Assessment of Self-Piercing Riveted Joints Using the Analytic Hierarchy Process
Abstract
1. Introduction
- (1)
- Less environmental pollution;
- (2)
- Can be used to join both similar and dissimilar materials;
- (3)
- No need for pre-drilling or punching holes;
- (4)
- No prerequisite for surface pre-treatment;
- (5)
- Capability to use lubricants and adhesives;
- (6)
- High speed production rate;
- (7)
- Long tool life;
- (8)
- High static and fatigue joint strengths;
- (9)
- Ability to automate and monitor the process easily.
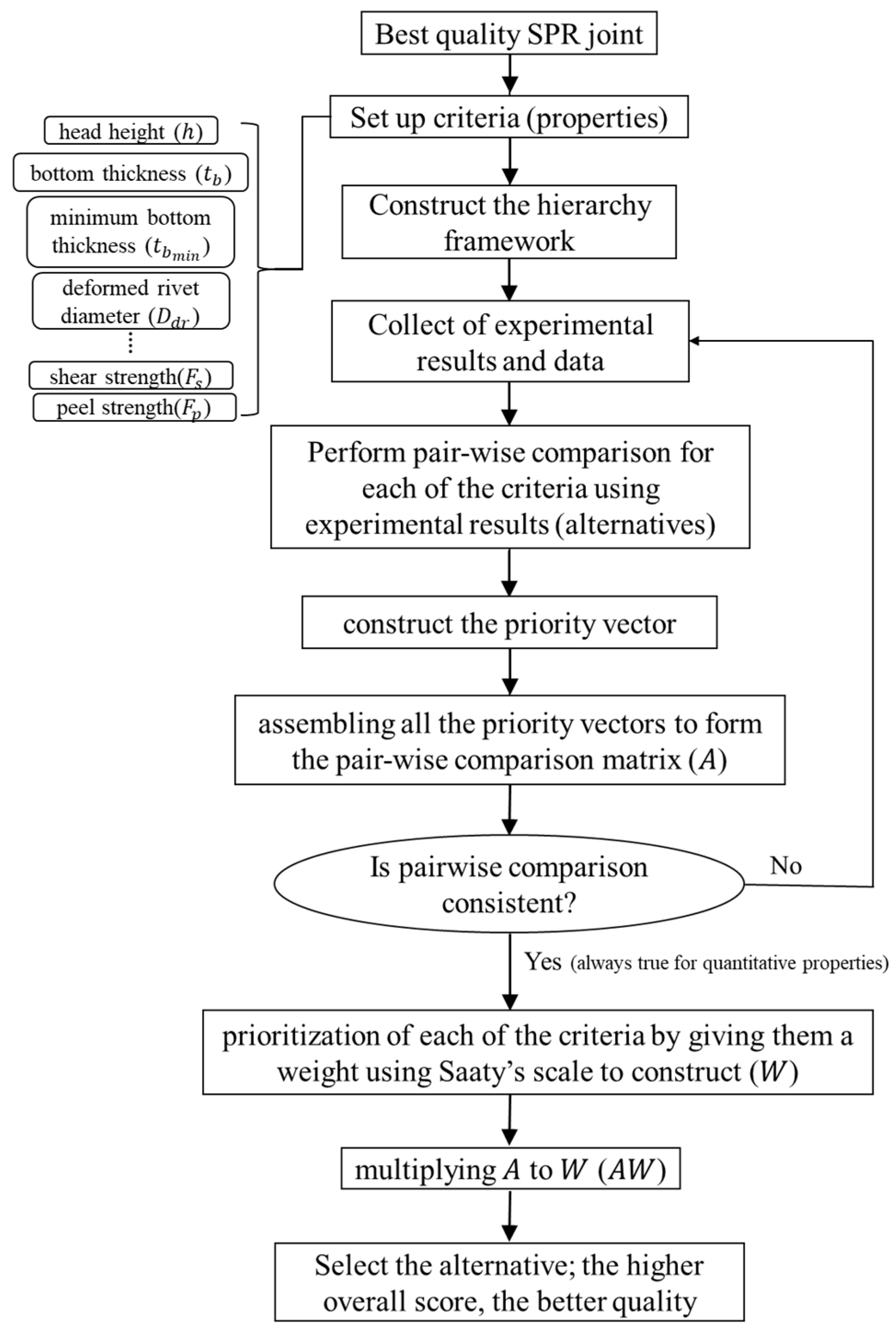
2. Theoretical Basis of the AHP
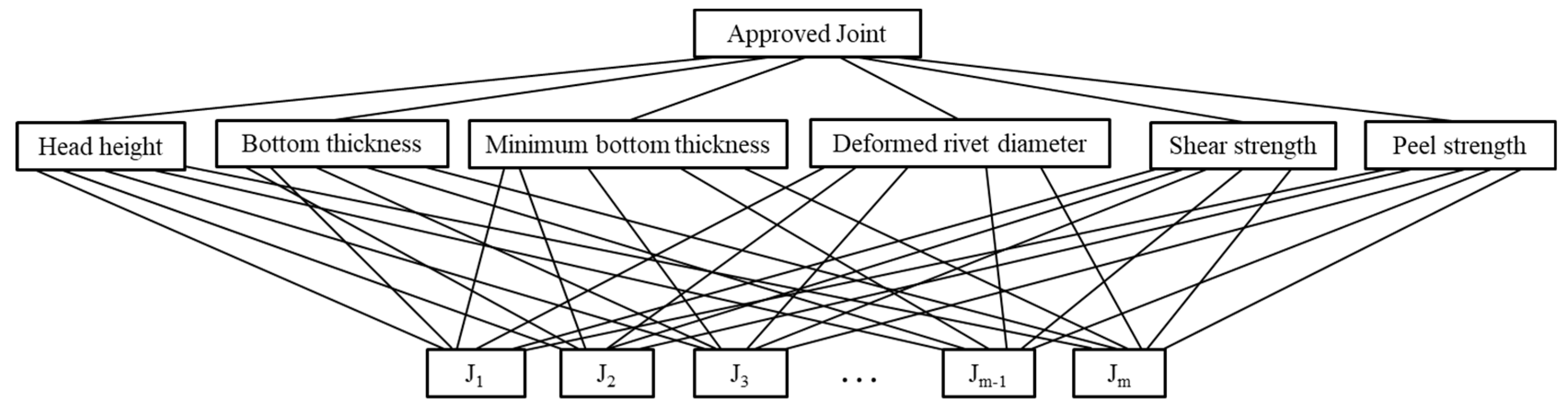
2.1. Problem Modelling
2.2. Pair-Wise Comparisons and Judgement Scales
2.3. Consistency
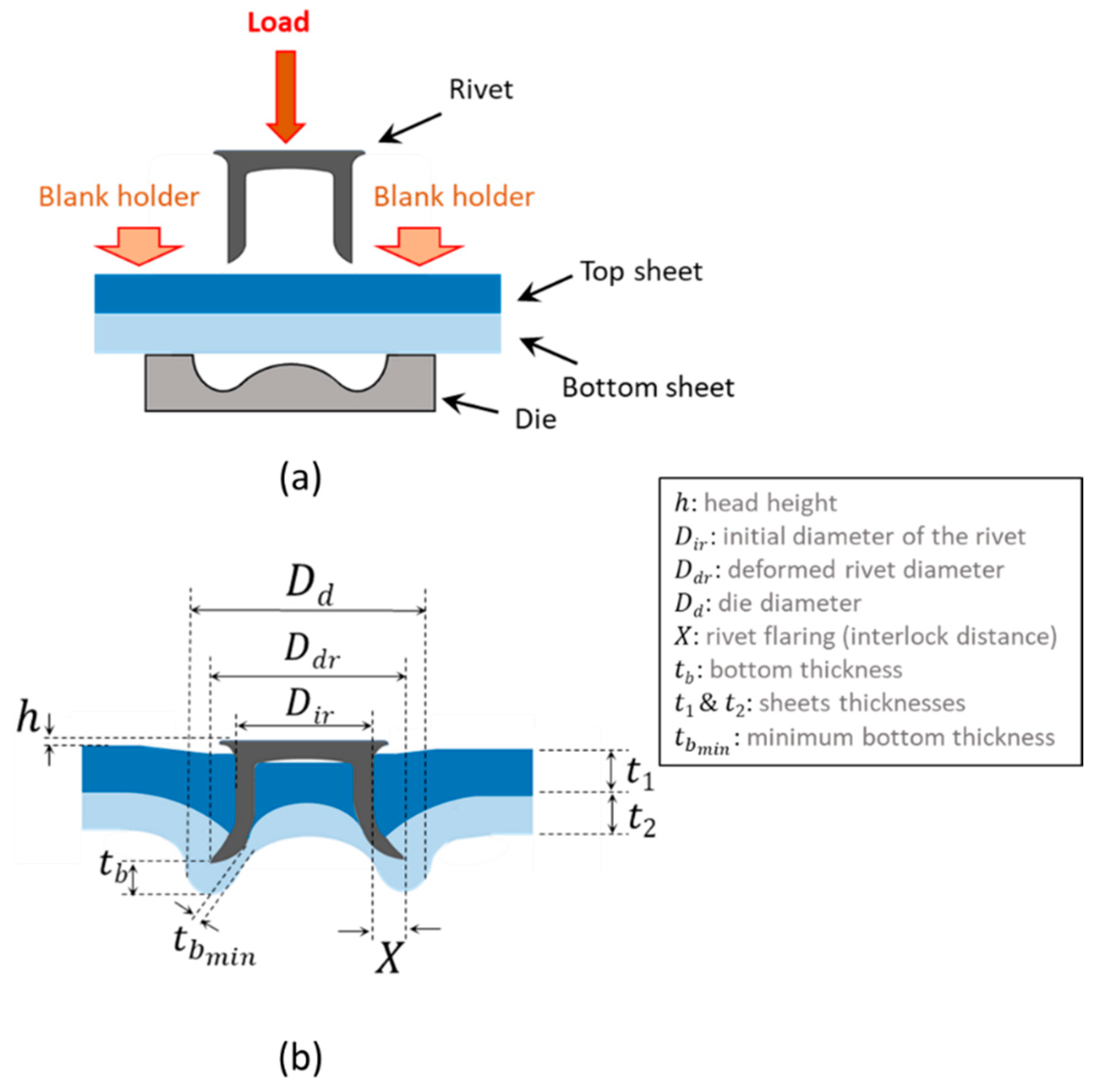
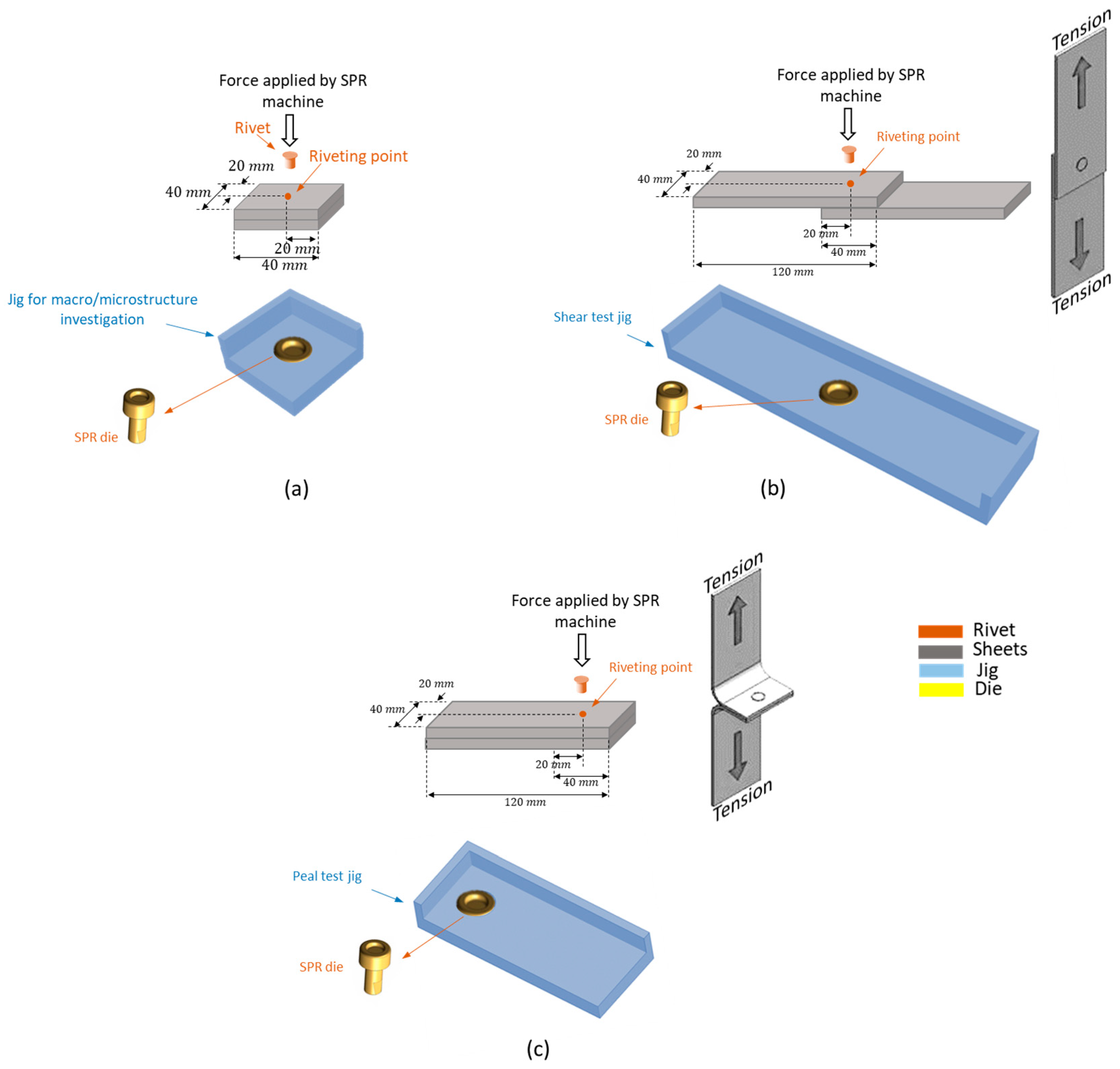
3. Experiments
3.1. Experimental Procedure
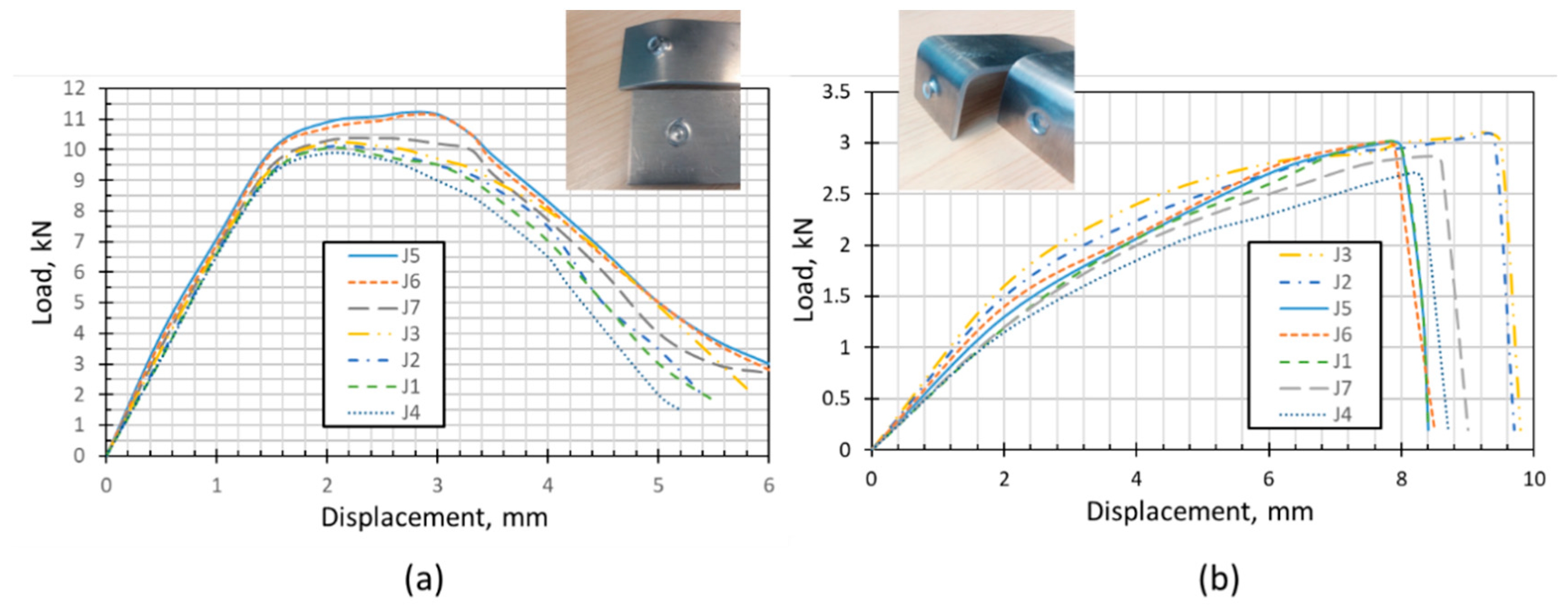
3.2. Experimental Results
- (1)
- Insufficient interlock;
- (2)
- The rivet tip breaking through into the die;
- (3)
- Rivet collapsing;
- (4)
- Under- or over-flashing of the head;
- (5)
- Excessive flaring;
- (6)
- Leg or tip tearing;
- (7)
- Formation of circumferential cracks;
- (8)
- Asymmetric deformation of the rivet;
- (9)
- Formation of bottom cracks.
4. SPR Joint Assessment Using AHP
4.1. Problem Modelling, Pair-Wise Comparison, Priority Derivation, and Consistency Evaluation
4.2. Ranking the Alternatives
5. Summary
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Cacko, R. Review of different material separation criteria in numerical modeling of the self-piercing riveting process—SPR. Arch. Civ. Mech. Eng. 2008, 8, 21–30. [Google Scholar] [CrossRef]
- Haque, R. Quality of self-piercing riveting (SPR) joints from cross-sectional perspective: A review. Arch. Civ. Mech. Eng. 2018, 18, 83–93. [Google Scholar] [CrossRef]
- Li, D.; Chrysanthou, A.; Patel, I.; Williams, G. Self-piercing riveting—A review. Int. J. Adv. Manuf. Technol. 2017, 92, 1777–1824. [Google Scholar] [CrossRef]
- Abe, Y.; Kato, T.; Mori, K. Self-piercing riveting of high tensile strength steel and aluminium alloy sheets using conventional rivet and die. J. Mater. Process. Technol. 2009, 209, 3914–3922. [Google Scholar] [CrossRef]
- de Rijck, J.J.M.; Homan, J.J.; Schijve, J.; Benedictus, R. The driven rivet head dimensions as an indication of the fatigue performance of aircraft lap joints. Int. J. Fatigue 2007, 29, 2208–2218. [Google Scholar] [CrossRef]
- Han, L.; Chrysanthou, A. Evaluation of quality and behaviour of self-piercing riveted aluminium to high strength low alloy sheets with different surface coatings. Mater. Des. 2008, 29, 458–468. [Google Scholar] [CrossRef]
- Ashby, M.F.; Bréchet, Y.J.M.; Cebon, D.; Salvo, L. Selection strategies for materials and processes. Mater. Des. 2004, 25, 51–67. [Google Scholar] [CrossRef]
- Chiner, M. Planning of expert systems for materials selection. Mater. Des. 1988, 9, 195–203. [Google Scholar] [CrossRef]
- Jahan, A.; Edwards, K.L.; Bahraminasab, M. 4—Multi-criteria decision-making for materials selection. In Multi-Criteria Decision Analysis for Supporting the Selection of Engineering Materials in Product Design, 2nd ed.; Jahan, A., Edwards, K.L., Bahraminasab, M., Eds.; Butterworth-Heinemann: Oxford, UK, 2016; pp. 63–80. [Google Scholar]
- Zafarani, H.; Hassani, A.; Bagherpour, E. Achieving a desirable combination of strength and workability in Al/SiC composites by AHP selection method. J. Alloys Compd. 2014, 589, 295–300. [Google Scholar] [CrossRef]
- Saaty, T.L. How to make a decision: The analytic hierarchy process. Eur. J. Oper. Res. 1990, 48, 9–26. [Google Scholar] [CrossRef]
- Brunelli, M. Introduction to the Analytic Hierarchy Process, 1st ed.; Springer: New York, NY, USA, 2015. [Google Scholar]
- Mansor, M.R.; Sapuan, S.M.; Zainudin, E.S.; Nuraini, A.A.; Hambali, A. Hybrid natural and glass fibers reinforced polymer composites material selection using Analytical Hierarchy Process for automotive brake lever design. Mater. Des. 2013, 51, 484–492. [Google Scholar] [CrossRef]
- Kiong, S.C.; Lee, L.Y.; Chong, S.H.; Azlan, M.A.; Nor, M.; Hisyamudin, N. Decision making with the analytical hierarchy process (AHP) for material selection in screw manufacturing for minimizing environmental impacts. Appl. Mech. Mater. 2013, 315, 57–62. [Google Scholar] [CrossRef]
- Di Angelo, L.; Di Stefano, P.; Fratocchi, L.; Marzola, A. An AHP-based method for choosing the best 3D scanner for cultural heritage applications. J. Cult. Herit. 2018, 34, 109–115. [Google Scholar] [CrossRef]
- Khorshidi, R.; Hassani, A.; Rauof, A.H.; Emamy, M. Selection of an optimal refinement condition to achieve maximum tensile properties of Al–15% Mg2Si composite based on TOPSIS method. Mater. Des. 2013, 46, 442–450. [Google Scholar] [CrossRef]
- Ishizaka, A.; Labib, A. Review of the main developments in the analytic hierarchy process. Expert Syst. Appl. 2011, 38, 14336–14345. [Google Scholar] [CrossRef]
- Saaty, T.L. Fundamentals of Decision Making, 1st ed.; RWS Publications: Pittsburgh, PA, USA, 1994. [Google Scholar]
- Dweiri, F.; Al-Oqla, F.M. Material selection using analytical hierarchy process. Int. J. Comput. Appl. Technol. 2016, 26, 182–189. [Google Scholar] [CrossRef]
- Perez-Vega, S.; Peter, S.; Salmeron-Ochoa, I.; Nieva-de la Hidalga, A.; Sharratt, P.N. Analytical hierarchy processes (AHP) for the selection of solvents in early stages of pharmaceutical process development. Process Saf. Environ. 2011, 89, 261–267. [Google Scholar] [CrossRef]
- Crawford, G.; Williams, C. A note on the analysis of subjective judgment matrices. J. Math. Psychol. 1985, 29, 387–405. [Google Scholar] [CrossRef]
- Saaty, T.L. A scaling method for priorities in hierarchical structures. Math. Psychol. 1977, 15, 234–281. [Google Scholar] [CrossRef]
- Peláez, J.I.; Lamata, M.T. A new measure of consistency for positive reciprocal matrices. Comput. Math. Appl. 2003, 46, 1839–1845. [Google Scholar] [CrossRef]
- Kwiesielewicz, M.; van Uden, E. Inconsistent and contradictory judgements in pairwise comparison method in the AHP. Comput. Oper. Res. 2004, 31, 713–719. [Google Scholar] [CrossRef]
- Karapetrovic, S.; Rosenbloom, E.S. A quality control approach to consistency paradoxes in AHP. Eur. J. Oper. Res. 1999, 119, 704–718. [Google Scholar] [CrossRef]
- Aguaron, J.; Moreno-Jiménez, J.M. The geometric consistency index: Approximated thresholds. Eur. J. Oper. Res. 2003, 147, 137–145. [Google Scholar] [CrossRef]




| Relative Importance (aij) | Description (i over j) |
|---|---|
| 1 | Equal importance |
| 2 | Weak |
| 3 | Moderate importance |
| 4 | Moderate plus |
| 5 | Strong importance |
| 6 | Strong plus |
| 7 | Very strong importance |
| 8 | Very, very strong |
| 9 | Absolute importance |
| n | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| k(n) | 3.147 | 3.526 | 3.717 | 3.755 | 3.755 | 3.744 | 3.733 | 3.709 | 3.698 | 3.685 | 3.674 | 3.663 | 3.646 | 3.646 |
| Joint | Die Type | Die Diameter, mm | Die Depth, mm | Rivet Type | Rivet Diameter, mm | Rivet Length, mm | Rivet Hardness, Hv | Velocity, mm/s | Force, Kgf |
|---|---|---|---|---|---|---|---|---|---|
| J1 | Flat bottomed die | 10 | 1.2 | flared hole- semi tubular | 5 | 7 | 420 | 360 | 82.8 |
| J2 | Flat bottomed die | 10 | 1.4 | flared hole- semi tubular | 5 | 8 | 440 | 360 | 82.4 |
| J3 | Flat bottomed die | 10 | 1.4 | flared hole- semi tubular | 5 | 6.5 | 440 | 360 | 85.4 |
| J4 | Flat bottomed die | 10 | 1.4 | flared hole- semi tubular | 5 | 6.5 | 440 | 340 | 77 |
| J5 | Flat bottomed die | 10 | 1.4 | flared hole- semi tubular | 5 | 6.5 | 460 | 350 | 82.6 |
| J6 | Flat bottomed die | 10 | 1.4 | flared hole- semi tubular | 5 | 6.5 | 460 | 345 | 80.7 |
| J7 | Flat bottomed die | 10 | 1.4 | flared hole- semi tubular | 5 | 6.5 | 460 | 340 | 78.9 |
| Joint | Head Height , mm | Bottom Thickness , mm | Minimum Bottom Thickness | Deformed Rivet Diameter , mm | Shear Strength , kN | Peel Strength , kN |
|---|---|---|---|---|---|---|
| J1 | ||||||
| J2 | ||||||
| J3 | ||||||
| J4 | ||||||
| J5 | ||||||
| J6 | ||||||
| J7 |
| Parameters | Head Height | Bottom Thickness | Minimum Bottom Thickness | Deformed Rivet Diameter | Shear Strength | Peel Strength |
|---|---|---|---|---|---|---|
| Head height | 1 | 2 | 1 | 3 | 0.5 | 0.5 |
| Bottom thickness | 0.5 | 1 | 0.5 | 2 | 0.33 | 0.33 |
| Minimum bottom thickness | 1 | 2 | 1 | 3 | 0.5 | 0.5 |
| Deformed rivet diameter | 0.33 | 0.5 | 0.33 | 1 | 0.25 | 0.25 |
| Shear strength | 2 | 3 | 0.5 | 4 | 1 | 1 |
| Peel strength | 2 | 3 | 0.5 | 4 | 1 | 1 |
| Rank | Final Priorities | Joint |
|---|---|---|
| 1 | 0.155 | J5 |
| 2 | 0.147 | J3 |
| 3 | 0.146 | J6 and J1 |
| 4 | 0.140 | J7 |
| 5 | 0.133 | J4 |
| 6 | 0.132 | J2 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bagherpour, E.; Huang, Y.; Fan, Z. Assessment of Self-Piercing Riveted Joints Using the Analytic Hierarchy Process. Metals 2019, 9, 760. https://doi.org/10.3390/met9070760
Bagherpour E, Huang Y, Fan Z. Assessment of Self-Piercing Riveted Joints Using the Analytic Hierarchy Process. Metals. 2019; 9(7):760. https://doi.org/10.3390/met9070760
Chicago/Turabian StyleBagherpour, Ebad, Yan Huang, and Zhongyun Fan. 2019. "Assessment of Self-Piercing Riveted Joints Using the Analytic Hierarchy Process" Metals 9, no. 7: 760. https://doi.org/10.3390/met9070760
APA StyleBagherpour, E., Huang, Y., & Fan, Z. (2019). Assessment of Self-Piercing Riveted Joints Using the Analytic Hierarchy Process. Metals, 9(7), 760. https://doi.org/10.3390/met9070760







