Finite Fracture Mechanics Assessment in Moderate and Large Scale Yielding Regimes
Abstract
1. Introduction
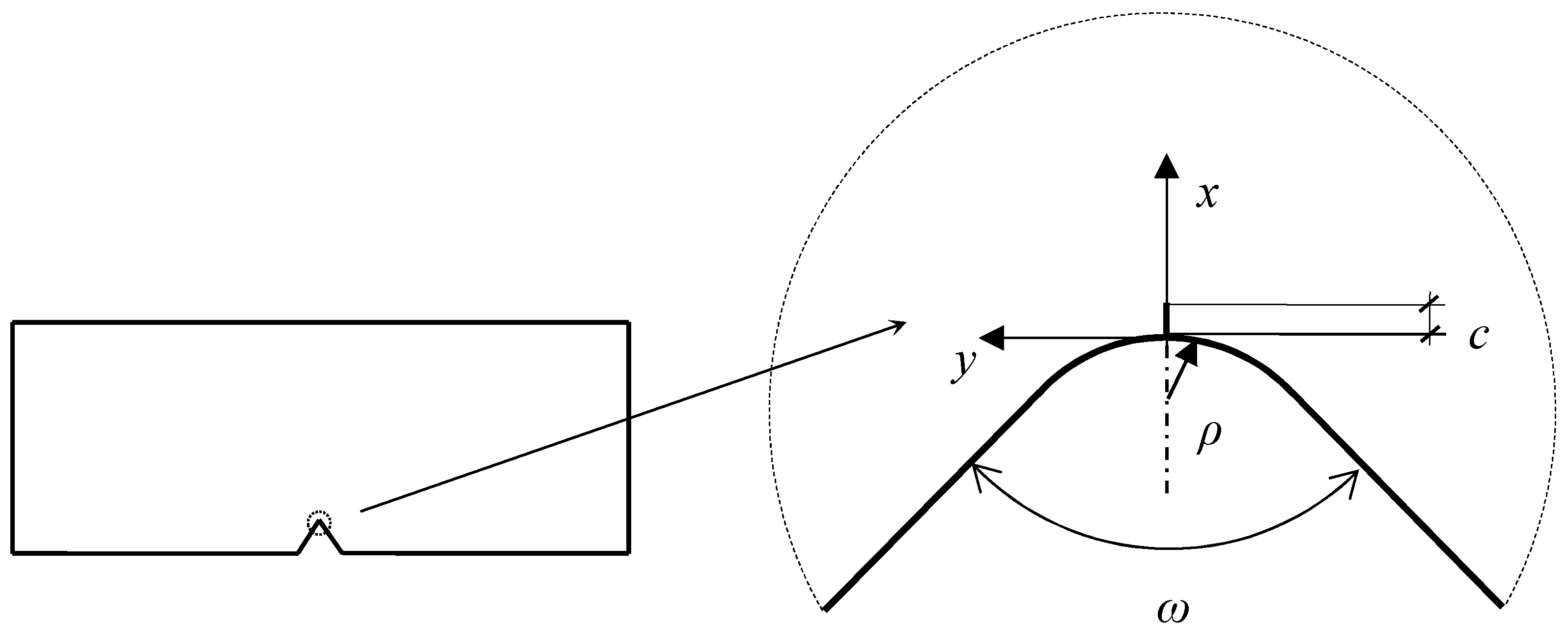
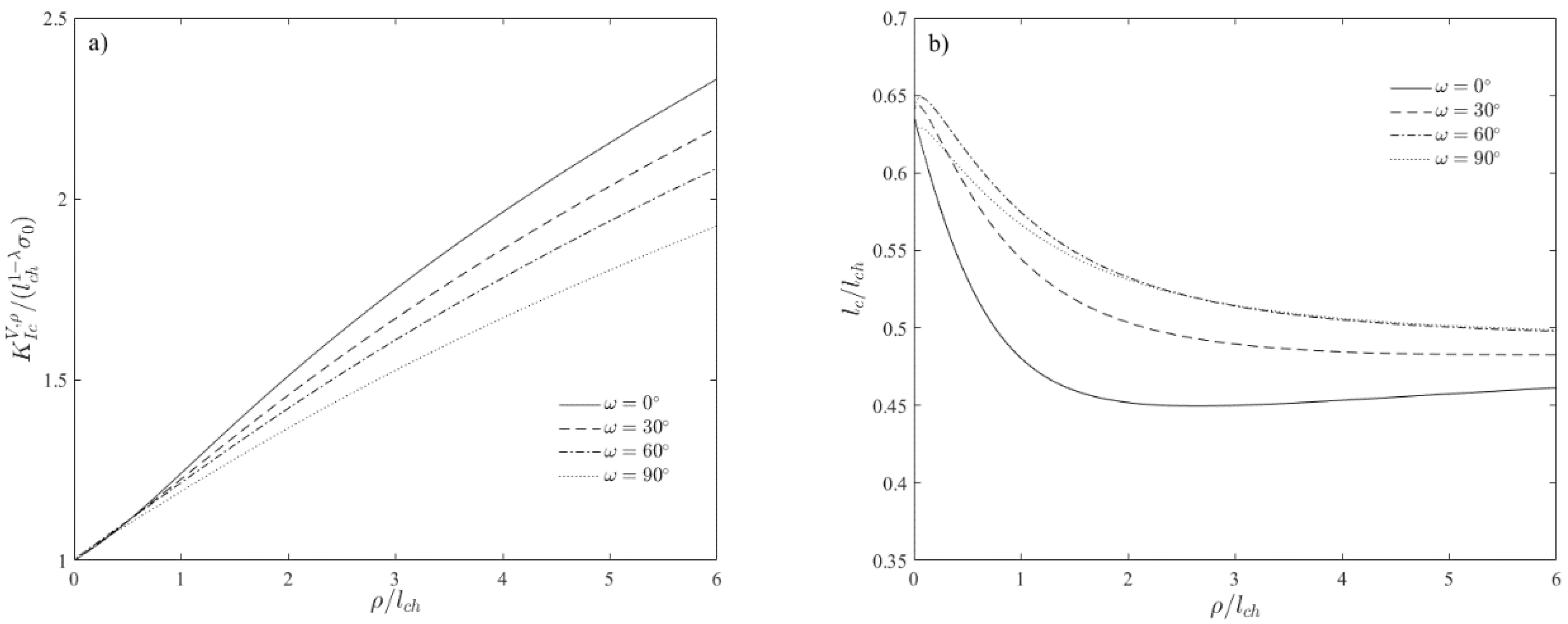
2. FFM Criteria
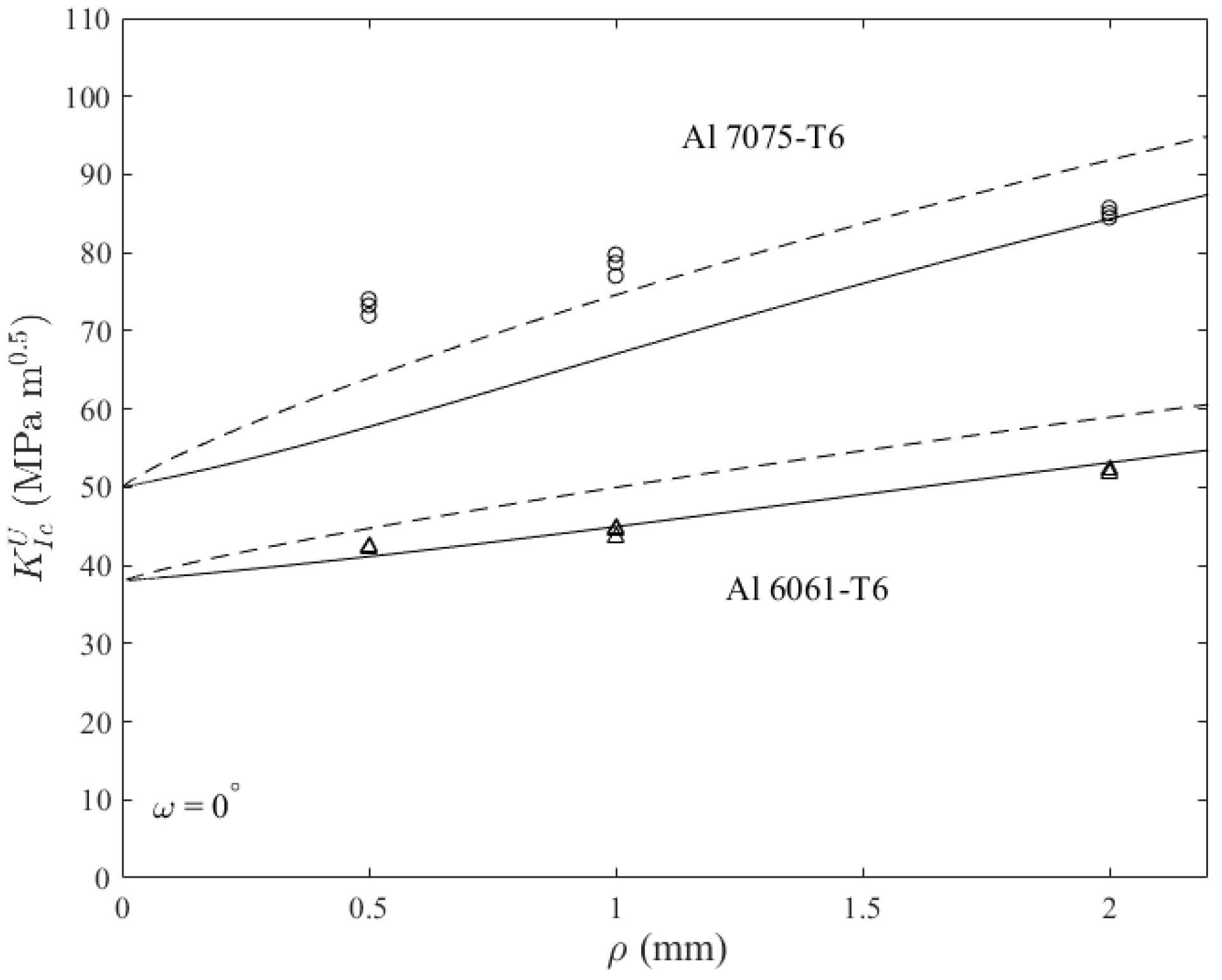
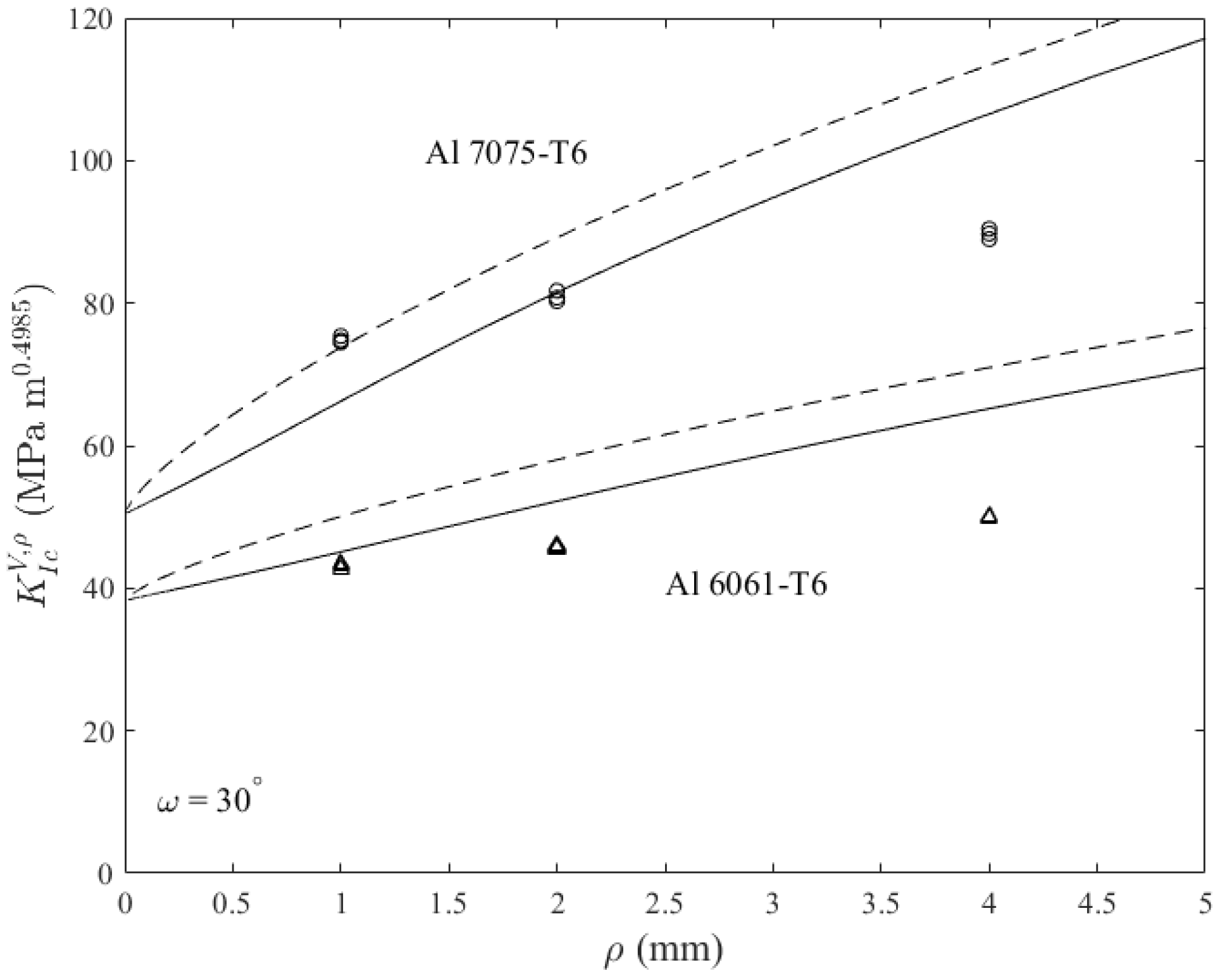
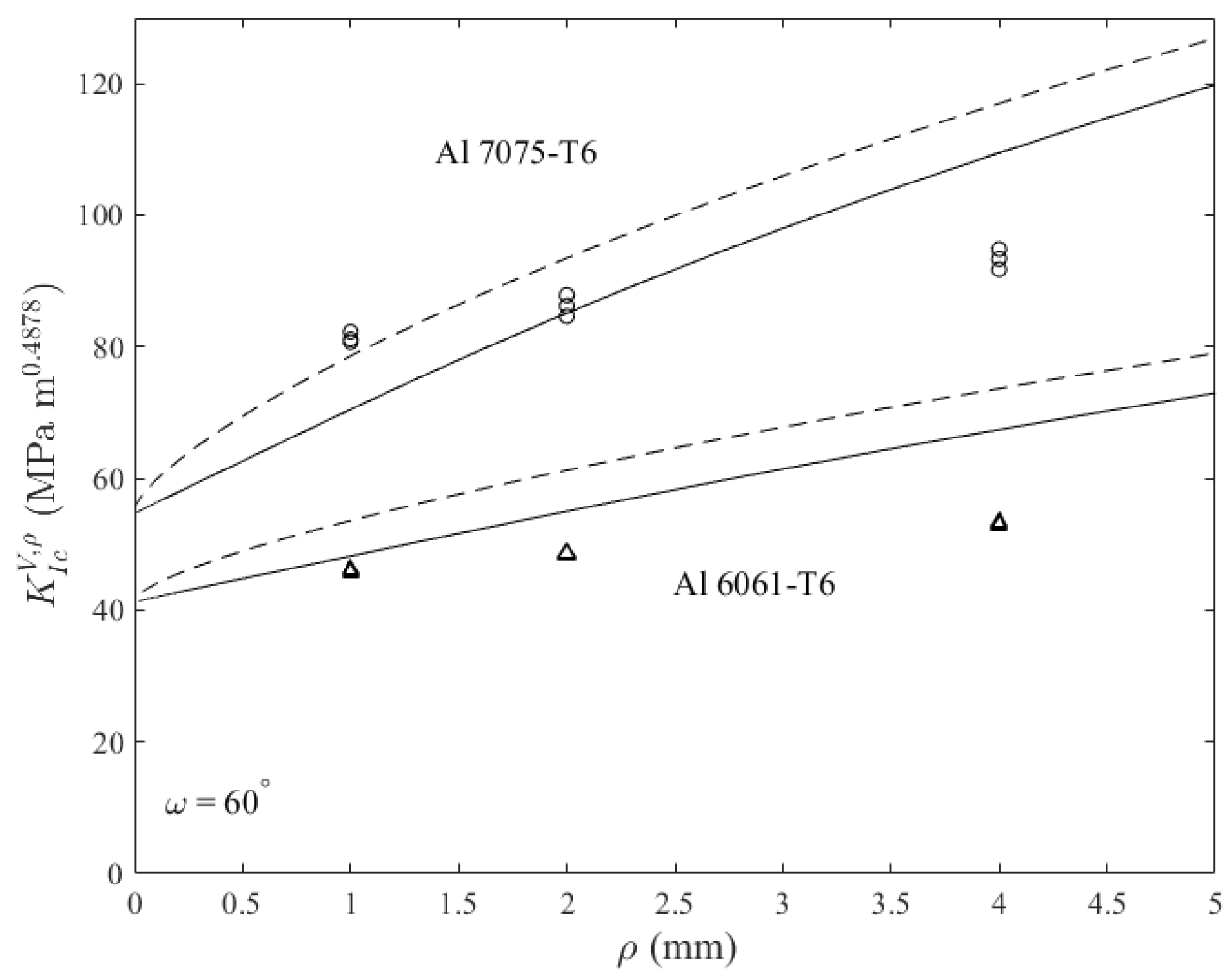
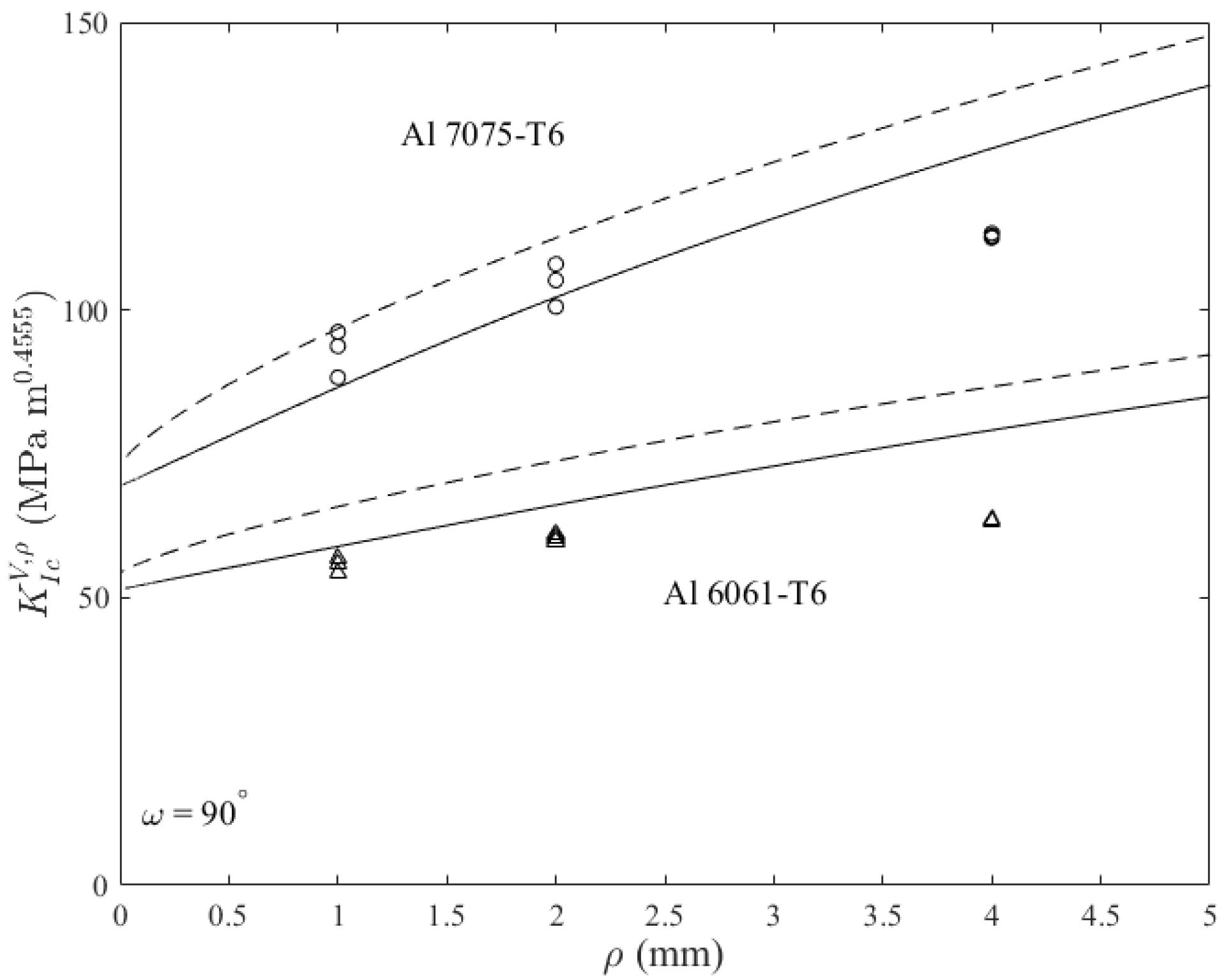
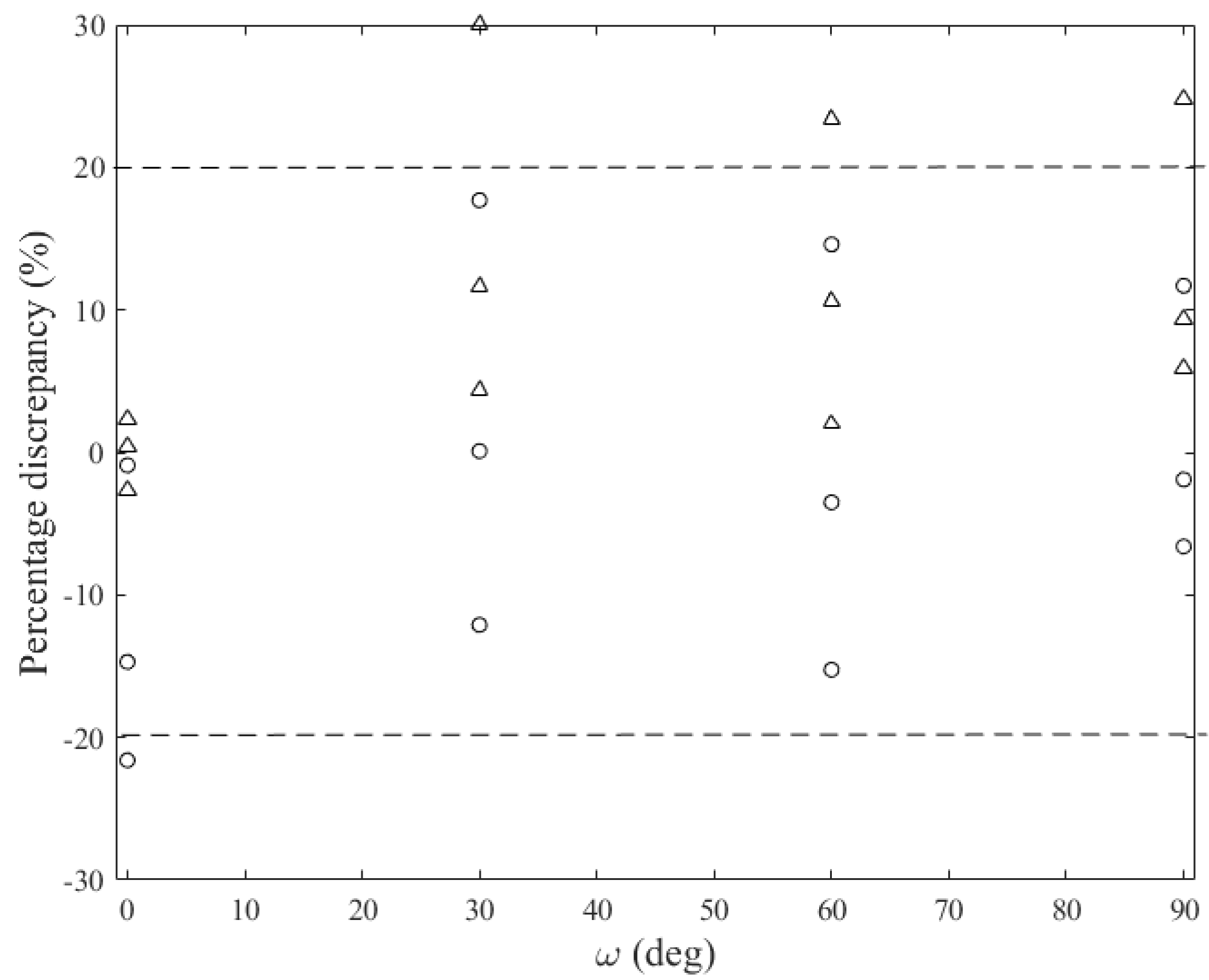
3. Comparison with Experimental Results
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Taylor, D. The Theory of Critical Distances: A New Perspective in Fracture Mechanics; Elsevier: Oxford, UK, 2006. [Google Scholar]
- Lazzarin, P.; Zambardi, R. A Finite-volume-energy based approach to predict the static and fatigue behaviour of components with sharp V-shaped notches. Int. J. Fract. 2002, 112, 275–298. [Google Scholar] [CrossRef]
- Seweryn, A.; Lukaszewicz, A. Verification of brittle fracture criteria for elements with V-shaped notches. Engng. Fract. Mech. 2002, 69, 1487–1510. [Google Scholar] [CrossRef]
- Seweryn, A. Brittle fracture criterion for structures with sharp notches. Eng. Fract. Mech. 1994, 47, 673–681. [Google Scholar] [CrossRef]
- Leguillon, D. Strength or toughness? A criterion for crack onset at a notch. Eur. J. Mech. A/Solids 2002, 21, 61–72. [Google Scholar] [CrossRef]
- Carpinteri, A.; Cornetti, P.; Pugno, N.; Sapora, A.; Taylor, D. Generalized fracture toughness for specimens with re-entrant corners: Experiments vs. theoretical predictions. Struct. Eng. Mech. 2009, 32, 609–620. [Google Scholar] [CrossRef]
- Sapora, A.; Firrao, D. Finite fracture mechanics predictions on the apparent fracture toughness of as-quenched Charpy V-type AISI 4340 steel specimens. Fatigue Fract. Eng. Mater. Struct. 2017, 40, 949–958. [Google Scholar] [CrossRef]
- Susmel, L.; Taylor, D. On the use of the theory of critical distances to predict static failures in ductile metallic materials containing different geometrical features. Eng. Fract. Mech. 2008, 75, 4410–4421. [Google Scholar] [CrossRef]
- Madrazo, V.; Cicero, S.; Carrascal, I.A. On the Point Method and the Line Method notch effect predictions in Al7075-T651. Eng. Fract. Mech. 2012, 79, 363–379. [Google Scholar] [CrossRef]
- Cicero, S.; Fuentes, J.D.; Procopio, I.; Madrazo, V.; González, P. Critical distance default values for structural steels and a simple formulation to estimate the apparent fracture toughness in U-notched conditions. Metals 2018, 8, 871. [Google Scholar] [CrossRef]
- Torabi, A.R.; Alaei, M. Mixed-mode ductile failure analysis of V-notched Al 7075-T6 thin sheets. Eng. Fract. Mech. 2015, 150, 70–95. [Google Scholar] [CrossRef]
- Torabi, A.R.; Habibi, R.; Hosseini, B.M. On the ability of the Equivalent Material Concept in predicting ductile failure of U-notches under moderate- and large-scale yielding conditions. Phys. Mesomech. 2015, 18, 337–347. [Google Scholar] [CrossRef]
- Torabi, A.R.; Alaei, M. Application of the equivalent material concept to ductile failure prediction of blunt V-notches encountering moderate-scale yielding. Int. J. Damage Mech. 2016, 25, 853–877. [Google Scholar] [CrossRef]
- Torabi, A.R.; Keshavarzian, M. Tensile crack initiation from a blunt V-notch border in ductile plates in the presence of large plasticity at the notch vicinity. Int. J. Terraspace Sci. Eng. 2016, 8, 93–101. [Google Scholar]
- Torabi, A.R. Estimation of tensile load-bearing capacity of ductile metallic materials weakened by a V-notch: The equivalent material concept. Mater. Sci. Eng. A 2012, 536, 249–255. [Google Scholar] [CrossRef]
- Torabi, A.R.; Berto, F.; Campagnolo, A. Elastic-plastic fracture analysis of notched Al 7075-T6 plates by means of the local energy combined with the equivalent material concept. Phys. Mesomech. 2016, 19, 204–214. [Google Scholar] [CrossRef]
- Fuentes, J.D.; Cicero, S.; Berto, F.; Torabi, A.R.; Madrazo, V.; Azizi, P. Estimation of Fracture Loads in AL7075-T651 Notched Specimens Using the Equivalent Material Concept Combined with the Strain Energy Density Criterion and with the Theory of Critical Distances. Metals 2018, 8, 87. [Google Scholar] [CrossRef]
- Muñoz-Reja, M.; Távara, L.; Mantič, V.; Cornetti, P. Crack onset and propagation at fibre–matrix elastic interfaces under biaxial loading using finite fracture mechanics. Compos. Part. A 2016, 82, 267–278. [Google Scholar] [CrossRef]
- Cornetti, P.; Sapora, A.; Carpinteri, A. Short cracks and V-notches: Finite Fracture Mechanics vs. Cohesive Crack Model. Eng. Fract. Mech. 2016, 168, 2–12. [Google Scholar] [CrossRef]
- Cornetti, P.; Muñoz-Reja, M.; Sapora, A.; Carpinteri, A. Finite fracture mechanics and cohesive crack model: Weight functions vs. cohesive laws. Int. J. Solid Struct. 2019, 156–157, 126–136. [Google Scholar] [CrossRef]
- Doitrand, A.; Estevez, R.; Leguillon, D. Comparison between cohesive zone and coupled criterion modeling of crack initiation in rhombus hole specimens under quasi-static compression. Theor. Appl. Fract. Mech. 2019, 99, 51–59. [Google Scholar] [CrossRef]
- Felger, J.; Stein, N.; Becker, W. Mixed-mode fracture in open-hole composite plates of finite-width: An asymptotic coupled stress and energy approach. Int. J. Solid. Struct. 2017, 122–123, 14–24. [Google Scholar] [CrossRef]
- Sapora, A.; Cornetti, P. Crack onset and propagation stability from a circular hole under biaxial loading. Int. J. Fract. 2019, 214, 97–104. [Google Scholar] [CrossRef]
- Doitrand, A.; Leguillon, D. 3D application of the coupled criterion to crack initiation prediction in epoxy/aluminum specimens under four point bending. Int. J. Solids Struct. 2018, 143, 175–182. [Google Scholar] [CrossRef]
- Stein, N.; Weißgraeber, P.; Becker, W. A model for brittle failure in adhesive lap joints of arbitrary joint configuration. Compos. Struct. 2015, 133, 707–718. [Google Scholar] [CrossRef]
- Felger, J.; Rosendahl, P.L.; Leguillon, D.; Becker, W. Predicting crack patterns at bi-material junctions: A coupled stress and energy approach. Int. J. Solids Struct. 2019, 164, 191–201. [Google Scholar] [CrossRef]
- Sapora, A.; Cornetti, P.; Carpinteri, A. Cracks at rounded V-notch tips: An analytical expression for the stress intensity factor. Int. J. Fract. 2014, 187, 285–291. [Google Scholar] [CrossRef]
- Carpinteri, A.; Cornetti, P.; Sapora, A. Brittle failures at rounded V-notches: A finite fracture mechanics approach. Int. J. Fract. 2011, 172, 1–8. [Google Scholar] [CrossRef]
- Filippi, S.; Lazzarin, P.; Tovo, R. Developments of some explicit formulas useful to describe elastic stress fields ahead of notches in plates. Int. J. Solid. Struct. 2002, 39, 4543–4565. [Google Scholar] [CrossRef]
| ω | λ | β | η | μ | m |
|---|---|---|---|---|---|
| 0° | 0.5000 | 1.000 | 1.000 | −0.5000 | 1.820 |
| 30° | 0.5015 | 1.005 | 1.034 | −0.4561 | 1.473 |
| 60° | 0.5122 | 1.017 | 0.9699 | −0.4057 | 1.338 |
| 90° | 0.5445 | 1.059 | 0.8101 | −0.3449 | 1.314 |
| Material | Al 7075-T6 | Al 6061-T6 |
|---|---|---|
| KIc (MPa √m) | 50 | 38 |
| σ0 (MPa) | 1845 | 1066 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Torabi, A.R.; Berto, F.; Sapora, A. Finite Fracture Mechanics Assessment in Moderate and Large Scale Yielding Regimes. Metals 2019, 9, 602. https://doi.org/10.3390/met9050602
Torabi AR, Berto F, Sapora A. Finite Fracture Mechanics Assessment in Moderate and Large Scale Yielding Regimes. Metals. 2019; 9(5):602. https://doi.org/10.3390/met9050602
Chicago/Turabian StyleTorabi, Ali Reza, Filippo Berto, and Alberto Sapora. 2019. "Finite Fracture Mechanics Assessment in Moderate and Large Scale Yielding Regimes" Metals 9, no. 5: 602. https://doi.org/10.3390/met9050602
APA StyleTorabi, A. R., Berto, F., & Sapora, A. (2019). Finite Fracture Mechanics Assessment in Moderate and Large Scale Yielding Regimes. Metals, 9(5), 602. https://doi.org/10.3390/met9050602







