Anelastic Behavior of Small Dimensioned Aluminum
Abstract
1. Introduction
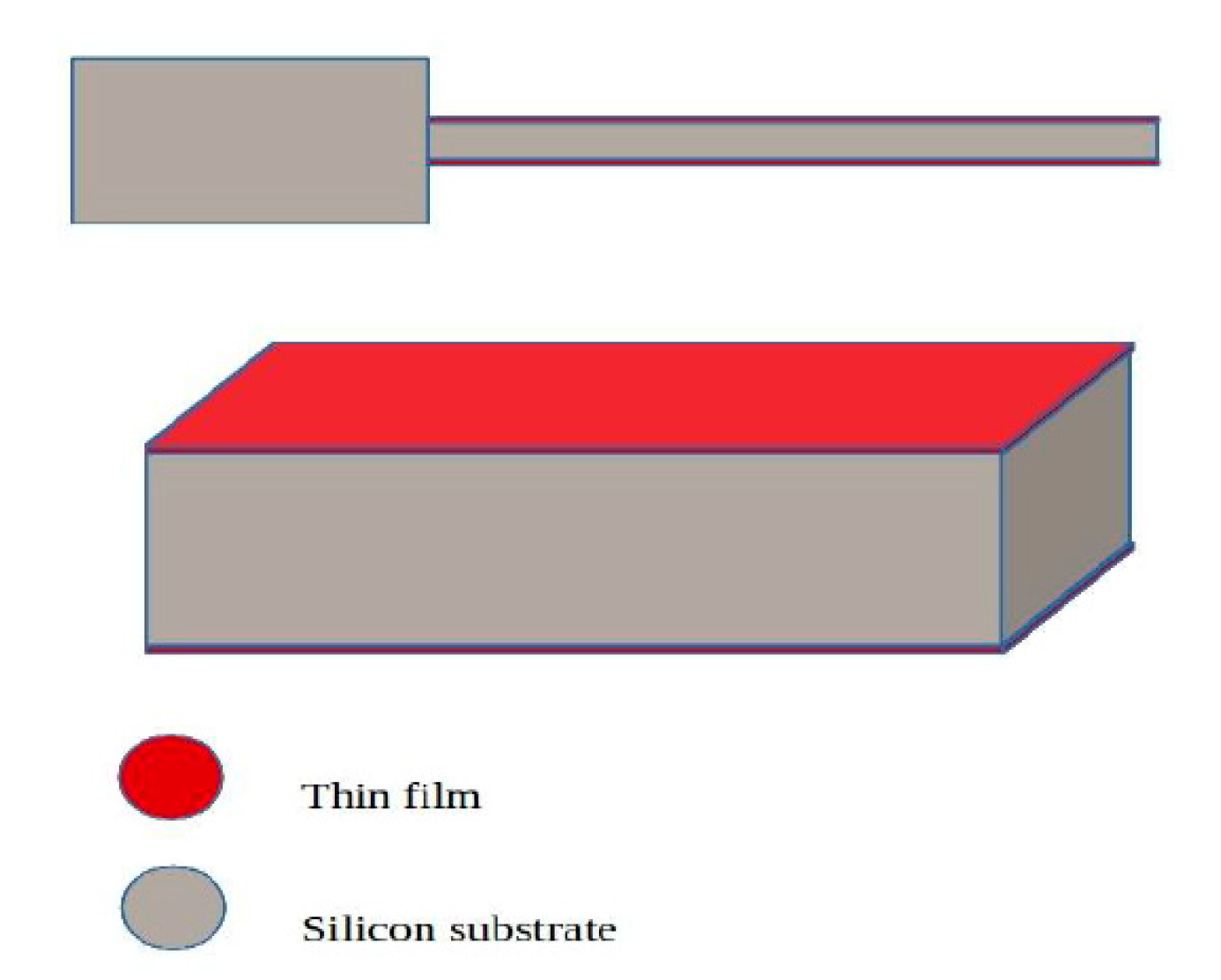
2. Materials and Methods
3. Results and Discussion
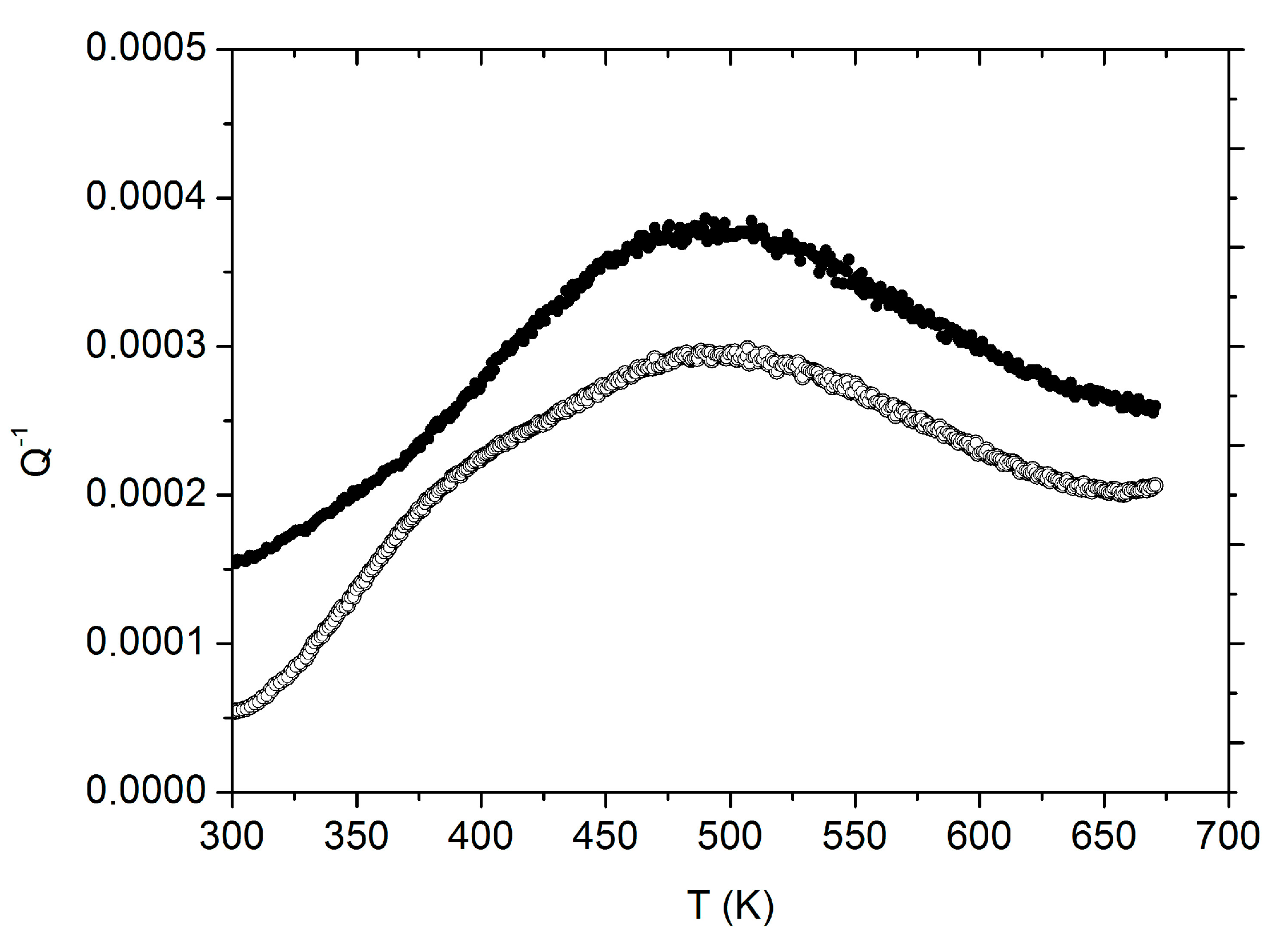
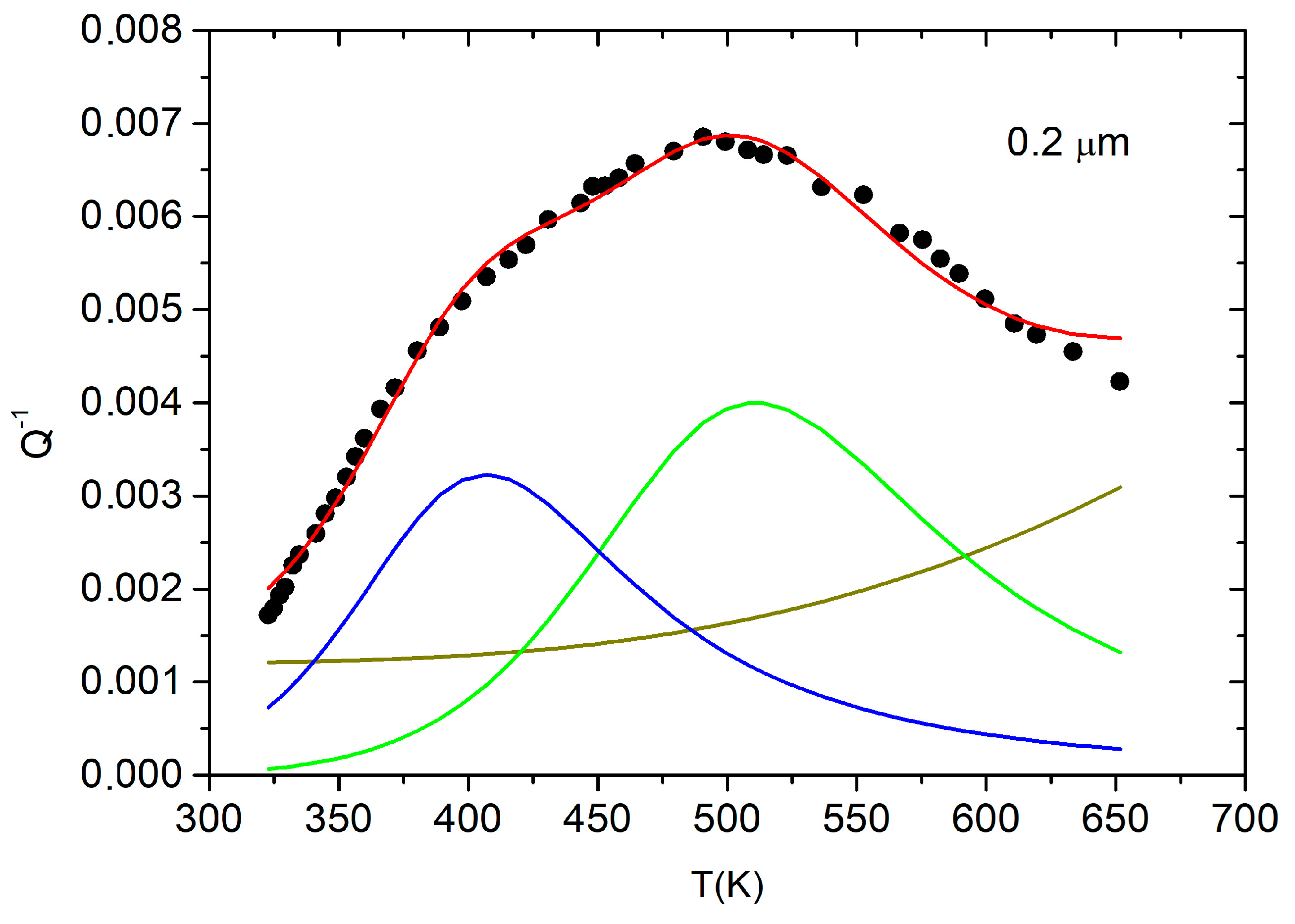
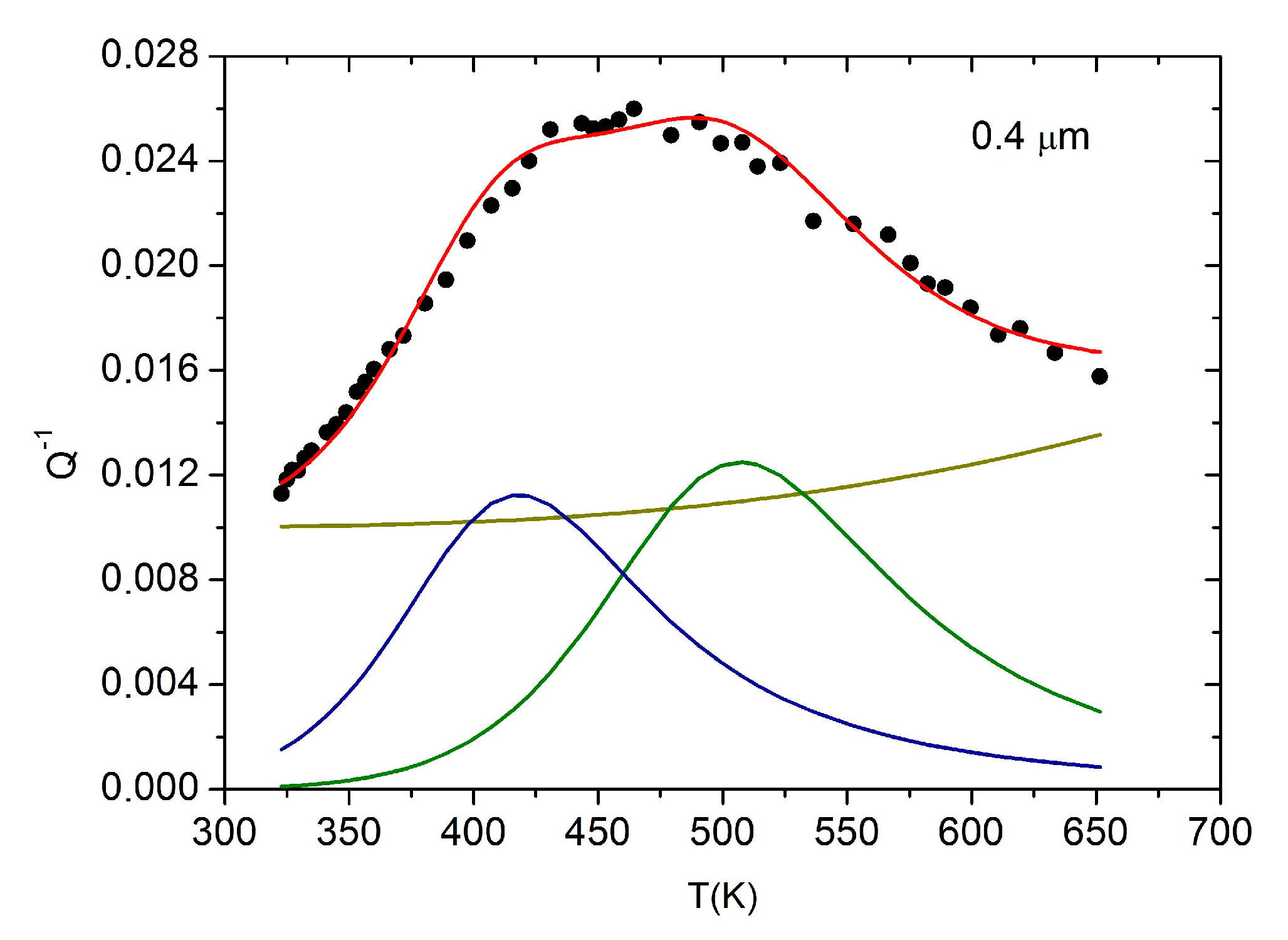
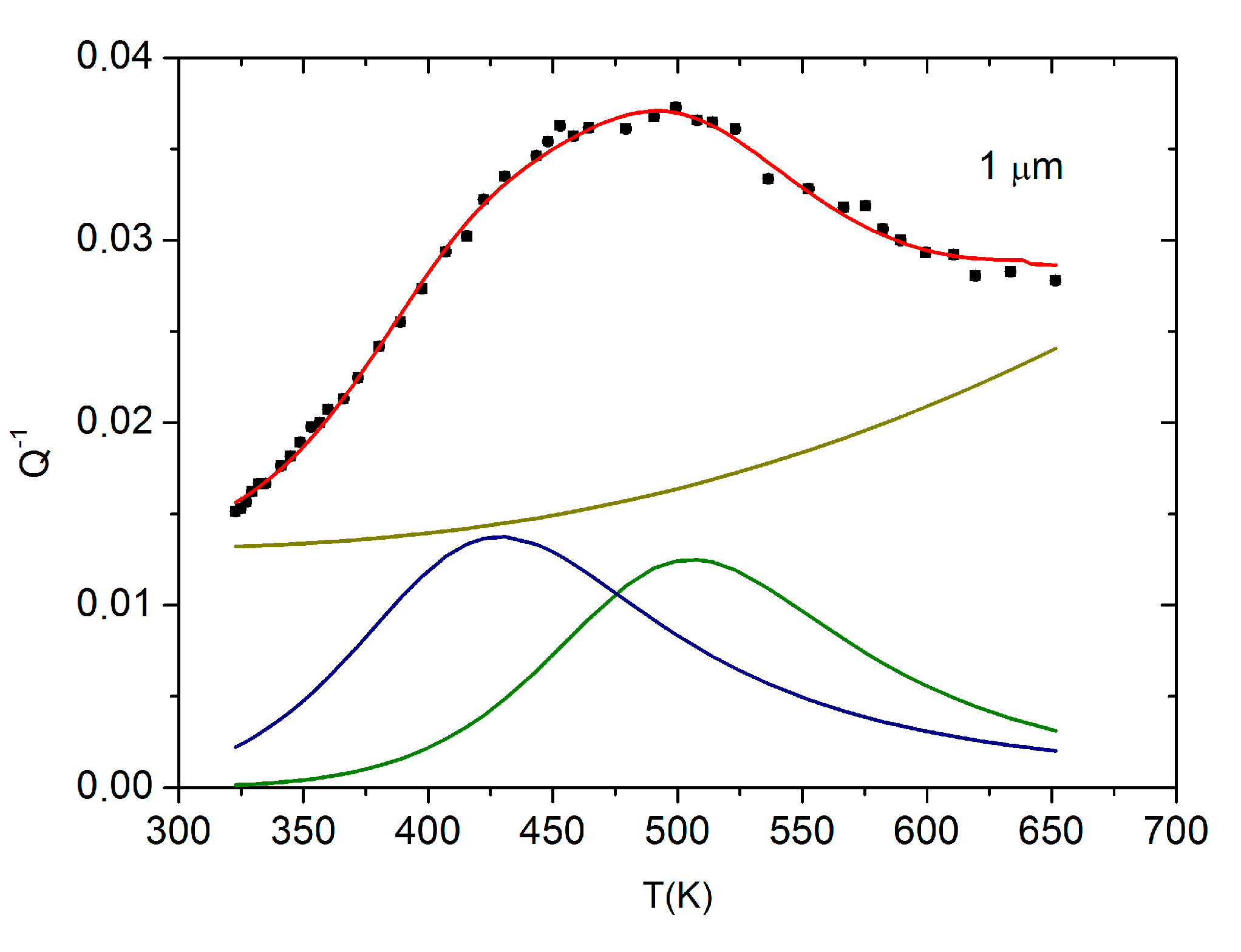
3.1. Deposited Films
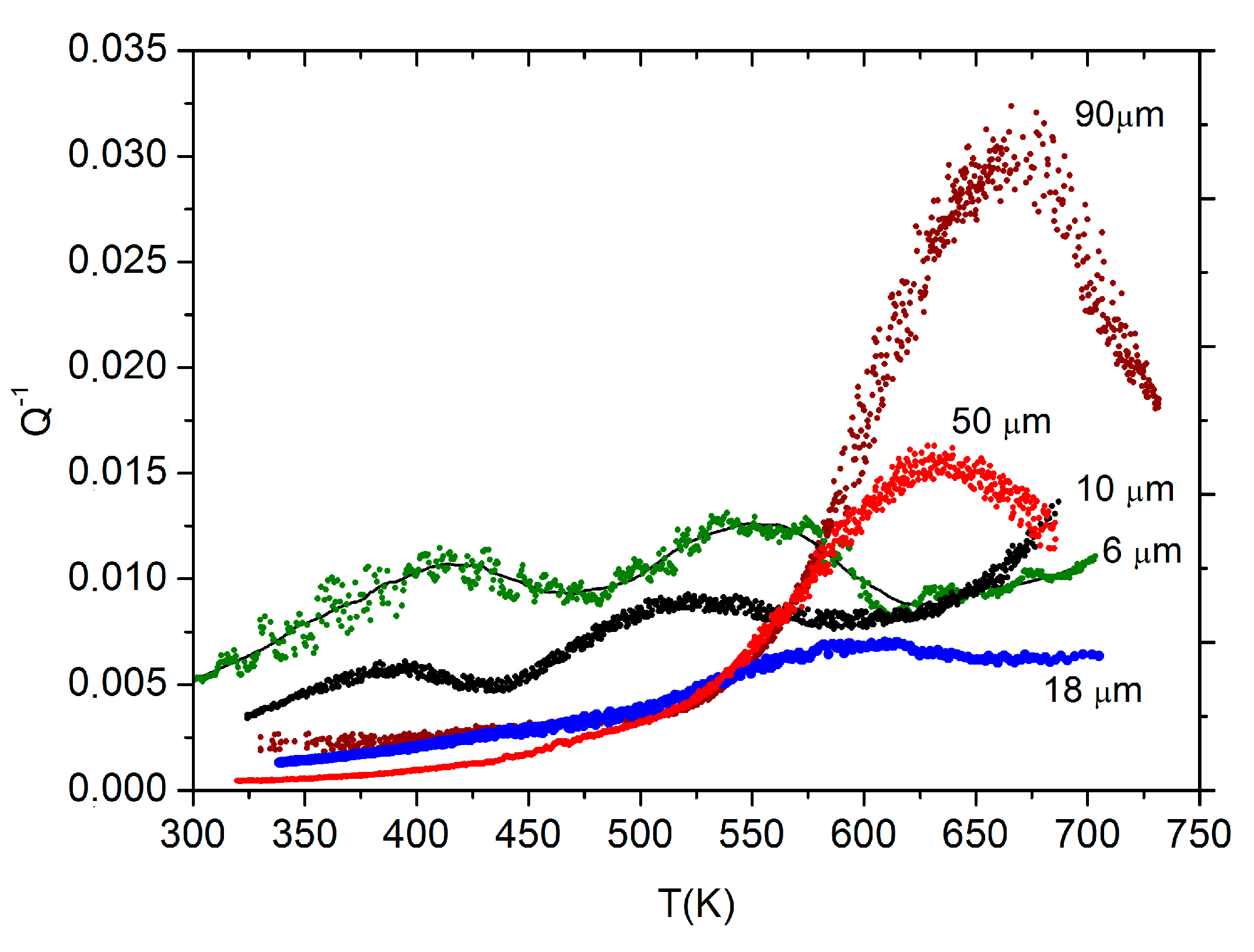
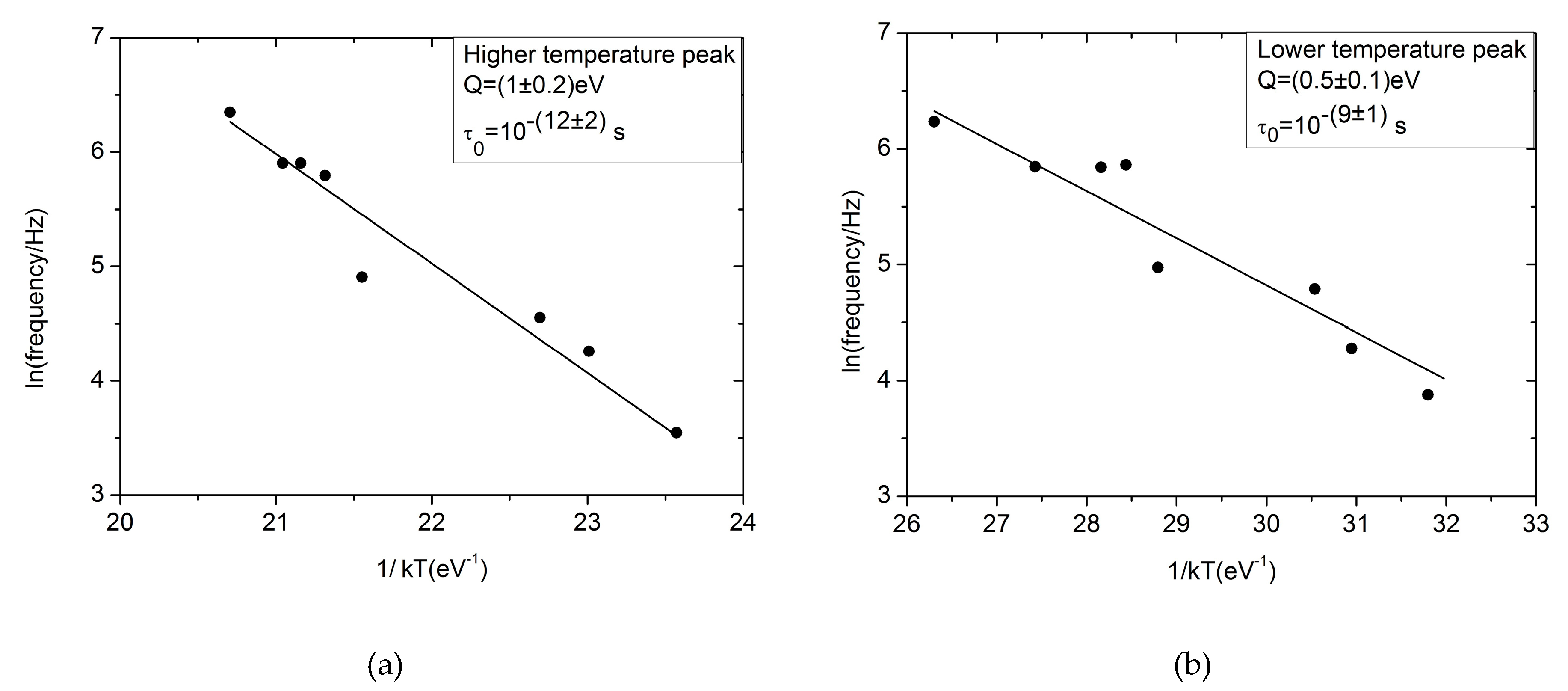
3.2. Free-Standing Films
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Uchic, M.D.; Dimiduk, D.M.; Florando, J.N.; Nix, W.D. Specimen dimensions influence strength and crystal plasticity. Science 2004, 305, 986–989. [Google Scholar] [CrossRef] [PubMed]
- Arzt, E. Size effects in materials due to microstructural and dimensional constraints: A comparative review. Acta Mater. 1998, 46, 5611–5626. [Google Scholar] [CrossRef]
- Kalman, A.J.; Verbruggen, A.H.; Janssen, G.C.A.M. Young’s modulus measurements and grain boundary sliding in free-standing thin metal films. Appl. Phys. Lett. 2001, 78, 2673. [Google Scholar] [CrossRef]
- Molotnikov, A.; Lapovok, R.; Davies, H.J.; Cao, C.W.; Estrin, Y. Size effect on the tensile strength of fine-grained copper. Scr. Mater. 2008, 9, 1182–1185. [Google Scholar] [CrossRef]
- Wei, X.; Lee, D.; Shim, S.; Chen, X.; Kysar, J.W. Plane-strain bulge test for nanocrystalline copper thin films. Scr. Mater. 2007, 57, 541–544. [Google Scholar] [CrossRef]
- Michel, J.F.; Picart, P. Size effects on the constitutive behaviour for brass in sheet metal forming. J. Mater. Proc. Technol. 2003, 141, 439–446. [Google Scholar] [CrossRef]
- Li, Q.; Anderson, P.M. Dislocation-based modeling of the mechanical behavior of epitaxial metallic multilayer thin films. Acta Mater. 2005, 53, 1121–1134. [Google Scholar] [CrossRef]
- Hosseini, E.; Kazeminezhad, M. A Dislocation-Based Model Considering Free Surface Theory Through HPT Process: Nano-Structured Ni. Trans. F: Nanotechnol. 2010, 17, 52–59. [Google Scholar]
- Baker, S.P.; Vinci, R.P.; Arias, T. Elastic and Anelastic Behavior of Materials in Small Dimensions. MRS Bull. 2002, 27, 26–29. [Google Scholar] [CrossRef]
- Berry, B.S.; Pritchet, W.C. Defect study of thin layers by the vibrating-reed technique. J. de Physique C5 1981, 42, 1111–1122. [Google Scholar] [CrossRef]
- Berry, B.S. Anelastic Relaxation and Diffusion in Thin-Layer Materials. In Diffusion Phenomena in Thin Films and Microelectronic Materials; Gupta, D., Ho, P.S., Eds.; Noyes Press: Park Ridge, NJ, USA, 1988; pp. 73–145. [Google Scholar]
- Bonetti, E.; Campari, E.G.; Enzo, S.; Groppelli, S.; Frattini, R.; Sberveglieri, G. Anelasticity and structural transformations of Fe and Al thin films and multilayers. Defect Diffus. Forum 1994, 106–107, 1–5. [Google Scholar] [CrossRef]
- Berry, B.S. Damping Mechanisms in Thin-Layer Materials. In M3D: Mechanics and Mechanisms of Material Damping; Kinra, V.K., Wolfenden, A., Eds.; ASTM STP 1169: Conshohocken, PA, USA, 1992; pp. 28–44. [Google Scholar]
- Prieler, M.; Bohn, H.G.; Schilling, W.; Trinkaus, H. Mat. Grain Boundary Sliding in Thin Substrate-Bonded AL Films. MRS Proc. 1993, 308, 305. [Google Scholar] [CrossRef]
- Prieler, M.; Bohn, H.G.; Schilling, W.; Trinkaus, H. Grain boundary sliding in thin substrate-bonded Al films. J. Alloys Compd. 1994, 211–212, 424–427. [Google Scholar] [CrossRef]
- Bohn, H.G.; Prieler, M.; Su, C.M.; Trinkaus, H.; Schilling, W. Internal friction effects due to grain boundary sliding in large- and small-grained aluminium. J. Phys. Chem. Solids 1994, 55, 1157–1164. [Google Scholar] [CrossRef]
- Heinen, D.; Bohn, H.G.; Schilling, W. Internal friction in free-standing thin Al films. J. Appl. Phys 1995, 78, 893–896. [Google Scholar] [CrossRef]
- Kê, T.S. Experimental evidence on the viscous behaviour of grain boundaries in metals. Phys. Rev. 1947, 71, 533–546. [Google Scholar] [CrossRef]
- Kong, Q.P.; Fang, Q.F. Progress in the investigations of grain boundary relaxation. Crit. Rev. Solid State Mater. Sci. 2016, 41, 192–216. [Google Scholar] [CrossRef]
- Jiang, W.B.; Kong, Q.P.; Magalas, L.B.; Fang, Q.F. The Internal Friction of Single Crystals, Bicrystals and Polycrystals of Pure Magnesium. Arch. Metall. Mater. 2015, 60, 371–375. [Google Scholar] [CrossRef]
- Kê, T.S.; Cui, P. Effect of solute atoms and precipitated particles on the optimum temperature of the grain boundary internal friction peak in Aluminum. Scr. Metall. Mater. 1992, 26, 1487. [Google Scholar]
- Choi, D.-h.; Kim, H.; Nix, W.D. Anelasticity and Damping of Thin Aluminum Films on Silicon Substrates. J. Microelectromech. Syst. 2004, 13, 230–237. [Google Scholar] [CrossRef]
- Nishino, Y. Mechanical Properties of Thin-Film Materials evaluated from Amplitude-Dependent Internal Friction. J. Electron. Mater. 1999, 28, 1023–1030. [Google Scholar] [CrossRef]
- Sosale, G.; Almecija, D.; Das, K.; Vengallatore, S. Mechanical spectroscopy of nanocrystalline aluminum films: effects of frequency and grain size on internal friction. Nanotechnology 2012, 23, 155701–155707. [Google Scholar] [CrossRef] [PubMed]
- Bonetti, E.; Campari, E.G.; Pasquini, L.; Savini, L. Automated resonant mechanical analyzer. Rev. Sci. Instr. 2001, 72, 2148. [Google Scholar] [CrossRef]
- No, M.L.; Esnouf, C.; San Juan, J.; Fantozzi, G. Dislocation motion in pure aluminium at 0.5 Tf: analysis from internal friction measurements. J. de Phys. 1985, 46, 347–350. [Google Scholar]
- Lee, L.C.S.; Morris, J.S. Anelasticity and grain boundary sliding. Proc. R. Soc. A 2010, 466, 2651–2671. [Google Scholar] [CrossRef]
- Levenson, L.L. Grain boundary diffusion activation energy derived from surface roughness measurements of aluminum thin films. Appl. Phys. Lett. 1989, 55, 2617–2619. [Google Scholar] [CrossRef]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Campari, E.G.; Amadori, S.; Bonetti, E.; Berti, R.; Montanari, R. Anelastic Behavior of Small Dimensioned Aluminum. Metals 2019, 9, 549. https://doi.org/10.3390/met9050549
Campari EG, Amadori S, Bonetti E, Berti R, Montanari R. Anelastic Behavior of Small Dimensioned Aluminum. Metals. 2019; 9(5):549. https://doi.org/10.3390/met9050549
Chicago/Turabian StyleCampari, Enrico Gianfranco, Stefano Amadori, Ennio Bonetti, Raffaele Berti, and Roberto Montanari. 2019. "Anelastic Behavior of Small Dimensioned Aluminum" Metals 9, no. 5: 549. https://doi.org/10.3390/met9050549
APA StyleCampari, E. G., Amadori, S., Bonetti, E., Berti, R., & Montanari, R. (2019). Anelastic Behavior of Small Dimensioned Aluminum. Metals, 9(5), 549. https://doi.org/10.3390/met9050549






