Mathematical Modeling of Postcombustion in an Electric Arc Furnace (EAF)
Abstract
:1. Introduction
2. Model Description
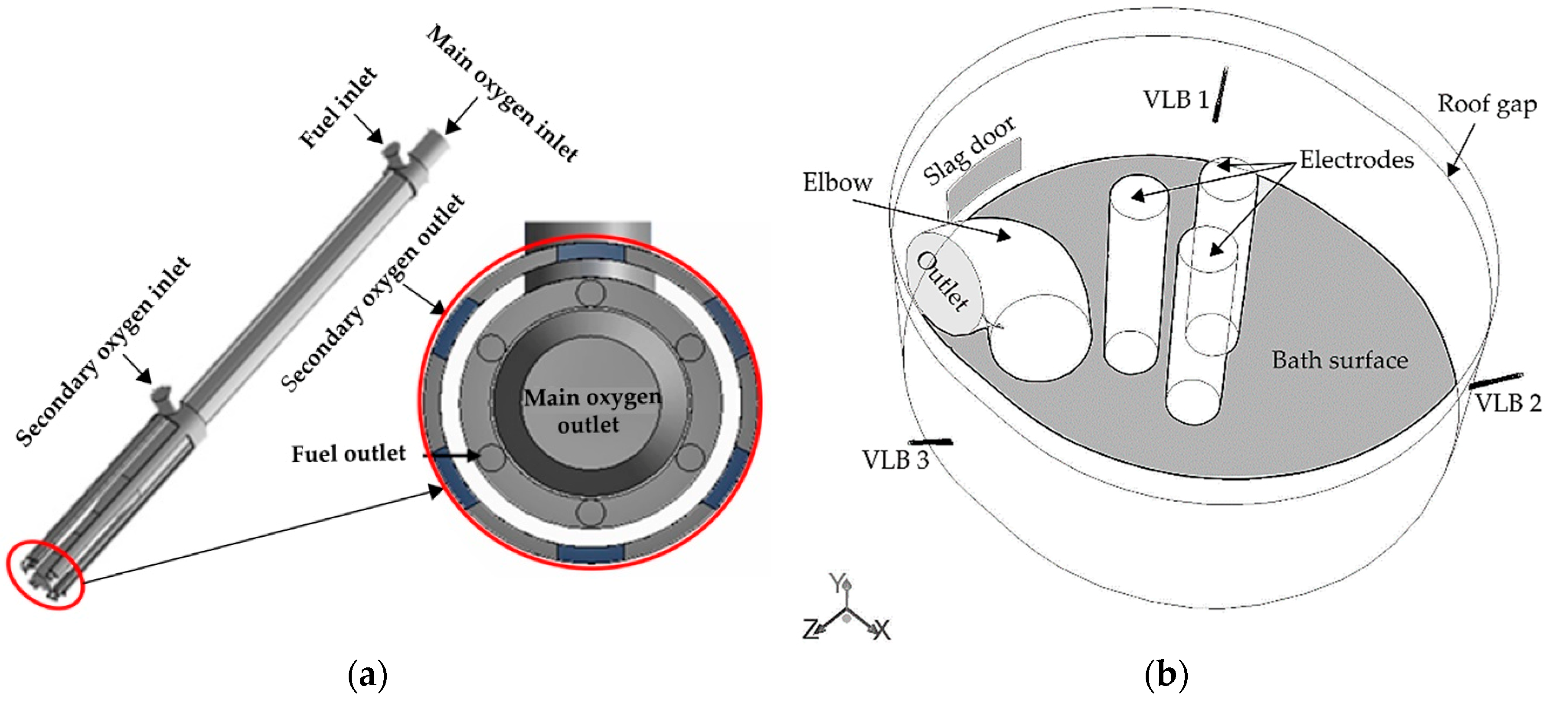
2.1. Computational Domain
- A flat molten bath surface
- A constant flow rate of CO from the molten bath surface
- No generation of NOx inside the furnace
2.2. Reactions and Governing Equations
2.3. Material Properties
2.4. Boundary Conditions
- Bottom: CO arises from the bottom surface of the domain. The flow rate of CO is mainly dependent on the decarburization rate and carbon-injection amount. A flow rate of 0.5 kg·s−1 from the molten bath for the burner mode (decarburization rate of 0.04% C min−1) and a flow rate of 1 kg·s−1 from the molten bath for the burner and lancing mode (decarburization rate of 0.08% C min−1) are assumed. It should be mentioned that these values are very dependent on the oxygen efficiency (the maximal possibility that the carbon in the melt reacts with the oxygen) which is difficult to measure. Temperature at the bottom surface is assigned to steel melting temperature 1773 K.
- VLB: Oxygen and methane gas are injected from three VLBs mounted at the wall at an angle of 40° to the molten bath surface.
- VLB walls: A constant temperature of 300 K is assigned to the VLB walls. No-slip and standard wall function.
- Slag door: For one of the cases, the air infiltration through the slag door was considered. The mass flow rate and temperature are assigned to values of 0.1 kg·s−1 and 800 K. In the other cases, the slag door was considered as a wall.
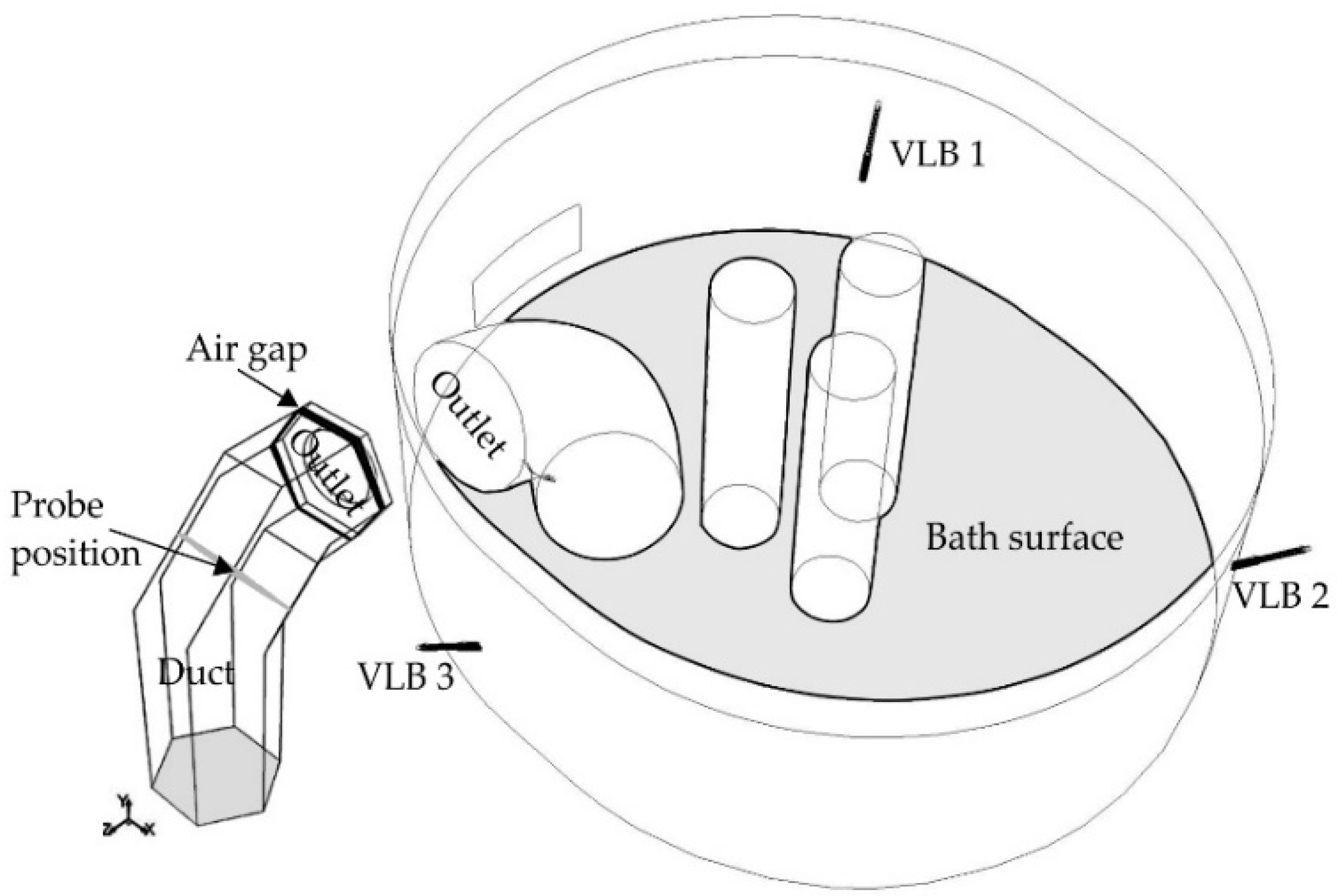
- Outlet: Pressure outlet where the off-gas chemical composition data from other EAFs are used for the backflow volume fractions of species. Temperature was specified from EAF data and low values for k and ε are applied as backflow condition.
- Electrodes: Zero heat flux is assumed on surfaces of the electrodes.
- Roof, side walls, and duct walls: A constant temperature of 1000 K is assigned to the side walls duct walls and roof. No-slip and standard wall function.
- Roof ring gap: The air ingresses through the roof ring gap which is specified as a mass flow rate inlet.
2.5. Case Studies
2.6. Calculation Procedure
3. Results and Discussion
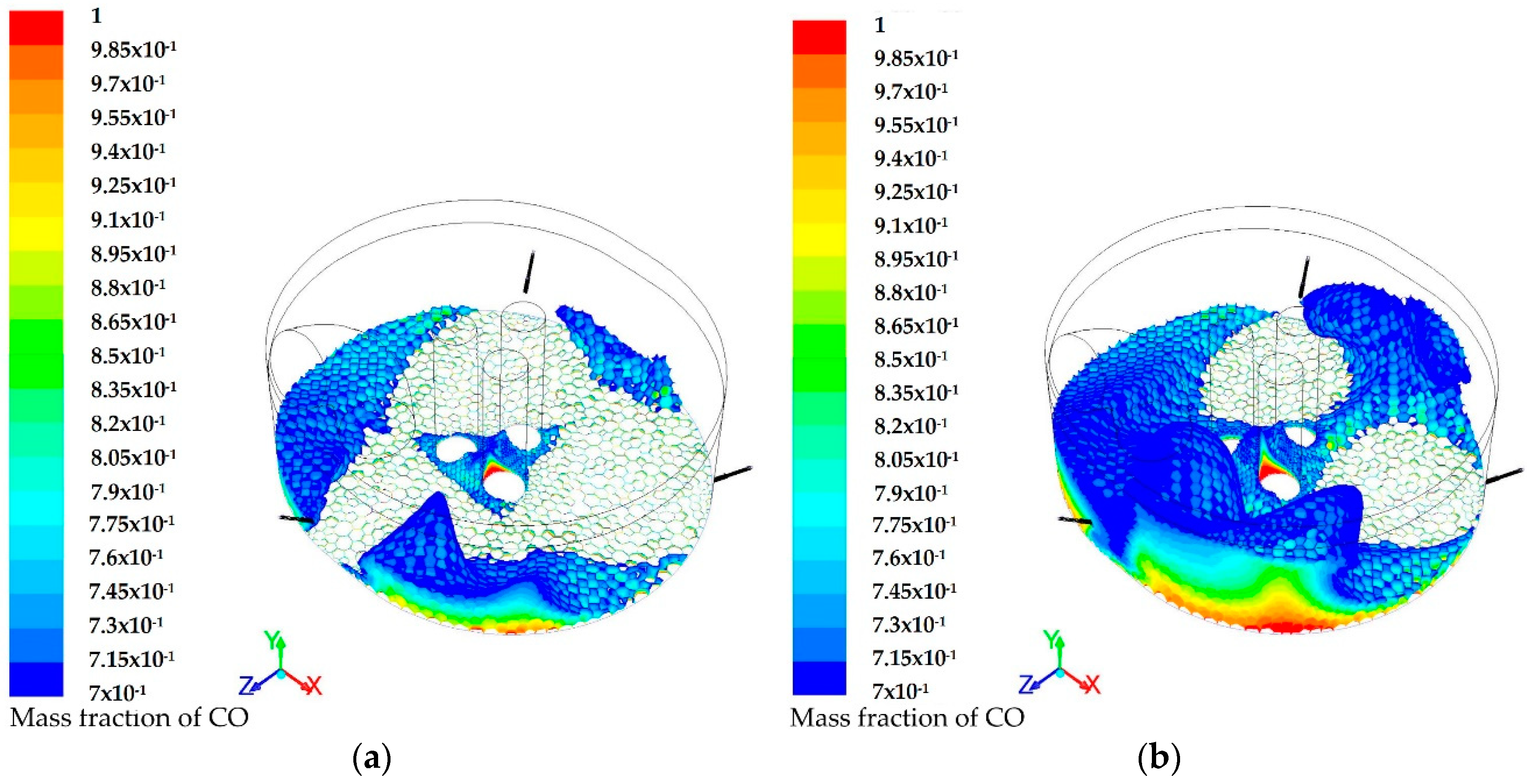
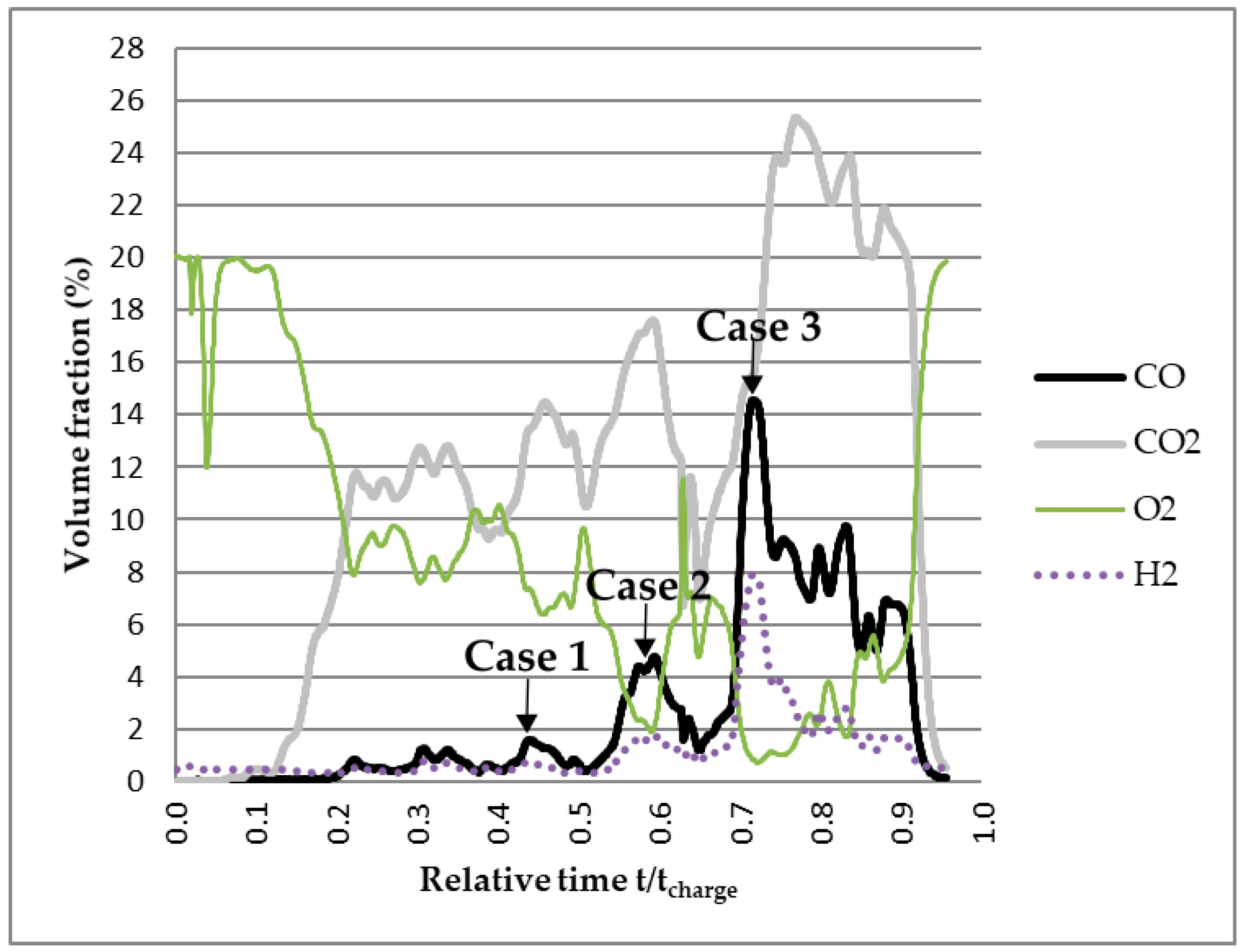
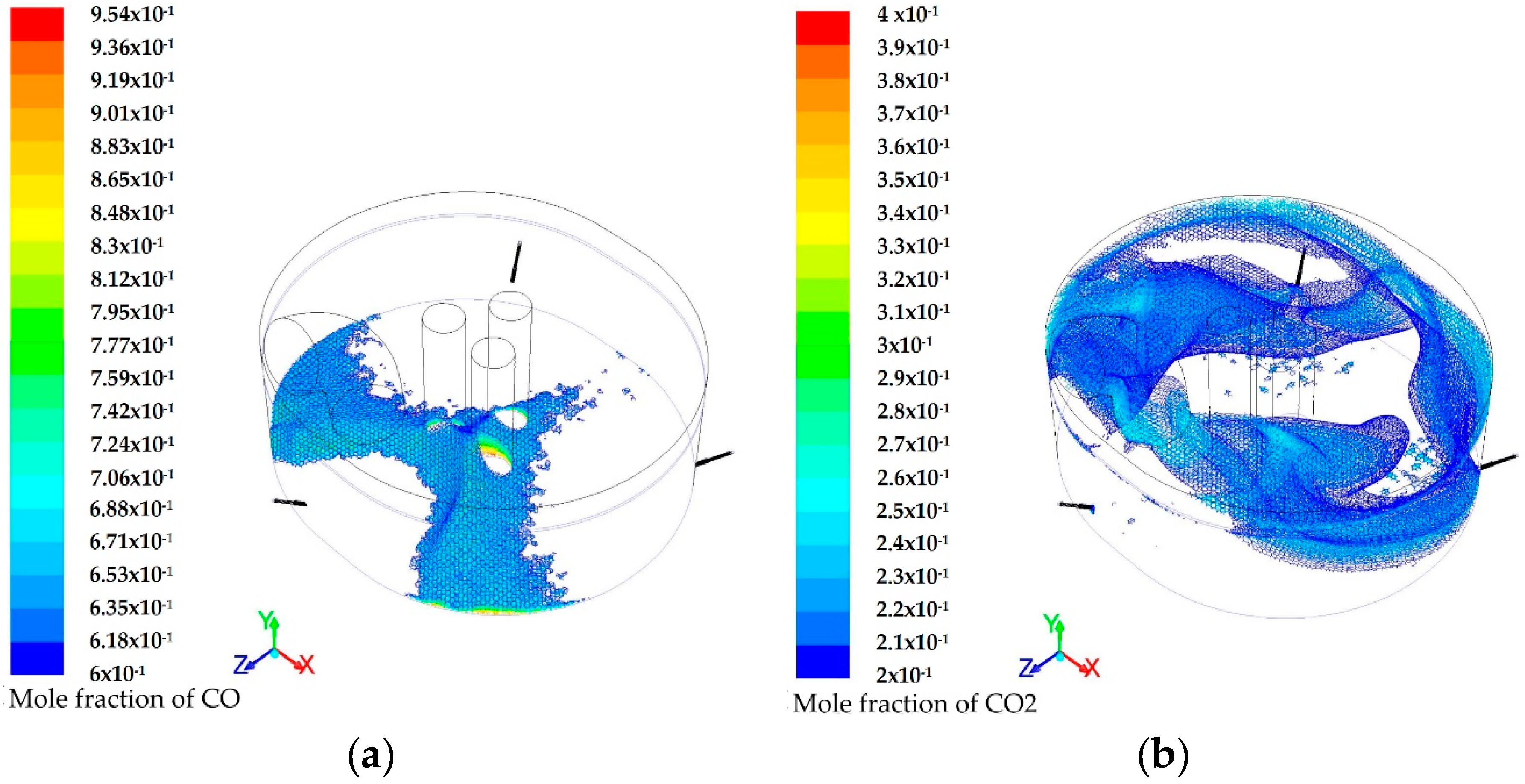
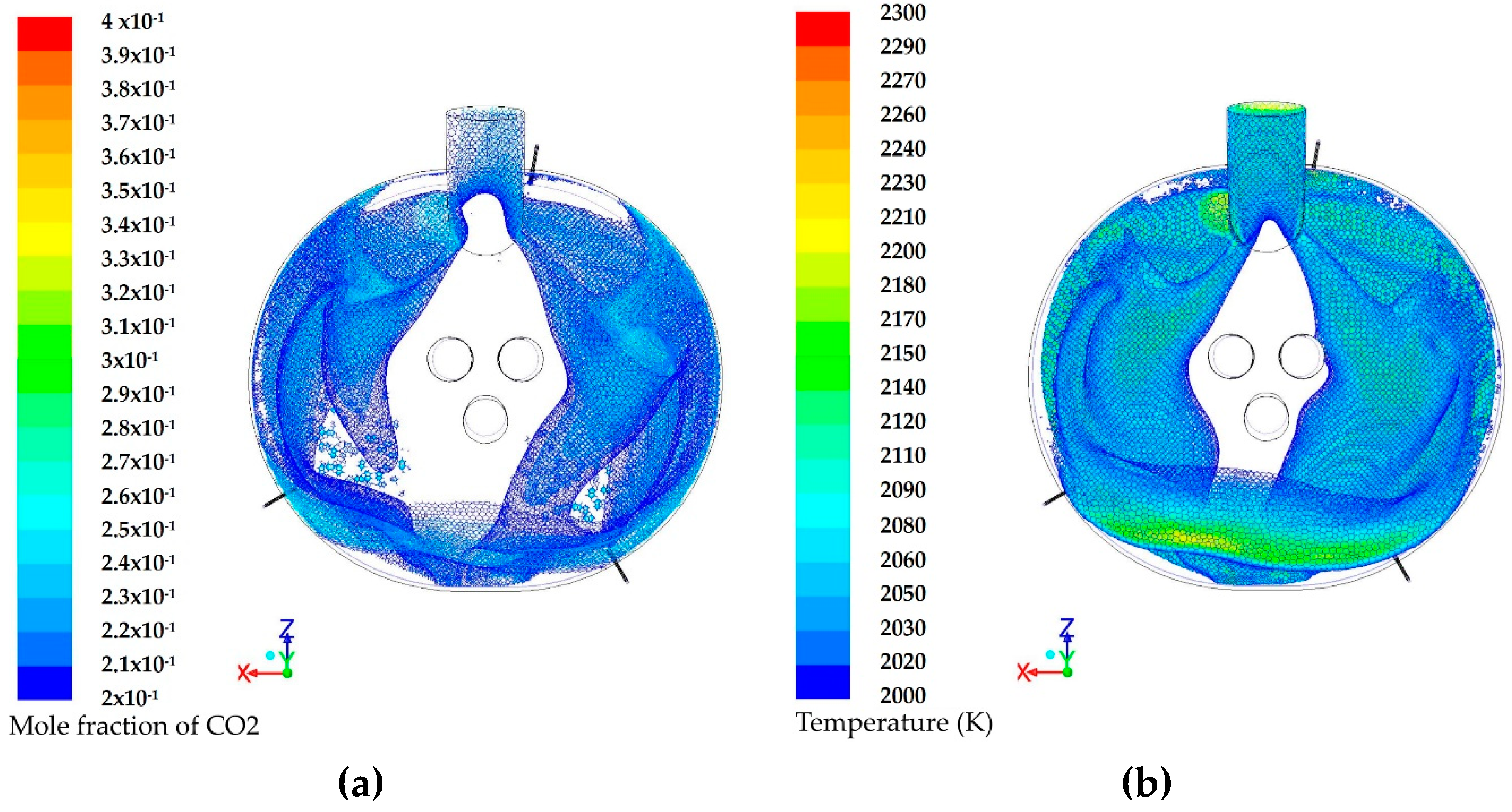
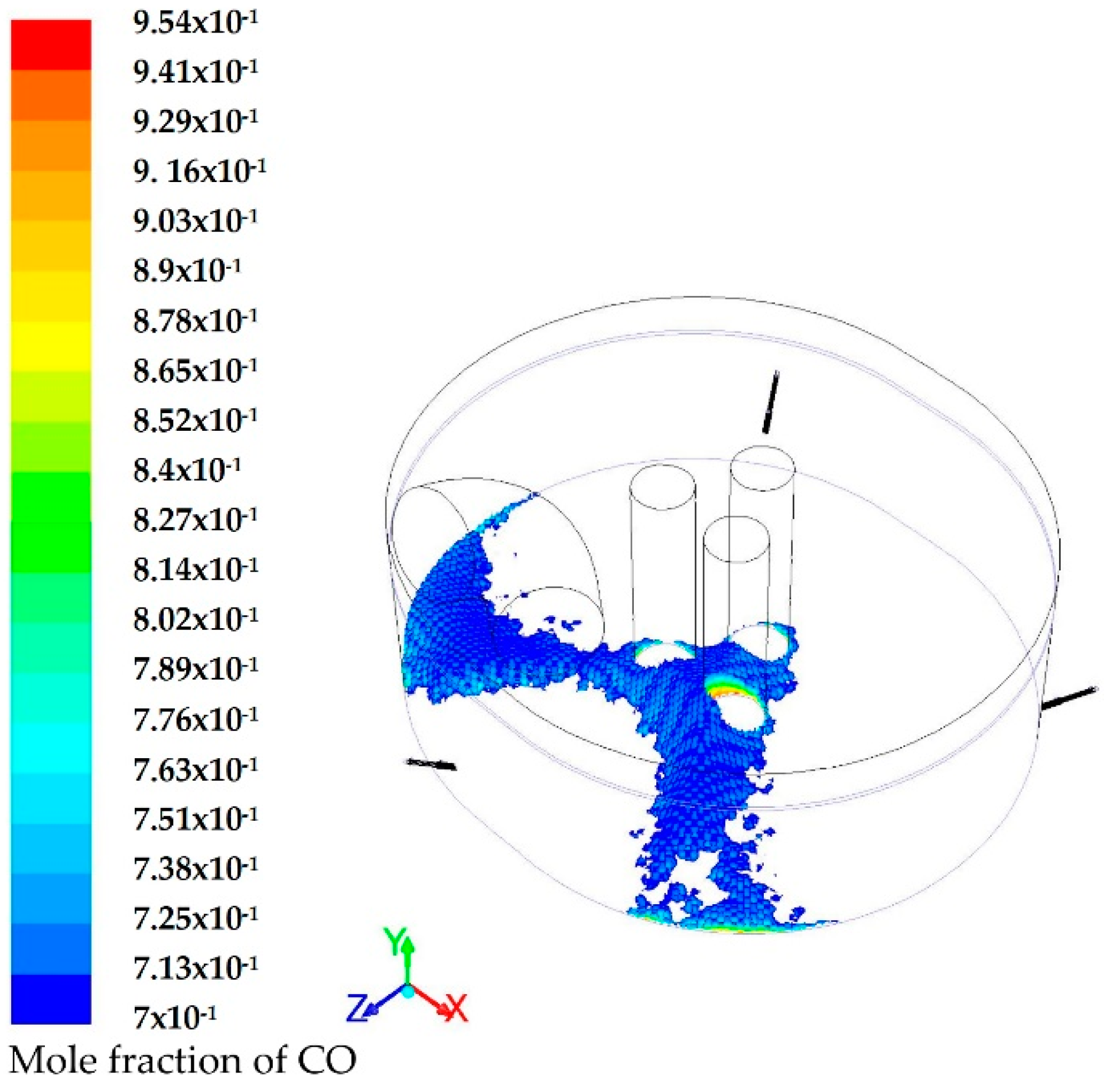
3.1. Modeling of the Reactions Inside the Furnace
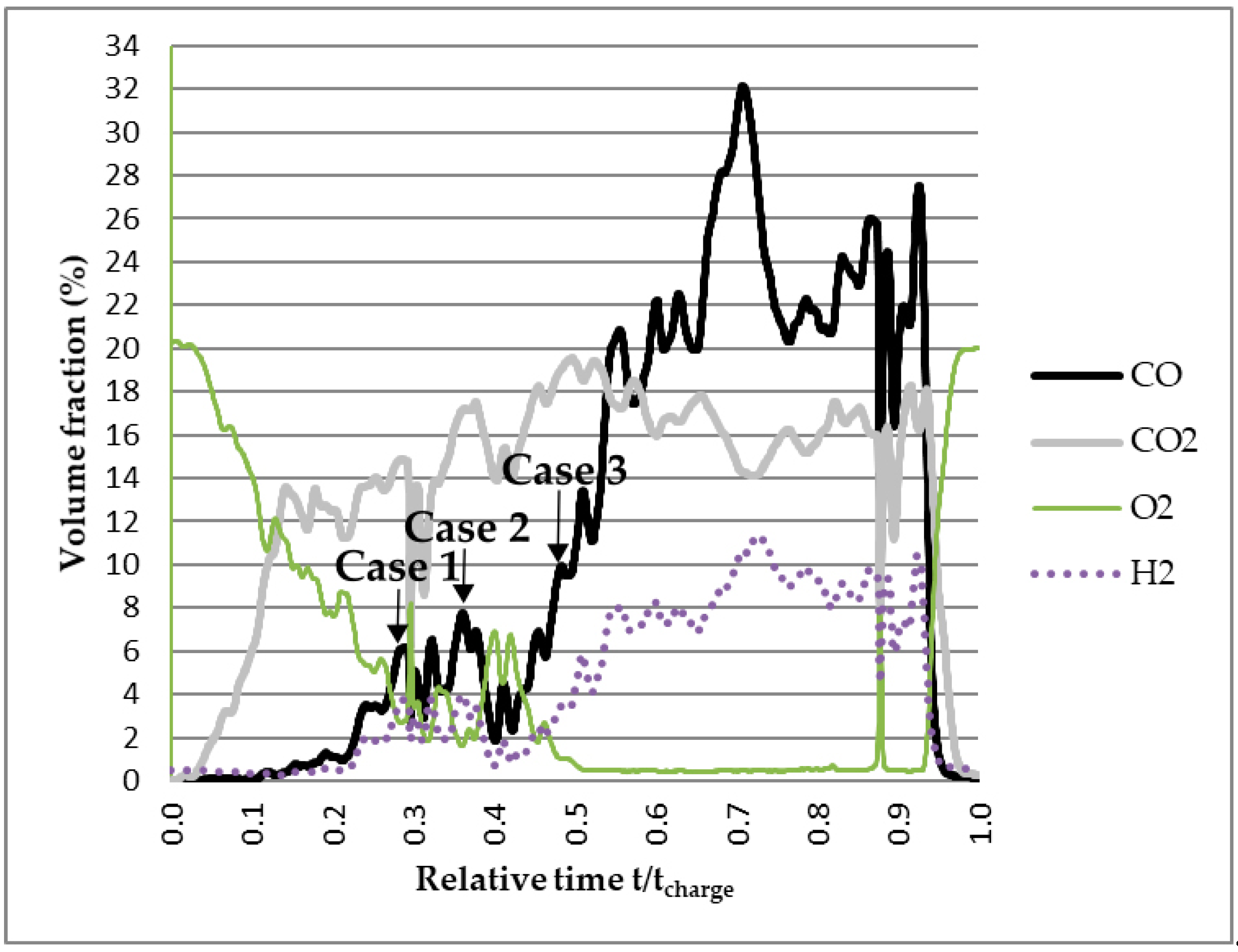
3.2. Modeling the Gas Flow in the Furnace based on the Off-Gas Measurements
3.3. Calculation of the Energy Available in Uncombusted CO Gas
4. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Grant, M.G. Principles and strategy of EAF post combustion. In Proceedings of the 58th Electric Furnace Conference and 17th Process Technology Conference, Orlando, FL, USA, 12–15 November 2000. [Google Scholar]
- Januard, F.; Bockel-Macal, S.; Vuillermoz, J.C.; Leurent, J.; Lebrun, C. Dynamic control of fossil fuel injections in EAF through continuous fumes monitoring. Revue Métall. 2006, 103, 275–280. [Google Scholar] [CrossRef]
- Li, Y.; Fruehan, R.J. Computational fluid dynamics simulation of post combustion in the electric arc furnace. Metall. Mater. Trans. B 2003, 34B, 333–343. [Google Scholar] [CrossRef]
- Zhonghua, W.; Mazumdar, D.; Mujumdar, A.S. Optimization of post combustion in an electric arc furnace for advanced steelmaking. In Proceedings of the 3rd International Conference on Processing Materials for Properties 2008, Bangkok, Thailand, 7–10 December 2008. [Google Scholar]
- Thomson, M.J.; Kournetas, N.G.; Evenson, E.; Sommerville, I.D.; McLean, A.; Guerard, J. Effect of oxyfuel burner ratio changes on energy efficiency in electric arc furnace at Co-Steel Lasco. Ironmak. Steelmak. 2001, 28, 266–272. [Google Scholar] [CrossRef]
- Chan, E.; Riley, M.; Thomson, M.J.; Evenson, E.J. Nitrogen Oxides (NOx) Formation and Control in an Electric Arc Furnace (EAF): Analysis with measurements and computational fluid dynamics (CFD) modeling. ISIJ 2004, 44, 429–438. [Google Scholar] [CrossRef]
- Opfermann, A.; Riedinger, D. Energy efficiency of electric arc furnace. In Proceedings of the 9th European Electric Steelmaking Conference, Krakow, Poland, 19–21 May 2008. [Google Scholar]
- Oseman, A.; Ridgeway, J. Performance of the New VLB System at CMC Steel South Carolina. In Proceedings of the AISTech Conference, St. Louis, MI, USA, 4–7 May 2009. [Google Scholar]
- Westbrook, C.K.; Dryer, F.K. Simplified reaction mechanisms for the oxidation of hydrocarbon. Combust. Sci. Technol. 1981, 27, 31–43. [Google Scholar] [CrossRef]
- ANSYS FLUENT. Theory and User’s Guide, Release 13.0.0. In Southpointe, 275 Technology Drive; ANSYS FLUENT: Canonsburg, PA, USA, 2010. [Google Scholar]
- Milewski, J.; Świrski, K.; Santarelli, M.; Leone, P. Advanced Methods of Solid Oxide Fuel Cell Modeling; Springer: London, UK, 2011; p. 201. [Google Scholar]
- Magnussen, B.F.; Hjertager, B.H. On Mathematical Models of Turbulent Combustion with Special Emphasis on soot Formation and Combustion. Symp. Combust. 1977, 16, 719–729. [Google Scholar] [CrossRef]
- Peters, A.A.F.; Weber, R. Mathematical modeling of a 2.25 MWt swirling natural gas flame. Part 1: eddy break-up concept for turbulent combustion; probability density function approach for nitric oxide formation. Combust. Sci. Technol. 1995, 110, 67–101. [Google Scholar] [CrossRef]
- Arzpeyma, N.; Ersson, M.; Jönsson, P.G. Modeling of Post Combustion inside the Off-Gas Dust System of the Ovako Electric Arc Furnace. In Proceedings of the 10th International Conference on CFD in Oil & Gas, Metallurgical and Process Industries SINTEF, Trondheim, Norway, 17–19 June 2014. [Google Scholar]
- Toulouevski, Y.N.; Zinurov, I.Y. Innovation in Electric Arc Furnaces; Springer: Heidelberg, Germany; Dordrecht, The Netherlands, 2010. [Google Scholar]
| Ref., Date | CFD Model | Dim | Reactions | Predictions | Combustion Source | Off-Gas Data | Domain |
|---|---|---|---|---|---|---|---|
| Li et al., 2003 [3] | Chemical-reaction Species Radiation | 3D | PC of CO Dissociation of CO2 de-PC | Temperature profile Mass transfer of CO, O2 and CO2 Radiation | Oxygen injectors | Y | Whole furnace |
| Chan et al., 2004 [6] | Species * Radiation | 3D | Combustion of CO, H2, and CH4 and NO formation | Temperature profile Mass transfer of NO, CO and O2 | Burner Oxygen lancing | Y | Whole furnace |
| Zhonghua et al., 2009 [4] | Species * Radiation | 3D | Combustion of CO | Mass transfer of CO and O2 | Oxygen injectors | N | Whole furnace |
| Current work | Species * Radiation | 3D | Combustion of CO, H2 and CH4 | Temperature profile Mass transfer of CO, O2 and CO2 | Secondary oxygen of the burner | Y | Whole furnace |
| Reaction | (1) | (2) |
|---|---|---|
| 2.119 | 2.239 | |
| E (J/kmol) | 2.027 | 1.7 |
| β | 0 | 0 |
| 1.3 | 0.25 | |
| - | 1 | |
| - | 0.5 | |
| 0.2 | - | |
| - | - | |
| - | - |
| Stage | Mode | Main Oxygen (kg·s−1) | Secondary Oxygen (kg·s−1) | Methane (kg·s−1) |
|---|---|---|---|---|
| Melting | Burner (B1) | 0.119 | 0.099 | 0.052 |
| Burner (B2) | 0.063 | 0.198 | 0.064 | |
| Burner (B3) | 0.198 | 0.063 | 0.064 | |
| Melting + Refining | Burner + Lancing (B+L1) | 0.317 | 0.059 | 0.052 |
| Burner + Lancing (B+L2) | 0.396 | 0.059 | 0.043 | |
| Refining | Lancing (L) | 0.634 | 0.04 | 0.023 |
| Case | CO Mass Flow Rate (kg·s−1) | Slag Door | Mode |
|---|---|---|---|
| 1 | 0.5 | Closed | B3 |
| 2 | 1 | Closed (one step reaction) | B + L1 |
| 3 | 1 | Open | B + L1 |
| 4 | 1 | Closed (O2 removal) | B + L1 |
| Case | N2 | CO | CO2 | PCR |
|---|---|---|---|---|
| 1 | - | 0.52 | 0.18 | 0.26 |
| 2 | - | 0.64 | 0.13 | 0.16 |
| 3 | 0.09 | 0.6 | 0.14 | 0.19 |
| 4 | - | 0.55 | 0.32 | 0.36 |
| Case | Composition at the Duct Inlet (mf) | Vin | Pout | Composition at the Probe (Avg. mf) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| CO | CO2 | O2 | H2 | CO | CO2 | O2 | H2 | |||
| 1 | 0.14 | 0.14 | 10−4 | 0.04 | 22 | −320 | 0.06 | 0.168 | 0.017 | 0.033 |
| 2 | 0.2 | 0.16 | 10−4 | 0.07 | 22 | −320 | 0.082 | 0.18 | 0.022 | 0.069 |
| 3 | 0.2 | 0.14 | 10−4 | 0.09 | 22 | −300 | 0.11 | 0.176 | 0.01 | 0.076 |
| Case | Composition at the Duct Inlet (mf) | Vin | Pout | Composition at the Probe (Avg. mf) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| CO | CO2 | O2 | H2 | CO | CO2 | O2 | H2 | |||
| 1 | 0.1 | 0.12 | 0.08 | 0.01 | 20 | −320 | 0.015 | 0.18 | 0.062 | 0.009 |
| 2 | 0.13 | 0.15 | 10−4 | 0.03 | 22 | −320 | 0.053 | 0.173 | 0.019 | 0.024 |
| 0.13 | 0.16 | 10−4 | 0.03 | 22 | −320 | 0.054 | 0.182 | 0.019 | 0.024 | |
| 3 | 0.24 | 0.12 | 10−5 | 0.09 | 22 | −300 | 0.146 | 0.161 | 0.007 | 0.077 |
| 0.25 | 0.12 | 10−5 | 0.09 | 22 | −300 | 0.155 | 0.161 | 0.007 | 0.077 | |
| Case | Air Flow Rate (Roof) (kg·s−1) | CO Flow Rate (Bottom) (kg·s−1) | N2 | CO | CO2 | H2O |
|---|---|---|---|---|---|---|
| 1 | 1.5 | 1 | 0.44 | 0.23 | 0.19 | 0.07 |
| 2 | 1.5 | 0.8 | 0.47 | 0.18 | 0.2 | 0.08 |
| 3 | 1.5 | 0.6 | 0.51 | 0.12 | 0.21 | 0.089 |
| 4 | 1.5 | 0.5 | 0.52 | 0.09 | 0.21 | 0.095 |
| 5 | 1.8 | 1 | 0.48 | 0.183 | 0.206 | 0.069 |
| 6 | 1.8 | 0.8 | 0.51 | 0.13 | 0.22 | 0.077 |
| 7 | 1.8 | 0.7 | 0.53 | 0.1 | 0.22 | 0.08 |
| 8 | 2 | 0.9 | 0.52 | 0.127 | 0.22 | 0.071 |
| Mode | Case | Air Flow Rate (Roof) (kg·s−1) | CO Flow Rate (Bottom) (kg·s−1) | N2 | CO | CO2 | H2O |
|---|---|---|---|---|---|---|---|
| B+L1 | 1 | 1.5 | 0.7 | 0.46 | 0.131 | 0.223 | 0.069 |
| 2 | 1.5 | 0.8 | 0.45 | 0.1551 | 0.219 | 0.066 | |
| B+L2 | 3 | 1.5 | 1.2 | 0.39 | 0.24 | 0.21 | 0.045 |
| 4 | 1.2 | 1 | 0.37 | 0.24 | 0.2 | 0.05 |
| Case | CO Flow Rate (kg·s−1) | Secondary Oxygen Flow Rate (kg·s−1) | CO | CO2 | O2 | PCR |
|---|---|---|---|---|---|---|
| 1 | 0.6 | 0.063 | 0.12 | 0.209 | 2 × 10−6 | 0.58 |
| 2 | 0.6 | 0.1 | 0.107 | 0.228 | 9 × 10−6 | 0.68 |
| Case | CO Flow Rate (kg·s−1) | Secondary Oxygen Flow Rate (kg·s−1) | CO | CO2 | O2 | PCR |
|---|---|---|---|---|---|---|
| 1 | 0.8 | 0.059 | 0.156 | 0.216 | 1.1 × 10−6 | 0.581 |
| 2 | 0.8 | 0.065 | 0.155 | 0.219 | 1.4 × 10−6 | 0.585 |
| 3 | 0.8 | 0.07 | 0.154 | 0.221 | 8 × 10−7 | 0.589 |
| 4 | 0.8 | 0.1 | 0.142 | 0.236 | 8 × 10−7 | 0.624 |
| Condition | Burner Mode | Burner + Lancing Mode |
|---|---|---|
| CO (mole fraction) | 0.09 | 0.156 |
| CO mass flow rate (kg·s−1) | 0.14 | 0.39 |
| Enthalpy of CO combustion (kWh·kg−1 of CO) | 2.39 | 2.39 |
| Capacity of CO combustion (MW) | 1.19 | 3.13 |
| CH4 mass flow rate (kg·s−1) | 0.06 | 0.05 |
| Enthalpy of reaction 1 (kWh/mole) | 0.24 | 0.24 |
| Capacity of reaction 1 (MW) | 3.35 | 2.77 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arzpeyma, N.; Ersson, M.; Jönsson, P.G. Mathematical Modeling of Postcombustion in an Electric Arc Furnace (EAF). Metals 2019, 9, 547. https://doi.org/10.3390/met9050547
Arzpeyma N, Ersson M, Jönsson PG. Mathematical Modeling of Postcombustion in an Electric Arc Furnace (EAF). Metals. 2019; 9(5):547. https://doi.org/10.3390/met9050547
Chicago/Turabian StyleArzpeyma, Niloofar, Mikael Ersson, and Pär G. Jönsson. 2019. "Mathematical Modeling of Postcombustion in an Electric Arc Furnace (EAF)" Metals 9, no. 5: 547. https://doi.org/10.3390/met9050547
APA StyleArzpeyma, N., Ersson, M., & Jönsson, P. G. (2019). Mathematical Modeling of Postcombustion in an Electric Arc Furnace (EAF). Metals, 9(5), 547. https://doi.org/10.3390/met9050547






