A Modified Johnson-Cook Model for Ferritic-Pearlitic Steel in Dynamic Strain Aging Regime
Abstract
1. Introduction
2. Experimental Method
3. Results and Discussion
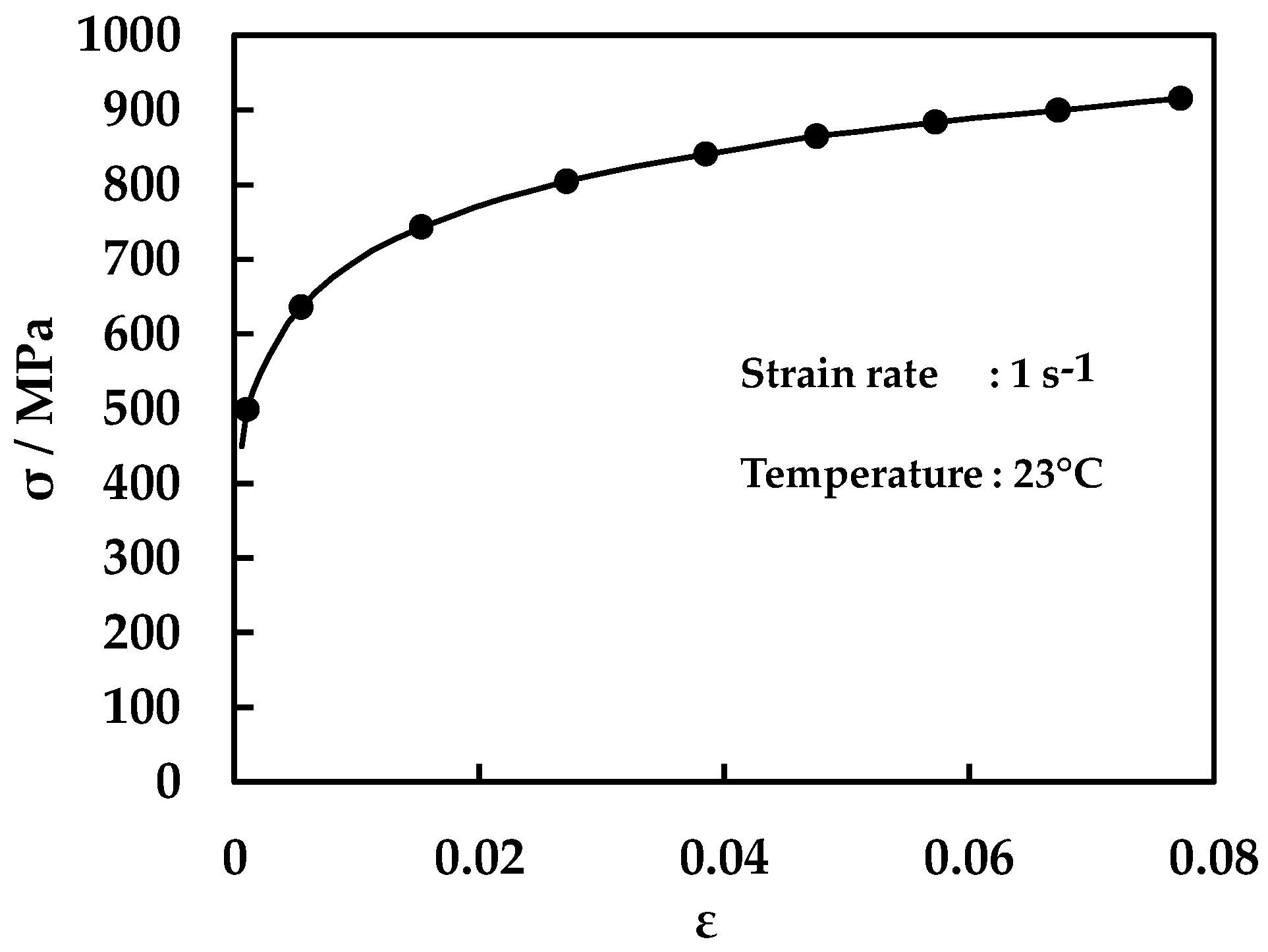
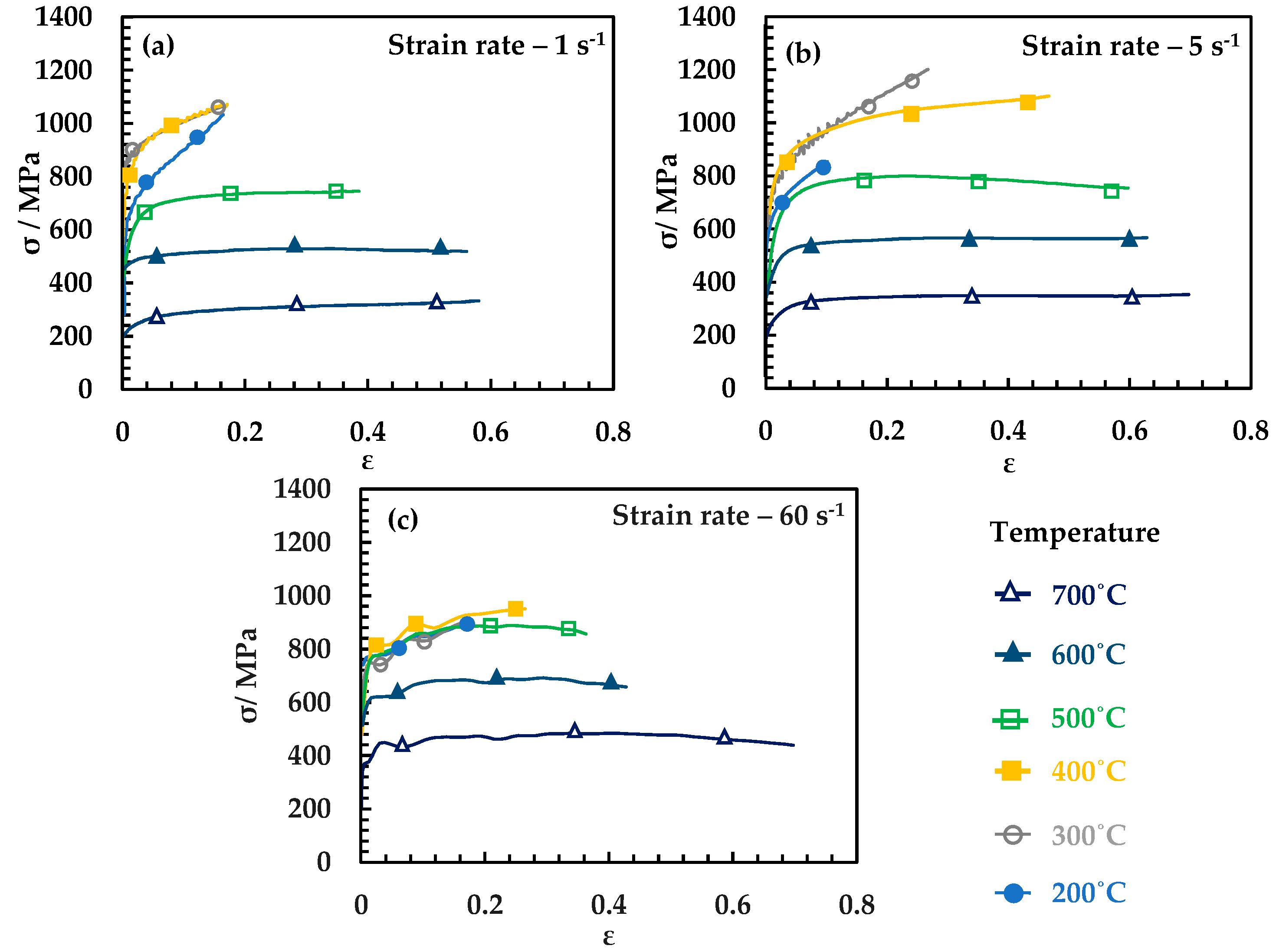
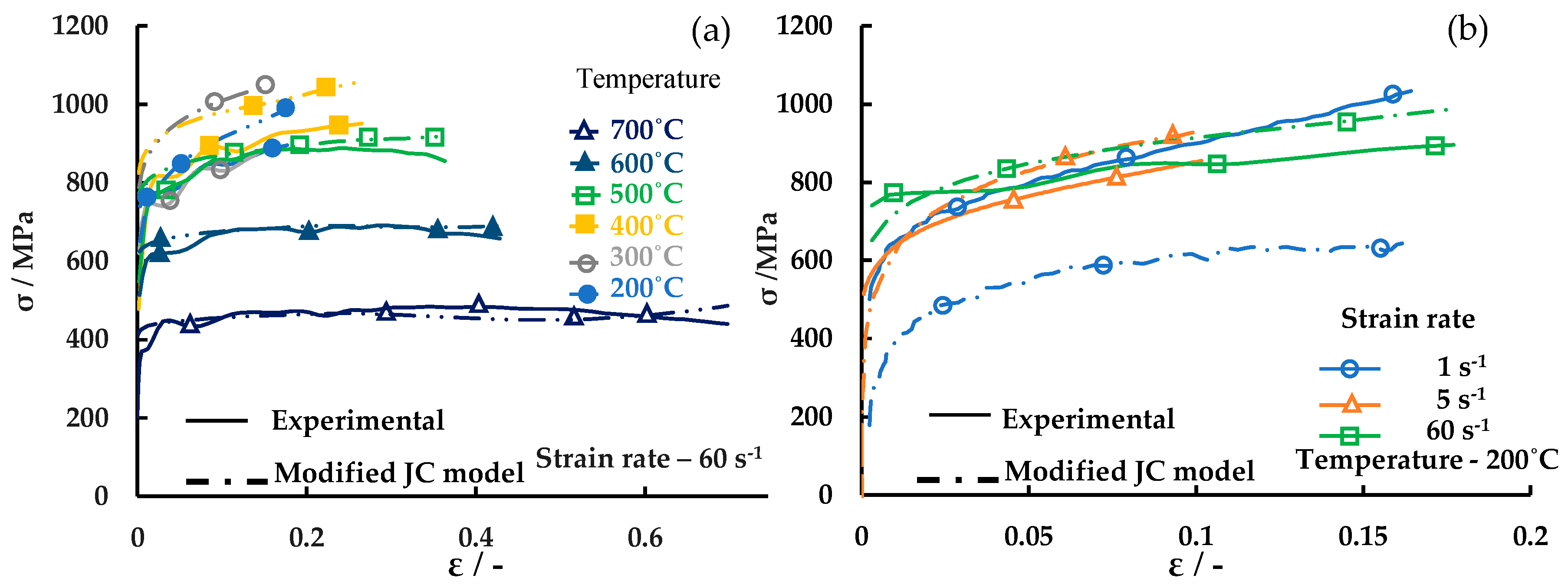
3.1. Experimental Results
- (a)
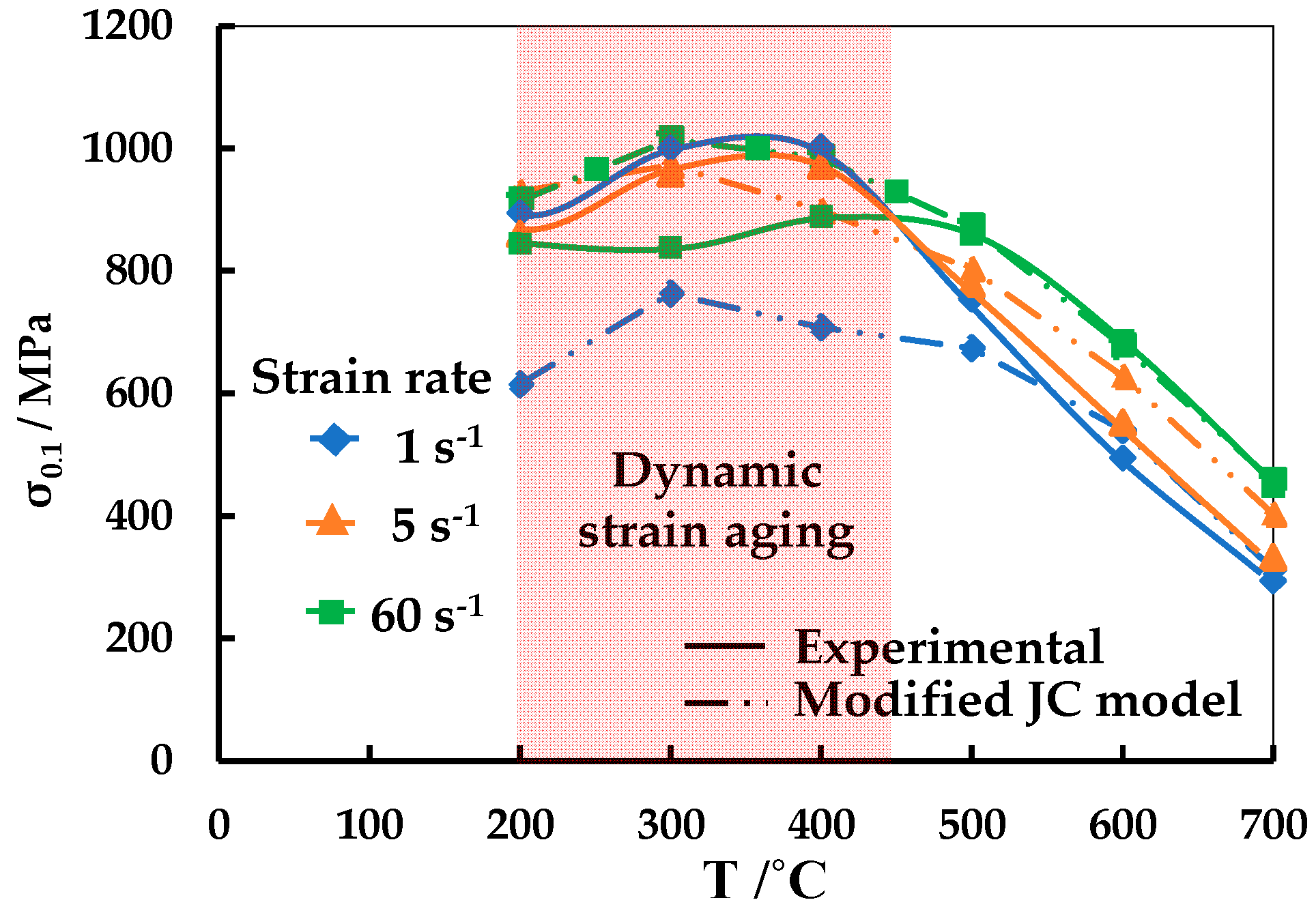
- Two temperature zones were identified with different flow behavior where the flow stress increased with temperature in the temperature zone (200–400 °C) and the flow stress decreased with temperature in the temperature zone (500–700 °C).
- (b)
- The flow stress decreased with increase in strain rate in the temperature range 200 °C to 400 °C.
- (c)
- The serrated flow was observed in the temperature range 200 °C to 300 °C.
3.2. Fitting of Flow Stress Curves to Original J-C Model
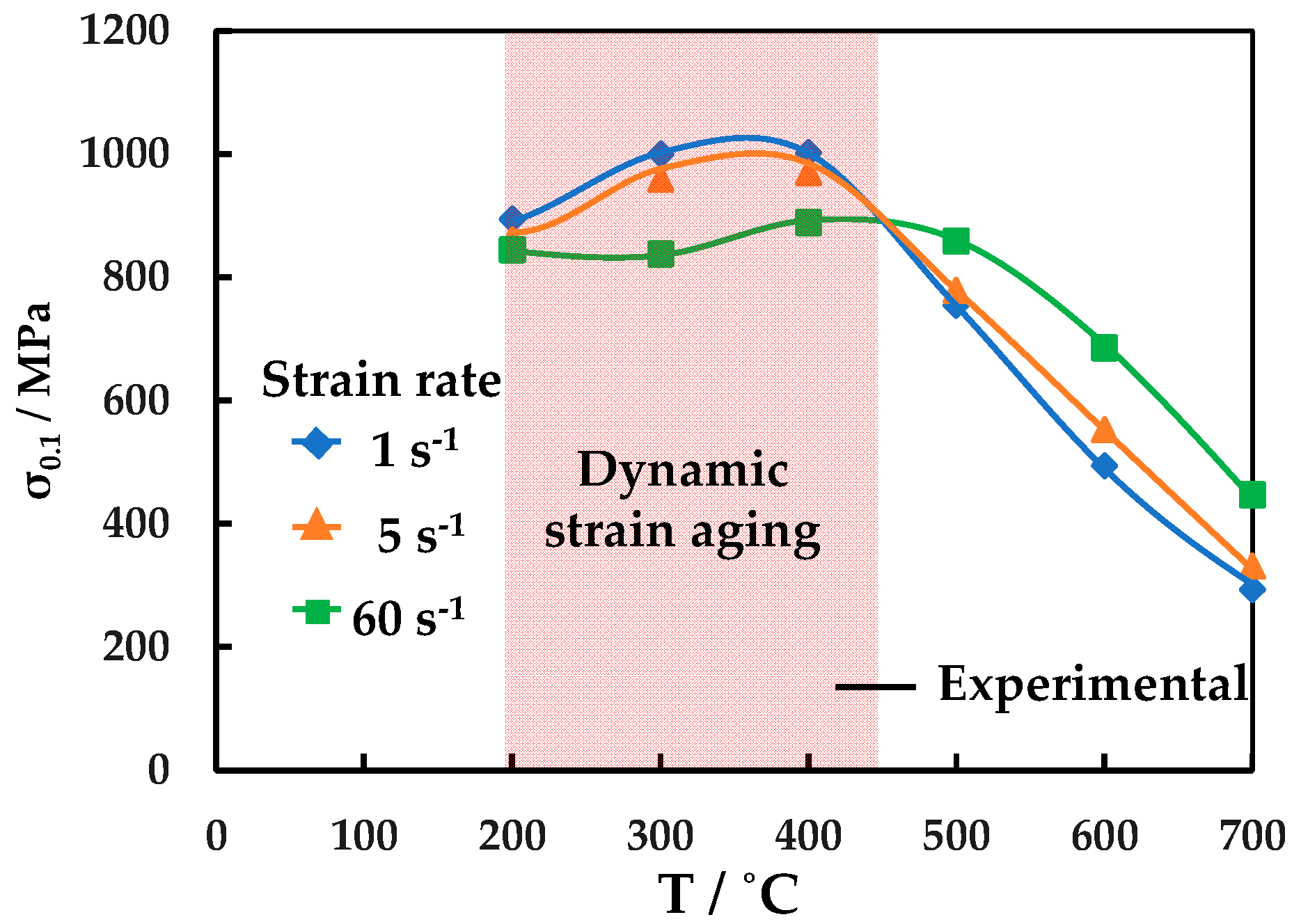
3.3. Influence of Temperature and Strain Rate on Flow Stress at a Strain of 0.1
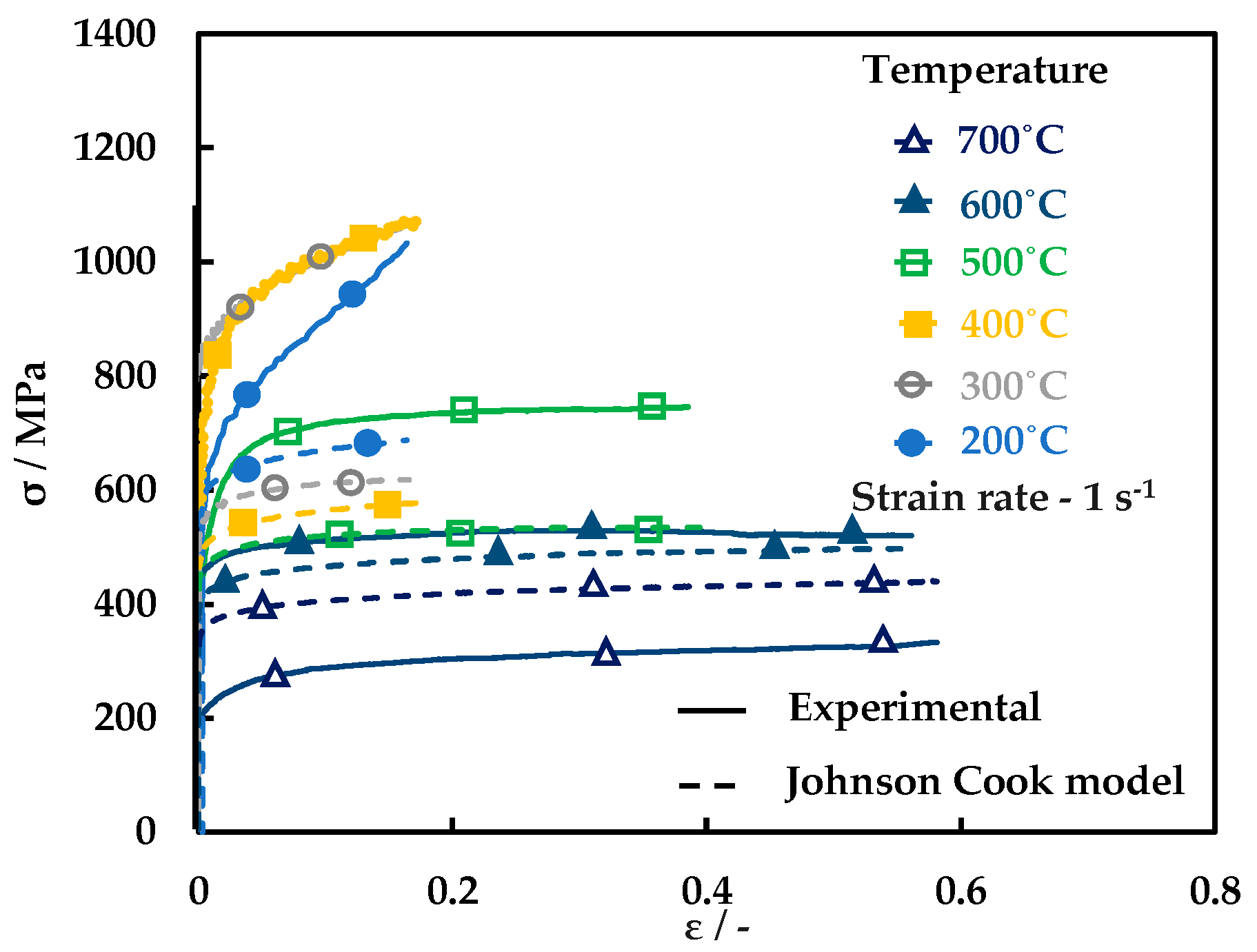
3.4. Fitting of Flow Stress Curves to Modified J-C Model
4. Conclusions
- True stress versus true plastic strain of C45E Steel shows the strain hardening behaviour is dependent on the temperature with the presence of two temperature zones (200–400 °C and 500–700 °C) with strain hardening being higher in the temperature range 200–400 °C and dynamic recovery active in the temperature range 500–700 °C.
- In the temperature range 200–400 °C, the presence of negative thermal softening, negative strain rate hardening and serrated flow indicates the presence of DSA.
- The general J-C model is unable to capture the strain hardening variation and the presence of DSA.
- The modification of J-C model’s strain hardening component with the parameters A and B as a function of temperature and strain rate using a polynomial function enables capturing the DSA qualitatively.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Arrazola, P.J.; Özel, T.; Umbrello, D.; Davies, M.; Jawahir, I.S. Recent advances in modelling of metal machining processes. CIRP Ann. Manuf. Technol. 2013, 62, 695–718. [Google Scholar] [CrossRef]
- Melkote, S.N.; Grzesik, W.; Outeiro, J.; Rech, J.; Schulze, V.; Attia, H.; Arrazola, P.J.; M’Saoubi, R.; Saldana, C. Advances in material and friction data for modelling of metal machining. CIRP Ann. Manuf. Technol. 2017, 66, 731–754. [Google Scholar] [CrossRef]
- Johnson, G.R.; Cook, W.H. A constitutive model and data for metals subjected to large strains, high strain rates and high temperatures. Proc. 7th Int. Symp. Ballist. 1983, 21, 541–547. [Google Scholar]
- Murugesan, M.; Jung, D.W. Johnson cook material and failure model parameters estimation of AISI-1045 medium carbon steel for metal forming applications. Materials 2019, 12, 609. [Google Scholar] [CrossRef]
- Rodríguez-Millán, M.; Díaz-Álvarez, J.; Bernier, R.; Rusinek, A.; Miguelez, M.; Cantero, J. Thermo-Viscoplastic Behavior of Ni-Based Superalloy Haynes 282 and Its Application to Machining Simulation. Metals 2017, 7, 561. [Google Scholar] [CrossRef]
- Ning, J.; Liang, S.Y. Predictive modeling of machining temperatures with force-temperature correlation using cutting mechanics and constitutive relation. Materials 2019, 12, 284. [Google Scholar] [CrossRef]
- Storchak, M.; Rupp, P.; Möhring, H.C.; Stehle, T. Determination of Johnson-Cook Constitutive Parameters for Cutting Simulations. Metals 2019, 9, 473. [Google Scholar] [CrossRef]
- Jaspers, S.P.F.C.; Dautzenberg, J.H. Material behaviour in conditions similar to metal cutting: Flow stress in the primary shear zone. J. Mater. Process. Technol. 2002, 122, 322–330. [Google Scholar] [CrossRef]
- Abouridouane, M.; Klocke, F.; Lung, D.; Adams, O. A new 3D multiphase FE model for micro cutting ferritic – pearlitic carbon steels. CIRP Ann. Manuf. Technol. 2012, 61, 71–74. [Google Scholar] [CrossRef]
- Courbon, C.; Mabrouki, T.; Rech, J.; Mazuyer, D.; Perrard, F.; D’Eramo, E.; Eramo, E.D.; D’Eramo, E.; Eramo, E.D.; D’Eramo, E.; et al. Towards a physical FE modelling of a dry cutting operation: Influence of dynamic recrystallization when machining AISI 1045. Procedia CIRP 2013, 8, 516–521. [Google Scholar] [CrossRef][Green Version]
- Sartkulvanich, P.; Koppka, F.; Altan, T. Determination of flow stress for metal cutting simulation - A progress report. J. Mater. Process. Technol. 2004, 146, 61–71. [Google Scholar] [CrossRef]
- Li, H.Y.; Wang, X.F.; Duan, J.Y.; Liu, J.J. A modified Johnson Cook model for elevated temperature flow behavior of T24 steel. Mater. Sci. Eng. A 2013, 577, 138–146. [Google Scholar] [CrossRef]
- Ee, K.C.; Dillon, O.W.; Jawahir, I.S. Finite element modeling of residual stresses in machining induced by cutting using a tool with finite edge radius. Int. J. Mech. Sci. 2005, 47, 1611–1628. [Google Scholar] [CrossRef]
- Wang, S.; Huang, Y.; Xiao, Z.; Liu, Y.; Liu, H. A Modified Johnson-Cook Model for Hot Deformation Behavior of 35CrMo Steel. Metals 2017, 7, 337. [Google Scholar] [CrossRef]
- Sajadifar, S.; Yapici, G. High Temperature Flow Response Modeling of Ultra-Fine Grained Titanium. Metals 2015, 5, 1315–1327. [Google Scholar] [CrossRef]
- Hor, A.; Morel, F.; Lebrun, J.L.; Germain, G. Modelling, identification and application of phenomenological constitutive laws over a large strain rate and temperature range. Mech. Mater. 2013, 64, 91–110. [Google Scholar] [CrossRef]
- Nemat-Nasser, S.; Guo, W.G. Thermomechanical response of HSLA-65 steel plates: Experiments and modeling. Mech. Mater. 2005, 37, 379–405. [Google Scholar] [CrossRef]
- Kim, I.S.; Kang, S.S. Dynamic strain aging in SA508-class 3 pressure vessel steel. Int. J. Press. Vessel. Pip. 1995, 62, 123–129. [Google Scholar] [CrossRef]
- Azizi-Alizamini, H.; Militzer, M.; Poole, W.J. Austenite formation in plain low-carbon steels. Metall. Mater. Trans. A Phys. Metall. Mater. Sci. 2011, 42, 1544–1557. [Google Scholar] [CrossRef]
- Hor, A.; Morel, F.; Lebrun, J.L.; Germain, G.; Miquelard-garnier, G.; Guinault, A.; Fromonteil, D.; Delalande, S.; Miquelard-garnier, G.; Guinault, A.; et al. An experimental investigation of the behaviour of steels over large temperature and strain rate ranges. Int. J. Mech. Sci. 2013, 67, 108–122. [Google Scholar] [CrossRef]
- Hokka, M.; Rämö, J.; Mardoukhi, A.; Vuoristo, T.; Roth, A.; Kuokkala, V.-T. Effects of Microstructure on the Dynamic Strain Aging in Ferritic-Pearlitic Steels. J. Dyn. Behav. Mater. 2018, 4, 452–463. [Google Scholar] [CrossRef]
- Li, C.C.; Leslie, W.C. Effects of dynamic strain aging on the subsequent mechanical properties of carbon steels. Metall. Trans. A 1978, 9, 1765–1775. [Google Scholar] [CrossRef]
- Abed, F.H.; Saffarini, M.H.; Abdul-Latif, A.; Voyiadjis, G.Z. Flow Stress and Damage Behavior of C45 Steel Over a Range of Temperatures and Loading Rates. J. Eng. Mater. Technol. 2017, 139, 021012. [Google Scholar] [CrossRef]
- Qingdong, Z.; Qiang, C.; Xiaofeng, Z. A Modified Johnson-Cook Model for Advanced High-Strength Steels Over a Wide Range of Temperatures. J. Mater. Eng. Perform. 2014, 23, 4336–4341. [Google Scholar] [CrossRef]


| C | Si | Mn | P | S | Cr | Ni | Mo | Fe |
|---|---|---|---|---|---|---|---|---|
| 0.44 | 0.24 | 0.66 | 0.006 | 0.031 | 0.13 | 0.19 | 0.03 | Balance |
| J-C Variant | A | B | n | C | m |
|---|---|---|---|---|---|
| GA Approach | 544 | 332 | 0.158 | 0.010 | 1 |
| Jaspers and Dautzenberg | 553 | 600 | 0.234 | 0.013 | 1 |
| A0 | A1 | A2 | A3 | A4 | B0 | B1 | B2 | B3 | B4 | n0 | n1 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| −763.44 | 41.04 | 9691 | −2.46 | −14.674 | 1390.6 | 182.6 | −3060.7 | −59.27 | 1751.24 | 0.07 | 1 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moris Devotta, A.; Sivaprasad, P.V.; Beno, T.; Eynian, M.; Hjertig, K.; Magnevall, M.; Lundblad, M. A Modified Johnson-Cook Model for Ferritic-Pearlitic Steel in Dynamic Strain Aging Regime. Metals 2019, 9, 528. https://doi.org/10.3390/met9050528
Moris Devotta A, Sivaprasad PV, Beno T, Eynian M, Hjertig K, Magnevall M, Lundblad M. A Modified Johnson-Cook Model for Ferritic-Pearlitic Steel in Dynamic Strain Aging Regime. Metals. 2019; 9(5):528. https://doi.org/10.3390/met9050528
Chicago/Turabian StyleMoris Devotta, Ashwin, P. V. Sivaprasad, Tomas Beno, Mahdi Eynian, Kjell Hjertig, Martin Magnevall, and Mikael Lundblad. 2019. "A Modified Johnson-Cook Model for Ferritic-Pearlitic Steel in Dynamic Strain Aging Regime" Metals 9, no. 5: 528. https://doi.org/10.3390/met9050528
APA StyleMoris Devotta, A., Sivaprasad, P. V., Beno, T., Eynian, M., Hjertig, K., Magnevall, M., & Lundblad, M. (2019). A Modified Johnson-Cook Model for Ferritic-Pearlitic Steel in Dynamic Strain Aging Regime. Metals, 9(5), 528. https://doi.org/10.3390/met9050528





