Effect of Elastic Module Degradation Measurement in Different Sizes of the Nonlinear Isotropic–Kinematic Yield Surface on Springback Prediction
Abstract
:1. Introduction
- (1)
- The new unloading elastic modulus is measured as a straight line between the stress forward and the non-zero residual stress.
- (2)
- Nonlinear regression analysis is used to fit the new model, which is a function of plastic strain.
- (3)
- The implementation of the new model is combined with von Mises yield criteria in finite element software.
- (4)
- The numerical integration of the algorithm stress update is implemented as an implicit integration.
- (5)
- The new model implements two types of nonlinear hardening models, the isotropic model and the combined hardening model, for comparative purposes.
- (6)
- A shell element is used with reduced integration (S4R) due to its efficiency in sheet metal simulation under plane stress conditions.
- (7)
- The extended Chord model was verified by comparing the U-draw bending of DP780 with the pre-strain result, which is available in the Numisheet benchmark 2011.
2. Methods
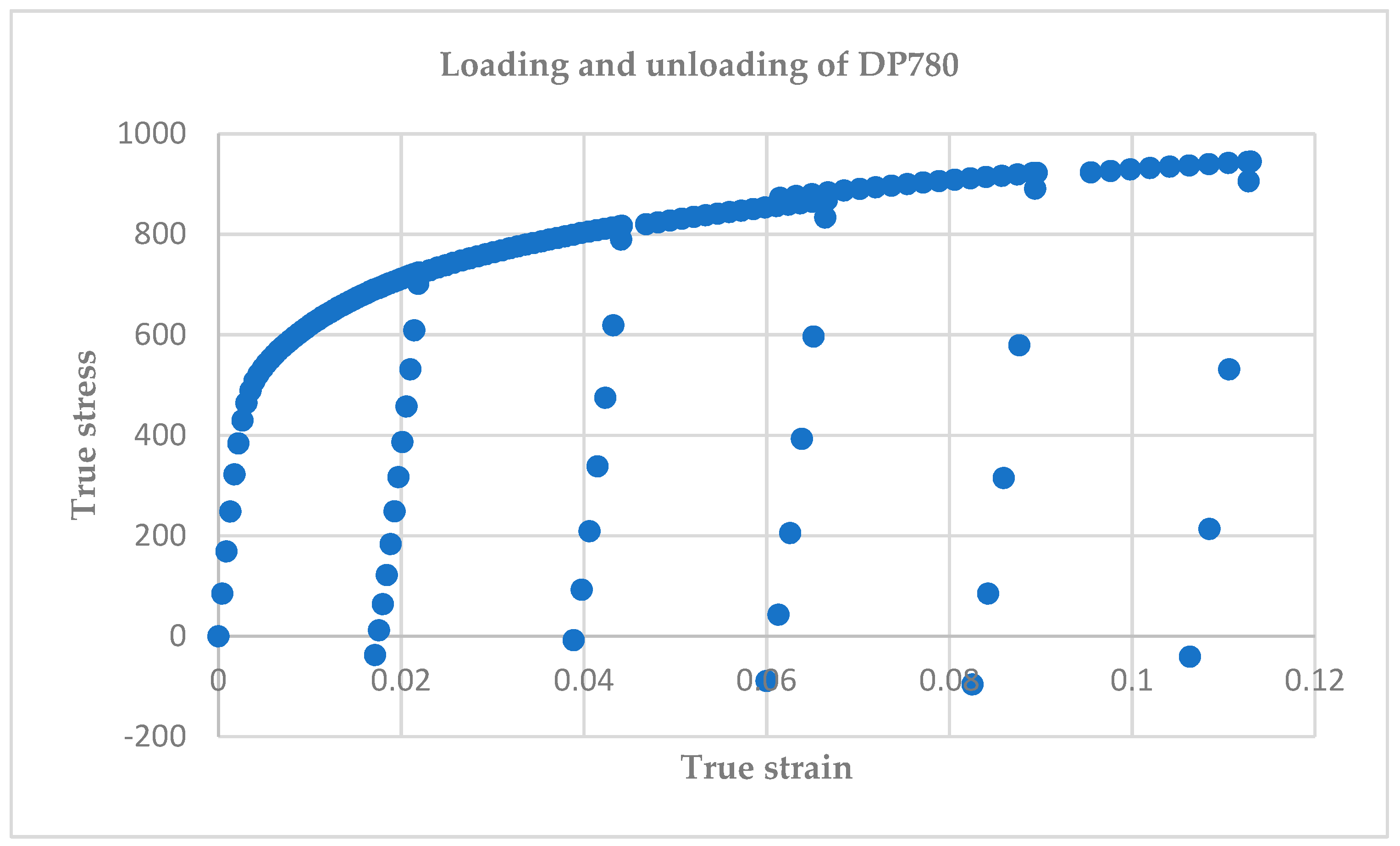
2.1. New Model Assumption and Statistical Analysis
2.2. Constitutive Models
2.3. Stress Integration
2.3.1. Elastic State Loading and Unloading
2.3.2. Elastic State Unloading and Reloading
2.3.3. Plastic State
3. Application
3.1. Description of Stress-Strain Curve of DP780 Sheet Steel
3.2. Finite Element Simulation to Evaluate New Model
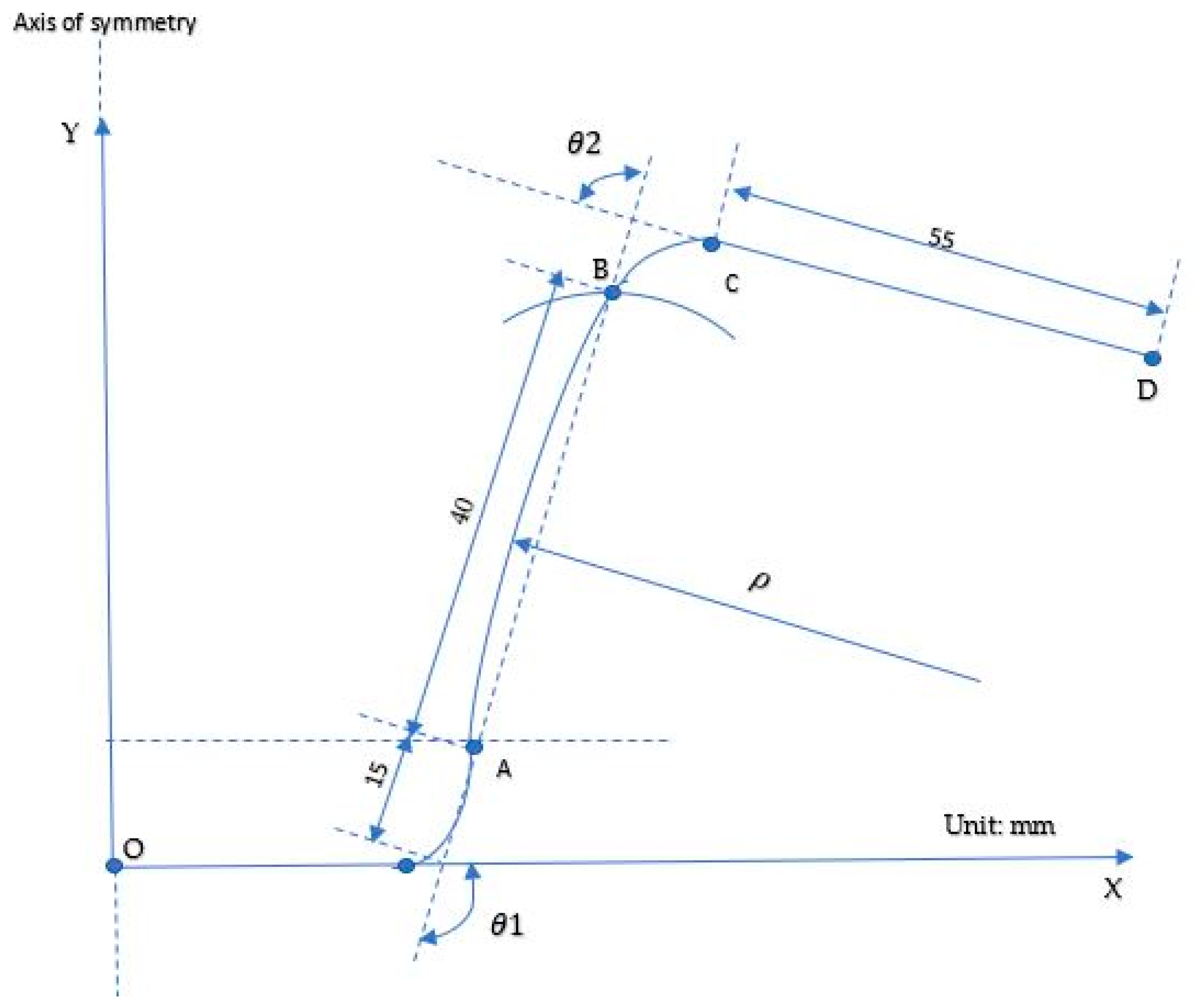
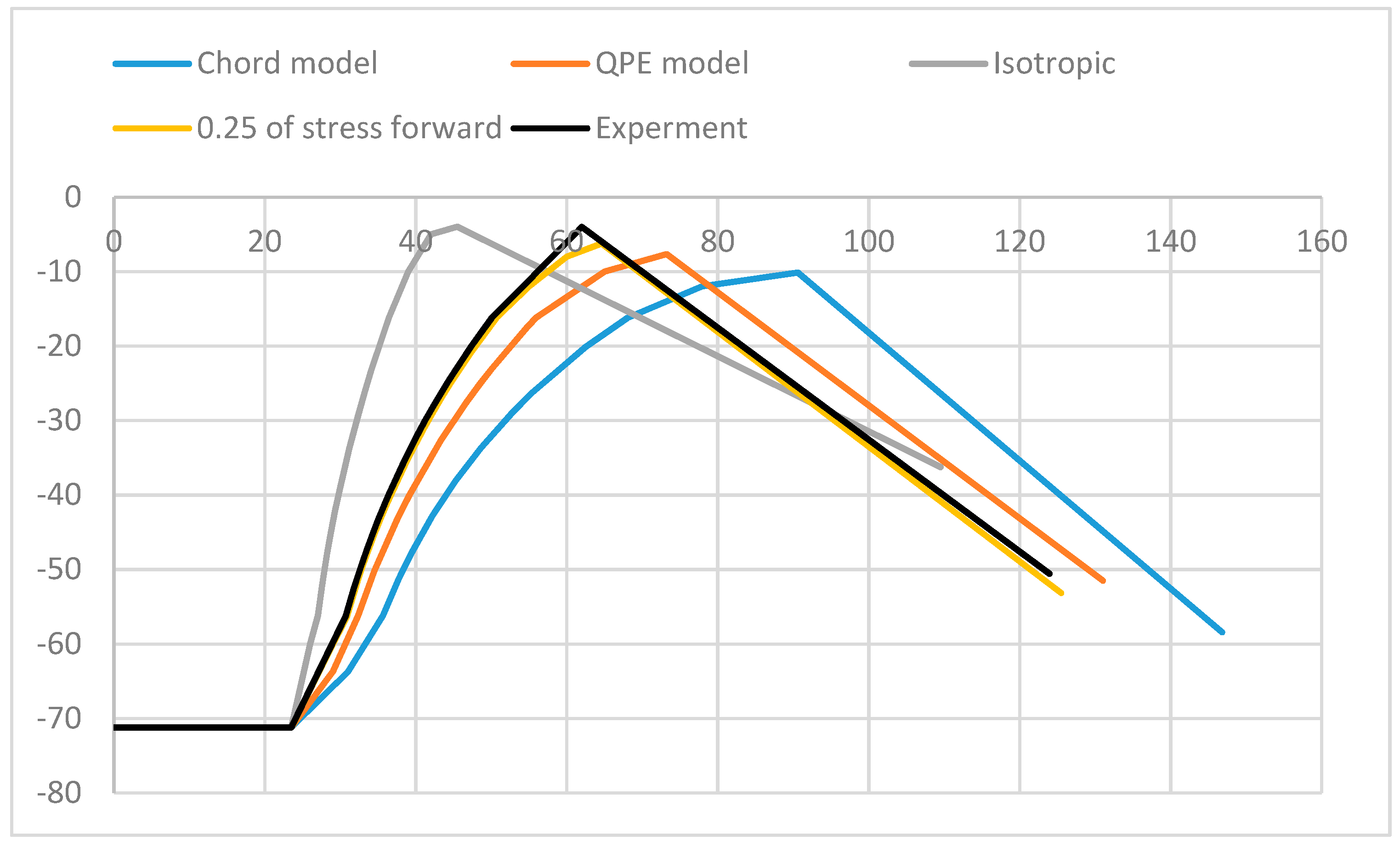
3.3. Draw-Bending Tests to Predict Springback
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Lems, W. The Change of Young’s Modulus after Deformation at Low Temperature and Its Recovery. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 1963. [Google Scholar]
- Morestin, F.; Boivin, M. On the necessity of taking into account the variation in the Young modulus with plastic strain in elastic-plastic software. Nucl. Eng. Des. 1996, 162, 107–116. [Google Scholar] [CrossRef]
- Yoshida, F.; Uemori, T.; Fujiwara, K. Elastic-plastic behavior of steel sheets under in plane cyclic tension-compression at large strain. Int. J. Plast. 2002, 18, 633–659. [Google Scholar] [CrossRef]
- Cleveland, R.M.; Ghosh, A.K. Inelastic effects on springback in metals. Int. J. Plast. 2002, 18, 769–785. [Google Scholar] [CrossRef]
- Yang, M.; Akiyama, Y.; Sasaki, T. Evaluation of change in material properties due to plastic deformation. J. Mater. Process. Technol. 2004, 151, 232–236. [Google Scholar] [CrossRef]
- Luo, L.; Ghosh, A.K. Elastic and inelastic recovery after plastic deformation of DQSK steel sheet. J. Eng. Mater. Technol. 2003, 125, 237–246. [Google Scholar] [CrossRef]
- Fei, D.; Hodgson, P. Experimental and numerical studies of springback in air v bending process for cold rolled TRIP steels. Nucl. Eng. Des. 2006, 236, 1847–1851. [Google Scholar] [CrossRef]
- Pérez, R.; Benito, J.A.; Prado, J.M. Study of the inelastic response of TRIP steels after plastic deformation. ISIJ Int. 2005, 45, 1925–1933. [Google Scholar] [CrossRef]
- Mendiguren, J.; Cortés, F.; Gómez, X.; Galdos, L. Elastic behaviour characterisation of TRIP 700 steel by means of loading–unloading tests. Mater. Sci. Eng. 2015, 634, 147–152. [Google Scholar] [CrossRef]
- Ghaei, A.; Green, D.E. Numerical implementation of Yoshida-Uemori two-surface plasticity model using a fully implicit integration scheme. Comput. Mater. Sci. 2010, 48, 195–205. [Google Scholar] [CrossRef]
- Ghaei, A.; Green, D.E.A. Taherizadeh, Semi-implicit numerical integration of Yoshida-Uemori two-surface plasticity model. Int. J. Mech. Sci. 2010, 52, 531–540. [Google Scholar] [CrossRef]
- Taherizadeh, A.; Ghaei, A.; Green, D.E.; Altenhof, W.J. Finite element simulation of springback for a channel draw process with drawbead using different hardening models. Int. J. Mech. Sci. 2009, 51, 314–325. [Google Scholar] [CrossRef]
- Ghaei, A. Numerical simulation of springback using an extended return mapping algorithm considering strain dependency of elastic modulus. Int. J. Mech. Sci. 2012, 65, 38–47. [Google Scholar] [CrossRef]
- Zang, S.L.; Lee, M.G.; Kim, J.H. Evaluating the significance of hardening behavior and unloading modulus under strain reversal in sheet springback prediction. Int. J. Mech. Sci. 2013, 77, 194–204. [Google Scholar] [CrossRef]
- Yu, H.Y. Variation of elastic modulus during plastic deformation and its influence on springback. Mater. Des. 2009, 30, 846–850. [Google Scholar] [CrossRef]
- Ghaei, A.; Green, D.E.; Thuillier, S.; Morestin, F. On the use of cyclic shear, bending and uniaxial tension–compression tests to reproduce the cyclic response of sheetmetals. Proc. Inst. Mech. Eng. 2015, 229, 453–462. [Google Scholar] [CrossRef]
- Lee, J.; Lee, J.-Y.; Barlat, F.; Wagoner, R.H.; Chung, K.; Lee, M.-G. Extension of quasi plastic–elastic approach to incorporate complex plastic flow behavior—Application to springback of advanced high-strength steels. Int. J. Plast. 2013, 45, 140–159. [Google Scholar] [CrossRef]
- Sun, L.; Wagoner, R.H. Complex unloading behavior: Nature of the deformation and its consistent constitutive representation. Int. J. Plast. 2011, 27, 1126–1144. [Google Scholar] [CrossRef]
- Chaboche, J.L. Time-Independent Constitutive Theories for Cyclic Plasticity. Int. J. Plast. 1986, 2, 149–188. [Google Scholar] [CrossRef]
- Zang, S.L.; Liang, J.; Guo, C. Constitutive model for spring-back prediction in which the change of Young’s modulus with plastic deformation is considered. Int. J. Mach. Tools Manuf. 2007, 47, 1791–1797. [Google Scholar] [CrossRef]
- Green, D.E.; Ghaei, A.; Aryanpour, A. Springback simulation of advanced high strength steels considering nonlinear elastic unloading-reloading behaviour. Mater. Des. 2015, 88, 461–470. [Google Scholar]
- Zajkani, A.; Hajbarati, H. Investigation of the variable elastic unloading modulus coupled with nonlinear kinematic hardening in springback measuring of advanced high-strength steel in U-shaped process. J. Manuf. Process. 2017, 25, 391–401. [Google Scholar] [CrossRef]
- Wagoner, R.H.; Chen, Z.; Gandhib, U.; Leec, J. Variation and consistency of Young’s modulus in steel. J. Mater. Process. Technol. 2016, 227, 227–243. [Google Scholar]



| DP780 | (MPa) | (MPa) | (MPa) | ||||
| 198,800 | 0.3 | 944 | 454 | ||||
| Chord Model | (MPa) | ||||||
| 460.7 | 39.7 | 152,100 | 96.5 | ||||
| QPE Model | (MPa) | (MPa) | (MPa) | ||||
| 431.62 | 39.7 | 96.9 | 17,135.3 | 95,000 | 254 | 39.7 | |
| Extended Model | (MPa) | ||||||
| (0.3% ) | 335.7 | 39.7 | 165,407 | 33,083 | 64.59 | 4673.86 | 39.7 |
| (0.25% ) | 350.2 | 39.7 | 163,271 | 35,291.7 | 70.5 | 3543.6 | 39.7 |
| (0.2% ) | 383.6 | 39.7 | 161,040.9 | 37,577.7 | 77.3 | 3115.9 | 39.7 |
| Parameters of Springback | Experiment | Isotropic Model | QPE | Chord Model | 20% | 25% | 30% |
|---|---|---|---|---|---|---|---|
| 115.8 | 103.25 | 119.4 | 105.26 | 120.5 | 116.3 | 111.03 | |
| 79.2 | 76.5 | 83.3 | 88.33 | 84.2 | 78.67 | 77.1 | |
| 118.2 | 190.49 | 108 | 82.65 | 105.26 | 117 | 131.89 | |
| Errors | |||||||
| 0% | 10.83% | 3.1% | 9.1% | 4% | 1.43% | 4.1% | |
| 0% | 3.4% | 5.17% | 11.48% | 6.31% | 2.7% | 3.65% | |
| 0% | 61.15% | 8.6% | 30% | 10.94% | 2.6% | 11.5% | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Baara, W.A.B.; Baharudin, B.T.H.T.b.; Anuar, M.K.; Ismail, M.I.S.b. Effect of Elastic Module Degradation Measurement in Different Sizes of the Nonlinear Isotropic–Kinematic Yield Surface on Springback Prediction. Metals 2019, 9, 511. https://doi.org/10.3390/met9050511
Baara WAB, Baharudin BTHTb, Anuar MK, Ismail MISb. Effect of Elastic Module Degradation Measurement in Different Sizes of the Nonlinear Isotropic–Kinematic Yield Surface on Springback Prediction. Metals. 2019; 9(5):511. https://doi.org/10.3390/met9050511
Chicago/Turabian StyleBaara, Wisam Ali Basher, B. T. Hang Tuah b. Baharudin, Mohd Khairol Anuar, and Mohd Idris Shah b. Ismail. 2019. "Effect of Elastic Module Degradation Measurement in Different Sizes of the Nonlinear Isotropic–Kinematic Yield Surface on Springback Prediction" Metals 9, no. 5: 511. https://doi.org/10.3390/met9050511
APA StyleBaara, W. A. B., Baharudin, B. T. H. T. b., Anuar, M. K., & Ismail, M. I. S. b. (2019). Effect of Elastic Module Degradation Measurement in Different Sizes of the Nonlinear Isotropic–Kinematic Yield Surface on Springback Prediction. Metals, 9(5), 511. https://doi.org/10.3390/met9050511





