Hot Deformation Behavior and Microstructure Evolution of a TiBw/Near α-Ti Composite with Fine Matrix Microstructure
Abstract
:1. Introduction
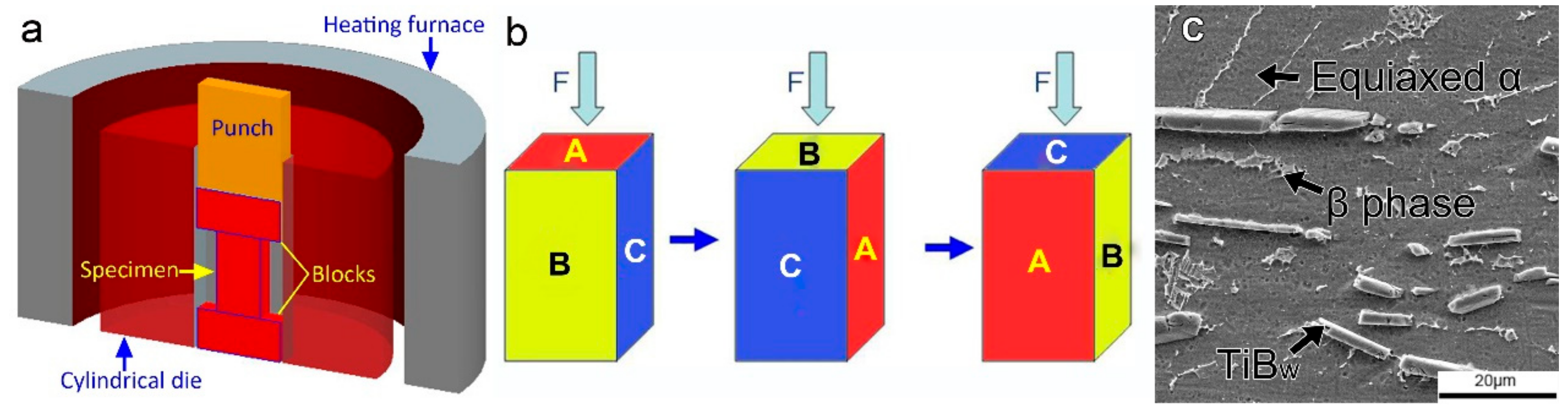
2. Experiment
3. Results and Discussion
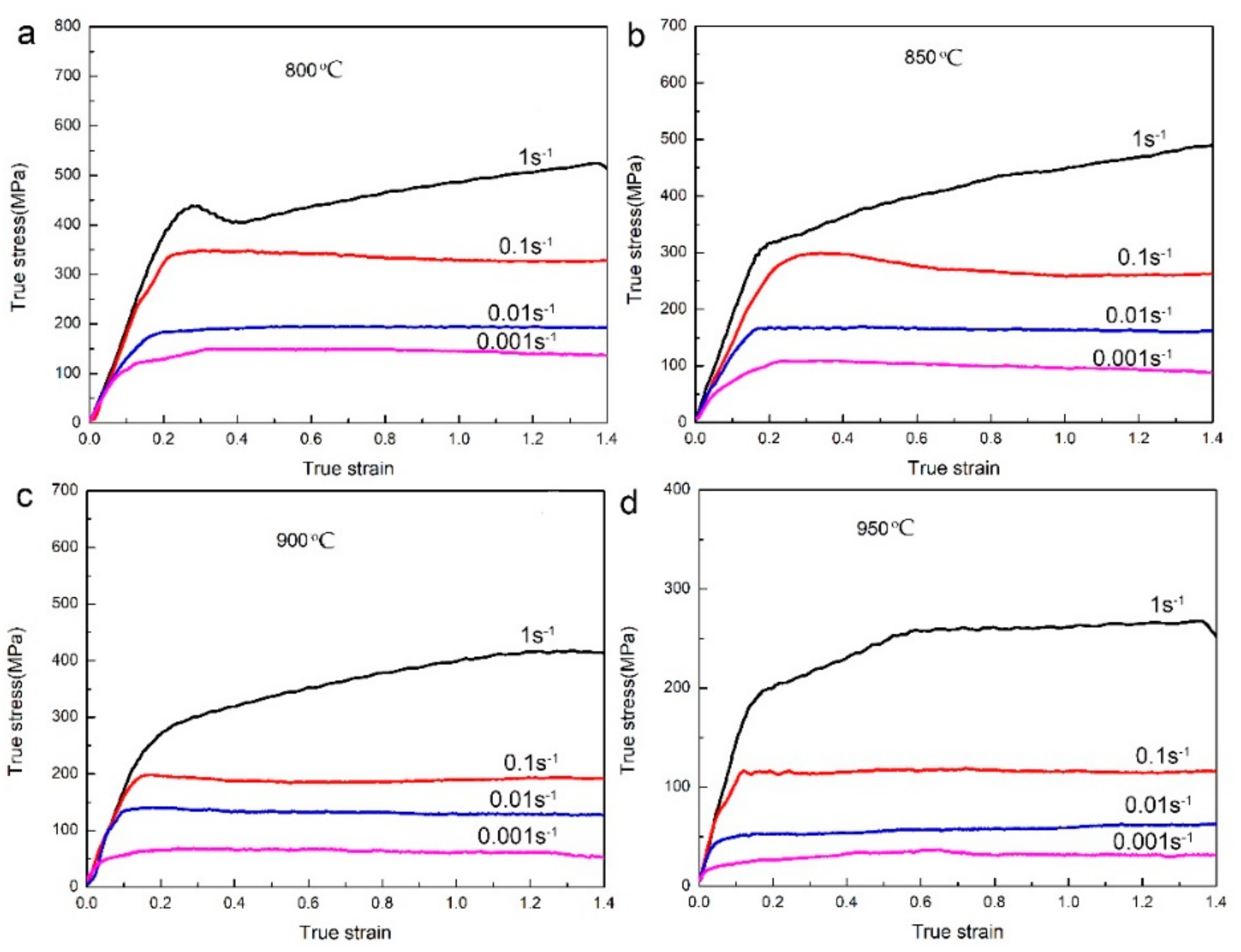
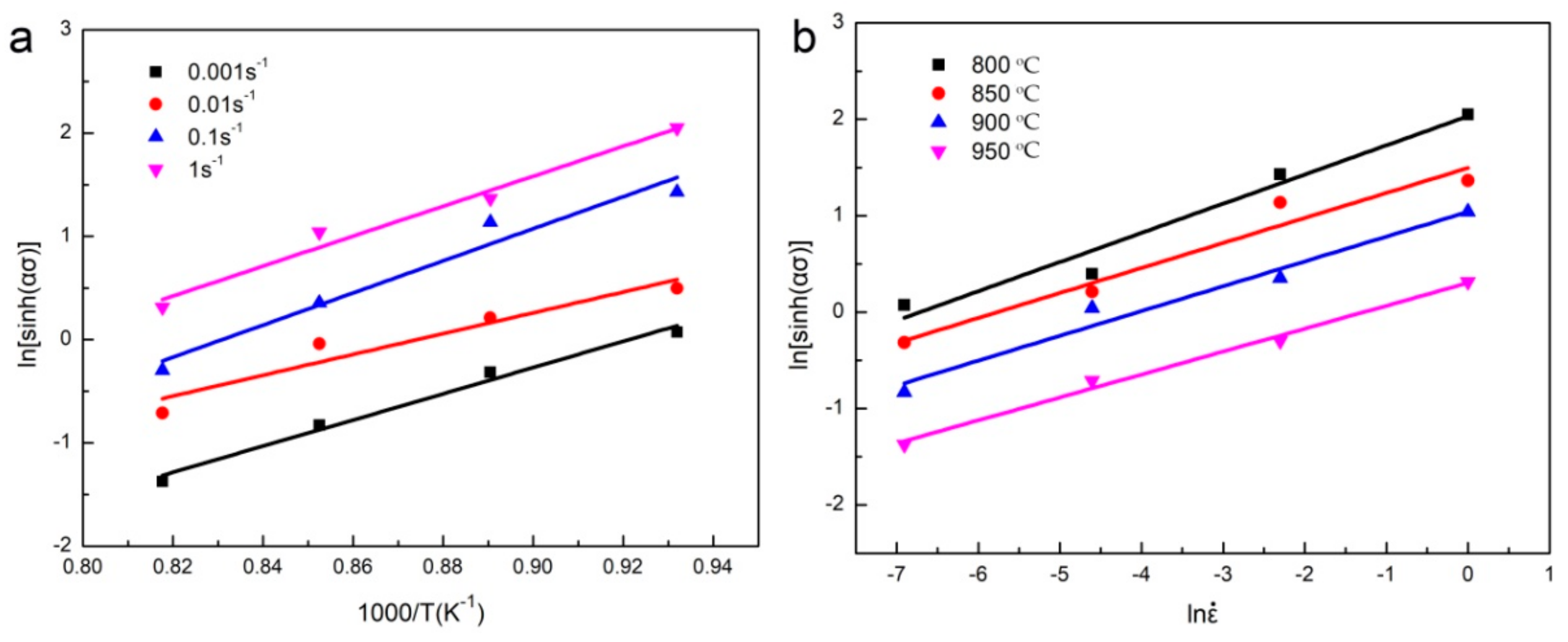
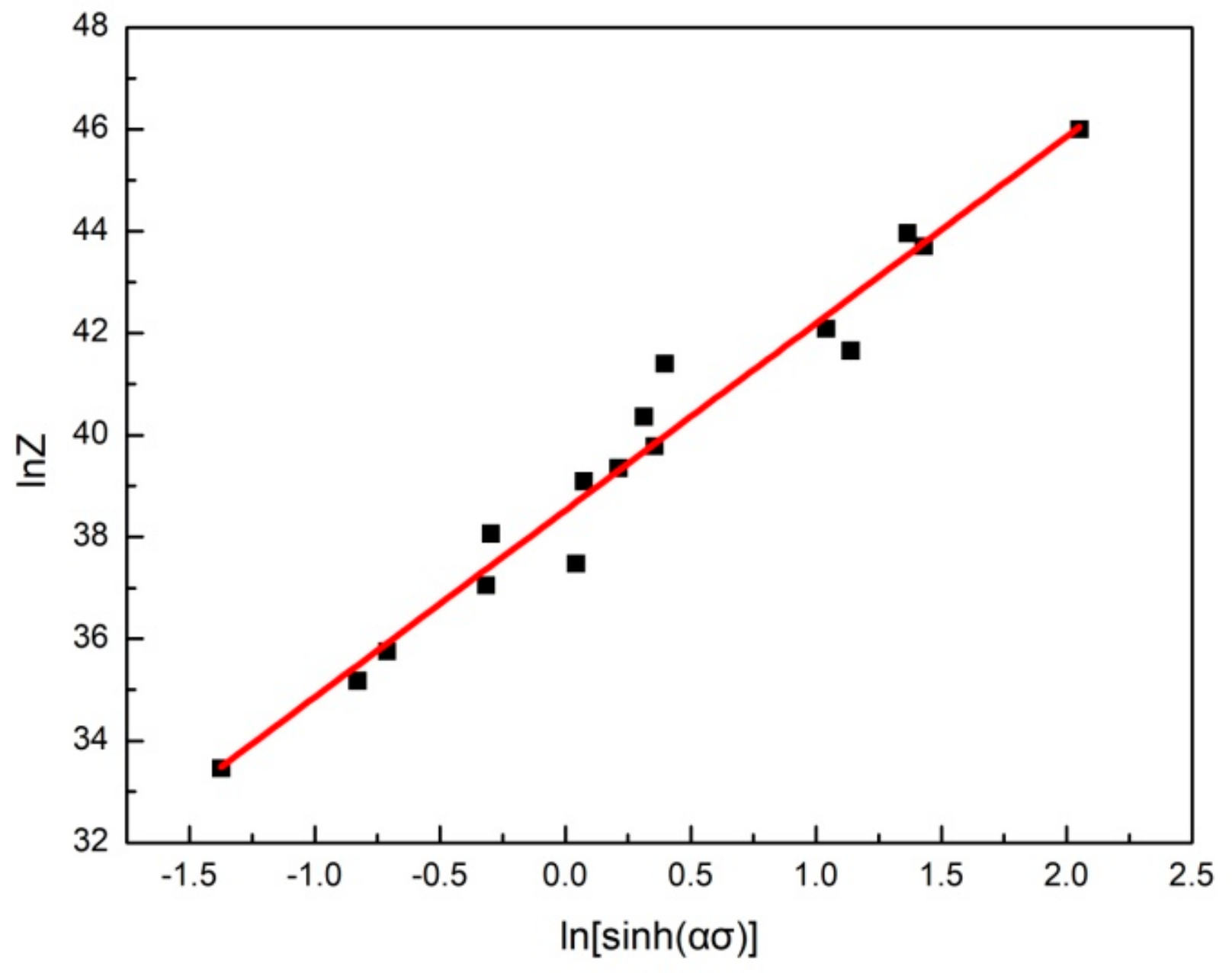
3.1. Flow Behavior and Kinetic Analysis
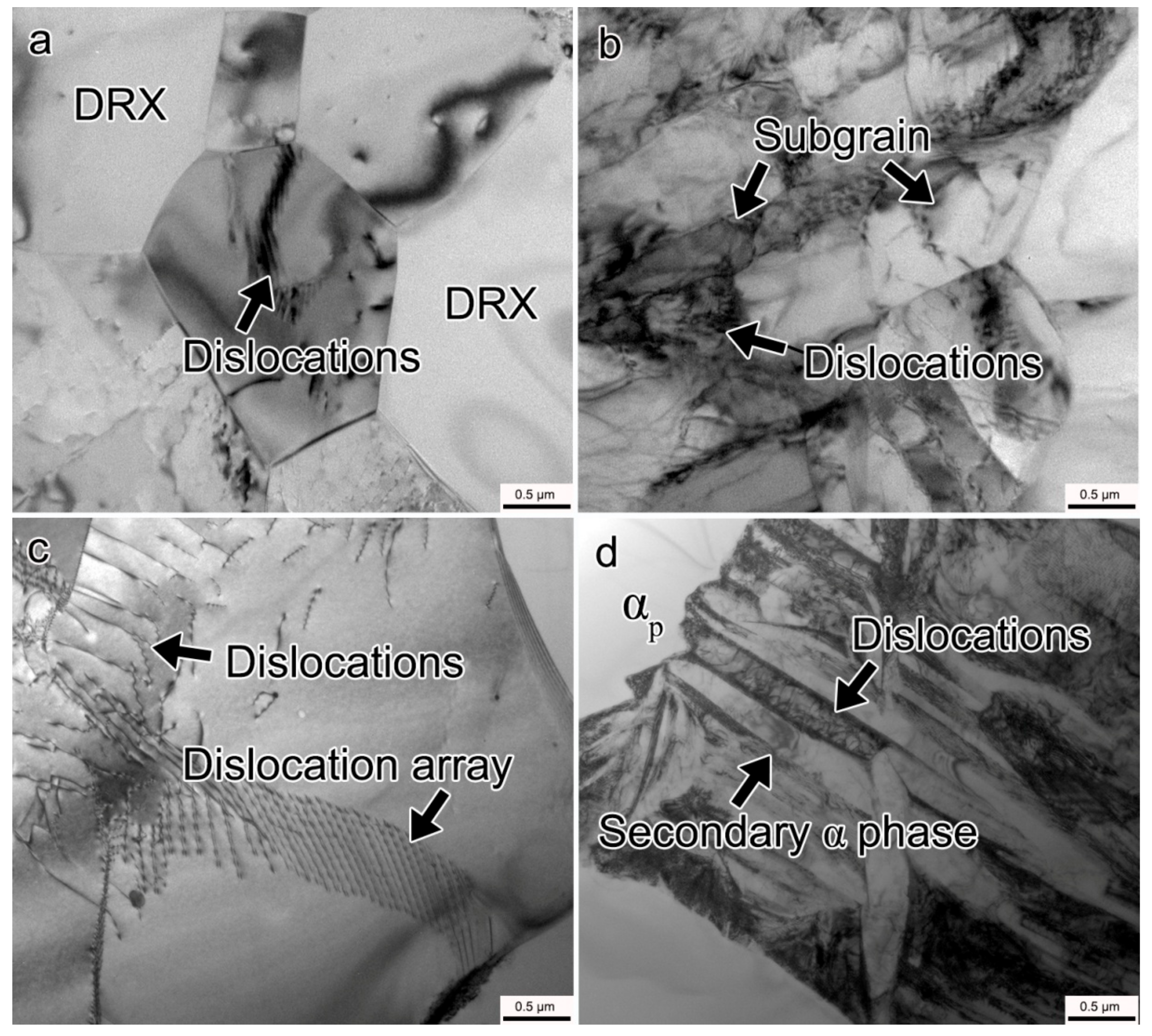
3.2. Microstructure Evolution
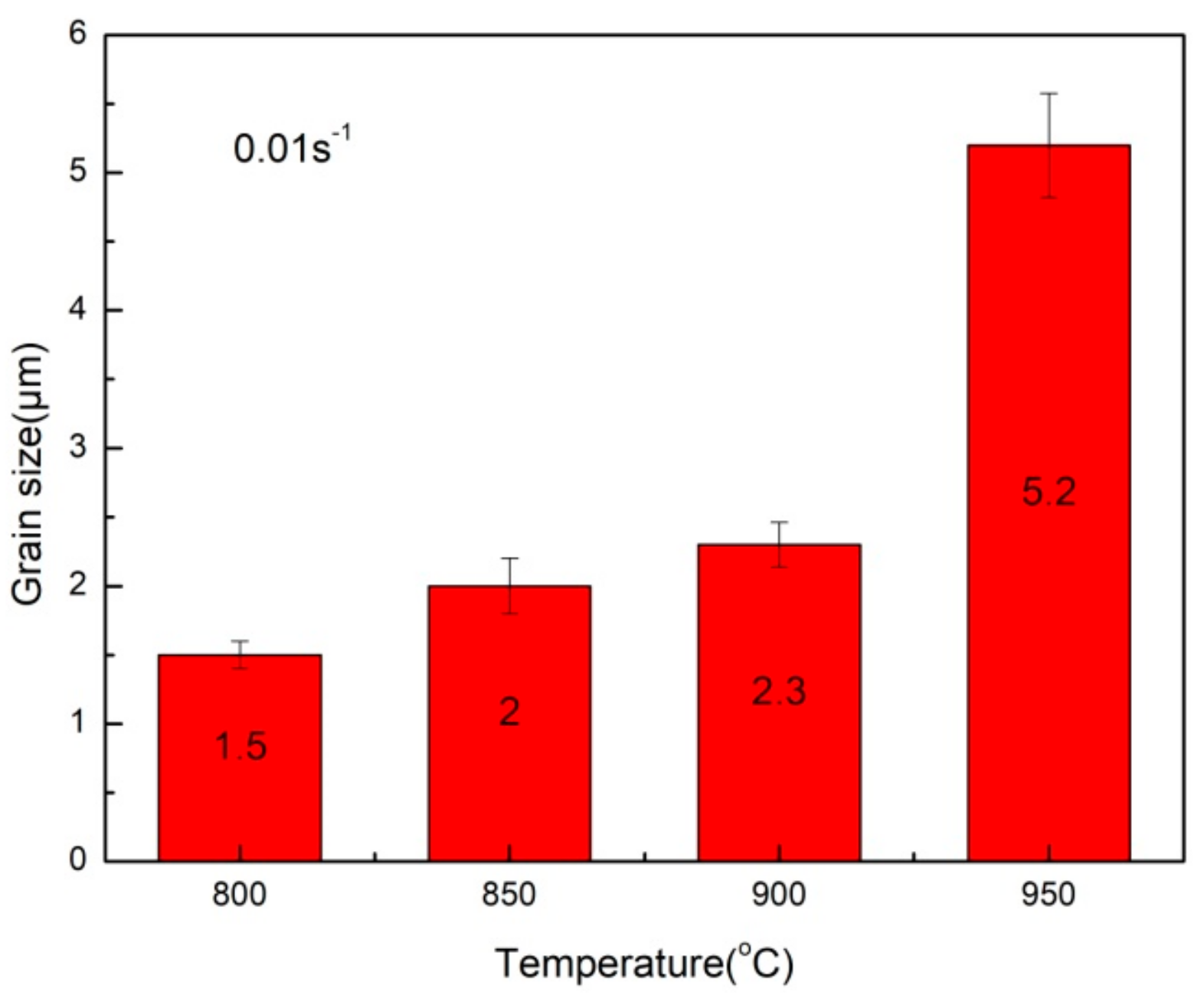
3.2.1. Effect of Deformation Temperature
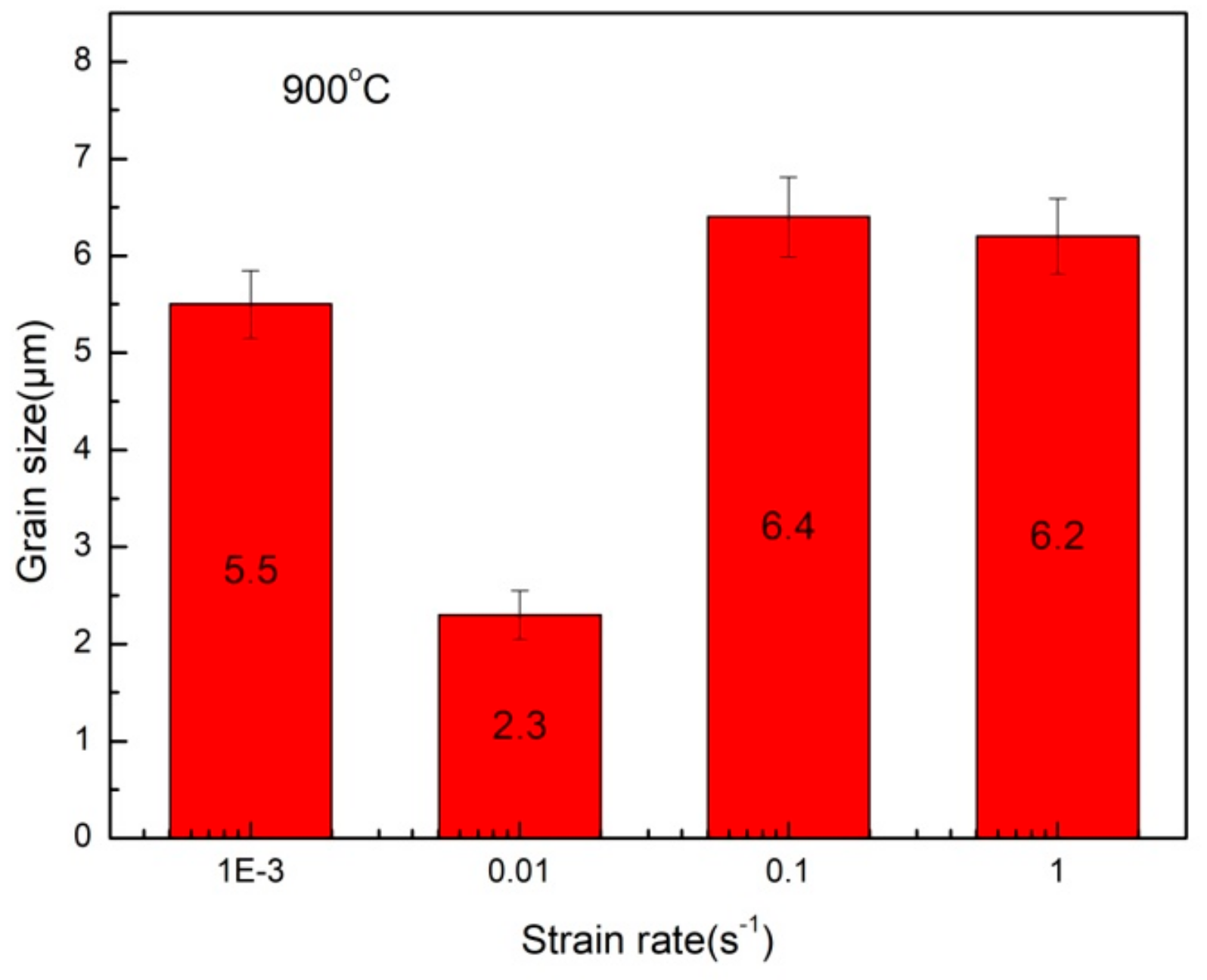
3.2.2. Effect of Strain Rate
3.3. Processing Map
4. Conclusions
- 1.
- During the plane strain compression test, the deformation temperature and strain rate have an obvious influence on the flow stress of the composite. The flow stress decreases as the temperature increases and the strain rate decreases. Flow stress curves exhibit typical work hardening characteristics at high strain rate (1 s−1), while flow steady state appears at low strain rate (<1 s−1). The flow hardening behavior is believed to be related to multiplication and pile up of dislocations at high strain rates.
- 2.
- Based on strain, strain rate and temperature, the constitutive equation of the 7.5 vol.% TiBw/near α-Ti composite was established:The deformation activation energy is 410.40 kJ/mol, which is lower than the activation energy of as-sintered and as-forged composite. The decrease of activation energy is related to the breaking of TiBw reinforcement during multi-directional forging and fine matrix microstructure which significantly improves the hot deformation ability of composite.
- 3.
- As the deformation temperature increases, the fraction of the primary α phase decreases and the dimension increases, corresponding to a decrease in flow stress. At 800–900 °C and 0.01 s−1 the matrix α grains are fine due to the occurrence of CDRX. The equiaxed α grain refine with increasing strain rate attributing to higher nucleation rate and insufficient time for grain growth. But the DRX cannot occur at high strain rates (>0.1 s−1).
- 4.
- The optimal hot processing window for 7.5 vol.% TiBw/near α-Ti composite is determined to be 800–950 °C/0.001–0.01 s−1, which is related to the CDRX of primary α grains or DRV/DRX of β phase. In addition, its instability mechanisms also include inhomogeneous deformation, voids and fracture or debonding of TiBw.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Chandran, K.S.R.; Panda, K.B.; Sahay, S.S. TiBw-reinforced Ti composites: Processing, properties, application prospects, and research needs. JOM 2004, 56, 42–48. [Google Scholar] [CrossRef]
- Guo, X.; Wang, L.; Wang, M.; Qin, J.; Zhang, D.; Lu, W. Effects of degree of deformation on the microstructure, mechanical properties and texture of hybrid-reinforced titanium matrix composites. Acta Mater. 2012, 60, 2656–2667. [Google Scholar] [CrossRef]
- Huang, L.J.; Geng, L.; Peng, H.X. Microstructurally inhomogeneous composites: Is a homogeneous reinforcement distribution optimal? Prog. Mater. Sci. 2015, 71, 93–168. [Google Scholar] [CrossRef]
- Huang, L.J.; Geng, L.; Li, A.B.; Yang, F.Y.; Peng, H.X. In situ TiBw/Ti–6Al–4V composites with novel reinforcement architecture fabricated by reaction hot pressing. Scr. Mater. 2009, 60, 996–999. [Google Scholar] [CrossRef]
- Ma, Z.Y.; Tjong, S.C.; Gen, L. In-situ Ti-TiB metal-matrix composite prepared by a reactive pressing process. Scr. Mater. 2000, 42, 367–373. [Google Scholar] [CrossRef]
- Madsen, A.; Ghonem, H. Effects of aging on the tensile and fatigue behavior of the near-α Ti-1100 at room temperature and 593 °C. Mater. Sci. Eng. A 1994, 177, 63–73. [Google Scholar] [CrossRef]
- Zhang, W.J.; Song, X.Y.; Hui, S.X.; Ye, W.J.; Wang, Y.L.; Wang, W.Q. Tensile behavior at 700 °C in Ti-Al-Sn-Zr-Mo-Nb-W-Si alloy with a bi-modal microstructure. Mater. Sci. Eng. A 2014, 595, 159–164. [Google Scholar] [CrossRef]
- Wang, T.; Guo, H.Z.; Wang, Y.W.; Peng, X.N.; Zhao, Y.; Yao, Z.K. The effect of microstructure on tensile properties, deformation mechanisms and fracture models of TG6 high temperature titanium alloy. Mater. Sci. Eng. A 2011, 528, 2370–2379. [Google Scholar] [CrossRef]
- Guo, C.; Zhang, C.; Han, J.; Zhang, S.; Fei, Y.; Chai, L.; Chen, Z. Effect of trace B on the microstructure and mechanical properties of a newly near α high temperature titanium alloy. Adv. Eng. Mater. 2017, 19, 1700490. [Google Scholar] [CrossRef]
- Tjong, S.C.; Mai, Y.W. Processing-structure-property aspects of particulate and whisker-reinforced titanium matrix composites. Compos. Sci. Technol. 2008, 68, 583–601. [Google Scholar] [CrossRef]
- Wanjara, P.; Jahazi, M.; Monajati, H.; Yue, S.; Immarigeon, J.-P. Hot working behavior of near-α alloy IMI834. Mater. Sci. Eng. A 2005, 396, 50–60. [Google Scholar] [CrossRef]
- Sun, X.; Li, H.; Han, Y.; Li, J.; Mao, J.; Lu, W. Compressive response and microstructural evolution of bimodal sized particulates reinforced (TiB + La2O3)/Ti composites. J. Alloys Compd. 2018, 732, 524–535. [Google Scholar] [CrossRef]
- Ma, F.; Shi, Z.; Ping, L.; Wei, L.; Liu, X.; Chen, X.; He, D.; Ke, Z.; Deng, P.; Di, Z. Strengthening effect of in situ TiC particles in Ti matrix composite at temperature range for hot working. Mater. Charact. 2016, 120, 304–310. [Google Scholar] [CrossRef]
- Ji, Z.; Shen, C.; Wei, F.; Li, H. Dependence of macro- and micro-properties on α plates in Ti-6Al-2Zr-1Mo-1V alloy with tri-modal microstructure. Metals 2018, 8, 299. [Google Scholar] [CrossRef]
- Cojocaru, V.; Șerban, N. Effects of solution treating on microstructural and mechanical properties of a heavily deformed new biocompatible Ti–Nb–Zr–Fe alloy. Metals 2018, 8, 297. [Google Scholar] [CrossRef]
- Prasad, Y.V.R.K.; Seshacharyulu, T.; Medeiros, S.C.; Frazier, W.G. Effect of preform microstructure on the hot working mechanisms in ELI grade Ti–6Al–4V: Transformed β v. equiaxed (α + β). Mater. Sci. Technol. 2010, 16, 511–516. [Google Scholar] [CrossRef]
- Zhao, Z.L.; Li, H.; Fu, M.W.; Guo, H.Z.; Yao, Z.K. Effect of the initial microstructure on the deformation behavior of Ti60 titanium alloy at high temperature processing. J. Alloys Compd. 2014, 617, 525–533. [Google Scholar] [CrossRef]
- Li, H.; Zhao, Z.; Guo, H.; Yao, Z.; Ning, Y.; Miao, X.; Ge, M. Effect of initial alpha lamellar thickness on deformation behavior of a near-α high-temperature alloy during thermomechanical processing. Mater. Sci. Eng. A 2016, 682, 345–353. [Google Scholar] [CrossRef]
- Zhang, Z.X.; Qu, S.J.; Feng, A.H.; Shen, J.; Chen, D.L. Hot deformation behavior of Ti-6Al-4V alloy: Effect of initial microstructure. J. Alloys Compd. 2017, 718, 170–181. [Google Scholar] [CrossRef]
- Zhang, C.J.; Xiang, L.; Zhang, S.Z.; Chai, L.; Chen, Z.; Kong, F.T.; Chen, Y.Y. Effects of direct rolling deformation on the microstructure and tensile properties of the 2.5 vol.% (TiBw + TiCp)/Ti composites. Mater. Sci. Eng. A 2017, 684, 645–651. [Google Scholar] [CrossRef]
- Zhang, C.J.; Qu, J.P.; Wu, J.; Zhang, S.Z.; Han, J.C.; Hayat, M.D.; Cao, P. A titanium composite with dual reinforcements of micrometer sized TiB and submicrometer sized Y2O3. Mater. Lett. 2018, 233, 242–245. [Google Scholar] [CrossRef]
- Wang, B.; Huang, L.J.; Geng, L.; Rong, X.D. Compressive behaviors and mechanisms of TiB whiskers reinforced high temperature Ti60 alloy matrix composites. Mater. Sci. Eng. A 2015, 648, 443–451. [Google Scholar] [CrossRef]
- Peng, L.; He, Z.; Yuan, S.; Shen, J. Tensile deformation behavior of Ti–22Al–25Nb alloy at elevated temperatures. Mater. Sci. Eng. A 2012, 556, 617–624. [Google Scholar]
- Han, J.; Lü, Z.; Zhang, C.; Zhang, S.; Zhang, H.; Lin, P.; Cao, P. The microstructural characterization and mechanical properties of 5 vol. % (TiBw + TiCp)/Ti composite produced by open-die forging. Metals 2018, 8, 485. [Google Scholar] [CrossRef]
- Cheng, L.; Xue, X.; Tang, B.; Liu, D.; Li, J.; Kou, H.; Li, J. Deformation behavior of hot-rolled IN718 superalloy under plane strain compression at elevated temperature. Mater. Sci. Eng. A 2014, 606, 24–30. [Google Scholar] [CrossRef]
- Jonas, J.J.; Sellars, C.M.; Tegart, W.J.M. Strength and structure under hot-working conditions. Metall. Rev. 1969, 14, 1–24. [Google Scholar]
- Quan, G.Z.; Wu, D.S.; Luo, G.C.; Xia, Y.F.; Jie, Z.; Liu, Q.; Lin, G. Dynamic recrystallization kinetics in α phase of as-cast Ti–6Al–2Zr–1Mo–1V alloy during compression at different temperatures and strain rates. Mater. Sci. Eng. A 2014, 589, 23–33. [Google Scholar] [CrossRef]
- Huang, G.; Han, Y.; Guo, X.; Di, Q.; Wang, L.; Lu, W.; Di, Z. Effects of extrusion ratio on microstructural evolution and mechanical behavior of in situ synthesized Ti–6Al–4V composites. Mater. Sci. Eng. A 2017, 688, 155–163. [Google Scholar] [CrossRef]
- Zherebtsov, S.; Murzinova, M.; Salishchev, G.; Semiatin, S.L. Spheroidization of the lamellar microstructure in Ti–6Al–4V alloy during warm deformation and annealing. Acta Mater. 2011, 59, 4138–4150. [Google Scholar] [CrossRef]
- Weiss, I.; Froes, F.H.; Eylon, D.; Welsch, G.E. Modification of alpha morphology in Ti–6Al–4V by thermomechanical processing. Metall. Trans. A 1986, 17, 1935–1947. [Google Scholar] [CrossRef]
- Zhang, R.; Wang, D.; Huang, L.; Yuan, S.; Geng, L. Deformation behaviors and microstructure evolution of TiBw/TA15 composite with novel network architecture. J. Alloys Compd. 2017, 722, 970–980. [Google Scholar] [CrossRef]
- Roy, S.; Suwas, S. The influence of temperature and strain rate on the deformation response and microstructural evolution during hot compression of a titanium alloy Ti–6Al–4V–0.1B. J. Alloys Compd. 2013, 548, 110–125. [Google Scholar] [CrossRef]
- Zhao, J.W.; Ding, H.; Hou, H.L.; Li, Z.Q. Influence of hydrogen content on hot deformation behavior and microstructural evolution of Ti600 alloy. J. Alloys Compd. 2010, 491, 673–678. [Google Scholar] [CrossRef]
- Wang, K.; Li, M.; Liu, Q. Evolution mechanisms of the primary α and β phases during α/β deformation of an α/β titanium alloy TC8. Mater. Charact. 2016, 120, 115–123. [Google Scholar] [CrossRef]
- Wang, X.; Jahazi, M.; Yue, S. Substructure of high temperature compressed titanium alloy IMI834. Mater. Sci. Eng. A 2006, 434, 188–193. [Google Scholar] [CrossRef]
- Prasad, Y.V.R.K.; Gegel, H.L.; Doraivelu, S.M.; Malas, J.C.; Morgan, J.T.; Lark, K.A.; Barker, D.R. Modeling of dynamic material behavior in hot deformation: Forging of Ti-6242. Metall. Trans. A 1984, 15, 1883–1892. [Google Scholar] [CrossRef]
- Kupradze, B.V.D. Dynamical problems in elasticity. In Progress in Solid Mechanics; North-Holland Publishing Company: Amsterdam, The Netherlands, 1963. [Google Scholar]
- Murty, S.V.S.N.; Rao, B.N.; Kashyap, B.P. Development and validation of a processing map for zirconium alloys. Model. Simul. Mater. Sci. Eng. 2002, 10, 503. [Google Scholar] [CrossRef]
- Sun, Y.; Zeng, W.D.; Zhao, Y.Q.; Zhang, X.M.; Shu, Y.; Zhou, Y.G. Research on the hot deformation behavior of Ti40 alloy using processing map. Mater. Sci. Eng. A 2011, 528, 1205–1211. [Google Scholar] [CrossRef]



© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, C.; Lian, Y.; Chen, Y.; Sun, Y.; Zhang, S.; Feng, H.; Zhou, Y.; Cao, P. Hot Deformation Behavior and Microstructure Evolution of a TiBw/Near α-Ti Composite with Fine Matrix Microstructure. Metals 2019, 9, 481. https://doi.org/10.3390/met9040481
Zhang C, Lian Y, Chen Y, Sun Y, Zhang S, Feng H, Zhou Y, Cao P. Hot Deformation Behavior and Microstructure Evolution of a TiBw/Near α-Ti Composite with Fine Matrix Microstructure. Metals. 2019; 9(4):481. https://doi.org/10.3390/met9040481
Chicago/Turabian StyleZhang, Changjiang, Yuzhou Lian, Yanfei Chen, Yonggang Sun, Shuzhi Zhang, Hong Feng, Yawei Zhou, and Peng Cao. 2019. "Hot Deformation Behavior and Microstructure Evolution of a TiBw/Near α-Ti Composite with Fine Matrix Microstructure" Metals 9, no. 4: 481. https://doi.org/10.3390/met9040481
APA StyleZhang, C., Lian, Y., Chen, Y., Sun, Y., Zhang, S., Feng, H., Zhou, Y., & Cao, P. (2019). Hot Deformation Behavior and Microstructure Evolution of a TiBw/Near α-Ti Composite with Fine Matrix Microstructure. Metals, 9(4), 481. https://doi.org/10.3390/met9040481






