Influence of Intergranular Mechanical Interactions on Orientation Stabilities during Rolling of Pure Aluminum
Abstract
:1. Introduction
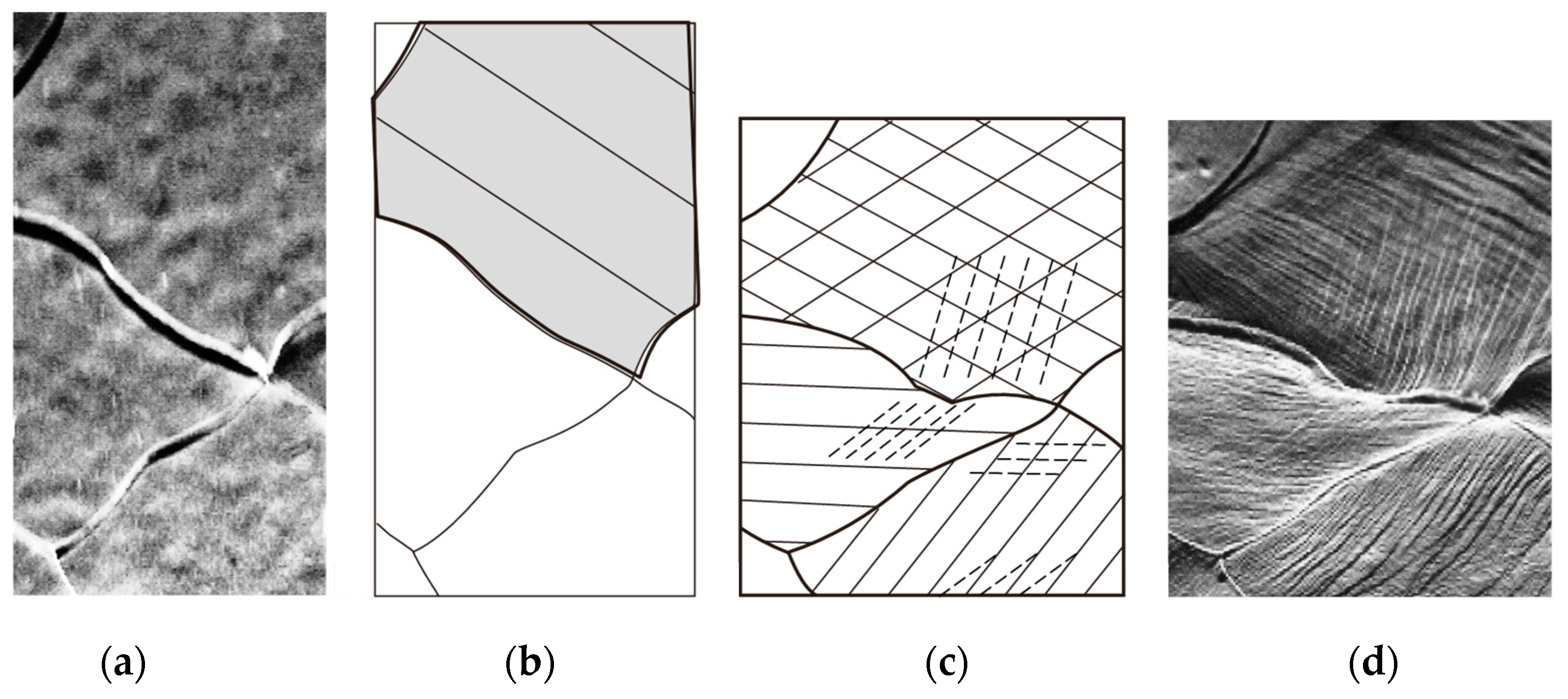
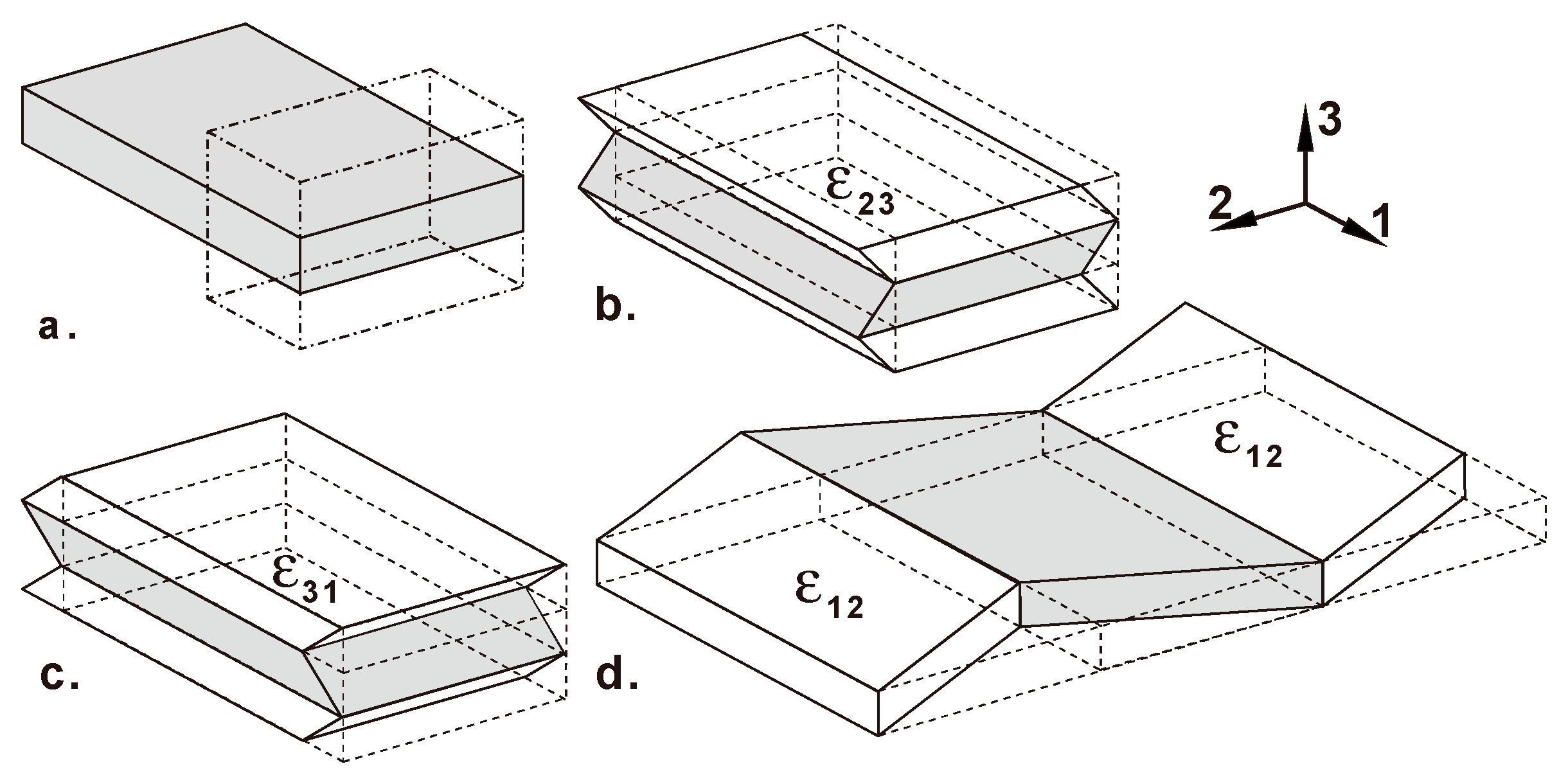
2. Intergranular Mechanical Interactions
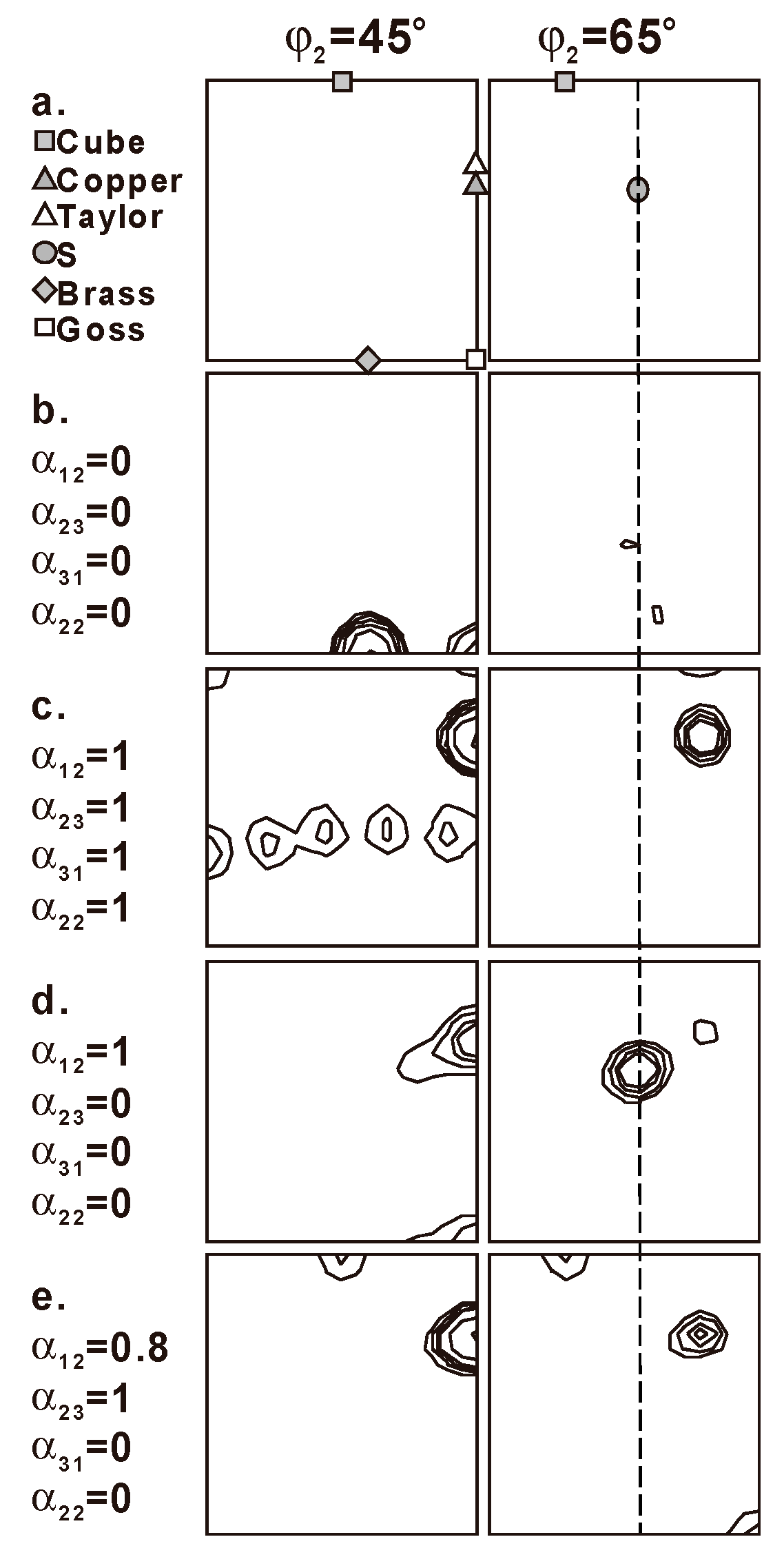
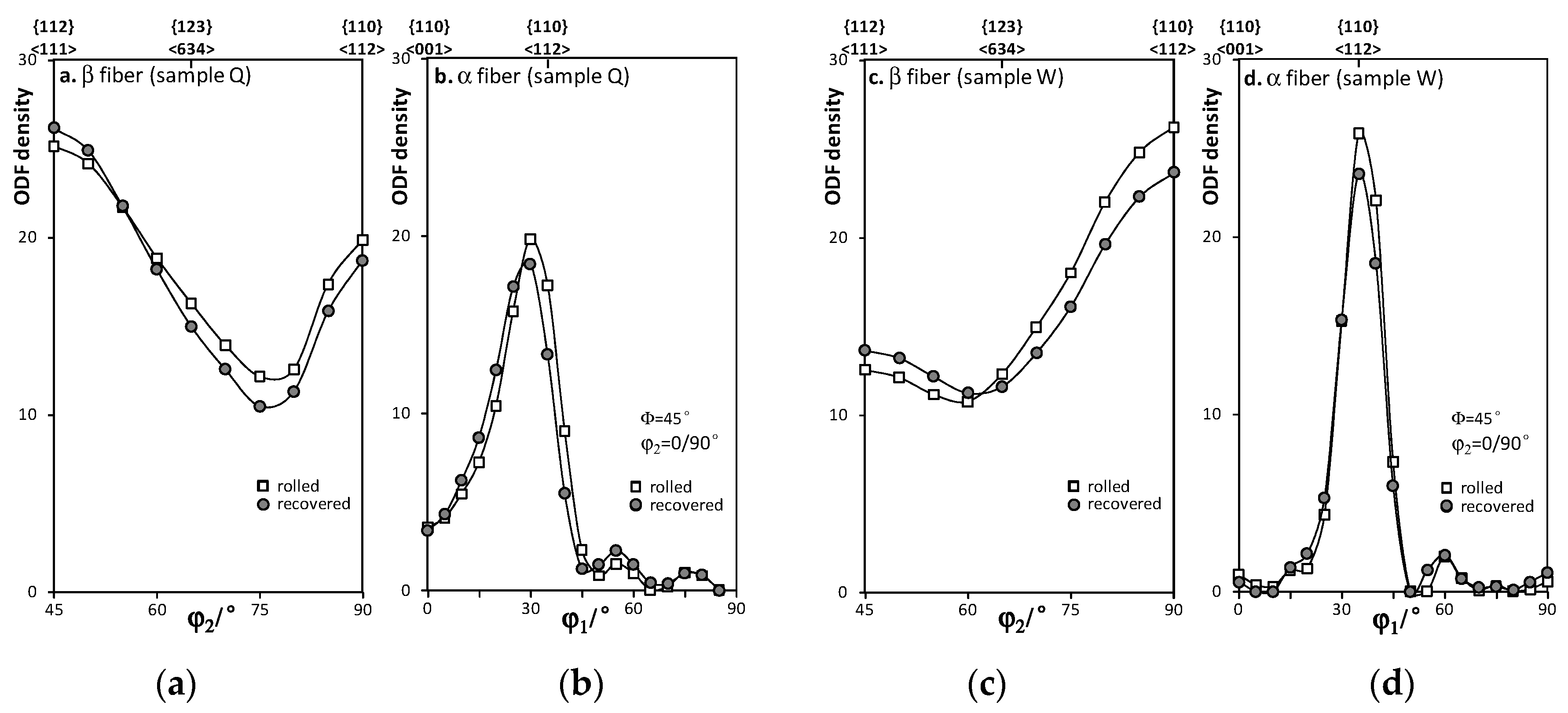
3. Orientation Stabilities during Rolling of Pure Aluminum
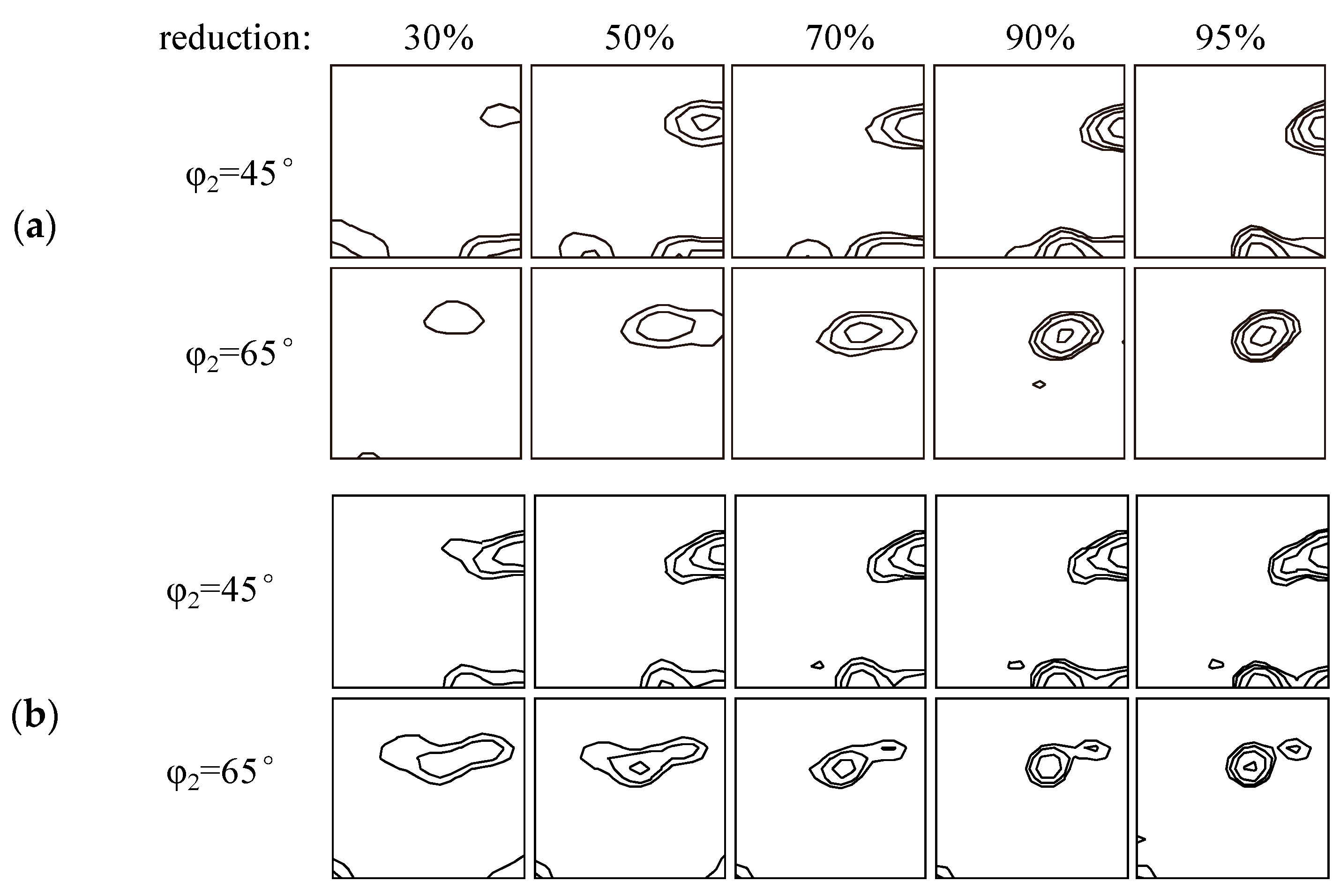
4. Simulation of Normal Rolling Texture in Pure Aluminum
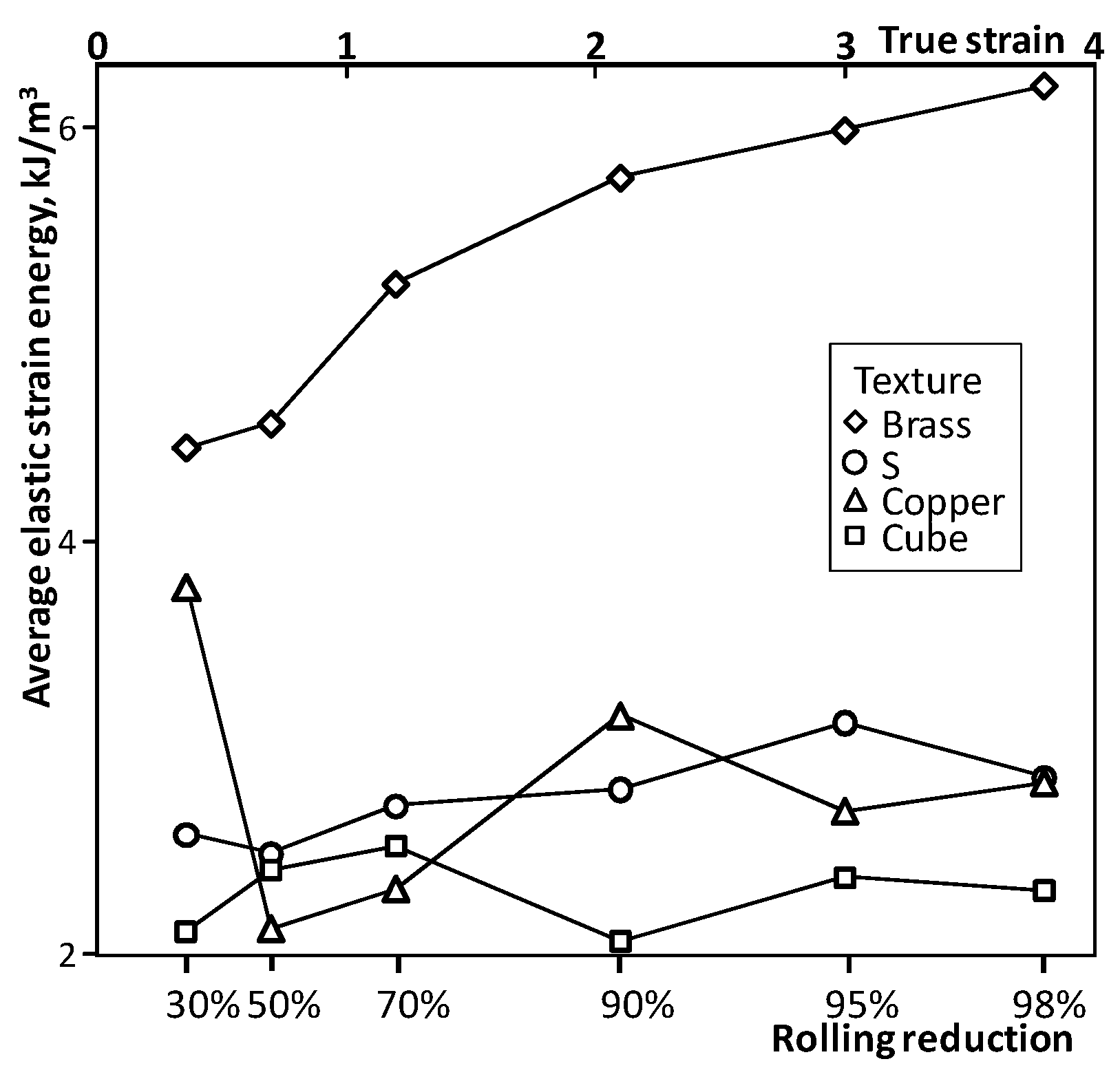
5. Orientation Dependency of Elastic Strain Energy after Rolling
6. Summary
Funding
Conflicts of Interest
References
- Taylor, G.I. Plastic strain in metals. J. Inst. Met. 1938, 62, 307–324. [Google Scholar]
- Lebensohn, R.A.; Tomé, C.N.; Castaňeda, P.P. Self-consistent modelling of the mechanical behaviour of viscoplastic polycrystals incorporating intragranular field fluctuations. Philoso. Mag. 2007, 87, 4287–4322. [Google Scholar] [CrossRef]
- Van Houtte, P.; Li, S.; Seefeldt, M.; Delannay, L. Deformation texture prediction: From the Taylor model to the advanced lamel model. Int. J. Plast. 2005, 21, 589–624. [Google Scholar] [CrossRef]
- Mu, S.; Tang, F.; Gottstein, G. A cluster-type grain interaction deformation texture model accounting for twinning-induced texture and strain-hardening evolution: Application to magnesium alloys. Acta Mater. 2014, 68, 310–324. [Google Scholar] [CrossRef]
- Mao, W. On the Taylor principles for plastic deformation of polycrystalline metals. Front. Mater. Sci. 2016, 10, 335–345. [Google Scholar] [CrossRef]
- Chapuis, A.; Liu, Q. Investigating the temperature dependency of plastic deformation in a Mg-3Al-1Zn alloy. Mater. Sci. Eng. A 2018, 725, 108–118. [Google Scholar] [CrossRef]
- Wronski, M.; Kumar, M.A.; Capolungo, L.; McCabe, R.J.; Wierzbanowski, K.; Tomé, C.N. Deformation behavior of CP-titanium: Experiment and crystal plasticity modeling. Mater. Sci. Eng. A 2018, 724, 289–297. [Google Scholar] [CrossRef]
- Chatterjeea, A.; Ghosh, A.; Moitra, A.; Bhaduri, A.K.; Mitra, R.; Chakrabarti, D. Role of hierarchical martensitic microstructure on localized deformation and fracture of 9Cr-1Mo steel under impact loading at different temperatures. Int. J. Plast. 2018, 104, 104–133. [Google Scholar] [CrossRef]
- Chelladurai, I.; Adams, D.; Fullwood, D.T.; Miles, M.P.; Niezgoda, S.; Beyerlein, I.J.; Knezevice, M. Modeling of trans-grain twin transmission in AZ31 via a neighborhood-based viscoplastic self-consistent model. Int. J. Plast. 2018, in press. [Google Scholar] [CrossRef]
- Zecevic, M.; Lebensohn, R.A.; McCabe, R.J.; Knezevic, M. Modeling of intragranular misorientation and grain fragmentation in polycrystalline materials using the viscoplastic self-consistent formulation. Int. J. Plast. 2018, 109, 193–211. [Google Scholar] [CrossRef]
- Mao, W. The currently predominant Taylor principles should be disregarded in the study of plastic deformation of metals. Front. Mater. Sci. 2018, 12, 322–326. [Google Scholar] [CrossRef]
- Mao, W.; Yu, Y. Effect of elastic reaction stress on plastic behaviors of grains in polycrystalline aggregate during tensile deformation. Mater. Sci. Eng. A 2004, 367, 277–281. [Google Scholar] [CrossRef]
- Mao, W. Intergranular mechanical equilibrium during the rolling deformation of polycrystalline metals based on Taylor principles. Mater. Sci. Eng. A 2016, 672, 129–134. [Google Scholar] [CrossRef]
- Hornbogen, E.; Warlimont, H. Metallkunde, 2nd ed.; Springer: New York, NY, USA, 1991; pp. 100–105. [Google Scholar]
- Sachs, G. Zur Ableitung einer Fließbedingdung. Zeitschrift des Vereines deutscher Ingeniere 1928, 72, 732–736. [Google Scholar]
- Mao, W. Rolling texture development in aluminum. Chin. J. Met. Sci. Tech. 1991, 7, 101–112. [Google Scholar]
- Mao, W. Modeling of rolling texture in aluminum. Mater. Sci. Eng. A 1998, 257, 171–177. [Google Scholar] [CrossRef]
- Hirsch, J.; Lücke, K. Mechanism of deformation and development of rolling texture in polycrystalline fcc metals-II. Acta Metall. 1998, 36, 2883–2904. [Google Scholar] [CrossRef]
- Mao, W.; Yang, P. Formation mechanisms of recrystallization textures in aluminum sheets based on theories of oriented nucleation and oriented growth. Trans. Nonferrous Met. Soc. China 2014, 24, 1635–1644. [Google Scholar] [CrossRef]
- Mao, W. Formation of recrystallization cube texture in high purity FCC metal sheets. J. Mater. Eng. Perf. 1999, 8, 556–560. [Google Scholar] [CrossRef]
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mao, W. Influence of Intergranular Mechanical Interactions on Orientation Stabilities during Rolling of Pure Aluminum. Metals 2019, 9, 477. https://doi.org/10.3390/met9040477
Mao W. Influence of Intergranular Mechanical Interactions on Orientation Stabilities during Rolling of Pure Aluminum. Metals. 2019; 9(4):477. https://doi.org/10.3390/met9040477
Chicago/Turabian StyleMao, Weimin. 2019. "Influence of Intergranular Mechanical Interactions on Orientation Stabilities during Rolling of Pure Aluminum" Metals 9, no. 4: 477. https://doi.org/10.3390/met9040477
APA StyleMao, W. (2019). Influence of Intergranular Mechanical Interactions on Orientation Stabilities during Rolling of Pure Aluminum. Metals, 9(4), 477. https://doi.org/10.3390/met9040477



