Close Range Explosive Loading on Steel Column in the Framework of Anisotropic Viscoplasticity
Abstract
:1. Introduction
2. Constitutive Assumptions
2.1. Introductory Remarks
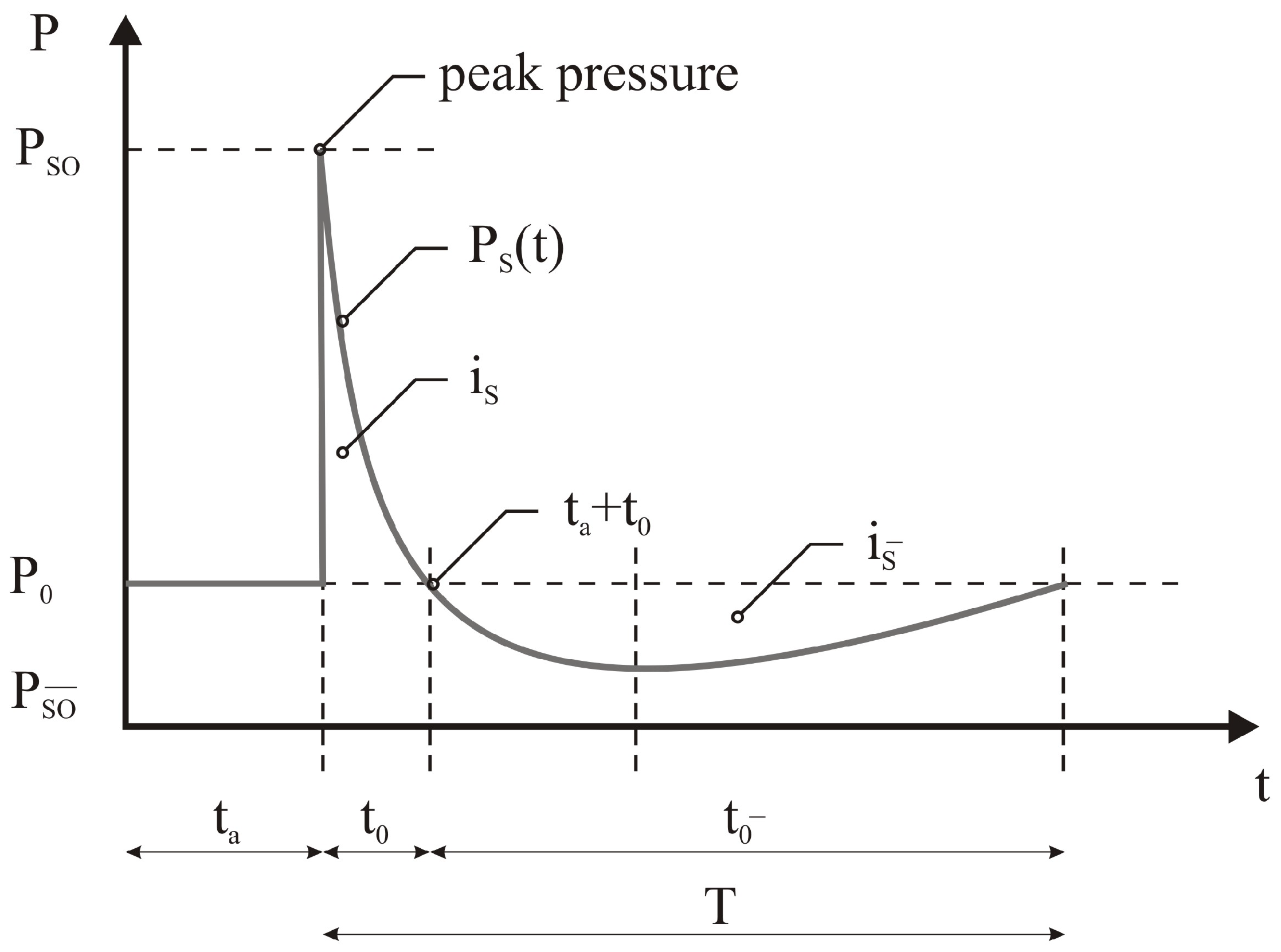
2.2. Description of the Surrounding Air and the Condensed Charge
2.3. Behavior of the Steel Column
- (i)
- Existence of the free energy function . Formally, we apply the following form (cf. [53] for extensive discussion on such an assumption):where denotes a set of internal state variables which describe the dissipation effects and is temperature.
- (ii)
- The axiom of objectivity (spatial covariance). The material model should be invariant with respect to any superposed motion (diffeomorphism).
- (iii)
- The axiom of the entropy production. For every regular process the constitutive functions should satisfy the second law of thermodynamics.
- (iv)
- The evolution equation for the internal state variable vector should be of the form:where evolution function has to be determined based on the experimental observations.
- (i)
- the field equations:
- (ii)
- the boundary conditions:
- (a)
- displacement is prescribed on a part of and tractions are prescribed on a part of , where and ,
- (b)
- heat flux is prescribed on , and
- (iii)
- the initial conditions are given for each particle at ,
- The elastic range is isotropic and independent of microdamage state, thus (for more general setup cf. [24]):where are Lam constants.
- The thermal expansion is isotropic, thus:where is the thermal expansion coefficient.
- The rate dependence of fracture porosity has the form [24]:where can be thought of as a quasi-static fracture porosity and denotes equivalent critical velocity of microdamage.
- The normalised directions of viscoplastic flow, under the above assumptions, are defined as:where represents the stress deviator, , are the first and the second invariants of Kirchhoff stress tensor and deviatoric part of the Kirchhoff stress tensor, respectively, .
- The microdamage mechanism assumes the growth term only ( while nucleation is replaced by the initial microdamage distribution assumption), therefore taking the additional assumptions [16,62]: (i) Velocity of the microdamage growth is coaxial with the principal directions of the stress state, and (ii) only positive (tension) principal stresses induces the growth of the microdamage, one has:where are the material parameters, and is the third invariant of deviatoric part of the Kirchhoff stress tensor.
- The tensor is a symmetric part of the fourth order unity tensor [16]:hence:and:where are the principal values of the Kirchhoff stress tensor.
- Lastly, for temperature evolution, the following relation is considered:
3. Numerical Prediction of Blast Effect on Steel Column
3.1. Introductory Remarks
- After the ignition moment in the centre of the explosive, the combustion wave goes through the charge domain, and then releases a high amount of kinetic and thermal energies;
- the transition phase generates a high pressure wave on the charge and ambient boundaries; and
- finally, the pressure reaches the obstacle boundaries and induces the thermomechanical process within its bounds, which is of strong wave character.
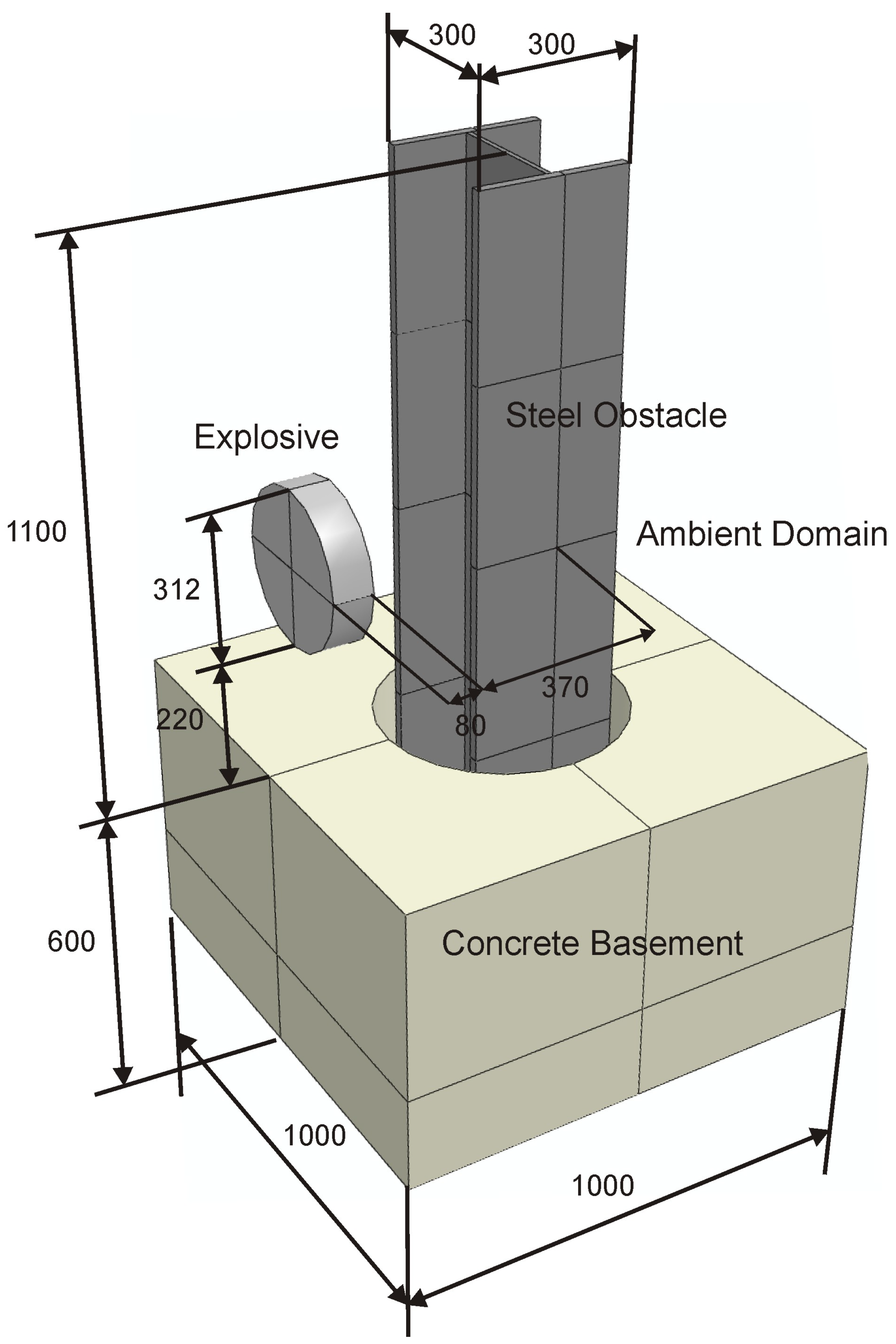
3.2. Steel Column Modeling Assumptions
3.3. Results
- High quality of the numerical results symmetry is observed,
- equivalent plastic strains are locally as high as ca. in the strain localization zones,
- the temperature in the strain localization zones is as high as ca. 800 C,
- the evolution of the porosity is restricted to the zones of high plastic strains,
- thermal stresses can be locally as high as 2000 MPa or more,
- the displacement field is localised in the zone of the evolving flying fragment, whereas in the remaining part for ms reaches ca. m,
- the strain hardening causes the Huber–Mises–Hencky stresses to be as high as ca. 900 MPa, and
- air pressure is highly scattered in the fluid domain and reaches locally 150 MPa (161 MPa according to the standards cf. [20]).
4. Experimental Validation
- High-speed camera Phantom v711 with mobile stand,
- Bosch GLM 80 Professional Laser Rangefinder, and
- ICP Free-field Blast Pressure “Pencil” Probe.
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Grimsmo, E.; Clausen, A.; Aalberg, A.; Langseth, M. A numerical study of beam-to-column joints subjected to impact. Eng. Struct. 2016, 120, 103–115. [Google Scholar] [CrossRef]
- Aune, V.; Valsamos, G.; Casadei, F.; Langseth, M.; Børvik, T. On the dynamic response of blast-loaded steel plates with and without pre-formed holes. Int. J. Impact Eng. 2017, 108, 27–46. [Google Scholar]
- Nassr, A.; Razaqpur, A.; Tait, M.; Campidelli, M.; Foo, S. Strength and stability of steel beam columns under blast load. Int. J. Impact Eng. 2013, 55, 34–48. [Google Scholar]
- Formica, G.; Sansalone, V.; Casciaro, R. A mixed solution strategy for the nonlinear analysis of brick masonry walls. Comput. Methods Appl. Mech. Eng. 2002, 191, 5847–5876. [Google Scholar] [CrossRef]
- Sabuwala, T.; Linzell, D.; Krauthammer, T. Finite element analysis of steel beam to column connections subjected to blast loads. Int. J. Impact Eng. 2005, 31, 861–876. [Google Scholar] [CrossRef]
- Rigby, S.; Tyas, A.; Bennett, T. Elastic-plastic response of plates subjected to cleared blast loads. Int. J. Impact Eng. 2014, 66, 37–47. [Google Scholar] [CrossRef]
- Neuberger, A.; Peles, S.; Rittel, D. Springback of circular clamped armor steel plates subjected to spherical air-blast loading. Int. J. Impact Eng. 2009, 36, 53–60. [Google Scholar] [CrossRef]
- Makarem, F.; Abed, F. Nonlinear finite element modeling of dynamic localizations in high strength steel columns under impact. Int. J. Impact Eng. 2013, 52, 47–61. [Google Scholar] [CrossRef]
- Denny, J.; Clubley, S. Long-duration blast loading & response of steel column sections at different angles of incidence. Eng. Struct. 2019, 178, 331–342. [Google Scholar]
- Fu, S.; Gao, X.; Chen, X. The similarity law and its verification of cylindrical lattice shell model under internal explosion. Int. J. Impact Eng. 2018, 122, 38–49. [Google Scholar] [CrossRef]
- Hadianfard, M.; Malekpour, S.; Momeni, M. Reliability analysis of H-section steel columns under blast loading. Struct. Saf. 2018, 75, 45–56. [Google Scholar] [CrossRef]
- Malachowski, J.; Klasztorny, M.; Mazurkiewicz, L.; Kołodziejczyk, D.; Niezgoda, T. Numerical assessment of the selected supporting element carrying capacity of critical infrastructure facility. J. Konbin 2013, 26, 29–42. [Google Scholar] [CrossRef]
- Sumelka, W. Role of Covariance in Continuum Damage Mechanics. ASCE J. Eng. Mech. 2013, 139, 1610–1620. [Google Scholar] [CrossRef]
- Sumelka, W.; Łodygowski, T. The influence of the initial microdamage anisotropy on macrodamage mode during extremely fast thermomechanical processes. Arch. Appl. Mech. 2011, 81, 1973–1992. [Google Scholar] [CrossRef]
- Perzyna, P. The Thermodynamical Theory of Elasto-Viscoplasticity. Eng. Trans. 2005, 53, 235–316. [Google Scholar]
- Glema, A.; Łodygowski, T.; Sumelka, W.; Perzyna, P. The Numerical Analysis of the Intrinsic Anisotropic Microdamage Evolution in Elasto-Viscoplastic Solids. Int. J. Damage Mech. 2009, 18, 205–231. [Google Scholar] [CrossRef]
- Lodygowski, T.; Rusinek, A.; Jankowiak, T.; Sumelka, W. Selected topics of high speed machining analysis. Eng. Trans. 2012, 60, 69–96. [Google Scholar]
- Litoński, J. Plastic flow of a Tube under Adiabatic Torsion. Bull. Acad. Pol. Sci. Ser. Sci. Tech. 1977, XXV, 7–14. [Google Scholar]
- Rusinek, A.; Klepaczko, J. Shear testing of a sheet steel at wide range of strain rates and a constitutive relation with strain-rate and temperature dependence of the flow stress. Int. J. Plast. 2001, 17, 87–115. [Google Scholar] [CrossRef]
- Sielicki, P.; Stachowski, M. Implementation of sapper-blast-module, a rapid prediction software for blast wave properties. Cent. Eur. J. Energ. Mater. 2015, 12, 473–486. [Google Scholar]
- US Army Manual, Department of The Army, The Navy, and The Air Force. Structures to Resist the Effects of Accidental Explosions; UFC 3-340-02; Department of The Army, The Navy, and The Air Force: Washington, DC, USA, 2008.
- Rankine, W. On the thermodynamic theory of waves of finite longitudinal disturbance. Philos. Transl. 1870, 160, 277–288. [Google Scholar]
- Sielicki, P. Masonry Failure under Unusual Impulse Loading; Publishing House of Poznan University of Technology: Poznan, Poland, 2013; ISBN 978-83-7775-274-6. [Google Scholar]
- Sumelka, W. The Constitutive Model of the Anisotropy Evolution for Metals with Microstructural Defects; Publishing House of Poznan University of Technology: Poznań, Poland, 2009. [Google Scholar]
- Brode, H. Numerical solutions of spherical blast waves. J. Appl. Phys. 1955, 26, 766. [Google Scholar] [CrossRef]
- Kingery, C.; Bulmash, G. Airblast Parameters From TNT Spherical Air Burst And Hemispherical Surface Burst; Ballistic Research Laboratory: Aberdeen Proving Ground, MD, USA, 1984. [Google Scholar]
- Abaqus 6.13. Documentation Collection. Available online: https://www.3ds.com/products-services/simulia/support/documentation/ (accessed on 11 March 2019).
- Wodarczyk, E. Wstp do Mechaniki Wybuchu; Wydawnictwo Naukowe PWN: Warszawa, Poland, 1994. (In Polish) [Google Scholar]
- Hallquist, J. LS-Dyna, Theoretical Manual; California Livermore Software Technology Corporation: Livermore, CA, USA, 2008. [Google Scholar]
- Jach, K. Komputerowe Modelowanie Dynamicznych Oddziaywa Cia Metod Punktw Swobodnych; PWN: Warsaw, Poland, 2000. (In Polish) [Google Scholar]
- Stenberg, D. Spherical Explosions and the Equation of State of Water; Lawrence Livermore National Laboratory: Livermore, CA, USA, 1978.
- Gathers, G. Shock Wave Physics and Equation of State Modelling; World Scientific Publishing Co., Pte. Ltd.: Singapore, 1994. [Google Scholar]
- Dobratz, B. Explosive Handbook; Lawrence Livermore National Laboratory: Livermore, CA, USA, 1981.
- Larcher, M.; Casadei, F. Explosions in Complex Geometries—A Comparison of Several Approaches. Int. J. Prot. Struct. 2010, 1, 169–195. [Google Scholar] [CrossRef]
- Rigby, S.; Sielicki, P. An investigation of TNT equivalence of hemispherical PE4 charges. Eng. Trans. 2014, 62, 423–435. [Google Scholar]
- Rigby, S.E.; Tyas, A.; Curry, R.J.; Langdon, G.S. Experimental Measurement of Specific Impulse Distribution and Transient Deformation of Plates Subjected to Near-Field Explosive Blasts. Exp. Mech. 2019, 59, 163–178. [Google Scholar] [CrossRef]
- Sumelka, W.; Łodygowski, T. Thermal stresses in metallic materials due to extreme loading conditions. ASME J. Eng. Mater. Technol. 2013, 135, 021009. [Google Scholar] [CrossRef]
- Łodygowski, T.; Sumelka, W. Damage Induced by Viscoplasitc Waves Interaction. Vib. Phys. Syst. 2012, 25, 23–32. [Google Scholar]
- Eftis, J.; Carrasco, C.; Osegueda, R. A constitutive-microdamage model to simulate hypervelocity projectile-target impact, material damage and fracture. Int. J. Plast. 2003, 19, 1321–1354. [Google Scholar] [CrossRef]
- Sumelka, W.; Łodygowski, T. Reduction of the number of material parameters by ANN approximation. Comput. Mech. 2013, 52, 287–300. [Google Scholar] [CrossRef]
- Nemat-Nasser, S.; Guo, W.G. Thermomechanical response of DH-36 steel plates over a wide range of strain rates and temperatures. Mech. Mater. 2003, 35, 1023–1047. [Google Scholar] [CrossRef]
- Nemat-Nasser, S.; Guo, W.G. Thermomechanical response of HSLA-65 steel plates: Experiments and modeling. Mech. Mater. 2005, 37, 379–405. [Google Scholar] [CrossRef]
- Moćko, W.; Kowalewski, Z. Application of FEM in the assessment of phenomena associated with dynamic investigations on a miniaturised ICT testing stand. Kovove Mater.-Metal. Mater. 2013, 51, 71–82. [Google Scholar]
- Perzyna, P. The Thermodynamical Theory of Elasto-viscoplasticity Accounting for Microshear Banding and Induced Anisotropy Effects. Mechanics 2008, 27, 25–42. [Google Scholar]
- Glema, A.; Łodygowski, T.; Sumelka, W. Nowacki’s Double Shear Test in the Framework of the Anisotropic Thermo-Elasto-Vicsoplastic Material Model. J. Theor. Appl. Mech. 2010, 48, 973–1001. [Google Scholar]
- Truesdell, C.; Noll, W. The non-linear field theories of mechanics. In Handbuch der Physik; Flügge, S., Ed.; Springer: Berlin, Germany, 1965; Volume III/3. [Google Scholar]
- Marsden, J.; Hughes, T. Mathematical Foundations of Elasticity; Prentice-Hall: Upper Saddle River, NJ, USA, 1983. [Google Scholar]
- Haupt, P. Continuum Mechanics and Theory of Materials, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2002. [Google Scholar]
- Lee, E. Elastic-plastic deformation at finite strain. ASME J. Appl. Mech. 1969, 36, 1–6. [Google Scholar] [CrossRef]
- Perzyna, P. Interactions of elastic-viscoplastic waves and localization phenomena in solids. In Proceedings of the IUTAM Symposium on Nonlinear Waves in Solids, Victoria, BC, Canada, 15–20 August 1995; pp. 114–121. [Google Scholar]
- Lu, J.; Papadopoulos, P. A covariant constitutive description of anisotropic non-linear elasticity. J. Appl. Math. Phys. (ZAMP) 2000, 51, 204–217. [Google Scholar] [CrossRef]
- Lu, J.; Papadopoulos, P. A covariant formulation of anisotropic finite plasticity: Theoretical developments. Comput. Methods Appl. Mech. Eng. 2004, 193, 5339–5358. [Google Scholar] [CrossRef]
- Duszek–Perzyna, M.; Perzyna, P. Analysis of anisotropy and plastic spin effects on localization phenomena. Arch. Appl. Mech. 1998, 68, 352–374. [Google Scholar] [CrossRef]
- Dornowski, W.; Perzyna, P. Analysis of the influence of various effects on cycle fatigue damage in dynamic process. Arch. Appl. Mech. 2002, 72, 418–438. [Google Scholar] [CrossRef]
- Dornowski, W.; Perzyna, P. Localized fracture phenomena in thermo-viscoplastic flow process under cyclic dynamic loadings. Acta Mech. 2002, 155, 233–255. [Google Scholar] [CrossRef]
- Glema, A.; Łodygowski, T.; Perzyna, P. Numerical investigation of dynamic shear bands in inelastic solids as a problem of mesomechanics. Comput. Mech. 2008, 41, 219–229. [Google Scholar] [CrossRef]
- Perzyna, P. Instability phenomena and adiabatic shear band localization in thermoplastic flow process. Acta Mech. 1994, 106, 173–205. [Google Scholar] [CrossRef]
- Łodygowski, T. Theoretical and Numerical Aspects of Plastic Strain Localization; Publishing House of Poznan University of Technology: Poznań, Poland, 1996; Volume 312. [Google Scholar]
- Shima, S.; Oyane, M. Plasticity for porous solids. Int. J. Mech. Sci. 1976, 18, 285–291. [Google Scholar] [CrossRef]
- Perzyna, P. Internal state variable description of dynamic fracture of ductile solids. Int. J. Solids Struct. 1986, 22, 797–818. [Google Scholar] [CrossRef]
- Perzyna, P. Constitutive modeling for brittle dynamic fracture in dissipative solids. Arch. Mech. 1986, 38, 725–738. [Google Scholar]
- Dornowski, W. Influence of Finite Deformations on the Growth Mechanism of Microvoids Contained in Structural Metals. Arch. Mech. 1999, 51, 71–86. [Google Scholar]
- Łodygowski, T.; Perzyna, P.; Lengnick, M.; Stein, E. Viscoplastic numerical analysis of dynamic plastic shear localization for a ductile material. Arch. Mech. 1994, 46, 541–557. [Google Scholar]
- Łodygowski, T. On avoiding of spurious mesh sensitivity in numerical analysis of plastic strain localization. Comput. Assist. Mech. Eng. Sci. 1995, 2, 231–248. [Google Scholar]
- Glema, A. Analysis of Wave Nature in Plastic Strain Localization in Solids; Rozprawy; Publishing House of Poznan University of Technology: Poznań, Poland, 2004; Volume 379. (In Polish) [Google Scholar]
- Benson, D.J. Computational methods in Lagrangian and Eulerian hydrocodes. Comput. Methods Appl. Mech. Eng. 1992, 99, 235–394. [Google Scholar] [CrossRef]
- Benson, D.J.; Okazawa, S. Contact in a multi-material Eulerian finite element formulation. Comput. Methods Appl. Mech. Eng. 2004, 193, 4277–4298. [Google Scholar] [CrossRef]


| Jones–Wilkins–Lee (JWL) Properties for TNT Explosive | ||
|---|---|---|
| A | Pa | |
| B | Pa | |
| - | ||
| - | ||
| - | ||
| 6930 | ||
| 1630 | ||
| 0 | Pa·s | |
| Ideal gas (IG) properties for Ambient Air | ||
| R | 287 | |
| 101,325 | ||
| 0 | ||
| Pa·s | ||
| Material Parameters for S355 Steel | |||
|---|---|---|---|
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sielicki, P.W.; Sumelka, W.; Łodygowski, T. Close Range Explosive Loading on Steel Column in the Framework of Anisotropic Viscoplasticity. Metals 2019, 9, 454. https://doi.org/10.3390/met9040454
Sielicki PW, Sumelka W, Łodygowski T. Close Range Explosive Loading on Steel Column in the Framework of Anisotropic Viscoplasticity. Metals. 2019; 9(4):454. https://doi.org/10.3390/met9040454
Chicago/Turabian StyleSielicki, Piotr Witold, Wojciech Sumelka, and Tomasz Łodygowski. 2019. "Close Range Explosive Loading on Steel Column in the Framework of Anisotropic Viscoplasticity" Metals 9, no. 4: 454. https://doi.org/10.3390/met9040454
APA StyleSielicki, P. W., Sumelka, W., & Łodygowski, T. (2019). Close Range Explosive Loading on Steel Column in the Framework of Anisotropic Viscoplasticity. Metals, 9(4), 454. https://doi.org/10.3390/met9040454






