Numerical Study on the Influence of a Swirling Flow Tundish on Multiphase Flow and Heat Transfer in Mold
Abstract
:1. Introduction
2. Model Description
2.1. Model Assumptions
- Steel and slag behave as an incompressible Newtonian fluids;
- Solidification in the mold is not considered;
- A constant molecular viscosity for steel and slag was assumed. This is due to that the maximum temperature difference in the mold is only 30 K between 1788 K and 1818 K. The viscosity change in this temperature range is not significant, and this can be seen from a previous study [10];
- A constant steel and slag density was used. The temperature influence on the steel density change was accounted for in the source term of the momentum equation;
- The SEN wall was assumed to be a smooth wall;
- Inclusions were assumed to be spherical.
2.2. Transport Equations
2.3. Interface Tracking
2.4. Turbulence Modeling
2.5. Heat Transfer
2.6. Lagrangian Particle Tracking Model
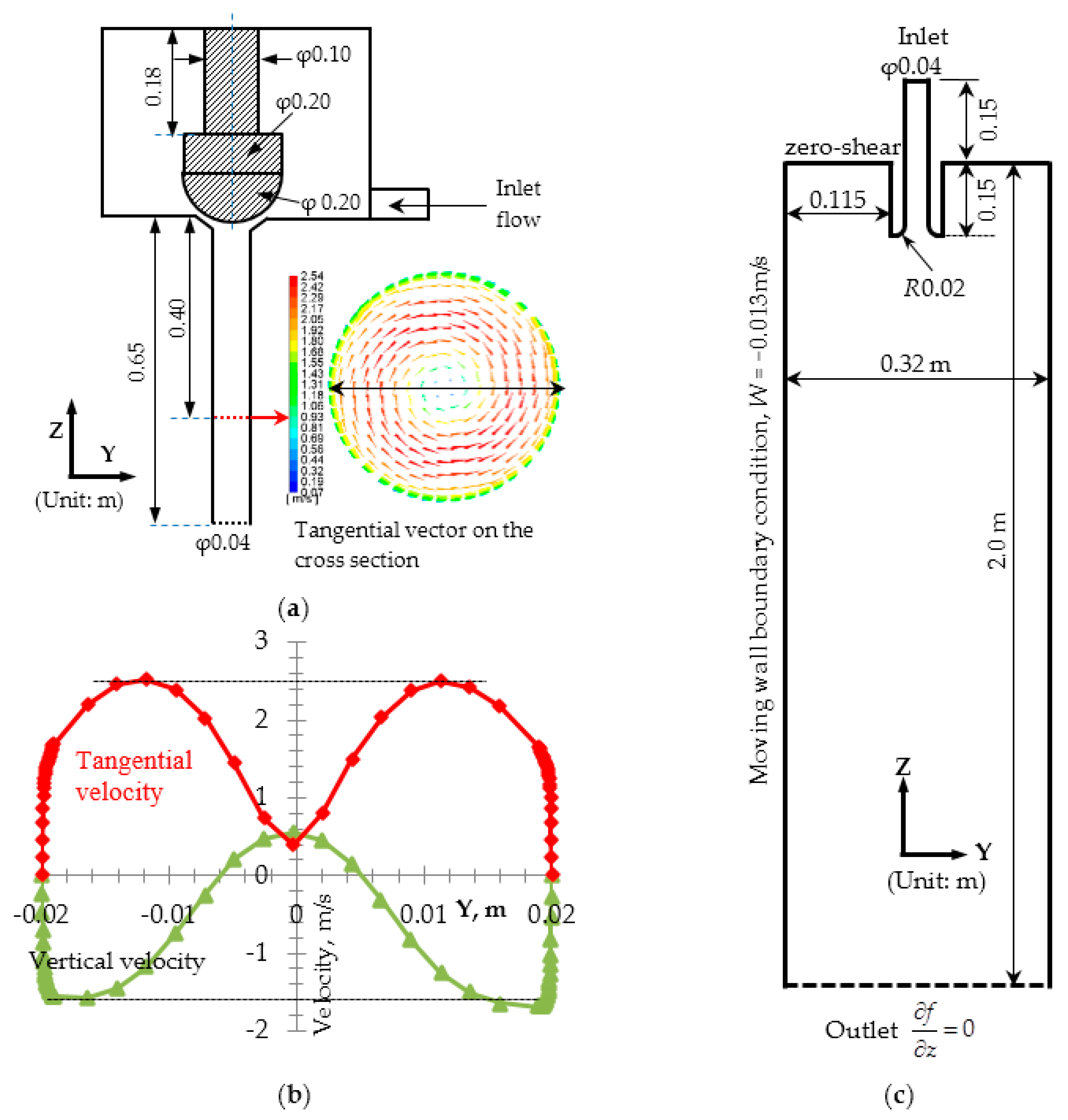
2.7. Boundary Conditions
2.8. Solution Method
3. Results and Discussion
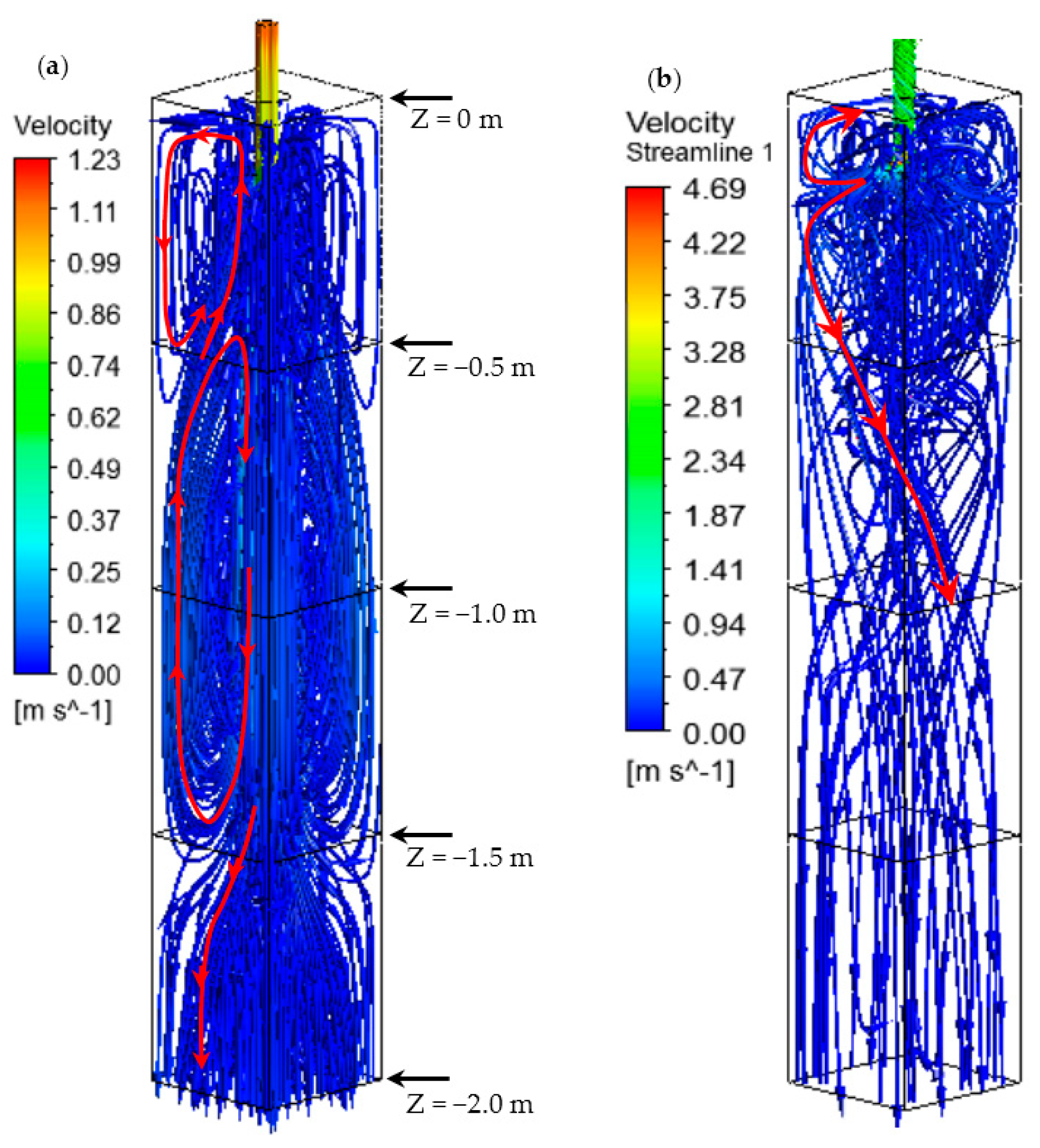
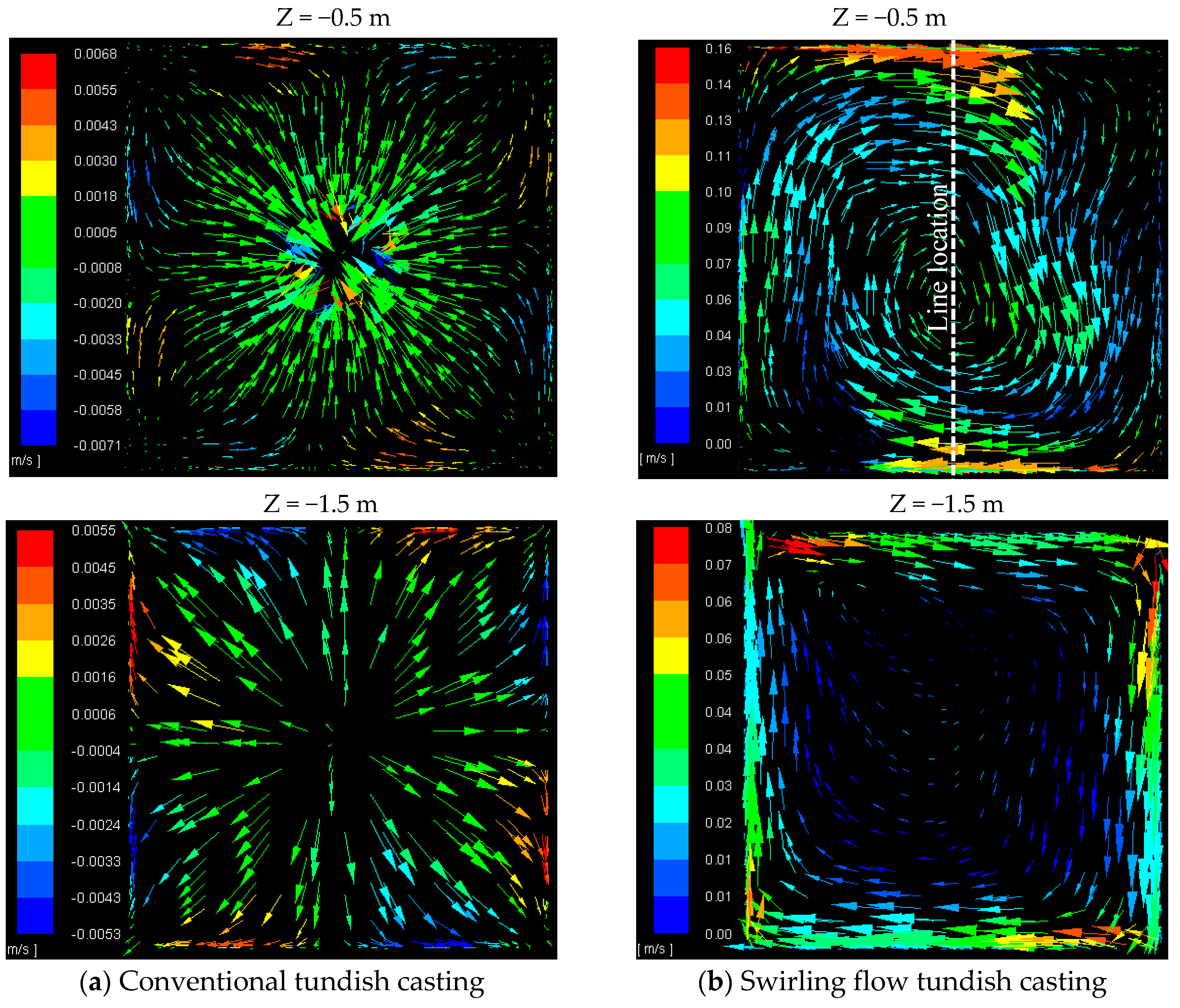
3.1. Steel Flow Paths
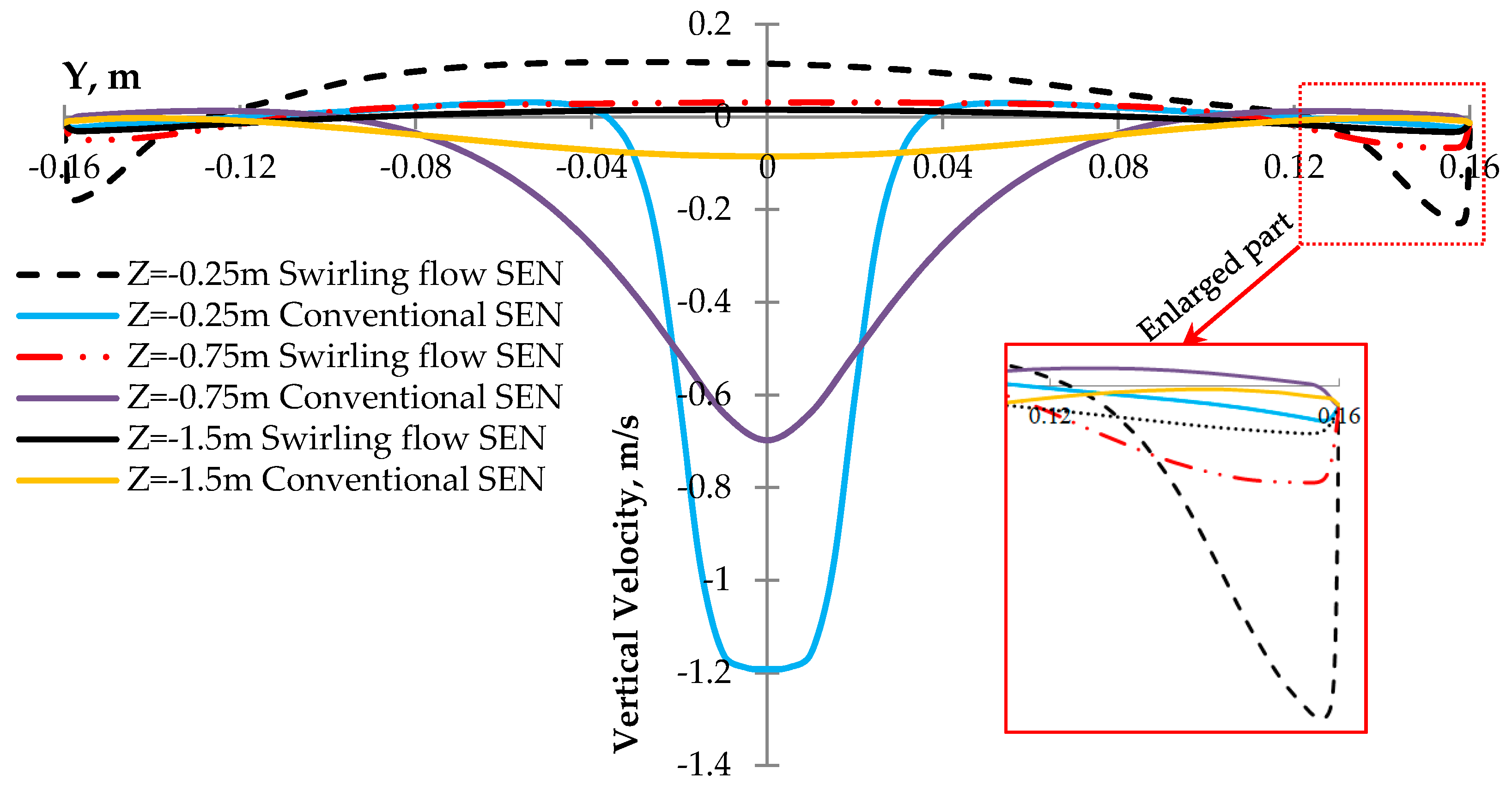
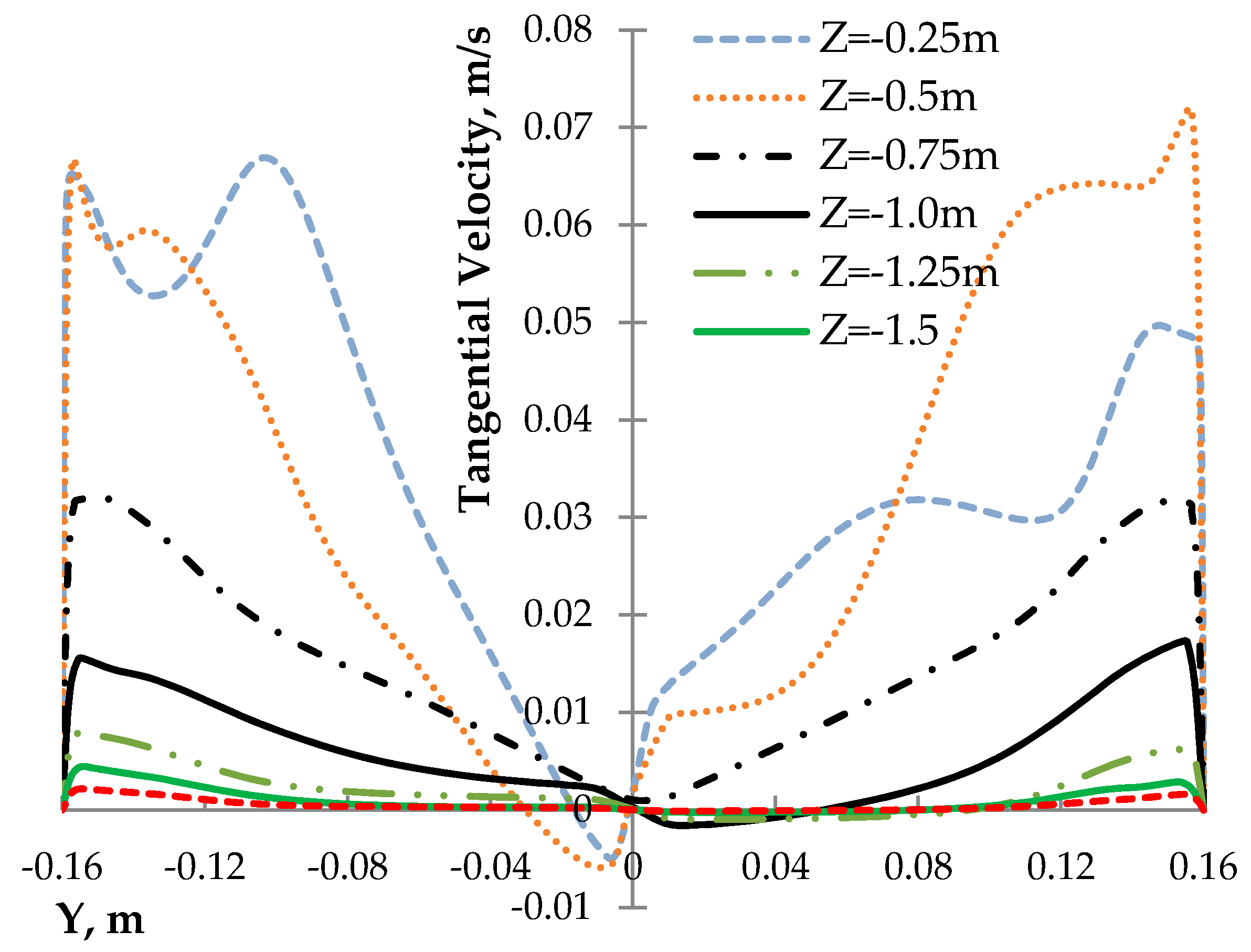
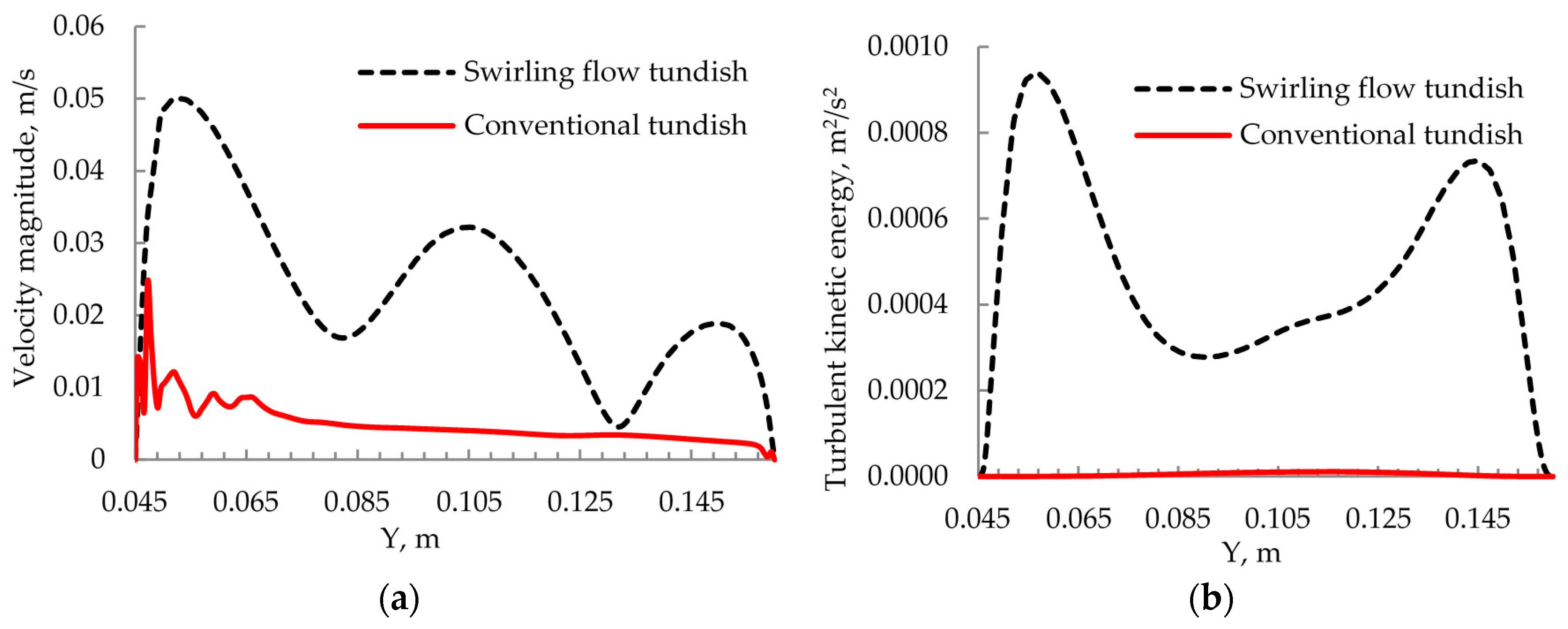
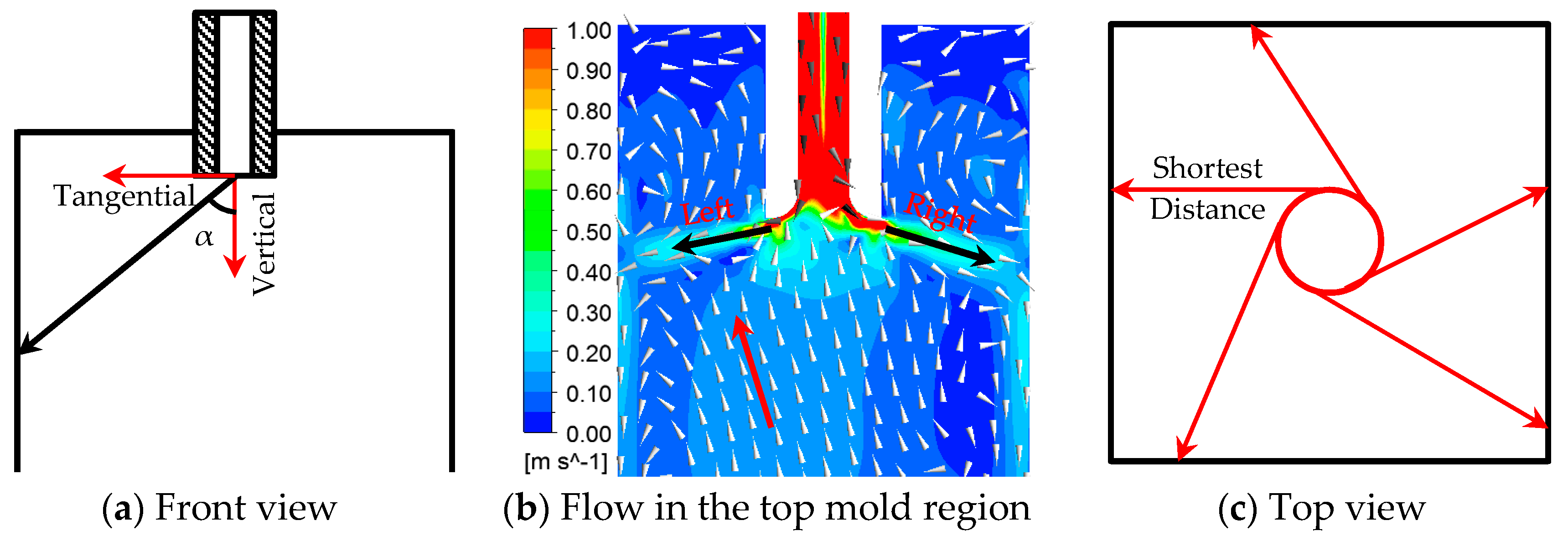
3.2. Steel Flow Velocity
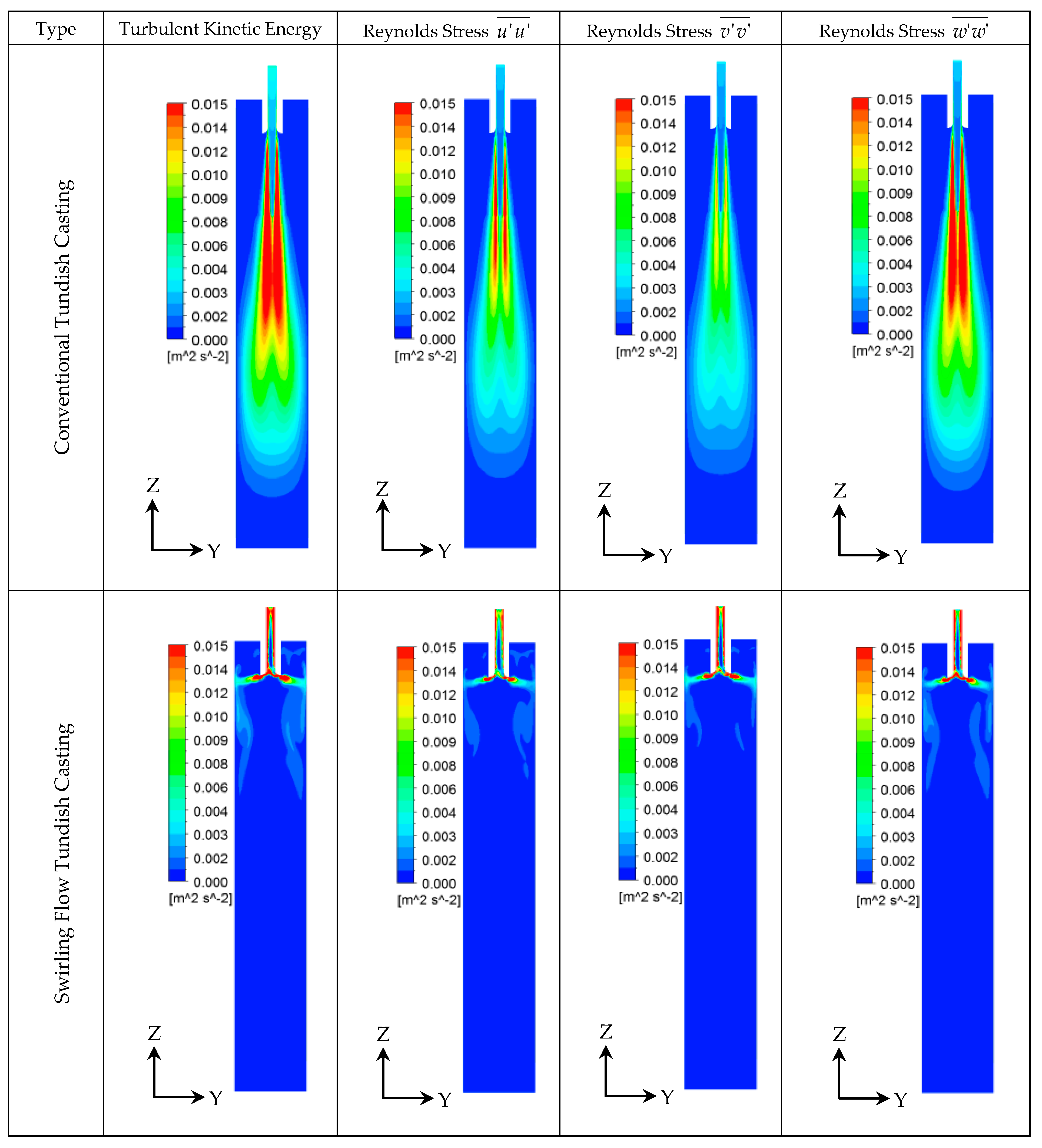
3.3. Turbulence Properties
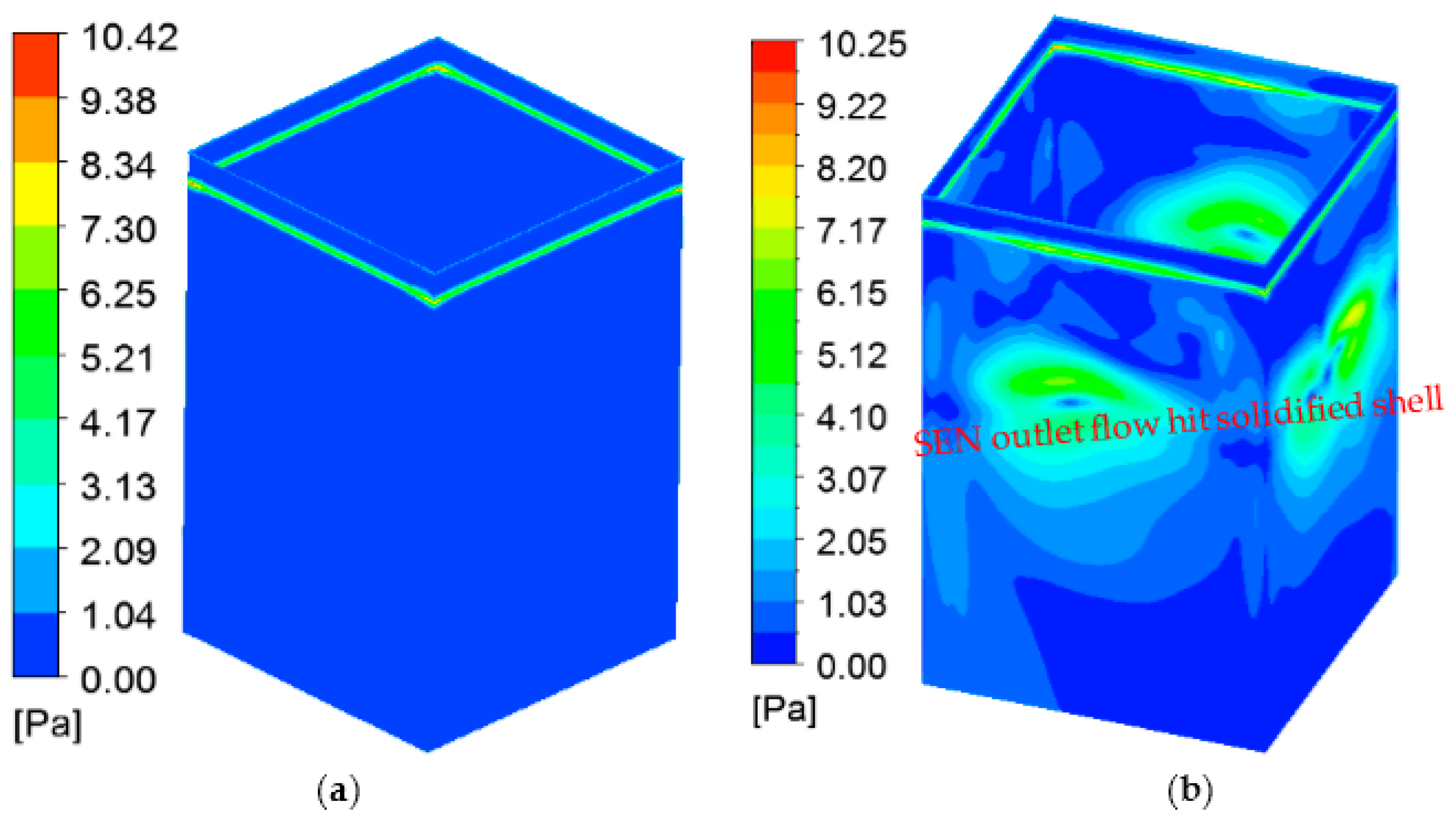
3.4. Steel/Slag Interface Phenomena
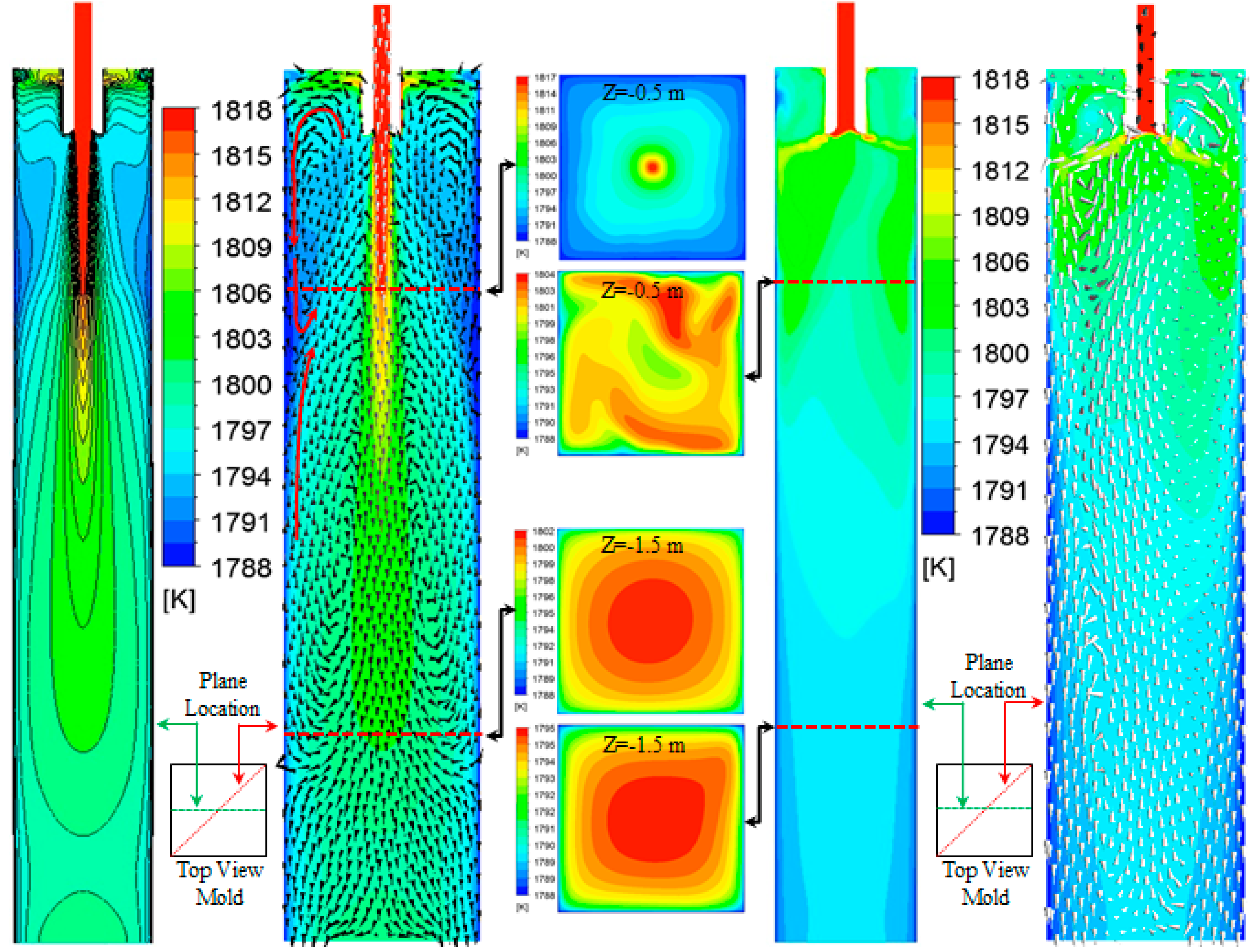
3.5. Temperature Distribution
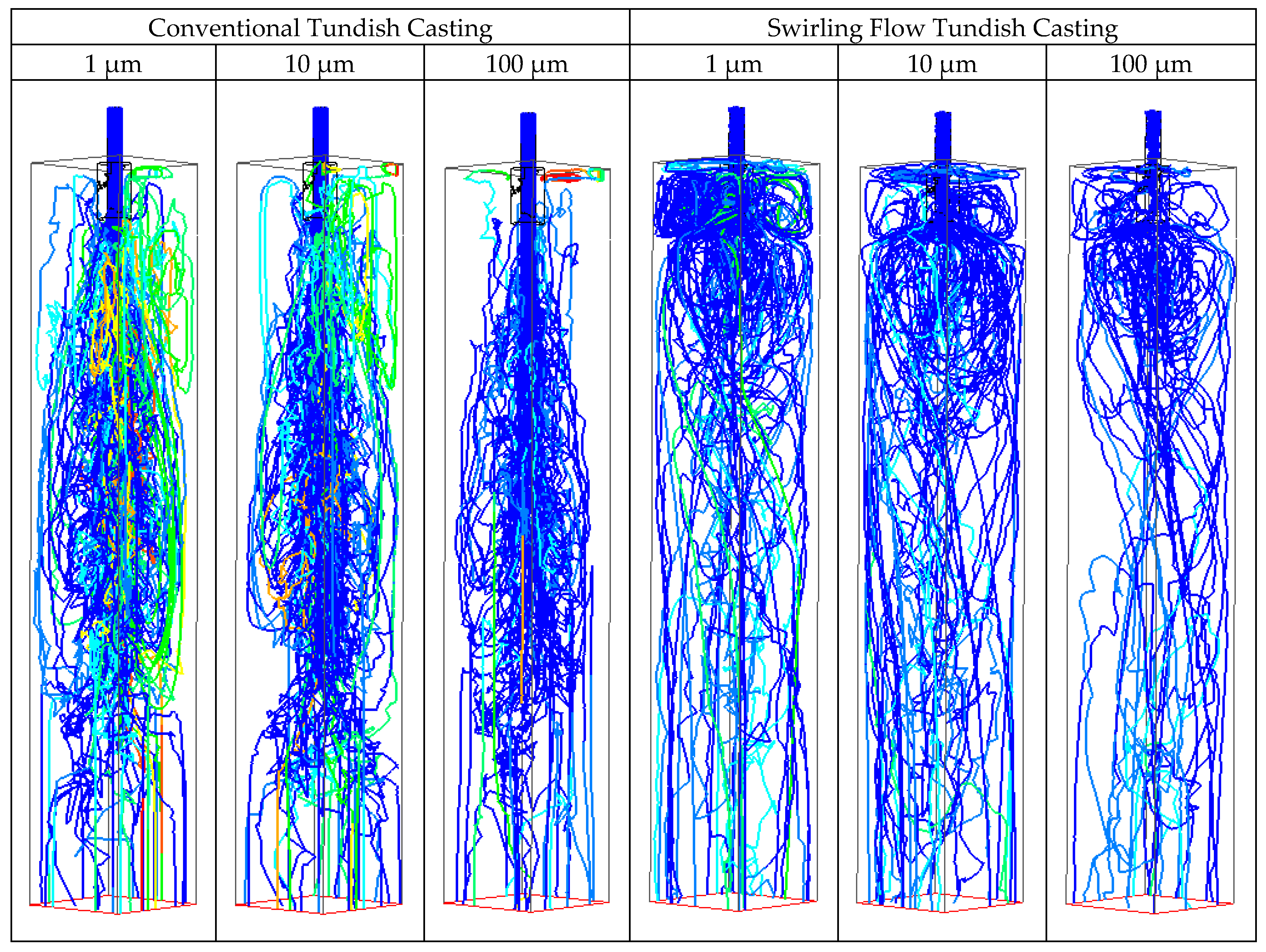
3.6. Inclusion Behavior in Mold
4. Concluding Discussion
5. Conclusions
- The new cylindrical tundish design for swirling flow casting significantly changed the flow behavior in the mold. The deep impingement jet in the mold disappeared, and the steel flow moved towards the solidified shell, due to the swirling flow effect. A large velocity in the vicinity of the solidified shell was obtained.
- The steel flow velocity in the top part of the mold was increased. The calculated Weber number was round 0.8, which indicates a small risk for the slag entrainment.
- With the swirling flow tundish casting, the temperature distribution became more uniform, and the dissipation of the steel superheat was accelerated. Furthermore, due to the high temperature steel directly flowing to the solidified shell, the temperature near the solidified shell was increased. A high temperature region was found at the top part of the mold, rather than in the deep center of the mold in a conventional tundish casting.
- Inclusion trajectories in the mold change a lot, due to the change of the SEN outlet flow pattern. Instead of moving deeply into the mold following the impingement jet, some inclusions tended to stay for a time at the top part of the mold. This may be helpful for their removal.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Szekely, J.; Yadoya, R.T. The physical and mathematical modelling of the flow field in the mold region of continuous casting systems. Part II. The mathematical representation of the turbulence flow field. Metall. Mater. Trans. 1973, 4, 1379–1388. [Google Scholar] [CrossRef]
- Xu, M.; Zhu, M. Transport phenomena in a Beam-Blank continuous casting mold with two types of submerged entry nozzle. ISIJ Int. 2015, 55, 791–798. [Google Scholar] [CrossRef]
- Thomas, B.G.; Mika, L.J.; Najjar, F.M. Simulation of fluid flow inside a continuous slab-casting machine. Metall. Mater. Trans. B 1990, 21, 387–400. [Google Scholar] [CrossRef]
- Calderon-Ramos, I.; Morales, R.D.; Garcia-Hernandez, S.; Ceballos-Huerta, A. Effects of immersion depth on flow turbulence of liquid steel in a slab mold using a nozzle with upward angle rectangular ports. ISIJ Int. 2014, 54, 1797–1806. [Google Scholar] [CrossRef]
- Calderon-Ramos, I.; Morales, R.D.; Salazar-Campoy, M. Modeling flow turbulence in a continuous casting slab mold comparing the use of two bifurcated nozzles with square and circular ports. Steel Res. Int. 2015, 86, 1610–1621. [Google Scholar] [CrossRef]
- Calderon-Ramos, I.; Morales, R.D. The role of submerged entry nozzle port shape on fluid flow turbulence in a slab mold. Metall. Mater. Trans. B 2015, 46, 1314–1325. [Google Scholar] [CrossRef]
- Salazar-Campoy, M.; Morales, R.D.; Najera-Bastida, A.; Cedillo-Hernandez, V.; Delgado-Pureco, J.C. A physical model to study the effects of nozzle design on dense two-phase flows in a slab mold casting Ultra-Low carbon steels. Metall. Mater. Trans. B 2017, 48, 1376–1389. [Google Scholar] [CrossRef]
- Sun, H.; Zhang, J. Macrosegregation improvement by swirling flow nozzle for bloom continuous castings. Metall. Mater. Trans. B 2014, 45, 936–946. [Google Scholar] [CrossRef]
- Sun, H.; Li, L. Application of swirling flow nozzle and investigation of superheat dissipation casting for bloom continuous casing. Ironmak. Steelmak. 2016, 43, 228–233. [Google Scholar] [CrossRef]
- Fang, Q.; Ni, H.; Zhang, H.; Wang, B.; Lv, Z. The effects of a submerged entry nozzle on flow and initial solidification in a continuous casting bloom mold with electromagnetic stirring. Metals 2017, 7, 146. [Google Scholar] [CrossRef]
- Thomas, B.G.; Dennisov, A.; Bai, H. Behavior of argon bubbles during continuous casting of steel. In Proceedings of the ISS 80th Steelmaking Conference, Chicago, IL, USA, 13–16 April 1997; pp. 375–384. [Google Scholar]
- Thomas, B.G.; Huang, X.; Sussman, R.C. Simulation of argon gas flow effects in a continuous slab caster. Metall. Mater. Trans. B 1994, 25, 527–547. [Google Scholar] [CrossRef]
- Li, B.; Okane, T.; Umeda, T. Modeling of biased flow phenomena associated with the effects of static magnetic-field application and argon gas injection in slab continuous casting of steel. Metall. Mater. Trans. B 2001, 32, 1053–1066. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, L. Fluid flow-related transport phenomena in steel slab continuous casting strands under electromagnetic brake. Metall. Mater. Trans. B 2011, 42, 1319–1351. [Google Scholar] [CrossRef]
- Liu, Z.; Li, B.; Jiang, M. Transient asymmetric flow and bubble transport inside a slab continuous casting mold. Metall. Mater. Trans. B 2014, 45, 675–697. [Google Scholar] [CrossRef]
- Liu, Z.; Li, L.; Qi, F.; Li, B.; Jiang, M.; Tsukihashi, F. Population balance modeling of polydispersed bubbly flow in continuous casting using multiple-size-group approach. Metall. Mater. Trans. B 2015, 46, 406–420. [Google Scholar] [CrossRef]
- Liu, Z.; Sun, Z.; Li, B. Modeling of quasi-four-phase flow in continuous casting mold using hybrid Eulerian and Lagrangian approach. Metall. Mater. Trans. B 2017, 48, 1248–1267. [Google Scholar] [CrossRef]
- Liu, Z.; Li, B. Large-Eddy simulation of transient horizontal gas–liquid flow in continuous casting using dynamic subgrid-scale model. Metall. Mater. Trans. B 2017, 48, 1833–1849. [Google Scholar] [CrossRef]
- Pfeiler, C.; Wu, M.; Ludwig, A. Influence of argon gas bubbles and non-metallic inclusions on the flow behavior in steel continuous casting. Mater. Sci. Eng. A 2005, 413–414, 115–120. [Google Scholar] [CrossRef]
- Yu, H.; Zhu, M. Numerical simulation of the effects of electromagnetic brake and argon gas injection on the three-dimensional multiphase flow and heat transfer in slab continuous casting mold. ISIJ Int. 2008, 48, 584–591. [Google Scholar] [CrossRef]
- Cho, S.; Kim, S.; Thomas, B.G. Transient fluid flow during steady continuous casting of steel slabs: Part I. measurements and modeling of two-phase flow. ISIJ Int. 2014, 54, 845–854. [Google Scholar] [CrossRef]
- Jin, K.; Thomas, B.G.; Ruan, X. Modeling and measurements of multiphase flow and bubble entrapment in steel continuous casting. Metall. Mater. Trans. B 2016, 47, 548–565. [Google Scholar] [CrossRef]
- Cho, S.; Thomas, B.G.; Kim, S. Transient two-phase flow in slide-gate nozzle and mold of continuous steel slab casting with and without double-ruler electro-magnetic braking. Metall. Mater. Trans. B 2016, 47, 3080–3098. [Google Scholar] [CrossRef]
- Cukierski, K.; Thomas, B.G. Flow control with local electromagnetic braking in continuous casting of steel slabs. Metall. Mater. Trans. B 2008, 39, 94–107. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, Y.; Zuo, X. Flow transport and inclusion motion in steel continuous-casting mold under submerged entry nozzle clogging condition. Metall. Mater. Trans. B 2008, 39, 534–550. [Google Scholar] [CrossRef]
- Gonzalez-Trejo, J.; Real-Ramirez, C.A.; Miranda-Tello, R.; Rivera-Perez, F.; Cervantes-De-La-Torre, F. Numerical and physical parametric analysis of a SEN with flow conditioners in slag continuous casting mold. Arch. Metall. Mater. 2017, 62, 927–946. [Google Scholar] [CrossRef]
- Miao, X.; Timmel, K.; Lucas, D.; Ren, Z.; Eckert, S.; Gerbeth, G. Effect of an electromagnetic brake on the turbulent melt flow in a continuous-casting mold. Metall. Mater. Trans. B 2012, 43, 954–972. [Google Scholar] [CrossRef]
- Liu, Z.; Li, L.; Li, B. Large eddy simulation of transient flow and inclusions transport in continuous casting mold under different electromagnetic brakes. JOM 2016, 68, 2180–2190. [Google Scholar] [CrossRef]
- Ha, M.Y.; Lee, H.G.; Seong, S.H. Numerical simulation of three-dimensional flow, heat transfer, and solidification of steel in continuous casting mold with electromagnetic brake. J. Mater. Process. Technol. 2003, 133, 322–339. [Google Scholar] [CrossRef]
- Yu, H.; Wang, B.; Li, H.; Li, J. Influence of electromagnetic brake on flow field of liquid steel in the slab continuous casting mold. J. Mater. Process. Technol. 2008, 202, 179–187. [Google Scholar]
- Yu, H.; Zhu, M. Three-dimensional magnetohydrodynamic calculation for coupling multiphase flow in round billet continuous casting mold with electromagnetic stirring. IEEE Trans. Magn. 2010, 46, 82–86. [Google Scholar]
- Yu, H.; Zhu, M. Influence of electromagnetic stirring on transport phenomena in round billet continuous casting mould and macrostructure of high carbon steel billet. Ironmak. Steelmak. 2012, 39, 574–584. [Google Scholar] [CrossRef]
- Liu, H.; Xu, M.; Qiu, S.; Zhang, H. Numerical simulation of fluid flow in a round bloom mold with In-Mold rotary electromagnetic stirring. Metall. Mater. Trans. B 2012, 43, 1657–1675. [Google Scholar] [CrossRef]
- Yokoya, S.; Takagi, S.; Iguchi, M.; Asako, Y.; Westoff, R.; Hara, S. Swirling effect in immersion nozzle on flow and heat transport in billet continuous casting mold. ISIJ Int. 1998, 38, 827–833. [Google Scholar] [CrossRef]
- Yokoya, S.; Takagi, S.; Iguchi, M.; Marukawa, K.; Yasugair, W.; Hara, S. Development of swirling flow generator in immersion nozzle. ISIJ Int. 2000, 40, 584–588. [Google Scholar] [CrossRef]
- Yokoya, S.; Takagi, S.; Kaneko, M.; Iguchi, M.; Marukawa, K.; Hara, S. Swirling flow effect in off-center immersion nozzle on bulk flow in billet continuous casting mold. ISIJ Int. 2001, 41, 1215–1220. [Google Scholar] [CrossRef]
- Yokoya, S.; Takagi, S.; Ootani, S.; Iguchi, M.; Marukawa, K.; Hara, S. Swirling flow effect in submerged entry nozzle on bulk flow in high throughput slab continuous casting mold. ISIJ Int. 2001, 41, 1208–1214. [Google Scholar] [CrossRef]
- Yokoya, S.; Jönsson, P.G.; Sasaki, K.; Tada, K.; Takagi, S.; Iguchi, M. The effect of swirl flow in an immersion nozzle on the heat and fluid flow in a billet continuous casting mold. Scan. J. Metall. 2004, 33, 22–28. [Google Scholar] [CrossRef]
- Tsukaguchi, Y.; Hayashi, H.; Kurimoto, H.; Yokoya, S.; Marukawa, K.; Tanaka, T. Development of swirling-flow submerged entry nozzles for slab casting. ISIJ Int. 2010, 50, 721–729. [Google Scholar] [CrossRef]
- Kholmatov, S.; Takagi, S.; Jonsson, L.; Jönsson, P.; Yokoya, S. Development of flow field and temperature distribution during changing divergent angle of the nozzle when using swirl flow in a square continuous casting billet mould. ISIJ Int. 2007, 47, 80–87. [Google Scholar] [CrossRef]
- Kholmatov, S.; Takagi, S.; Jönsson, P.; Jonsson, L.; Yokoya, S. Influence of aspect ratio on fluid flow and heat transfer in mould when using swirl flow during casting. Steel Res. Int. 2008, 79, 698–707. [Google Scholar] [CrossRef]
- Kholmatov, S.; Takagi, S.; Jonsson, L.; Jönsson, P.; Yokoya, S. Effect of nozzle angle on flow field and temperature distribution in a billet mould when using swirl flow. Steel Res. Int. 2008, 79, 31–39. [Google Scholar] [CrossRef]
- Geng, D.; Lei, H.; He, J.; Liu, H. Effect of electromagnetic swirling flow in slide-gate SEN on flow field in square billet continuous casting mold. Acta Metall. Sin. (Engl. Lett.) 2012, 25, 347–356. [Google Scholar]
- Wondrak, Th.; Eckert, S.; Galindo, V.; Gerbeth, G.; Stefani, F.; Timmel, K.; Peyton, A.J.; Yin, W.; Riaz, S. Liquid metal experiments with swirling flow submerged entry nozzle. Ironmak. Steelmak. 2012, 39, 1–9. [Google Scholar] [CrossRef]
- Li, D.; Su, Z.; Chen, J.; Wang, Q.; Yang, Y.; Nakajima, K.; Marukaw, K.; He, J. Effects of electromagnetic swirling flow in submerged entry nozzle on square billet continuous casting of steel process. ISIJ Int. 2013, 53, 1187–1194. [Google Scholar] [CrossRef]
- Yang, Y.; Jönsson, P.G.; Ersson, M.; Su, Z.; He, J.; Nakajima, K. The Influence of swirl flow on the flow field, temperature field and inclusion behavior when using a half type electromagnetic swirl flow generator in a submerged entry and mold. Steel Res. Int. 2015, 86, 1312–1327. [Google Scholar] [CrossRef]
- Ni, P.; Jonsson, L.; Ersson, M.; Jönsson, P. A new tundish design to produce a swirling flow in the SEN during continuous casting of steel. Steel Res. Int. 2016, 87, 1356–1365. [Google Scholar] [CrossRef]
- Ni, P.; Jonsson, L.; Ersson, M.; Jönsson, P. Non-Metallic inclusion behaviors in a new tundish and SEN design using a swirling flow during continuous casting of steel. Steel Res. Int. 2017, 88, 1600155. [Google Scholar] [CrossRef]
- Ni, P.; Wang, D.; Jonsson, L.; Ersson, M.; Zhang, T.; Jönsson, P. Numerical and physical study on a cylindrical tundish design to produce a swirling flow in the SEN during continuous casting of steel. Metall. Mater. Trans. B 2017, 48, 2695–2706. [Google Scholar] [CrossRef]
- Wang, S.; Yang, V.; Hsiao, G.; Hsieh, S.; Mongia, H.C. Large-eddy simulation of gas-turbine swirl injector flow dynamics. J. Fluid Mech. 2007, 583, 99–122. [Google Scholar] [CrossRef]
- Weber, R.; Visser, B.M.; Boysan, F. Assessment of turbulence modeling for engineering predictions of swirling vortices in the near burner zone. Int. J. Heat Fluid Flow 1990, 11, 225–235. [Google Scholar] [CrossRef]
- Hoekstra, A.; Derksen, J.; Van Den Akker, H. An experimental and numerical study on turbulent swirling flow in gas cyclones. Chem. Eng. Sci. 1999, 54, 2055–2065. [Google Scholar] [CrossRef]
- Jakirlic, S.; Hanjalic, K.; Tropea, C. Modeling rotating and swirling turbulent flows: A perpetual challenge. AIAA J. 2002, 40, 1984–1996. [Google Scholar] [CrossRef]
- Patankar, S.V. Numerical Heat Transfer and Fluid Flow; Hemispere Publishing Corp.: New York, NY, USA, 1980. [Google Scholar]
- ANSYS. Fluent Theory Guide; Release 18.0; ANSYS: Canonsburg, PA, USA, 2017. [Google Scholar]
- Versteeg, H.K.; Malalasekera, W. An Introduction to Computational Fluid Dynamics: The Finite Volume Method, 2nd ed.; Pearson Education Limited: London, UK, 2007; p. 80. [Google Scholar]
- Launder, B.E.; Reece, G.J.; Rodi, W. Progress in the development of a Reynolds-stress turbulence closure. J. Fluid Mech. 1975, 68, 537–566. [Google Scholar] [CrossRef]
- Lien, F.S.; Leschziner, M.A. Assessment of turbulence-transport models including non-linear RNG eddy-viscosity formulation and second-moment closure for flow over a backward-facing step. Comput. Fluids 1994, 23, 983–1004. [Google Scholar] [CrossRef]
- Shih, T.-H.; Liou, W.W.; Shabbir, A.; Yang, Z.; Zhu, J. A new k-ε eddy viscosity model for high Reynolds number turbulent flows. Comput. Fluids 1995, 24, 227–238. [Google Scholar] [CrossRef]
- ANSYS. Fluent User’s Guide; Release 18.0; ANSYS: Canonsburg, PA, USA, 2017. [Google Scholar]
- Ni, P.; Ersson, M.; Jonsson, L.; Jönsson, P. A study on the nonmetallic inclusion motions in a swirling flow submerged entry nozzle in a new cylindrical Tundish design. Metall. Mater. Trans. B 2018, 49, 723–736. [Google Scholar] [CrossRef]
- Saffman, P.G. The lift on a small sphere in a slow shear flow. J. Fluid Mech. 1965, 22, 385–400. [Google Scholar] [CrossRef]
- Morsi, S.A.; Alexander, A.J. An investigation of particle trajectories in two-phase flow systems. J. Fluid Mech. 1972, 55, 193–208. [Google Scholar] [CrossRef]
- Willers, B.; Barna, M.; Reiter, J.; Eckert, S. Experimental investigations of rotary electromagnetic mould stirring in continuous casting using a cold liquid metal model. ISIJ Int. 2017, 57, 468–477. [Google Scholar] [CrossRef]
- Jonsson, L.; Jönsson, P. Modeling of fluid flow conditions around the slag/metal interface in a gas-stirred ladle. ISIJ Int. 1996, 36, 1127–1134. [Google Scholar] [CrossRef]
- Shannon, G.N.; Sridhar, S. Film-drainage, separation and dissolution of Al2O3 inclusions at steel/interfaces. High Temp. Mater. Process. 2005, 24, 111–124. [Google Scholar] [CrossRef]
- Ni, P.; Ersson, M.; Jonsson, L.; Jönsson, P.G. Application of a swirling flow producer in a conventional tundish during continuous casting of steel. ISIJ Int. 2017, 57, 2175–2184. [Google Scholar] [CrossRef]
- Bai, H.; Ersson, M.; Jönsson, P. Experimental validation and numerical analysis of the swirling flow in a submerged entry nozzle and mold by using a reverse turboswirl in a billet continuous casting process. Steel Res. Int. 2017, 88, 1600399. [Google Scholar] [CrossRef]


| Parameters | Symbols | Steel | Slag |
|---|---|---|---|
| Density, kg/m3 | ρo | 7000 | 2600 |
| Viscosity, kg/(m·s) | µ | 0.0064 | 0.09 |
| Thermal conductivity, W/(m·K) | k | 35 | 1.1 |
| Specific heat, J/(kg·K) | cp | 628 | 1200 |
| Thermal expansion coefficient, 1/K | β | 10−4 | - |
| Interfacial tension, N/m | σ | 1.6 | |
| Operating temperature, K | To | 1788 | |
| Turbulent Prandtl number | Prt | 0.85 | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ni, P.; Ersson, M.; Jonsson, L.T.I.; Zhang, T.-a.; JÖNSSON, P.G. Numerical Study on the Influence of a Swirling Flow Tundish on Multiphase Flow and Heat Transfer in Mold. Metals 2018, 8, 368. https://doi.org/10.3390/met8050368
Ni P, Ersson M, Jonsson LTI, Zhang T-a, JÖNSSON PG. Numerical Study on the Influence of a Swirling Flow Tundish on Multiphase Flow and Heat Transfer in Mold. Metals. 2018; 8(5):368. https://doi.org/10.3390/met8050368
Chicago/Turabian StyleNi, Peiyuan, Mikael Ersson, Lage Tord Ingemar Jonsson, Ting-an Zhang, and Pär Göran JÖNSSON. 2018. "Numerical Study on the Influence of a Swirling Flow Tundish on Multiphase Flow and Heat Transfer in Mold" Metals 8, no. 5: 368. https://doi.org/10.3390/met8050368
APA StyleNi, P., Ersson, M., Jonsson, L. T. I., Zhang, T.-a., & JÖNSSON, P. G. (2018). Numerical Study on the Influence of a Swirling Flow Tundish on Multiphase Flow and Heat Transfer in Mold. Metals, 8(5), 368. https://doi.org/10.3390/met8050368







