An Equivalent Calculation Method for Press-Braking Bending Analysis of Integral Panels
Abstract
:1. Introduction
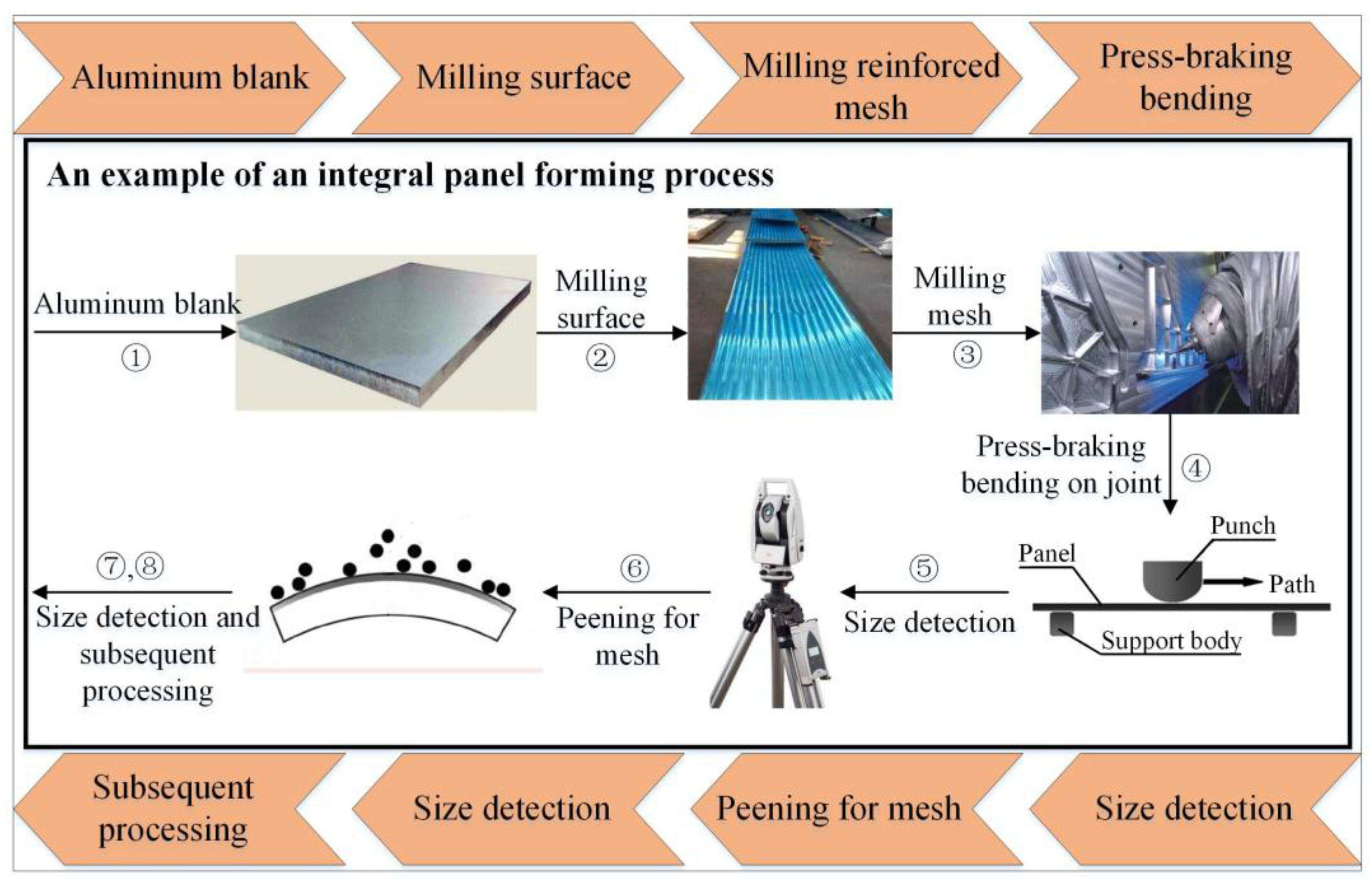
2. Press-Braking Bending Process
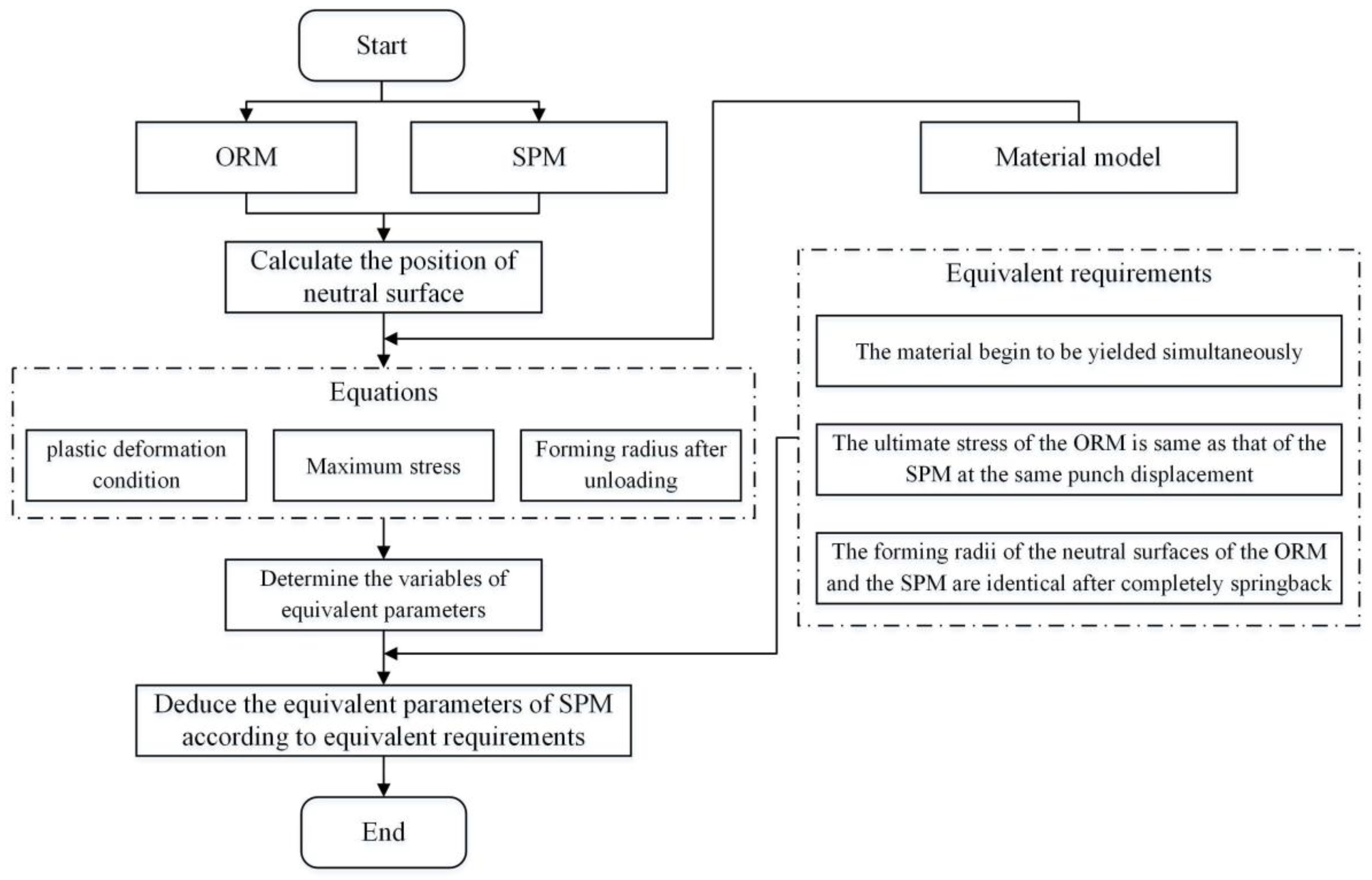
3. Development of Equivalent Model
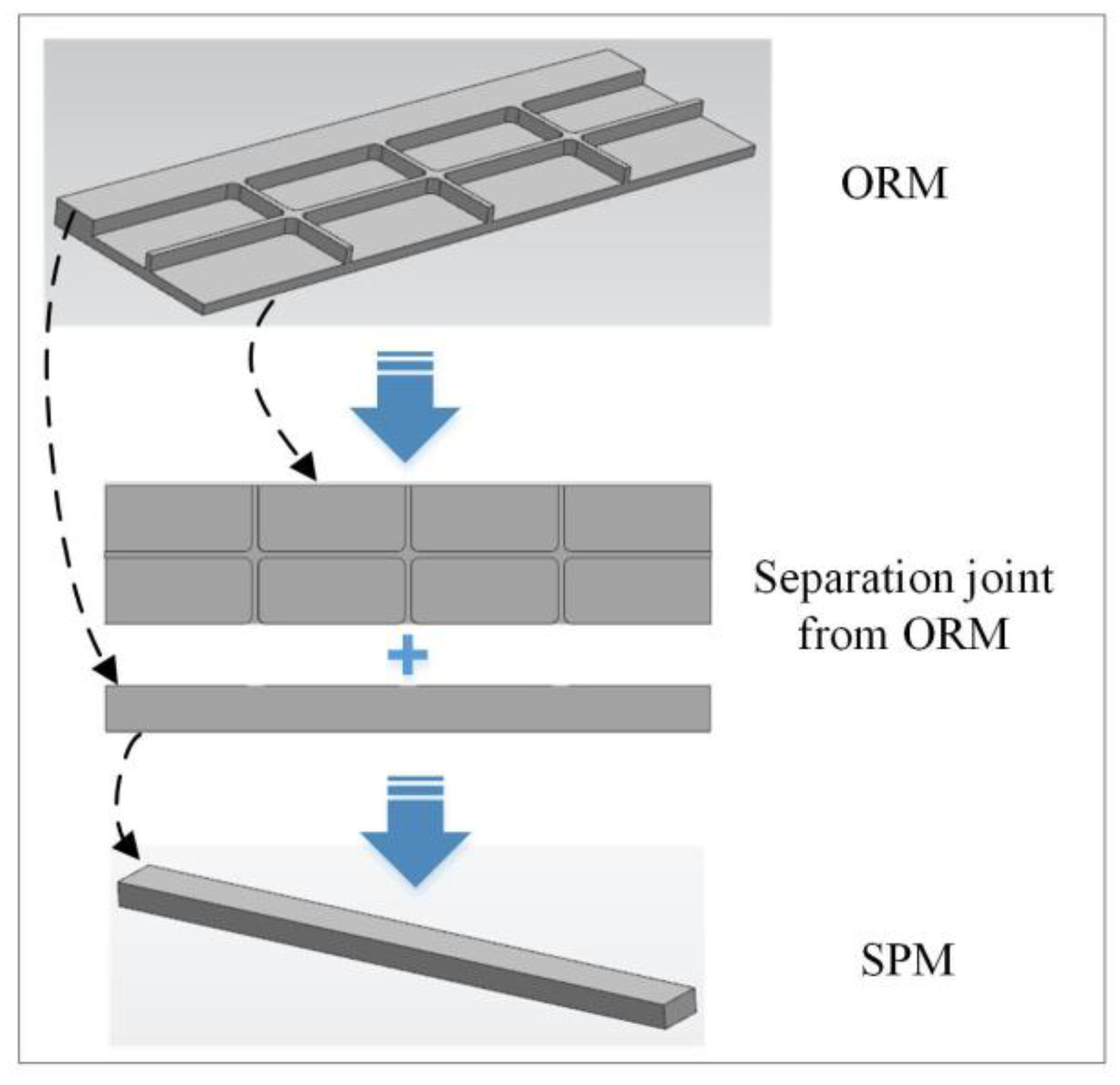
3.1. Equivalent Requirements
3.2. Method
3.2.1. Bending Analysis of SPM
- The material is isotropic and homogeneous.
- The plane section remains planar throughout deformation and springback.
- The change of thickness during bending is ignored.
- The neutral surface of bending is assumed to stay at the same position.
- The rolling direction of the material does not have a major impact on this forming process.
3.2.2. Bending Analysis of ORM
3.2.3. Equivalent Parameters
4. Simulation and Experimental Verification
4.1. FE Simulation Model
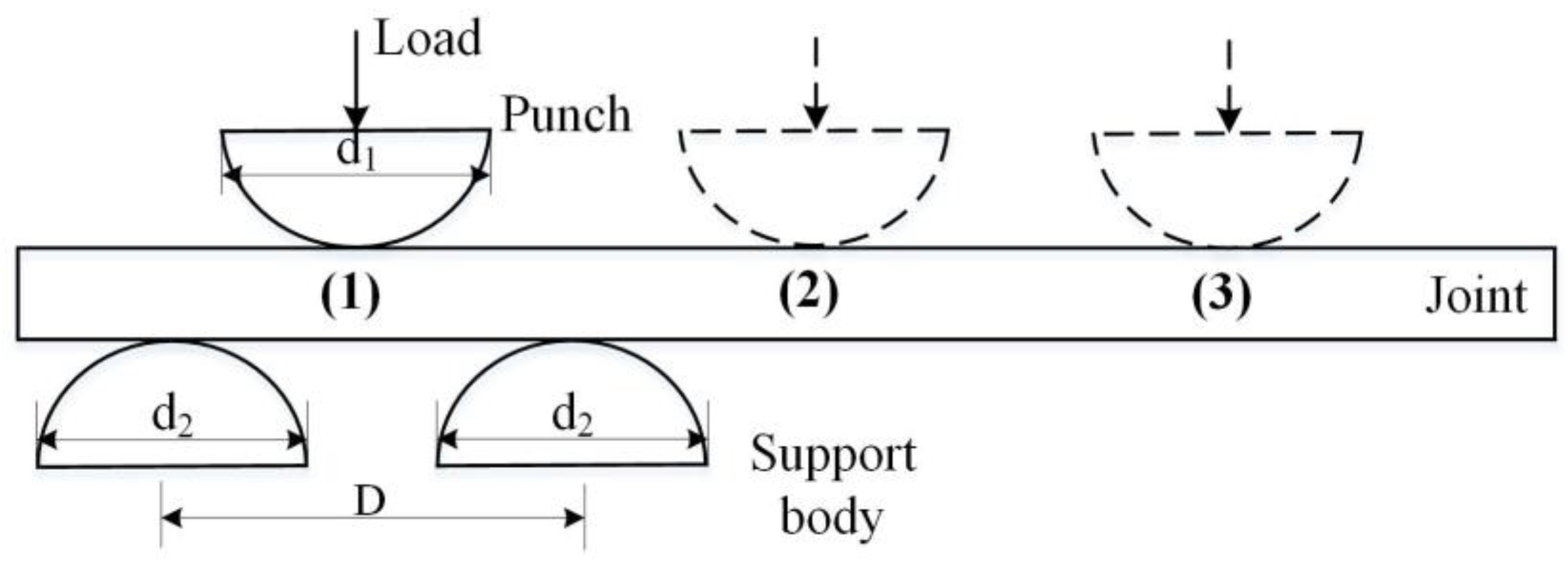
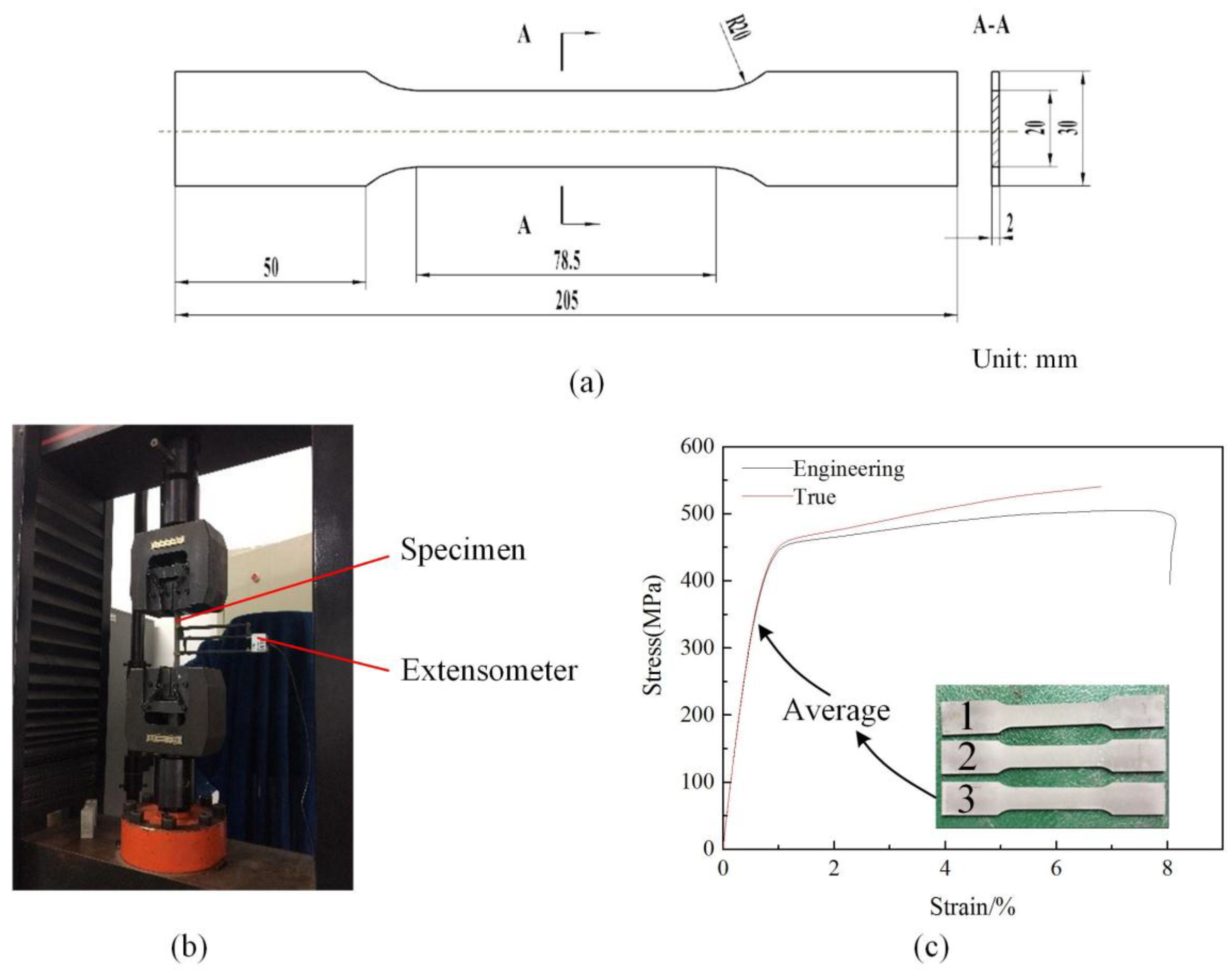
4.2. Bending Experiment
5. Results and Discussion
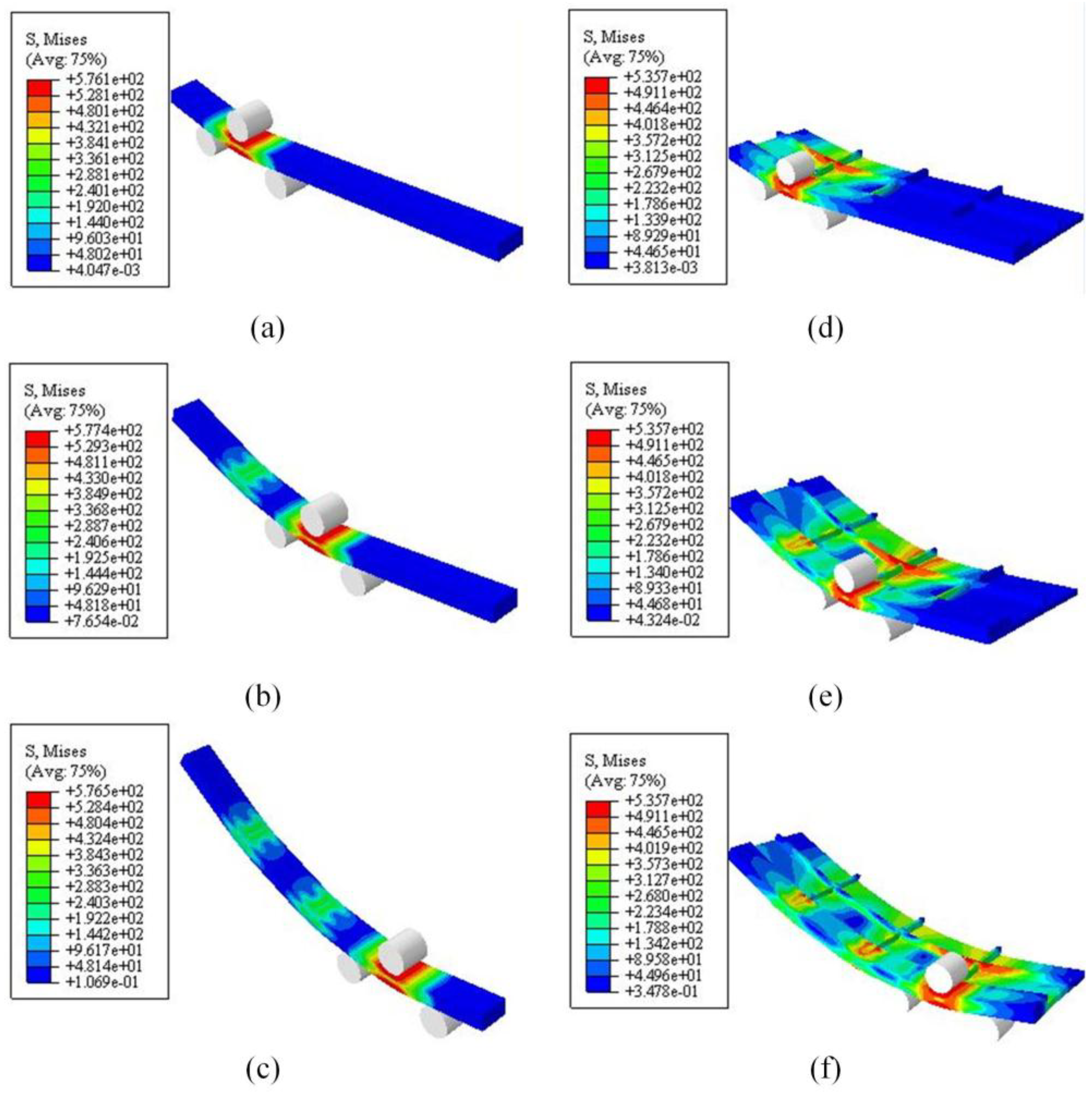
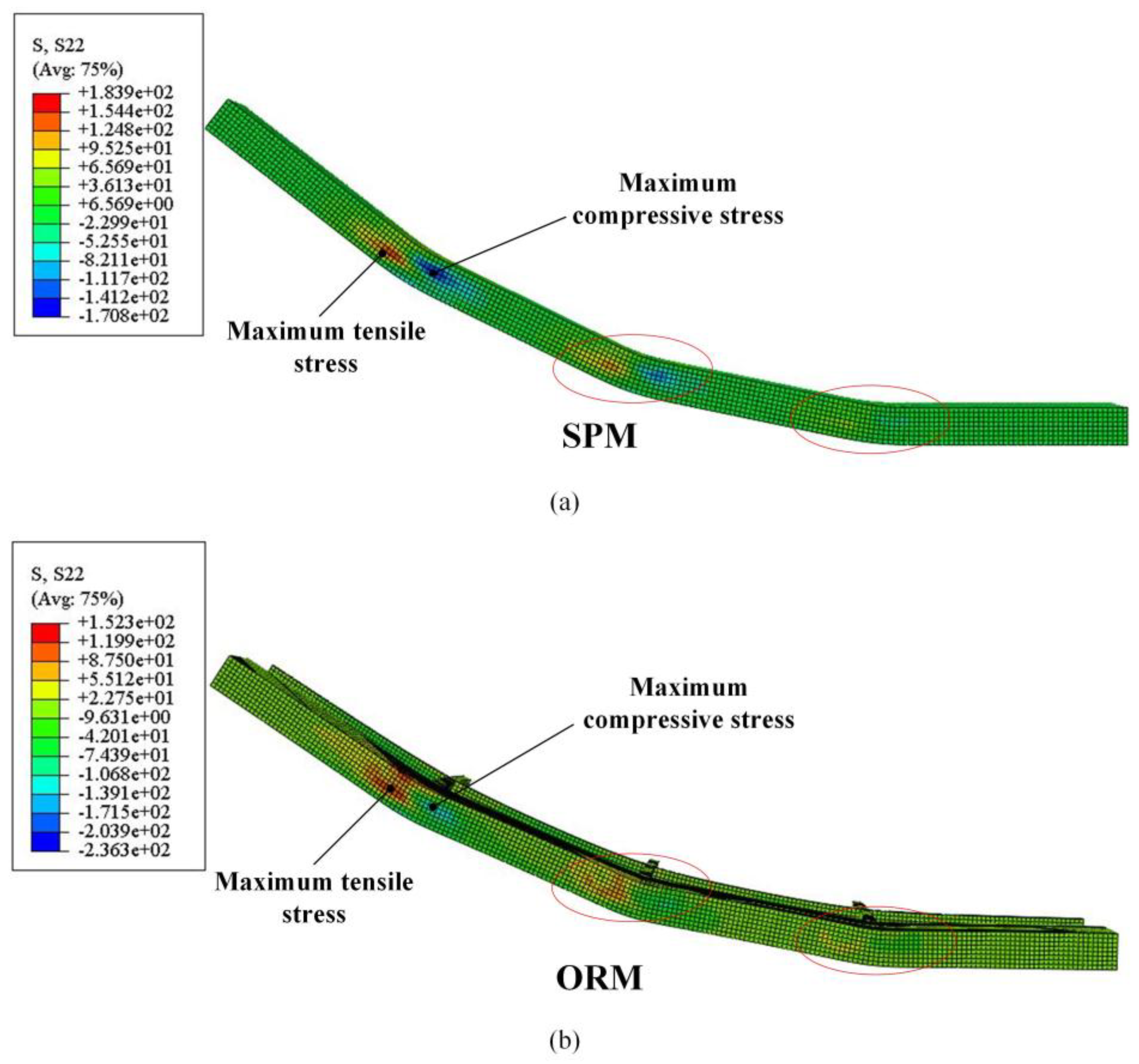
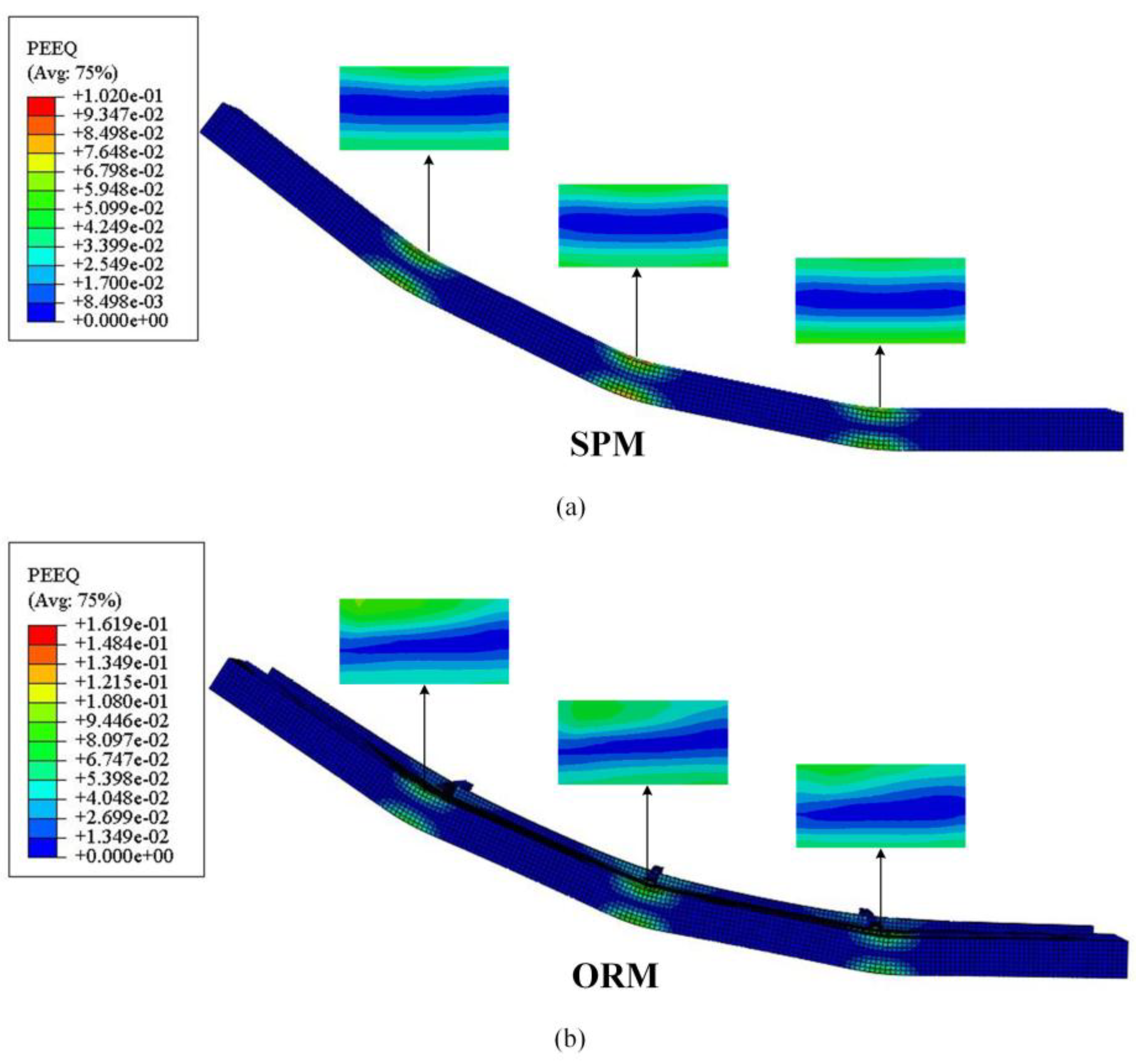
5.1. Distribution of Stress and Strain
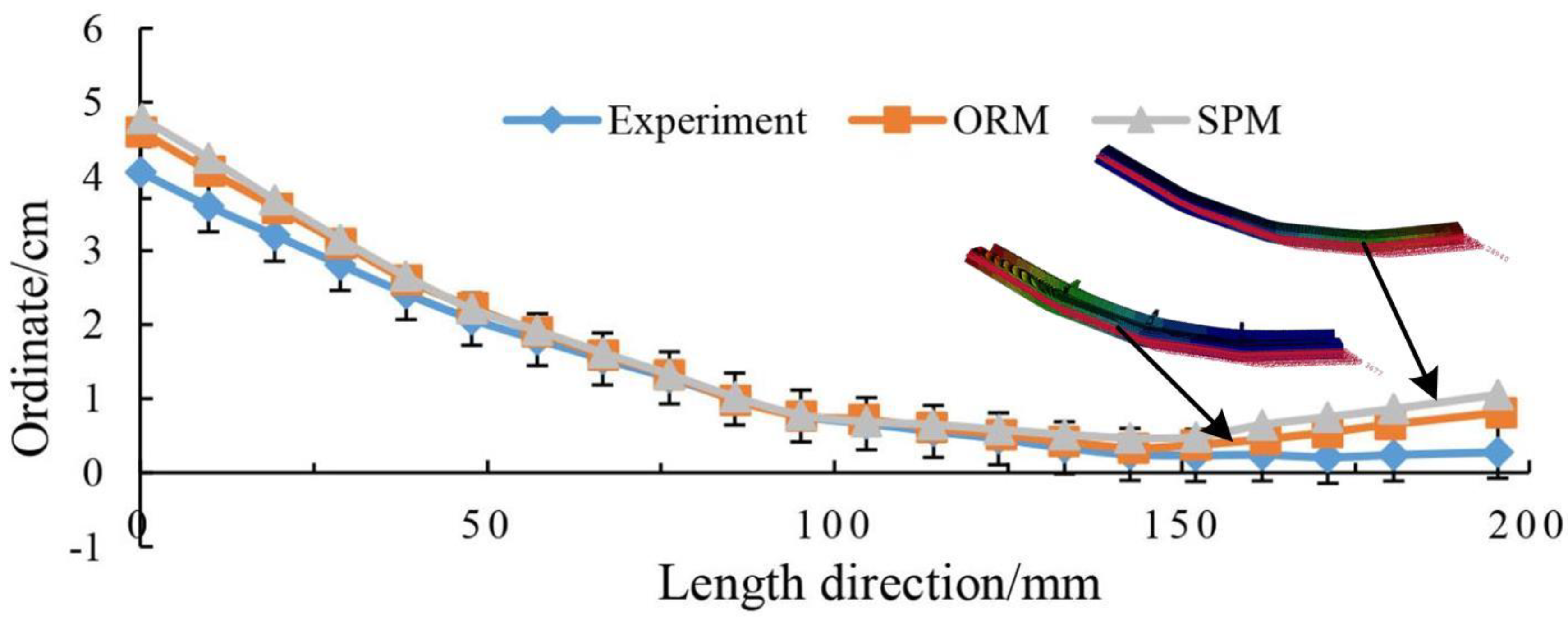
5.2. Contours of the Forming Workpieces
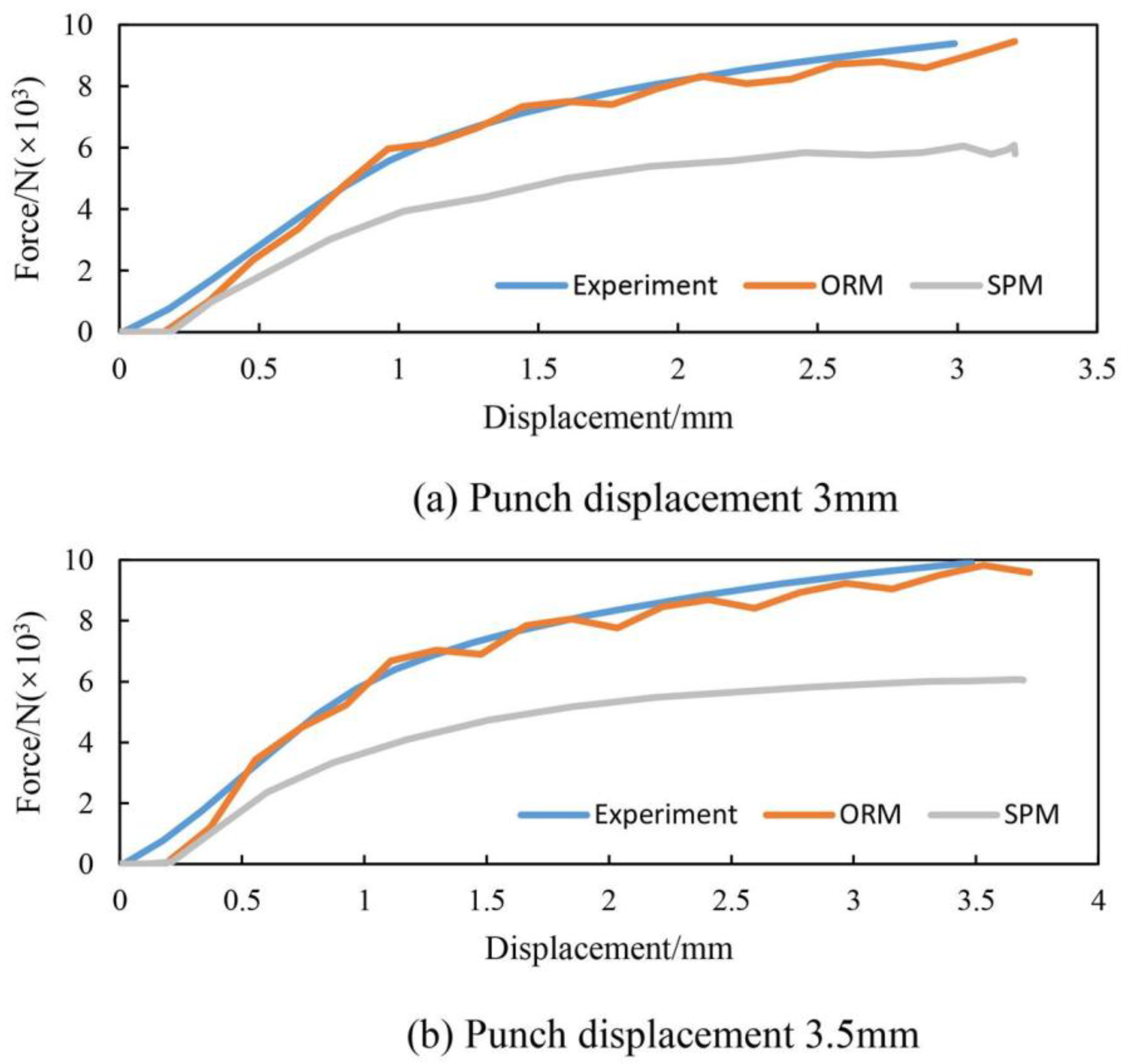
5.3. Comparing the Reaction Force between FE Simulation and Experiment
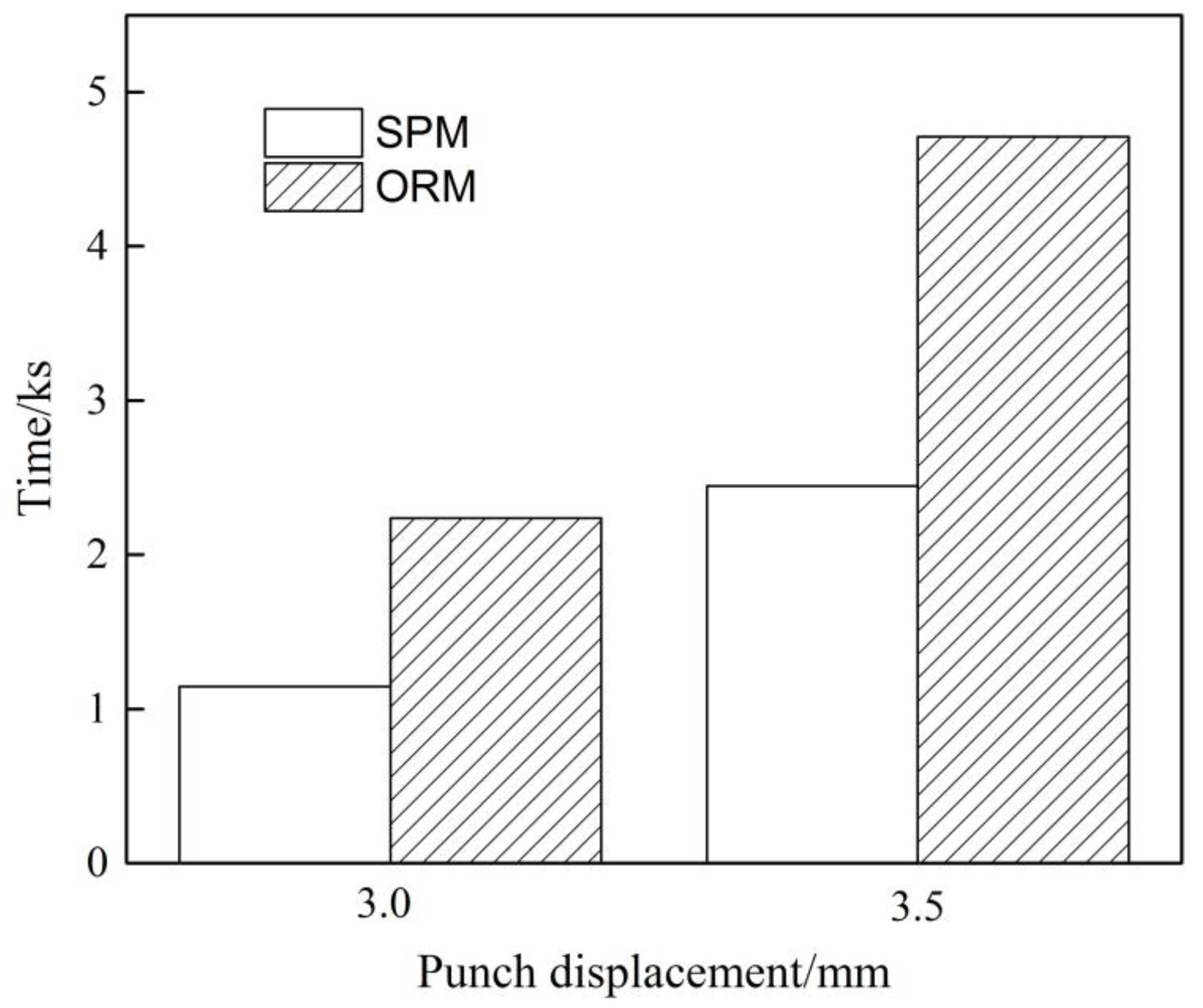
5.4. Efficiency Analysis
6. Conclusions
- (1)
- With the detailed analysis of the bending forming and springback of the SPM and ORM, the equivalent parameters for the SPM including the yield stress , hardening coefficient and hardening exponent are determined and obtained according to the equivalent requirements.
- (2)
- The FE simulation is carried out to simulate the bending forming of the ORM and the SPM. The simulation results indicate that the maximum relative error of Mises stress between the SPM and ORM is 7.78%, and the calculated error of contours between ORM and SPM is less than 13.17%.
- (3)
- The fact that the SPM has a similar stress distribution and contour curve comparing with the ORM under the same forming parameters, suggests that the SPM can replace the ORM in the FE simulation to avoid a large number of mesh generation and in the optimization of bending process to lower the amount of iterative calculation.
- (4)
- Compared with ORM, the calculating efficiency of the FE simulation with SPM is improved significantly (by more than 48%), while ensuring simulation accuracy.
Author Contributions
Funding
Conflicts of Interest
References
- Zeng, Y.S.; Huang, X. Forming technologies of large integral panel. Acta Aeronaut. Astronaut. Sin. 2008, 29, 721–727. [Google Scholar]
- Luo, H.; Li, W.D.; Li, C.; Wan, M. Investigation of creep-age forming of aluminum lithium alloy stiffened panel with complex structures and variable curvature. Int. J. Adv. Manuf. Technol. 2017, 91, 3265–3271. [Google Scholar] [CrossRef]
- Liu, C.G.; Li, J.; Dong, Y.N.; Zhang, X.G.; Yue, T. Fracture prediction in the forming of aircraft Al stiffeners using multi-point dies. Int. J. Adv. Manuf. Technol. 2017, 90, 3109–3118. [Google Scholar] [CrossRef]
- Thipprakmas, S. Finite element analysis of punch height effect on V-bending angle. Mater. Des. 2010, 31, 1593–1598. [Google Scholar] [CrossRef]
- Kuroda, K.; Kawakami, T.; Okui, T.; Akiyama, M.; Kiuchi, M. Influential factor to dimensional precision of cold-drawn tubes. Proc. Inst. Mech. Eng. B J. Eng. 2015, 229, 100–109. [Google Scholar] [CrossRef]
- Panthi, S.K.; Ramakrishnan, N.; Ahmed, M.; Singh, S.S.; Goel, M.D. Finite Element Analysis of sheet metal bending process to predict the springback. Mater. Des. 2010, 31, 657–662. [Google Scholar] [CrossRef]
- Li, W.D.; Wan, M. Press bending equivalent simulation model of integrally reinforced panel. J. Beijing. Univ. Aeronaut. Astronaut. 2014, 40, 1537–1542. [Google Scholar]
- Chongthairungruang, B.; Uthaisangsuk, V.; Suranuntchai, S.; Jirathearanat, S. Springback prediction in sheet metal forming of high strength steels. Mater. Des. 2013, 50, 253–266. [Google Scholar] [CrossRef]
- Cao, T.S. Models for ductile damage and fracture prediction in cold bulk metal forming processes: A review. Int. J. Mater. Form. 2015, 10, 1–33. [Google Scholar] [CrossRef]
- Wen, H.B.; Li, W.D.; Wan, M. Prediction and analysis of stiffener buckling in press bend forming of integral panels. J. Plast. Eng. 2013, 20, 56–60. [Google Scholar]
- Benedetti, M.; Fontanari, V.; Monelli, B.; Tassan, M. Single-point incremental forming of sheet metals: Experimental study and numerical simulation. Proc. Inst. Mech. Eng. B J. Eng. 2017, 231, 301–312. [Google Scholar] [CrossRef]
- Fu, Z.M.; Tian, X.L.; Chen, W.; Hu, B.K.; Yao, X.Y. Analytical modeling and numerical simulation for three-roll bending forming of sheet metal. Int. J. Adv. Manuf. Technol. 2013, 69, 1639–1647. [Google Scholar] [CrossRef]
- Xia, J.; Lu, S.H. 3D FEM Simulation and Experimental Research of Springback in Bending Process of Aluminum Alloy Sheet. Key Eng. Mater. 2010, 431–432, 487–490. [Google Scholar]
- Muhammad, A.A.; Ala, Q. Numerical simulation of sheet metal forming: A review. Int. J. Adv. Manuf. Technol. 2017, 89, 1235–1250. [Google Scholar]
- Ghaei, A.; Green, D.E.; Aryanpour, A. Springback simulation of advanced high strength steels considering nonlinear elastic unloading—Reloading behavior. Mater. Des. 2015, 88, 461–470. [Google Scholar] [CrossRef]
- Tran, Q.H.; Champliaud, H.; Feng, Z.K.; Dao, T.M. Analysis of the asymmetrical roll bending process through dynamic FE simulations and experimental study. Int. J. Adv. Manuf. Technol. 2014, 75, 1233–1244. [Google Scholar] [CrossRef]
- Zhao, G.Y.; Liu, Y.L.; Yang, H.; Lu, C.H.; Gu, R.J. Three-dimensional finite-elements modeling and simulation of rotary-draw bending process for thin-walled rectangular tube. Mater. Sci. Eng. A Struct. 2009, 499, 257–261. [Google Scholar] [CrossRef]
- Fu, Z.M.; Chen, W.; Tian, X.L.; Hu, B.K. Modeling and simulation for multiple-step incremental air-bending forming of sheet metal. Int. J. Adv. Manuf. Technol. 2014, 72, 561–570. [Google Scholar] [CrossRef]
- Fu, Z.M.; Mo, J.H. Multiple-Step Incremental Air-Bending Forming of High-Strength Sheet Metal Based on Simulation Analysis. Mater. Manuf. Process. 2010, 25, 808–816. [Google Scholar] [CrossRef]
- Henrard, C.; Bouffioux, C.; Eyckens, P.; Sol, H.; Duflou, J.R.; Houtte, P.V.; Bael, A.V.; Duchêne, L.; Habraken, A.M. Forming forces in single point incremental forming: Prediction by finite element simulations, validation and sensitivity. Comput. Mech. 2011, 47, 573–590. [Google Scholar] [CrossRef]
- Bui, Q.V.; Ponthot, J.P. Numerical simulation of cold roll-forming processes. J. Mater. Process. Technol. 2008, 202, 275–282. [Google Scholar] [CrossRef]
- Yan, Y.; Wan, M.; Wang, H.B. FEM equivalent model for press bend forming of aircraft integral panel. Trans. Nonferrous Met. Soc. 2009, 19, 414–421. [Google Scholar] [CrossRef]
- Xia, L.J.; Jin, X.D.; Wang, Y.B. The equivalent analysis of honeycomb sandwich plates for satellite structure. J. Shanghai Jiaotong Univ. 2003, 37, 999–1001. [Google Scholar]
- Zhang, T.L.; Ding, Y.L.; Jin, H.B. Comparative analysis of equivalent models for honeycomb sandwich plates. Chin. J. Appl. Mech. 2011, 28, 275–282. [Google Scholar]
- Liang, S.; Chen, H.L.; Chen, T.N.; Liang, T.X. Analytical study of the equivalent elastic parameters for a honeycomb core. J. Aeronaut. Mater. 2004, 24, 26–31. [Google Scholar]
- Chen, X.A.; Zhang, Y.Y.; Hu, G.T.; Zeng, Q.N.; Liu, H.; Fang, J.Z. Analysis of Equivalent Parameters for Honeycomb Sandwich Mirror. Adv. Mater. Res. 2014, 842, 397–400. [Google Scholar] [CrossRef]
- Yang, J.S.; Li, D.L.; Ma, L.; Zhang, S.Q.; Schröder, K.U.; Schmidt, R. Numerical static and dynamic analyses of improved equivalent models for corrugated sandwich structures. Mech. Adv. Mater. Struct. 2018, 1–12. [Google Scholar] [CrossRef]
- Trzepiecinski, T.; Lemu, H.G. Effect of Computational Parameters on Springback Prediction by Numerical Simulation. Metals(Basel) 2017, 7, 380. [Google Scholar] [CrossRef]
- Wagoner, R.H.; LI, M. Simulation of springback: Through-thickness integration. Int. J. Plast. 2007, 23, 345–360. [Google Scholar] [CrossRef]
- Lai, S.B.; Yu, D.Y.; Chen, T.X. Plastic Equivalent Model for Integrally Stiffened Panel in Bending Forming. J. Astronaut. 2012, 33, 809–815. [Google Scholar]
- Abebe, M.; Yoon, J.S.; Kang, B.S. Radial Basis Functional Model of Multi-Point Dieless Forming Process for Springback Reduction and Compensation. Metals (Basel) 2017, 7, 528. [Google Scholar] [CrossRef]
- Feng, Z.K.; Champliaud, H. Three-stage process for improving roll bending quality. Simul. Model. Pract. Theory 2011, 19, 887–898. [Google Scholar] [CrossRef]
- Feng, Z.K.; Champliaud, H. Modeling and simulation of asymmetrical three-roll bending process. Simul. Model. Pract. Theory 2011, 19, 1913–1917. [Google Scholar] [CrossRef]
- Tan, J.Q.; Zhan, M.; Gao, P.F.; Li, H.W. Electromagnetic Forming Rules of a Stiffened Panel with Grid Ribs. Metals (Basel). 2017, 7, 559. [Google Scholar] [CrossRef]
- Anokye-Siribor, K.; Singh, U.P. A new analytical model for pressbrake forming using in-process identification of material characteristics. J. Mater. Process. Technol. 2000, 99, 103–112. [Google Scholar] [CrossRef]
- Liu, B.; Villavicencio, R.; Soares, C.G. Experimental and numerical analysis of residual stresses and strains induced during cold bending of thick steel plates. Mar. Struct. 2018, 57, 121–132. [Google Scholar] [CrossRef]
- Jiang, Z.Q.; Yang, H.; Zhan, M.; Yue, Y.B.; Liu, J.; Xu, X.D.; Li, G.J. Establishment of a 3D FE model for the bending of a titanium alloy tube. Int. J. Mech. Sci. 2010, 52, 1115–1124. [Google Scholar] [CrossRef]
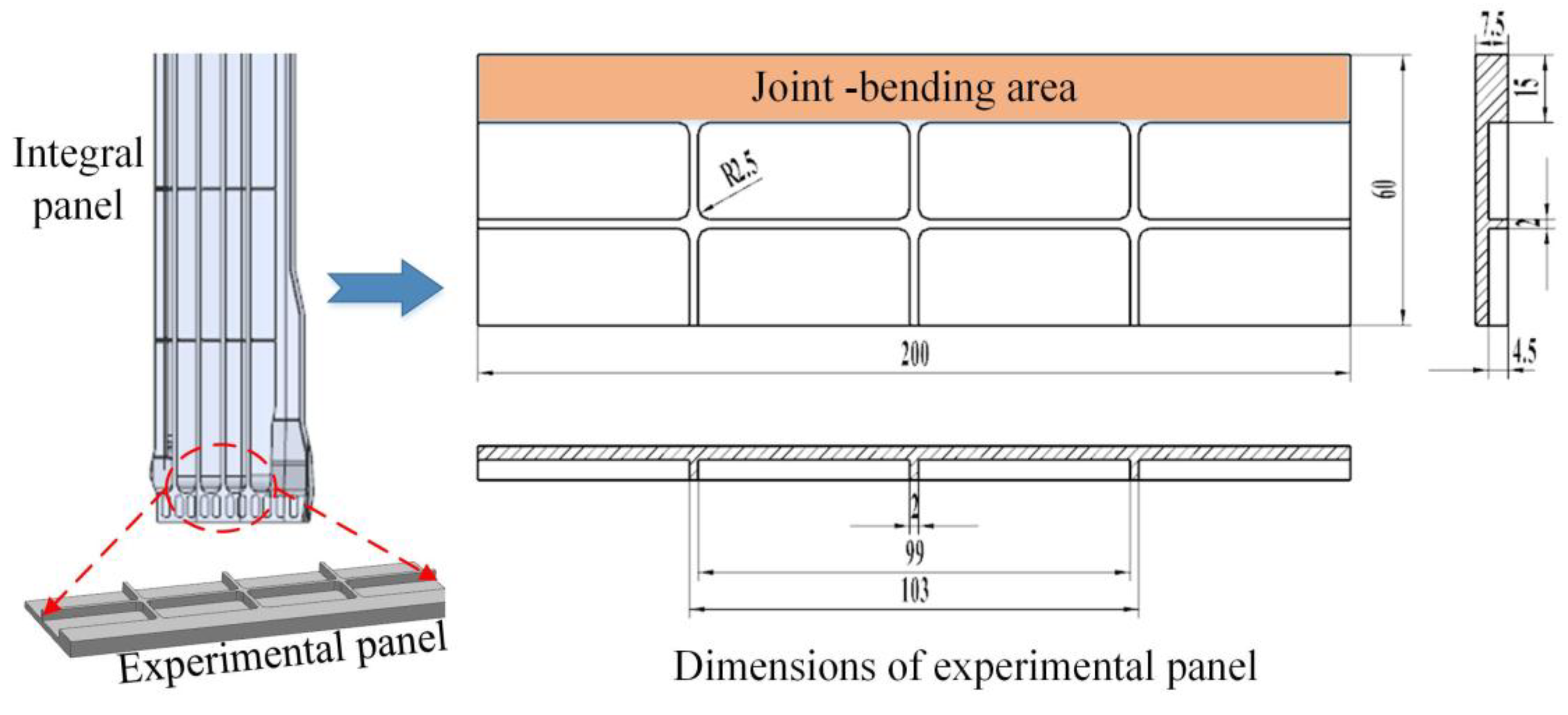
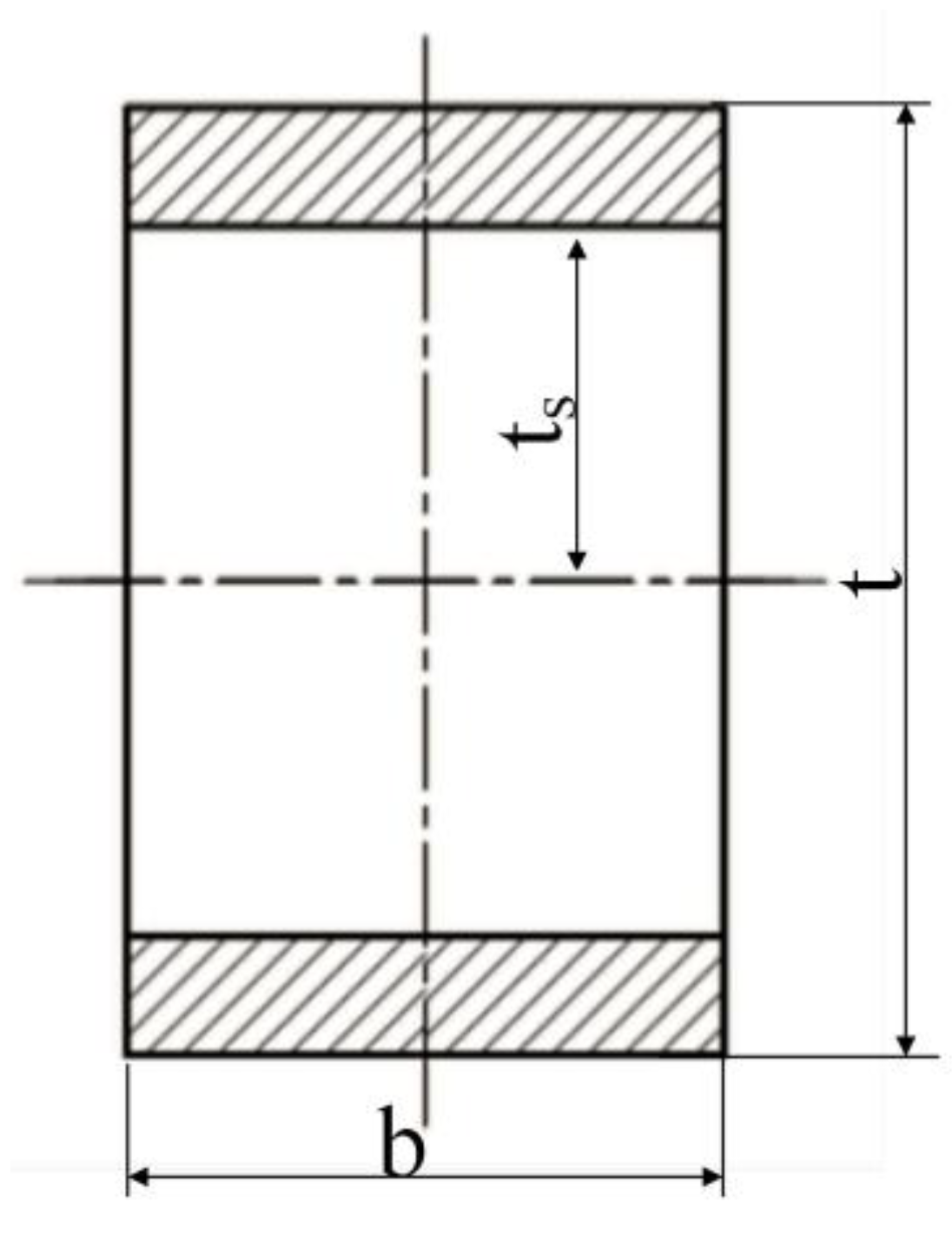
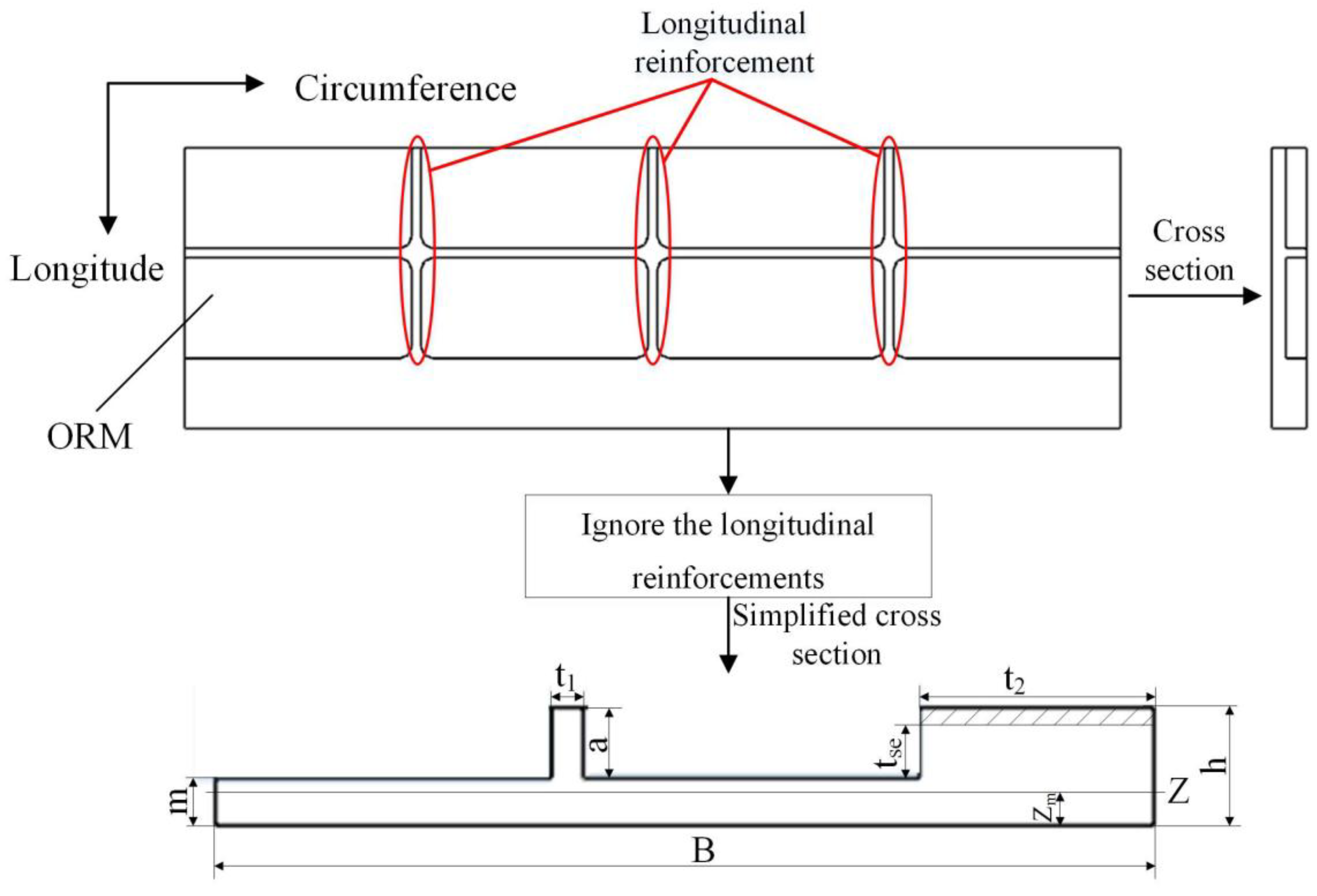
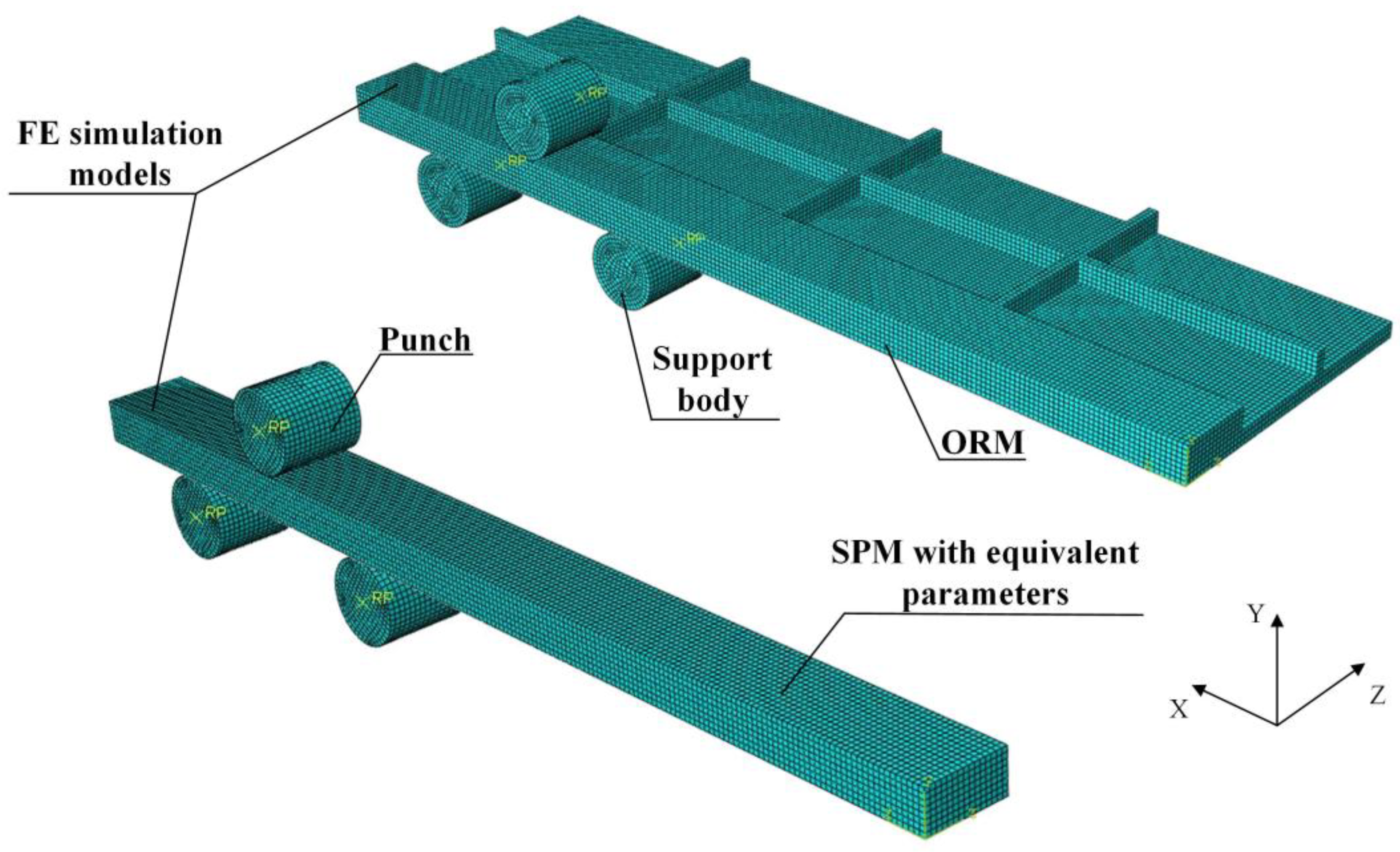
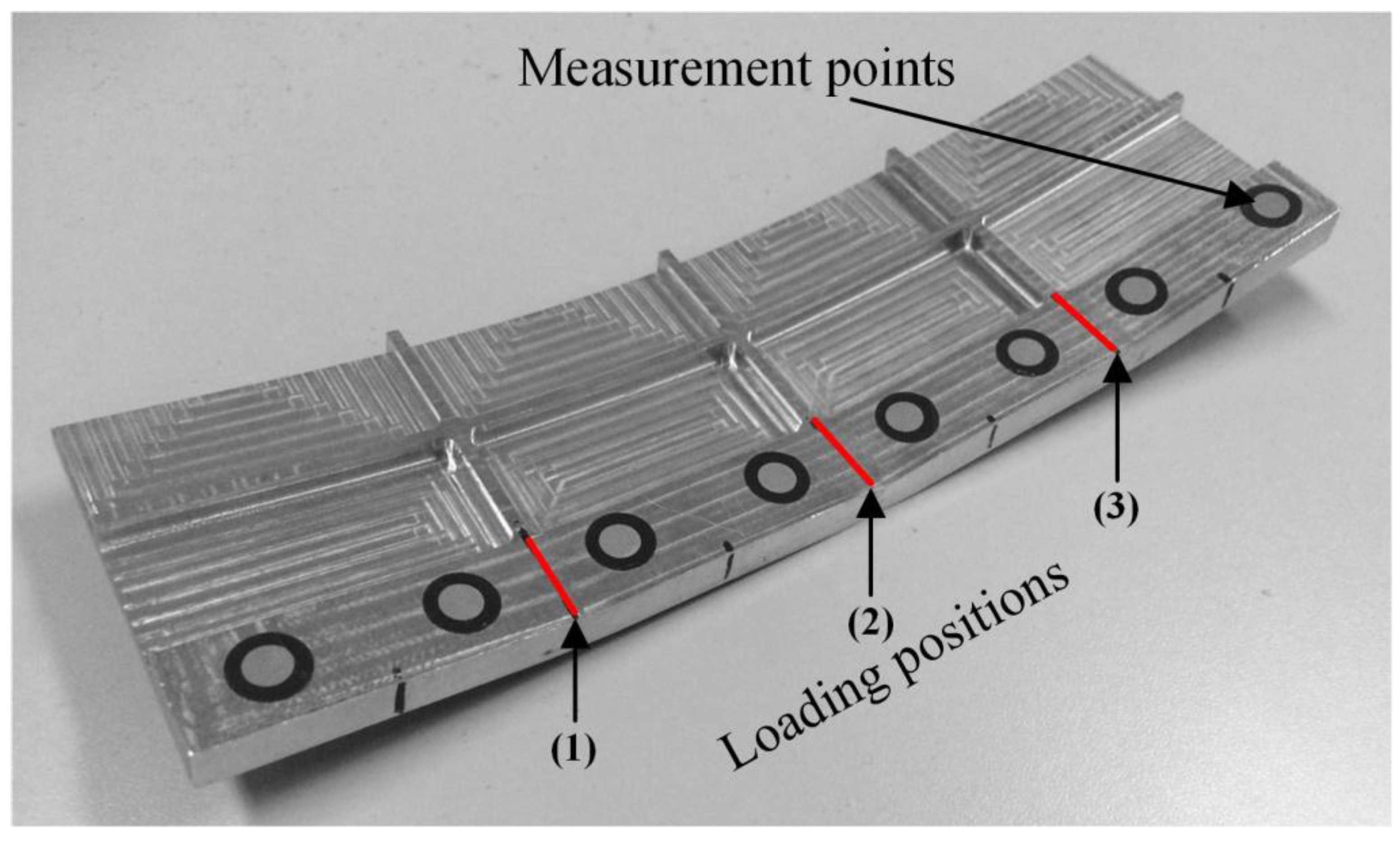
| Items | Parameters | Values | Items | Parameters | Values | ||
|---|---|---|---|---|---|---|---|
| FE model parameters | ORM | L | 200 mm | Material properties | ORM | 66,000 MPa | |
| B | 60 mm | 0. 33 | |||||
| h | 7.5 mm | 442 MPa | |||||
| t1 | 2 mm | 778.8 | |||||
| t2 | 15 mm | 0.73 | |||||
| a | 4.5 mm | SPM | 66,000 MPa | ||||
| SPM | l | 200 mm | 0.33 | ||||
| b | 15 mm | 339.87 MPa | |||||
| t | 7.5 mm | 363.635 | |||||
| Tools | d1,d2 | 15 mm | 0.148 | ||||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, M.; Tian, X.; Li, W.; Shi, X. An Equivalent Calculation Method for Press-Braking Bending Analysis of Integral Panels. Metals 2018, 8, 364. https://doi.org/10.3390/met8050364
Zhang M, Tian X, Li W, Shi X. An Equivalent Calculation Method for Press-Braking Bending Analysis of Integral Panels. Metals. 2018; 8(5):364. https://doi.org/10.3390/met8050364
Chicago/Turabian StyleZhang, Min, Xitian Tian, Wupeng Li, and Xiaolin Shi. 2018. "An Equivalent Calculation Method for Press-Braking Bending Analysis of Integral Panels" Metals 8, no. 5: 364. https://doi.org/10.3390/met8050364
APA StyleZhang, M., Tian, X., Li, W., & Shi, X. (2018). An Equivalent Calculation Method for Press-Braking Bending Analysis of Integral Panels. Metals, 8(5), 364. https://doi.org/10.3390/met8050364




