Rheological Characterization of Semi-Solid Metals: A Review
Abstract
1. Introduction
2. Rheological Classification of SSM
3. Experimental Methods for the Measurements of Rheological Properties
3.1. Shear Experiments in Rotational Rheometers
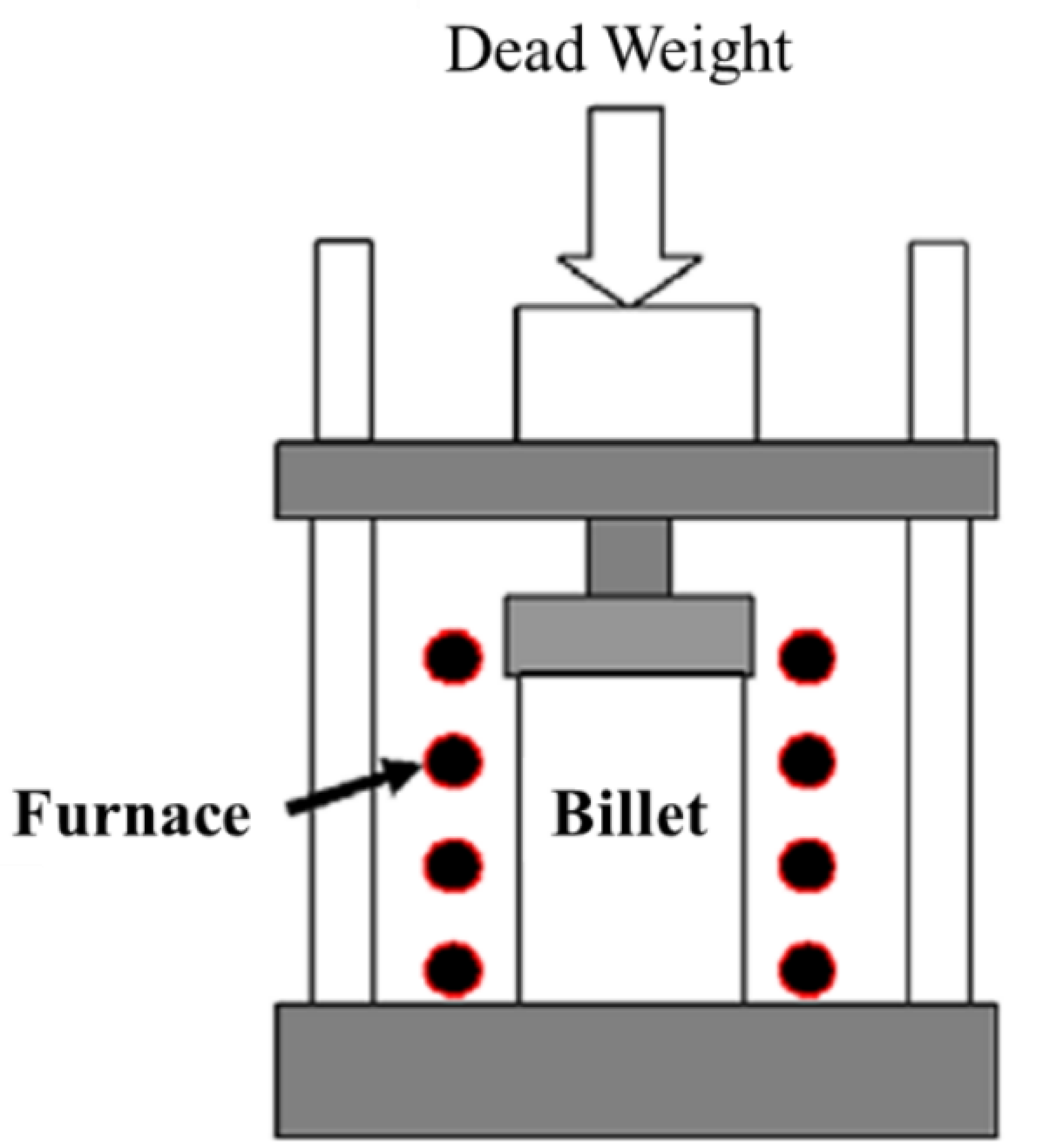
3.2. Compression Tests
4. Modelling of Rheological Properties
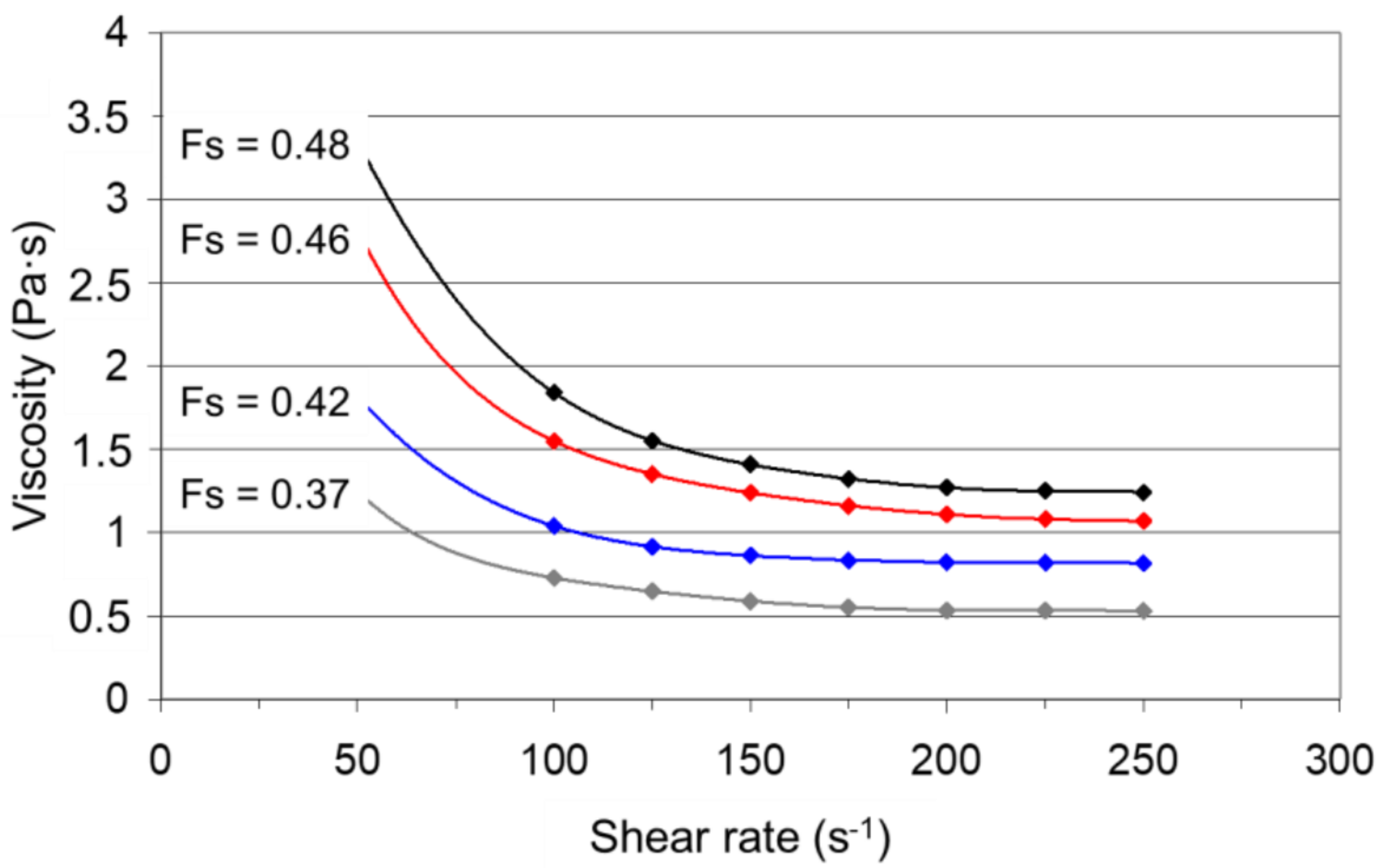
5. Steady State Condition: Time-Independent Properties
6. Non-Viscous Properties
6.1. Yield Stress
- the static one is a constant value and it is achieved after long resting time,
- the dynamic yield stress holds for the period where the yield stress increases with time when the material is in rest after being sheared and
- the isostructural one corresponding to the value which would be measured immediately after shearing the material.
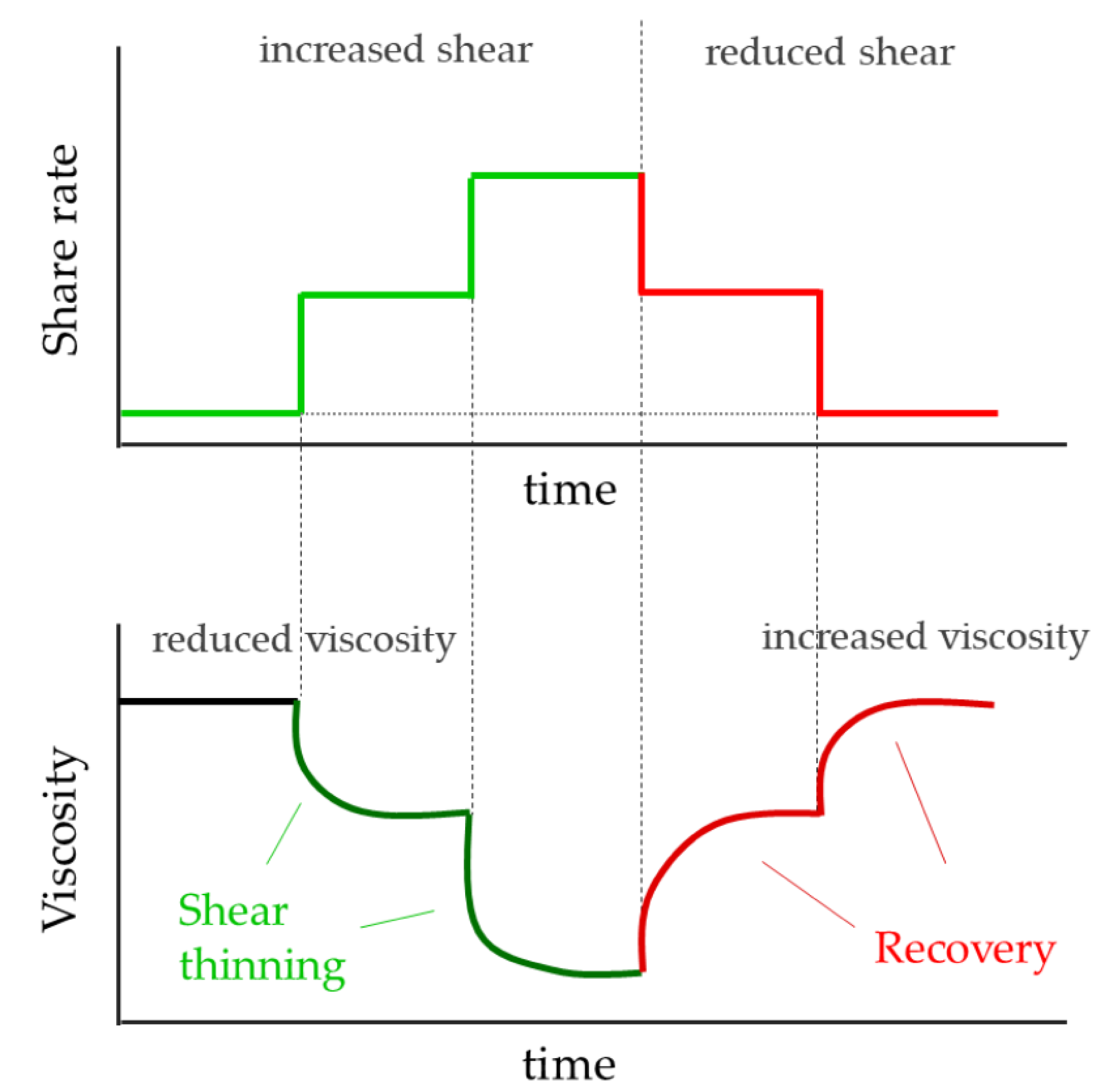
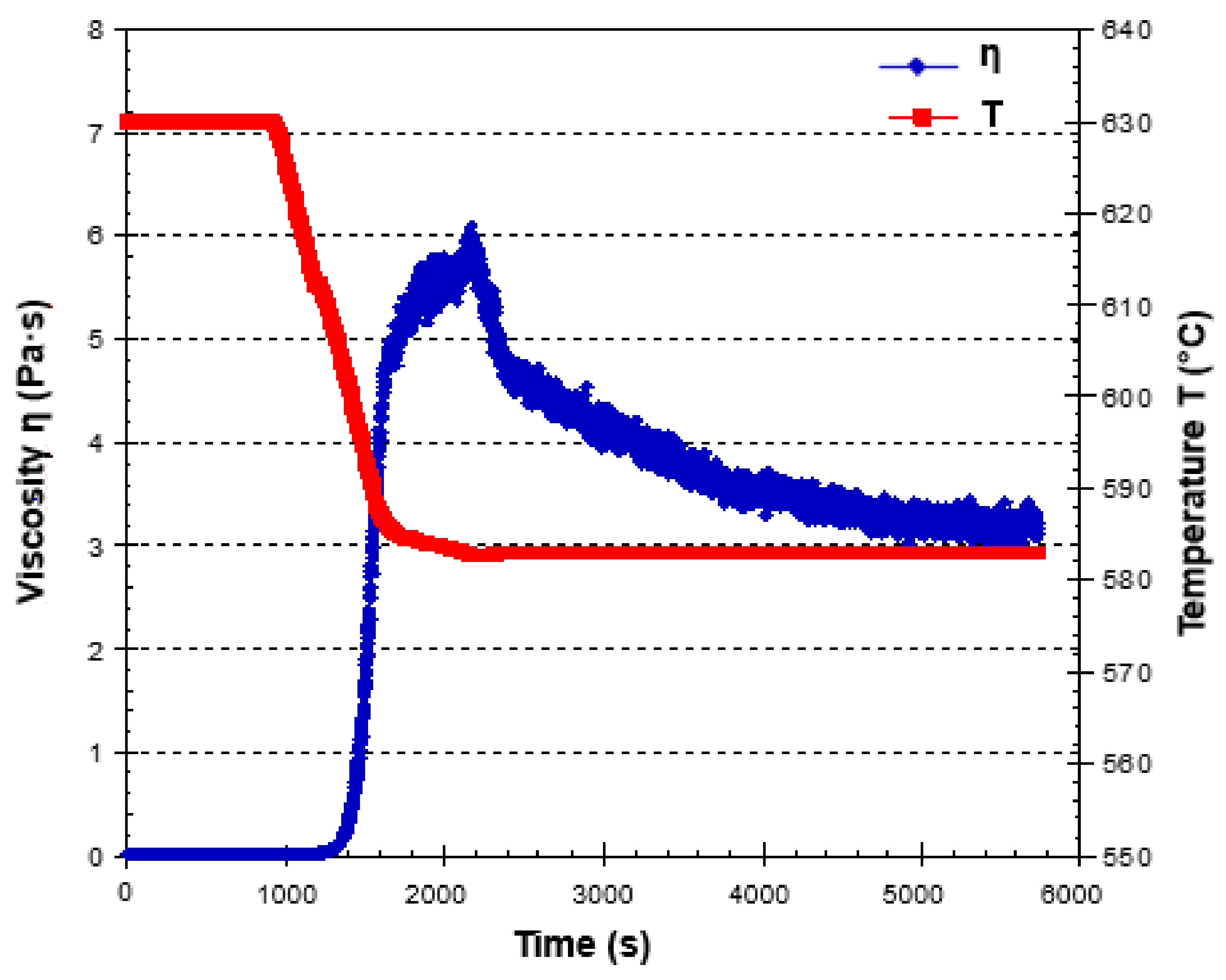
6.2. Transient Behavior: Time-Dependent Properties
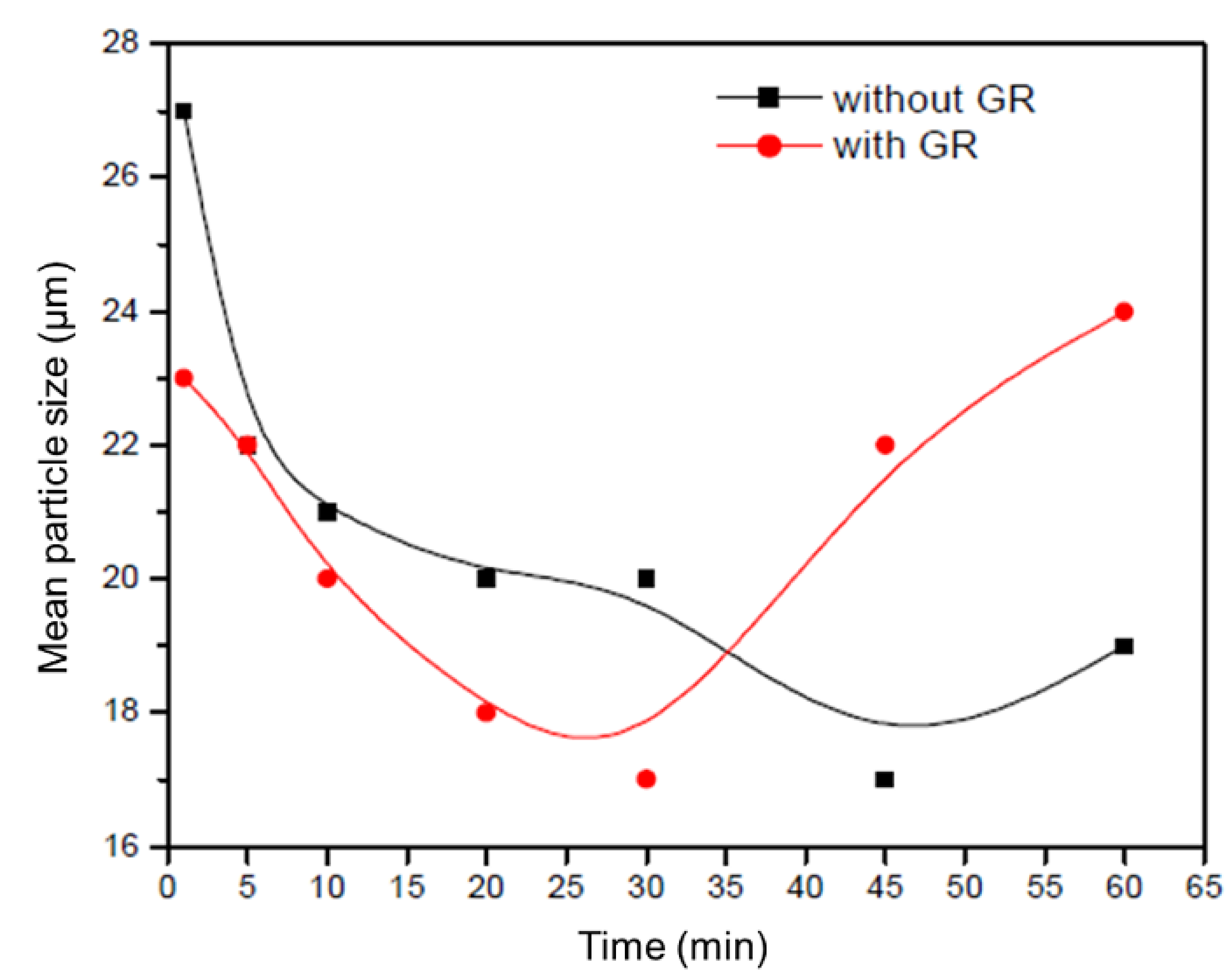
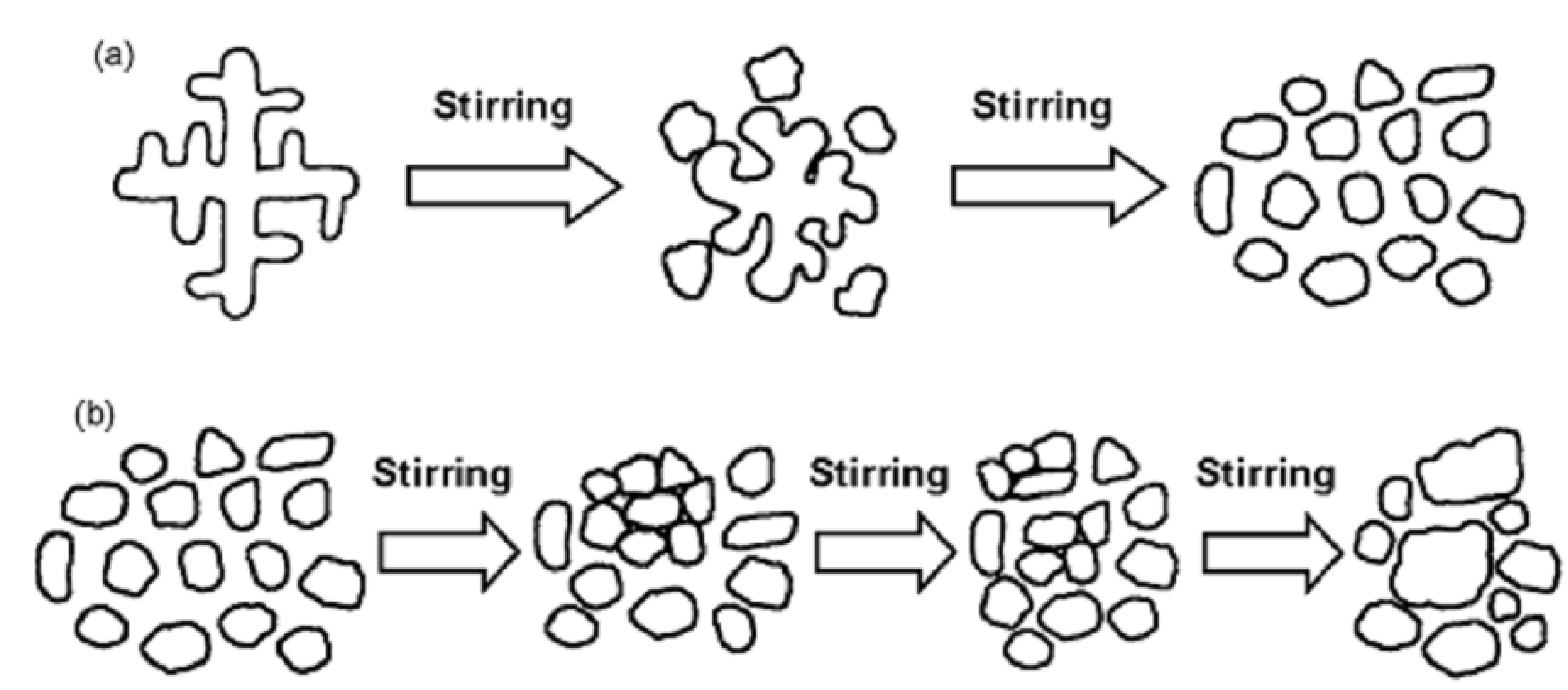
7. Ostwald Ripening
8. Summary
Conflicts of Interest
References
- Flemings, M.C. Behavior of metal alloys in the semisolid state. Metall. Trans. A 1991, 22, 957–981. [Google Scholar] [CrossRef]
- Hirt, G.; Kopp, R. Thixoforming: Semi-Solid Metal Processing; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2009. [Google Scholar]
- Pola, A.; Montesano, L.; Tocci, M.; La Vecchia, G.M. Influence of Ultrasound Treatment on Cavitation Erosion Resistance of AlSi7 Alloy. Materials 2017, 10, 256. [Google Scholar] [CrossRef] [PubMed]
- Barnes, H.A.; Hutton, J.F.; Walters, K. An Introduction to Rheology; Elsevier Science: Amsterdam, The Netherlands, 1993. [Google Scholar]
- Bakhtiyarov, S.I.; Overfelt, R.A. Measurement of liquid metal viscosity by rotational technique. Acta Mater. 1999, 47, 4311–4319. [Google Scholar] [CrossRef]
- Modigell, M.; Koke, J. Rheological modelling on semi-solid metal alloys and simulation of thixocasting processes. J. Mater. Process. Tech. 2001, 111, 53–58. [Google Scholar] [CrossRef]
- Atkinson, H.V. Modelling the semisolid processing of metallic alloys. Prog. Mater. Sci. 2005, 50, 341–412. [Google Scholar] [CrossRef]
- Atkinson, H.; Favier, V. Does Shear Thickening Occur in Semisolid Metals? Metall. Mater. Trans. A 2016, 47, 1740–1750. [Google Scholar] [CrossRef]
- Lashkari, O.; Ghomashchi, R. The implication of rheology in semi-solid metal processes: An overview. J. Mater. Process. Tech. 2007, 182, 229–240. [Google Scholar] [CrossRef]
- Kirkwood, D.H.; Suery, M.; Kapranos, P.; Atkinson, H.V.; Young, K.P. Semi-Solid Processing of Alloys; Springer: Berlin, Germany, 2009. [Google Scholar]
- McLelland, A.R.A.; Henderson, N.G.; Atkinson, H.V.; Kirkwood, D.H. Anomalous rheological behaviour of semi-solid alloy slurries at low shear rates. Mater. Sci. Eng. A 1997, 232, 110–118. [Google Scholar] [CrossRef]
- Hirt, G.; Uggowitzer, P.J.; Bleck, W.; Friedrich, B.; Schneider, J.M.; Modigell, M.; Kopp, R.; Bobzin, K.; Telle, R.; Bührig-Polaczek, A.; et al. Final Report of the Joint Research Program SFB289 Forming of Metals in the Semi-Solid State and Their Properties; RWTH-Aachen University: Aachen, Germany, 2007. [Google Scholar]
- Quaak, C.J.; Katgermann, L.; Kool, W.H. Viscosity Evaluation of Partially Solidified Aluminium Slurries after a Shear Rate Jump. In Proceedings of the 4th International Conference on Semi-Solid Processing of Alloys and Composites, Sheffield, UK, 19–21 June 1996. [Google Scholar]
- Windhab, E.J. Process–Structure–Rheology Relationships of Multiphase Food Systems. In Proceedings of the 1st International Symposium on Food Rheology and Structure, Zurich, Switzerland, 16–21 March 1997. [Google Scholar]
- Modigell, M.; Hufschmidt, M. Dynamic and Static Yield Stress of Metallic Suspensions. Solid State Phenom. 2006, 116–117, 587–590. [Google Scholar] [CrossRef]
- Moll, A.; Modigell, M. Yield stress phenomena in semi-solid alloys. Int. J. Mater. Form. 2010, 3, 779–782. [Google Scholar] [CrossRef]
- Koke, J.; Modigell, M. Flow behaviour of semi-solid metal alloys. J. Non-Newton. Fluid. Mech. 2003, 112, 141–160. [Google Scholar] [CrossRef]
- Koke, J. Rheologie Teilerstarrter Metalllegierungen; Fortschr.-Ber. VDI Reihe 5 Nr. 620; VDI Verlag: Düsseldorf, Germany, 2001; Volume 620. [Google Scholar]
- Harboe, S.J. Investigation of Rheological and Microstructural Properties of Semi-Solid Aluminium Copper Alloy during Isothermal Shear; Shaker Verlag GmbH: Aachen, Germany, 2017. [Google Scholar]
- Zabler, S.; Rueda, A.; Rack, A.; Riesemeier, H.; Zaslansky, P.; Manke, I.; Garcia-Moreno, F.; Benhart, J. Coarsening of grain-refined semi-solid Al-Ge32 alloy: X-ray microtomography and in situ radiography. Acta Mater. 2007, 55, 5045–5055. [Google Scholar] [CrossRef]
- Cai, B.; Karagadde, S.; Rowley, D.; Marrow, T.J.; Connolley, T.; Lee, P.D. Time-resolved synchrotron tomographic quantification of deformation-induced flow in a semi-solid equiaxed dendritic Al-Cu alloy. Scr. Mater. 2015, 103, 69–72. [Google Scholar] [CrossRef]
- Kareh, K.M.; Lee, P.D.; Atwood, R.C.; Connolley, T.; Gourlay, C.M. Revealing the micromechanisms behind semi-solid metal deformation with time-resolved X-ray tomography. Nat. Commun. 2014, 5, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Terzi, S.; Salvo, L.; Suery, M.; Dahle, A.; Boller, E. In situ microtomography investigation of microstructural evolution in Al-Cu alloys during holding in semi-solid state. Trans. Nonferr. Metals Soc. China 2010, 20, s734–s738. [Google Scholar] [CrossRef]
- Modigell, M.; Pola, A.; Suery, M.; Zang, C. Investigation of correlations between shear history and microstructure of semi-solid alloys. Solid State Phenom. 2013, 192–193, 251–256. [Google Scholar] [CrossRef]
- Kang, C.G.; Choi, J.S.; Kim, K.H. The effect of strain rate on macroscopic behavior in the compression forming of semi-solid aluminum alloy. J. Mater. Process. Tech. 1999, 88, 159–168. [Google Scholar] [CrossRef]
- Macosko, C.W. Rheology—Principles, Measurements, and Applications; Wiley-VCH, Inc.: Hoboken, NJ, USA, 1994. [Google Scholar]
- Van Wazer, J.R.; Lyons, J.; Lim, K.; Colwell, R.E. Viscosity and Flow Measurements; Wiley: New York, NY, USA, 1963. [Google Scholar]
- Schummer, P.; Worthoff, R.H. An elementary method for the evaluation of a flow curve. Chem. Eng. Sci. 1978, 33, 759–763. [Google Scholar] [CrossRef]
- Alexandrou, A.N.; Georgiou, G.C.; Economides, E.-A.; Modigell, M. Determining true material constants of semisolid slurries from rotational rheometer data. Solid State Phenom. 2016, 256, 153–172. [Google Scholar] [CrossRef]
- Alexandrou, A.N.; Georgiou, G. On the early breakdown of semisolid suspensions. J. Non-Newton. Fluid Mech. 2007, 142, 199–206. [Google Scholar] [CrossRef]
- Modigell, M.; Pape, L. A comparison of measuring devices used to prevent wall slip in viscosity measurements of metallic suspensions. Solid State Phenom. 2008, 141–143, 307–312. [Google Scholar] [CrossRef]
- Kiljański, T. A method for correction of the wall-slip effect in a Couette rheometer. Rheol. Acta 1989, 28, 61–64. [Google Scholar] [CrossRef]
- Harboe, S.; Modigell, M. Wall slip of semi-solid A356 in couette rheometers. AIP Conf. Proc. 2011, 1353, 1075–1080. [Google Scholar] [CrossRef]
- Tocci, M.; Zang, C.; Cadórniga Zueco, I.; Pola, A.; Modigell, M. Rheological properties of liquid metals and semisolid materials at low solid fraction. Solid State Phenom. 2016, 256, 133–138. [Google Scholar] [CrossRef]
- Solek, K.; Rogal, L.; Kapranos, P.; Solek, K.P.; Rogal, L.; Kapranos, P. Evolution of Globular Microstructure and Rheological Properties of Stellite 21 Alloy after Heating to Semisolid State. J. Mater. Eng. Perform. 2017, 26, 115–122. [Google Scholar] [CrossRef][Green Version]
- Yekta, F.H.; Vanini, A.S. Simulation the Flow of Semi-Solid Steel Alloy Using an Enhanced Model. Metals Mater. Int. 2015, 21, 913–922. [Google Scholar] [CrossRef]
- Modigell, M.; Volkmann, T.; Zang, C. A High -Precision Rotational Rheometer for Temperatures up to 1700 °C. Solid State Phenom. 2013, 192–193, 359–364. [Google Scholar] [CrossRef]
- Laxmanan, V.; Flemings, M.C. Deformation of Semi-Solid Sn-15 Pct Pb Alloy. Metall. Trans. A 1980, 11, 1927–1937. [Google Scholar] [CrossRef]
- Nafisi, S.; Lashkari, O.; Ghomashchi, R.; Ajersch, F.; Charette, A. Microstructure and rheological behavior of grain refined and modified semi-solid A356 Al–Si slurries. Acta Mater. 2006, 54, 3503–3511. [Google Scholar] [CrossRef]
- Hu, X.G.; Zhu, Q.; Atkinson, H.V.; Lu, H.X.; Zhang, F.; Dong, H.B.; Kang, Y.L. A time-dependent power law viscosity model and its application in modelling semi-solid die casting of 319s alloy. Acta Mater. 2017, 124, 410–420. [Google Scholar] [CrossRef]
- Becker, E.; Favier, V.; Bigot, R.; Cezard, P.; Langlois, L. Impact of experimental conditions on material response during forming of steel in semi-solid state. J. Mater. Process. Tech. 2010, 210, 1482–1492. [Google Scholar] [CrossRef]
- Becker, E.; Langlois, L.; Favier, V.; Bigot, R. Thermomechanical modelling and simulation of C38 thixoextrusion steel. Solid State Phenom. 2015, 217–218, 130–137. [Google Scholar] [CrossRef]
- Shimahara, H.; Baadjou, R.; Kopp, R.; Hirt, G. Investigation of flow behavior and microstructure on X210CrW12 steel in semi-solid state. Solid State Phenom. 2006, 116–117, 189–192. [Google Scholar] [CrossRef]
- Liu, T.Y.; Atkinson, H.V.; Kapranos, P.; Kirkwood, D.H.; Hogg, S.C. Rapid Compression of Aluminum Alloys and Its Relationship to Thixoformability. Metall. Mater. Trans. A 2003, 34, 1545–1554. [Google Scholar] [CrossRef]
- Hogg, S.C.; Atkinson, H.V.; Kapranos, P. Semi-Solid Rapid Compression Testing of Spray-Formed Hypereutectic Al-Si Alloys. Metall. Mater. Trans. A 2004, 35, 899–910. [Google Scholar] [CrossRef]
- Favier, V.; Atkinson, H.V. Micromechanical modelling of the elastic–viscoplastic response of metallic alloys under rapid compression in the semi-solid state. Acta Mater. 2011, 59, 1271–1280. [Google Scholar] [CrossRef]
- Kim, W.Y.; Kang, C.G.; Kim, B.M. The effect of the solid fraction on rheological behavior of wrought aluminum alloys in incremental compression experiments with a closed die. Mat. Sci. Eng. A 2007, 447, 1–10. [Google Scholar] [CrossRef]
- Joly, P.A.; Mehrabian, R. The rheology of a partially solid alloy. J. Mater. Sci. 1976, 11, 1393–1418. [Google Scholar] [CrossRef]
- Blanco, A.; Azpilgain, Z.; Lozares, J.; Kapranos, P.; Hurtado, I. Rheological characterization of A201 aluminum alloy. Trans. Nonferr. Metals Soc. China 2010, 20, 1638–1642. [Google Scholar] [CrossRef]
- Heidary, D.S.B.; Akhlaghi, F. Experimental Investigation on the Rheological Behavior of Hypereutectic Al-Si Alloys by a Precise Rotational Viscometer. Metall. Mater. Trans. A 2010, 41, 3435–3442. [Google Scholar] [CrossRef]
- Chhabra, R.P.; Richardson, J.F. Non-Newtonian Flow in the Process Industries; Butterworth Heinemann: Oxford, UK, 2004. [Google Scholar]
- Burgos, G.R.; Alexandrou, A.N.; Entov, V. Thixotropic rheology of semisolid metal suspensions. J. Mater. Process. Tech. 2001, 110, 164–176. [Google Scholar] [CrossRef]
- Burgos, G.R.; Alexandrou, A.N. Flow development of Herschel-Bulkley fluids in a sudden three-dimensional square expansion. J. Rheol. 1999, 43, 485–498. [Google Scholar] [CrossRef]
- Ahmed, A.; Alexandrou, A.N. Processing of semi-solid materials using a shear-thickening Bingham fluid model. Am. Soc. Mech. Eng. Fluids Eng. Div. 1994, 179, 83–87. [Google Scholar]
- Barnes, H.A. Thixotropy—A review. J. Non-Newton. Fluid Mech. 1997, 70, 1–33. [Google Scholar] [CrossRef]
- Denny, D.A.; Brodkey, R.S. Kinetic Interpretation of Non-Newtonian Flow. J. Appl. Phys. 1962, 33, 2269–2274. [Google Scholar] [CrossRef]
- Moore, F. The rheology of ceramic slips and bodies. Trans. Brit. Ceram. Soc. 1959, 58, 470–494. [Google Scholar]
- Tonmukayakul, N.; Pan, Q.Y.; Alexandrou, A.N.; Apelian, D. Transient Flow Characteristics and Properties of Semi Solid Aluminium Alloy A356. In Proceedings of the 8th International Conference on Semi-Solid Processing of Alloys and Composites, Limassol, Cyprus, 21–23 September 2004; pp. 167–172. [Google Scholar]
- Petera, J.; Kotynia, M. The numerical simulation of the thixoforming. Inzynieria Chem. Proces. 2001, 22, 1103–1108. [Google Scholar]
- Modigell, M.; Koke, J. Time-Dependent Rheological Properties of Semi-Solid Metal Alloys. Mech. Time-Depend. Mater. 1999, 3, 15–30. [Google Scholar] [CrossRef]
- Cross, M.M. Rheology of Non-Newtonian Fluids: A New Flow Equation for Pseudoplastic Systems. J. Colloidal Sci. 1965, 20, 417–437. [Google Scholar] [CrossRef]
- Liu, T.Y. Rheology of Semisolid Alloys under Rapid Change in Shear Rate. Ph.D. Thesis, University of Sheffield, Sheffield, UK, 2002. [Google Scholar]
- Lashkari, O.; Ajersch, F.; Charette, A.; Chen, X.-G. Microstructure and rheological behavior of hypereutectic semi-solid Al–Si alloy under low shear rates compression test. Mater. Sci. Eng. A 2008, 492, 377–382. [Google Scholar] [CrossRef]
- Das, P.; Samanta, S.K.; Dutta, P. Rheological Behavior of Al-7Si-0.3Mg Alloy at Mushy State. Metall. Mater. Trans. B 2015, 46, 1302–1313. [Google Scholar] [CrossRef]
- Brabazon, D.; Browne, D.J.; Carr, A.J. Experimental investigation of the transient and steady state rheological behaviour of Al-Si alloys in the mushy state. Mater. Sci. Eng. A 2003, 356, 69–80. [Google Scholar] [CrossRef]
- Tocci, M.; Pola, A.; La Vecchia, G.M.; Modigell, M. Characterization of a New Aluminium Alloy for the Production of Wheels by Hybrid Aluminium Forging. Procedia Eng. 2015, 109, 303–311. [Google Scholar] [CrossRef][Green Version]
- Fukui, Y.; Nara, D.; Kumazawa, N. Evaluation of the Deformation Behavior of a Semi-solid Hypereutectic Al-Si Alloy Compressed in a Drop-Forge Viscometer. Metall. Mater. Trans. A 2015, 46, 1908–1916. [Google Scholar] [CrossRef]
- Azzi, L.; Ajersch, F. Analytical Modeling of the Rheological Behavior of Semisolid Metals and Composites. Metall. Mater. Trans. B 2006, 37, 1067–1074. [Google Scholar] [CrossRef]
- Cheng, D.C.-H. Yield stress: A time-dependent property and how to measure it. Rheol. Acta 1986, 25, 542–554. [Google Scholar] [CrossRef]
- Barnes, H.A.; Walters, K. The yield stress myth? Rheol. Acta 1985, 24, 323–326. [Google Scholar] [CrossRef]
- Barnes, H.A. The yield stress—A review or ‘παντα ρει’—Everything flows? J. Non-Newton. Fluid Mech. 1999, 81, 133–178. [Google Scholar] [CrossRef]
- Pan, Q.Y.; Apelian, D.; Alexandrou, A.N. Yield Behavior of Commercial Al-Si Alloys in the Semisolid State. Metall. Mater. Trans. B 2004, 35, 1187–1202. [Google Scholar] [CrossRef]
- Solek, K. Identification of the steel viscosity and dynamic yield stress for the numerical modelling of casting simulations in the semi-solid state. Arch. Metall. Mater. 2017, 62, 195–200. [Google Scholar] [CrossRef]
- Harboe, S.; Modigell, M. Yield stress in semi-solid alloys—The dependency on time and deformation history. Key Eng. Mater. 2013, 554–557, 523–535. [Google Scholar] [CrossRef]
- Hufschmidt, M.; Modigell, M.; Petera, J. Modelling and simulation of forming processes of metallic suspensions under non-isothermal conditions. J. Non-Newton. Fluid Mech. 2006, 134, 16–26. [Google Scholar] [CrossRef]
- Gautham, B.P.; Kapur, P.C. Rheological model for short duration response of semi-solid metals. Mater. Sci. Eng. A 2005, 393, 223–228. [Google Scholar] [CrossRef]
- Liu, T.Y.; Atkinson, H.V.; Ward, P.J.; Kirkwood, D.H. Response of Semi-solid Sn-15 Pct Pb to Rapid Shear-Rate Changes. Metall. Mater. Trans. A 2003, 34, 409–417. [Google Scholar] [CrossRef][Green Version]
- Simlandi, S.; Barman, N.; Chattopadhyay, H. Study on Rheological Behavior of Semisolid A356 Alloy during Solidification. Trans. Indian Inst. Metals 2012, 65, 809–814. [Google Scholar] [CrossRef]
- Pouyafar, V.; Sadough, S.A. An Enhanced Herschel–Bulkley Model for Thixotropic Flow Behavior of Semisolid Steel Alloys. Metall. Mater. Trans. B 2013, 44, 1304–1310. [Google Scholar] [CrossRef]
- Liang, L.; Mian, Z. Theoretical research on rheological behavior of semisolid slurry of magnesium alloy AZ91D. Comput. Mater. Sci. 2015, 102, 202–207. [Google Scholar] [CrossRef]
- Omar, M.Z.; Atkinson, H.V.; Kapranos, P. Thixotropy in Semisolid Steel Slurries under Rapid Compression. Metall. Mater. Trans. A 2011, 42, 2807–2819. [Google Scholar] [CrossRef]
- Kirkwood, D.H.; Ward, P.J. Numerical Modelling of Semi-Solid Flow under Processing Conditions. Fundam. Thixoforming Process. 2004, 75, 519–524. [Google Scholar] [CrossRef]
- Becker, E.; Bigot, R.; Rivoirard, S.; Faverolle, P. Experimental investigation of the thixoforging of tubes of low-carbon steel. J. Mater. Process. Tech. 2018, 252, 485–497. [Google Scholar] [CrossRef]
- Lozares, J.; Azpilgain, Z.; Hurtado, I.; Ortubay, R.; Berrocal, S. Thixo Lateral Forging of a Commercial Automotive Spindle From LTT45 Steel Grade. Key Eng. Mater. 2012, 504–506, 357–360. [Google Scholar] [CrossRef]
- Quaak, C.J. Rheology of Partially Solidified Aluminium Alloys and Composites. Ph.D. Thesis, Technische Univesiteit Delft, Delft, The Netherlands, 1996. [Google Scholar]
- Peng, H.; Wang, K.K. Steady State and Transient Rheological Behaviour of a Semi-Solid Tin-Lead Alloy in Simple Shear Flow. In Proceedings of the 4th International Conference Semi-Solid Processing of Alloys and Composites, Sheffield, UK, 19–21 June 1996; pp. 2–9. [Google Scholar]
- Bührig-Polaczek, A.; Afrath, C.; Modigell, M.; Pape, L. Comparison of rheological measurement techniques for semi-solid aluminium alloys. Solid State Phenom. 2006, 116–117, 610–613. [Google Scholar] [CrossRef]
- Tadros, T. (Ed.) Ostwald Ripening. In Encyclopedia of Colloid and Interface Science, 1st ed.; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Courtney, T.H. Microstructural evolution during liquid phase sintering: Part II. Microstructural coarsening. Metall. Trans. A 1976, 8, 685–689. [Google Scholar] [CrossRef]
- Courtney, T.H. A reanalysis of the kinetics of neck growth during liquid phase sintering. Metall. Trans. A 1977, 8, 671–677. [Google Scholar] [CrossRef]
- Poirier, D.R.; Ganesan, S.; Andrews, M.; Ocansey, P. Isothermal coarsening of dendritic equiaxial grains in Al–15.6 wt %Cu alloy. Mater. Sci. Eng. A 1991, 148, 289–297. [Google Scholar] [CrossRef]
- Bender, W.; Ratke, L. Ostwald ripening of liquid phase sintered Cu Co dispersions at high volume fractions. Acta Mater. 1998, 46, 1125–1133. [Google Scholar] [CrossRef]
- Limodin, N.; Salvo, L.; Suery, M.; DiMichiel, M. In situ investigation by X-ray tomography of the overall and local microstructural changes occurring during partial remelting of an Al–15.8 wt % Cu alloy. Acta Mater. 2007, 55, 3177–3191. [Google Scholar] [CrossRef]
- Terzi, S.; Salvo, L.; Suery, M.; Dahle, A.K.; Boller, E. Coarsening mechanisms in a dendritic Al–10% Cu alloy. Acta Mater. 2010, 58, 20–30. [Google Scholar] [CrossRef]
- Lifshitz, I.M.; Sloyozov, V.V. The kinetics of precipitation from supersaturated solid solutions. J. Phys. Chem. Solids 1961, 19, 35–50. [Google Scholar] [CrossRef]
- Wagner, C. Theorie der alterung von niederschlägen durch umlösung. Z. Elektrochem. 1961, 65, 581–591. [Google Scholar]
- Modigell, M.; Pola, A. Modeling of shear induced coarsening effects in semi-solid alloys. Trans. Nonferr. Metals Soc. China 2010, 20, 1696–1701. [Google Scholar] [CrossRef]
- Yang, Y.S.; Tsao, C.-Y.A. Viscosity and structure variations of Al–Si alloy in the semi-solid state. J. Mater. Sci. 1997, 32, 2087–2092. [Google Scholar] [CrossRef]
- Sukumaran, K.; Pai, B.C.; Chakraborty, M. The effect of isothermal mechanical stirring on an Al–Si alloy in the semisolid condition. Mater. Sci. Eng. A 2004, 369, 275–283. [Google Scholar] [CrossRef]
- Barman, N.; Dutta, P. Rheology of A356 Alloy during Solidification under Stirring. Trans. Indian Inst. Metals 2014, 67, 101–104. [Google Scholar] [CrossRef]
- Rogal, L.; Dutkiewicz, J.; Atkinson, H.V.; Lityńska-Dobrzyńska, L.; Czeppe, T.; Modigell, M. Characterization of semi-solid processing of aluminium alloy 7075 with Sc and Zr additions. Mater. Sci. Eng. A 2013, 580, 362–373. [Google Scholar] [CrossRef]
- Chen, H.I.; Chen, J.C.; Liao, J.J. The influence of shearing conditions on the rheology of semi-solid magnesium alloy. Mater. Sci. Eng. A 2008, 487, 114–119. [Google Scholar] [CrossRef]


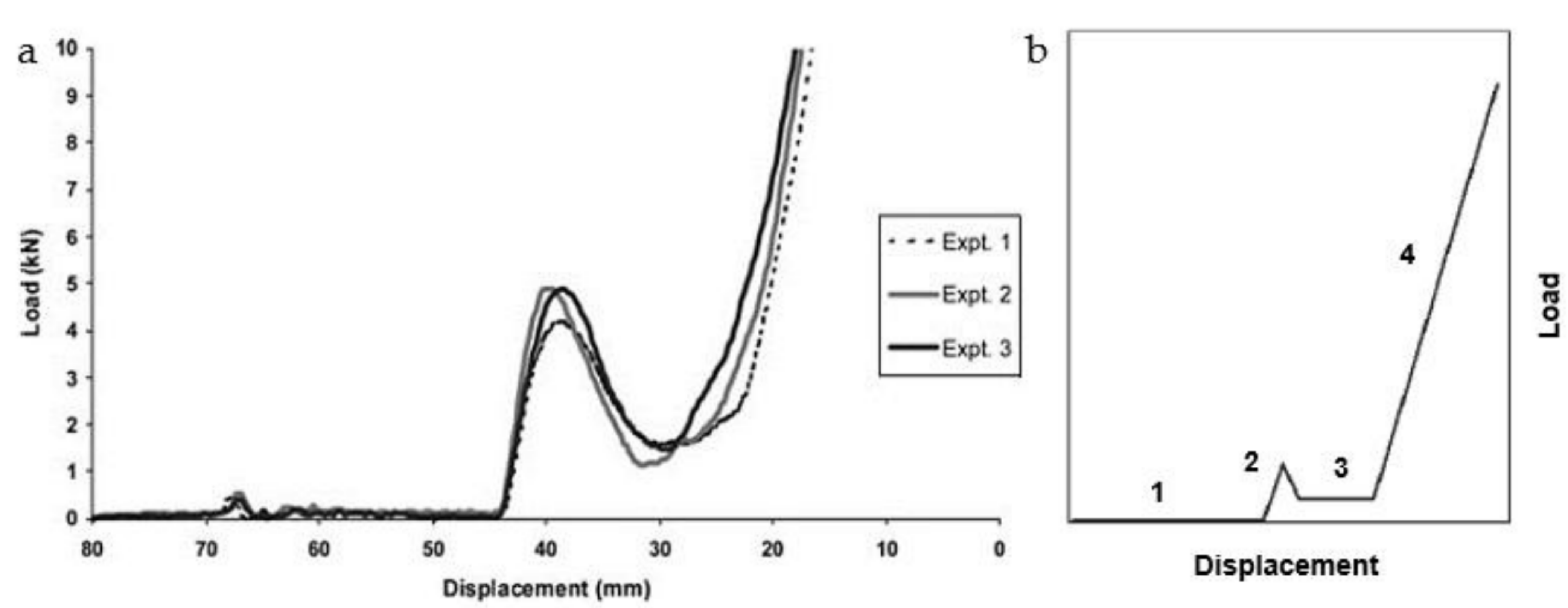
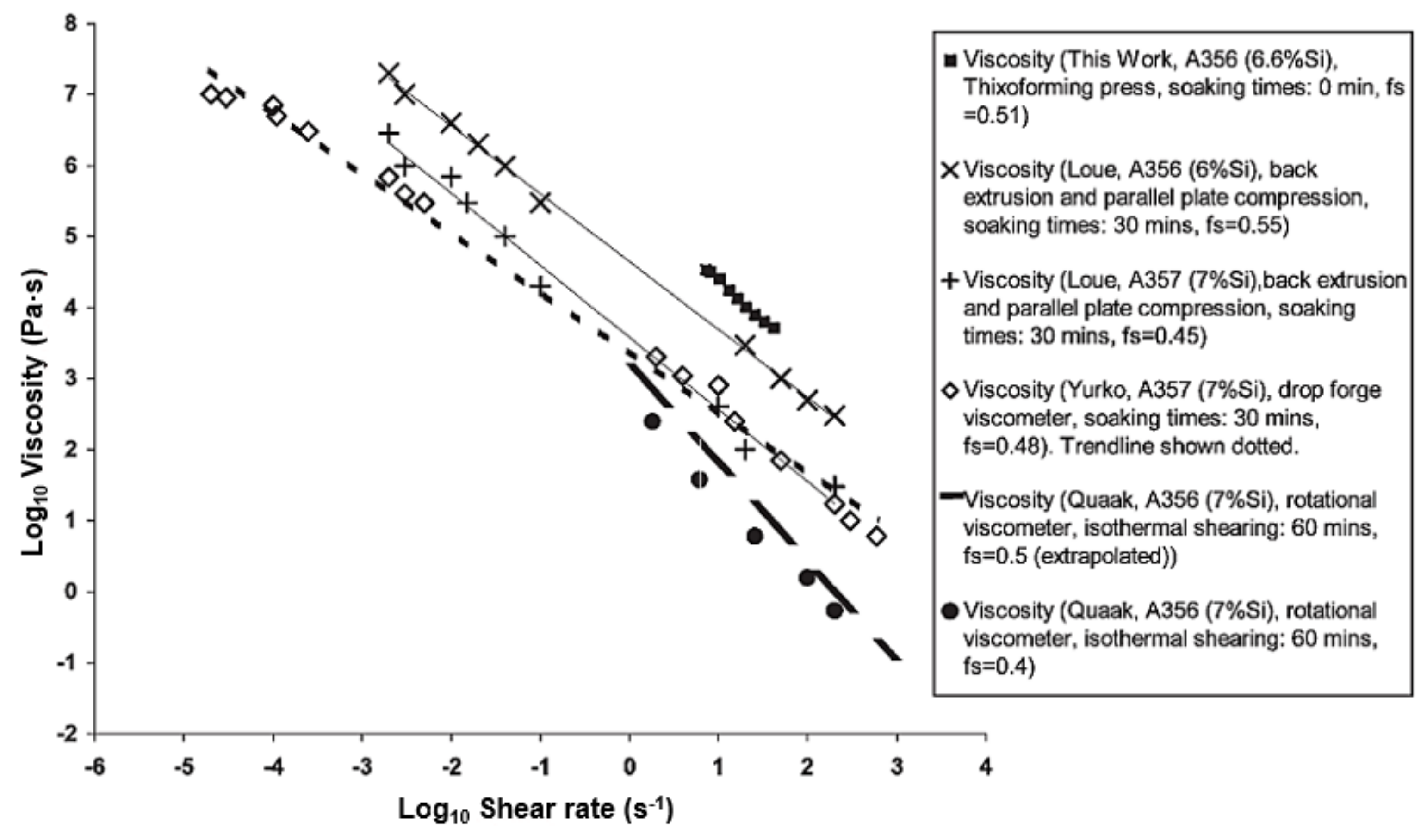
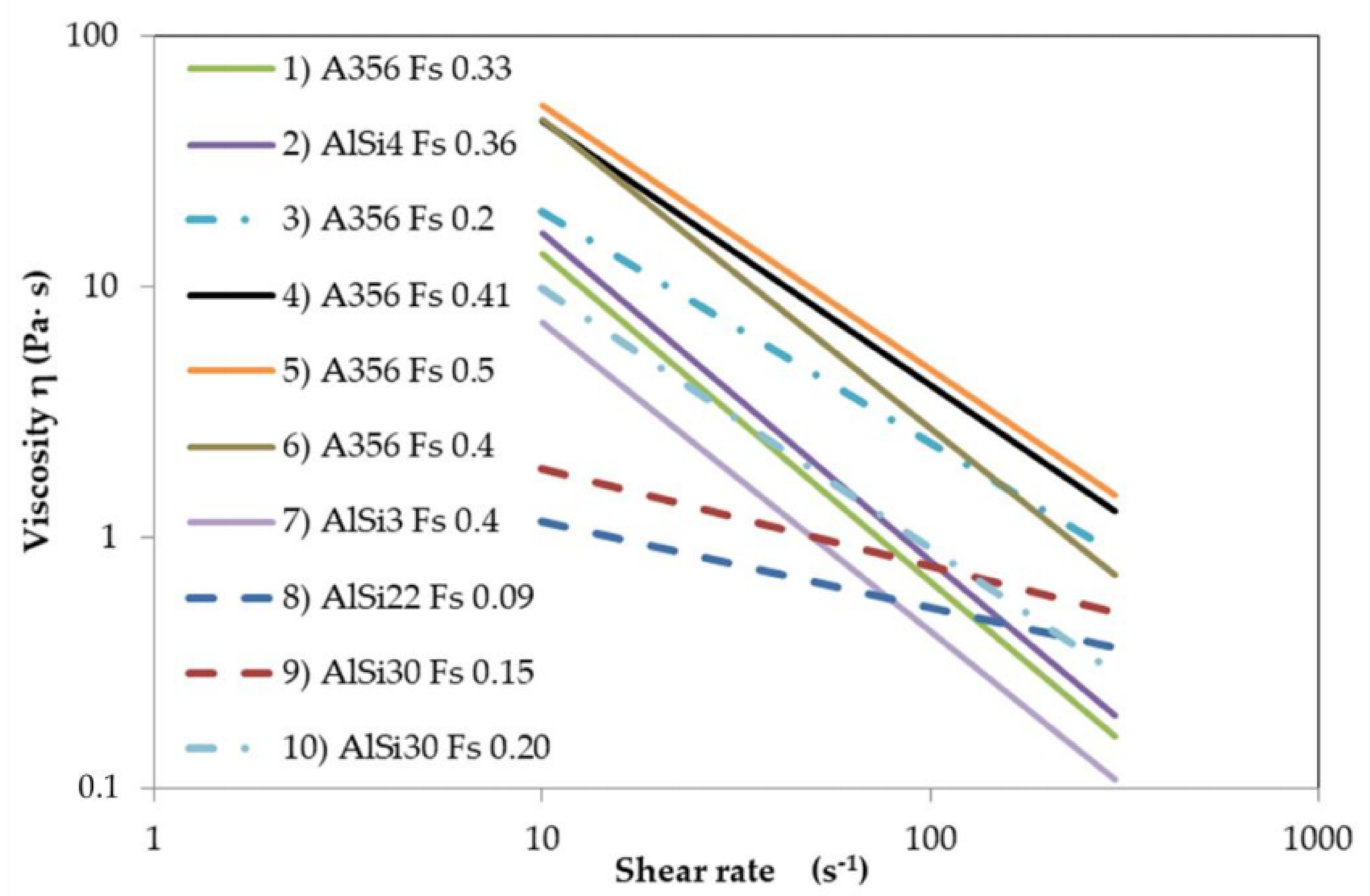
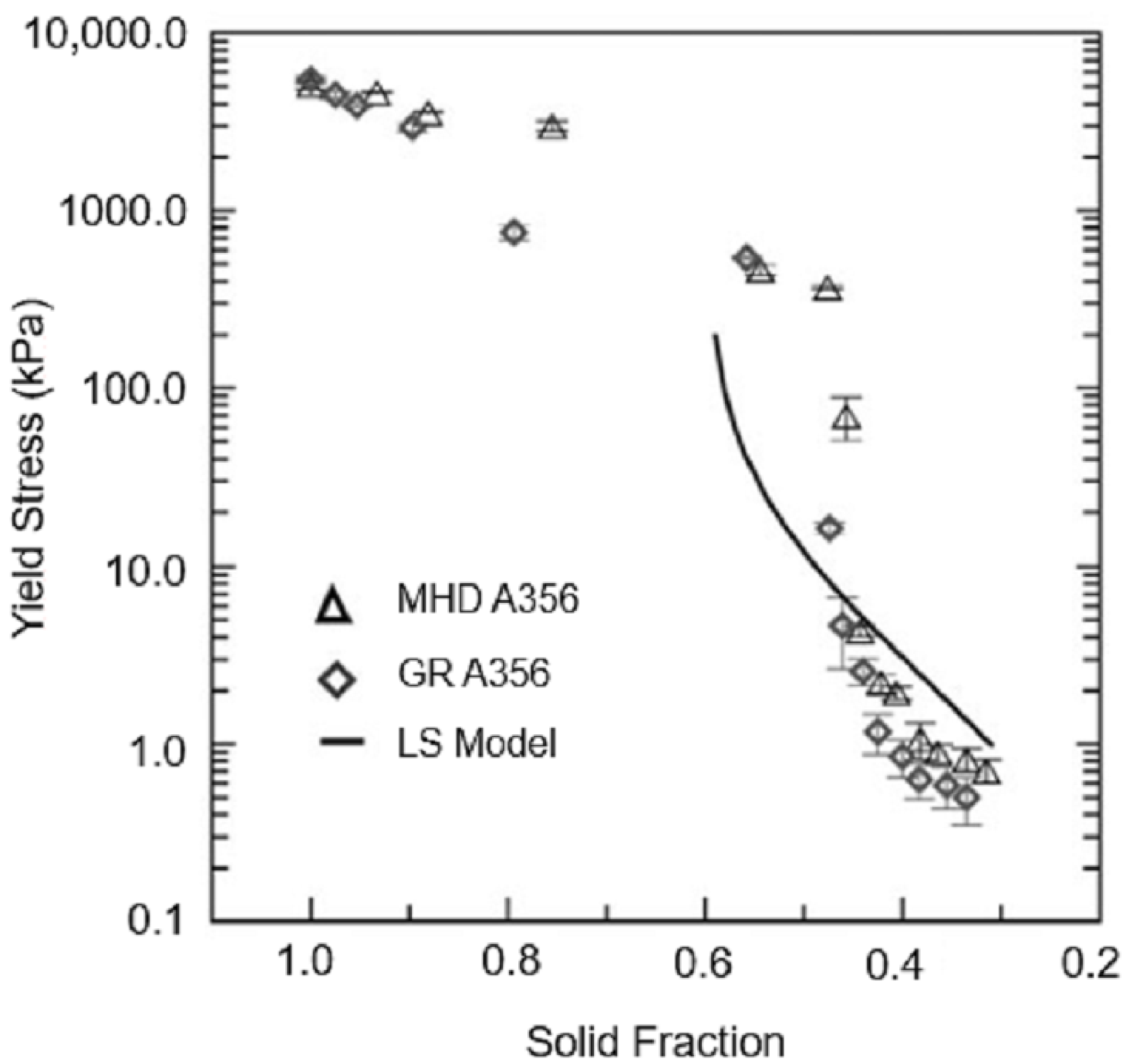
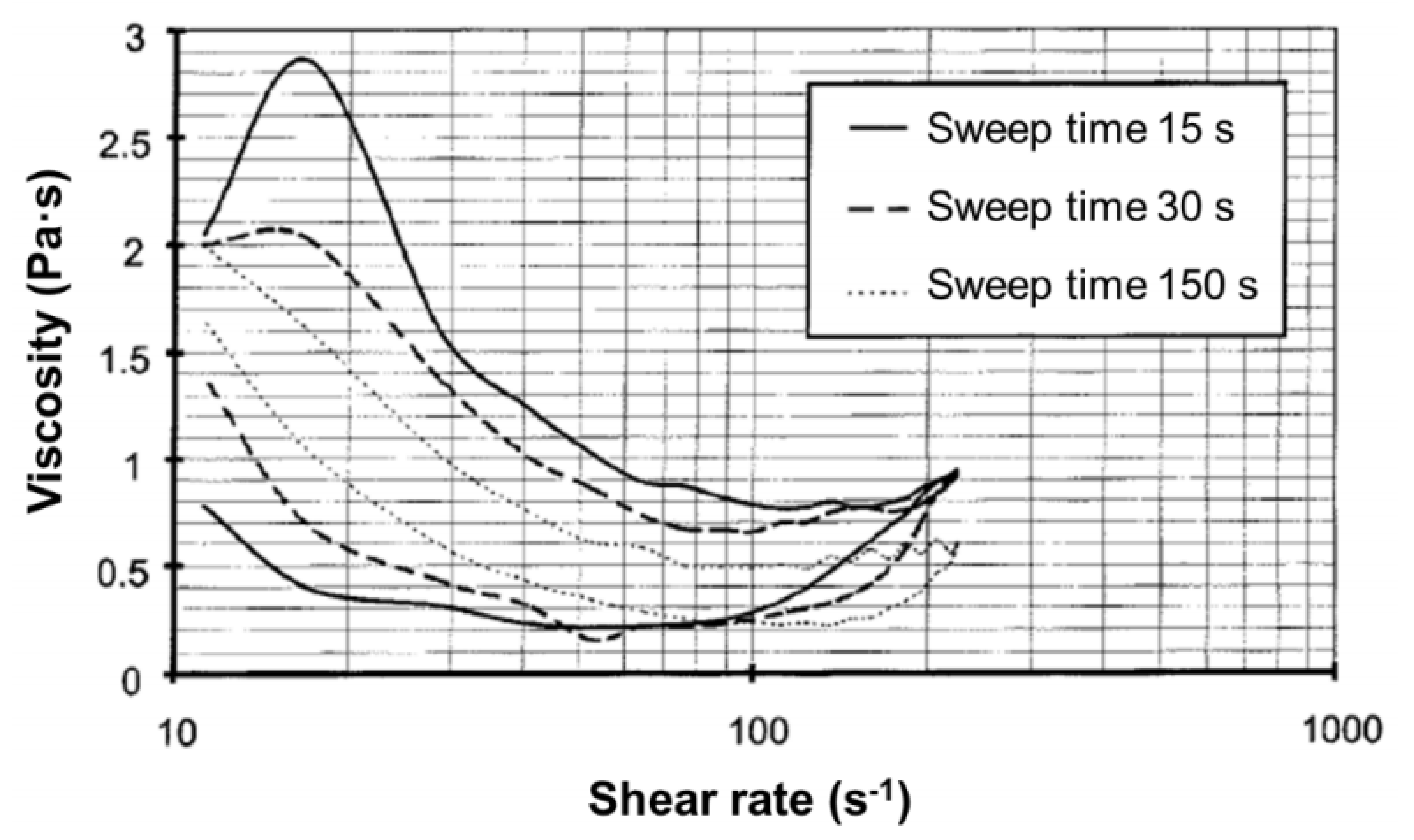
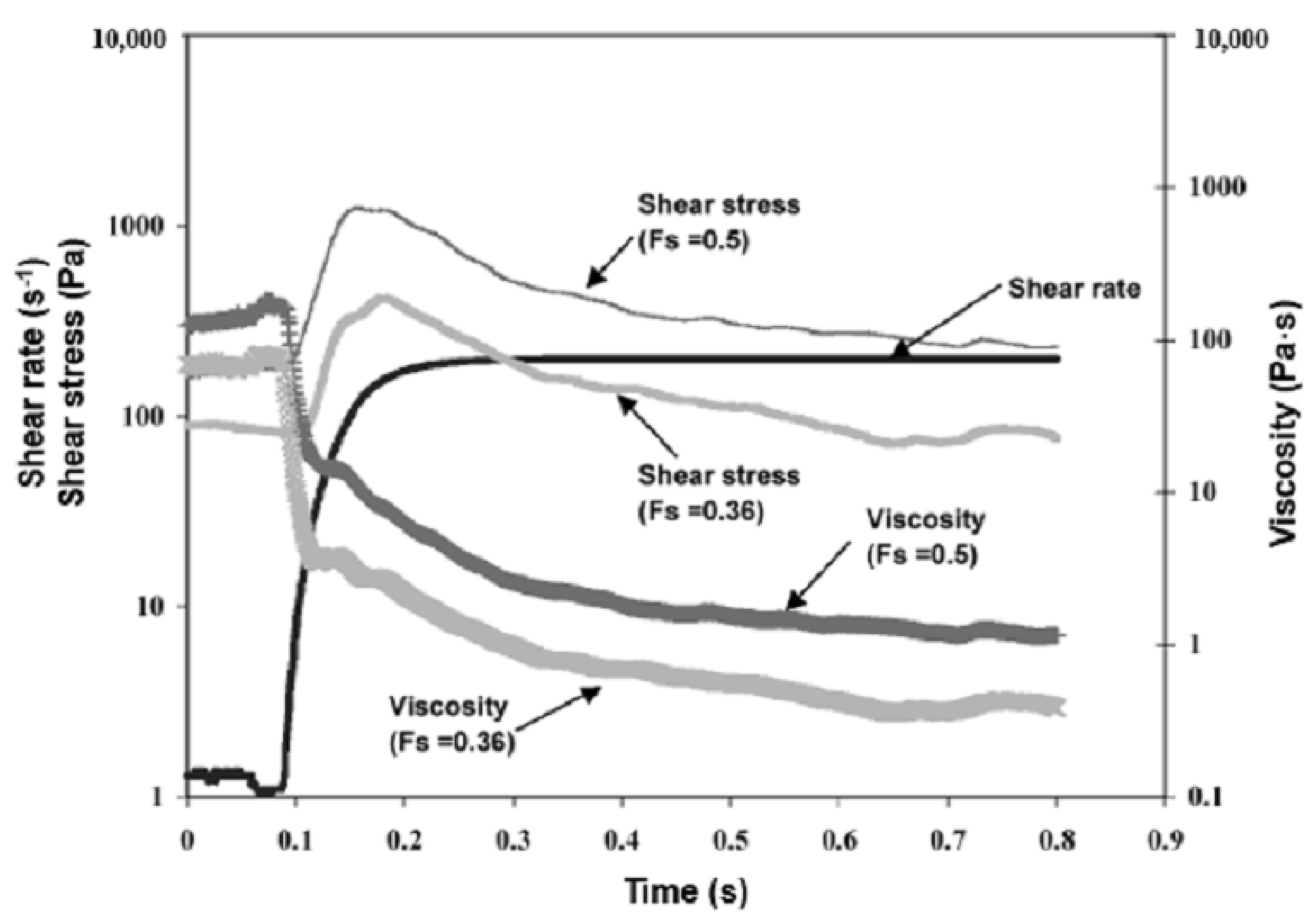
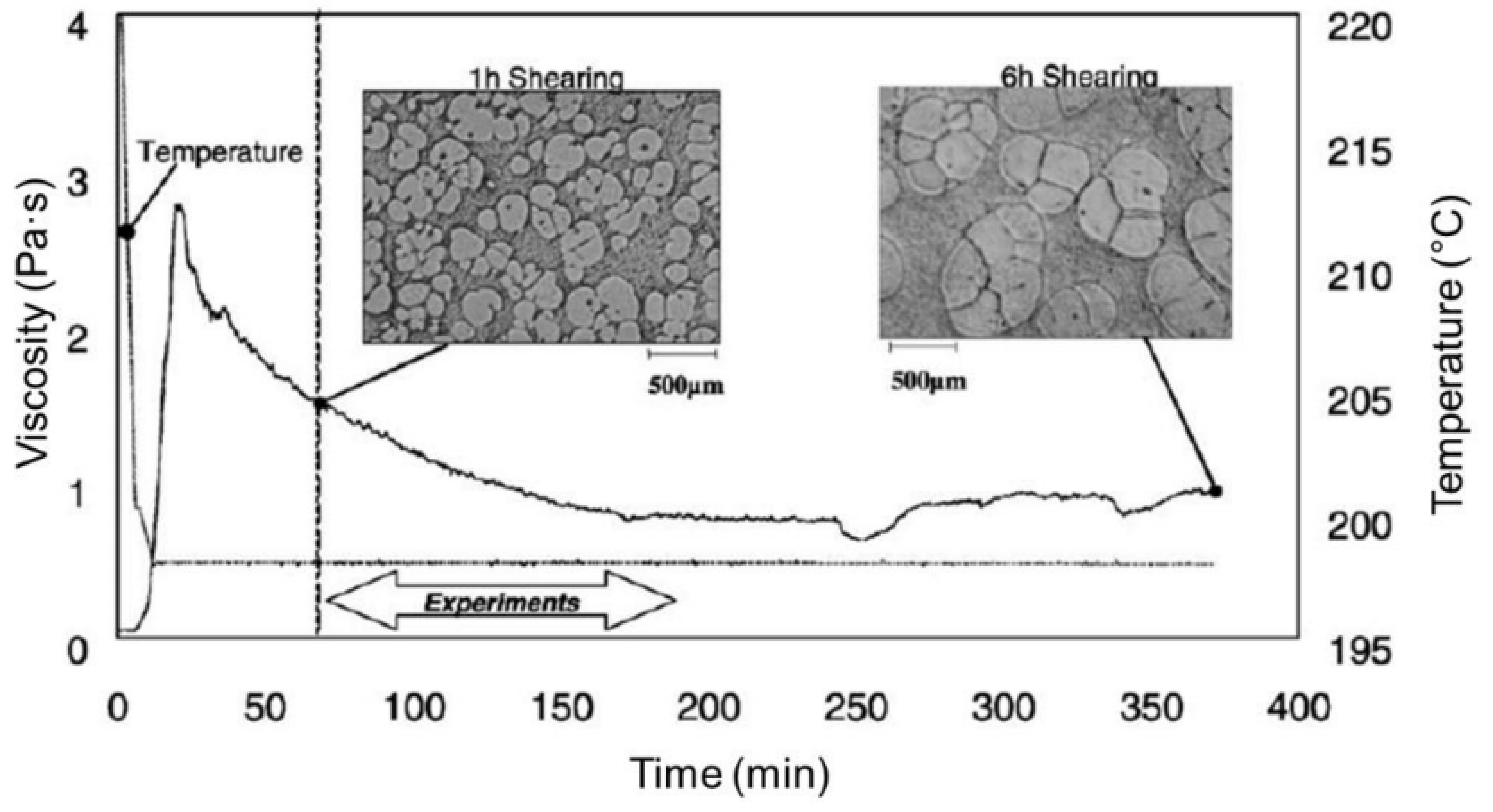
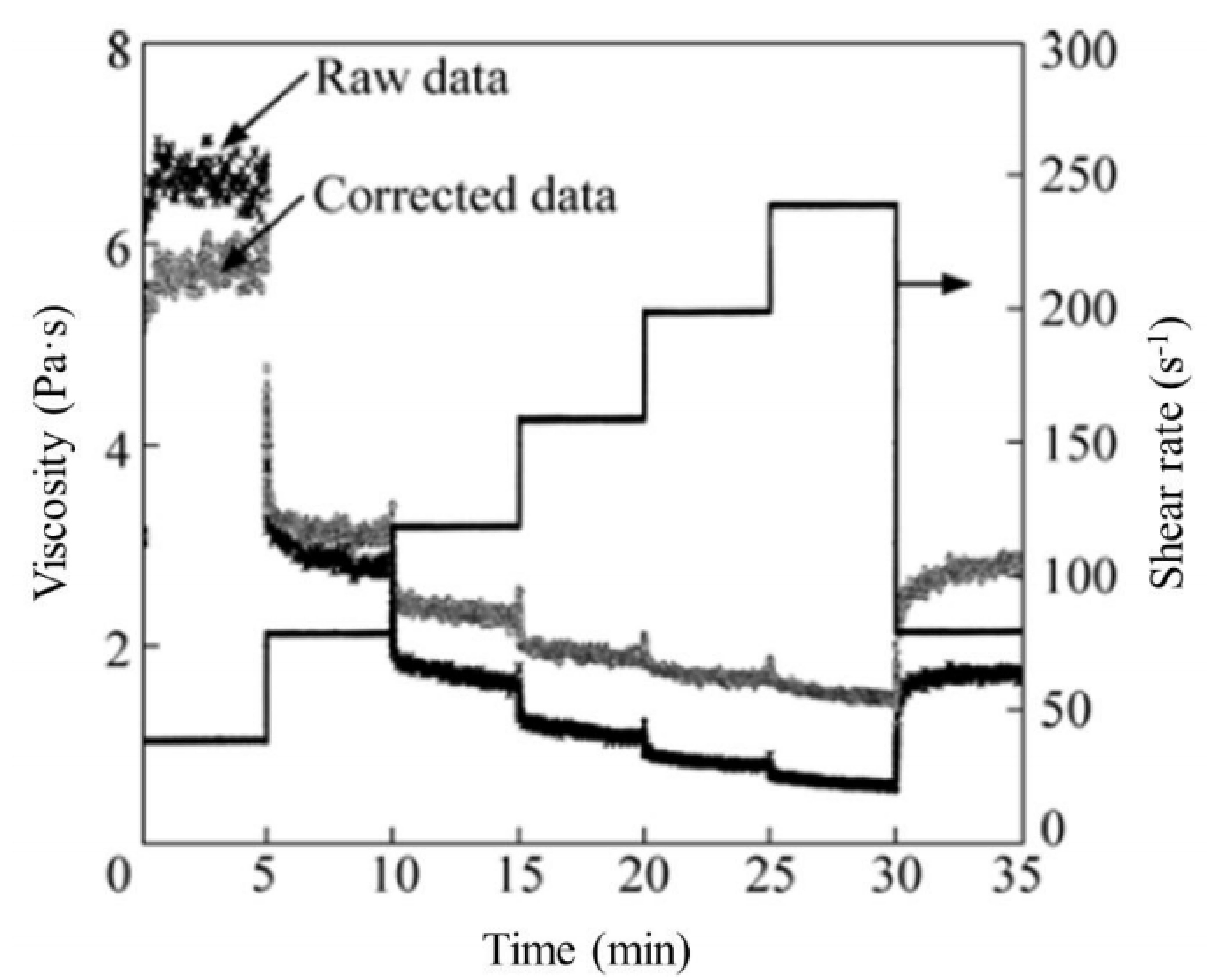
| Alloy | Solid Fraction (-) | Shear Rate Range (s−1) | Flow Index m (Pa·sn) | Shear Exponent n − 1 (-) | Source | |
|---|---|---|---|---|---|---|
| 1 | A356 | 0.33 | 3.1–124.8 | 269 | −1.3 | [65] |
| 2 | AlSi4 | 0.36 | 3.1–124.8 | 325 | −1.3 | [65] |
| 3 | A356 | 0.2 | 0–1500 | 166 | −0.92 | [64] |
| 4 | A356 | 0.41 | 0–1500 | 509 | −1.05 | [64] |
| 5 | A356 | 0.5 | 0–1500 | 589 | −1.05 | [64] |
| 6 | A356 | 0.4 | 10–300 | 789 | −1.23 | [66] |
| 7 | AlSi3 | 0.4 | 10–300 | 122 | −1.23 | [66] |
| - | A201 (AlCu4.5) | 0.35 | 60–260 | - | −1.35 | [49] |
| - | A201 (AlCu4.5) | 0.45 | 60–260 | - | −1.49 | [49] |
| 8 | AlSi22 | 0.09 | 10–50 | 2.53 | −0.34 | [50] |
| 9 | AlSi30 | 0.15 | 10–50 | 4.63 | −0.39 | [50] |
| 10 | AlSi30 | 0.20 | 10–50 | 109 | −1.04 | [50] |
| Alloy | Solid Fraction (-) | Shear Rate Range (s−1) | Flow Index m (Pa·sn) | Shear Exponent n − 1 (-) | Source |
|---|---|---|---|---|---|
| 6061 | 0.5–0.9 | 0.01–2 | 104–106 | From −2 to −1 according to the solid fraction | [47] |
| 7075 | 0.5–0.9 | 0.01–2 | 104–105 | approx. −2.5 | [47] |
| 2024 | 0.5–0.9 | 0.01–2 | 103–105 | From −2.75 to −2.5 according to the solid fraction | [47] |
| AlSi25 | Various T (°C) | 10–3000 | 1.78 × 107 | −1.5 | [67] |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Modigell, M.; Pola, A.; Tocci, M. Rheological Characterization of Semi-Solid Metals: A Review. Metals 2018, 8, 245. https://doi.org/10.3390/met8040245
Modigell M, Pola A, Tocci M. Rheological Characterization of Semi-Solid Metals: A Review. Metals. 2018; 8(4):245. https://doi.org/10.3390/met8040245
Chicago/Turabian StyleModigell, Michael, Annalisa Pola, and Marialaura Tocci. 2018. "Rheological Characterization of Semi-Solid Metals: A Review" Metals 8, no. 4: 245. https://doi.org/10.3390/met8040245
APA StyleModigell, M., Pola, A., & Tocci, M. (2018). Rheological Characterization of Semi-Solid Metals: A Review. Metals, 8(4), 245. https://doi.org/10.3390/met8040245






