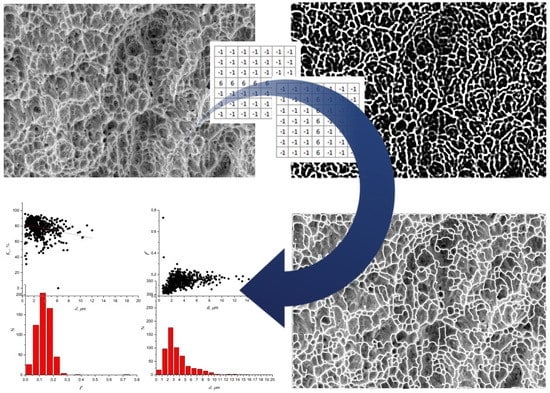
Automated Method for Fractographic Analysis of Shape and Size of Dimples on Fracture Surface of High-Strength Titanium Alloys
Abstract
:1. Introduction
2. Investigation of Static Stretching and Dynamic Non-Equilibrium Process (DNP) of Alloys VT23 and VT23M
- 1
- Static stretching to fracture (VT23M and VT23);
- 2
- Impact toughness testing (VT22M):
- -
- in the initial state;
- -
- after DNP.
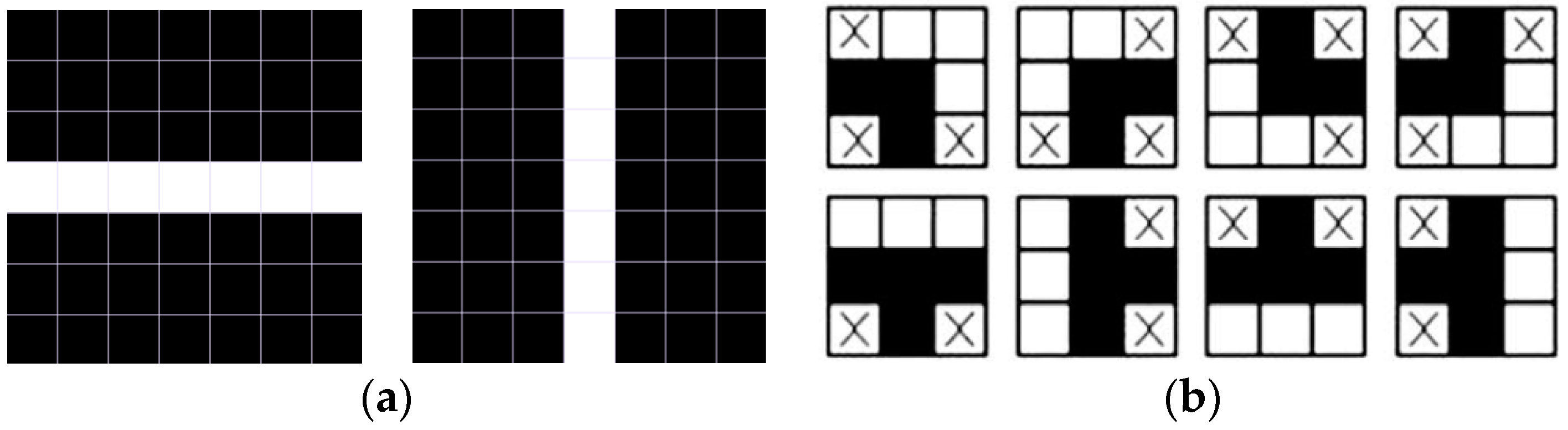
3. Algorithm for Image Analysis
3.1. Algorithm
- area ;
- coefficient of roundness ;
- visual depth in units of image intensity.
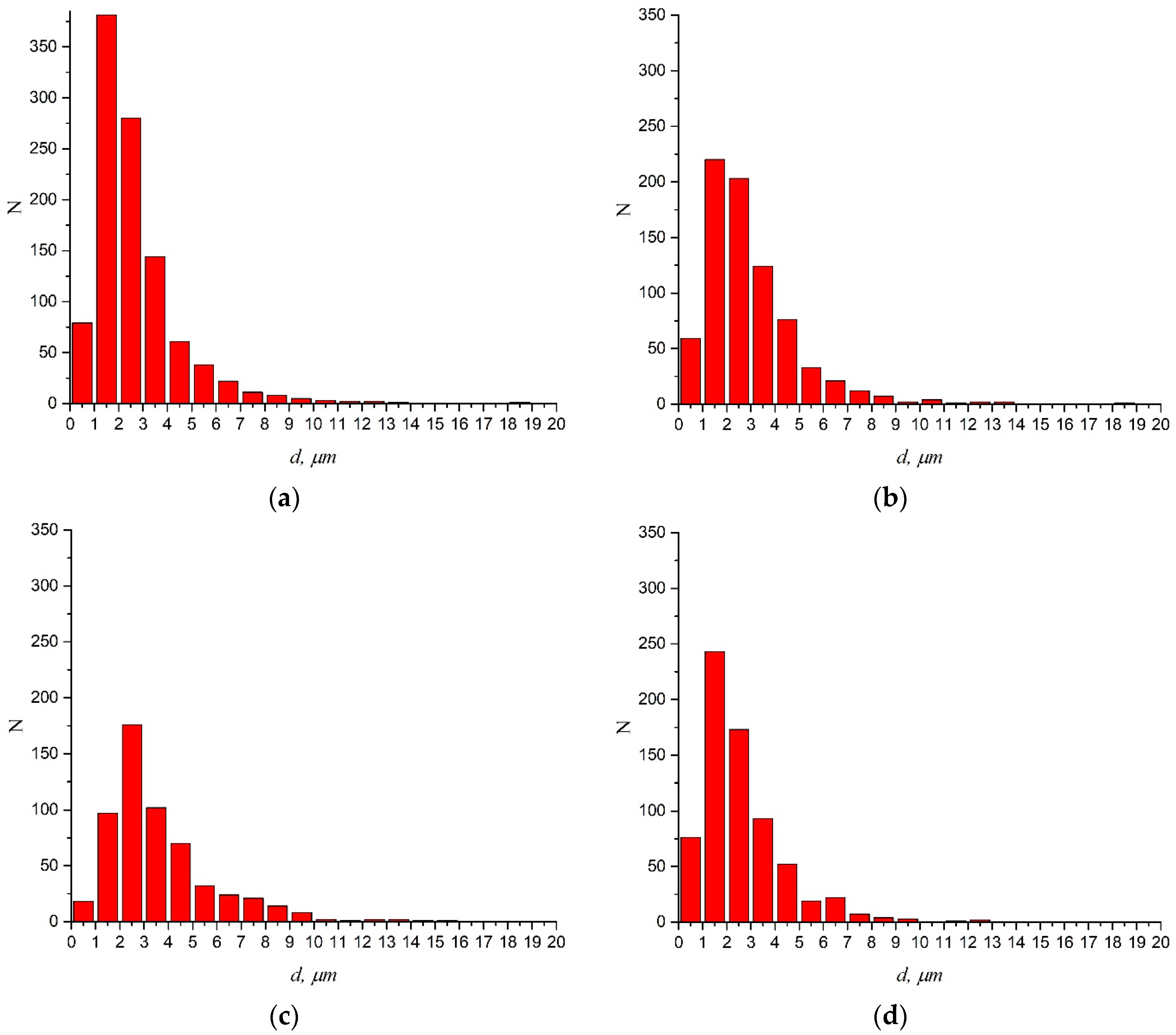
3.2. Equivalent Diameters of Dimples Analysis
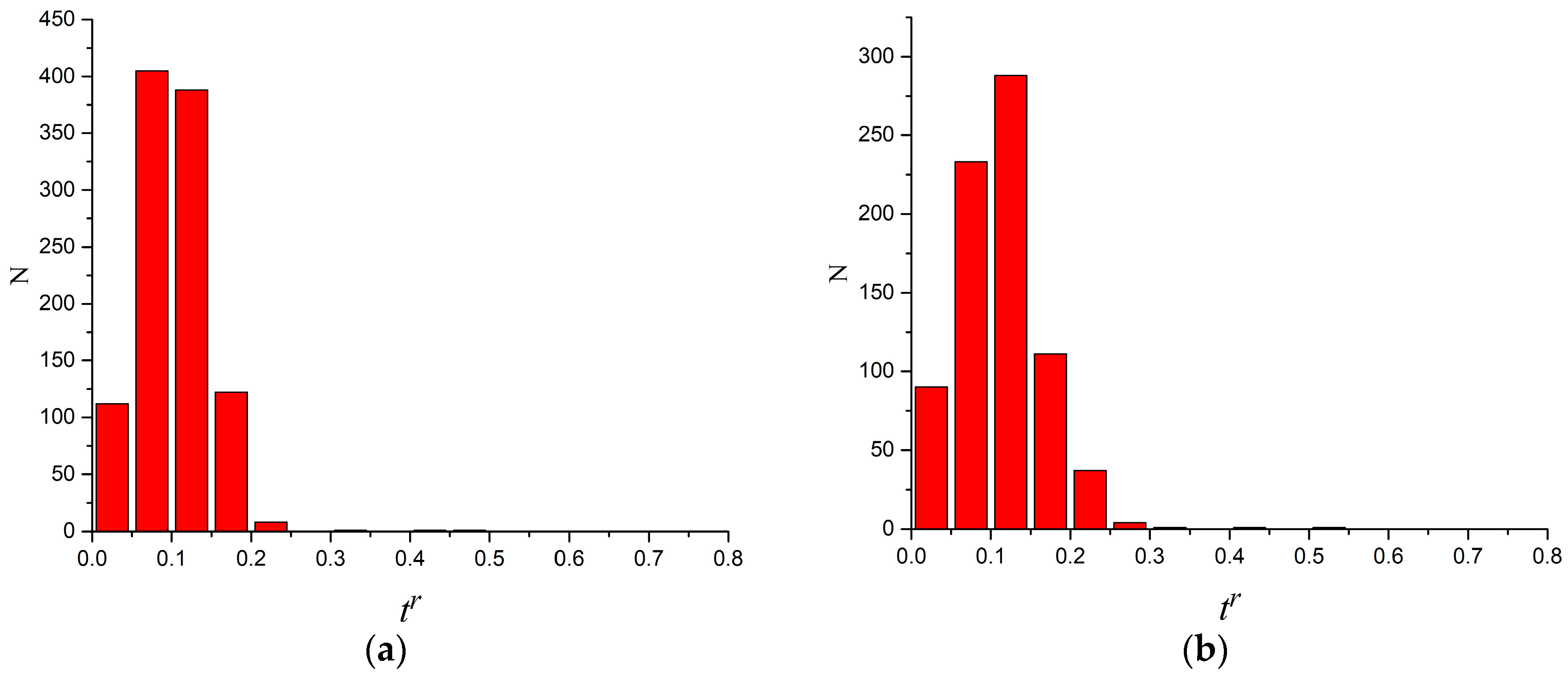
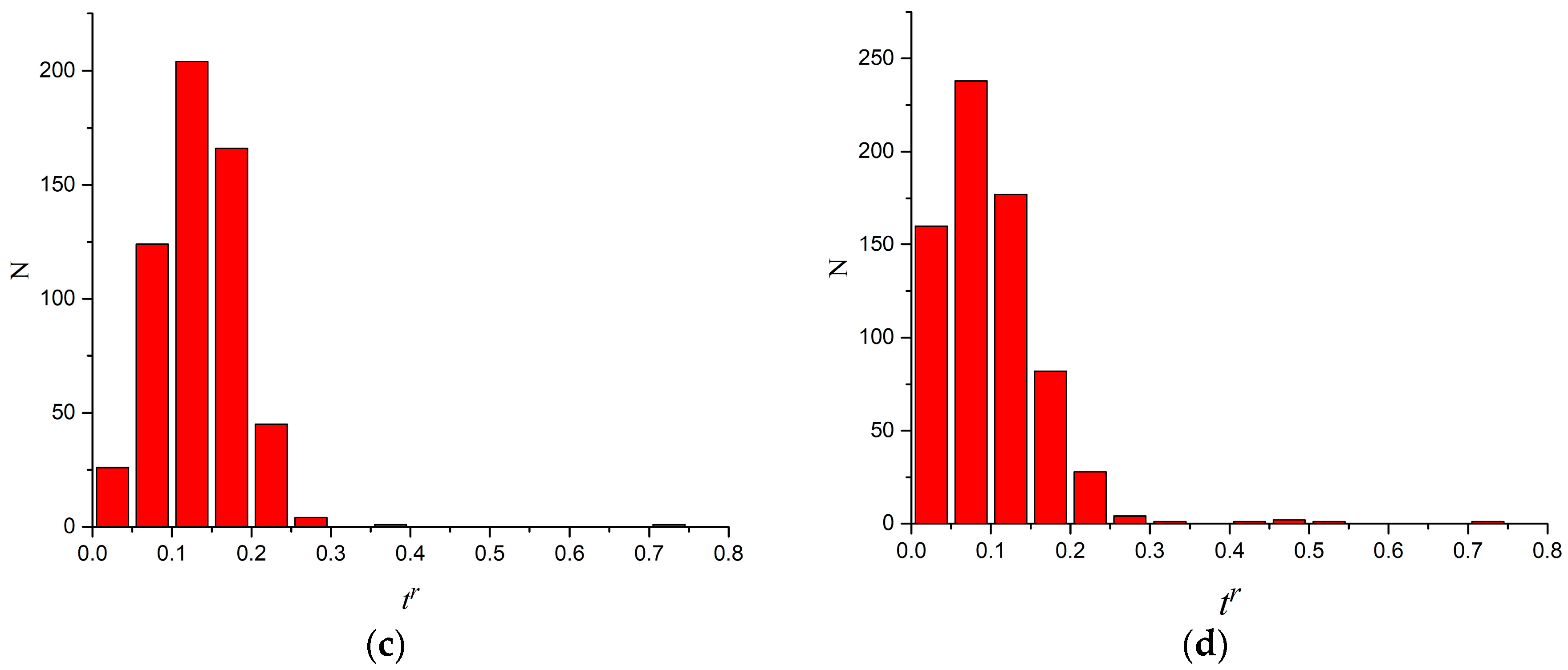
3.2.1. Static Stretching
3.2.2. Impact Toughness
4. Macroparameters as an Integral Indicator
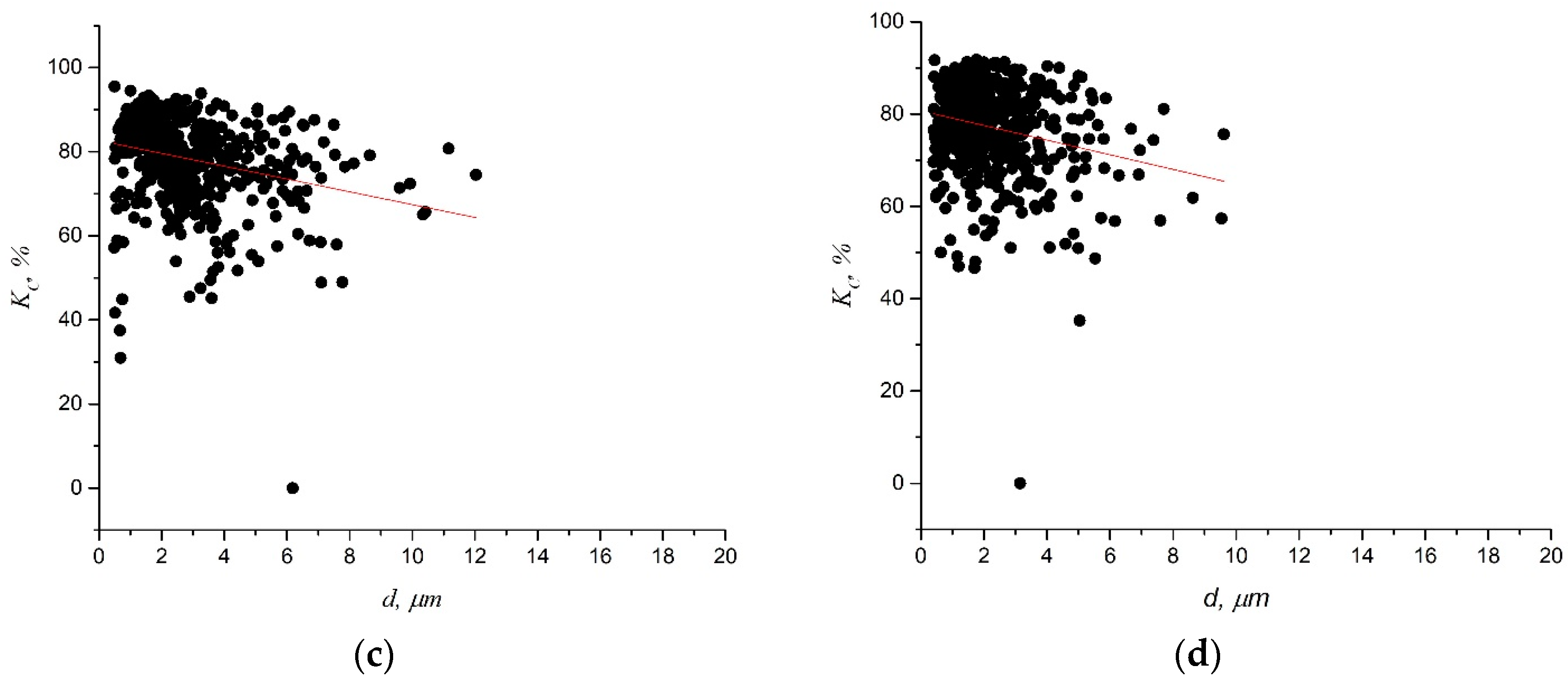
4.1. Shape and Depth of Dimples
4.1.1. Static Stretching
4.1.2. Impact Toughness
4.2. Additional Characteristic of the Surface
4.2.1. Relative Share of the Surface Covered with Dimples and Average Dimple Size
4.2.2. Static Stretching
4.2.3. Impact Toughness
5. Conclusions
Author Contributions
Conflicts of Interest
References
- Broek, D. The role of inclusions in ductile fracture and fracture toughness. Eng. Fract. Mech. 1973, 5, 57–66. [Google Scholar] [CrossRef]
- Garrison, W.M., Jr.; Wojcieszynski, A.L. A discussion of the spacing of inclusions in the volume and of the spacing of inclusion nucleated voids on fracture surfaces of steels. Mater. Sci. Eng. A 2009, 505, 52–61. [Google Scholar] [CrossRef]
- Srivastava, A.; Ponson, L.; Osovski, S.; Bouchaud, E.; Tvergaard, V.; Needleman, A. Effect of inclusion density on ductile fracture toughness and roughness. J. Mech. Phys. Solids 2014, 63, 62–79. [Google Scholar] [CrossRef]
- Osovski, S.; Srivastava, A.; Ponson, L.; Bouchaud, E.; Tvergaard, V.; Ravi-Chandar, K.; Needleman, A. The effect of loading rate on ductile fracture toughness and fracture surface roughness. J. Mech. Phys. Solids 2015, 76, 20–46. [Google Scholar] [CrossRef]
- Kim, J.; Gao, X.; Srivatsan, T.S. Modeling of void growth in ductile solids: Effects of stress triaxiality and initial porosity. Eng. Fract. Mech. 2004, 71, 379–400. [Google Scholar] [CrossRef]
- Kruglova, A.; Roland, M.; Diebels, S.; Dahmen, T.; Slusallek, P.; Mücklich, F. Modelling and characterization of ductile fracture surface in Al-Si alloys by means of Voronoi tessellation. Mater. Charact. 2017, 131, 1–11. [Google Scholar] [CrossRef]
- Osovski, S.; Srivastava, A.; Williams, J.C.; Needleman, A. Grain boundary crack growth in meta-stable titanium beta alloys. Acta Mater. 2015, 82, 167–178. [Google Scholar] [CrossRef]
- Underwood, E. Quantitative fractography. In Applied Metallography; Voort, G.V., Ed.; Springer: Berlin, Germany, 1986; pp. 101–122. [Google Scholar]
- Li, X.; Tian, J.; Kang, Y.; Wang, Z. Quantitative analysis of fracture surface by roughness and fractal method. Scr. Metall. Mater. 1995, 33, 803–809. [Google Scholar] [CrossRef]
- Kosarevych, R.Y.; Student, O.Z.; Svirs’ka, L.M.; Rusyn, B.P.; Nykyforchyn, H.M. Computer analysis of characteristic elements of fractographic images. Mat. Sci. 2013, 48, 474–481. [Google Scholar] [CrossRef]
- Gonzalez, R.C.; Woods, R.E. Digital Image Processing, 3rd ed.; Pearson Education: London, UK, 2008. [Google Scholar]
- Maruschak, P.; Konovalenko, I.; Prentkovskis, O.; Tsyrulnyk, O. Digital analysis of shape and size of dimples of ductile tearing on fracture surface of long-operated steel. Procedia Eng. 2016, 134, 437–442. [Google Scholar] [CrossRef]
- Dutta, S.; Das, A.; Barat, K.; Roy, H. Automatic characterization of fracture surfaces of AISI 304LN stainless steel using image texture analysis. Measurement 2012, 45, 1140–1150. [Google Scholar] [CrossRef]
- Bastidas-Rodriguez, M.X.; Prieto-Ortiz, F.A.; Espejo, E. Fractographic classification in metallic materials by using computer vision. Eng. Fail. Anal. 2016, 59, 237–252. [Google Scholar] [CrossRef]
- Kosarevych, R.J.; Rusyn, B.P.; Korniy, V.V.; Kerod, T.I. Image segmentation based on the evaluation of the tendency of image elements to form clusters with the help of point field characteristics. Cybern. Syst. Anal. 2015, 51, 704–713. [Google Scholar] [CrossRef]
- Kudrya, A.V.; Sokolovskaya, E.A.; Trachenko, V.A.; Le Hai, N.; Skorodumov, S.V.; Papina, K.B. Measurement of nonuniformity of fracture in structural steels with heterogeneous structure. Met. Sci. Heat Treat. 2015, 57, 190–196. [Google Scholar] [CrossRef]
- Maruschak, P.; Konovalenko, I.; Prentkovskis, O.; Chausov, M.; Pylypenko, A. Methods and some results of automated analysis of ductile failure mechanisms of titanium alloy VT-22. Procedia Eng. 2016, 134, 475–480. [Google Scholar] [CrossRef]
- Chausov, M.G.; Maruschak, P.O.; Hutsaylyuk, V.; Śnieżek, L.; Pylypenko, A.P. Effect of complex combined loading mode on the fracture toughness of titanium alloys. Vacuum 2018, 147, 51–57. [Google Scholar] [CrossRef]
- Chausov, M.G.; Maruschak, P.O.; Pylypenko, A.P.; Berezin, V.B.; Prentkovskis, O. Structural self-organization of titanium alloys under impulse force action. Mater. Test. 2017, 59, 567–569. [Google Scholar] [CrossRef]
- Marushchak, P.O.; Konovalenko, I.V. Computer evaluation of the depth of thermomechanical fatigue cracks according to their length. Mater. Sci. 2012, 48, 54–64. [Google Scholar] [CrossRef]
- Konovalenko, I.V.; Marushchak, P.O.; Bishchak, R.T. Automated estimation of damage to the surface of gas main by corrosion pittings. Mater. Sci. 2014, 49, 493–500. [Google Scholar] [CrossRef]
- Ohashi, M. Extreme value analysis of ductile fracture surface by dimpled rupture associated with fracture behavior of tensile specimens. J. Mater. Sci. 2007, 42, 9877–9887. [Google Scholar] [CrossRef]
- Maruschak, P.; Menou, A.; Chausov, M.; Mocharskyi, V. Fractographic analysis of surface and failure mechanisms of nanotitanium after laser shock-wave treatment. Key Eng. Mater. 2014, 592–593, 346–349. [Google Scholar] [CrossRef]
- Rittel, D.; Osovski, S. Dynamic failure by adiabatic shear banding. Int. J. Fract. 2010, 162, 177–185. [Google Scholar] [CrossRef]
- Yasniy, P.; Maruschak, P.; Bishchak, R.; Hlado, V.; Pylypenko, A. Damage and fracture of heat resistance steel under cyclic thermal loading. Theor. Appl. Fract. Mech. 2009, 52, 22–25. [Google Scholar] [CrossRef]
- Faleskog, J.; Gao, X.; Shih, C.F. Cell model for nonlinear fracture analysis—I. Micromechanics calibration. Int. J. Fract. 1998, 89, 355–373. [Google Scholar] [CrossRef]
- Romanova, V.; Balokhonov, R.; Panin, A.; Kazachenok, M.; Kozelskaya, A. Micro-and mesomechanical aspects of deformation-induced surface roughening in polycrystalline titanium. Mater. Sci. Eng. A. 2017, 697, 248–258. [Google Scholar] [CrossRef]


| Fe | Cr | Mo | V | Ti | Al |
|---|---|---|---|---|---|
| 0.5–0.8 | 1.0–1.4 | 1.8–2.5 | 4.3–5.0 | 86.0–89.3 | 4.4–6.3 |
| Titanium Alloys | Mechanical Properties | ||
|---|---|---|---|
| σys, MPa | σus, MPa | δ, % | |
| VT23 | 980–1180 | 1080–1280 | 15 |
| VT23M | 1000–1150 | 1080–1180 | 20 |
| Schemes of Deformation | Relative Strain, ε, % | , μm | N, pcs | Relative Shares of Dimples, Sr, % | Relative Shares of Interstices, Sb, % | |
|---|---|---|---|---|---|---|
| Static fracture | VT23 | 17.40 | 2.84 | 1038 | 74.04 | 25.96 |
| VT23M | 22.30 | 3.13 | 767 | 75.19 | 24.81 | |
| Impact fracture | VT23M | - | 3.75 | 571 | 80.22 | 19.78 |
| VT23M after DNP | - | 2.74 | 695 | 75.59 | 24.41 | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Konovalenko, I.; Maruschak, P.; Prentkovskis, O. Automated Method for Fractographic Analysis of Shape and Size of Dimples on Fracture Surface of High-Strength Titanium Alloys. Metals 2018, 8, 161. https://doi.org/10.3390/met8030161
Konovalenko I, Maruschak P, Prentkovskis O. Automated Method for Fractographic Analysis of Shape and Size of Dimples on Fracture Surface of High-Strength Titanium Alloys. Metals. 2018; 8(3):161. https://doi.org/10.3390/met8030161
Chicago/Turabian StyleKonovalenko, Ihor, Pavlo Maruschak, and Olegas Prentkovskis. 2018. "Automated Method for Fractographic Analysis of Shape and Size of Dimples on Fracture Surface of High-Strength Titanium Alloys" Metals 8, no. 3: 161. https://doi.org/10.3390/met8030161
APA StyleKonovalenko, I., Maruschak, P., & Prentkovskis, O. (2018). Automated Method for Fractographic Analysis of Shape and Size of Dimples on Fracture Surface of High-Strength Titanium Alloys. Metals, 8(3), 161. https://doi.org/10.3390/met8030161