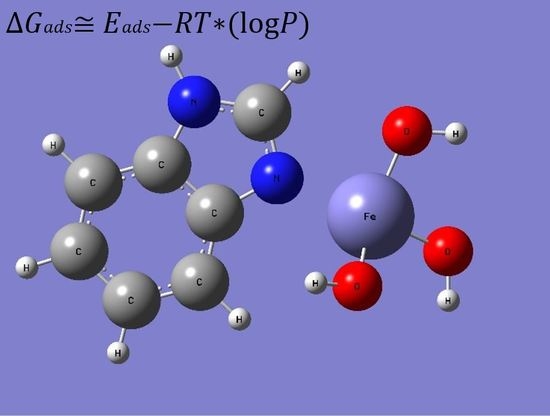
Interaction of Model Inhibitor Compounds with Minimalist Cluster Representations of Hydroxyl Terminated Metal Oxide Surfaces
Abstract
:1. Introduction
2. Computational Methods
3. Results
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Obot, I.B. Recent advances in computational design of organic materials for corrosion protection of steel in aqueous media. In Developments in Corrosion Protection; Aliofkhazraei, M., Ed.; Intech: London, UK, 2014. [Google Scholar]
- Papavinasam, S. Corrosion Control in the Oil and Gas Industry; Elsevier: London, UK, 2014; p. 374. [Google Scholar]
- Taylor, C.D.; Chandra, A.; Vera, J.; Sridhar, N. A Multiphysics Perspective on Mechanistic Models for Chemical Corrosion Inhibitor Performance. J. Electrochem. Soc. 2015, 162, C369. [Google Scholar] [CrossRef]
- Gece, G. The use of quantum chemical methods in corrosion inhibitor studies. Corros. Sci. 2008, 50, 2981–2992. [Google Scholar] [CrossRef]
- Durnie, W.; de Marco, R.; Jefferson, A.; Kinsella, B. Development of a Structure-Activity Relationship for Oil Field Corrosion Inhibitors. J. Electrochem. Soc. 1999, 146, 1751–1756. [Google Scholar] [CrossRef]
- Ramakrishnan, S.K.; Martin, M.; Cloitre, T.; Firlej, L.; Gergely, C. Design rules for metal binding biomolecules: Understanding of amino acid adsorption on platinum crystallographic facets from density functional calculations. Phys. Chem. Chem. Phys. 2015, 17, 4193–4198. [Google Scholar] [CrossRef] [PubMed]
- Khaled, K.F.; Sherik, A. Using neural networks for corrosion inhibition efficiency prediction during corrosion of steel in chloride solutions. Int. J. Electrochem. Sci. 2013, 8, 9918. [Google Scholar]
- El Ashry, E.S.H.; el Nemr, A.; Essawy, S.A.; Ragab, S. Corrosion inhibitors part V: QSAR of benzimidazole and 2-substituted derivatives as corrosion inhibitors by using the quantum chemical parameters. Prog. Organ. Coat. 2008, 61, 11–20. [Google Scholar] [CrossRef]
- El Ashry, E.S.H.; Senior, S.A. QSAR of lauric hydrazide and its salts as corrosion inhibitors by using the quantum chemical and topological descriptors. Corros. Sci. 2011, 53, 1025–1034. [Google Scholar] [CrossRef]
- Lukovits, I.; Shaban, A.; Kalman, E. Thiosemicarbazides and thiosemicarbazones: Non-linear quantitative structure-efficiency model of corrosion inhibition. Electrochim. Acta 2005, 50, 4128–4133. [Google Scholar] [CrossRef]
- Khalil, N. Quantum chemical approach of corrosion inhibition. Electrochim. Acta 2003, 48, 2635–2640. [Google Scholar] [CrossRef]
- Arshadi, M.R.; Lashgari, M.; Parsafar, G.A. Cluster approach to corrosion inhibition problems: Interaction studies. Mater. Chem. Phys. 2004, 86, 311–314. [Google Scholar] [CrossRef]
- Arslan, T.; Kandemirli, F.; Ebenso, E.E.; Love, I.; Alemu, H. Quantum chemical studies on the corrosion inhibition of some sulphonamides on mild steel in acidic medium. Corros. Sci. 2009, 51, 35–47. [Google Scholar] [CrossRef]
- Du, L.; Zhao, H.; Hu, H.; Yang, J. Quantum chemical and molecular dynamics studies of imidazoline derivatives as corrosion inhibitor and quantitative structure-activity relationship (QSAR) analysis using the support vector machine (SVM) method. J. Theor. Comp. Chem. 2014, 13, 1450012. [Google Scholar] [CrossRef]
- Plimpton, S.J. Fast Parallel Algorithms for Short-Range Molecular Dynamics. J. Comp. Phys. 1995, 117, 1. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmuller, J. Efficient Iterative Schemes for Ab initio Total-Energy Calculations Using a Plane-Wave Basis Set. Phys. Rev. B 1996, 54, 11169. [Google Scholar] [CrossRef]
- Kresse, G. Furthmüller, Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. J. Comput. Mat. Sci. 1996, 54, 11169–11186. [Google Scholar]
- Kresse, G.; Hafner, J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B 1993, 47, 558–561. [Google Scholar] [CrossRef]
- Finsgar, M.; Lesar, A.; Kokalj, A.; Milosev, I. A comparative electrochemical and quantum chemical calculation study of BTAH and BTAOH as copper corrosion inhibitors in near neutral chloride solution. Electrochim. Acta 2008, 53, 8287–8297. [Google Scholar] [CrossRef]
- Peljhan, S.; Kokalj, A. DFT study of gas-phase adsorption of benzotriazole on Cu(111), Cu(100), Cu(110), and low coordinated defects thereon. Phys. Chem. Chem. Phys. 2011, 13, 20408–20417. [Google Scholar] [CrossRef] [PubMed]
- Mondal, S.K.; Taylor, S.R. The identification and characterization of organic corrosion inhibitors: Correlation of a computational model with experimental results. J. Electrochem. Soc. 2014, 161, C476–C485. [Google Scholar] [CrossRef]
- Kokalj, A. Is the analysis of molecular electronic structure of corrosion inhibitors sufficient to predict the trend of their inhibition performance? Electrochim. Acta 2010, 56, 745. [Google Scholar] [CrossRef]
- Winkler, D.A.; Breedon, M.; Hughes, A.E.; Burden, F.R.; Barnard, A.S.; Harvey, T.G.; Cole, I. Towards chromate-free corrosion inhibitors: Structure-property models for organic alternatives. Green Chem. 2014, 16, 3349–3357. [Google Scholar] [CrossRef]
- Winkler, D.A.; Breedon, M.; White, P.; Hughes, A.E.; Sapper, E.D.; Cole, I. Using high throughput experimental data and in silico models to discover alternatives to toxic chromate corrosion inhibitors. Corros. Sci. 2016, 106, 229–235. [Google Scholar] [CrossRef]
- Chen, F.F.; Breedon, M.; Sapper, E.D.; Ganther, W.; Lau, D.; Cole, I. A microclimate model to simulate neutral salt spray testing for corrosion inhibitor evaluation and functional coating development. Prog. Org. Coat. 2017, 111, 327–335. [Google Scholar] [CrossRef]
- Chen, F.F.; Breedon, M.; White, P.; Chu, C.; Mallick, D.; Thomas, S.; Sapper, E.D.; Cole, I. Correlation between molecular features and electrochemical properties using an artificial neural network. Mater. Des. 2016, 112, 410–418. [Google Scholar] [CrossRef]
- Sangster, J. Octanol-Water Partition Coefficients: Fundamentals and Physical Chemistry; John Wiley & Sons: Chichester, UK, 1997. [Google Scholar]
- Feng, L.J.; Yang, H.Y.; Wang, F.H. Experimental and theoretical studies for corrosion inhibition of carbon steel by imidazoline derivative in 5% NaCl saturated Ca(OH)2 solution. Electrochim. Acta 2011, 58, 427–436. [Google Scholar] [CrossRef]
- Blajiev, O.; Hubin, A. Inhibition of copper corrosion in chloride solutions by amino-mercapto-thiadiazol and methyl-mercapto-thiadiazol: An impedance spectroscopy and a quantum-chemical investigation. Electrochim. Acta 2004, 49, 2761–2770. [Google Scholar] [CrossRef]
- Arrouvel, C.; Diawara, B.; Costa, D.; Marcus, P. DFT periodic study of the adsorption of glycine on the anhydrous and hydroxylated (0001) surfaces of alpha-alumina. J. Phys. Chem. C 2007, 111, 18164–18173. [Google Scholar] [CrossRef]
- Borck, O.; Hyldgaard, P.; Schroder, E. Adsorption of methylamine on alpha-Al2O3(0001) and alpha-Cr2O3(0001): Density functional theory. Phys. Rev. B 2007, 75. [Google Scholar] [CrossRef]
- Motta, A.; Gaigeot, M.P.; Costa, D. Ab Initio Molecular Dynamics Study of the AlOOH Boehmite/Water Interface: Role of Steps in Interfacial Grotthus Proton Transfers. J. Phys. Chem. C 2012, 116, 12514–12524. [Google Scholar] [CrossRef]
- Gao, Y.Y.; Zhao, N.; Wei, W.; Sun, Y.H. Ab initio DFT study of urea adsorption and decomposition on the ZnO (10-1 0) surface. Comput. Theor. Chem. 2012, 992. [Google Scholar] [CrossRef]
- Irrera, S.; Costa, D.; Ogle, K.; Marcus, P. Molecular modelling by DFT of 1,2-diaminoethane adsorbed on the Zn-terminated and O-terminated, anhydrous and hydroxylated ZnO (0001) surface. Superlattices Microstruct. 2009, 46, 19–24. [Google Scholar] [CrossRef]
- Islam, M.M.; Diawara, B.; Marcus, P.; Costa, D. Synergy between iono-covalent bonds and van der Waals interactions in SAMs formation: A first-principles study of adsorption of carboxylic acids on the Zn-ZnO(0001) surface. Catal. Today 2011, 177, 39–49. [Google Scholar] [CrossRef]
- Tang, W.D.; Gao, Y.Y.; Wei, W.; Sun, Y.H. Adsorption of Urea onto a ZnO(10-10) Surface. Acta Phys. Chim. Sin. 2010, 26, 1373–1377. [Google Scholar]
- Costa, D.; Marcus, P. Adsorption of Organic Inhibitor Molecules on Metal and Oxidized Surfaces Studied by Atomistic Theoretical Methods. In Molecular Modeling of Corrosion Processes; Taylor, C.D., Marcus, P., Eds.; ECS-Wiley: Hoboken, NJ, USA, 2015. [Google Scholar]
- Kokalj, A.; Peljhan, S. Density Functional Theory Study of Adsorption of Benzotriazole on Cu2O Surfaces. J. Phys. Chem. C 2015, 119, 11625–11635. [Google Scholar] [CrossRef]
- Kovacevic, N.; Kokalj, A. DFT Study of Interaction of Azoles with Cu(111) and Al(111) Surfaces: Role of Azole Nitrogen Atoms and Dipole-Dipole Interactions. J. Phys. Chem. C 2011, 115, 24189–24197. [Google Scholar] [CrossRef]
- Masel, R.I. Principles of Adsorption and Reaction on Solid Surfaces; Wiley: Hoboken, NJ, USA, 1996. [Google Scholar]
- Levine, I.N. Quantum Chemistry; Prentice Hall: Upper Saddle River, NY, USA, 2000. [Google Scholar]
- Gaussian 09W, Gaussian, Inc.: Wallingford, CT, USA, 2009.
- Becke, A.D. Density-Functional Thermochemistry. III. The Role of Exact Exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
- Hay, P.J.; Wadt, W.R. Ab initio effective core potentials for molecular calculations. Potentials for the transition metal atoms Sc to Hg. J. Chem. Phys. 1985, 82, 270. [Google Scholar] [CrossRef]
- Hay, P.J.; Wadt, W.R. Ab initio effective core potentials for molecular calculations. Potentials for main group elements Na to Bi. J. Chem. Phys. 1985, 82, 284. [Google Scholar]
- Hay, P.J.; Wadt, W.R. Ab initio effective core potentials for molecular calculations. Potentials for K to Au including the outermost core orbitals. J. Chem. Phys. 1985, 82, 299. [Google Scholar] [CrossRef]
- Cramer, C.J.; Truhlar, D.G. Density functional theory for transition metals and transition metal chemistry. Phys. Chem. Chem. Phys. 2009, 11, 10757–10816. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; Truhlar, D.G. Density Functionals with Broad Applicability in Chemistry. Acc. Chem. Res. 2008, 41, 157–167. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; Truhlar, D.G. Applications and validations of the Minnesota density functionals. Chem. Phys. Lett. 2011, 502, 1–13. [Google Scholar] [CrossRef]
- Ramachandran, S.; Jovancicevic, V. Molecular modeling of the inhibition of mild steel carbon dioxide corrosion by imidazolines. Corros. Sci. 1999, 55, 259–267. [Google Scholar] [CrossRef]
- Thierry, D.; Leygraf, C. Enhanced Raman scattering of 1,2,4 triazole and imidazole adsorbed on microlithographically prepared copper surfaces. J. Electrochem. Soc. 1986, 133, 2236–2239. [Google Scholar] [CrossRef]
- Martinez, J.A.; Yilmaz, D.E.; Liang, T.; Sinnott, S.B.; Phillpot, S.R. Fitting empirical potentials: Challenges and methodologies. Curr. Opin. Solid State Mater. Sci. 2013, 17, 263–270. [Google Scholar] [CrossRef]
- Bukowska, J.; Kudelski, A.; Jockowska, K. The use of surface enhanced Raman scattering to prove the interaction of imidazole with the silver electrode surface. J. Electroanal. Chem. Interfacial Electrochem. 1991, 309, 251. [Google Scholar] [CrossRef]
- Loo, B.H.; Tse, Y.; Parsons, K.; Adelman, C.; El-Hage, A.; Lee, Y.G. Surface-enhanced Raman spectroscopy of imidazole adsorbed on electrode and colloidal surfaces of Cu, Ag, and Au. J. Raman Spectrosc. 2006, 37, 299–304. [Google Scholar] [CrossRef]
- Kovacevic, N.; Milosev, I.; Kokalj, A. How relevant is the adsorption bonding of imidazoles and triazoles for their corrosion inhibition of copper? Corros. Sci. 2017, 124, 25–34. [Google Scholar] [CrossRef]
- Taylor, C.D.; Chandra, A.; Vera, J.; Sridhar, N. Design and prediction of corrosion inhibitors from quantum chemistry. II. A general framework for prediction of effective oil/water partition coefficients and speciation from quantum chemistry. J. Electrochem. Soc. 2015, 162, C347–C353. [Google Scholar] [CrossRef]
- Marenich, A.V.; Cramer, C.J.; Truhlar, D.G. Universal Solvation Model Based on Solute Electron Density and on a Continuum Model of the Solvent Defined by the Bulk Dielectric Constant and Atomic Surface Tensions. J. Phys. Chem. B 2009, 113, 6378–6396. [Google Scholar] [CrossRef] [PubMed]
- Taylor, C.D.; Kelly, R.G.; Neurock, M. A first-principles analysis of the chemisorption of hydroxide on copper under electrochemical conditions: A probe of the electronic interactions that control chemisorption at the electrochemical interface. J. Electroanal. Chem. 2007, 607, 167–174. [Google Scholar] [CrossRef]
- Anderson, A.B.; Debnath, N.C. Mechanism of iron dissolution and passivation in an aqueous environment: Active and transition ranges. J. Am. Chem. Soc. 1983, 105, 18–22. [Google Scholar] [CrossRef]
- Kovačević, N.; Kokalj, A. Analysis of molecular electronic structure of imidazole- and benzimidazole-based inhibitors: A simple recipe for qualitative estimation of chemical hardness. Corros. Sci. 2011, 53, 909–921. [Google Scholar] [CrossRef]
- Sun, S.; Geng, Y.; Tian, L.; Chen, S.; Yan, Y.; Hu, S. Density functional theory study of imidazole, benzimidazole and 2-mercaptobenzimidazole adsorption onto clean Cu(111) surface. Corros. Sci. 2012, 63, 140–147. [Google Scholar] [CrossRef]
- Jiang, Y.; Adams, J.B.; Sun, D.H. Benzotriazole adsorption on Cu2O(111) surfaces: A first-principles study. J. Phys. Chem. B 2004, 108, 12851–12857. [Google Scholar] [CrossRef]
- Mobin, M.; Parveen, M.; Rafiquee, M.Z.A. Inhibition of mild steel corrosion using l-histidine and synergistic surfactants additives. J. Mater. Eng. Perform. 2013, 22, 548–556. [Google Scholar] [CrossRef]
- Deltombe, E.; de Zoubov, N.; Pourbaix, M. Atlas of Electrochemical Equilibria in Aqueous Solution; NACE: Houston, TX, USA, 1974. [Google Scholar]
- Mendes, J.O.; da Silva, E.C.; Rocha, A.B. On the nature of inhibition performance of imidazole on iron surface. Corros. Sci. 2012, 57, 254–259. [Google Scholar] [CrossRef]
- Milosev, I.; Kovacevic, N.; Kokalj, A. Electrochemical and Spectroscopic Study of Benzotriazole Films Formed on Copper, Copper-zinc Alloys and Zinc in Chloride Solution. Acta Chim. Slov. 2016, 63, 544–559. [Google Scholar] [PubMed]
- Xhanari, K.; Finsgar, M. Organic corrosion inhibitors for aluminum and its alloys in chloride and alkaline solutions: A review. Arabian J. Chem. 2016, in press. [Google Scholar] [CrossRef]
- Schmitt, G. Application of inhibitors for acid media: Report prepared for the European Federation of Corrosion Working Party on Inhibitors. Br. Corros. J. 1984, 19, 165–176. [Google Scholar] [CrossRef]
- Frankel, G.; Li, T.; Scully, J.R. Perspective—Localized corrosion: Passive film breakdown vs. pit growth stability. J. Electrochem. Soc. 2017, 164, C180–C181. [Google Scholar] [CrossRef]
- Frankel, G.; Thornton, G.; Street, S.; Rayment, T.; Williams, D.; Cook, A.; Davenport, A.; Gibbon, S.; Engelberg, D.; Ornek, C.; et al. Localised corrosion: General discussion. Faraday Discuss. 2015, 180, 381–414. [Google Scholar] [CrossRef] [PubMed]
- Frankel, G.S.; Scully, J.R.; Jahnes, C.V. Repassivation of pits in aluminum thin films. J. Electrochem. Soc. 1996, 143, 1834–1840. [Google Scholar] [CrossRef]
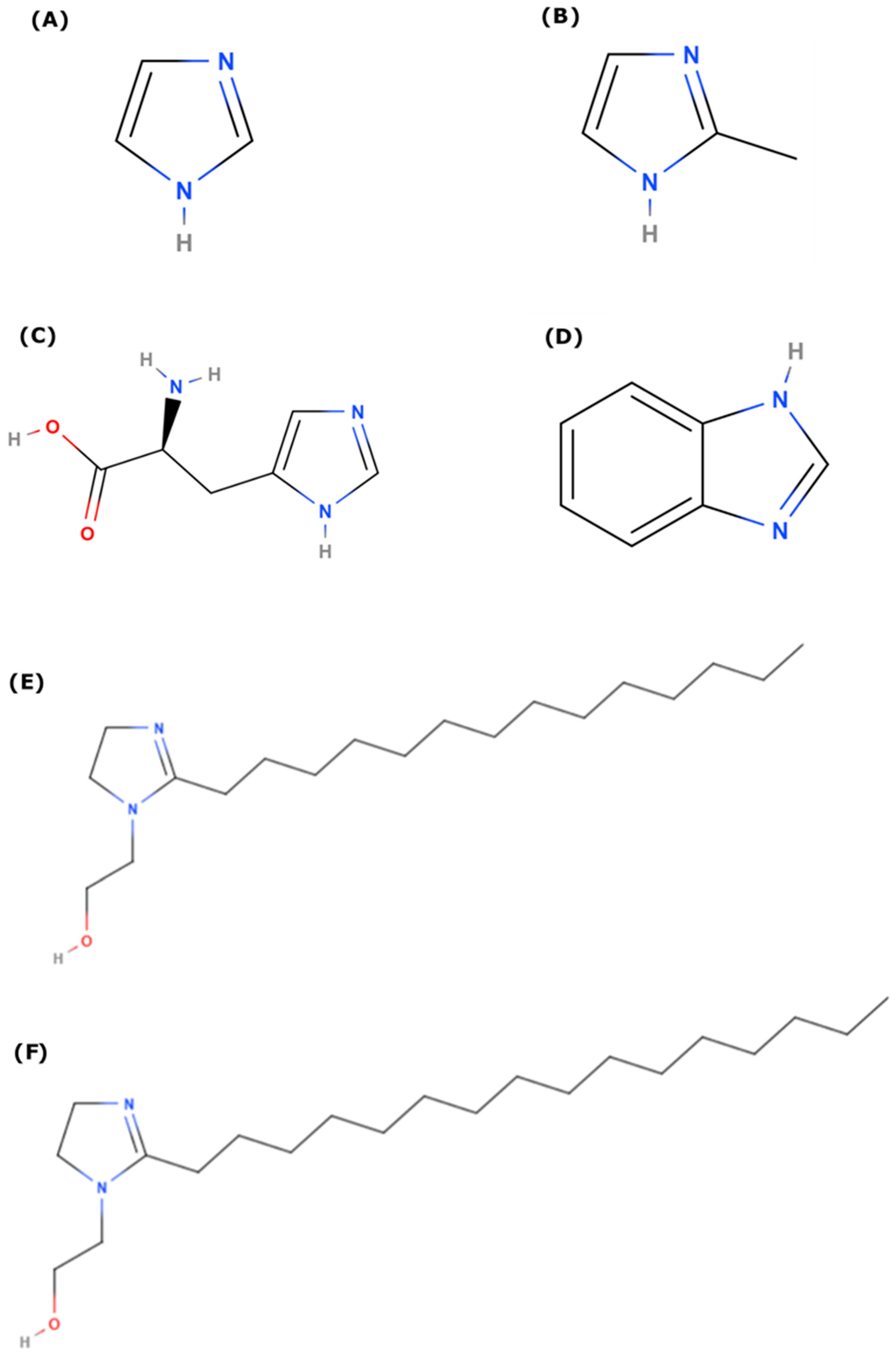
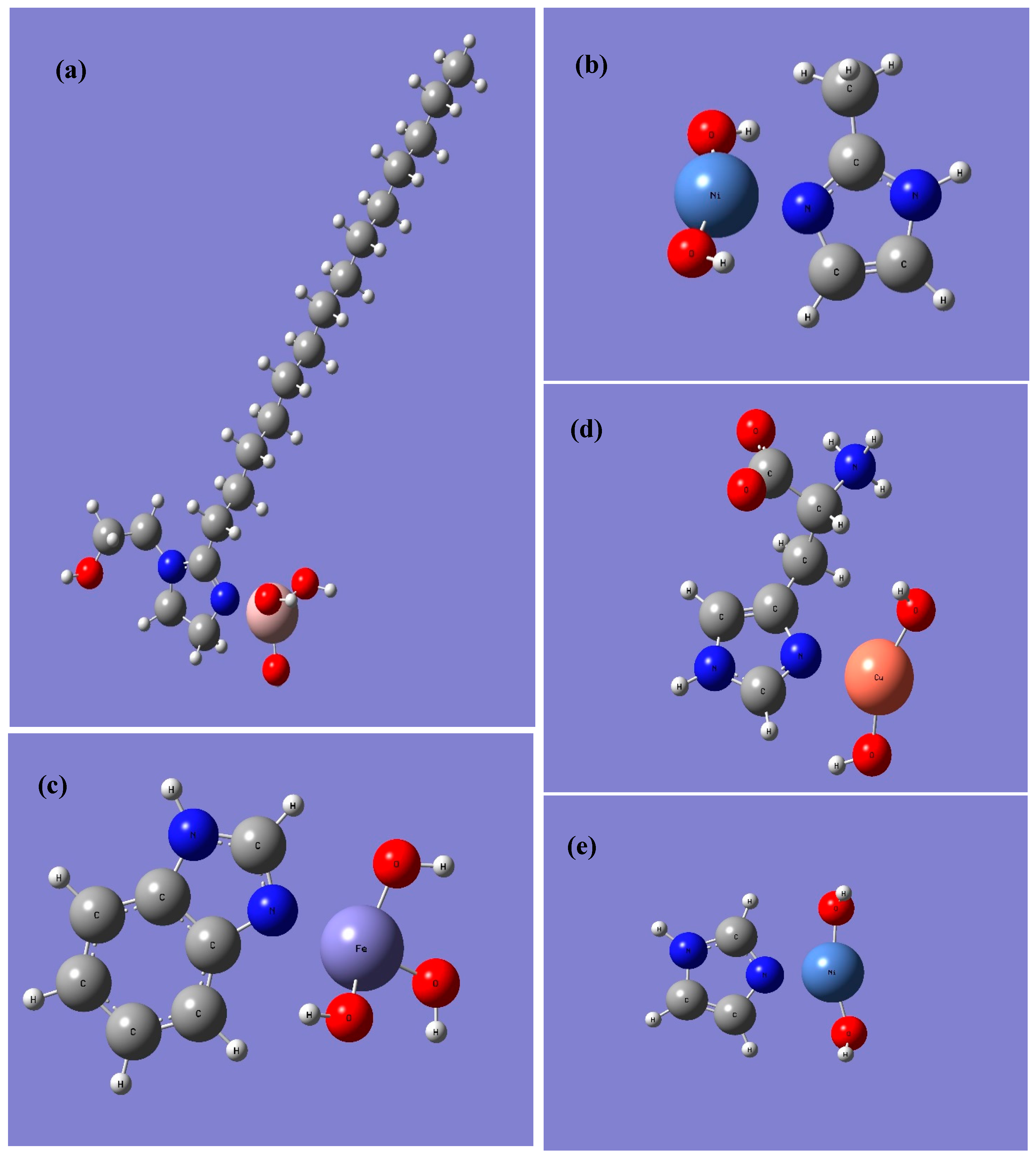
| Binding Energy in Vacuum (kJ/mol) | ||||||
|---|---|---|---|---|---|---|
| Metal Hydroxide | Corrosion Inhibitor | |||||
| IMZ (A) | Me-IMZ (B) | BI (C) | l-HIS (D) | IMZ_C14 (E) | IMZ_C16 (F) | |
| Cu(OH)2 | 103 | 110 | 107 | 92 | 125 | 125 |
| Fe(OH)3 | 139 | 157 | 146 | 158 | -- | -- |
| Al(OH)3 | 148 | 163 | 152 | 189 | 195 | 195 |
| Ni(OH)2 | 176 | 186 | 183 | 209 | 202 | 200 |
| Binding Energy in Presence of Water (kJ/mol) | ||||||
|---|---|---|---|---|---|---|
| Metal Hydroxide | Corrosion Inhibitor | |||||
| IMZ (A) | Me-IMZ (B) | BI (C) | l-HIS (D) | IMZ_C14 (E) | IMZ_C16 (F) | |
| Cu(OH)2 | 87 | 91 | 84 | 88 | 95 | 97 |
| Fe(OH)3 | 81 | 89 | 78 | 97 | -- | -- |
| Al(OH)3 | 152 | 161 | 151 | 165 | 177 | 183 |
| Ni(OH)2 | 169 | 172 | 165 | 177 | 178 | 180 |
| Corrosion Inhibitor | Hydrophobicity (log P) | |
|---|---|---|
| with Reference to n-Octanol | with Reference to Hexane | |
| IMZ (A) | 0.04 | −4.2 |
| Me-IMZ (B) | −0.16 | −5.28 |
| BI (C) | 1.73 | −2.02 |
| L-His (D) | −3.76 | −16.31 |
| IMZ_C14 (E) | 11.26 | 2.73 |
| IMZ_C16 (F) | 13.62 | 6.1 |
| Metal Hydroxide | Free Energy of Adsorption at 298 K (kJ/mol) | |||||
|---|---|---|---|---|---|---|
| IMZ (A) | Me-IMZ (B) | BI (C) | l-HIS (D) | IMZ_C14 (E) | IMZ_C16 (F) | |
| Cu(OH)2 | −88 | −91 | −88 | −79 | −122 | −131 |
| Fe(OH)3 | −81 | −88 | −83 | −87 | -- | -- |
| Al(OH)3 | −152 | −161 | −155 | −156 | −205 | −217 |
| Ni(OH)2 | −169 | −172 | −169 | −168 | −206 | −214 |
| Metal Hydroxide | Free Energy of Adsorption at 298 K (kJ/mol) | |||||
|---|---|---|---|---|---|---|
| IMZ (A) | Me-IMZ (B) | BI (C) | l-HIS (D) | IMZ_C14 (E) | IMZ_C16 (F) | |
| Cu(OH)2 | −77 | −78 | −79 | −47 | −101 | −112 |
| Fe(OH)3 | −70 | −76 | −73 | −56 | -- | -- |
| Al(OH)3 | −142 | −148 | −146 | −125 | −183 | −199 |
| Ni(OH)2 | −158 | −159 | −160 | −136 | −185 | −195 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Taylor, C.D.; Kurapati, Y.; Mondal, S.K. Interaction of Model Inhibitor Compounds with Minimalist Cluster Representations of Hydroxyl Terminated Metal Oxide Surfaces. Metals 2018, 8, 81. https://doi.org/10.3390/met8020081
Taylor CD, Kurapati Y, Mondal SK. Interaction of Model Inhibitor Compounds with Minimalist Cluster Representations of Hydroxyl Terminated Metal Oxide Surfaces. Metals. 2018; 8(2):81. https://doi.org/10.3390/met8020081
Chicago/Turabian StyleTaylor, Christopher D., Yathish Kurapati, and Sujit K. Mondal. 2018. "Interaction of Model Inhibitor Compounds with Minimalist Cluster Representations of Hydroxyl Terminated Metal Oxide Surfaces" Metals 8, no. 2: 81. https://doi.org/10.3390/met8020081
APA StyleTaylor, C. D., Kurapati, Y., & Mondal, S. K. (2018). Interaction of Model Inhibitor Compounds with Minimalist Cluster Representations of Hydroxyl Terminated Metal Oxide Surfaces. Metals, 8(2), 81. https://doi.org/10.3390/met8020081