Elastic and Plastic Behavior of the QE22 Magnesium Alloy Reinforced with Short Saffil Fibers and SiC Particles
Abstract
:1. Introduction
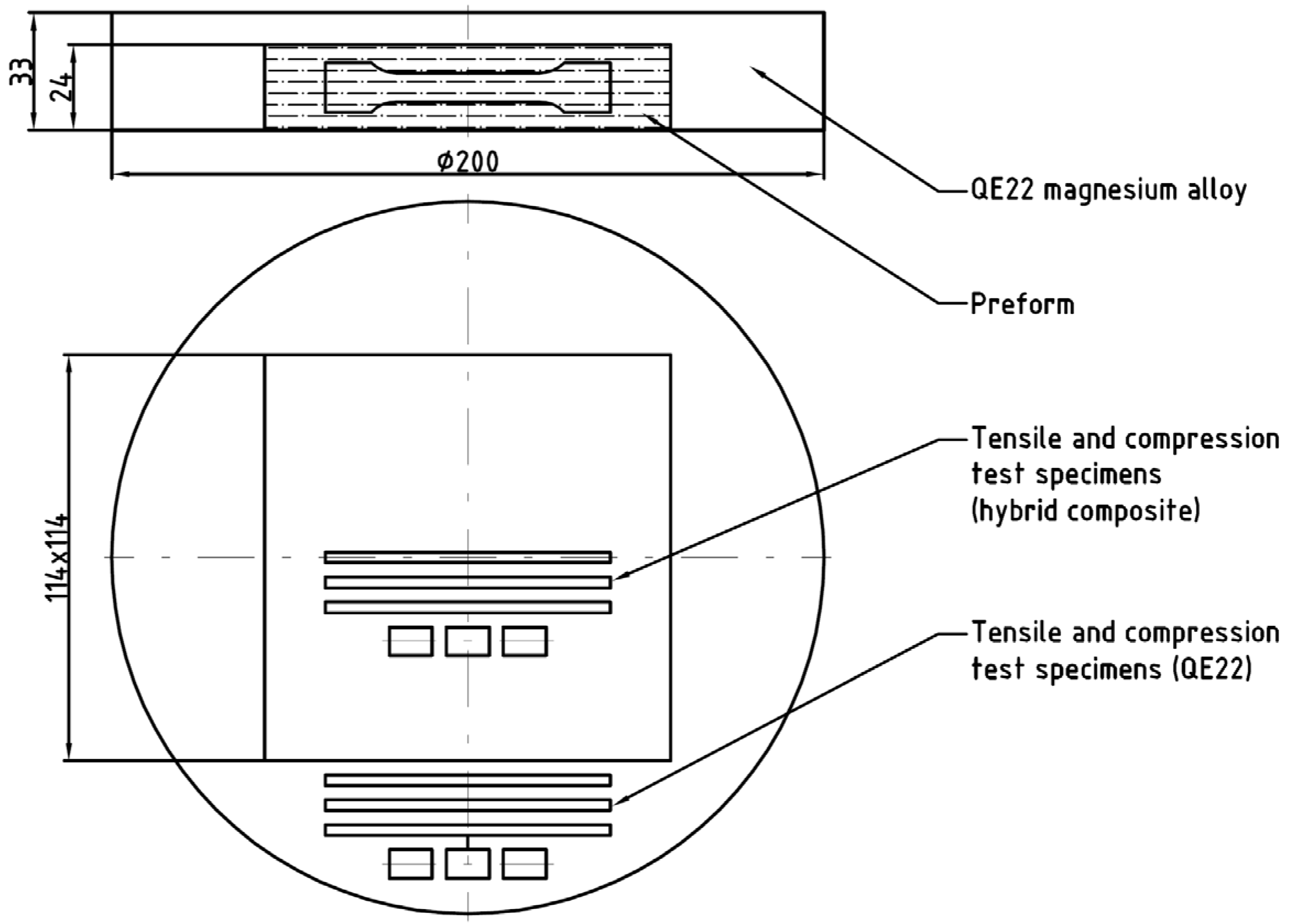
2. Experimental Material and Procedure
3. Results and Discussion
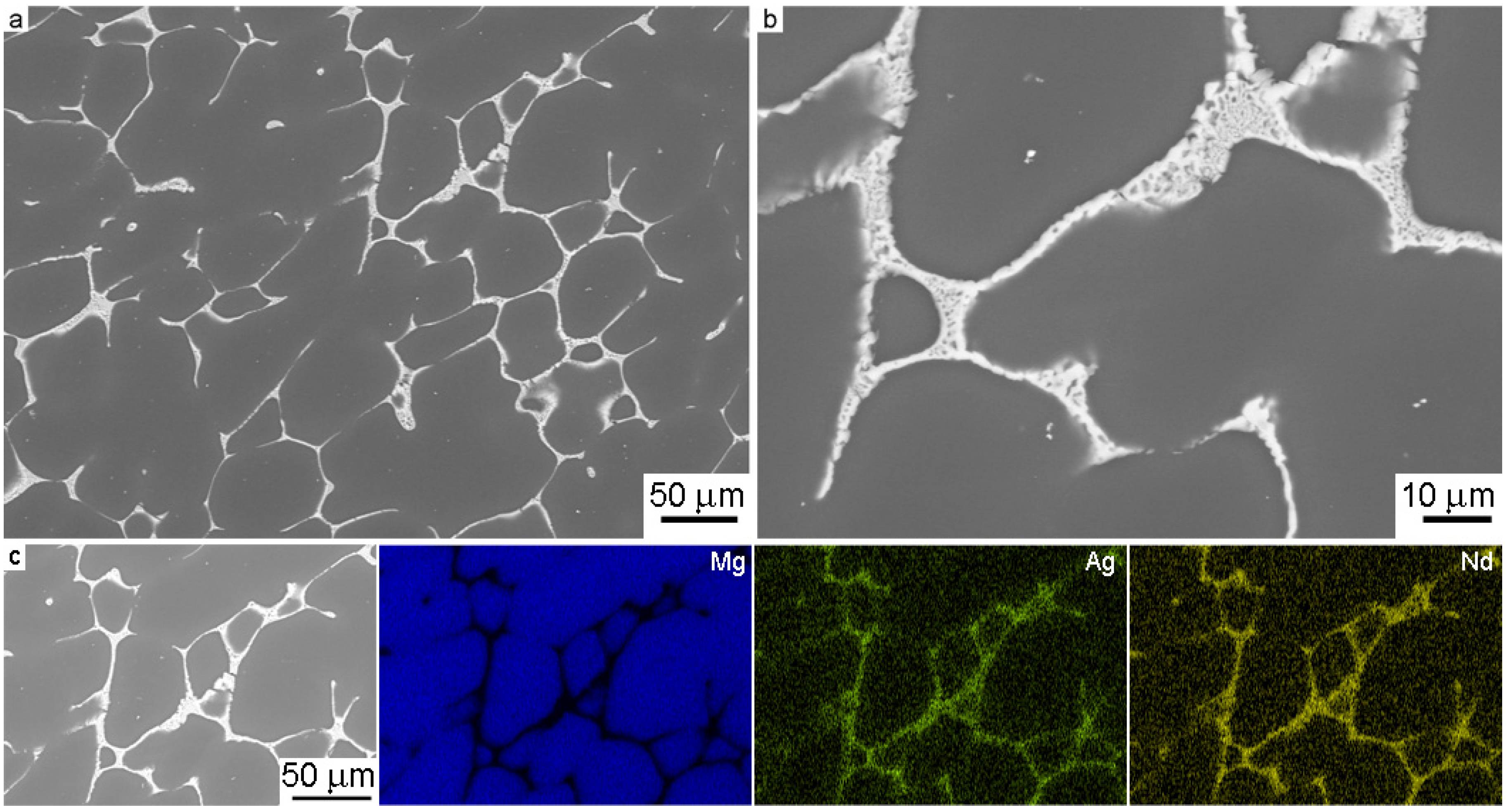
3.1. Microstructure Analysis
3.2. Elastic Properties
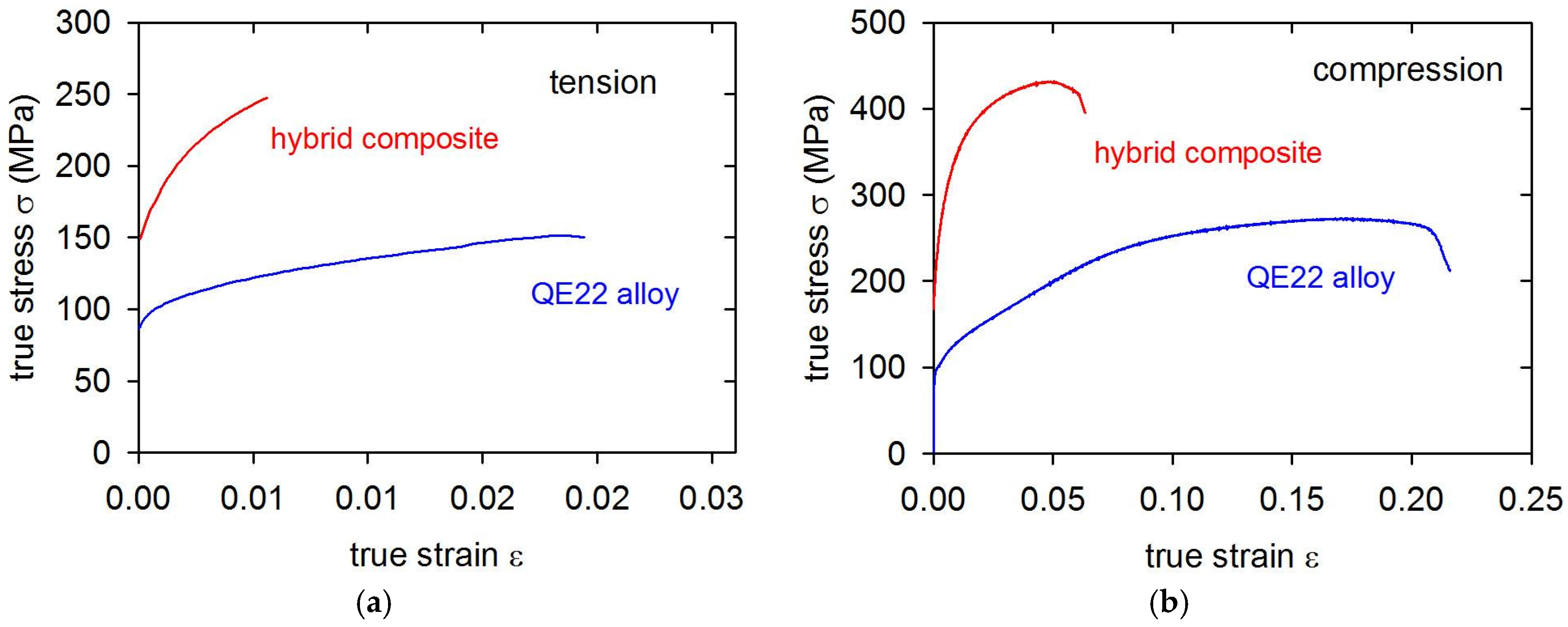
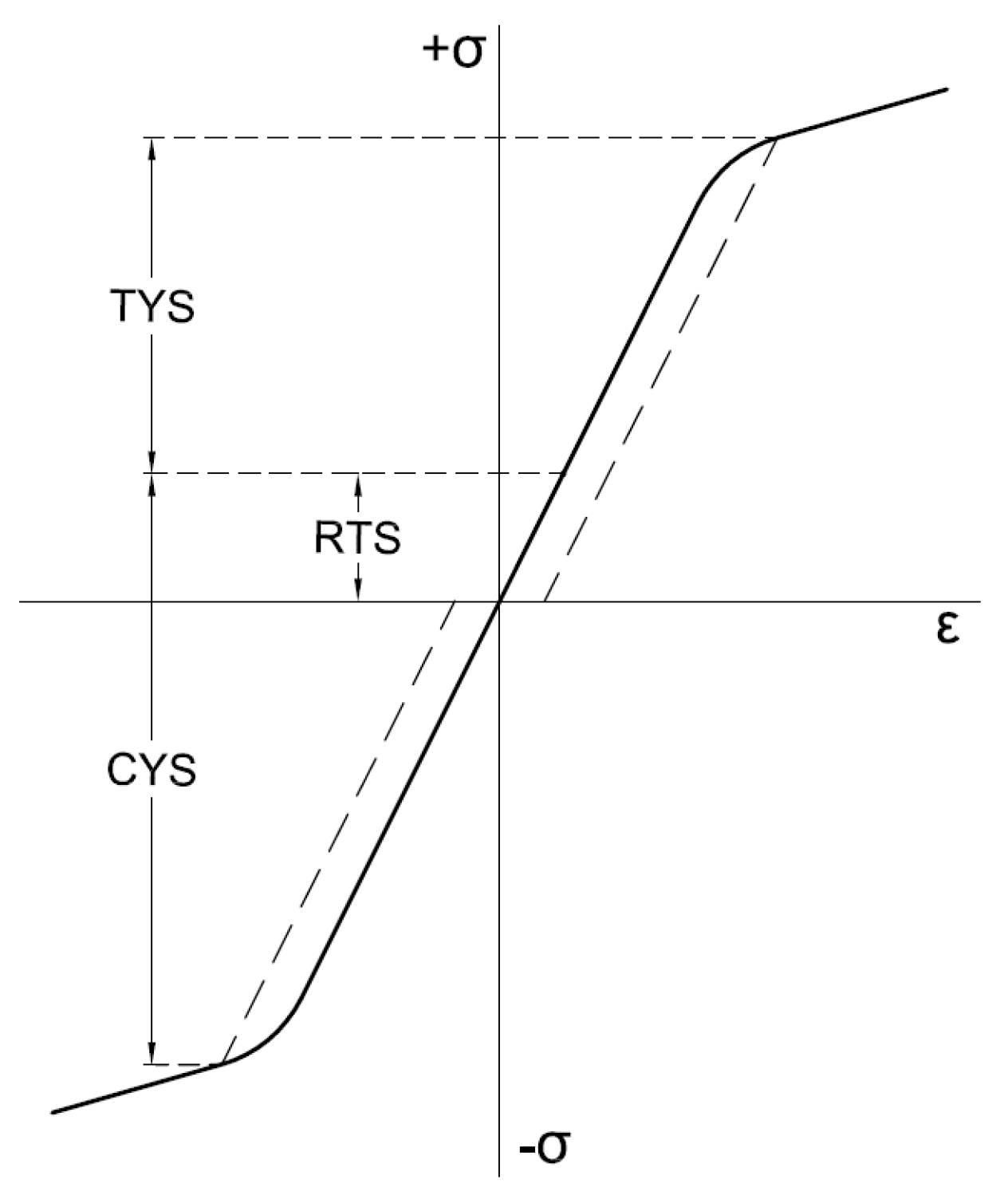
3.3. Plastic Deformation
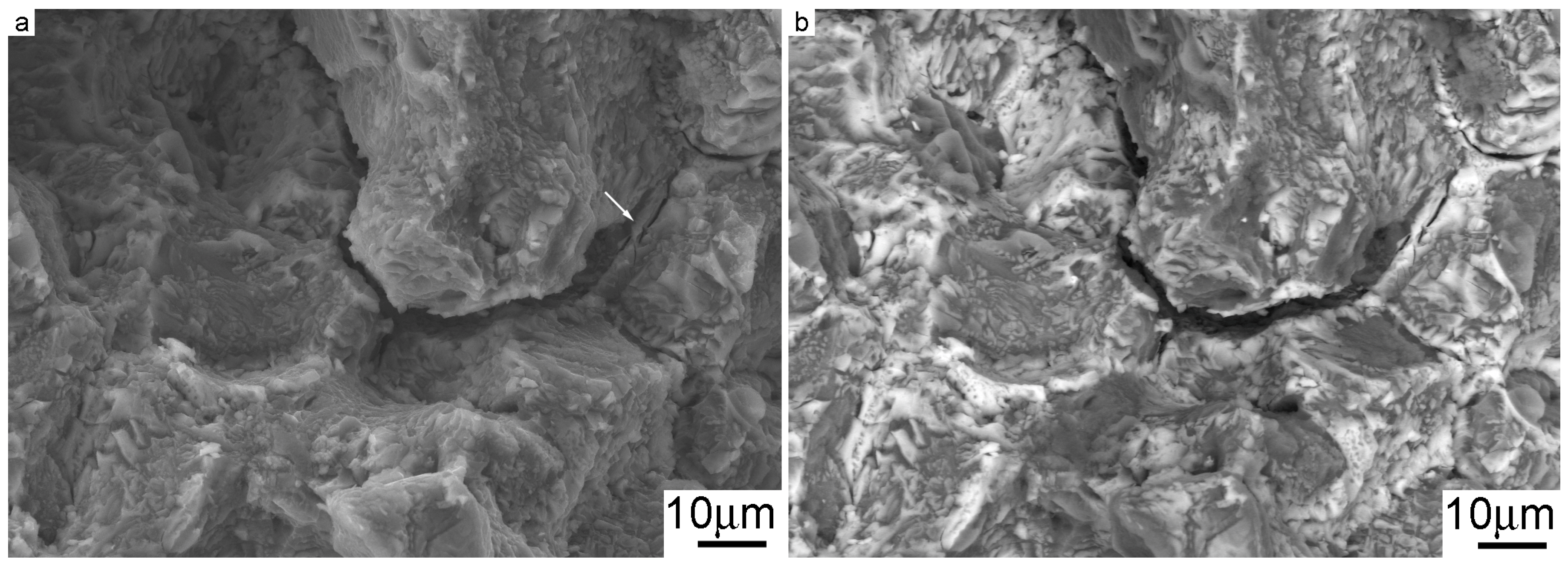
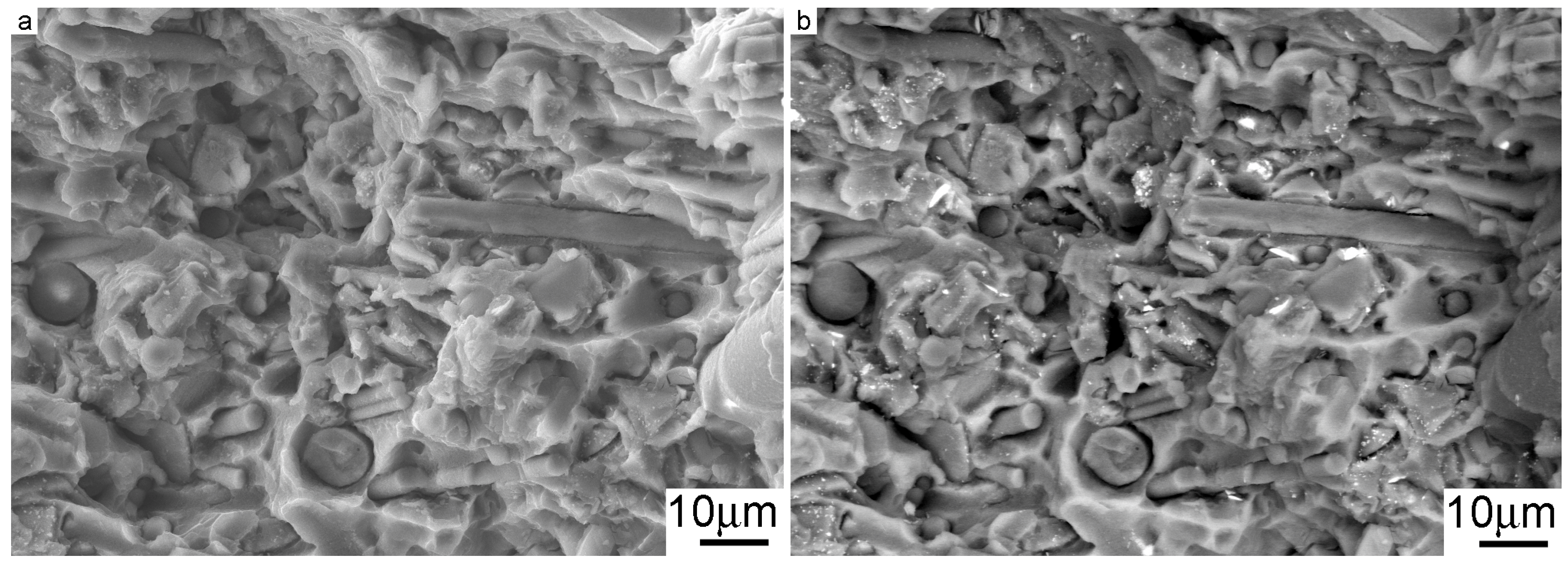
3.4. Fractographic Analysis
4. Conclusions
- Young’s modulus measurements exhibited anisotropy owing to the 2D fiber distribution.
- The Halpin–Tsai–Kardos self-consistent model was successfully used to model the Young’s modulus anisotropy, and the results are in good agreement with the experimentally obtained data.
- The presence of reinforcing fibers and particles substantially increased both tensile and compression deformation flow stresses.
- The ductility of the hybrid composite was radically decreased compared to the cast matrix alloy.
- The load transfer, the increased dislocation density, and the Hall–Petch strengthening are the main reinforcing mechanisms in the case of studied hybrid composite.
- Fracture of the matrix is mainly intercrystalline due to brittle eutectics present at the grain boundaries.
- Fracture of the hybrid composite is transcrystalline; no pulling out of the reinforcing fibers or particles was observed.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Polmear, I.J. Magnesium Alloys and Their Applications; Mordike, B.L., Hehmann, F., Eds.; DGM: Oberursel, Germany, 1992; p. 201. ISBN 978-3883551845. [Google Scholar]
- Advesian, M.M. ASM Speciality Handbook: Magnesium and Magnesium Alloys; Advesian, M.M., Baker, H., Eds.; ASM International: Russell Township, OH, USA, 1999; ISBN 978-0-87170-657-7. [Google Scholar]
- Kainer, K.U. Magnesium Alloys and Their Applications; Mordike, B.L., Hehmann, F., Eds.; DGM: Oberursel, Germany, 1992; p. 415. ISBN 978-3883551845. [Google Scholar]
- Oakley, R.; Cochrane, R.F.; Stevens, R. Recent developments in magnesium matrix composites. Key Eng. Mater. 1995, 104–107, 387–416. [Google Scholar] [CrossRef]
- Dey, A.; Pandey, K.M. Magnesium metal matrix composites—A review. Rev. Adv. Mater. Sci. 2015, 42, 58–67. [Google Scholar]
- Park, Y.; Cho, K.; Park, I.; Park, Y. Fabrication and mechanical properties of magnesium matrix composite reinforced with Si coated carbon nanotubes. Procedia Eng. 2011, 10, 1446–1450. [Google Scholar] [CrossRef]
- Jiang, Q.C.; Wang, H.Y.; Ma, B.X.; Wang, Y.; Zhao, F. Fabrication of B4C particulate reinforced magnesium matrix composite by powder metallurgy. J. Alloy. Compd. 2005, 386, 177–181. [Google Scholar] [CrossRef]
- Han, G.Q.; Shen, J.H.; Ye, X.X.; Chen, B.; Imai, H.; Kondoh, K.; Du, W.B. The influence of CNTs on the microstructure and ductility of CNT/Mg composites. Mater. Lett. 2016, 181, 300–304. [Google Scholar] [CrossRef]
- Han, B.C.; Dunand, D.Q. Microstructure and mechanical properties of magnesium containing high volume fractions of yttria dispersoids. Mater. Sci. Eng. A 2000, 277, 297–304. [Google Scholar] [CrossRef]
- Yu, W.; Zhao, H.; Hu, X. Anisotropic mechanical and physical properties in textured Ti2AlC reinforced AZ91D magnesium composite. J. Alloy. Compd. 2018, 732, 894–901. [Google Scholar] [CrossRef]
- Chawla, K.K. Materials Science and Technology; Cahn, R.W., Haasen, P., Kramer, E.J., Eds.; Wiley-VCH: Weinheim, Germany, 1993; Volume 13, pp. 121–182. [Google Scholar]
- Hassan, S.F.; Gupta, M. Development of high performance magnesium nano-composites using nano-Al2O3 as reinforcement. Mater. Sci. Eng. A 2005, 392, 163–168. [Google Scholar] [CrossRef]
- Trojanová, Z.; Gärtnerová, V.; Lukáč, P.; Drozd, Z. Mechanical properties of Mg alloys composites reinforced with short Saffil® fibres. J. Alloy. Compd. 2004, 378, 19–26. [Google Scholar] [CrossRef]
- Trojanová, Z.; Száraz, Z.; Lábár, J.; Lukáč, P. Deformation behaviour of an AS21 alloy reinforced by short Saffil fibres and SiC particles. J. Mater. Process. Technol. 2005, 162–163, 131–138. [Google Scholar] [CrossRef]
- Ho, K.F.; Gupta, M.; Srivatsan, T.S. The mechanical behavior of magnesium alloy AZ91 reinforced with fine copper particulates. Mater. Sci. Eng. A 2004, 369, 302–308. [Google Scholar] [CrossRef]
- Jayalakshmi, S.; Kailas, S.V.; Seshan, S. Tensile behaviour of squeeze cast AM100 magnesium alloy and its Al2O3 fibre reinforced composites. Compos. Part A 2002, 33, 1135–1140. [Google Scholar] [CrossRef]
- Trojanová, Z.; Drozd, Z.; Kúdela, S.; Száraz, Z.; Lukáč, P. Strengthening in Mg–Li matrix composites. Compos. Sci. Technol. 2009, 67, 1965–1973. [Google Scholar] [CrossRef]
- Manoharan, M.; Lim, S.C.V.; Gupta, M. Application of a model for the work hardening behavior to Mg/SiC composites synthesized using a fluxless casting proces. Mater. Sci. Eng. A 2002, 333, 243–249. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, Q.; Hu, H. Tensile behaviour and microstructure of magnesium AM60-based hybrid composite containing Al2O3 fibres and particles. Mater. Sci. Eng. A 2014, 607, 269–276. [Google Scholar] [CrossRef]
- Kumar, S.R.; Panigrahi, M.K.; Thakur, S.K.; Kainer, K.U.; Chakraborty, M.; Dhindaw, B.K. Characterization of stress in reinforcements in magnesium based squeeze infiltrated cast hybrid composites. Mater. Sci. Eng. A 2006, 415, 207–212. [Google Scholar] [CrossRef]
- Kumar, S.; Dieringa, H.; Kainer, K.U. Effect of particulate content on the thermal cycling behaviour of the magnesium alloy based hybrid composites. Compos. Part A 2005, 36, 321–325. [Google Scholar] [CrossRef]
- Svoboda, M.; Pahutová, M.; Kuchařová, K.; Sklenička, V.; Kainer, K.U. Microstructure and creep behaviour of magnesium hybrid composites. Mater. Sci. Eng. A 2007, 462, 220–224. [Google Scholar] [CrossRef]
- Arunachaleswaran, A.; Pereira, I.M.; Dieringa, H.; Huang, Y.; Hort, N.; Dhindaw, B.K.; Kainer, K.U. Creep behavior of AE42 based hybrid composites. Mater. Sci. Eng. A 2007, 460–461, 268–276. [Google Scholar] [CrossRef]
- Arunachaleswaran, A.; Dhindaw, B.K.; Dieringa, H.; Hort, N.; Kainer, K.U. Microstructure characterisation and creep properties of AE42 based hybrid composites prepared by squeeze casting process. Trans. Indian Inst. Met. 2007, 60, 87–91. [Google Scholar]
- Roy, S.; Gebert, J.-M.; Stasiuk, G.; Piat, R.; Weidenmann, K.A.; Wanner, A. Complete determination of elastic moduli of interpenetrating metal/ceramic composites using ultrasonic techniques and micromechanical modelling. Mater. Sci. Eng. A 2011, 528, 8226–8235. [Google Scholar] [CrossRef]
- Trojanová, Z.; Drozd, Z.; Minárik, P.; Lukáč, P.; Kasakewitsch, A. Influence of texture on the thermal expansion coefficient of Mg/BN nanocomposite. Thermochim. Acta 2016, 644, 69–75. [Google Scholar] [CrossRef]
- Penchal Reddy, M.; Shakoor, R.A.; Parande, G.; Manakari, V.; Ubaid, F.; Modamed, A.M.A.; Gupta, M. Enhanced performance of nano-sized SiC reinforced Al metal matrix nanocomposites synthesized through microwave sintering and hot extrusion techniques. Prog. Nat. Sci. 2017, 27, 606–614. [Google Scholar] [CrossRef]
- Chen, Y.; Tekumalla, S.; Guo, Y.B.; Shabadi, R.; Shim, V.P.W.; Gupta, M. The dynamic compressive response of a high-strength magnesium alloy and its nanocomposite. Mater. Sci. Eng. A 2017, 702, 65–72. [Google Scholar] [CrossRef]
- Gupta, M.; Wong, W.L.E. Magnesium-based nanocomposites: Lightweight materials of the future. Mater. Charact. 2015, 105, 30–46. [Google Scholar] [CrossRef]
- Casati, R.; Vedani, M. Metal Matrix Composites Reinforced by Nano-Particles—A Review. Metals 2014, 4, 65–83. [Google Scholar] [CrossRef]
- Jayakumar, J.; Raghunath, B.K.; Rao, T.H. Recent Development and Challenges in Synthesis of Magnesium Matrix Nano Composites—A Review. Int. J. Latest Res. Sci. Technol. 2012, 1, 164–171. [Google Scholar]
- Zhao, C.; Wu, H.; Ni, J.; Zhang, S.; Zhang, X. Development of PLA/Mg composite for orthopedic implant: Tunable degradation and enhanced mineralization. Compos. Sci. Technol. 2017, 147, 8–15. [Google Scholar] [CrossRef]
- Trojanová, Z.; Ferkel, H.; Lukáč, P.; Riehemann, W. Two new high-damping magnesium composites. Phys. Status Solidi 2002, 193, 205–210. [Google Scholar] [CrossRef]
- Kiehn, J.; Smola, B.; Vostrý, P.; Stulíková, I.; Kainer, K.U. Microstructure Changes in Isochronally Annealed Alumina Fibre Reinforced Mg-Ag-Nd-Zr Alloy. Phys. Status Solidi 1997, 164, 709–723. [Google Scholar] [CrossRef]
- Magnesium Elektron® QE22 Casting Alloy. Available online: http://www.matweb.com/search/datasheettext.aspx?matguid=05ed4d435e5648058e27e84284aaceae (accessed on 15 January 2018).
- Saffil—Specific Property Information. Available online: http://www.saffil.com/index/fibre_home/property_information.aspx (accessed on 15 January 2018).
- Property of Silicon Carbide (SiC). Available online: http://www.qualitymaterial.net/news_list85.html (accessed on 15 January 2018).
- Halpin, J.C. Effect of Environmental Factors on Composite Materials; Technical Report AFML-TR-67-423; US Air Force Material Laboratory: Dayton, OH, USA, 1969. [Google Scholar]
- Halpin, J.C.; Kardos, J.L. Halpin-Tsai equations: A review. Polym. Eng. Sci. 1976, 16, 344–352. [Google Scholar] [CrossRef]
- Mendelson, S. Dislocations Dissociations in hcp Metals. J. Appl. Phys. 1970, 41, 1893–1910. [Google Scholar] [CrossRef]
- Máthis, K.; Čapek, J.; Zdražilová, Z.; Trojanová, Z. Investigation of tension-compression asymmetry of magnesium by use of the acoustic emission technique. Mater. Sci. Eng. A 2011, 528, 5904–5907. [Google Scholar] [CrossRef]
- Arsenault, R.J.; Shi, N. Dislocation generation due to differences between the coefficients of thermal expansion. Mater. Sci. Eng. 1986, 81, 175–187. [Google Scholar] [CrossRef]
- Ashby, M.F. The deformation of plastically non-homogeneous materials. Philos. Mag. 1970, 21, 399–424. [Google Scholar] [CrossRef]
- Taya, M.; Arsenault, R.J. A comparison between a shear lag type model and an Eshelby type model in predicting the mechanical properties of a short fiber composite. Scr. Metall. 1987, 21, 349–354. [Google Scholar] [CrossRef]
- Ryu, H.J.; Cha, S.I.; Hong, S.H. Generalized shear-lag model for load transfer in SiC/Al metal-matrix composites. J. Mater. Res. 2003, 18, 2851–2858. [Google Scholar] [CrossRef]
- Zhang, C.Y.; Qiu, Y.P. Modified shear lag model for fibers and fillers with irregular cross-sectional shapes. J. Adhes. Sci. Technol. 2003, 17, 397–408. [Google Scholar] [CrossRef]
- Karbhari, V.M.; Wilkins, D.J. An “engineering” modification to the shear-lag model as applied to whisker and particulate reinforced composites. Scr. Metall. Mater. 1991, 25, 707–712. [Google Scholar] [CrossRef]
- Nardone, V.C.; Prewo, K.M. On the strength of discontinuous silicon carbide reinforced aluminum composites. Scr. Metall. 1986, 20, 43–48. [Google Scholar] [CrossRef]
- Aikin, R.M., Jr.; Christodoulou, L. The role of equiaxed particles on the yield stress of composites. Scr. Metall. Mater. 1991, 25, 9–14. [Google Scholar] [CrossRef]
- Arsenault, R.J.; Wang, L.; Feng, C.R. Strengthening of composites due to microstructural changes in the matrix. Acta Metall. Mater. 1991, 39, 47–57. [Google Scholar] [CrossRef]
- Armstrong, R.W. Theory of the Tensile Ductile-Brittle Behaviour of Polycrystalline h.c.p. Materials with Application to Beryllium. Acta Metall. 1986, 16, 347–355. [Google Scholar] [CrossRef]
- Scattergood, R.O.; Bacon, D.J. The Orowan mechanism in anisotropic crystals. Philos. Mag. A 1975, 31, 179–198. [Google Scholar] [CrossRef]
- Yeh, Y.-H.; Nakashima, H.; Kurishita, H.; Goto, S.; Yoshinaga, H. Absence of Threshold Stress for High-Temperature Creep of Dispersion- and Solution-Hardened Al-3.1 at % Mg-1.3 vol % be Alloy. Mater. Trans. 1990, 31, 778–785. [Google Scholar] [CrossRef]
- Delannay, F. Thermal Stresses and Thermal Expansion in MMCs. In Comprehensive Composite Materials; Clyne, T.W., Ed.; Elsevier: Amsterdam, The Netherlands, 2000; Volume 3, ISBN 978-0-08-042993-9. [Google Scholar]
- Pekguleryuz, M.O.; Kainer, K.U.; Kaya, A. (Eds.) Fundamentals of Magnesium Alloy Metallurgy, 1st ed.; Woodhead Publishing: Cambridge, UK, 2013; ISBN 9780857097293. [Google Scholar]
- Rudajevová, A.; Gärtnerová, V.; Jäger, A.; Lukáč, P. Influence of the thermal strain on the dilatation characteristics of Mg8Li and Mg10Li alloys. Kov. Mater. 2004, 42, 185–192. [Google Scholar]
- Lide, D.R. (Ed.) Handbook of Chemistry and Physics, 73rd ed.; CRC Press: Boca Raton, FL, USA, 1992; ISBN 978-0849304736. [Google Scholar]
- Ono, N.; Nakamura, K.; Miura, S. Influence of Grain Boundaries on Plastic Deformation in Pure Mg and AZ31 Mg Alloy Polycrystals. Mater. Sci. Forum 2003, 419–422, 195–200. [Google Scholar] [CrossRef]
- Lavrentev, F.F.; Pokhil, Y.A. Relation of dislocation density in different slip systems to work-hardening parameters for magnesium crystals. Mater. Sci. Eng. 1975, 18, 261–270. [Google Scholar] [CrossRef]
- Cáceres, C.H.; Lukáč, P. Strain hardening behaviour and the Taylor factor of pure magnesium. Philos. Mag. 2008, 88, 977–989. [Google Scholar] [CrossRef]
- Farkas, G.; Trojanová, Z.; Száraz, Z.; Minárik, P.; Máthis, K. Effect of the fiber orientation on the deformation mechanisms of magnesium-alloy based fiber reinforced composite. Mater. Sci. Eng. A 2015, 643, 25–31. [Google Scholar] [CrossRef]
- Trojanová, Z.; Farkas, G.; Máthis, K.; Lukáč, P. Hardening and softening in an AJ51 magnesium alloy reinforced with Saffil fibres. In Magnesium Technology 2014; Alderman, M., Manuel, M.V., Hort, N., Neelameggham, N.R., Eds.; TMS (The Mineral, Metals and Materials Society): Pittsburgh, PA, USA, 2014; pp. 435–440. ISBN 9781118888162. [Google Scholar]
- Farkas, G.; Choe, H.; Máthis, K.; Száraz, Z.; Noh, Y.; Trojanová, Z.; Minárik, P. In situ investigation of deformation mechanisms in magnesium-based metal matrix composites. Met. Mater. Int. 2015, 21, 652–658. [Google Scholar] [CrossRef]
- Lilholt, H. Additive strengthening. In Deformation of Multi-Phase and Particle Containing Materials, Proceedings of the 4th Risø International Symposium on Metallurgy and Materials Science, Risø, Roskilde, Denmark, 5–9 September 1983; Bilde-Sørensen, J.B., Hansen, N., Horsewell, A., Leffers, T., Lilholt, H., Eds.; Risø National Laboratory: Roskilde, Denmark, 1983; pp. 381–392. [Google Scholar]
- Clyne, T.W.; Whithers, P.J. An Introduction to Metal Matrix Composites; Cambridge University Press: Cambridge, UK, 1993; ISBN 9780511623080. [Google Scholar]
- Khan, F.; Panigradi, S.K. Age hardening, fracture behavior and mechanical properties of QE22 Mg alloy. J. Magnes. Alloy. 2015, 3, 210–217. [Google Scholar] [CrossRef]

| Em | ESaffil | ESiC | EH(ROM) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| GPa | GPa | GPa | GPa | GPa | GPa | GPa | GPa | GPa | GPa |
| 44.1 | 300 | 410 | 61.42 | 48.6 | 76.5 | 61.5 | 74.5 | 71.1 | 118.5 |
| [35] | [36] | [37] | - | - | - | - | - | - | - |
| Material | TYS | CYS | UTS | UCS | εf | εf |
|---|---|---|---|---|---|---|
| MPa | MPa | MPa | MPa | Tension | Compression | |
| QE22 alloy | 108.3 | 100.5 | 151.4 | 260.3 | 0.02 | 0.22 |
| composite | 207.6 | 243.4 | 247.3 | 431.4 | 0.006 | 0.06 |
| Mechanism | Equation | Symbols |
|---|---|---|
| Increased dislocation density due to thermal strain ΔαΔT | b Burgers vector of dislocations, B = 12 (p) B = 10 (f), t minimum size of (f) or (p) | |
| Dislocation geometrically necessary | εp plastic strain, νf,p volume fraction of fibers/particles | |
| Enhanced dislocation density | α1 constant, m Taylor factor, G shear modulus | |
| Load transfer | L fibers length, d fibers diameter | |
| Hall–Petch strengthening | d1, d2 grain sizes, Ky Hall–Petch constant | |
| Orowan strengthening | Λ distance between particles or fibers ends | |
| Residual thermal stresses | σm yield stress in matrix |
| α (QE22) | α (Saffil) | α (SiC) | Ky (Mg) | α1 | G | b | m |
|---|---|---|---|---|---|---|---|
| K−1 | K−1 | K−1 | MPa⋅mm1/2 | - | GPa | m | - |
| 26 × 10−6 | 6 × 10−6 | 6.6 × 10−6 | 10 | 0.35 | 17 | 3.2 × 10−10 | 4.5 |
| [55] | [56] | [57] | [58] | [59] | - | - | [60] |
| Deformation Mode | YS (A) | YS (M) | ΔσLT | ΔσD | ΔσOR | ΔσGS | <σm>max | σtot | YS (ex) |
|---|---|---|---|---|---|---|---|---|---|
| MPa | MPa | MPa | MPa | MPa | MPa | MPa | MPa | MPa | |
| tension | 108.3 | 144.2 | 29.2 + 10.8 | 35.9 | 2 | 25.2 | - | 202.4 | 207.6 |
| compresion | 100.5 | 136.4 | 27.6 +10.2 | 35.9 | 2 | 25.2 | 26.9 | 229.3 | 243.4 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zapletal, J.; Trojanová, Z.; Doležal, P.; Fintová, S.; Knapek, M. Elastic and Plastic Behavior of the QE22 Magnesium Alloy Reinforced with Short Saffil Fibers and SiC Particles. Metals 2018, 8, 133. https://doi.org/10.3390/met8020133
Zapletal J, Trojanová Z, Doležal P, Fintová S, Knapek M. Elastic and Plastic Behavior of the QE22 Magnesium Alloy Reinforced with Short Saffil Fibers and SiC Particles. Metals. 2018; 8(2):133. https://doi.org/10.3390/met8020133
Chicago/Turabian StyleZapletal, Josef, Zuzanka Trojanová, Pavel Doležal, Stanislava Fintová, and Michal Knapek. 2018. "Elastic and Plastic Behavior of the QE22 Magnesium Alloy Reinforced with Short Saffil Fibers and SiC Particles" Metals 8, no. 2: 133. https://doi.org/10.3390/met8020133
APA StyleZapletal, J., Trojanová, Z., Doležal, P., Fintová, S., & Knapek, M. (2018). Elastic and Plastic Behavior of the QE22 Magnesium Alloy Reinforced with Short Saffil Fibers and SiC Particles. Metals, 8(2), 133. https://doi.org/10.3390/met8020133






