Characteristics of Metal Magnetic Memory Testing of 35CrMo Steel during Fatigue Loading
Abstract
1. Introduction
2. Experimental Procedures
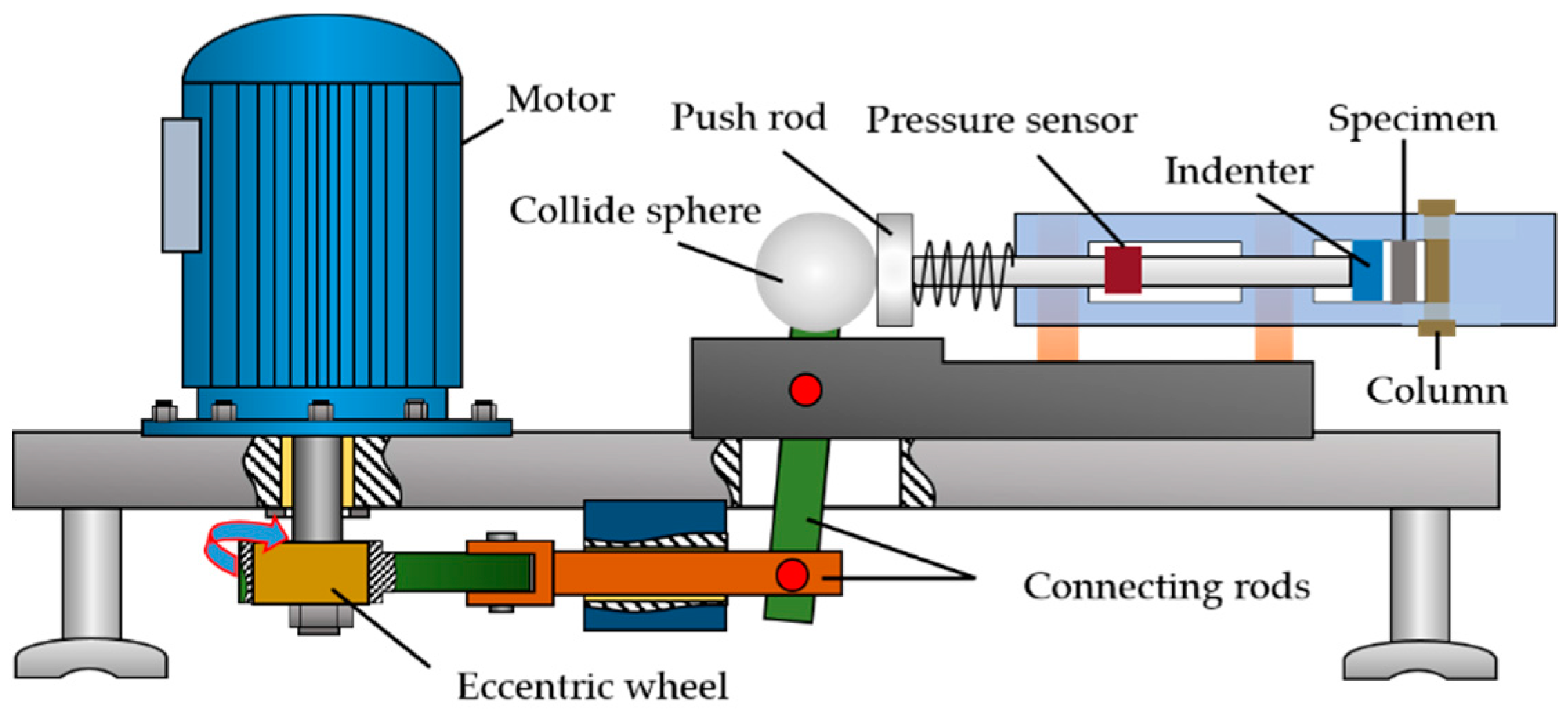
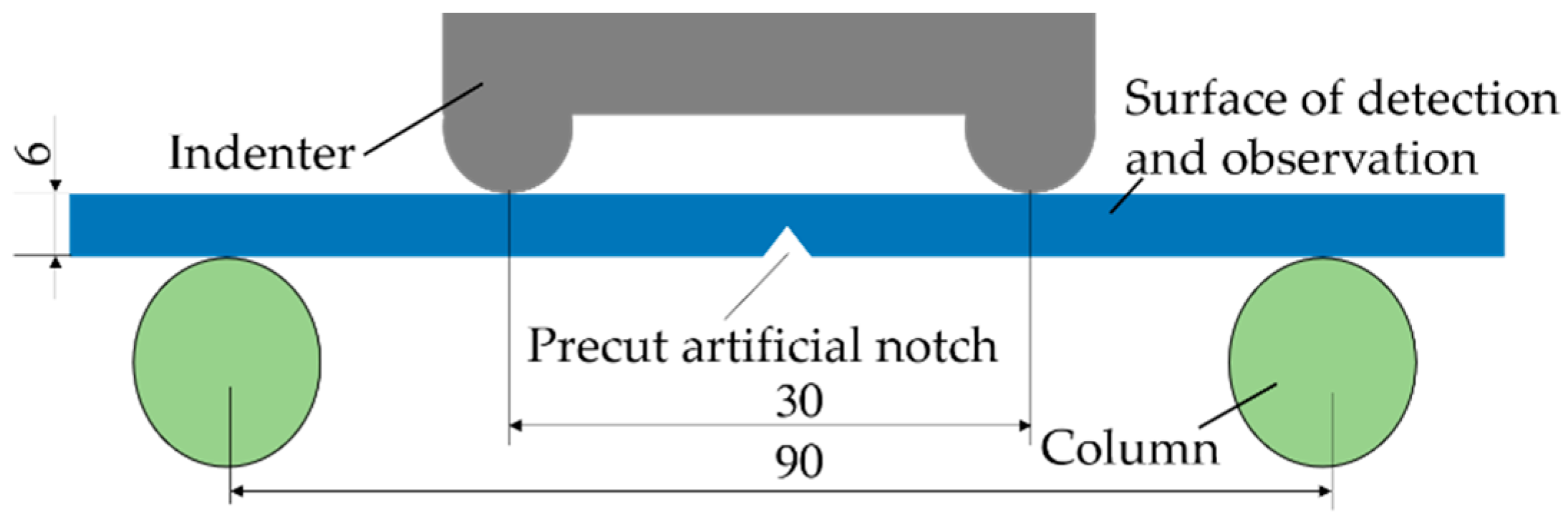
2.1. Experimental Instrument
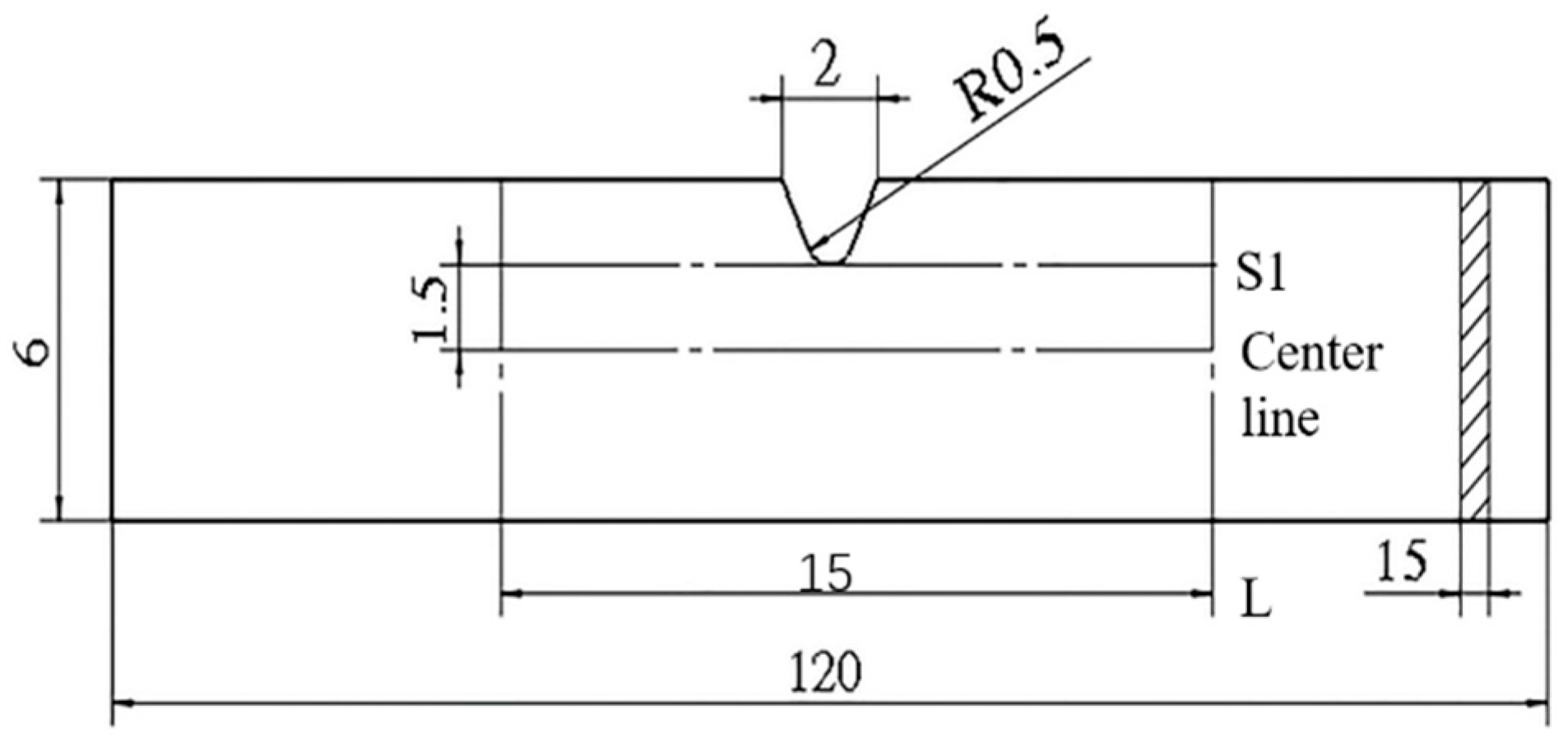
2.2. Specimen Preparation
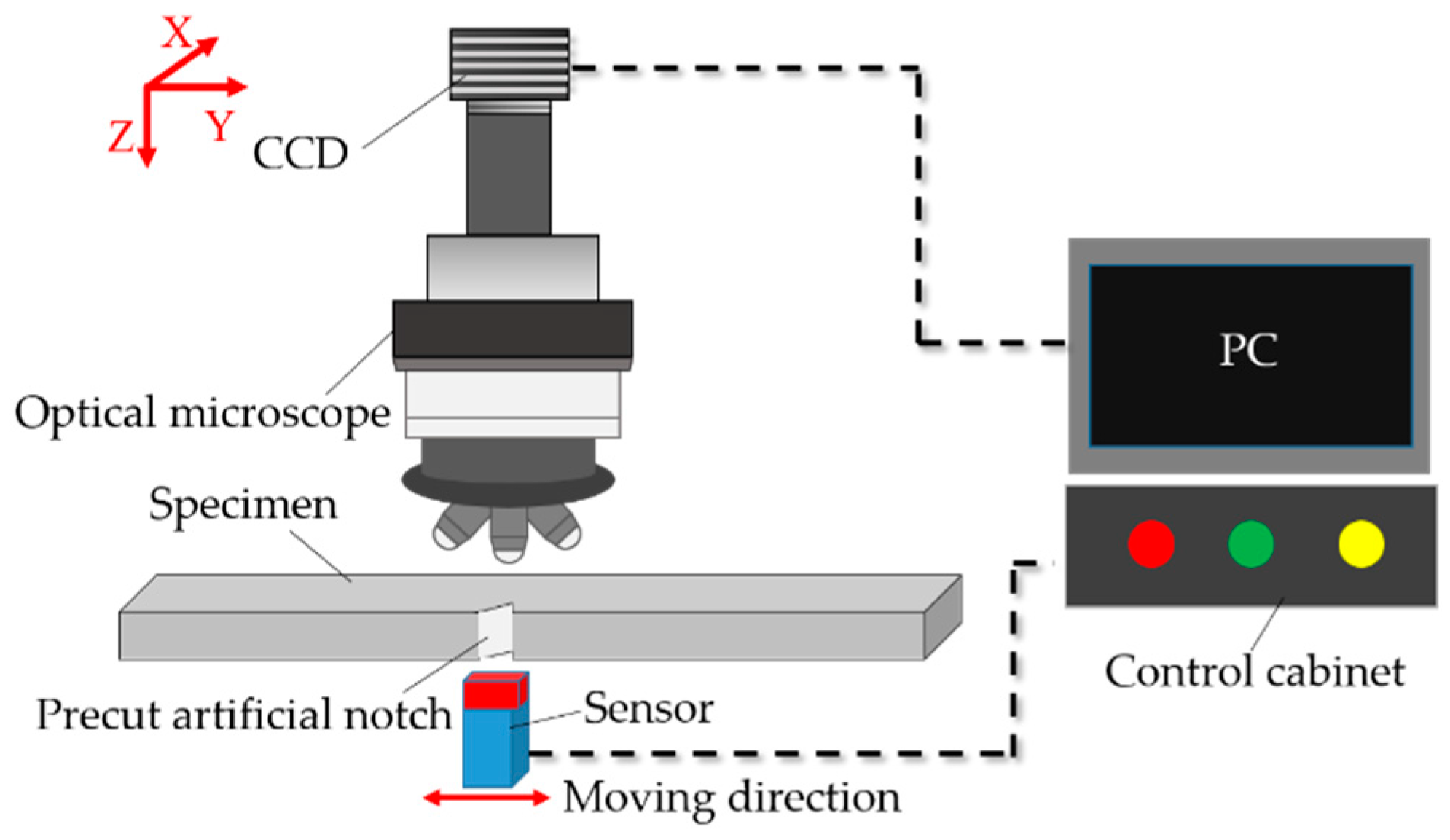
2.3. Arrangement
3. Results and Discussion
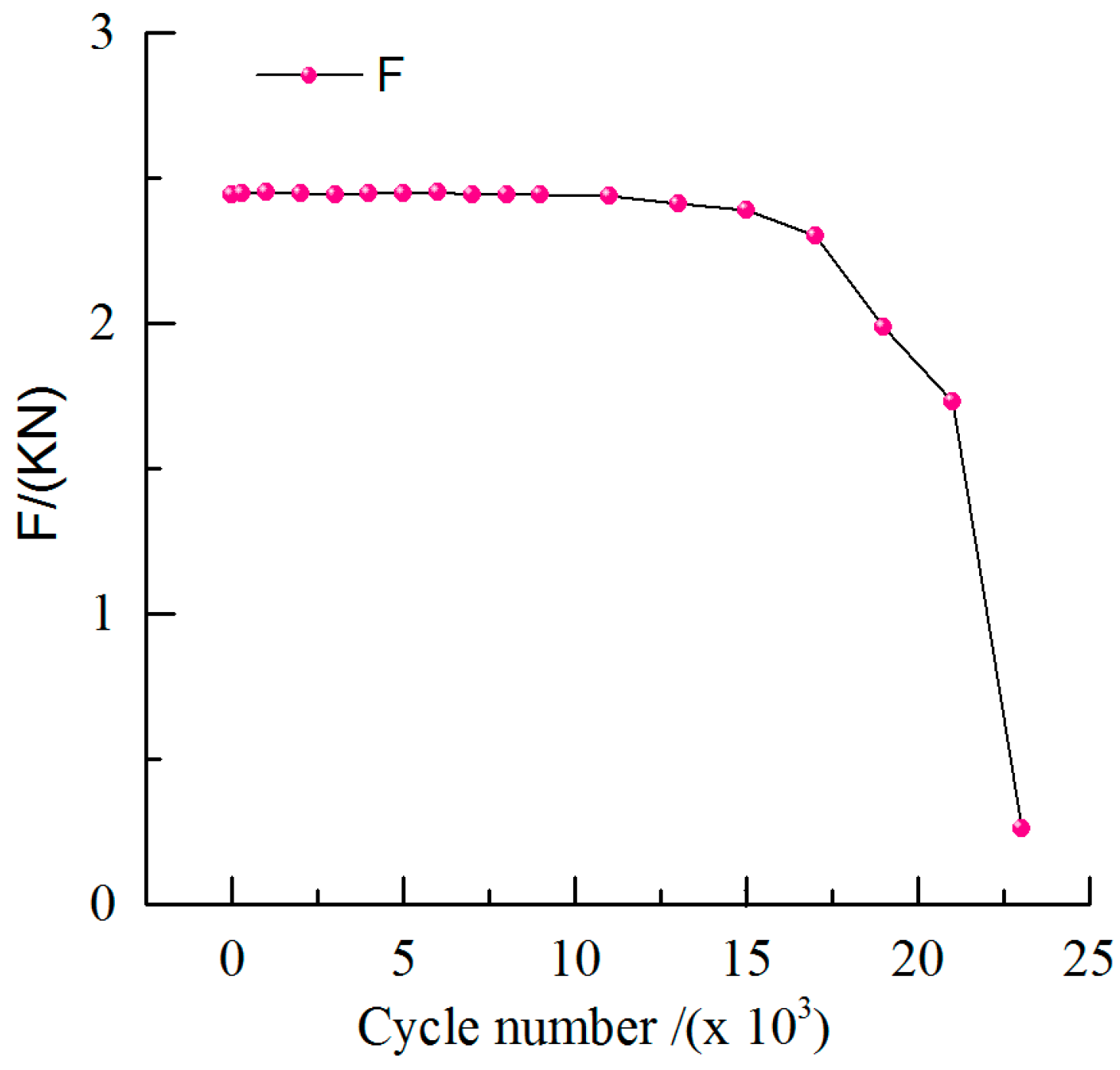
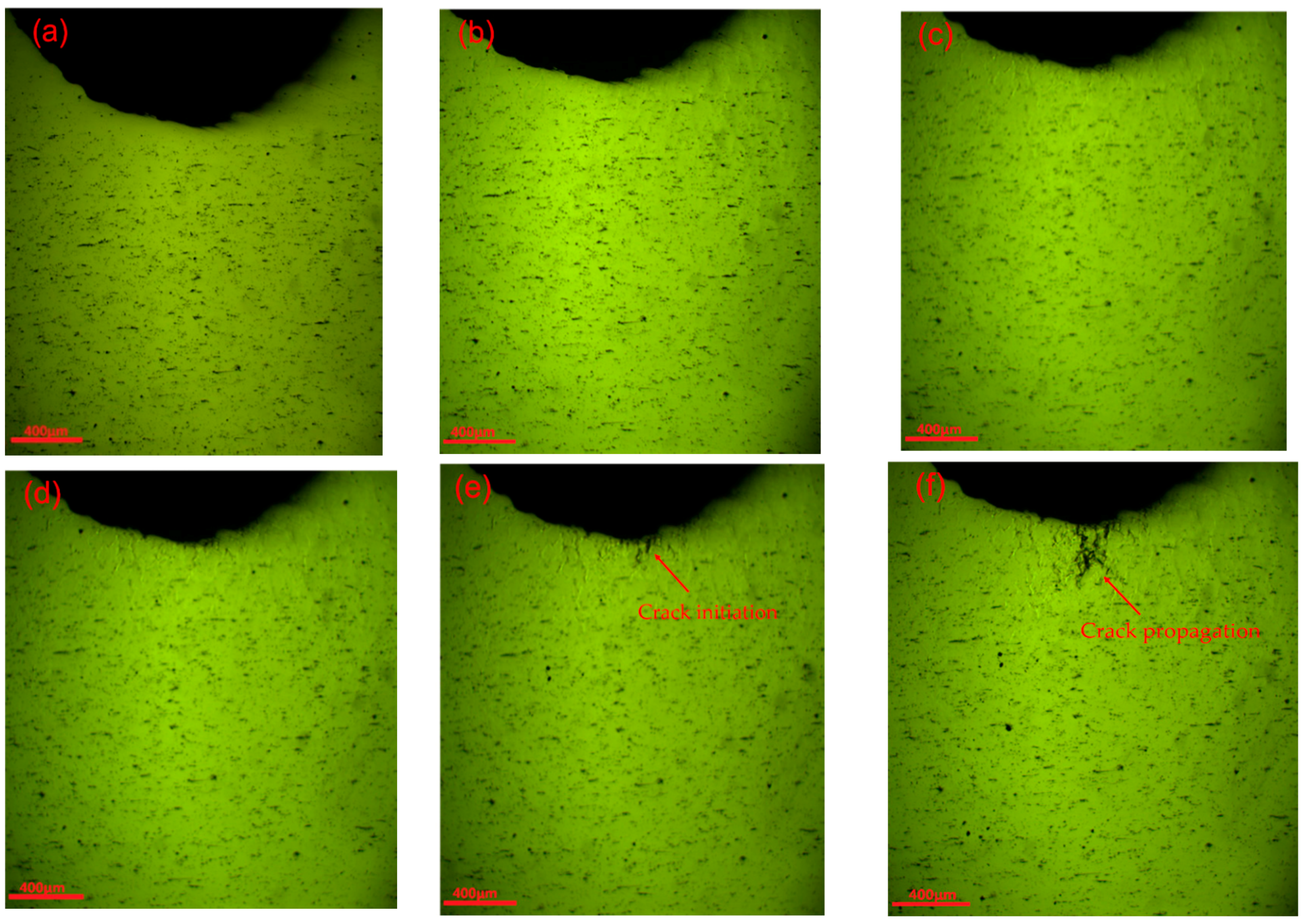
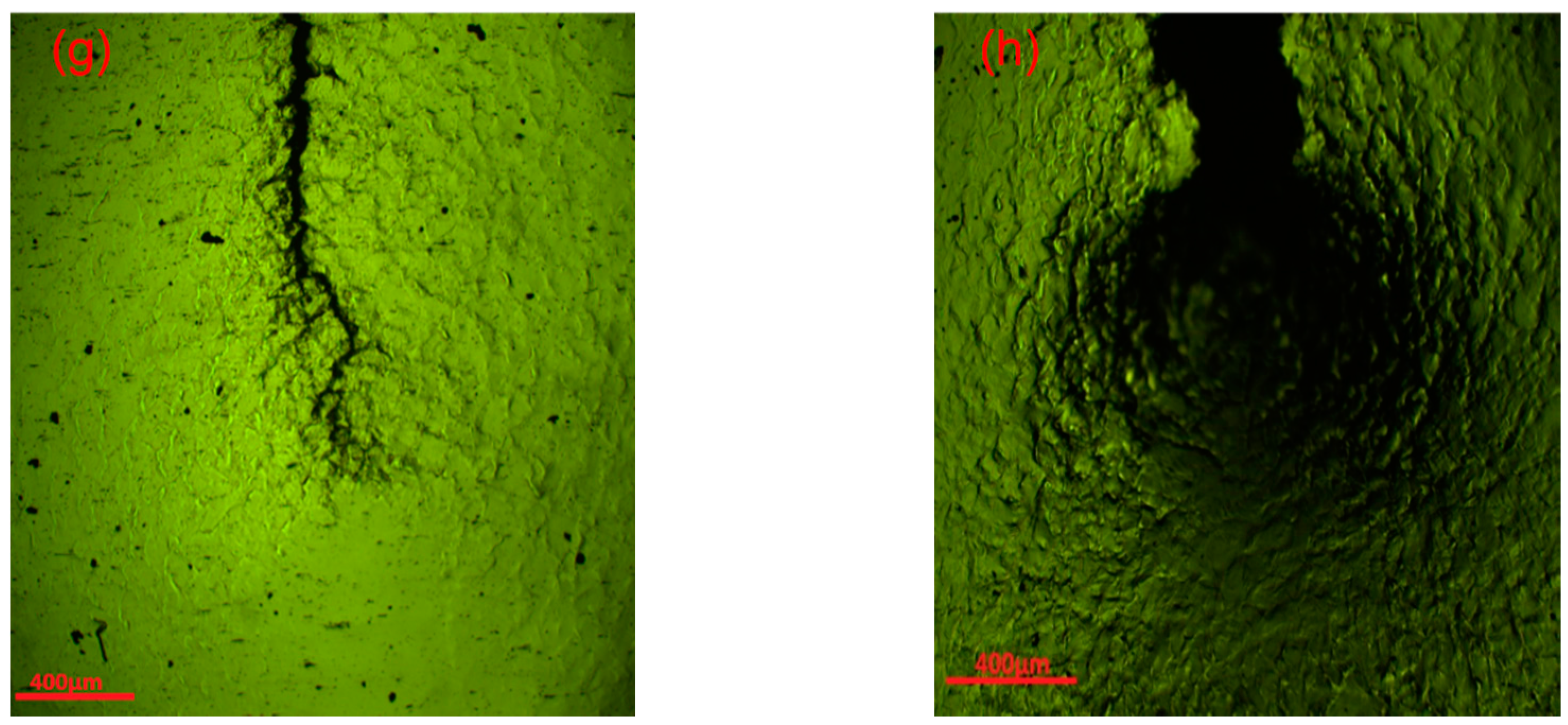
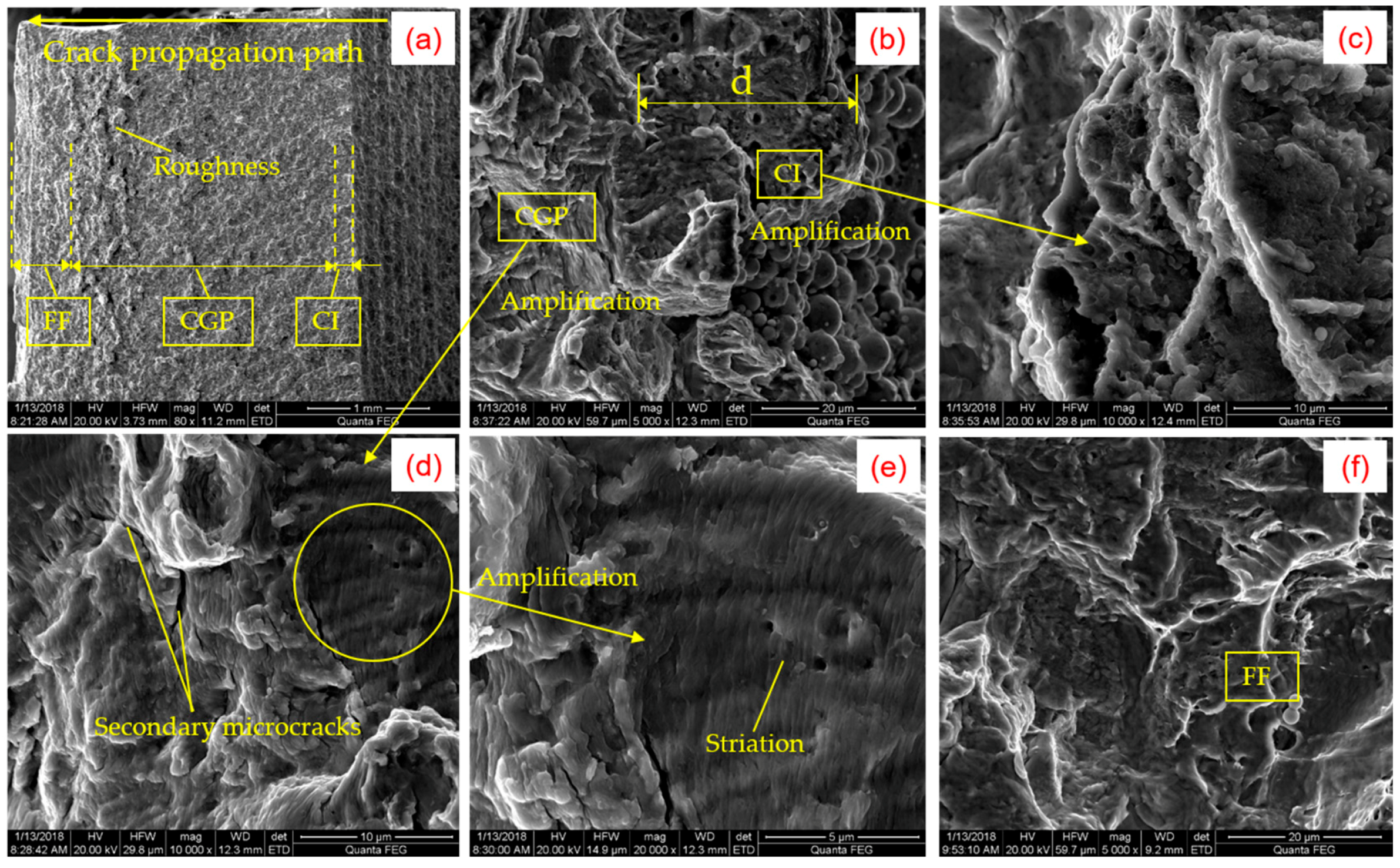
3.1. Morphology of the Specimen’s Surface
3.2. MMM Signals
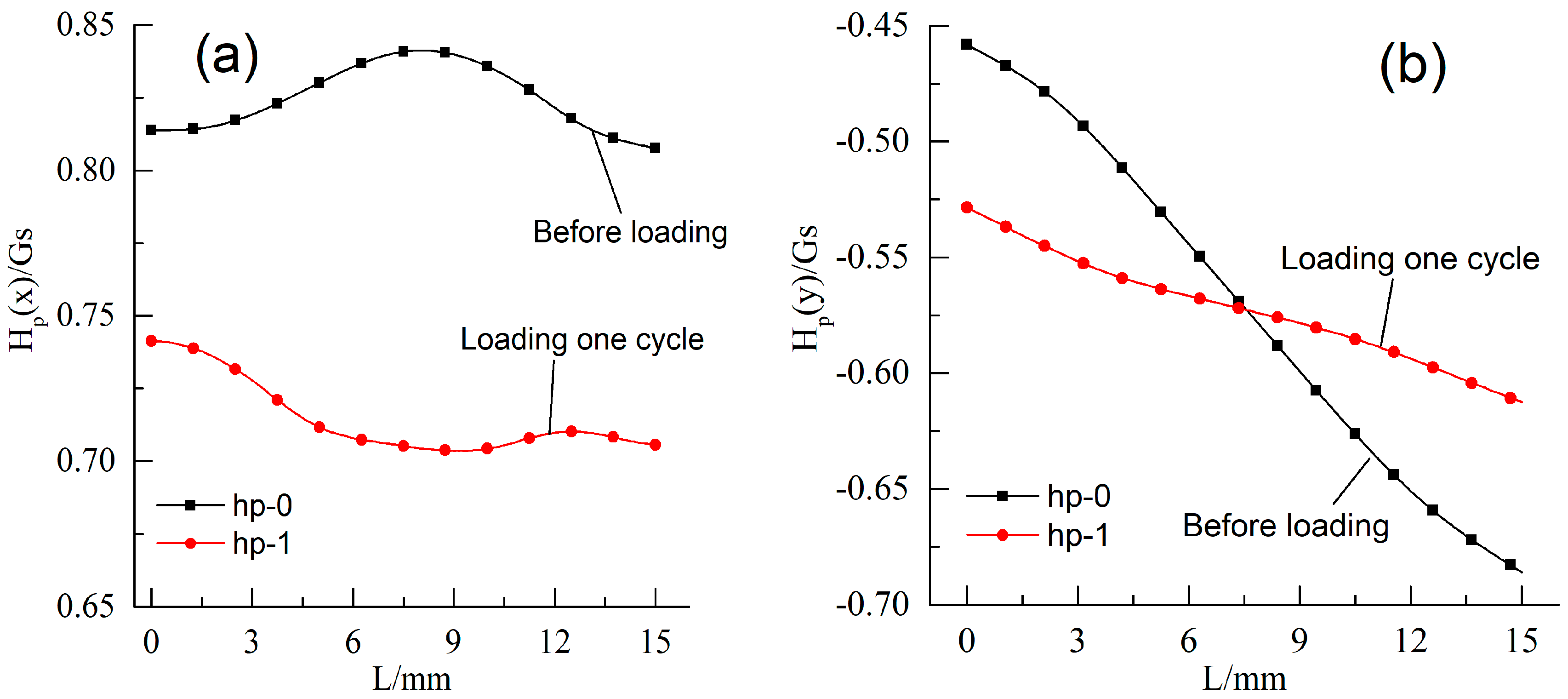
3.2.1. Before and after Loading
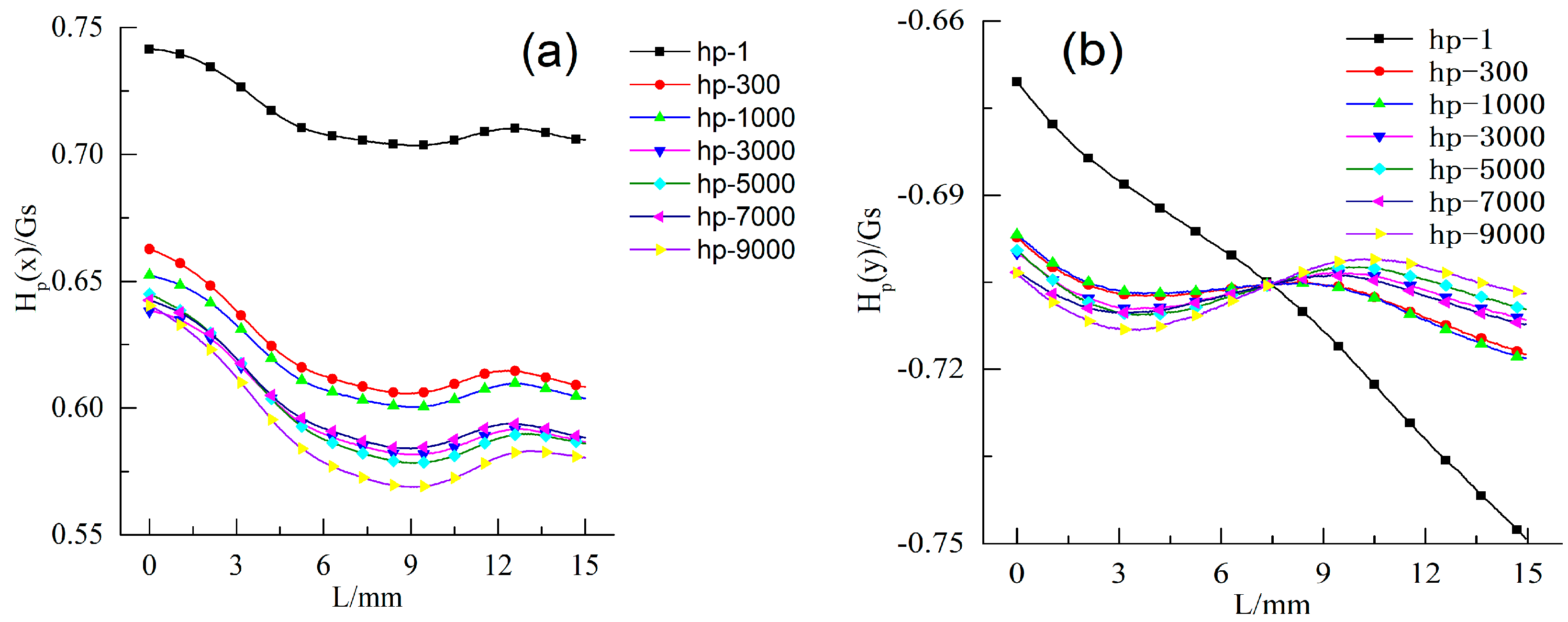
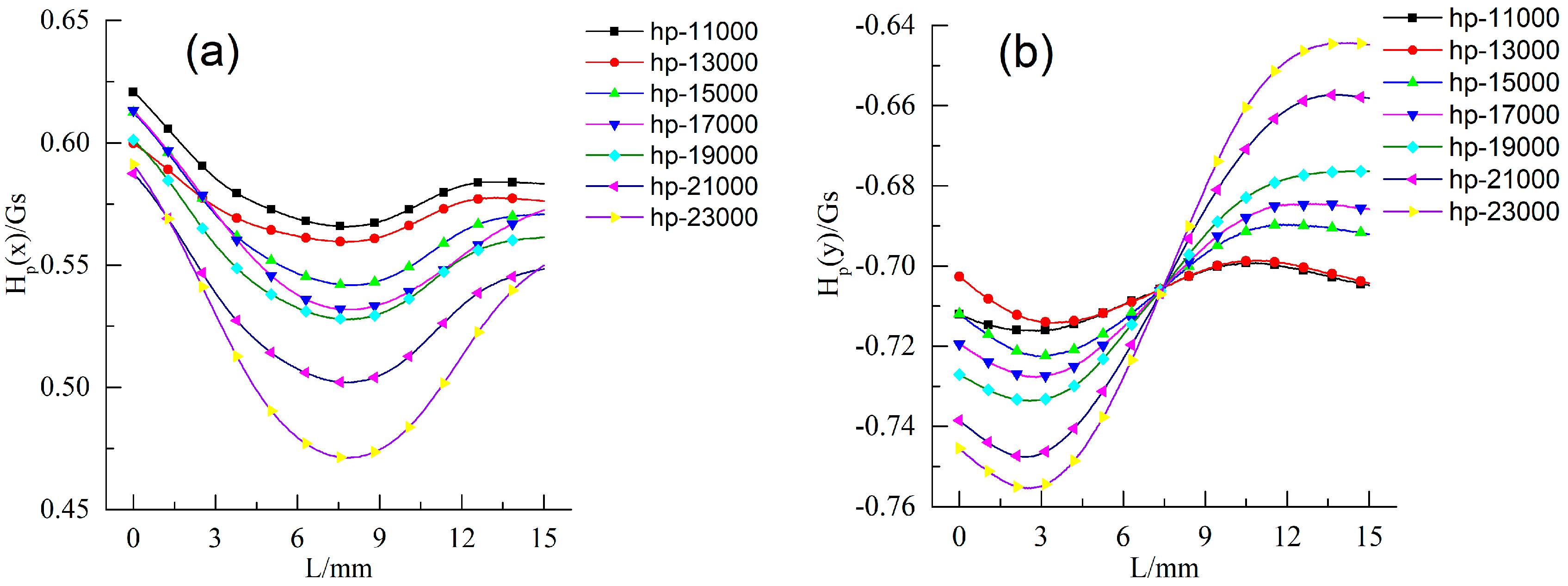
3.2.2. Cyclic Procedure
3.3. MMM Signal Characteristics
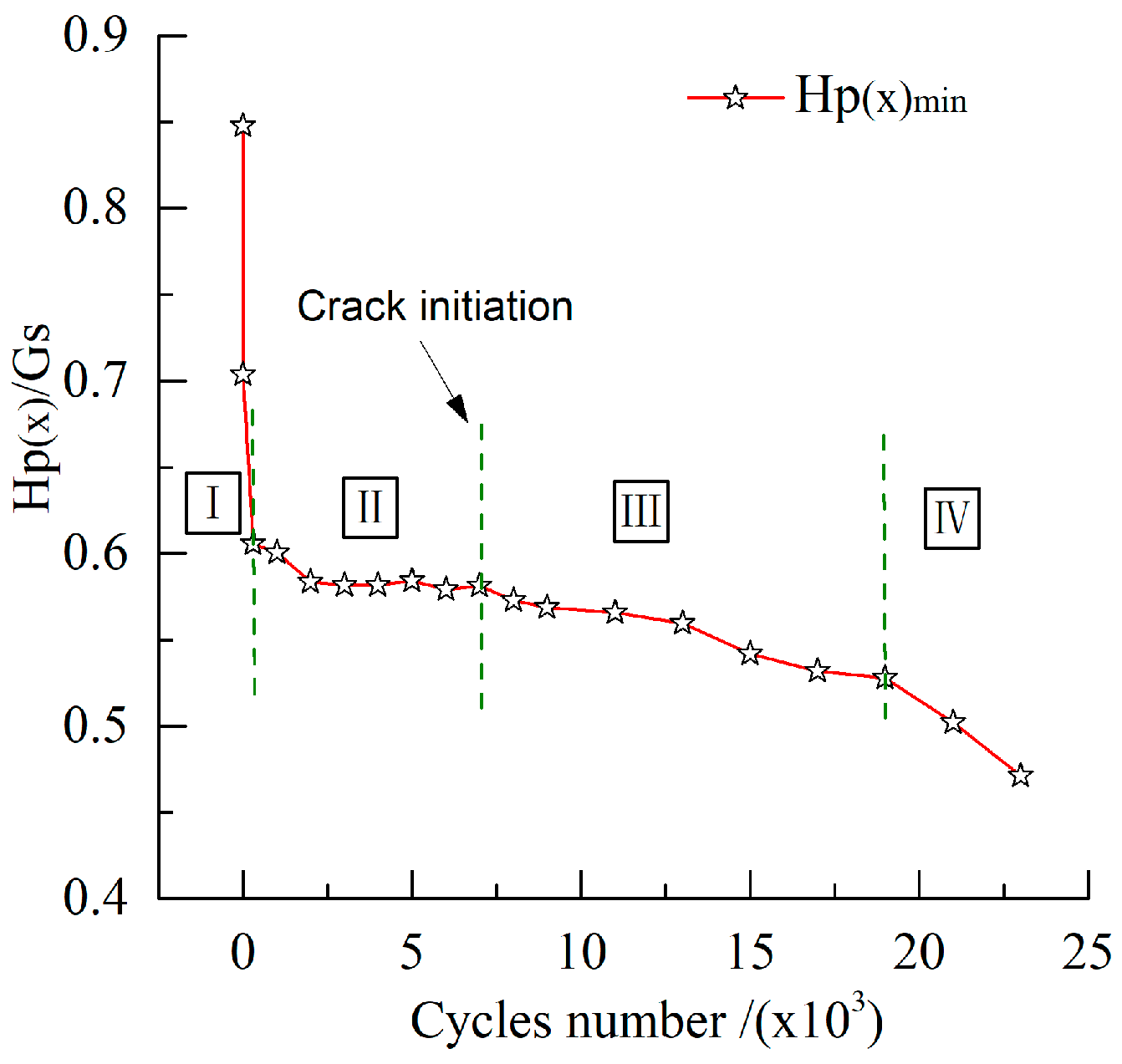
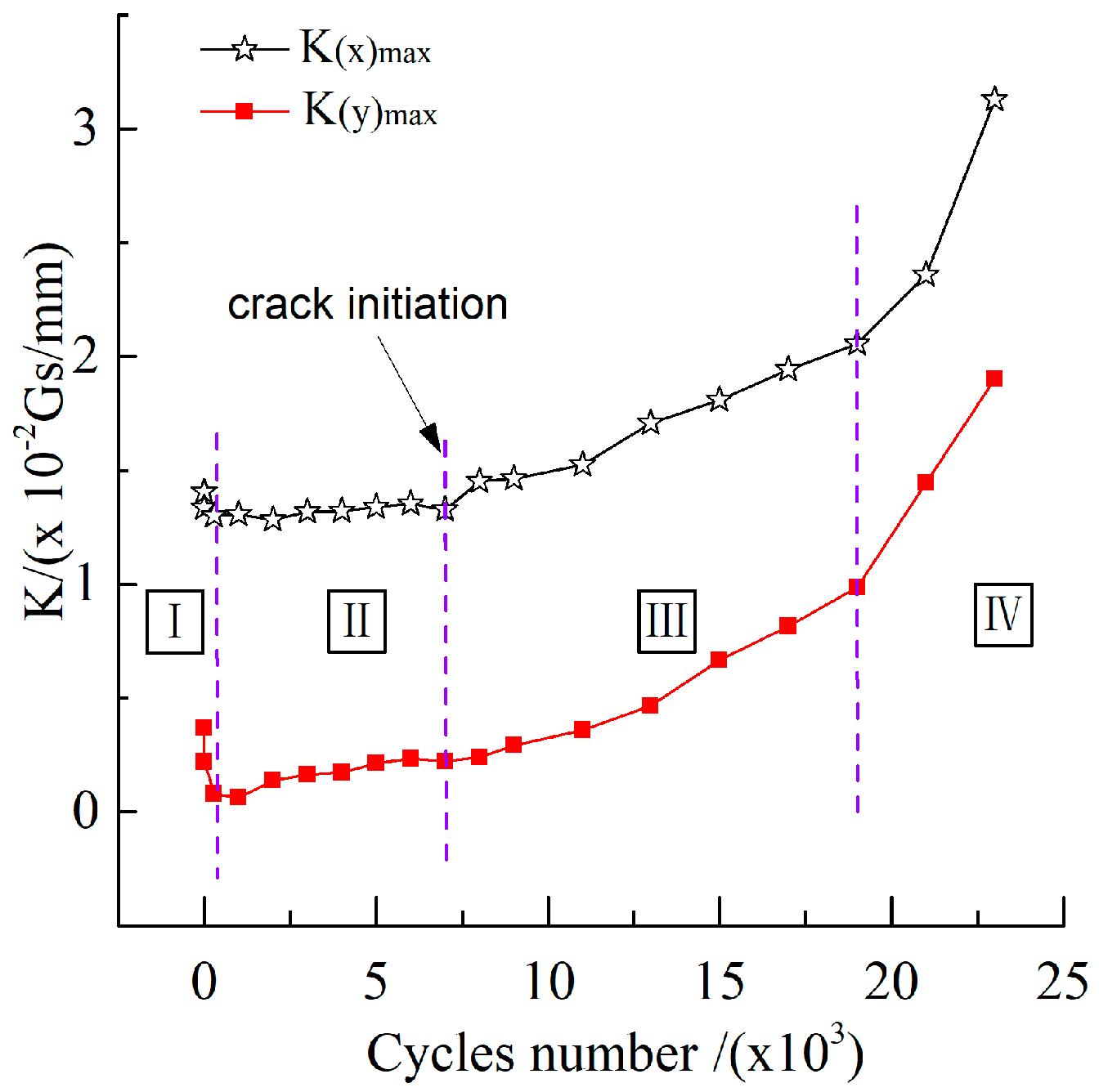
3.3.1. Variation of MMM Signal Characteristics during the Fatigue Process
- The initial stage I (1 to 300 cycles),
- The steady stage II (300 to 7000 cycles),
- The steady growth stage III (7000 to 19,000 cycles), and
- The rapid growth stage IV (19,000 to 23,000 cycles).
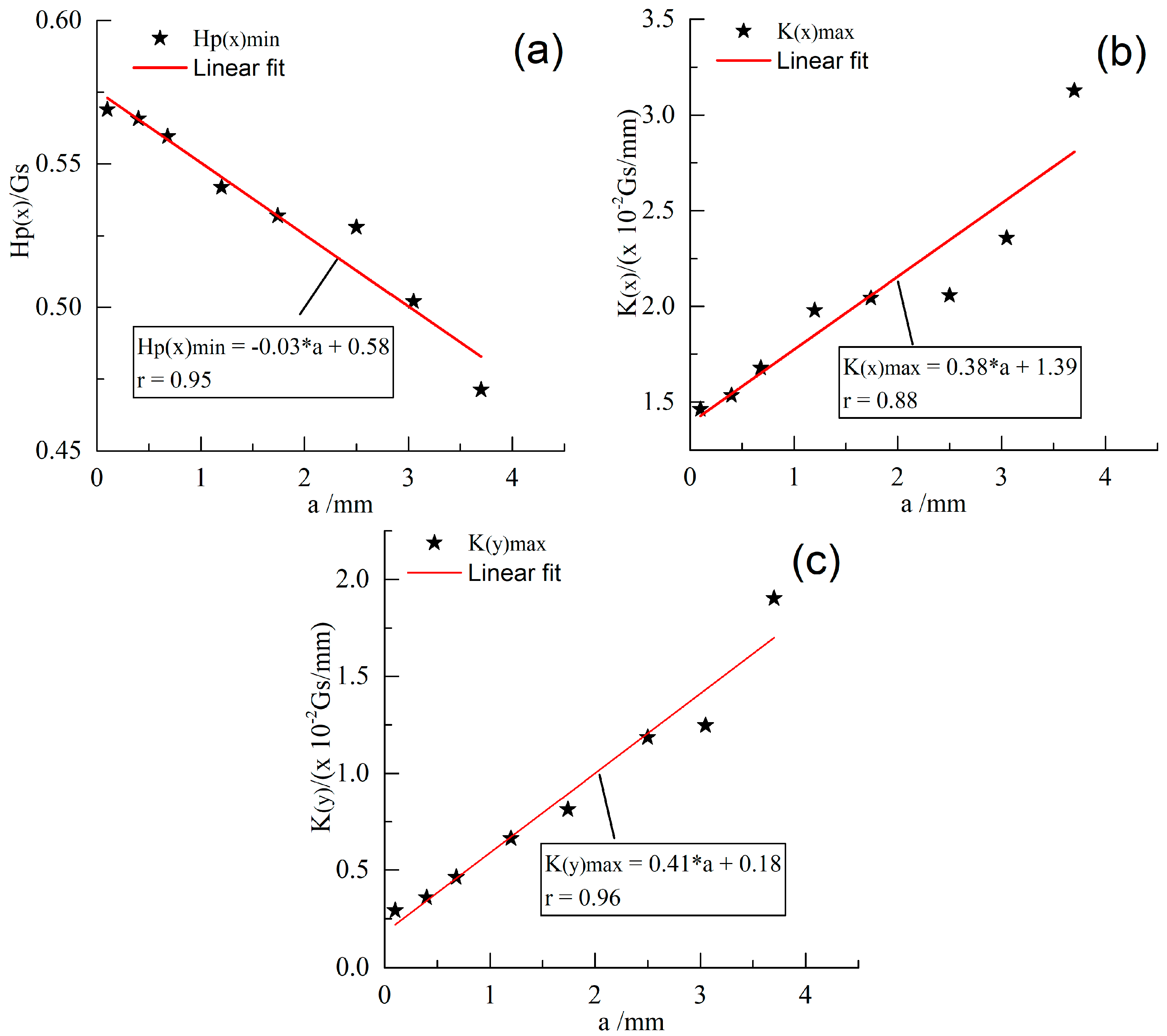
3.3.2. Relationship between Characteristics and Fatigue Crack Length
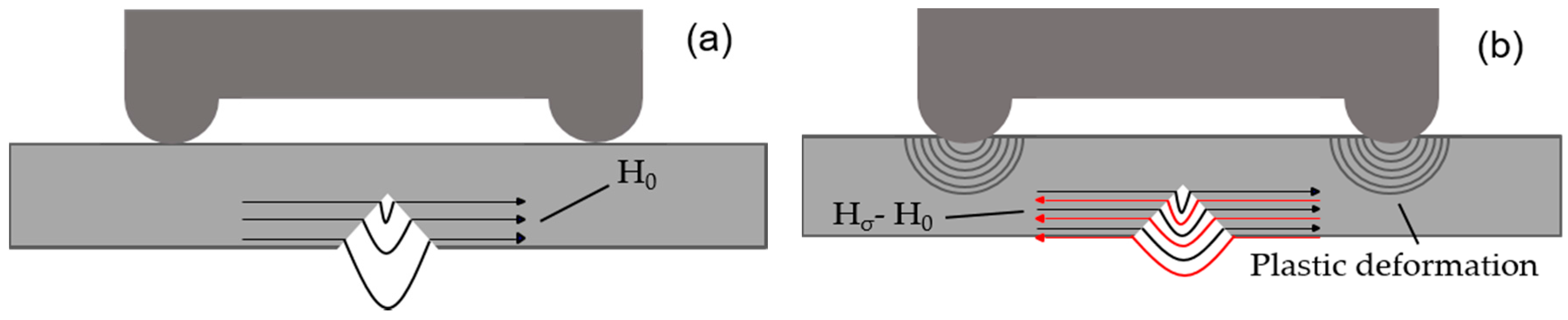
3.4. Discussion
4. Conclusions
- The variations of MMM signal characteristics could be explained by the changes of morphology on specimen surface during fatigue process. At the initial stage, the characteristics decreased significantly with the increase of plastic deformation on the specimen’s surface because of the opposite direction between the equivalent magnetic field and the initial magnetic field. After that, the characteristics remained constant due to the appearance of dislocation blocking. After crack initiation, the characteristics entered a steady growth stage and the K(x)max and K(y)max values began to increase, while Hp(x)min continued to decline. Approaching fracture, the fatigue specimen generated serious irreversible deformation, and the variation tendency of K(x)max, K(y)max, Hp(x)min sped up. The results indicated that MMM signal characteristics could reflect fatigue process, including crack initiation, which had great significance to prevent fatigue failure of ferromagnetic materials, including drillstrings. Additionally, the combination of Hp(x) and Hp(y) signals to evaluate fatigue damage could reduce the probability of missing crack initiation, compared with the detection results from Hp(y) signals only.
- Fatigue crack initiation occurred at the surface/sub-surface of the specimen, fatigue striations and the secondary crack were observed at the crack propagation zone, and the final fracture surface had an obvious ductile dimpled morphology. At the end of crack propagation zone, the surface of fracture was rough, which corresponded to the rapid growth stage of MMM signal characteristics. The results showed that the variations of MMM signal characteristics were related to the morphology of fatigue fracture. In addition, the result of metallographical structure observation showed that the crack mechanism was transcrystalline rupture.
- The fitting results showed that the length of crack propagation “a” had a good linear relationship with the values of Hp(x)min, K(x)max and K(y)max. The results of the whole fatigue test indicated that it was possible to detect microcracks and predict the residual life of drillstrings. However, a large number of investigations have to be conducted if we intend to achieve these potential functions, including the size and the initial residual magnetic field of testing objects. These issues will be studied in the future by experimentation.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Cirimello, P.; Otegui, J.L. Oil well drill bit failure during pull out: Redesign to reduce its consequences. Eng. Fail. Anal. 2017, 83, 75–87. [Google Scholar] [CrossRef]
- Zamani, S.M.; Hassanzadeh-Tabrizi, S.A. Failure analysis of drill pipe: A review. Eng. Fail. Anal. 2016, 59, 605–623. [Google Scholar] [CrossRef]
- Baryshnikov, A.; Calderoni, A. A new approach to the analysis of drillstring fatigue behavior. SPE Drill. Complet. 2013, 12, 77–84. [Google Scholar] [CrossRef]
- Dao, N.H.; Sellami, H. Stress intensity factors and fatigue growth of a surface crack in a drill pipe during rotary drilling operation. Eng. Fract. Mech. 2012, 96, 626–640. [Google Scholar] [CrossRef]
- Dale, B.A. An experimental investigation of fatigue-crack growth in drillstring tubulars. SPE Drill. Eng. 1988, 3, 356–362. [Google Scholar] [CrossRef]
- Ojanomare, C.; Cornetti, P. Fatigue crack growth analysis of drill pipes during rotary drilling operations by the multiple reference state weight function approach. Eng. Fail. Anal. 2017, 74, 11–34. [Google Scholar] [CrossRef]
- Santus, C.; Bertini, L. Torsional strength comparison between two assembling techniques for aluminium drill pipe to steel tool joint connection. Int. J. Press. Vessels Pip. 2009, 86, 177–186. [Google Scholar] [CrossRef]
- Dubov, A.A. A study of metal properties using the method of magnetic memory. Met. Sci. Heat Treat. 1997, 39, 401–402. [Google Scholar] [CrossRef]
- Wilson, J.W.; Tian, G.Y. Residual magnetic field sensing for stress measurement. Sens. Actuators A Phys. 2007, 135, 381–387. [Google Scholar] [CrossRef]
- Shi, P.P.; Jin, K. A magnetomechanical model for the magnetic memory method. Int. J. Mech. Sci. 2017, 124–125, 229–241. [Google Scholar] [CrossRef]
- Ariffin, A.; Ahmad, I.M. Detection of cracked position due to cyclic loading for ferromagnetic materials based on magnetic memory method. Jurnal Teknologi 2015, 75, 67–70. [Google Scholar] [CrossRef]
- Shen, G.T.; Hu, B. Investigation on metal magnetic memory signal during loading. Int. J. Appl. Electromagn. Mech. 2010, 33, 1329–1334. [Google Scholar] [CrossRef]
- Rieger, G.; Ludwig, K. GMR sensors for contactless position detection. Sens. Actuators A Phys. 2001, 91, 7–11. [Google Scholar] [CrossRef]
- Chen, L.; Que, P.W. A giant-magnetoresistance sensor for magnetic-flux-leakage nondestructive testing of a pipeline. Russ. J. Nondestruct. Test. 2005, 41, 462–465. [Google Scholar] [CrossRef]
- Dong, L.H.; Xu, B.S. Stress dependence of the spontaneous stray field signals of ferromagnetic steel. NDT E Int. 2009, 42, 323–327. [Google Scholar] [CrossRef]
- Huang, H.H.; Yang, C. Magnetic memory signals variation induced by applied magnetic field and static tensile stress in ferromagnetic steel. J. Magn. Magn. Mater. 2016, 416, 213–219. [Google Scholar] [CrossRef]
- Dong, L.H.; Xu, B. Variation of stress-induced magnetic signals during tensile testing of ferromagnetic steels. NDT E Int. 2008, 41, 184–189. [Google Scholar] [CrossRef]
- Wang, Z.D.; Yao, K. Theoretical studies of metal magnetic memory technique on magnetic flux leakage signals. NDT E Int. 2010, 43, 354–359. [Google Scholar] [CrossRef]
- Jian, X.L.; Jian, X.C. Experiment on relationship between the magnetic gradient of low carbon steel and its stress. J. Magn. Magn. Mater. 2009, 321, 3600–3606. [Google Scholar] [CrossRef]
- Li, J.W.; Zhong, S. The variation of surface magnetic field induced by fatigue stress. J. Nondestruct. Eval. 2013, 32, 238–241. [Google Scholar] [CrossRef]
- Leng, J.C.; Xu, M.Q. Magnetic field variation induced by cyclic bending stress. NDT E Int. 2009, 42, 410–414. [Google Scholar] [CrossRef]
- Shi, C.L.; Dong, S.Y. Stress concentration degree affects spontaneous magnetic signals of ferromagnetic steel under dynamic tension load. NDT E Int. 2010, 43, 8–12. [Google Scholar] [CrossRef]
- Dong, L.H.; Xu, B.S. Monitoring fatigue crack propagation of ferromagnetic materials with spontaneous abnormal magnetic signals. Int. J. Fatigue 2008, 30, 1599–1605. [Google Scholar] [CrossRef]
- Huang, H.H.; Jiang, S.L. Investigation of magnetic memory signals induced by dynamic bending load in fatigue crack propagation process of structural steel. J. Nondestruct. Eval. 2014, 33, 407–412. [Google Scholar] [CrossRef]
- Huang, H.H.; Qian, Z.C. Magnetic memory signals of ferromagnetic weldment induced by dynamic bending load. Nondestruct. Test. Eval. 2017, 32, 166–184. [Google Scholar] [CrossRef]
- Wang, Z.D.; Deng, B. Physical model of plastic deformation on magnetization in ferromagnetic materials. J. Appl. Phys. 2011, 109, 083928. [Google Scholar] [CrossRef]
- Lo, C.C.H.; Kinser, E. Modeling the interrelating effects of plastic deformation and stress on magnetic properties of materials. J. Appl. Phys. 2003, 93, 6626–6628. [Google Scholar] [CrossRef]
- Mishnev, R.; Dudova, N. Low cycle fatigue behavior of a 10Cr–2W–Mo–3Co–NbV steel. Int. J. Fatigue 2016, 83, 344–355. [Google Scholar] [CrossRef]
- Atapek, Ş.H.; Pantelakis, S.G.Ş. Fractographical analysis of fatigue failed Cu–2.55Ni–0.55Si alloy. Theor. Appl. Fract. Mech. 2016, 83, 60–66. [Google Scholar] [CrossRef]
- Liu, X.L.; Zhang, Z. Fatigue Fractography Quantitative Analysis; National Defense Industry Press: Beijing, China, 2010; pp. 26–31. ISBN 978-7-118-07062-0. [Google Scholar]
- Lynch, S. Some fractographic contributions to understanding fatigue crack growth. Int. J. Fatigue 2017, 104, 12–26. [Google Scholar] [CrossRef]
- Jiang, S.T.; Li, W. Magnetic Physics of the Condensed Matter; Science Press: Beijing, China, 2003; pp. 258–289. ISBN 7-03-011190-7. [Google Scholar]
- Ren, W.; Sun, J. Experimental study on effect of stress on magnetic domain structure under geomagnetic condition. J. Mech. Eng. 2013, 49, 8–13. [Google Scholar] [CrossRef]
- Jiles, D.C.; Atherton, D.L. Theory of ferromagnetic hysteresis. J. Magn. Magn. Mater. 1986, 61, 48–60. [Google Scholar] [CrossRef]
- Jiles, D.C.; Li, L. A new approach to modeling the magneto-mechanical effect. J. Appl. Phys. 2004, 95, 7058–7060. [Google Scholar] [CrossRef]
- Jiles, D.C.; Devine, M.K. Recent developments in modeling of the stress derivative of magnetization in ferromagnetic materials. Am. Inst. Phys. 1994, 76, 7015–7017. [Google Scholar] [CrossRef]



| Material | C | Si | Mn | P | S | Cr | Mo |
|---|---|---|---|---|---|---|---|
| 35CrMo | 0.32~0.40 | 0.17~0.37 | 0.40~0.70 | ≤0.035 | ≤0.035 | 0.80~1.10 | 0.15~0.25 |
| Material | Yield Strength σs (MPa) | Ultimate Strength σb (MPa) | Impact Toughness Value аkv (J/cm2) |
|---|---|---|---|
| 35CrMo | ≥835 | ≥985 | ≥78 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, Z.; Fan, J.; Wu, S.; Dai, H.; Liu, S. Characteristics of Metal Magnetic Memory Testing of 35CrMo Steel during Fatigue Loading. Metals 2018, 8, 119. https://doi.org/10.3390/met8020119
Hu Z, Fan J, Wu S, Dai H, Liu S. Characteristics of Metal Magnetic Memory Testing of 35CrMo Steel during Fatigue Loading. Metals. 2018; 8(2):119. https://doi.org/10.3390/met8020119
Chicago/Turabian StyleHu, Zhibin, Jianchun Fan, Shengnan Wu, Haoyuan Dai, and Shujie Liu. 2018. "Characteristics of Metal Magnetic Memory Testing of 35CrMo Steel during Fatigue Loading" Metals 8, no. 2: 119. https://doi.org/10.3390/met8020119
APA StyleHu, Z., Fan, J., Wu, S., Dai, H., & Liu, S. (2018). Characteristics of Metal Magnetic Memory Testing of 35CrMo Steel during Fatigue Loading. Metals, 8(2), 119. https://doi.org/10.3390/met8020119




