Magnetic Hysteresis and Barkausen Noise in Plastically Deformed Steel Sheets
Abstract
:1. Introduction
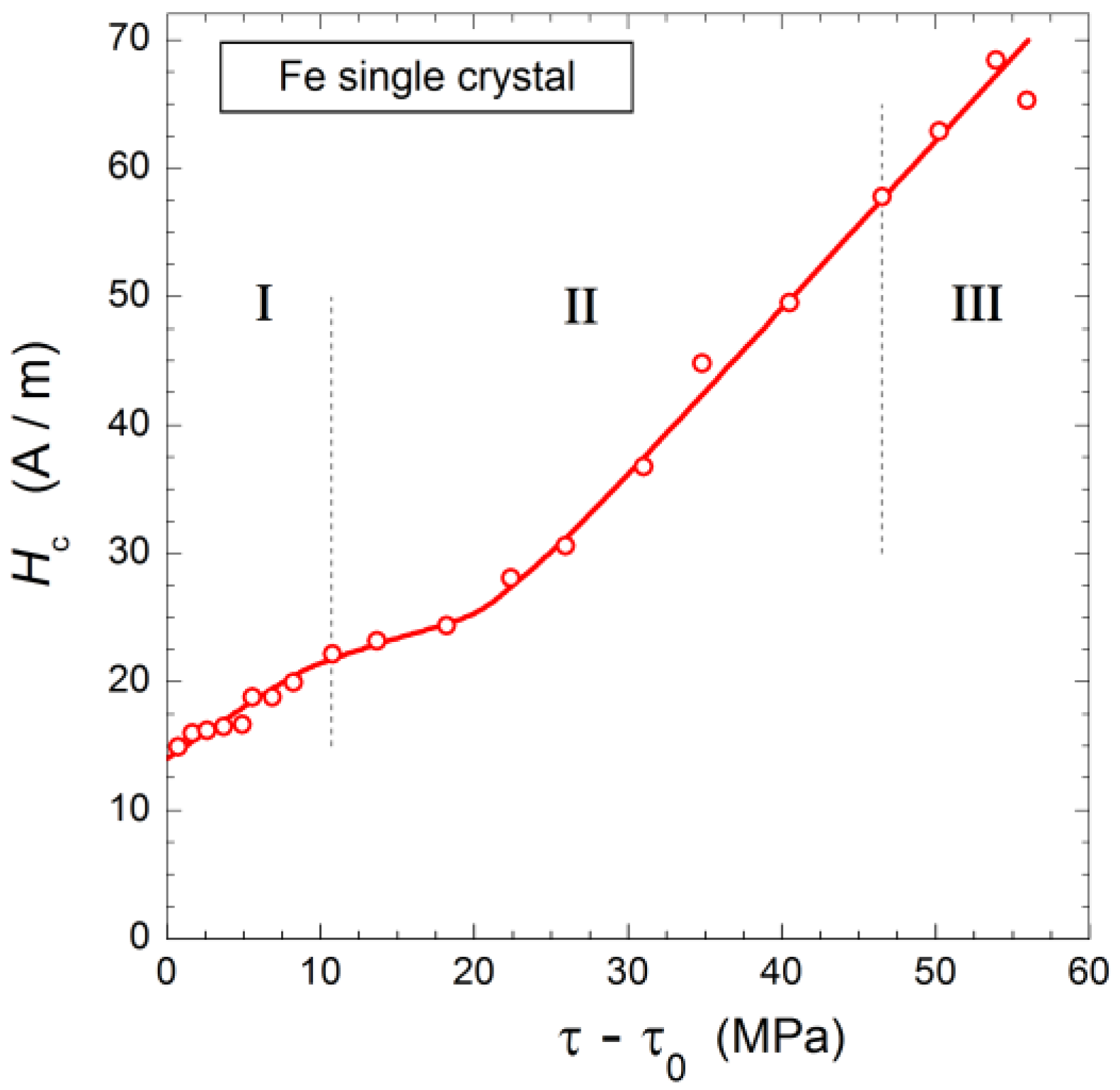
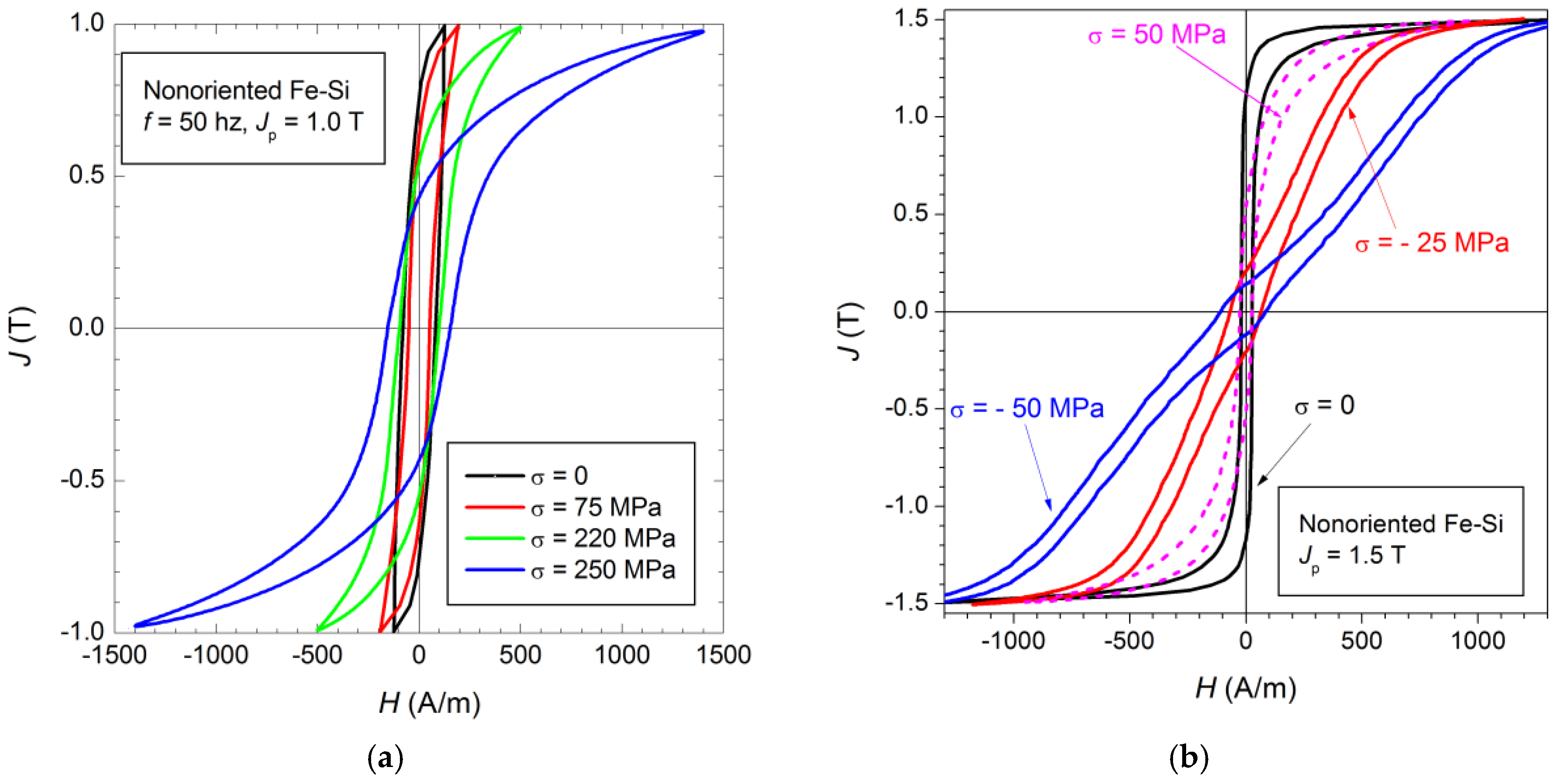
2. Dislocations, Residual Stress, Hysteresis Loop and Coercivity
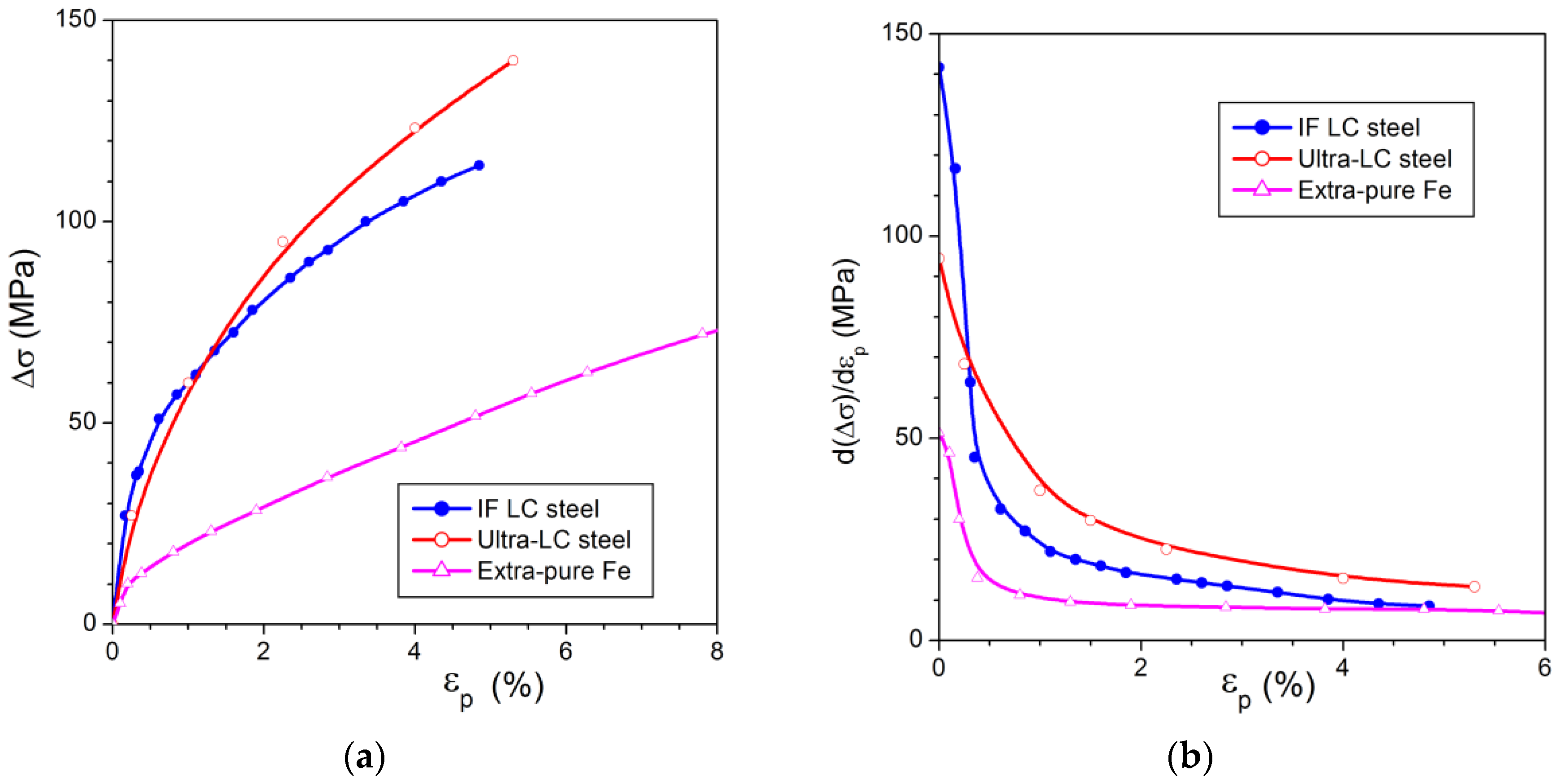
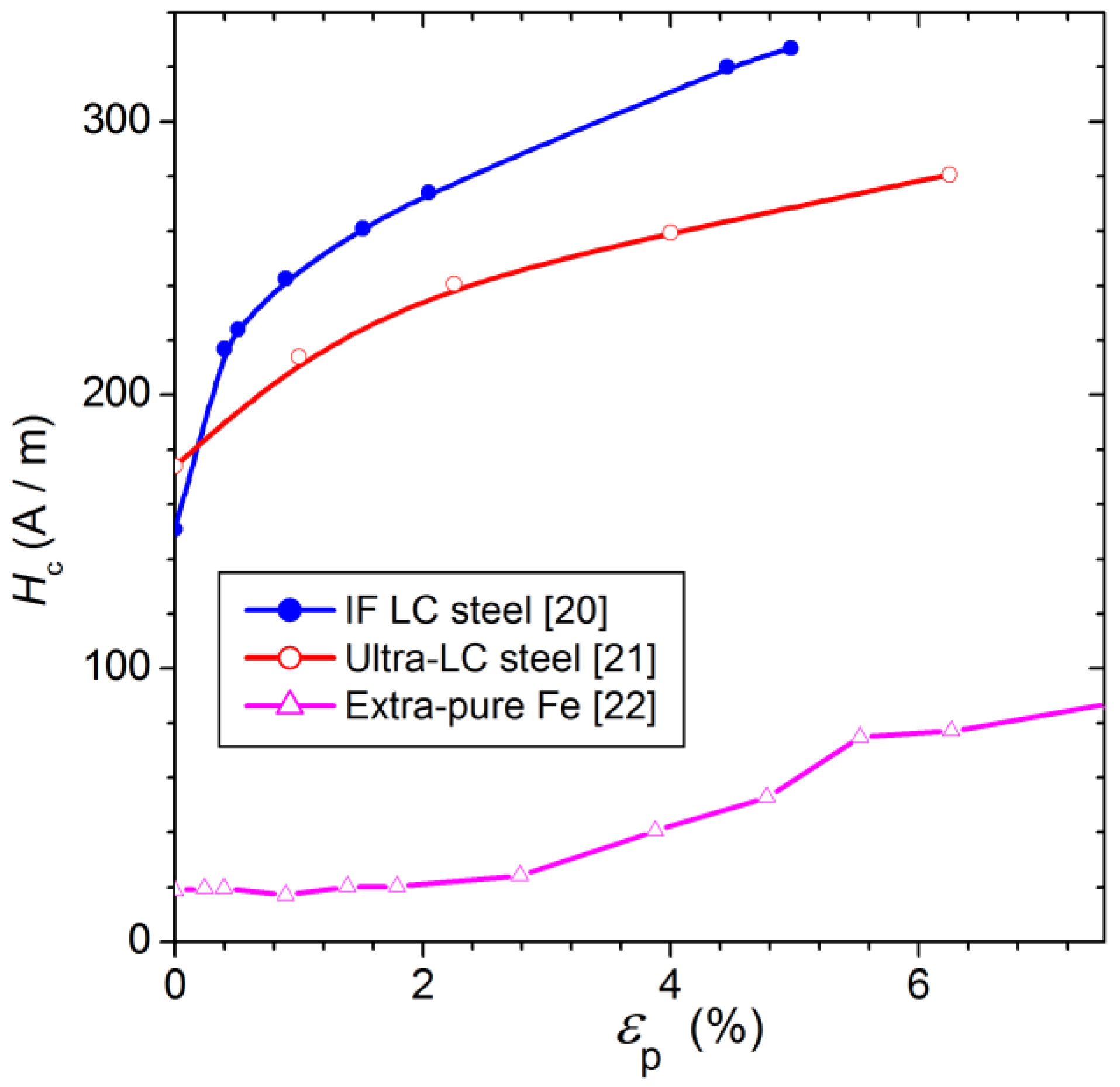
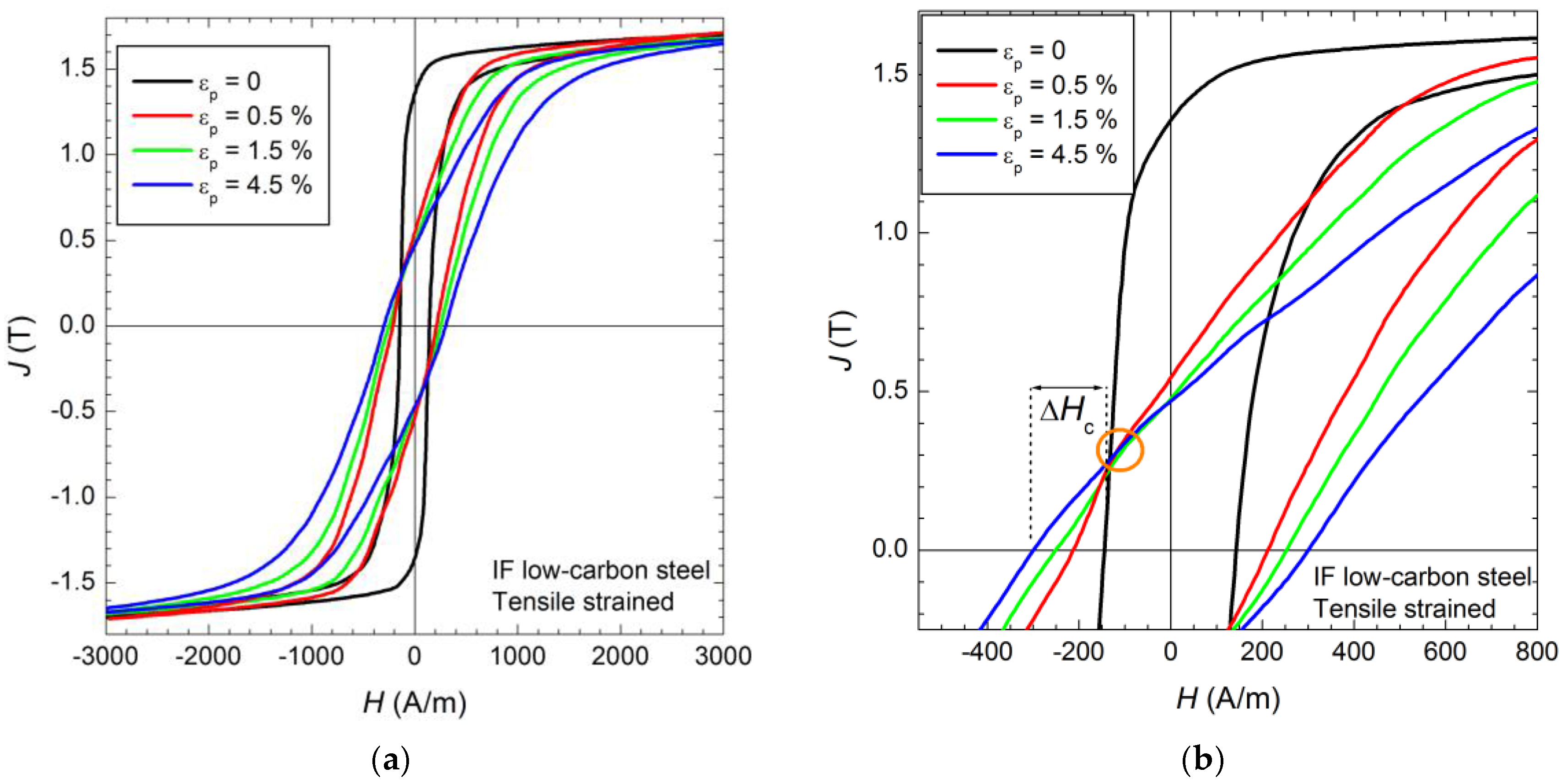
2.1. Plastic Strain and Magnetization Process
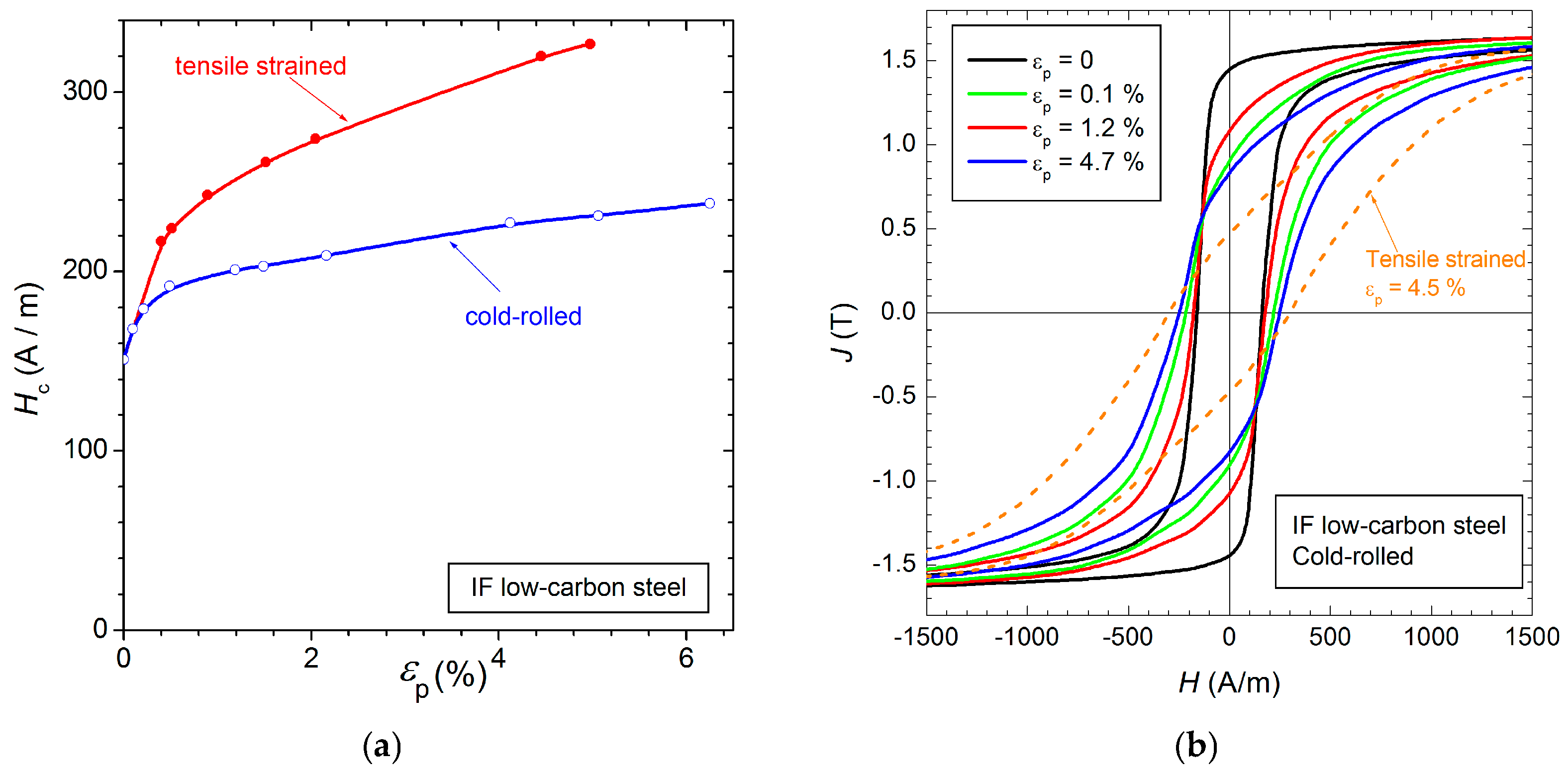
2.2. Tensile Straining versus Cold-Rolling
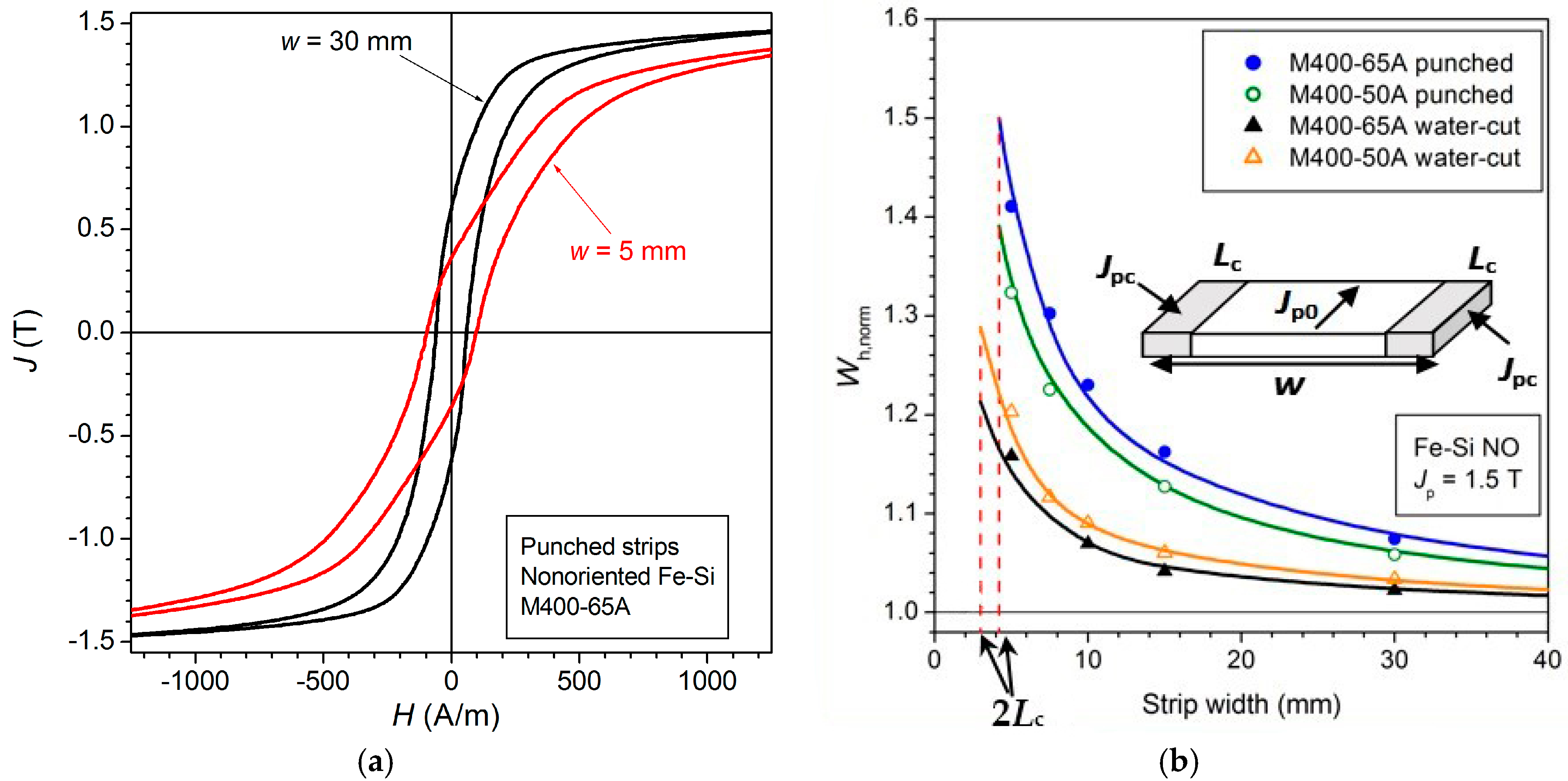
2.3. Strain Hardening by Cutting
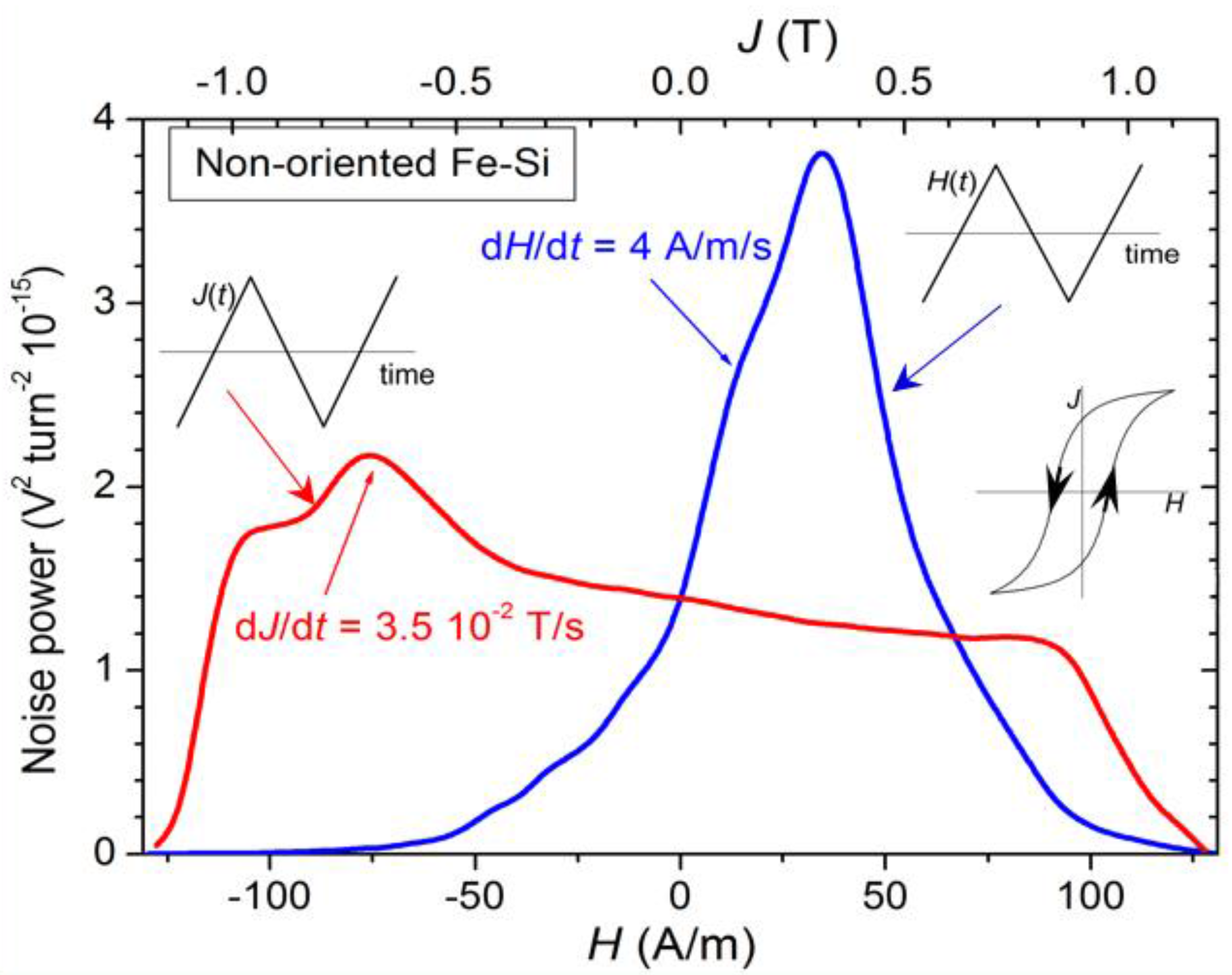
3. Barkhausen Noise in Plastically Deformed Steels
3.1. Properties and Measurement of the Barkhausen Noise
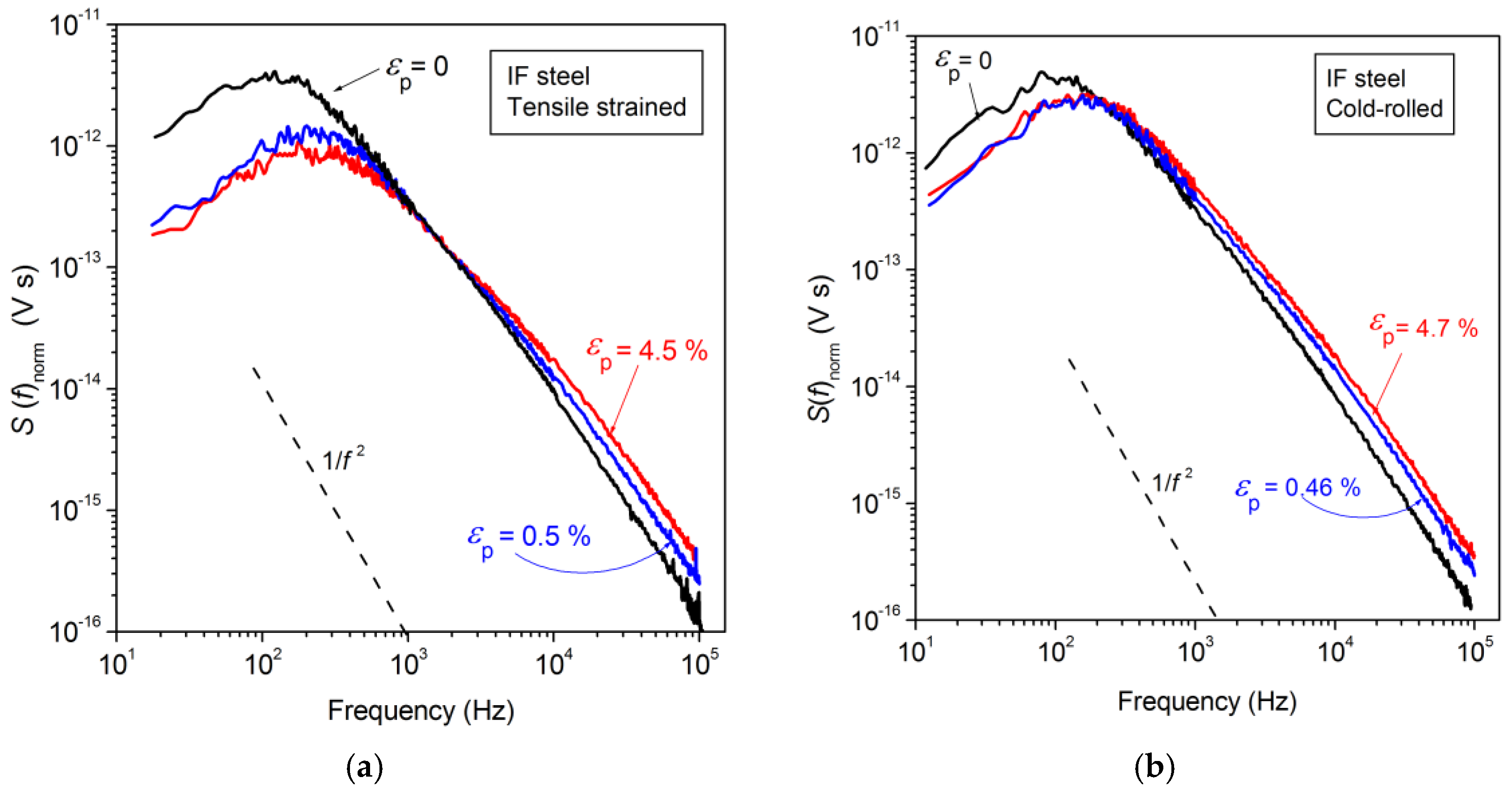
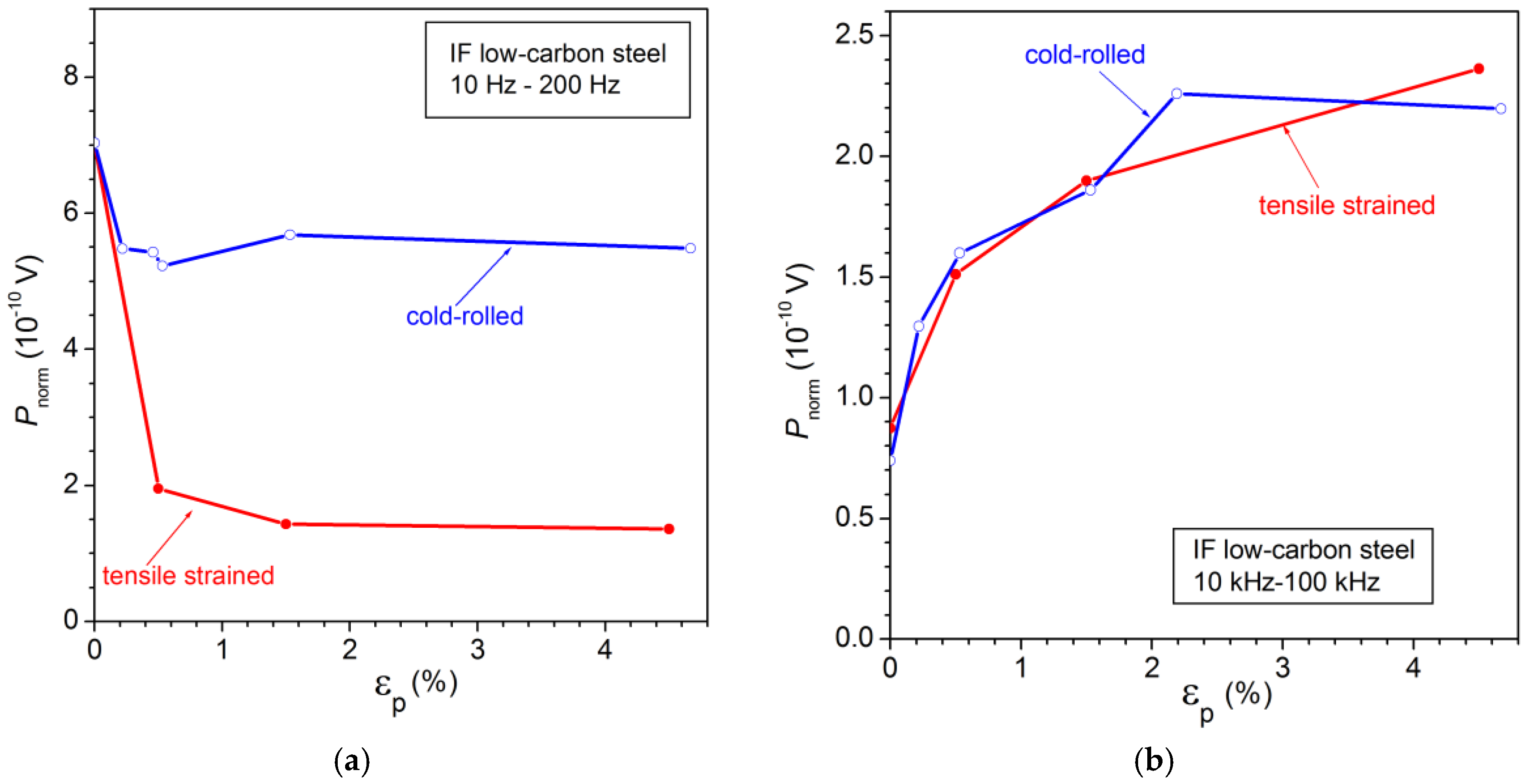
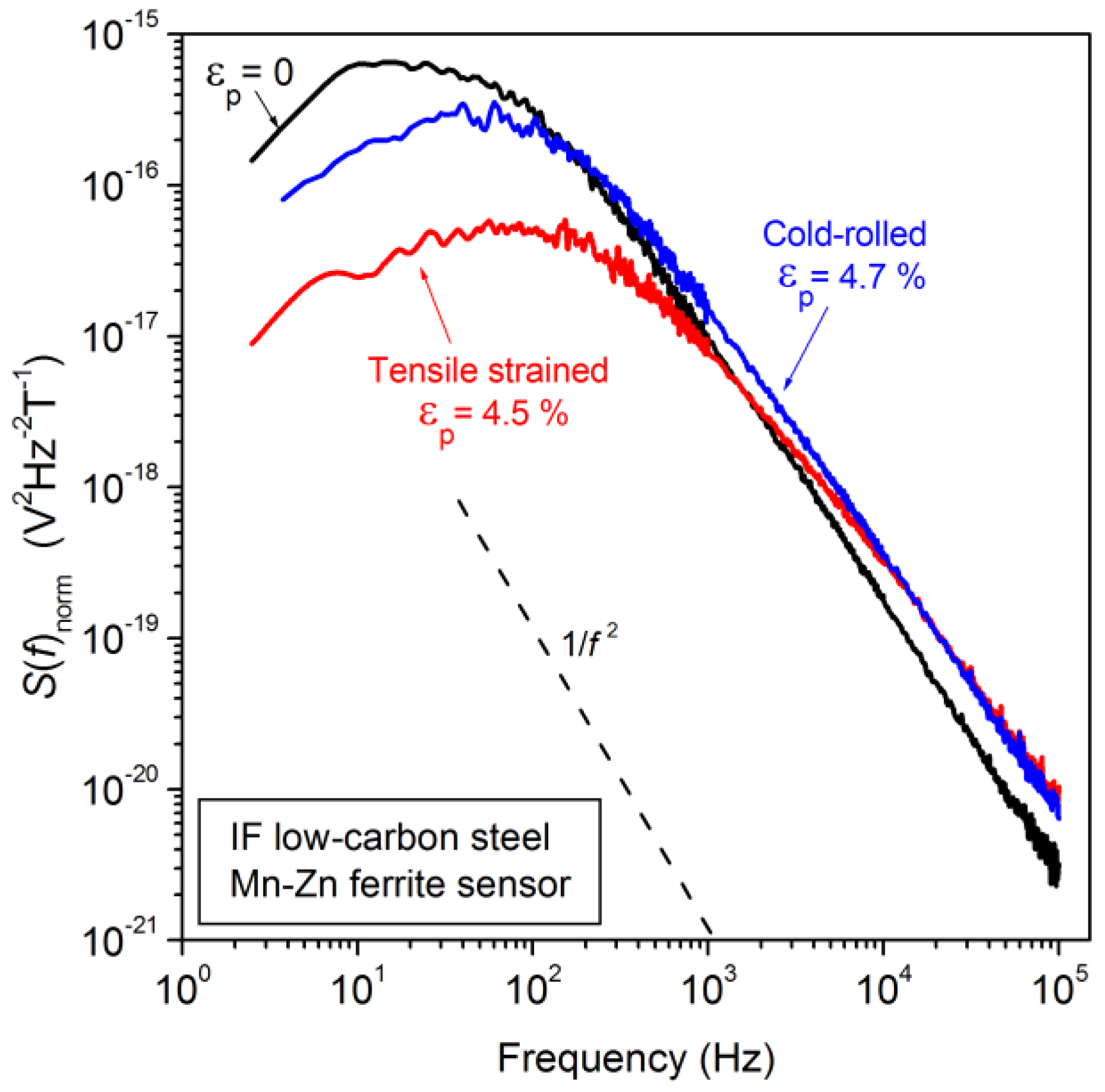
3.2. The Spectral Density of the Barkhausen Noise
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Bertotti, G.; Fiorillo, F. Crystalline Fe-Si, Fe-Al, and Fe-Si-Al alloys. In Landolt-Börnstein, Magnetic Properties of Metals; Wijn, H.P.J., Ed.; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 1994; Group III; Volume 19, pp. 33–143. ISBN 3-540-55590-0. [Google Scholar]
- Takahashi, N.; Suga, Y.; Kobayashi, H. Recent developments in grain-oriented silicon steel. J. Magn. Magn. Mater. 1996, 160, 98–101. [Google Scholar] [CrossRef]
- Gmyrek, Z.; Cavagnino, A.; Ferraris, L. Estimation of the magnetic properties of the damaged area resulting from the punching process: Experimental research and FEM modeling. IEEE Trans. Ind. Appl. 2013, 49, 2069–2077. [Google Scholar] [CrossRef]
- Girgis, R.S.; te Nijenhuis, E.G.; Gramm, K.; Wrethag, J.E. Experimental investigations on effect of core production attributes on transformer core loss performance. IEEE Trans. Magn. 1998, 13, 526–531. [Google Scholar] [CrossRef]
- Takahashi, S.; Kobayashi, S.; Kikuchi, H.; Kamada, Y. Relationship between mechanical and magnetic properties in cold rolled low carbon steel. J. Appl. Phys. 2006, 100, 113908. [Google Scholar] [CrossRef]
- O’Sullivan, D.; Cotterell, M.; Meszaros, I. The characterization of work-hardened austenitic stainless steel by NDT micromagnetic techniques. NDT E Int. 2004, 37, 265–269. [Google Scholar] [CrossRef]
- Kleber, X.; Vincent, A. On the role of residual internal stresses and dislocations on Barkhausen noise in plastically deformed steel. NDT E Int. 2004, 37, 439–445. [Google Scholar] [CrossRef]
- Liu, T.; Kikuchi, H.; Kamada, Y.; Ara, K.; Kobayashi, S.; Takahashi, S. Comprehensive analysis of Barkhausen noise properties in the cold rolled mild steel. J. Magn. Magn. Mater. 2007, 310, e989–e991. [Google Scholar] [CrossRef]
- Manjanna, J.; Kobayashi, S.; Kamada, Y.; Takahashi, S.; Kikuchi, H. Martensitic transformation in SUS 316LN austenitic stainless steel at RT. J. Mater. Sci. 2008, 43, 2659–2665. [Google Scholar] [CrossRef]
- Kypris, O.; Nlebedim, I.C.; Jiles, D. Measuring stress variation with depth using Barkhausen signal. J. Magn. Magn. Mater. 2016, 407, 377–395. [Google Scholar] [CrossRef]
- Ktena, A.; Hristoforou, E.; Gerhardt, G.J.L.; Missell, F.P.; Landgraf, F.J.G.; Rodrigues, D.L.; Alberteris-Campos, M. Barkhausen noise as a microstructure characterization tool. Physica B 2014, 435, 109–112. [Google Scholar] [CrossRef]
- Park, D.G.; Jeong, H.T.; Hong, J.H. A study on the radiation damage and recovery of neutron irradiated vessel steel using magnetic Barkhausen noise. J. Appl. Phys. 1999, 85, 5726–5728. [Google Scholar] [CrossRef]
- Clapham, L.; Jagadish, C.; Atherton, D.L. The influence of pearlite on Barkhausen noise generation in plain carbon steels. Acta Metall. Mater. 1991, 39, 1555–1562. [Google Scholar] [CrossRef]
- Palit Sagar, S.; Parida, N.; Das, S.; Dobmann, G.; Bhattacharya, D.K. Magnetic Barkhausen emission to evaluate fatigue damage in a low carbon structural steel. Int. J. Fatigue 2005, 27, 317–322. [Google Scholar] [CrossRef]
- Blaow, M.; Evans, J.T.; Shaw, B.A. Surface decarburisation of steel detected by magnetic Barkhausen emission. J. Mater. Sci. 2005, 40, 5517–5520. [Google Scholar] [CrossRef]
- Vincent, A.; Pasc, L.; Morin, M.; Kleber, X.; Delnondedieu, M. Magnetic Barkhausen noise from strain-induced martensite during low cycle fatigue of 304L austenitic stainless steel. Acta Mater. 2005, 53, 4579–4591. [Google Scholar] [CrossRef]
- Ilker Yelbay, H.; Cam, I.; Hakan Gür, C. Non-destructive determination of residual stress state in steel weldments by Magnetic Barkhausen Noise technique. NDT E Int. 2010, 43, 29–33. [Google Scholar] [CrossRef]
- Bilger, H.; Träuble, H. Temperatur und Verformungsabhängigkeit der Koerzitivfeldstärke von Eisen-Einkristallen. Phys. Status Solidi 1965, 10, 755–764. [Google Scholar] [CrossRef]
- Traüble, H. The influence of crystal defects on magnetization processes in ferromagnetic single crystals. In Magnetism and Metallurgy; Berkowitz, A.E., Kneller, E., Eds.; Academic Press: New York, NY, USA; London, UK, 1969; Volume 2, pp. 622–687, Library of Congress Catalog Card 69-13488. [Google Scholar]
- Küpferling, M.; Appino, C.; Basso, V.; Bertotti, G.; Fiorillo, F.; Meilland, P. Magnetic hysteresis in plastically deformed low-carbon steel laminations. J. Magn. Magn. Mater. 2007, 316, e854–e857. [Google Scholar] [CrossRef]
- Swartzendruber, L.J.; Hicho, G.E.; Chopra, H.D.; Leigh, S.D.; Adam, G.; Tsory, E. Effect of plastic strain on magnetic and mechanical properties of ultralow carbon sheet steel. J. Appl. Phys. 1997, 81, 4263–4265. [Google Scholar] [CrossRef]
- Astié, B.; Degauque, J.; Porteseil, J.L.; Vergne, R. Influence of the dislocation structures on the magnetic and magnetomechanical properties of high-purity iron. IEEE Trans. Magn. 1981, 17, 2929–2931. [Google Scholar] [CrossRef]
- Krause, R.F.; Cullity, B.D. Formation of uniaxial anisotropy in nickel by plastic deformation. J. Appl. Phys. 1968, 39, 356–358. [Google Scholar] [CrossRef]
- Perevertov, O. Influence of the residual stress on the magnetization process in mild steel. J. Phys. D Appl. Phys. 2007, 40, 949–954. [Google Scholar] [CrossRef]
- Stupakov, O.; Uchimoto, T.; Takagi, T. Magnetic anisotropy of plastically deformed low-carbon steel. J. Phys. D Appl. Phys. 2010, 43, 195003. [Google Scholar] [CrossRef]
- Silva, E.M.; Paula, A.M.R.; Leite, J.P.; Leite, J.P.; Andrade, L.S.S.; de Albuquerque, V.H.C.; Tavares, J.M.R.S. Detection of the magnetic easy direction in steels using induced magnetic fields. Metals 2016, 6, 317. [Google Scholar] [CrossRef]
- Permiakov, V.; Dupré, L.; Makaveev, D.; Melkebeek, J. Dependence of power losses on tensile stress for Fe-Si nonoriented steel up to destruction. J. Appl. Phys. 2002, 91, 7854–7856. [Google Scholar] [CrossRef]
- LoBue, M.; Basso, V.; Fiorillo, F.; Bertotti, G. Power losses and magnetization process in Fe-Si non-oriented electrical steels under compressive and tensile stresses. J. Magn. Magn. Mater. 2000, 215–216, 124–126. [Google Scholar] [CrossRef]
- Hattori, N.; Matsumoto, R.; Utsunomiya, H. Residual Stress Distribution through Thickness in Cold-Rolled Aluminum Sheet. Key Eng. Mater. 2014, 622–623, 1000–1007. [Google Scholar] [CrossRef]
- Ossart, F.; Hug, E.; Hubert, O.; Buvat, C.; Billardon, R. Effect of punching on electrical steels: Experimental and numerical coupled analysis. IEEE Trans. Magn. 2000, 36, 3137–3140. [Google Scholar] [CrossRef]
- Hofman, M.; Naumoski, H.; Herr, U.; Herzog, H. Magnetic properties of electrical steel sheets in respect of cutting: Micromagnetic analysis and macromagnetic modeling. IEEE Trans. Magn. 2016, 52, 2000114. [Google Scholar] [CrossRef]
- Crevecoeur, G.; Dupré, L.; Vandenbossche, L.; van de Walle, R. Local Identification of Magnetic Hysteresis Properties Near Cutting Edges of Electrical Steel Sheets. IEEE Trans. Magn. 2008, 44, 1010–1013. [Google Scholar] [CrossRef]
- Zhao, H.; Ferrara, E.; Manescu Paltanea, V.; Paltanea, G.; Gavrila, H.; Fiorillo, F. Effect of punching and water-jet cutting methods on magnetization curve and energy losses of non-oriented magnetic steel sheets. Int. J. Appl. Electromagn. Mech. 2017, 55, 69–76. [Google Scholar] [CrossRef]
- Piotrowski, L.; Augustyniak, B.; Chmielewski, M.; Hristoforou, E.V.; Kosmas, K. Evaluation of Barkhausen noise and magnetoacoustic emission signals properties for plastically deformed Armco iron. IEEE Trans. Magn. 2010, 46, 239–242. [Google Scholar] [CrossRef]
- Bertotti, G.; Fiorillo, F.; Sassi, M.P. Barkhausen noise and domain structure dynamics in Si.Fe at different points of the magnetization curve. J. Magn. Magn. Mater. 1981, 23, 136–148. [Google Scholar] [CrossRef]
- Bertotti, G. Hysteresis on Magnetism; Academic Press: San Diego, CA, USA, 1998; pp. 288–294. ISBN 0-12-093270-9. [Google Scholar]
- Küpferling, M.; Fiorillo, F.; Basso, V.; Bertotti, G.; Meilland, P. Barkhausen noise in plastically deformed low-carbon steels. J. Magn. Magn. Mater. 2008, 320, e527–e530. [Google Scholar] [CrossRef]
- Bertotti, G.; Fiorillo, F.; Rietto, A.M. Microscopic and macroscopic aspects of the magnetization process in Si-Fe single crystals. IEEE Trans. Magn. 1984, 20, 1481–1483. [Google Scholar] [CrossRef]


© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fiorillo, F.; Küpferling, M.; Appino, C. Magnetic Hysteresis and Barkausen Noise in Plastically Deformed Steel Sheets. Metals 2018, 8, 15. https://doi.org/10.3390/met8010015
Fiorillo F, Küpferling M, Appino C. Magnetic Hysteresis and Barkausen Noise in Plastically Deformed Steel Sheets. Metals. 2018; 8(1):15. https://doi.org/10.3390/met8010015
Chicago/Turabian StyleFiorillo, Fausto, Michaela Küpferling, and Carlo Appino. 2018. "Magnetic Hysteresis and Barkausen Noise in Plastically Deformed Steel Sheets" Metals 8, no. 1: 15. https://doi.org/10.3390/met8010015
APA StyleFiorillo, F., Küpferling, M., & Appino, C. (2018). Magnetic Hysteresis and Barkausen Noise in Plastically Deformed Steel Sheets. Metals, 8(1), 15. https://doi.org/10.3390/met8010015




