Simulation of Crack Initiation and Propagation in the Crystals of a Beam Blank
Abstract
:1. Introduction
2. Establishment of a Polycrystalline Model
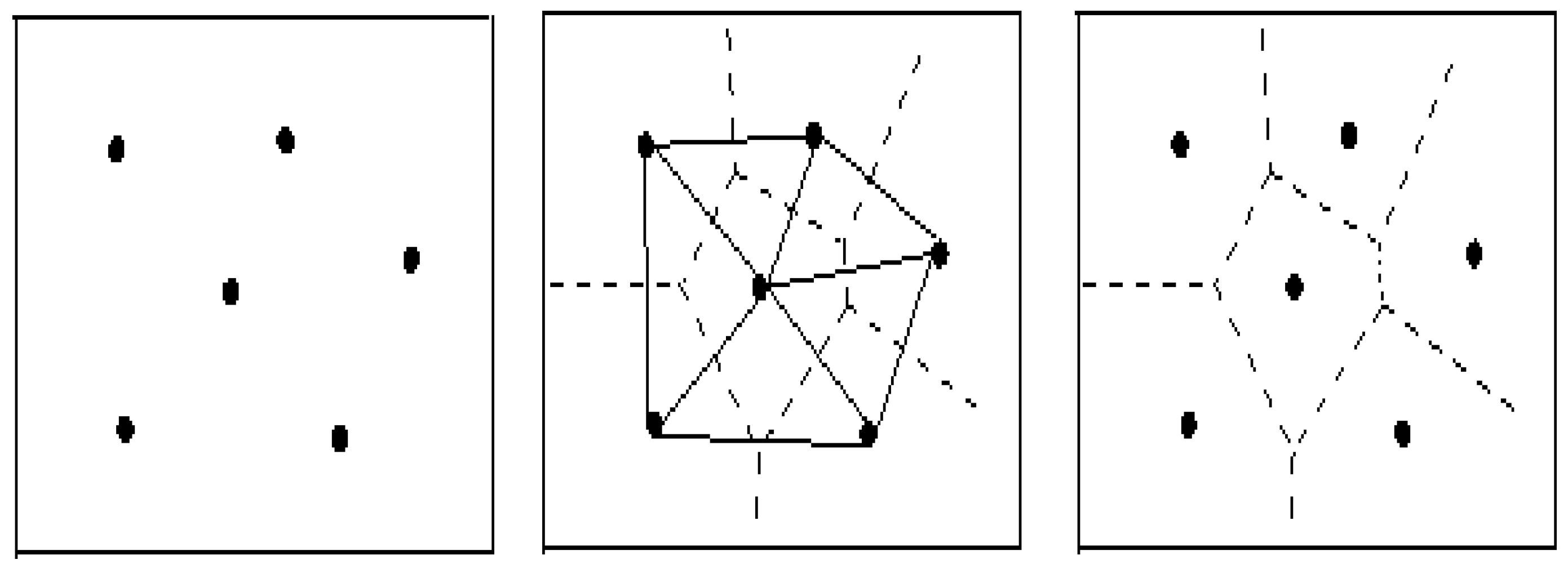
2.1. Polycrystalline Model with Cracks
2.2. Polycrystalline Model with Pores
2.3. Polycrystalline Model with Inclusions
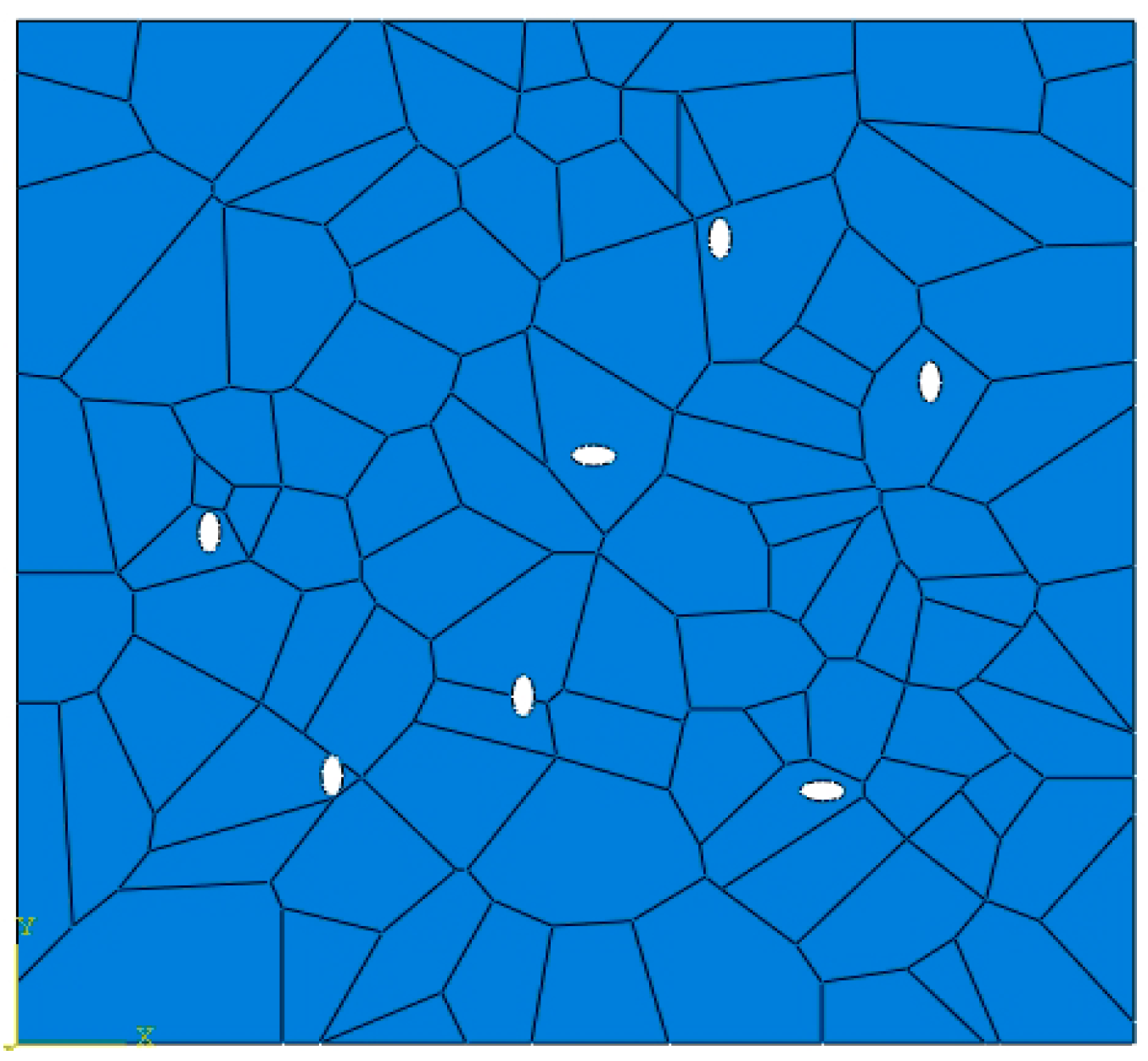
2.4. Meshing and Initial Boundary Conditions
3. Analysis of Crack Initiation and Propagation in a Crystal
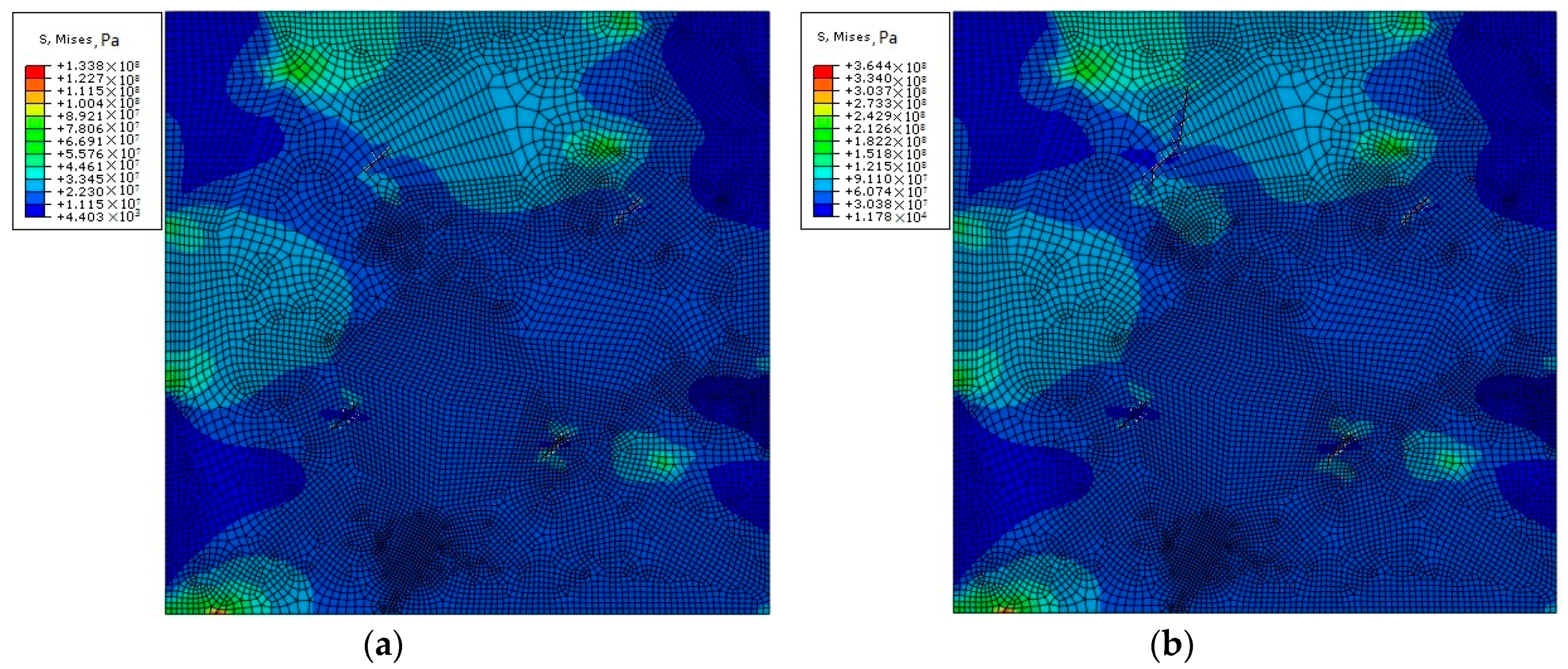
3.1. Stress and Strain Analysis of Defect-Free Crystals
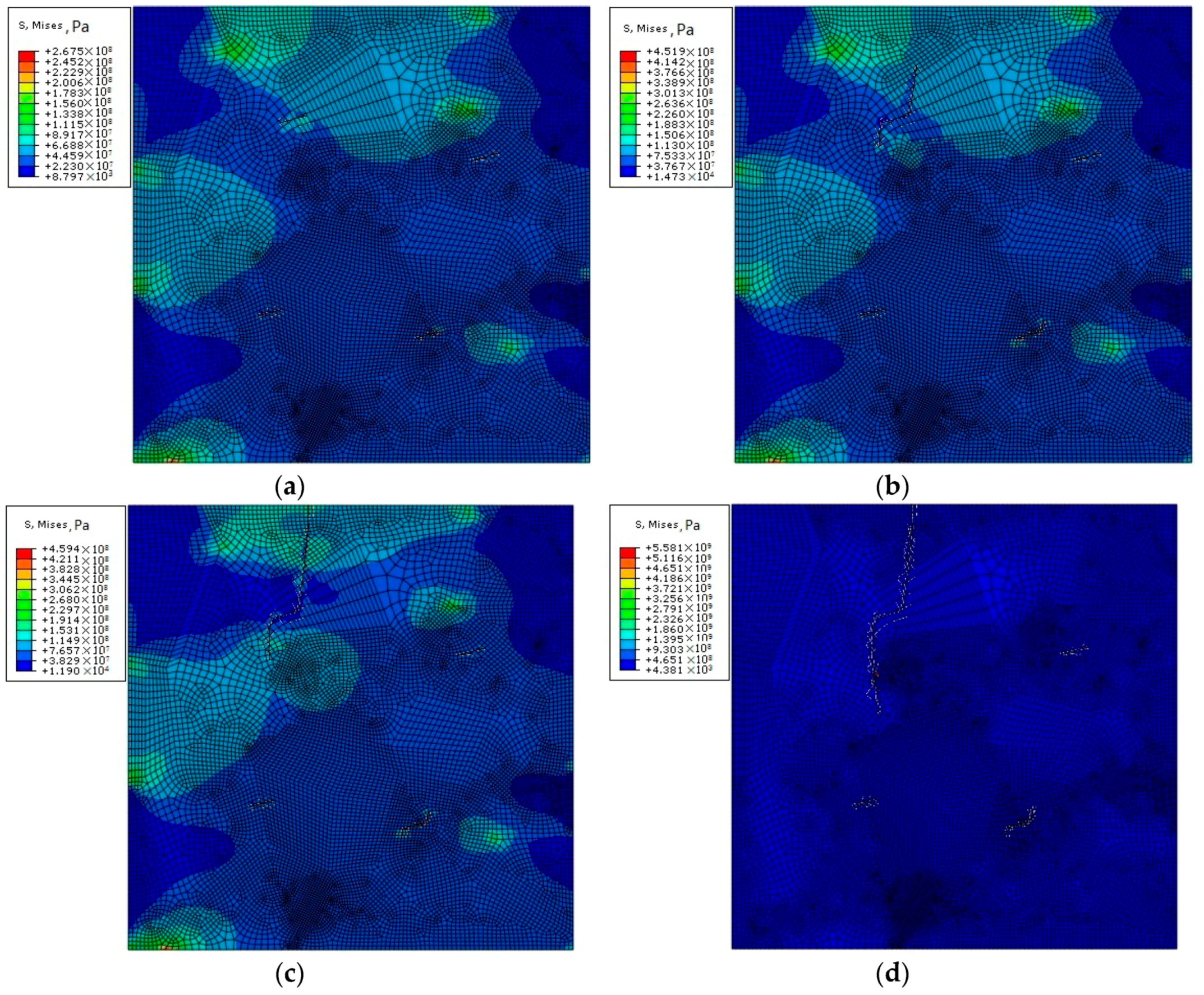
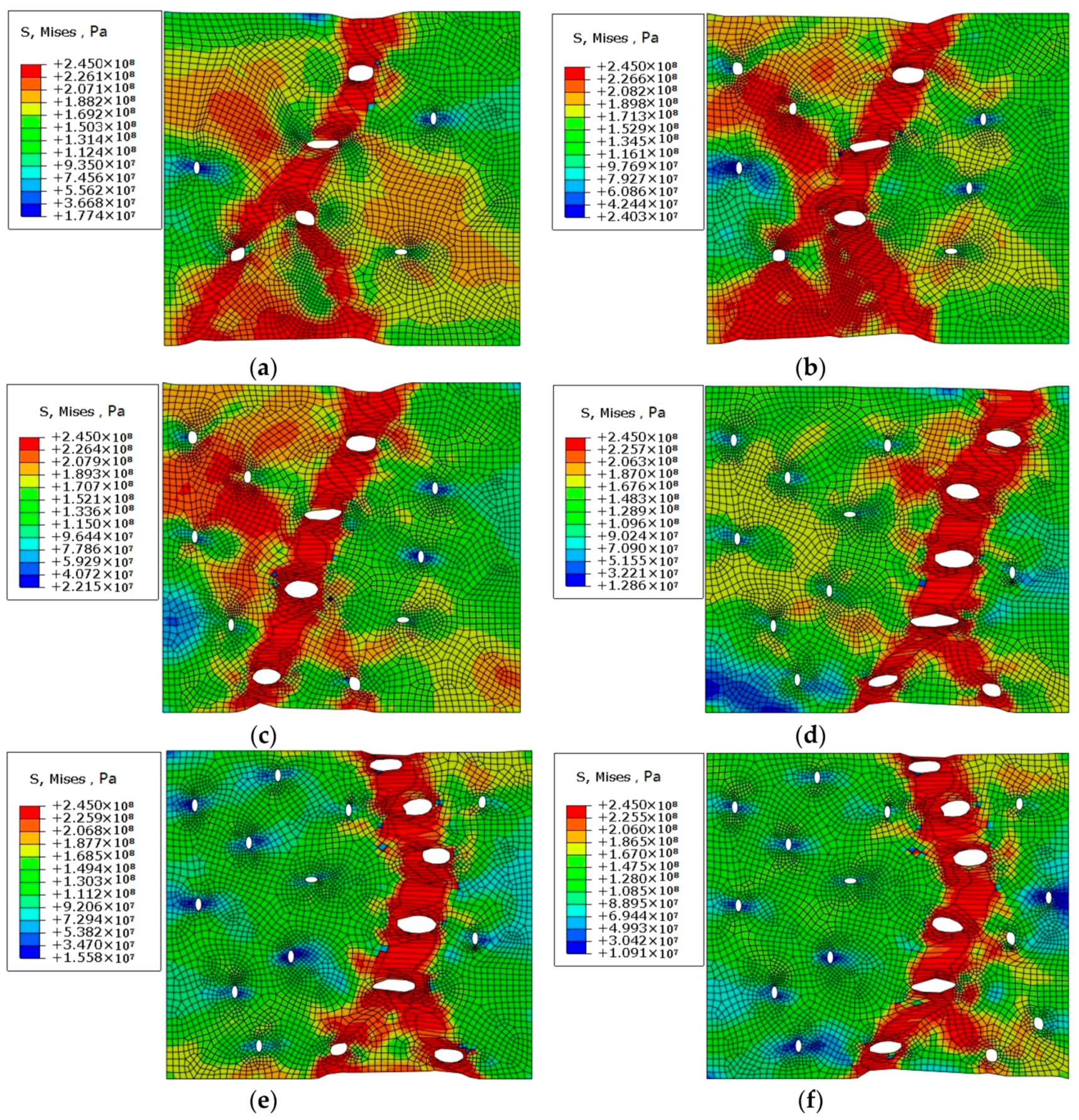
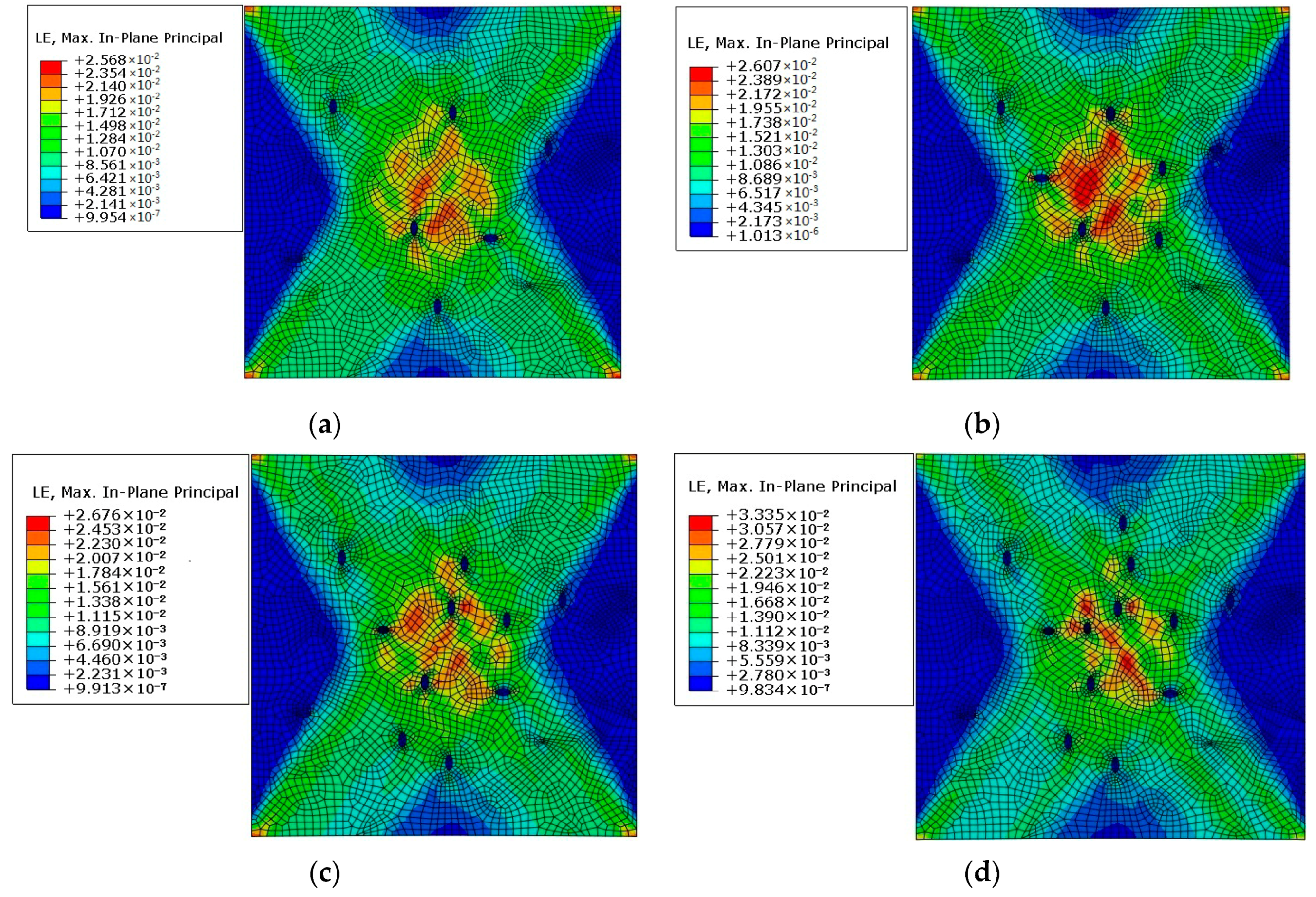
3.2. Analysis of a Polycrystalline Model with Multiple Cracks
- The amount of crack propagation at the grain boundary is higher than that in the crystal.
- The angle and tensile stress of the crack are unrelated to the direction of crack propagation, and their influence on crack propagation is mainly reflected in the time and sequence of the crack propagation and the final crack propagation displacement.
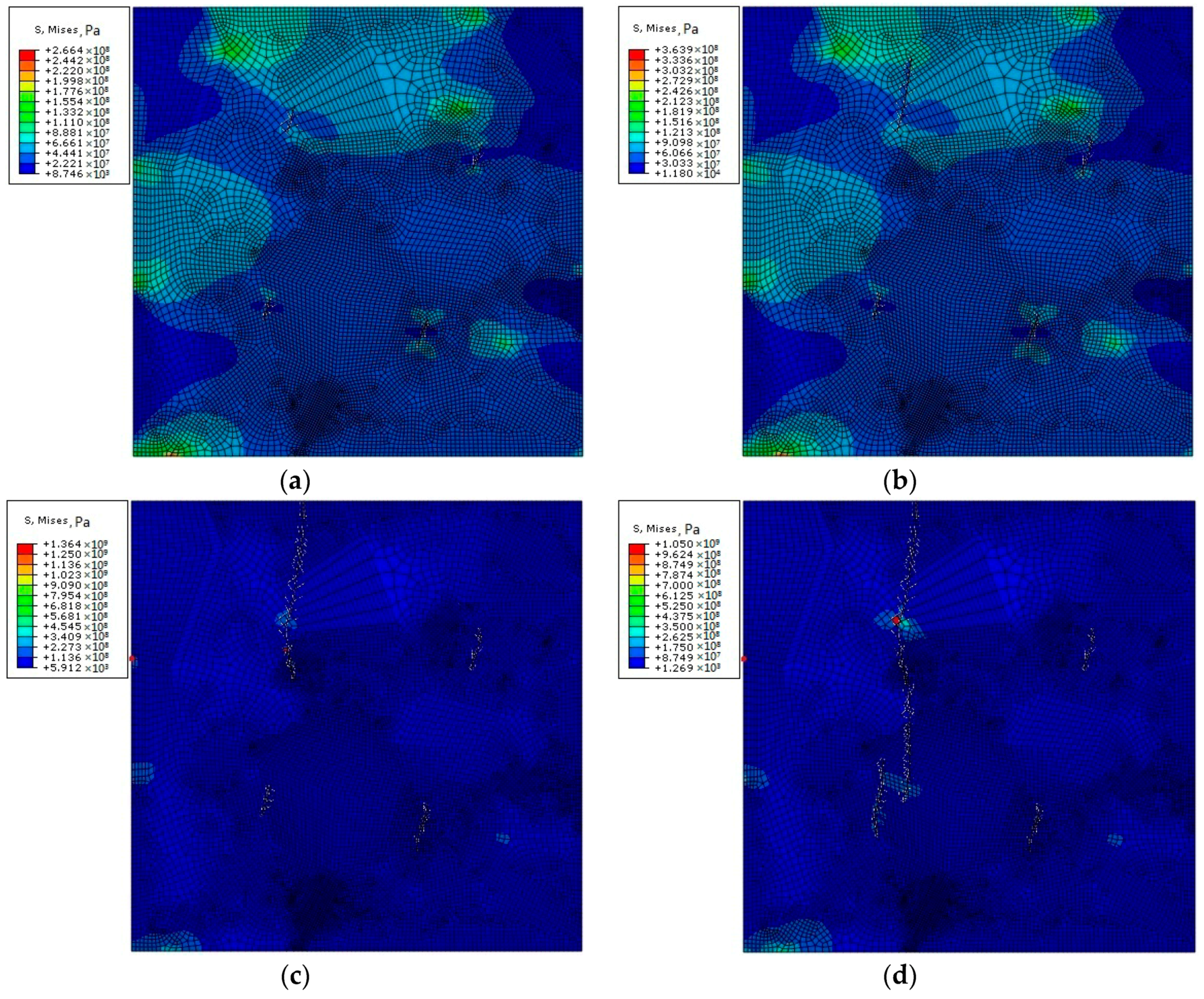
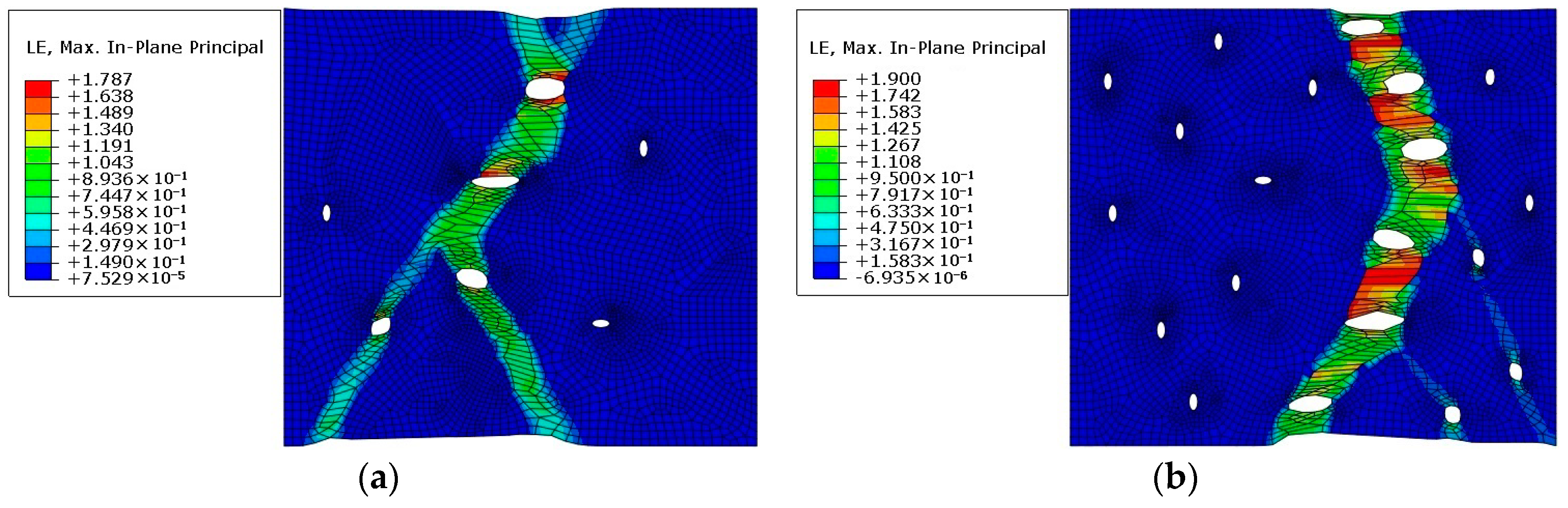
3.3. Analysis of a Polycrystalline Model of Different Porosities
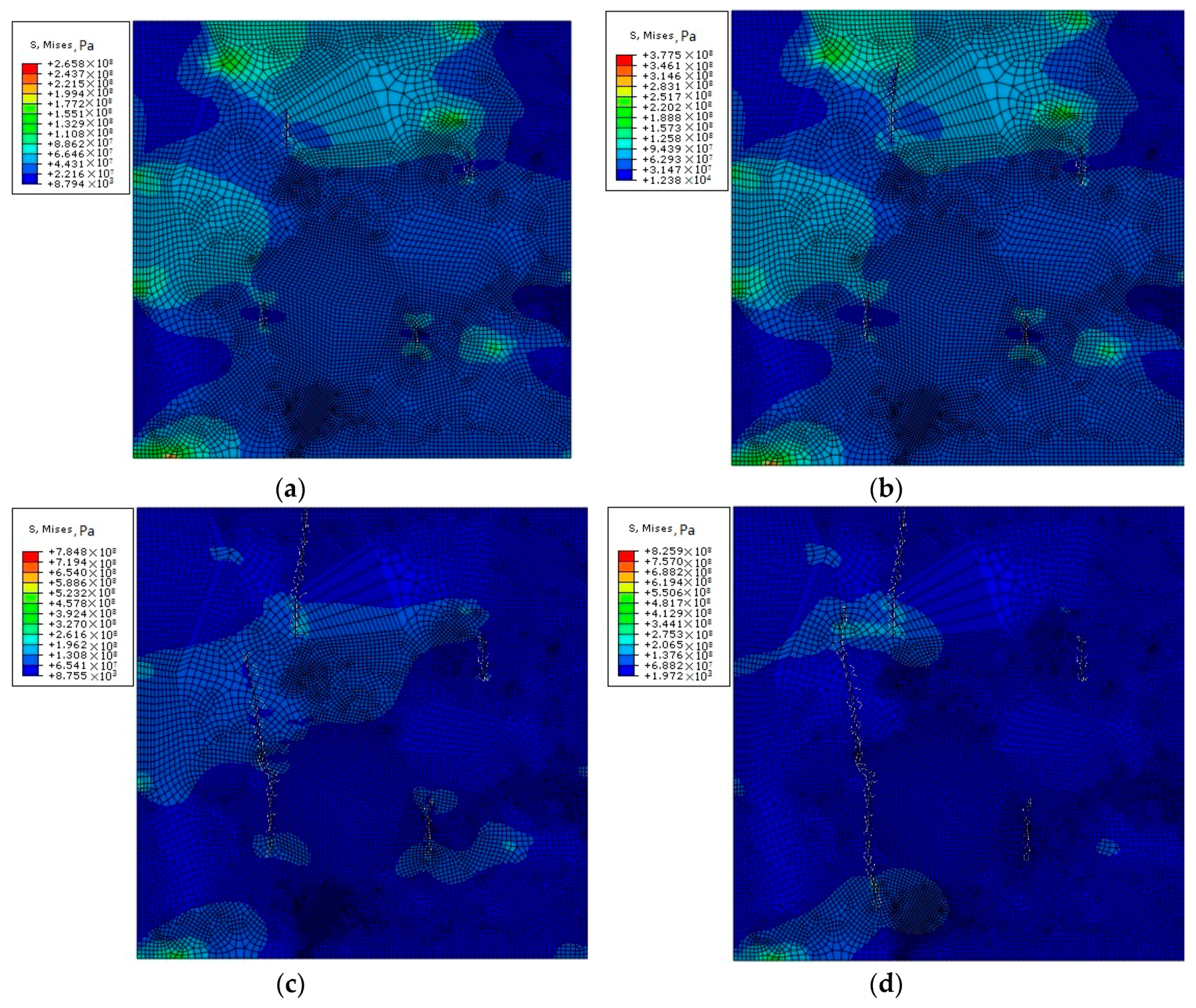
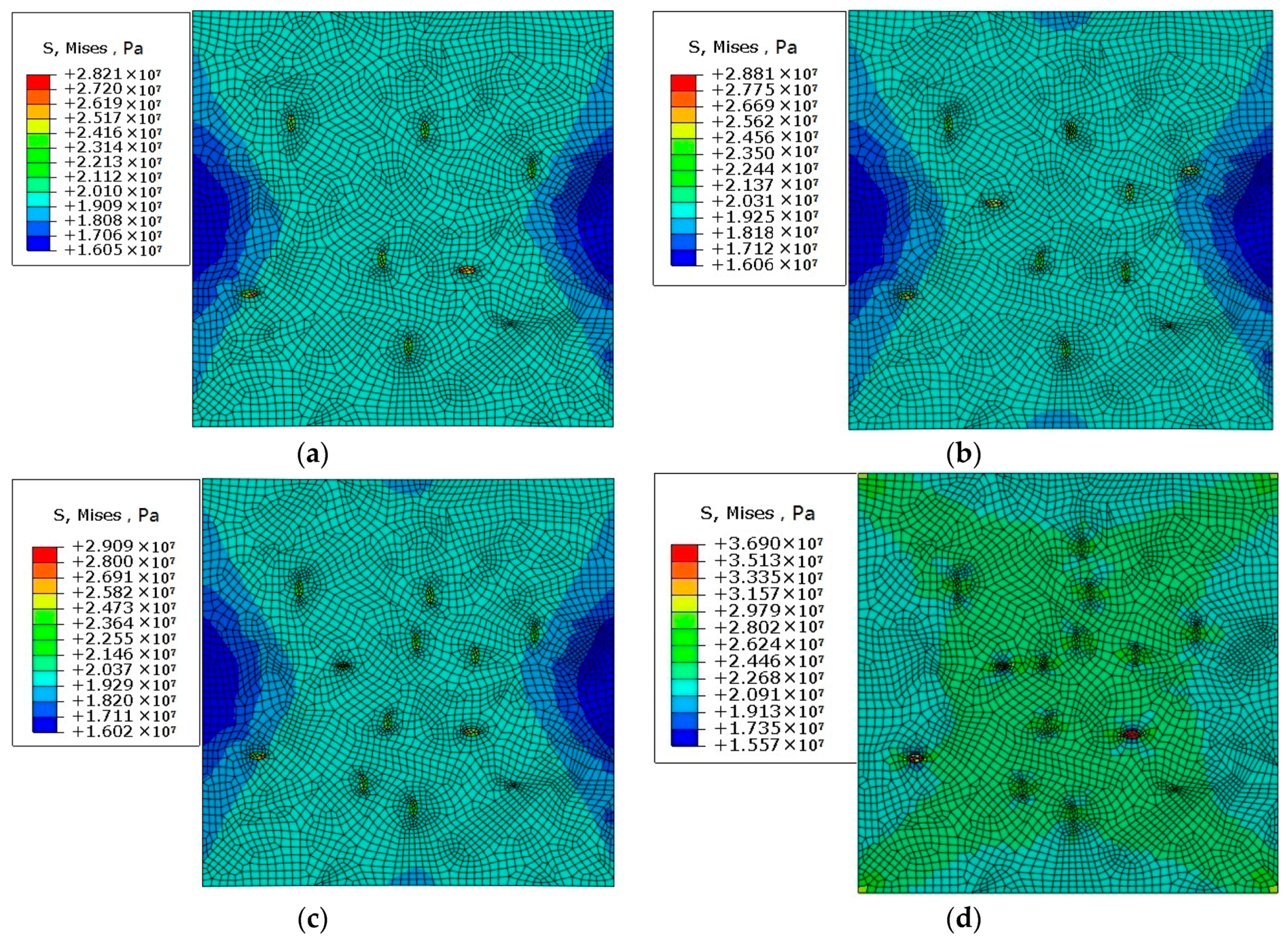
3.4. Analysis of Polycrystal Model with Different Proportion Inclusions
4. Conclusions
- The stress at the crystal boundary is much greater than that in the crystal after loading on the defect-free polycrystalline model.
- Crack propagation occurs at the crystal boundary prior to that in the crystal, and the propagation of the former is greater than that of the latter.
- The direction of crack propagation is basically along the direction perpendicular to the tensile stress, and the amount of crack propagation along this direction is also the greatest.
- When a polycrystalline model with pores is subjected to tensile stress, stress concentration occurs at the position where the end of pores is perpendicular to the stress direction, and the propagation and aggregation direction of the pores are basically perpendicular to the direction of the tensile stress. When the pores ends are parallel to the stress direction, the stress values at these locations are relatively small.
- When a polycrystalline model with impurities is subjected to a force, a large stress concentration will occur at the impurities, while the strain generated by the impurities is the smallest. This often causes the crack to propagate along the direction of the impurities, thus causing damage to and fracturing of the material.
- Both inclusions and pores affect crack initiation and propagation. Through mesoscopic simulation, it was found that the influence of pores on cracks is greater than that of inclusions.
- The simulation of mesoscopic crack initiation and propagation of a beam blank can provide theoretical guidance for the generation of macrocracks and process optimization.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Xu, M.G.; Zhu, M.Y. Transport Phenomena in a Beam-Blank Continuous Casting Mold and a New Design of Submerged Entry Nozzle. ISIJ Int. 2015, 55, 791–798. [Google Scholar] [CrossRef]
- Xu, H.L.; Wen, G.H.; Sun, W.; Wang, K.Z.; Yan, B. Analysis of thermal behavior for beam blank continuous casting mold. J. Iron Steel Res. Int. 2010, 17, 17–22. [Google Scholar] [CrossRef]
- Lee, J.E.; Yeo, T.J.; Kyu Hwan, O.H.; Yoon, J.K.; Yoon, U.S. Prediction of cracks in continuously cast steel beam blank through fully coupled analysis of fluid flow, heat transfer, and deformation behavior of a solidifying shell. Metall. Mater. Trans. A 2000, 31, 225–237. [Google Scholar] [CrossRef]
- Xu, H.L. Simulation and Optimization of Cooling Process for Continuous Casting Beam Blank. Ph.D. Thesis, Chongqing University, Chongqing, China, 2010. [Google Scholar]
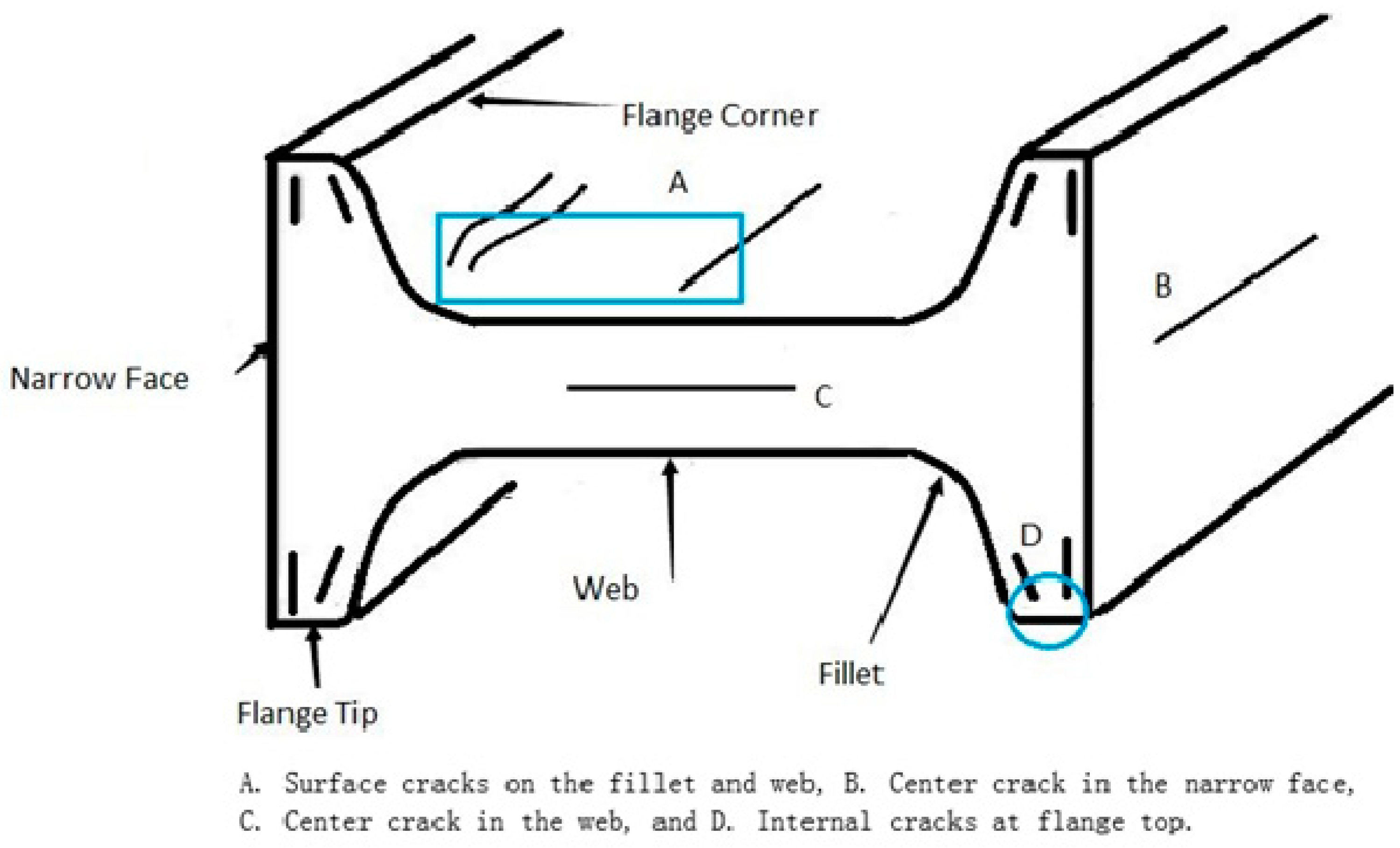
- Yang, G.Y.; Zhu, L.G.; Chen, W.; Yu, X.W.; He, B.M. Initiation of Surface Cracks on Beam Blank in the Mold during Continuous Casting. Metals 2018, 8, 712. [Google Scholar] [CrossRef]
- Lv, M.; Lu, B.; Wang, X.X.; Shan, Z.G.; Zhang, Q.; Chen, Y.S. Research and control on web plate crack of the large type beam blank. Iron Steel 2010, 45, 99–102. [Google Scholar] [CrossRef]
- Wu, J.; Xu, W.; Yang, Y.D. Technics study of reduing longitudinal surface crack of beam blank. Iron Steel 2009, 45, 95–97. [Google Scholar] [CrossRef]
- Xu, H.L.; Wen, G.H.; Sun, W.; Wang, K.Z.; Yan, B.; Luo, W. Thermal behaviour of moulds with different water channels and their influence on quality in continuous casting of beam blanks. Ironmak. Steelmak. 2013, 37, 380–386. [Google Scholar] [CrossRef]
- Du, Y.P.; Yang, J.W.; Shi, R.; Cui, X.C. Effect of submerged entry nozzle (sen) parameters and shape on 3-d fluid flow in mould for beam blank continuous casting. Acta Metall. Sin. 2004, 17, 705–712. [Google Scholar]
- De Santis, M.; Cristallini, A.; Rinaldi, M.; Sgrò, A. Modelling-based innovative feeding strategy for beam blanks mould casting aimed at as-cast surface quality improvement. ISIJ Int. 2014, 54, 496–503. [Google Scholar] [CrossRef]
- Lasko, G.; Weber, U.; Schmauder, S. Finite Element Simulations of Crack Propagation in Al2O3/6061 Al Composites. Acta Metall. Sin. 2014, 27, 853–861. [Google Scholar] [CrossRef]
- Jiang, Z.W.; Wan, S.; Cheng, C. Analysis of the Crack Propagation Based on Extended Finite Method. Appl. Mech. Mater. 2013, 275–277, 169–173. [Google Scholar] [CrossRef]
- Wang, G.X.; Schwalbe, K.H. A study of the transition from intercrystalline to transcrystalline fatigue crack propagation in different ageing conditions of the alloy Cu-35%Ni-3.5%Cr. Int. J. Fatigue 1993, 15, 3–8. [Google Scholar] [CrossRef]
- Shen, J.L. Study on Simulation of Surface Cracks Growth for Continuous Casting Q235 Slab. Mater’s Thesis, Chongqing University, Chongqing, China, 2013. [Google Scholar]
- Xue, F.M.; Li, F.G.; Li, J.; He, M.; Yuan, Z.W.; Wang, R.T. Numerical modeling crack propagation of sheet metal forming based on stress state parameters using xfem method. Comput. Mater. Sci. 2013, 69, 311–326. [Google Scholar] [CrossRef]
- Wang, F.G. Crack Initiatiation and Propagation of Duplex Stainless Steel Finite Element Simulation. Master’s Thesis, Xi’an Technological University, Xi’an, China, 2014. [Google Scholar]
- Chen, L.Y.; Zhu, Y.C. Cause for bubbles occurring in top CC slab & countermeasures. Contin. Cast. 1999, 2, 19–20. [Google Scholar] [CrossRef]
- Geng, M.S.; Wang, X.H.; Zhang, J.M.; Wang, W.J.; Liu., Z.M. Study of Surface Blow Hole Defects of Continuous Casting Slab. Iron Steel 2010, 45, 45–50. [Google Scholar] [CrossRef]
- Yang, G.Y.; Zhu, L.G.; Chen, W.; Yu, X.W.; Guo, G.X. Propagation of Surface Cracks on Beam Blank in the Mould during Continuous Casting. Ironmak. Steelmak. 2018. [Google Scholar] [CrossRef]










| Parameter | Data |
|---|---|
| Steel grade | Q235B |
| Steel compositions | C: 0.19%, Mn: 0.43%, Si: 0.20%, P: 0.025%, S: 0.007% |
| Elastic Modulus of matrix (Em) | 206 GPa [16] |
| Elastic Modulus of inclusion (Ei) | 20,600 GPa [16] |
| Poisson’s ratio (ν) | 0.28 [16] |
| Specific heat (Cp) | 687 J/kg·°C [14] |
| Thermal conductivity (λ) | 32 W/m·°C [14] |
| Thermal expansion Coefficient (α) | 1.30 × 10−5 m/K [14] |
| Ultimate tensile strength (σb) | 390 MPa [14] |
| Yield stress (σs) | 235 MPa [14] |
| The density of strand (ρ) | 7400 kg/m3 [14] |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, G.; Zhu, L.; Chen, W.; Guo, G.; He, B. Simulation of Crack Initiation and Propagation in the Crystals of a Beam Blank. Metals 2018, 8, 905. https://doi.org/10.3390/met8110905
Yang G, Zhu L, Chen W, Guo G, He B. Simulation of Crack Initiation and Propagation in the Crystals of a Beam Blank. Metals. 2018; 8(11):905. https://doi.org/10.3390/met8110905
Chicago/Turabian StyleYang, Gaiyan, Liguang Zhu, Wei Chen, Gaoxiang Guo, and Baomin He. 2018. "Simulation of Crack Initiation and Propagation in the Crystals of a Beam Blank" Metals 8, no. 11: 905. https://doi.org/10.3390/met8110905
APA StyleYang, G., Zhu, L., Chen, W., Guo, G., & He, B. (2018). Simulation of Crack Initiation and Propagation in the Crystals of a Beam Blank. Metals, 8(11), 905. https://doi.org/10.3390/met8110905




