Numerical Simulation of Electromagnetic Field in Round Bloom Continuous Casting with Final Electromagnetic Stirring
Abstract
:1. Introduction
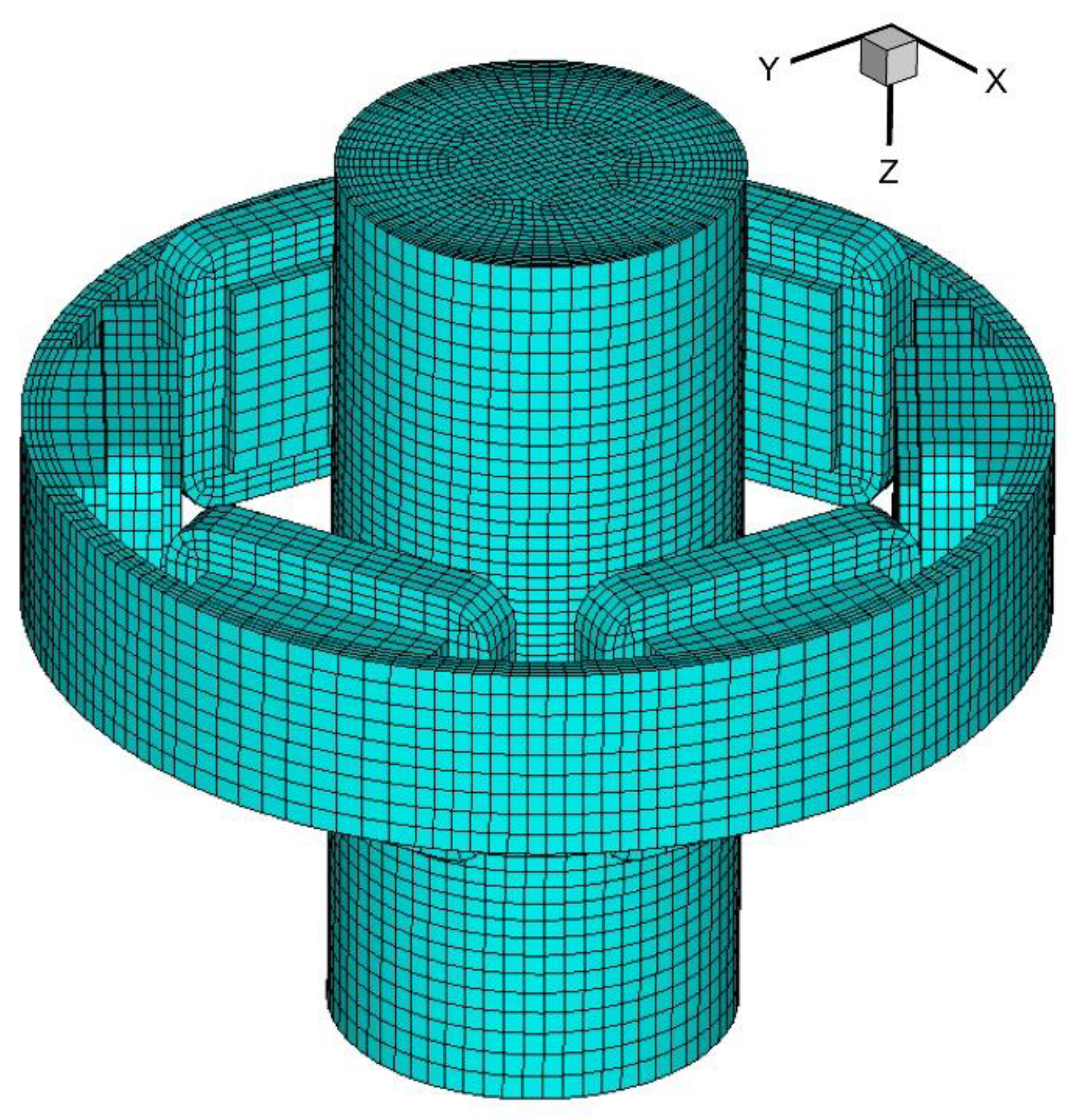
2. Mathematical Model
2.1. Basic Assumption
- In the F-EMS process, the magnetic Reynolds number (about 0.1) is far less than the shielding parameter (about 10) [10,12] and the angular frequency of the current intensity is much larger than the angular velocity of the molten steel; thus, the influence of the molten steel flow on the electromagnetic field is negligible [13]. Therefore, this problem can be decomposed into an electromagnetic problem and a fluid flow problem to be solved separately. In the present paper, only the electromagnetic field was calculated without regard to the flow field and solidification.
- Since the current frequency of F-EMS is generally in the range of 4 Hz to 10 Hz, which belongs to the magnetic quasi-static field, the displacement current is ignored [8].
- Both the outer shell and the cooling water jacket of the stirrer are approximated as an air zone for the benefit of the calculations.
- The curve of the strand is negligible.
2.2. Control Equations
2.3. Boundary Conditions
2.4. Physical Properties
2.5. Solution
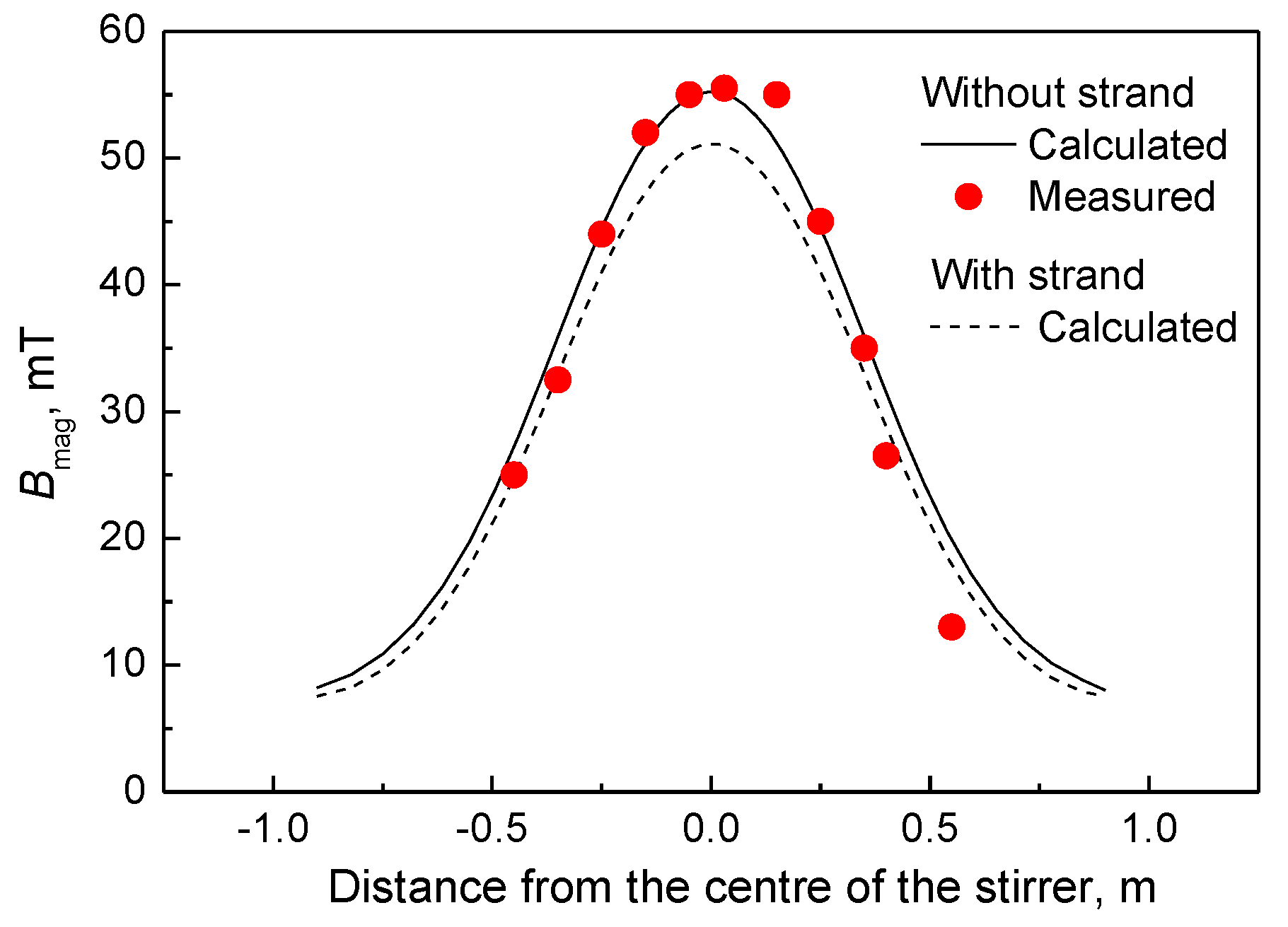
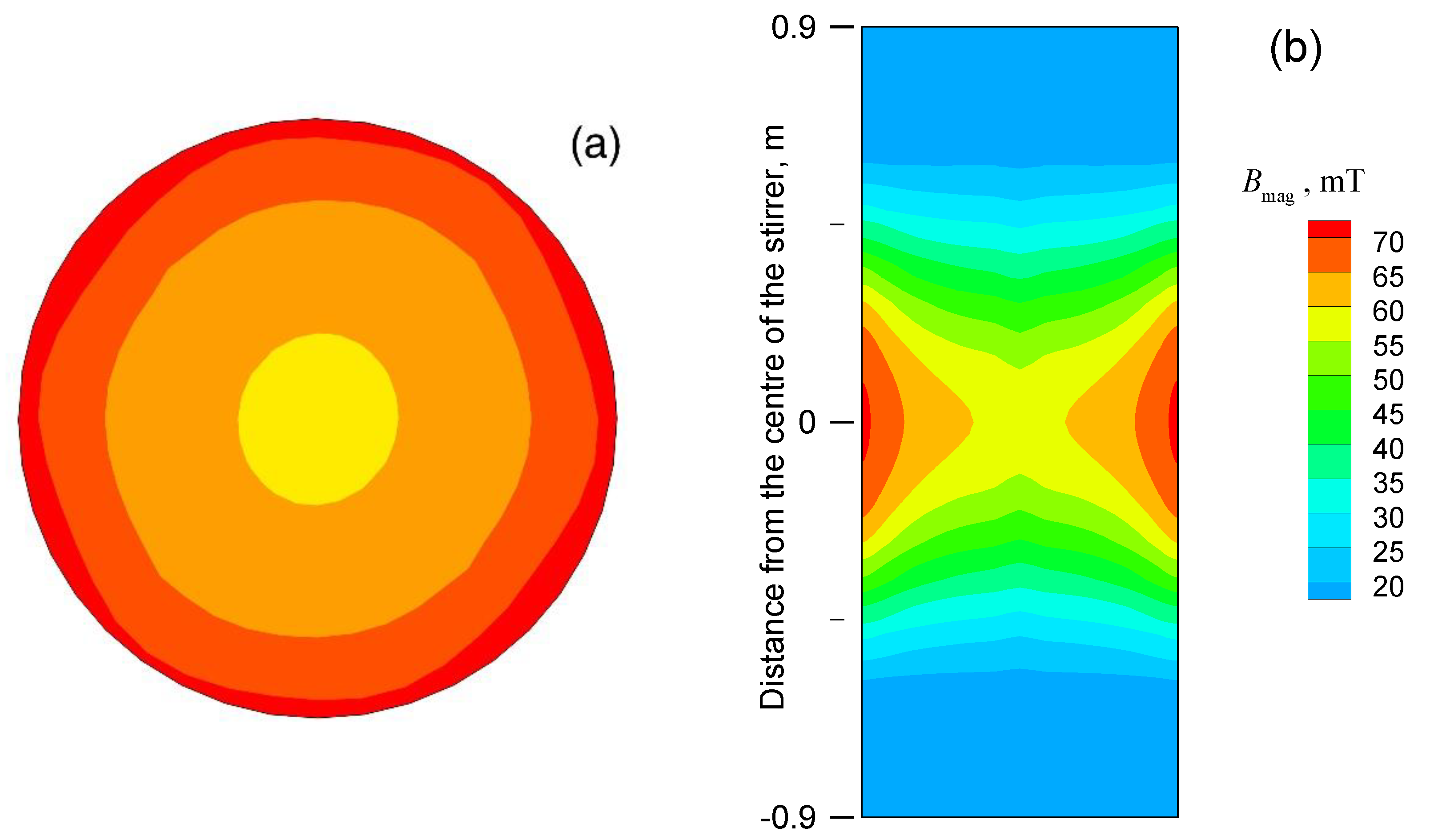
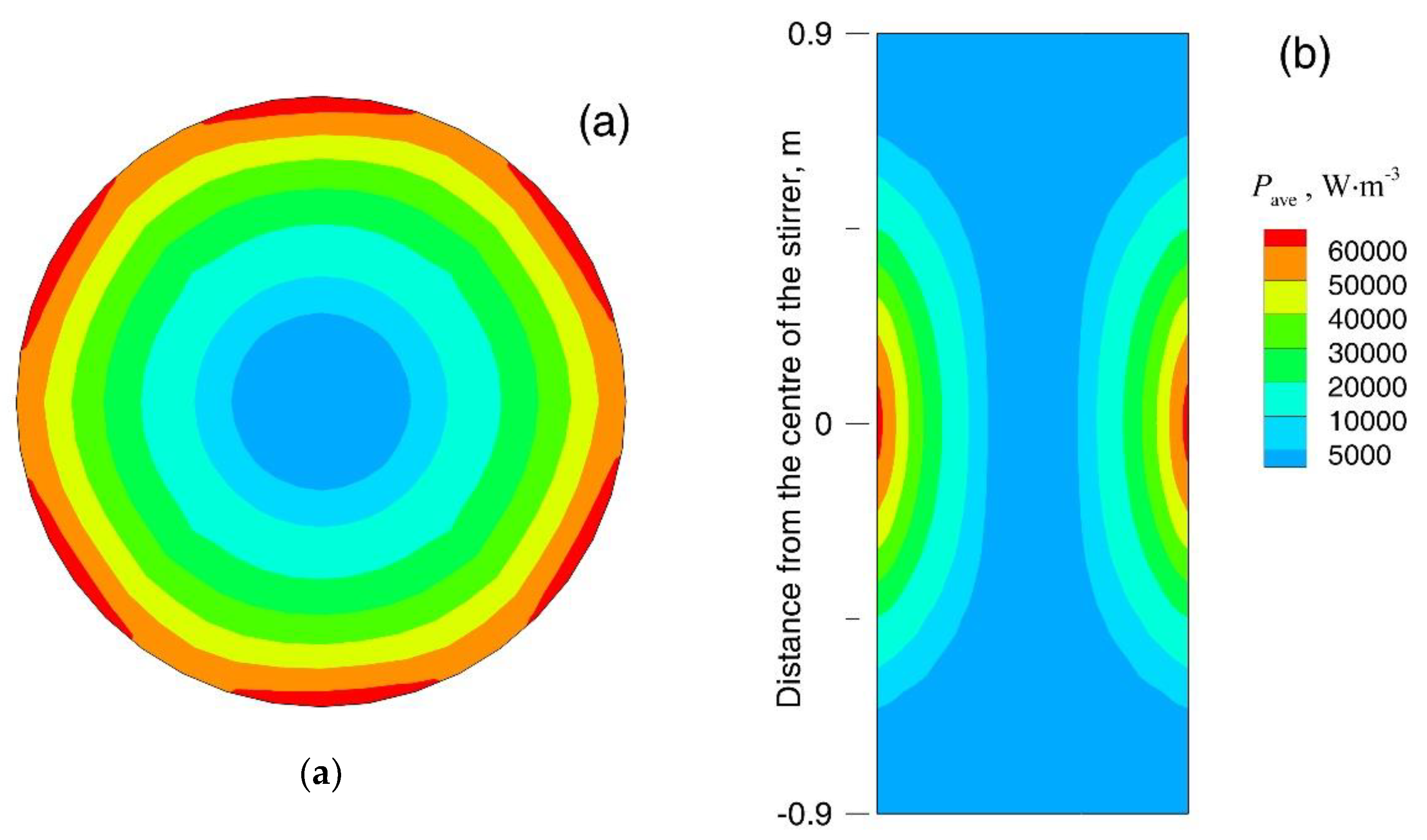
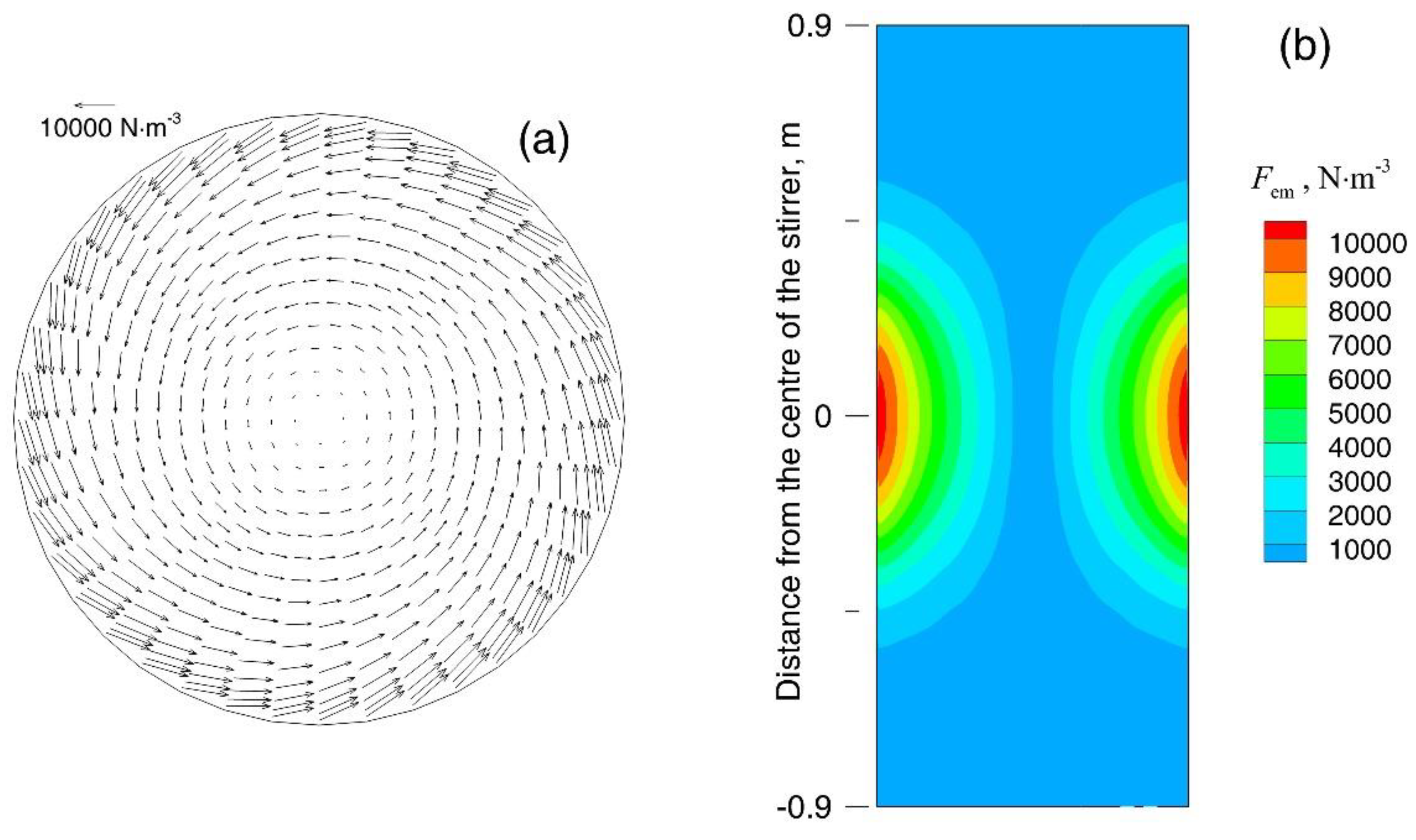
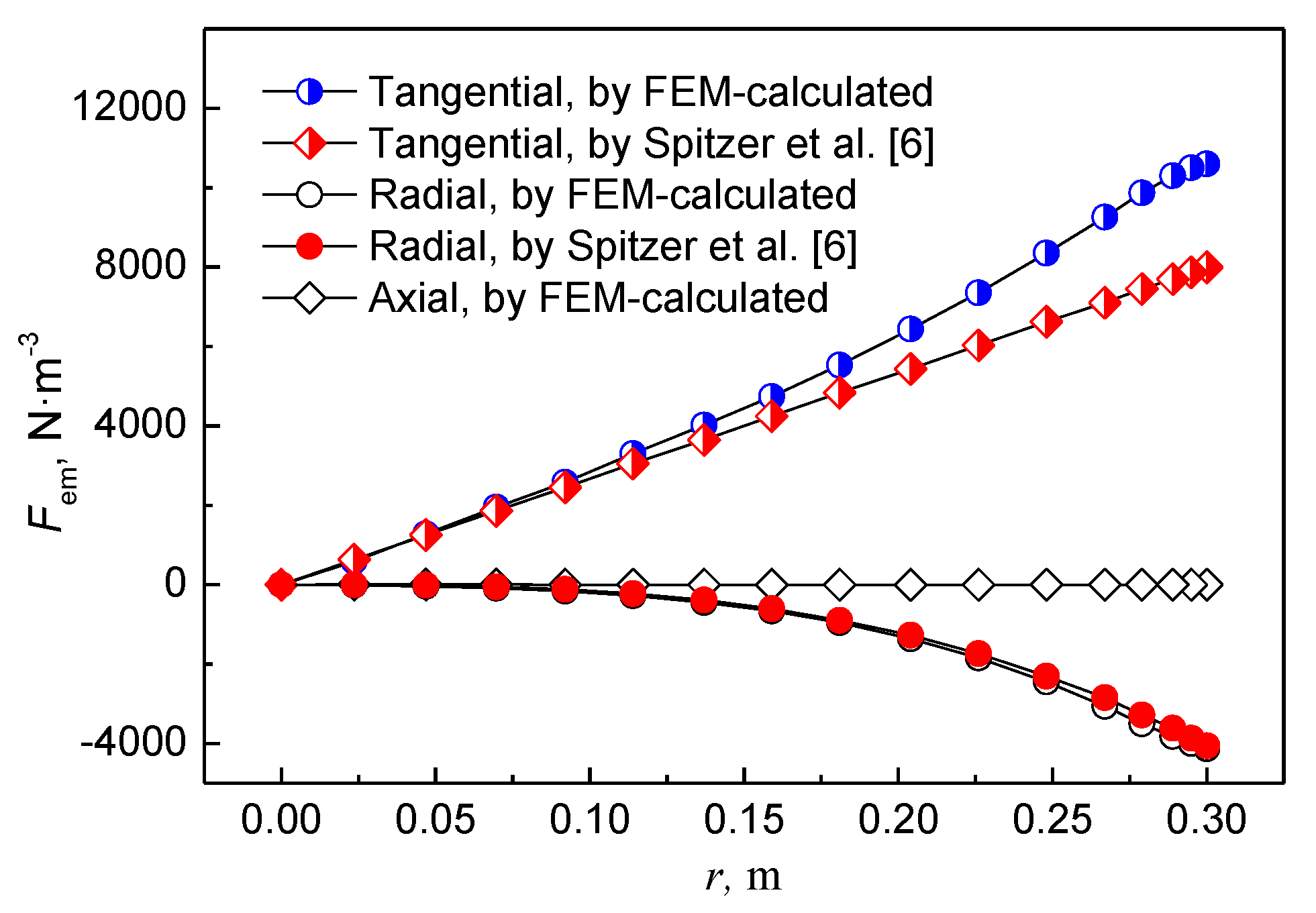
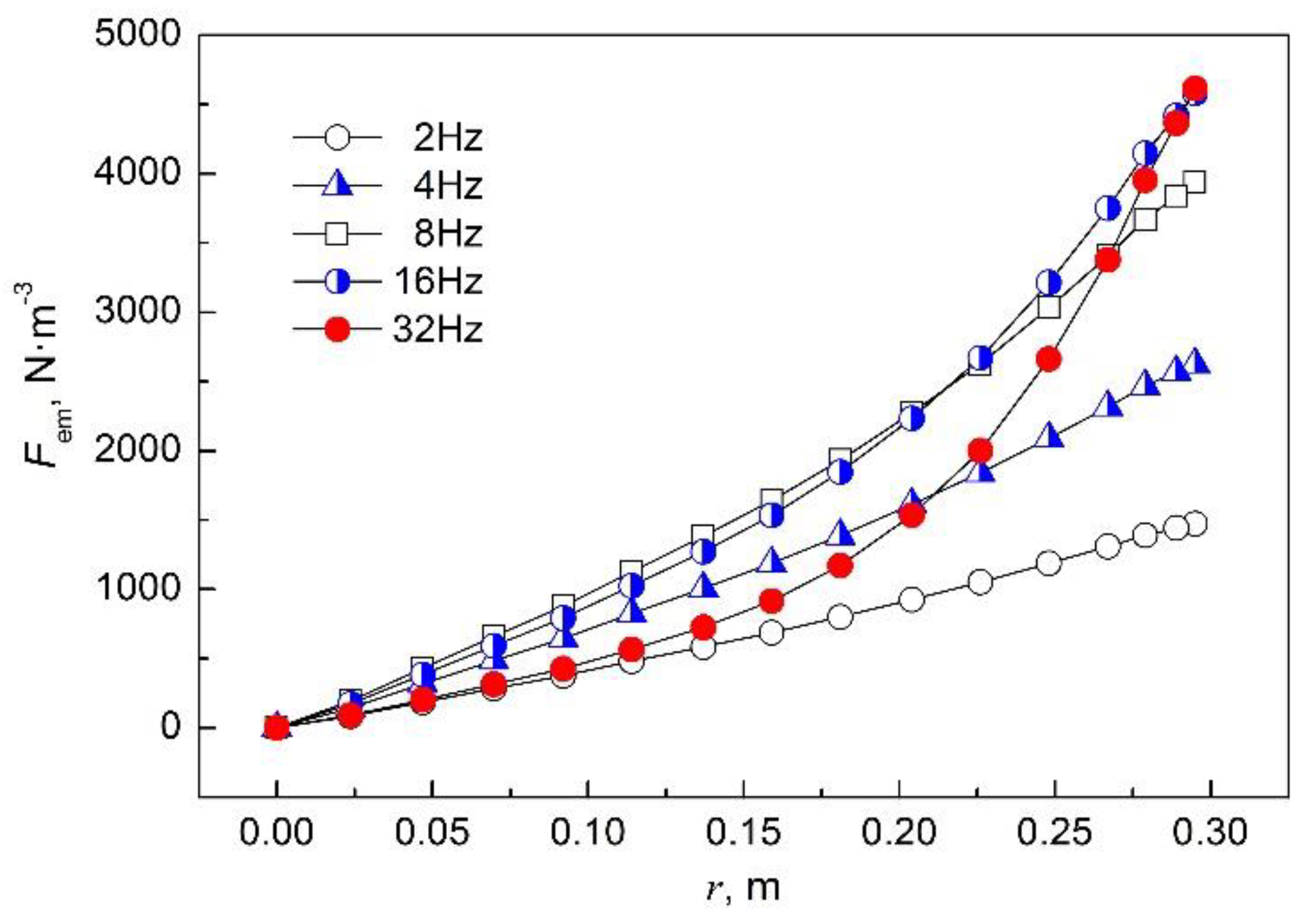
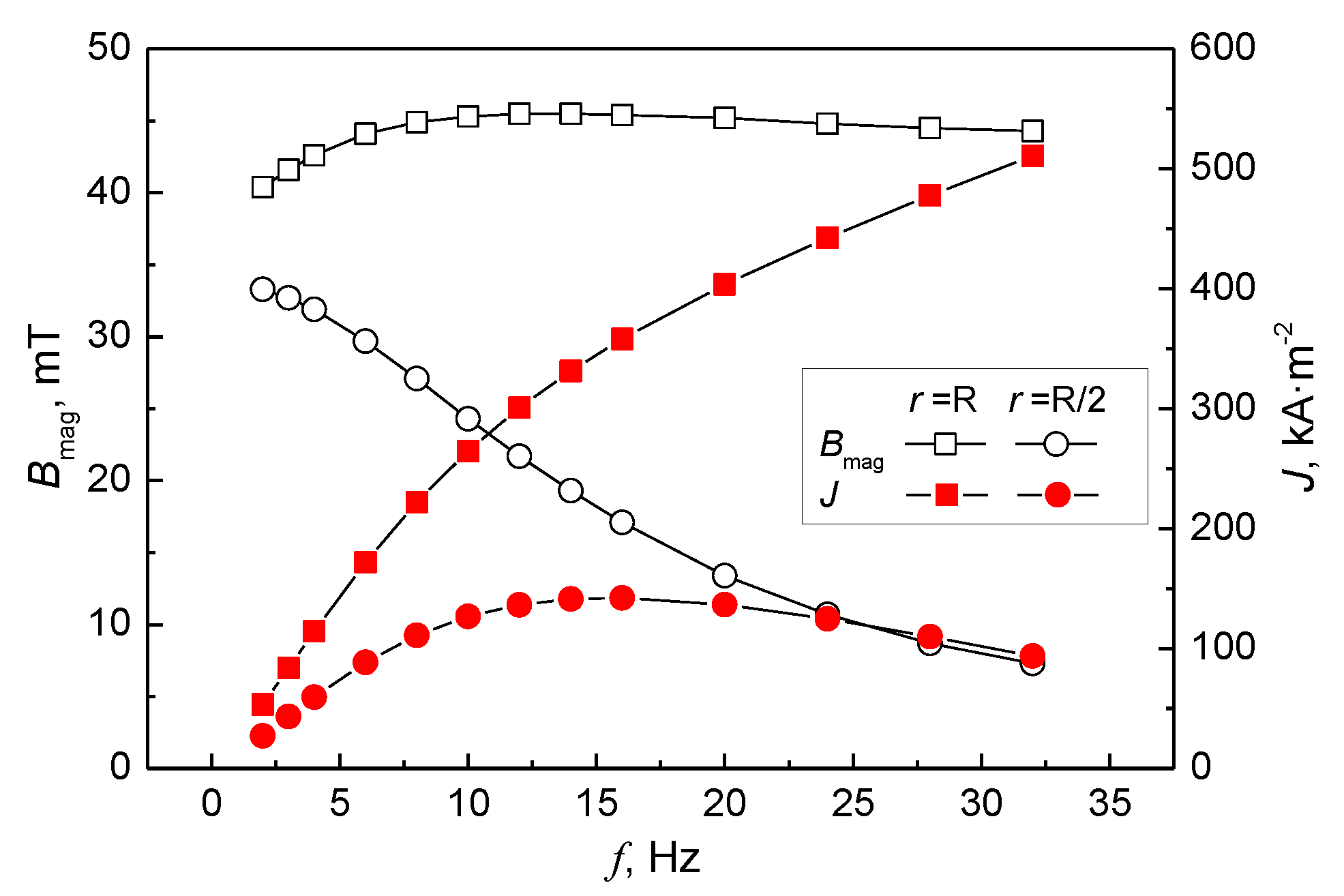
3. Results and Discussion
4. Conclusions
- The Joule heat generated by F-EMS in a continuous casting strand is very small, and its influence on the secondary cooling heat transfer in the stirring zone can be ignored.
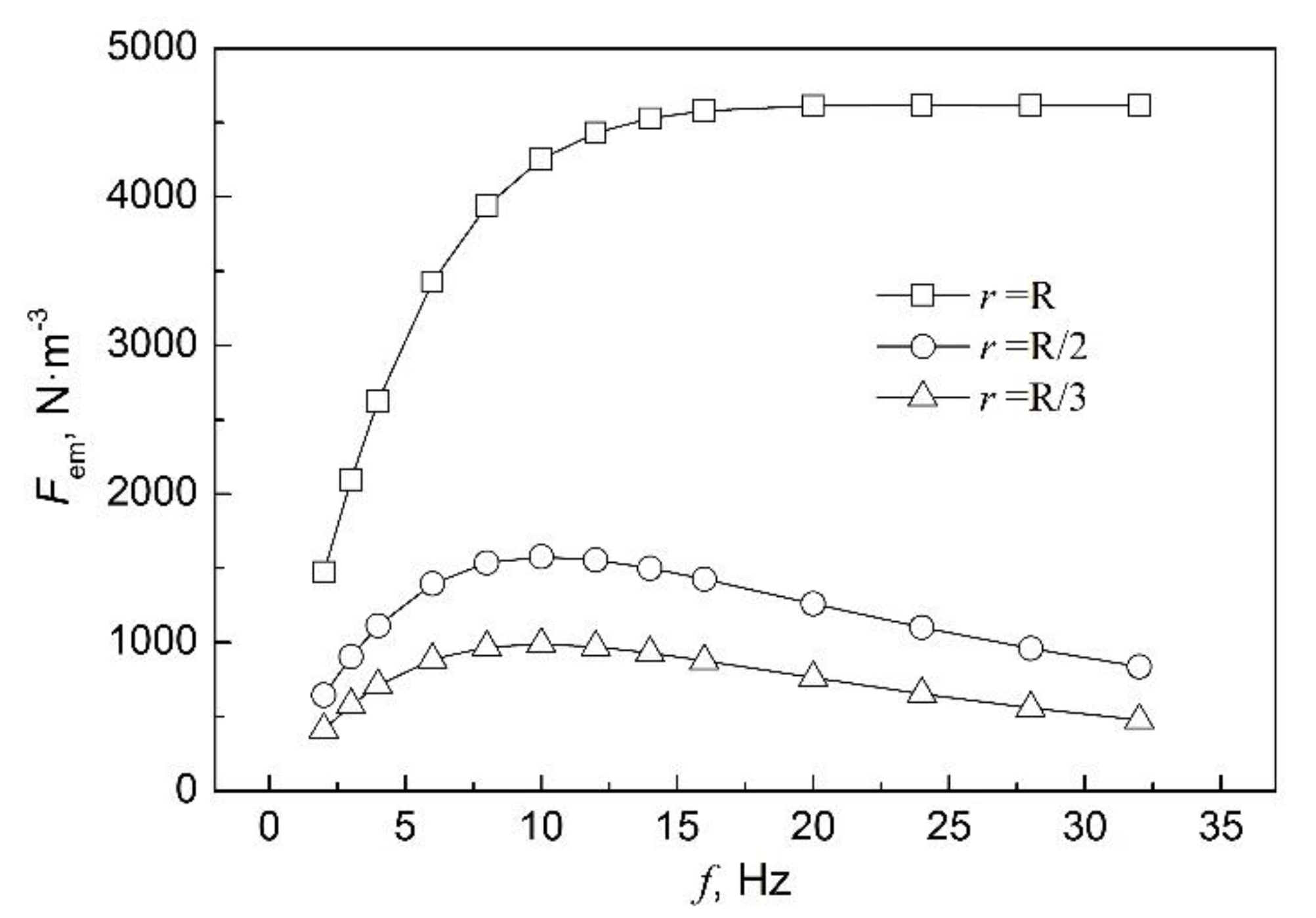
- Since the electromagnetic force generated by F-EMS usually provides stirring action in a region less than R/2 of a round bloom, it is feasible to calculate it approximately using the analytical formula for the infinite-length stirring system.
- With increase in current frequency, the electromagnetic force density at R/2 and R/3 of the strand first increases and then decreases, and it reaches a maximum at 10 Hz. The results of the calculations show that the optimal current frequency of F-EMS is 10 Hz in continuous casting of a Φ600 mm round bloom.
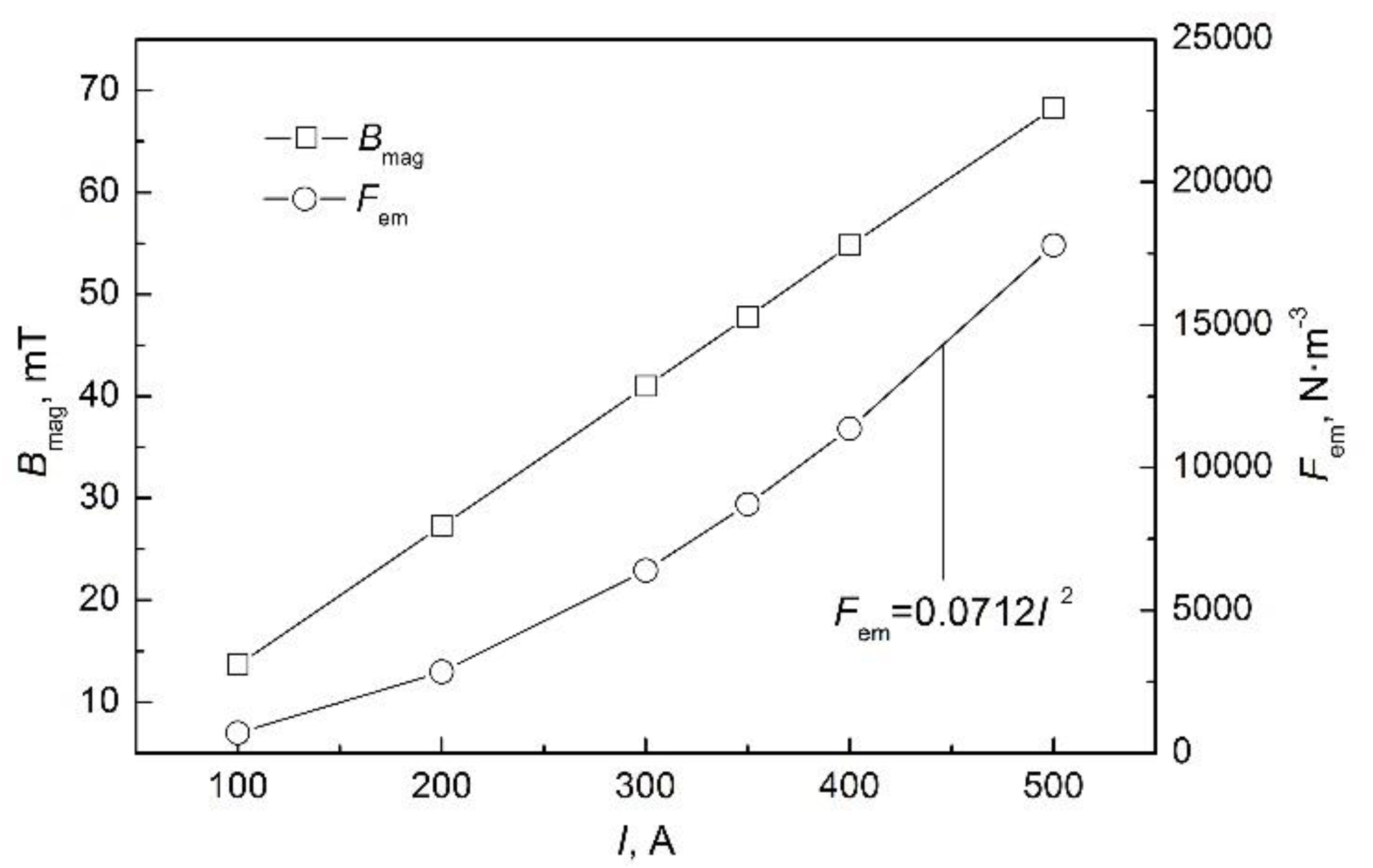
- The magnetic flux density increases linearly with current intensity, while the electromagnetic force density has a quadratic relationship with current intensity.
Author Contributions
Funding
Conflicts of Interest
References
- Barna, M.; Javurek, M.; Reiter, J.; Watzinger, J.; Kaufmann, B.; Kirschen, M. Continuous casting of round bloom strands with mould-electromagnetic stirring numerical simulations with a full coupling method. World Iron Steel 2012, 12, 29–33. [Google Scholar]
- Hanley, P.J.; Kollberg, S.G. Electromagnetic methods for continuous casting. In The Making, Shaping and Treating of Steel, 11th ed.; Cramb, A.W., Ed.; Association for Iron & Steel Technology: Pittsburgh, PA, USA, 2003; pp. 287–297. ISBN 978-0-930767-04-4. [Google Scholar]
- Sun, H.; Li, L.; Cheng, X.; Qiu, W.; Liu, Z.; Zeng, L. Reduction in macrosegregation on 380 mm× 490 mm bloom caster equipped combination M+F-EMS by optimising casting speed. Ironmak. Steelmak. 2015, 42, 439–449. [Google Scholar] [CrossRef]
- Mizukami, H.; Komatsu, M.; Kitagawa, T.; Kawakami, K. Effect of electromagnetic stirring at the final stage of solidification of continuously cast strand. Tetsu-to-Hagane 1984, 70, 194–200. [Google Scholar] [CrossRef]
- Xiao, C.; Zhang, J.; Luo, Y.; Wei, X.; Wu, L.; Wang, S. Control of macrosegregation behavior by applying final electromagnetic stirring for continuously cast high carbon steel billet. J. Iron Steel Res. Int. 2013, 20, 13–20. [Google Scholar] [CrossRef]
- Spitzer, K.H.; Dubke, M.; Schwerdtfeger, K. Rotational electromagnetic stirring in continuous casting of round strands. Metall. Trans. B 1986, 17, 119–131. [Google Scholar] [CrossRef]
- Vynnycky, M. On an anomaly in the modeling of electromagnetic stirring in continuous casting. Metall. Mater. Trans. B 2018, 49, 399–410. [Google Scholar] [CrossRef]
- Trindade, L.B.; Vilela, A.C.F.; Filho, Á.F.F.; Vilhena, M.T.M.B.; Soares, R.B. Numerical model of electromagnetic stirring for continuous casting billets. IEEE Trans. Magn. 2002, 38, 3658–3660. [Google Scholar] [CrossRef]
- Yu, H.Q.; Zhu, M.Y. Influence of electromagnetic stirring on transport phenomena in round billet continuous casting mould and macrostructure of high carbon steel billet. Ironmak. Steelmak. 2012, 39, 574–584. [Google Scholar] [CrossRef]
- Liu, H.; Xu, M.; Qiu, S.; Zhang, H. Numerical simulation of fluid flow in a round bloom mold with in-mold rotary electromagnetic stirring. Metall. Mater. Trans. B 2012, 43, 1657–1675. [Google Scholar] [CrossRef]
- Jiang, D.; Zhu, M. Center segregation with final electromagnetic stirring in billet continuous casting process. Metall. Mater. Trans. B 2017, 48, 444–455. [Google Scholar] [CrossRef]
- Marioni, L. Computational Modelling and Electromagnetic-CFD Coupling Incasting Processes; PSL Research University: Paris, France, 17 November 2017. [Google Scholar]
- Davidson, P.A.; Hunt, J.C.R. Swirling recirculating flow in a liquid-metal column generated by a rotating magnetic field. J. Fluid Mech. 1987, 185, 67–106. [Google Scholar] [CrossRef]
- Ren, B.Z.; Chen, D.F.; Wang, H.D.; Long, M.J.; Han, Z.W. Numerical simulation of fluid flow and solidification in bloom continuous casting mould with electromagnetic stirring. Ironmak. Steelmak. 2015, 42, 401–408. [Google Scholar] [CrossRef]
- Barna, M.; Javurek, M.; Reiter, J.; Lechner, M. Numerical simulations of mould electromagnetic stirring for round bloom strands. Berg Huettenmaenn. Monatsh. 2009, 154, 518–522. [Google Scholar] [CrossRef]
- Mao, B.; Ren, B.; Han, Z.; Cao, J.; Feng, K. Numerical simulation for heat transfer during solidification of round bloom continuous casting. Ind. Heat. 2012, 41, 50–53. [Google Scholar] [CrossRef]
- Guo, G.; Ma, H.; Zhang, J.; Huang, L. The relationship of thermophysical properties to microstructure of high-carbon steel. Phys. Test. Chem. Anal. 2006, 42, 167–170. [Google Scholar]
- Long, M.; Dong, Z.; Sheng, J.; Chen, D.; Chen, C. Universal secondary cooling structure for round blooms continuous casting of steels in various diameters. Steel Res. Int. 2015, 86, 154–162. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ren, B.; Chen, D.; Xia, W.; Wang, H.; Han, Z. Numerical Simulation of Electromagnetic Field in Round Bloom Continuous Casting with Final Electromagnetic Stirring. Metals 2018, 8, 903. https://doi.org/10.3390/met8110903
Ren B, Chen D, Xia W, Wang H, Han Z. Numerical Simulation of Electromagnetic Field in Round Bloom Continuous Casting with Final Electromagnetic Stirring. Metals. 2018; 8(11):903. https://doi.org/10.3390/met8110903
Chicago/Turabian StyleRen, Bingzhi, Dengfu Chen, Wentang Xia, Hongdan Wang, and Zhiwei Han. 2018. "Numerical Simulation of Electromagnetic Field in Round Bloom Continuous Casting with Final Electromagnetic Stirring" Metals 8, no. 11: 903. https://doi.org/10.3390/met8110903
APA StyleRen, B., Chen, D., Xia, W., Wang, H., & Han, Z. (2018). Numerical Simulation of Electromagnetic Field in Round Bloom Continuous Casting with Final Electromagnetic Stirring. Metals, 8(11), 903. https://doi.org/10.3390/met8110903




