Ferrite-to-Austenite and Austenite-to-Martensite Phase Transformations in the Vicinity of a Cementite Particle: A Molecular Dynamics Approach
Abstract
1. Introduction
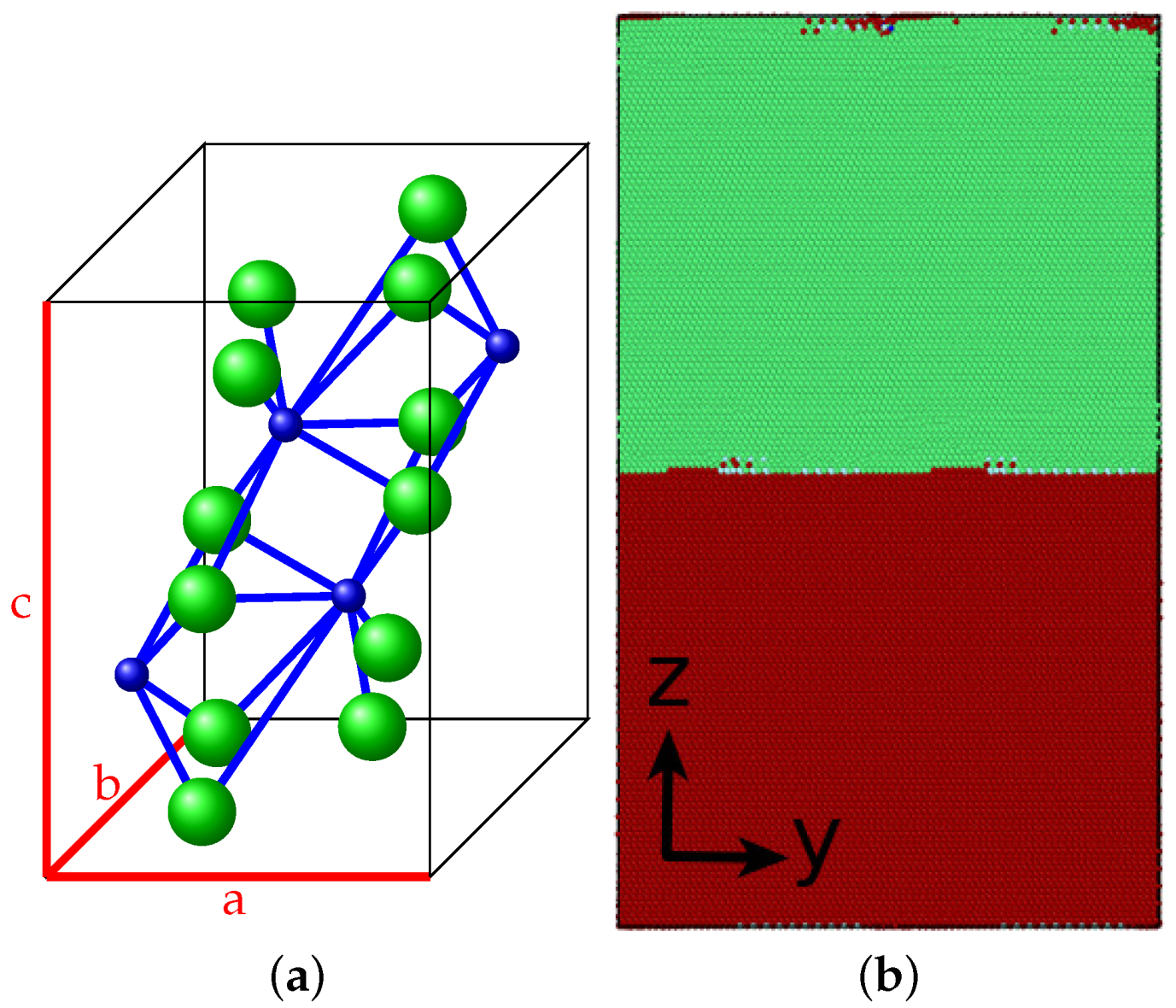
2. Simulation Method
2.1. Interatomic Interaction Potentials
2.2. Cementite–Fe Interface
3. Results
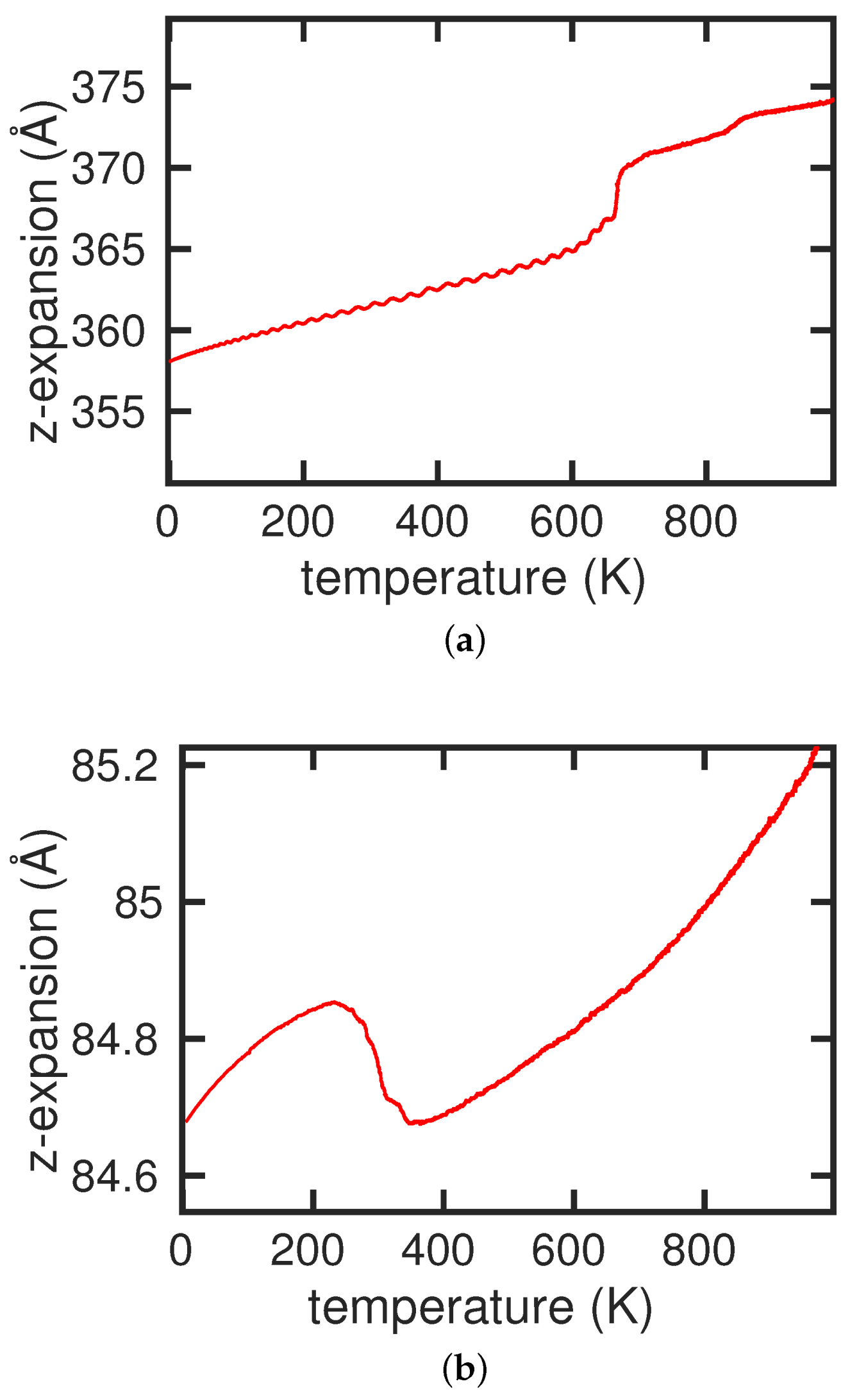
3.1. Pure Cementite Properties
3.2. Cementite–Iron Interface
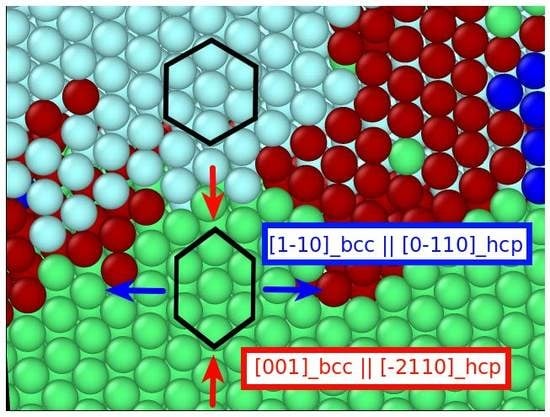
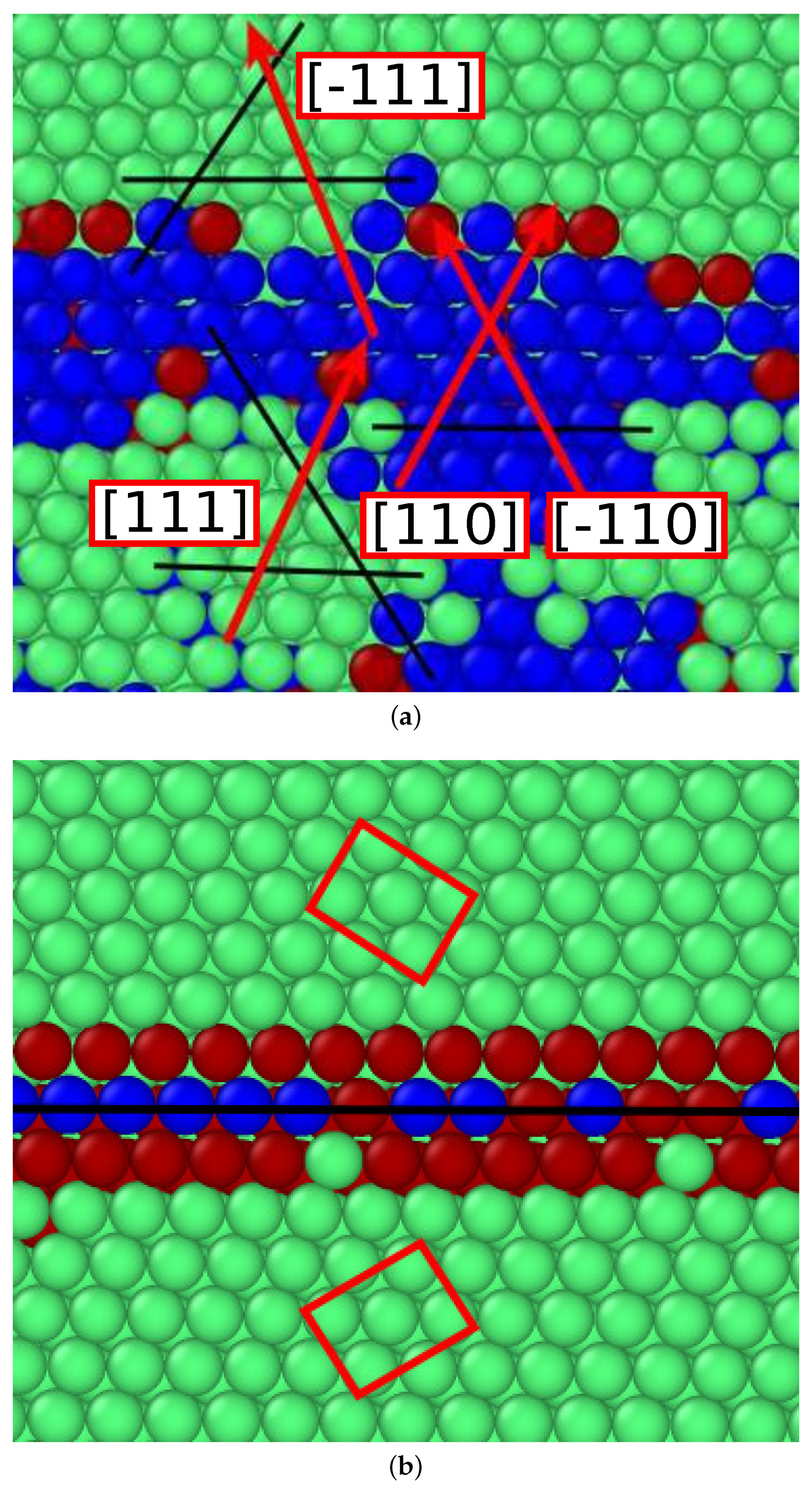
3.2.1. Cementite–Ferrite Interface
3.2.2. Cementite–Austenite Interface
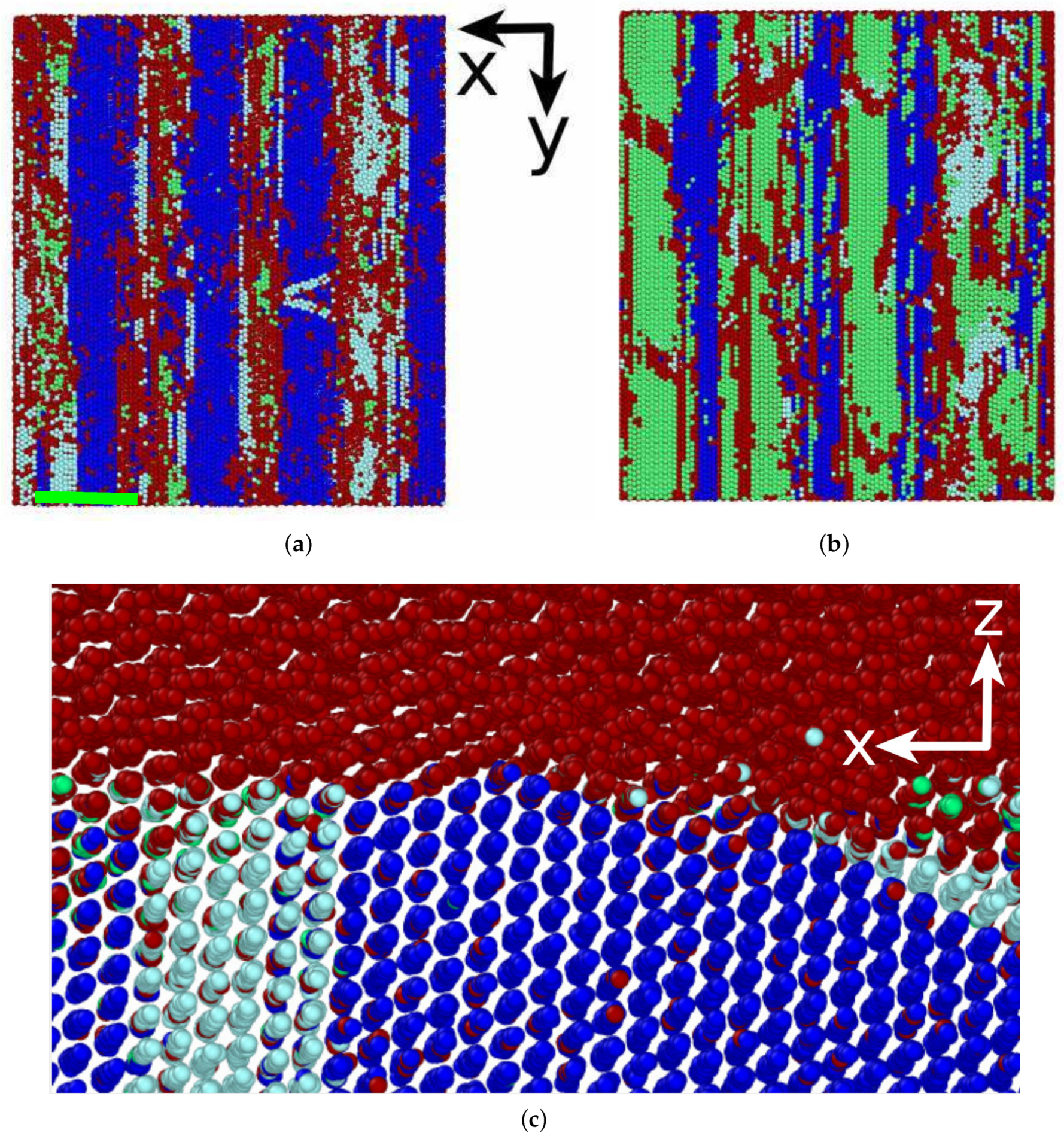
3.3. Phase Transformation
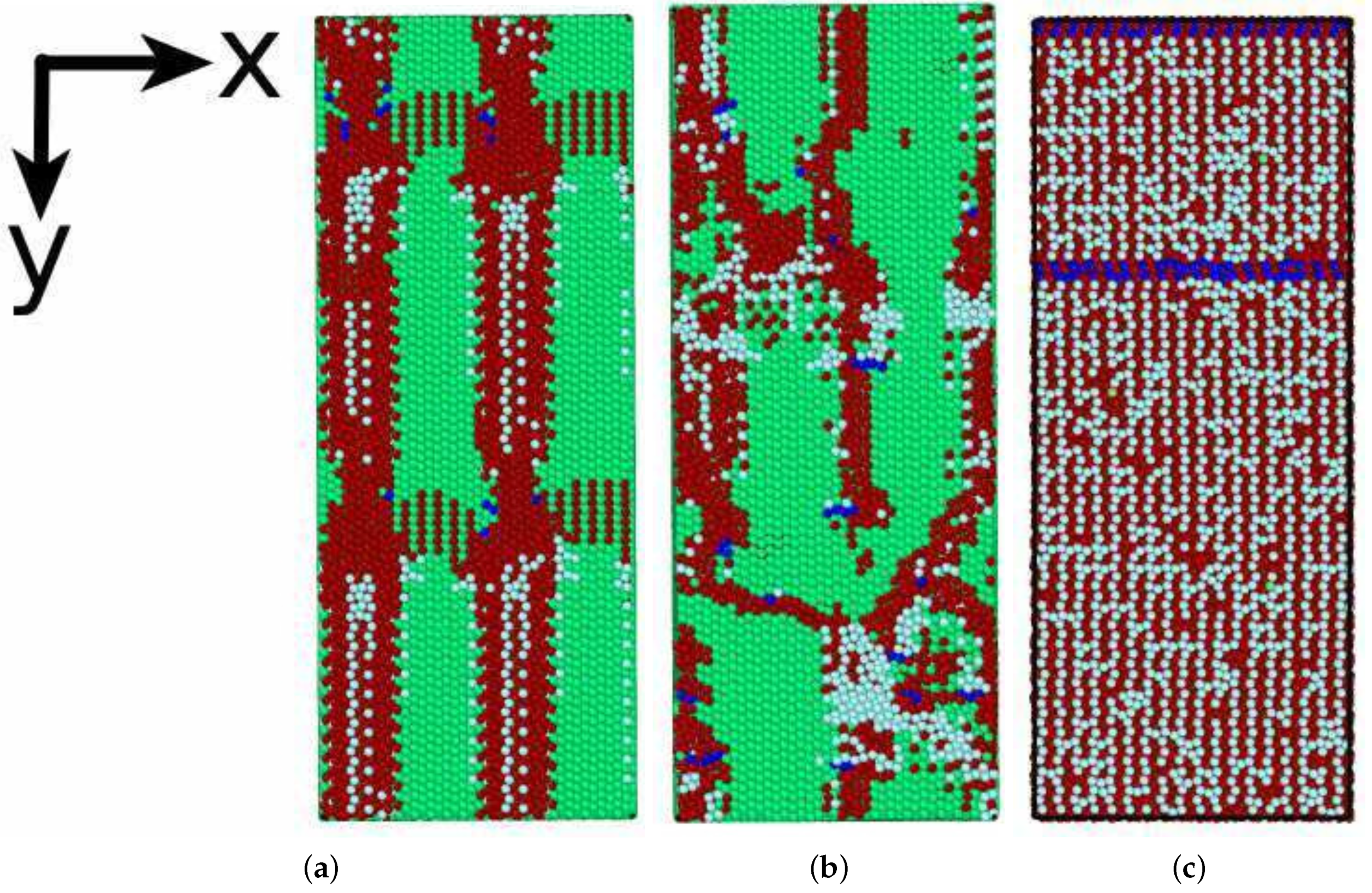
3.3.1. Austenitic Transformation
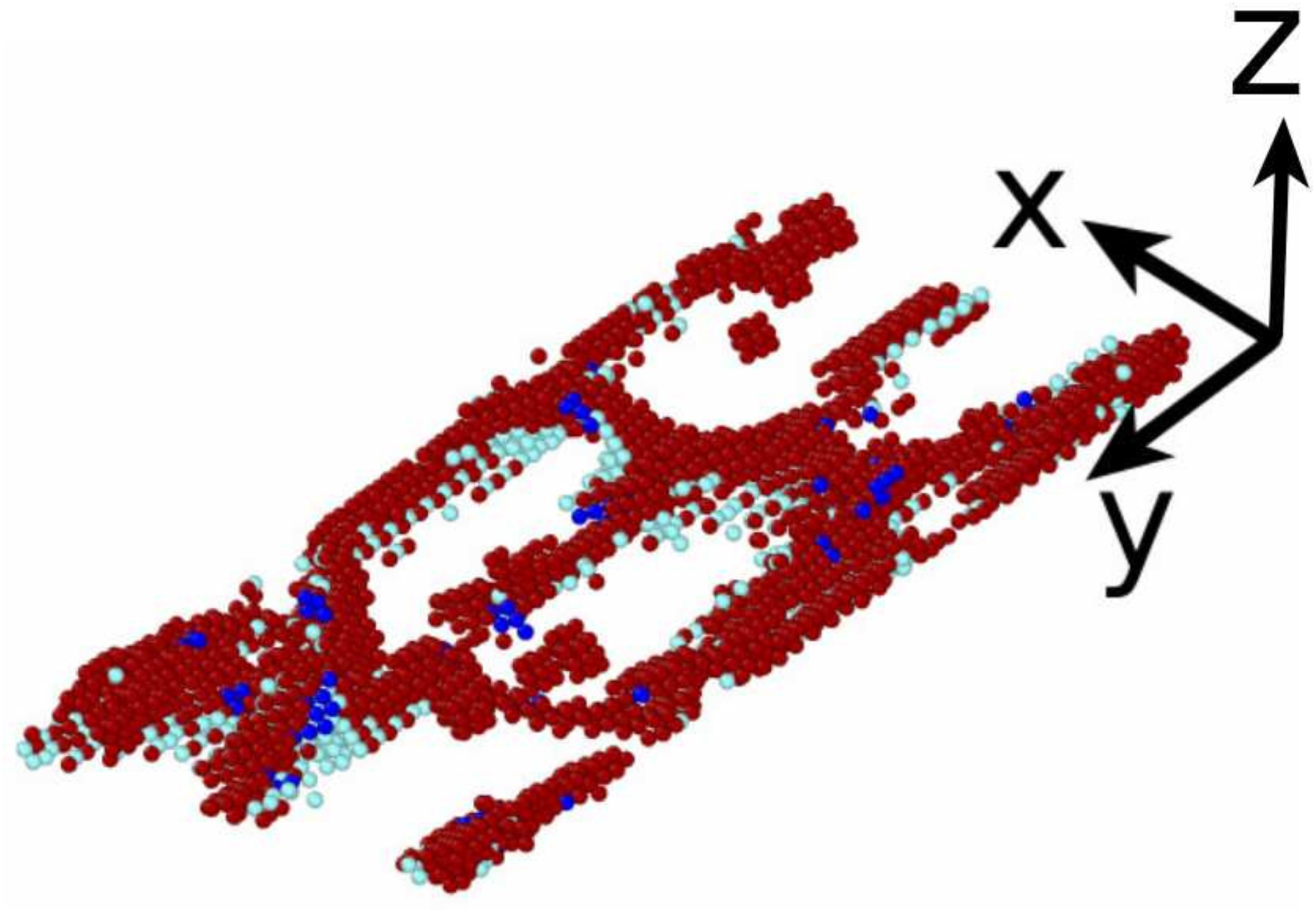
3.3.2. Martensitic Transformation
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Yang, Z.; Johnson, R.A. An eam simulation of the α–γ iron interface. Model. Simul. Mater. Sci. Eng. 1993, 1, 707. [Google Scholar] [CrossRef]
- Bos, C.; Sietsma, J.; Thijsse, B.J. Molecular dynamics simulation of interface dynamics during the fcc-bcc transformation of a martensitic nature. Phys. Rev. B 2006, 73, 104117. [Google Scholar] [CrossRef]
- Sandoval, L.; Urbassek, H.M.; Entel, P. Solid-solid phase transitions and phonon softening in an embedded-atom method model for iron. Phys. Rev. B 2009, 80, 214108. [Google Scholar] [CrossRef]
- Sandoval, L.; Urbassek, H.M. Transformation pathways in the solid-solid phase transitions of iron nanowires. Appl. Phys. Lett. 2009, 95, 191909. [Google Scholar] [CrossRef]
- Sandoval, L.; Urbassek, H.M.; Entel, P. The Bain versus Nishiyama-Wassermann path in the martensitic transformation of Fe. New J. Phys. 2009, 11, 103027. [Google Scholar] [CrossRef]
- Urbassek, H.M.; Sandoval, L. Molecular dynamics modeling of martensitic transformations in steels. Phase Transformations in Steels; Pereloma, E., Edmonds, D.V., Eds.; Woodhead Publishing Limited: Cambridge, UK, 2012; Volume 2, pp. 433–463. [Google Scholar]
- Wang, B.; Urbassek, H.M. Phase transitions in an Fe system containing a bcc/fcc phase boundary: An atomistic study. Phys. Rev. B 2013, 87, 104108. [Google Scholar] [CrossRef]
- Wang, B.; Urbassek, H.M. Role of the Surface in Solid–Solid Phase Transitions: Molecular Dynamics Study of the α–γ Transition in Fe. Metall. Mater. Trans. A 2016, 47, 2471–2480. [Google Scholar] [CrossRef]
- Meiser, J.; Urbassek, H.M. Martensitic transformation of pure iron at a grain boundary: Atomistic evidence for a two-step Kurdjumov–Sachs-Pitsch pathway. AIP Adv. 2016, 6, 085017. [Google Scholar] [CrossRef]
- Karewar, S.; Sietsma, J.; Santofimia, M.J. Effect of pre-existing defects in the parent fcc phase on atomistic mechanisms during the martensitic transformation in pure Fe: A molecular dynamics study. Acta Mater. 2018, 142, 71–81. [Google Scholar] [CrossRef]
- Wang, B.; Urbassek, H.M. Atomistic dynamics of the bcc ↔ fcc phase transition in iron: Competition of homo- and heterogeneous phase growth. Comput. Mater. Sci. 2014, 81, 170–177. [Google Scholar] [CrossRef]
- Meyer, R.; Entel, P. Martensite-austenite transition and phonon dispersion curves of Fe1 − xNix studied by molecular-dynamics simulations. Phys. Rev. B 1998, 57, 5140. [Google Scholar] [CrossRef]
- Wang, B.; Sak-Saracino, E.; Gunkelmann, N.; Urbassek, H.M. Molecular-dynamics study of the α↔γ phase transition in Fe-C. Comput. Mater. Sci. 2014, 82, 399–404. [Google Scholar] [CrossRef]
- Wang, B.; Sak-Saracino, E.; Sandoval, L.; Urbassek, H.M. Martensitic and austenitic phase transformations in Fe-C nanowires. Model. Simul. Mater. Sci. Eng. 2014, 22, 045003. [Google Scholar] [CrossRef]
- Sak-Saracino, E.; Urbassek, H.M. Temperature-induced phase transformation of Fe1 − xNix alloys: Molecular-dynamics approach. Eur. Phys. J. B 2015, 88, 169. [Google Scholar] [CrossRef]
- Toji, Y.; Matsuda, H.; Herbig, M.; Choi, P.P.; Raabe, D. Atomic-scale analysis of carbon partitioning between martensite and austenite by atom probe tomography and correlative transmission electron microscopy. Acta Mater. 2014, 65, 215–228. [Google Scholar] [CrossRef]
- Toji, Y.; Miyamoto, G.; Raabe, D. Carbon partitioning during quenching and partitioning heat treatment accompanied by carbide precipitation. Acta Mater. 2015, 86, 137–147. [Google Scholar] [CrossRef]
- Castro Cerda, F.M.; Goulas, C.; Sabirov, I.; Papaefthymiou, S.; Monsalve, A.; Petrov, R.H. Microstructure, texture and mechanical properties in a low carbon steel after ultrafast heating. Mater. Sci. Eng. A 2016, 672, 108–120. [Google Scholar] [CrossRef]
- Castro Cerda, F.M.; Schulz, B.; Papaefthymiou, S.; Artigas, A.; Monsalve, A.; Petrov, R.H. The Effect of Ultrafast Heating on Cold-Rolled Low Carbon Steel: Formation and Decomposition of Austenite. Metals 2016, 6, 321. [Google Scholar] [CrossRef]
- Bouzouni, M.; Papaefthymiou, S. Preliminary Study of Carbide Dissolution during an Ultra-Fast Heat Treatment in Chromium Molybdenum Steel. Int. J. Metall. Met. Phys. 2017, 2, 005. [Google Scholar]
- Bouzouni, M.; Papaefthymiou, S. Modeling of the Steel Microstructure Gained after the Application of an Ultra-Fast Heat Treatment. J. Nanosci. Adv. Tech. 2017, 2, 15–19. [Google Scholar] [CrossRef]
- Papaefthymiou, S.; Goulas, C.; Cerda, F.M.C.; Geerlofs, N.; Petrov, R. The Effect of Heating Rate on the Microstructure of a Soft-Annealed Medium Carbon Steel. Steel Res. Int. 2017, 88, 1700158. [Google Scholar] [CrossRef]
- Cerda, F.M.C.; Vercruysse, F.; Goulas, C.; Schulz, B.; Petrov, R.H. ‘Flash’ Annealing in a Cold-Rolled Low Carbon Steel Alloyed With Cr, Mn, Mo, and Nb: Part I—Continuous Phase Transformations. Steel Res. Int. 2018. [Google Scholar] [CrossRef]
- Ghaemifar, S.; Mirzadeh, H. Refinement of Banded Structure via Thermal Cycling and Its Effects on Mechanical Properties of Dual Phase Steel. Steel Res. Int. 2018, 89, 1700531. [Google Scholar] [CrossRef]
- Papaefthymiou, S.; Bouzouni, M.; Petrov, R.H. Study of Carbide Dissolution and Austenite Formation during Ultra—Fast Heating in Medium Carbon Chromium Molybdenum Steel, Metals. Metals 2018, 8, 646. [Google Scholar] [CrossRef]
- Howe, J.M.; Spanos, G. Atomic structure of the austenite-cementite interface of proeutectoid cementite plates. Philos. Mag. A 1999, 79, 9. [Google Scholar] [CrossRef]
- Shtansky, D.V.; Nakai, K.; Ohmori, Y. Mechanism and crystallography of ferrite precipitation from cementite in an Fe-Cr-C alloy during austenitization. Philos. Mag. A 1999, 79, 1655. [Google Scholar]
- Gerstein, G.; Nürnberger, F.; Dudzinski, W.; Grygier, D.; Schaper, M.; Milenin, A. Structural evolution of thin lamellar cementite during cold drawing of eutectoid steels. Procedia Eng. 2014, 81, 694–699. [Google Scholar] [CrossRef]
- Zhou, D.S.; Shiflet, G.J. Ferrite: cementite crystallography in pearlite. Metall. Mater. Trans. A 1992, 23, 1259–1269. [Google Scholar] [CrossRef]
- Bagaryatsky, Y.A. Possible mechanism of martensite decomposition. Dokl. Akad. Nauk. SSSR 1950, 73, 1161–1164. [Google Scholar]
- Petch, N.J. The orientation relationships between cementite and α-iron. Acta Cryst. 1953, 6, 96. [Google Scholar] [CrossRef]
- Pitsch, W. Der Orientierungszusammenhang zwischen Zementit und Ferrit im Perlit. Acta Metall. 1962, 10, 79–80. [Google Scholar] [CrossRef]
- Ghosh, G. A first-principles study of cementite (Fe3C) and its alloyed counterparts: Elastic constants, elastic anisotropies, and isotropic elastic moduli. AIP Adv. 2015, 5, 087102. [Google Scholar] [CrossRef]
- Ledbetter, H. Polycrystalline elastic constants of in situ cementite (Fe3C). Mat. Sci. Eng. A 2010, 527, 2657. [Google Scholar] [CrossRef]
- Liyanage, L.S.I.; Kim, S.G.; Houze, J.; Kim, S.; Tschopp, M.A.; Baskes, M.I.; Horstemeyer, M.F. Structural, elastic, and thermal properties of cementite (Fe3C) calculated using a modified embedded atom method. Phys. Rev. B 2014, 89, 094102. [Google Scholar] [CrossRef]
- Ghaffarian, H.; Taheri, A.K.; Ryu, S.; Kang, K. Nanoindentation study of cementite size and temperature effects in nanocomposite pearlite: A molecular dynamics simulation. Curr. Appl. Phys. 2016, 16, 1015–1025. [Google Scholar] [CrossRef]
- Nematollahi, G.A.; von Pezold, J.; Neugebauer, J.; Raabe, D. Thermodynamics of carbon solubility in ferrite and vacancy formation in cementite in strained pearlite. Acta Mater. 2013, 61, 1773–1784. [Google Scholar] [CrossRef]
- Kim, J.; Kang, K.; Ryu, S. Characterization of the misfit dislocations at the ferrite/cementite interface in pearlitic steel: An atomistic simulation study. Int. J. Plast. 2016, 83, 302–312. [Google Scholar] [CrossRef]
- Levchenko, E.V.; Evteev, A.V.; Belova, I.V.; Murch, G.E. Molecular dynamics simulation and theoretical analysis of carbon diffusion in cementite. Acta Mater. 2009, 57, 846. [Google Scholar] [CrossRef]
- Evteev, A.; Levchenko, E.; Belova, I.; Murch, G. Atomic Mechanism of Carbon Diffusion in Cementite. Defect Diffus. Forum 2008, 277, 101. [Google Scholar] [CrossRef]
- Nose, S. A unified formulation of the constant temperature molecular dynamics methods. J. Chem. Phys. 1984, 81, 511. [Google Scholar] [CrossRef]
- Hoover, W.G. Canonical dynamics: equilibrium phase-space distribution. Phys. Rev. A 1985, 31, 1695. [Google Scholar] [CrossRef]
- Plimpton, S. Fast Parallel Algorithms for Short-Range Molecular Dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Stukowski, A. Visualization and analysis of atomistic simulation data with OVITO—The Open Visualization Tool. Model. Simul. Mater. Sci. Eng. 2010, 18, 015012. [Google Scholar] [CrossRef]
- Faken, D.; Jonsson, H. Systematic analysis of local atomic structure combined with 3D computer graphics. Comput. Mater. Sci. 1994, 2, 279–286. [Google Scholar] [CrossRef]
- Honeycutt, J.D.; Andersen, H.C. Molecular dynamics study of melting and freezing of small Lennard-Jones clusters. J. Phys. Chem. 1987, 91, 4950–4963. [Google Scholar] [CrossRef]
- Johnson, R.A.; Dienes, G.J.; Damask, A.C. Calculations of the energy and migration characteristics of carbon and nitrogen in alpha-iron and vanadium. Acta Metall. 1964, 12, 1215. [Google Scholar] [CrossRef]
- Sak-Saracino, E.; Urbassek, H.M. Free energies of austenite and martensite Fe-C alloys: an atomistic study. Philos. Mag. 2014, 94, 933–945. [Google Scholar] [CrossRef]
- Sak-Saracino, E.; Urbassek, H.M. The α↔γ transformation of an Fe1 − xCrx alloy: A molecular-dynamics approach. Int. J. Mod. Phys. C 2016, 27, 1650124. [Google Scholar] [CrossRef]
- Gunkelmann, N.; Ledbetter, H.; Urbassek, H.M. Experimental and atomistic study of the elastic properties of α′ Fe-C martensite. Acta Mater. 2012, 60, 4901–4907. [Google Scholar] [CrossRef]
- Janßen, J.; Gunkelmann, N.; Urbassek, H.M. Influence of C concentration on elastic moduli of α′-Fe1 − xCx alloys. Philos. Mag. 2016, 96, 1448–1462. [Google Scholar] [CrossRef]
- Eckstein, W. Computer Simulation of Ion-Solid Interactions; Springer: Berlin, Germany, 1991. [Google Scholar]
- Andersen, H.H.; Sigmund, P. Defect distributions in channeling experiments. Nucl. Instr. Meth. 1965, 38, 238. [Google Scholar] [CrossRef]
- Hestenes, M.R.; Stiefel, E. Methods of Conjugate Gradients for Solving Linear Systems. J. Res. Natl. Bur. Stand. 1952, 49, 409. [Google Scholar] [CrossRef]
- Wood, I.G.; Vocadlo, L.; Knight, K.S.; Dobson, D.P.; Marshall, W.G.; Price, G.D.; Brodholt, J. Thermal expansion and crystal structure of cementite, Fe3C, between 4 and 600 K determined by time-of-flight neutron powder diffraction. J. Appl. Crystallogr. 2004, 37, 82–90. [Google Scholar] [CrossRef]
- Henriksson, K.O.E.; Nordlund, K. Simulations of cementite: An analytical potential for the Fe-C system. Phys. Rev. B 2009, 79, 144107. [Google Scholar] [CrossRef]
- Mookherjee, M. Elasticity and anisotropy of Fe3C at high pressures. Am. Mineral. 2011, 96, 1530–1536. [Google Scholar] [CrossRef]
- Meyer, R. Computersimulationen Martensitischer Phasenübergänge in Eisen-Nickel- und Nickel-Aluminium- Legierungen. Ph.D. Thesis, University Duisburg, Duisburg, Germany, 1995. [Google Scholar]
- Freitas, R.; Asta, M.; de Koning, M. Nonequilibrium free-energy calculation of solids using LAMMPS. Comput. Mater. Sci. 2016, 112, 333. [Google Scholar] [CrossRef]
- Wang, B.; Urbassek, H.M. Computer simulation of strain-induced phase transformations in thin Fe films. Model. Simul. Mater. Sci. Eng. 2013, 21, 085007. [Google Scholar] [CrossRef]
- Sak-Saracino, E.; Urbassek, H.M. Effect of uni- and biaxial strain on phase transformations in Fe thin films. Int. J. Comp. Mat. Sci. Eng. 2016, 5, 1650001. [Google Scholar] [CrossRef]
- Mao, H.K.; Bassett, W.A.; Takahashi, T. Effect of pressure on crystal structure and lattice parameters of iron up to 300 kbar. J. Appl. Phys. 1967, 38, 272. [Google Scholar] [CrossRef]
- Wang, F.M.; Ingalls, R. Iron bcc-hcp transition: Local structure from x-ray-absorption fine structure. Phys. Rev. B 1998, 57, 5647. [Google Scholar] [CrossRef]
- Nishiyama, Z. Mechanism of transformation from face-centred to body-centred cubic lattice. Sci. Rep. Tohoku Imp. Univ. 1934, 23, 637. [Google Scholar]
- Wassermann, G. Einfluß der α–γ-Umwandlung eines irreversiblen Nickelstahls auf Kristallorientierung und Zugfestigkeit. Arch. Eisenhüttenwes 1933, 6, 347. [Google Scholar] [CrossRef]
- Kurdjumov, G.V.; Sachs, G. Über den Mechanismus der Stahlhärtung. Z. Phys. 1930, 64, 325–343. [Google Scholar] [CrossRef]


© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Meiser, J.; Urbassek, H.M. Ferrite-to-Austenite and Austenite-to-Martensite Phase Transformations in the Vicinity of a Cementite Particle: A Molecular Dynamics Approach. Metals 2018, 8, 837. https://doi.org/10.3390/met8100837
Meiser J, Urbassek HM. Ferrite-to-Austenite and Austenite-to-Martensite Phase Transformations in the Vicinity of a Cementite Particle: A Molecular Dynamics Approach. Metals. 2018; 8(10):837. https://doi.org/10.3390/met8100837
Chicago/Turabian StyleMeiser, Jerome, and Herbert M. Urbassek. 2018. "Ferrite-to-Austenite and Austenite-to-Martensite Phase Transformations in the Vicinity of a Cementite Particle: A Molecular Dynamics Approach" Metals 8, no. 10: 837. https://doi.org/10.3390/met8100837
APA StyleMeiser, J., & Urbassek, H. M. (2018). Ferrite-to-Austenite and Austenite-to-Martensite Phase Transformations in the Vicinity of a Cementite Particle: A Molecular Dynamics Approach. Metals, 8(10), 837. https://doi.org/10.3390/met8100837