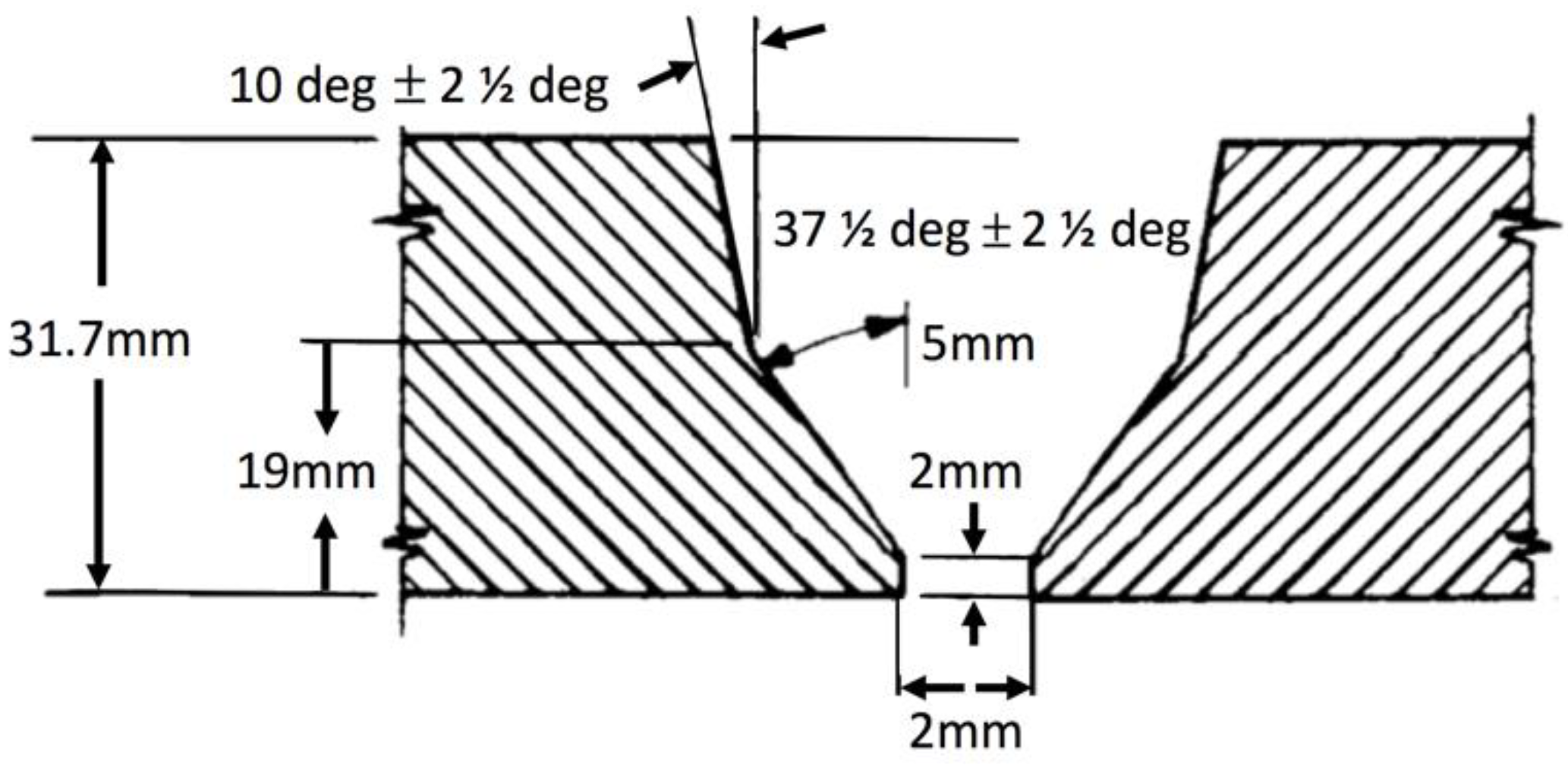
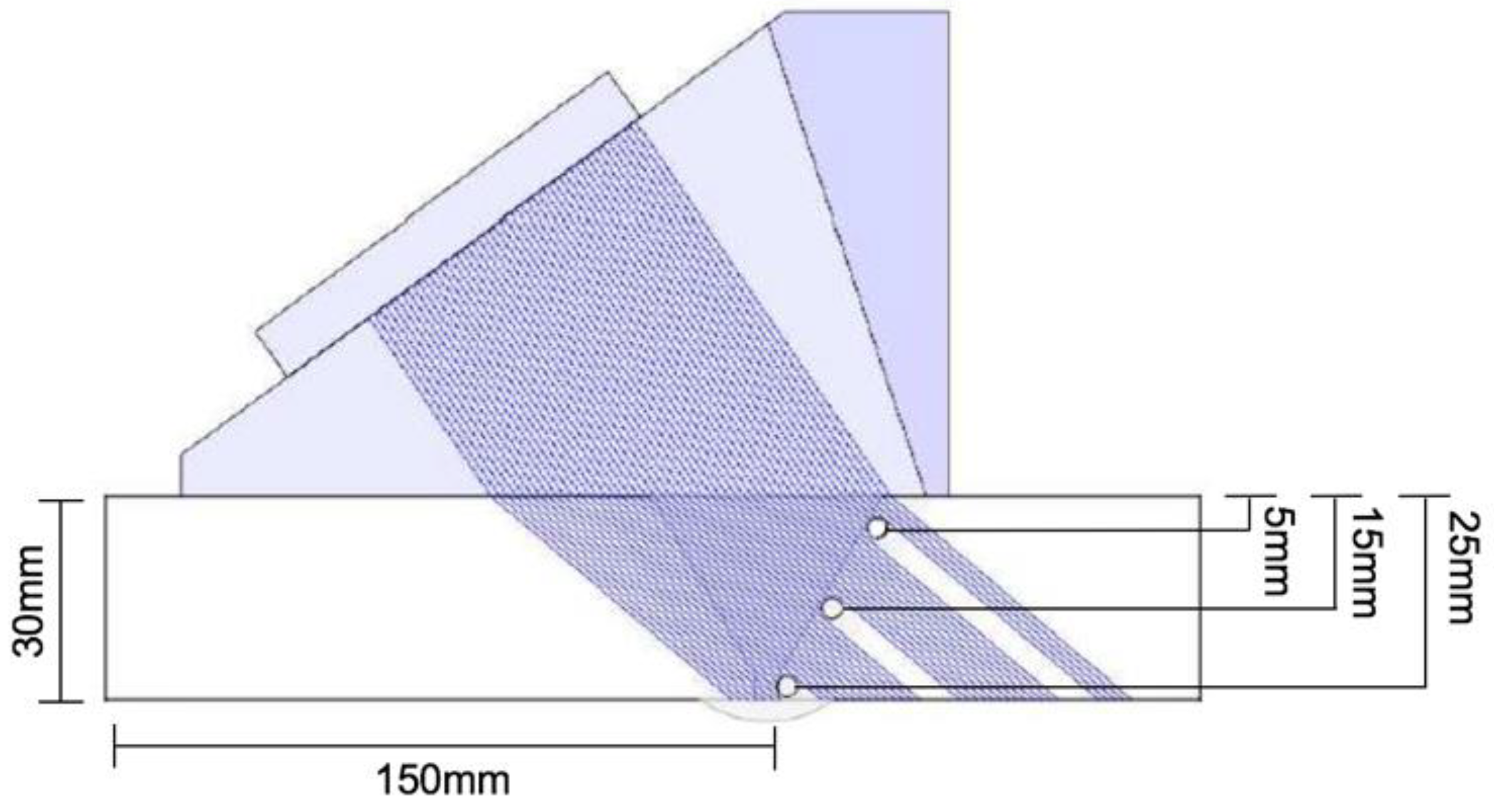
Figure 1.
Design of the 9% Ni steel circumferential pipe butt joint.
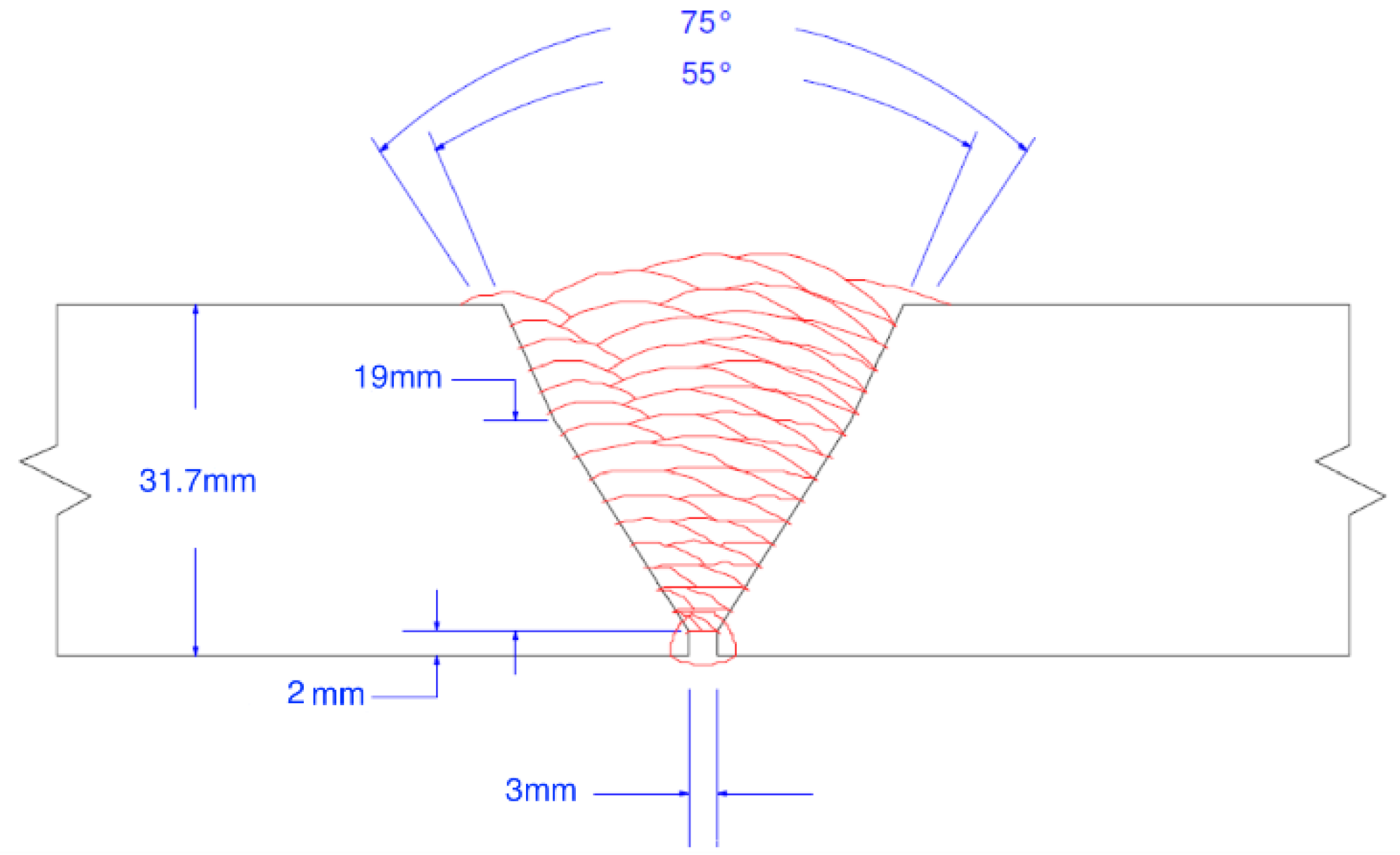
Figure 2.
Illustration of the butt joint weld passes distribution.
Figure 3.
Macrograph of the 9% Ni steel pipe welded butt joint showing the weld passes highlighted by CAD drawing overlay and the directions of dendrite growth ((a), arrows) and SEM micrograph of the HAZ near the fusion line (b).
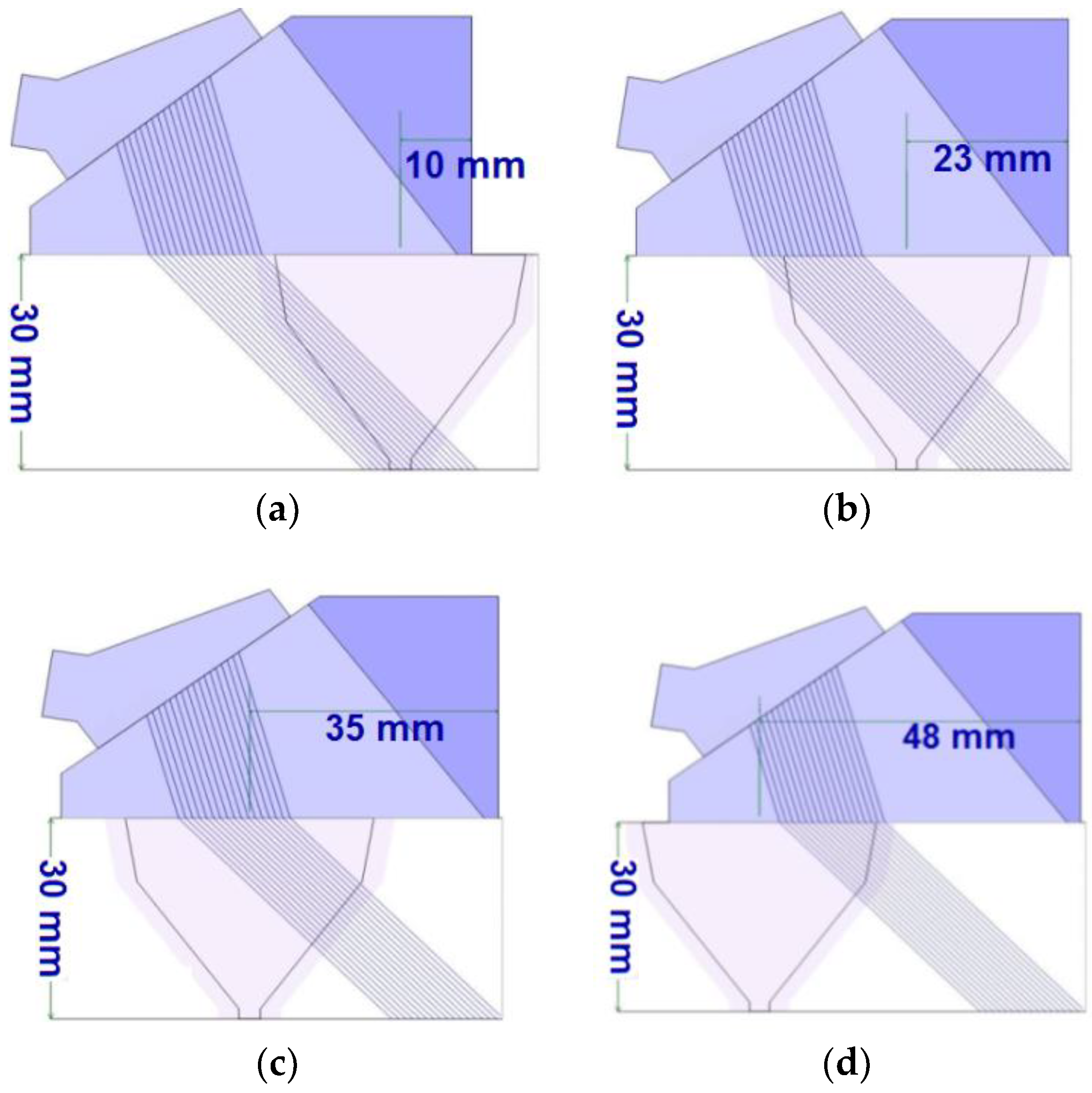
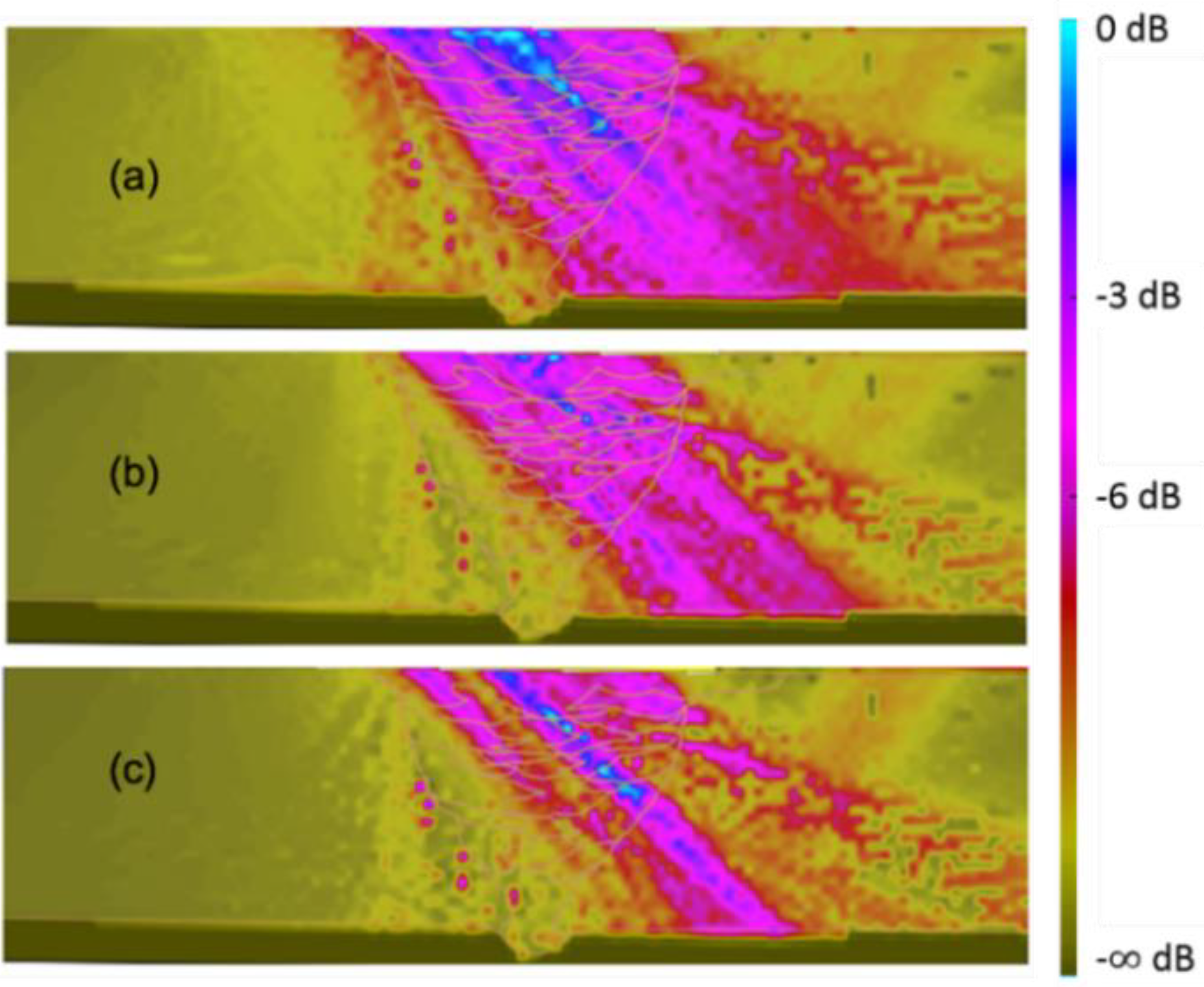
Figure 4.
Simulation of inspection with scanning angle of 45° and 16 active elements. Indexes: (a) 10 mm, (b) 23 mm, (c) 35 mm and (d) 48 mm.
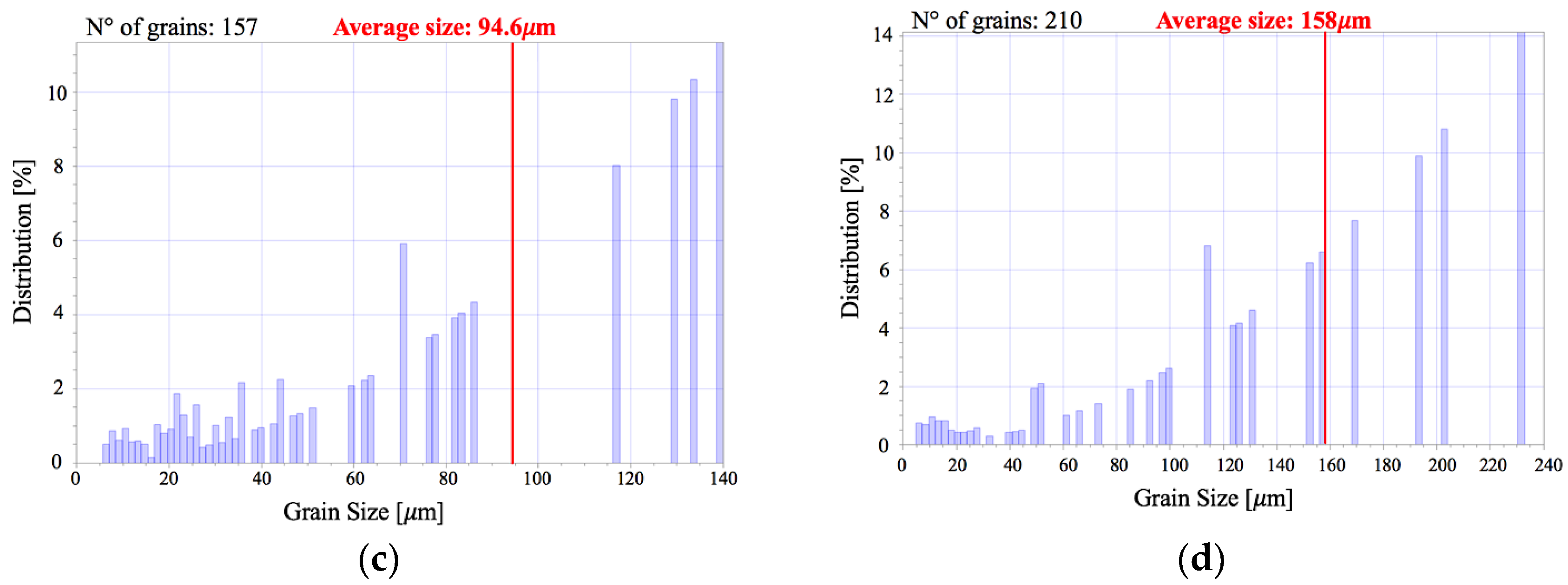
Figure 5.
EBSD images of the (a) fusion line and the (b) weld metal. Below the EBSD images, are the distributions of grain size in the respective regions (c,d).
Figure 6.
Longitudinal wave inspection. Scanning angle of 45°, index 23 mm. Number of elements: (a) 16, (b) 24 and (c) 32.
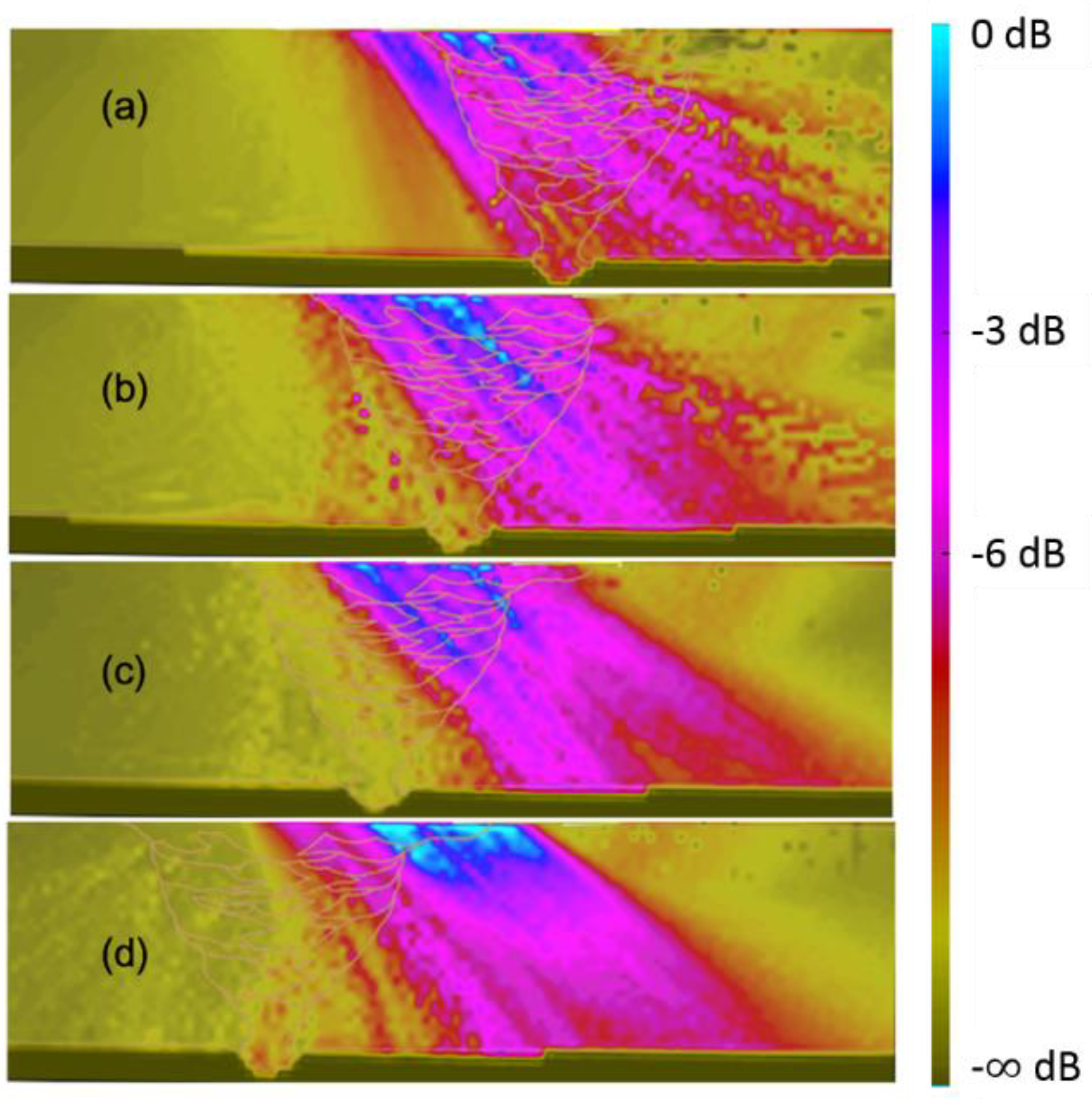
Figure 7.
Longitudinal wave inspection. Scanning angle of 45° with 16 elements. Indexes: (a) 10 mm, (b) 23 mm, (c) 35 mm and (d) 48 mm.
Figure 8.
Longitudinal wave inspection. Scanning angle of 48°, index 22 mm. Number of elements: (a) 16, (b) 24 and (c) 32.
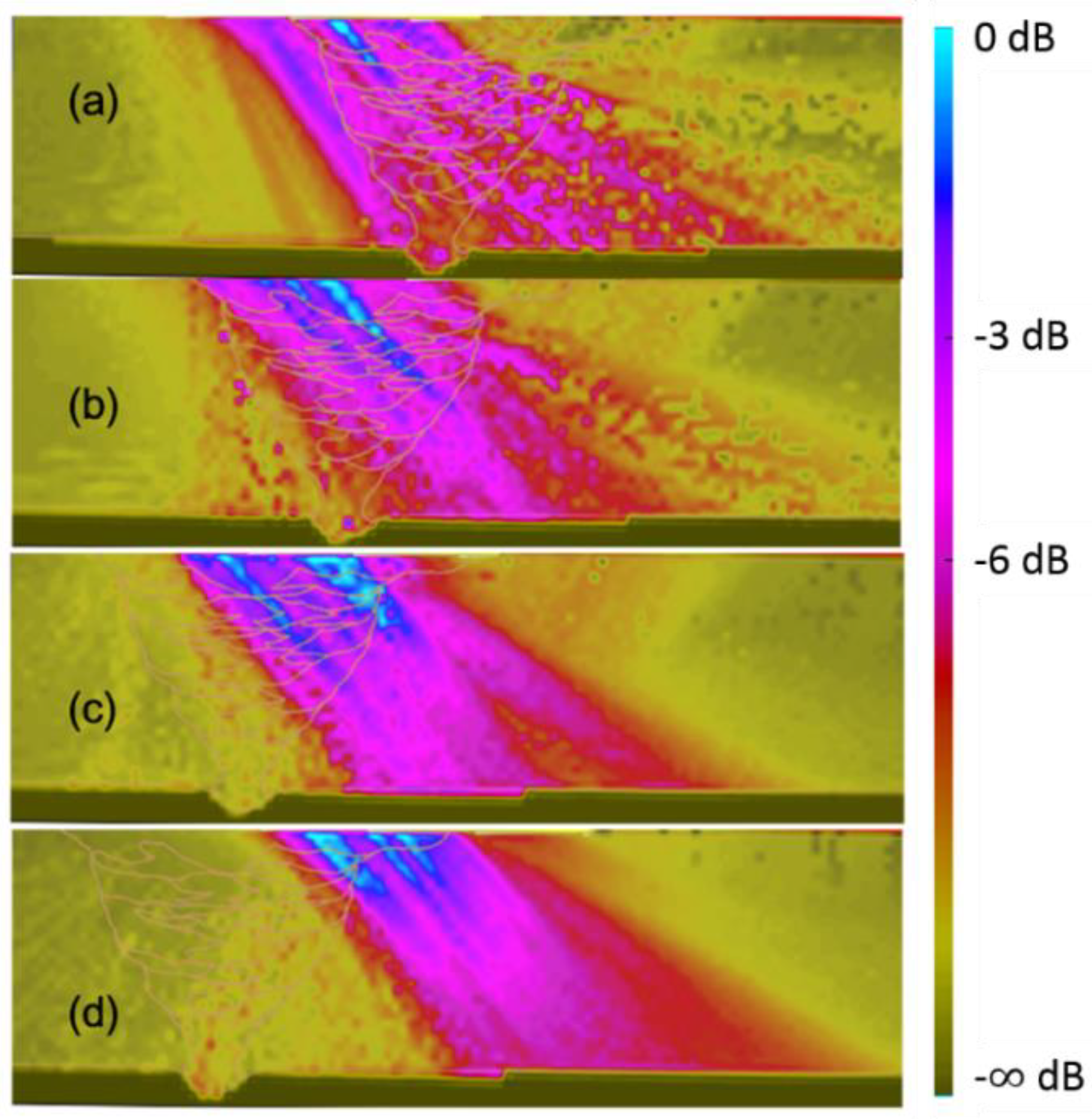
Figure 9.
Longitudinal wave inspection. Scanning angle of 48° with 16 elements. Indexes: (a) 8 mm, (b) 22 mm, (c) 35 mm and (d) 49 mm.
Figure 10.
Longitudinal wave inspection. Scanning angle of 52°, index 18 mm. Number of elements: (a) 16, (b) 24 and (c) 32.
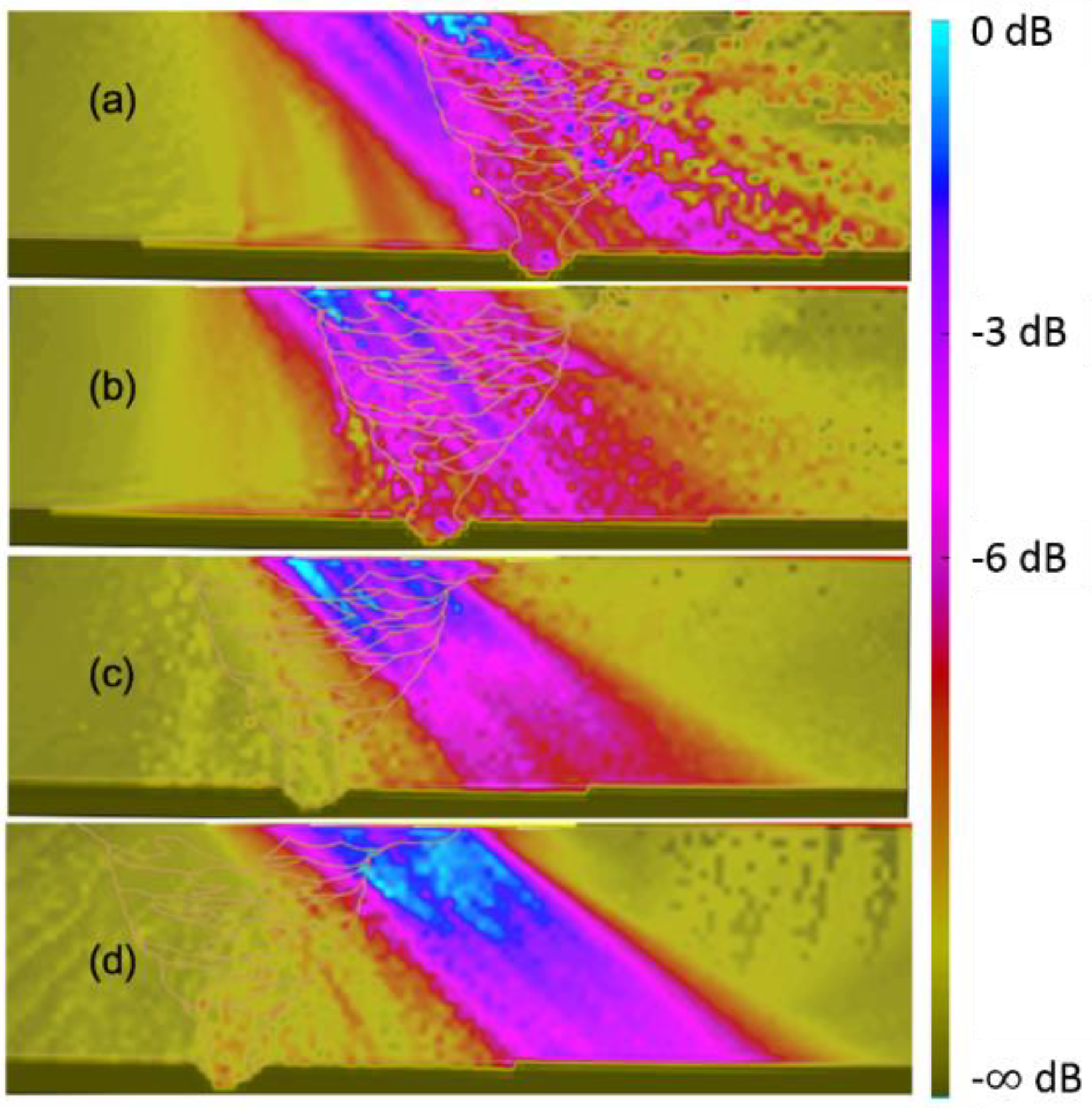
Figure 11.
Longitudinal wave inspection. Scanning angle of 52°, with 16 elements. Indexes: (a) 3 mm, (b) 18 mm, (c) 32 mm and (d) 46 mm.
Figure 12.
Simulation of sensitivity calibration with longitudinal waves in the calibration block, withdrawn from the 9% Ni quenched and tempered steel pipe joint welded with GTAW and SMAW processes using Ni-based superalloy 625 as the filler metal.
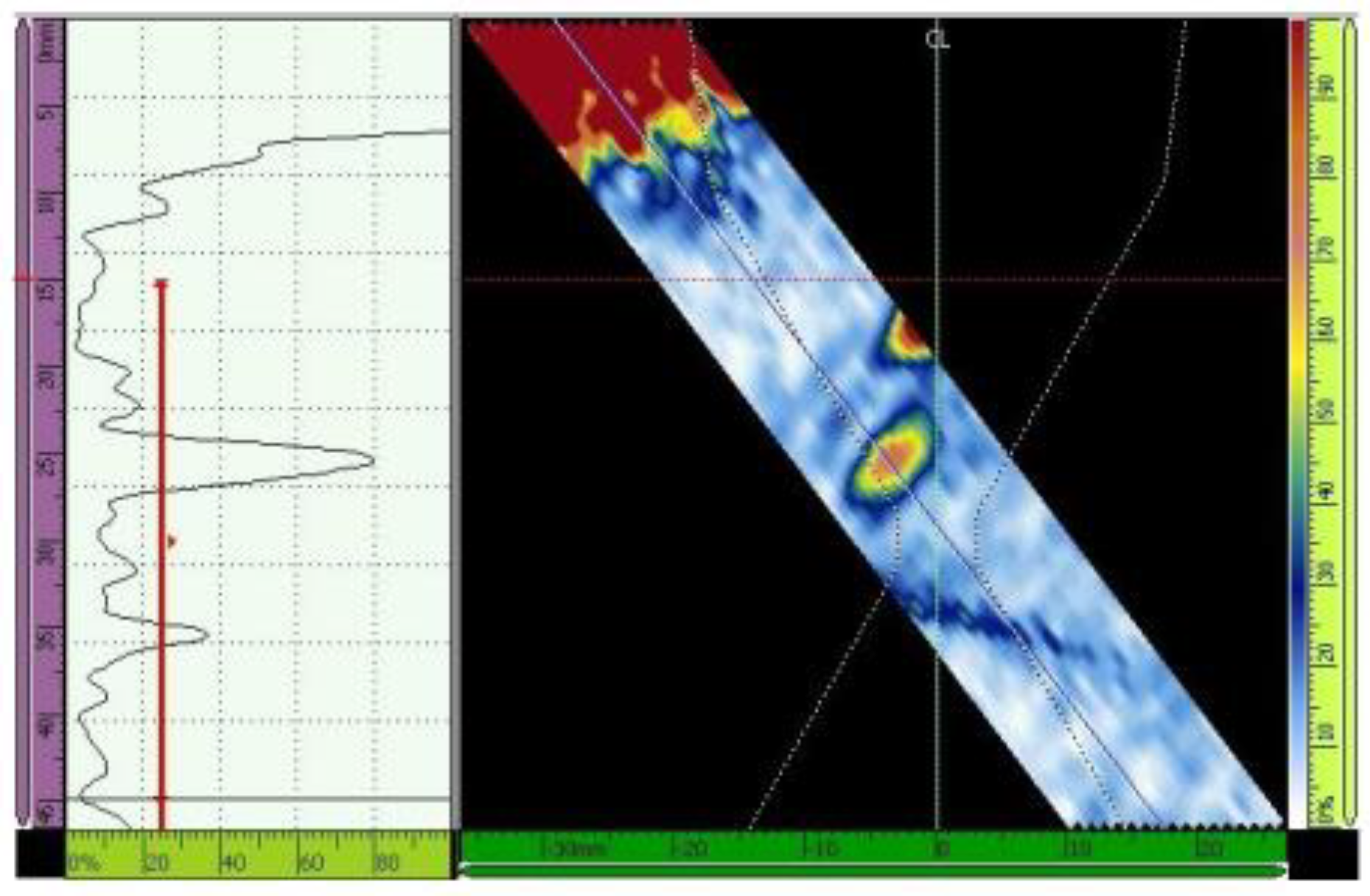
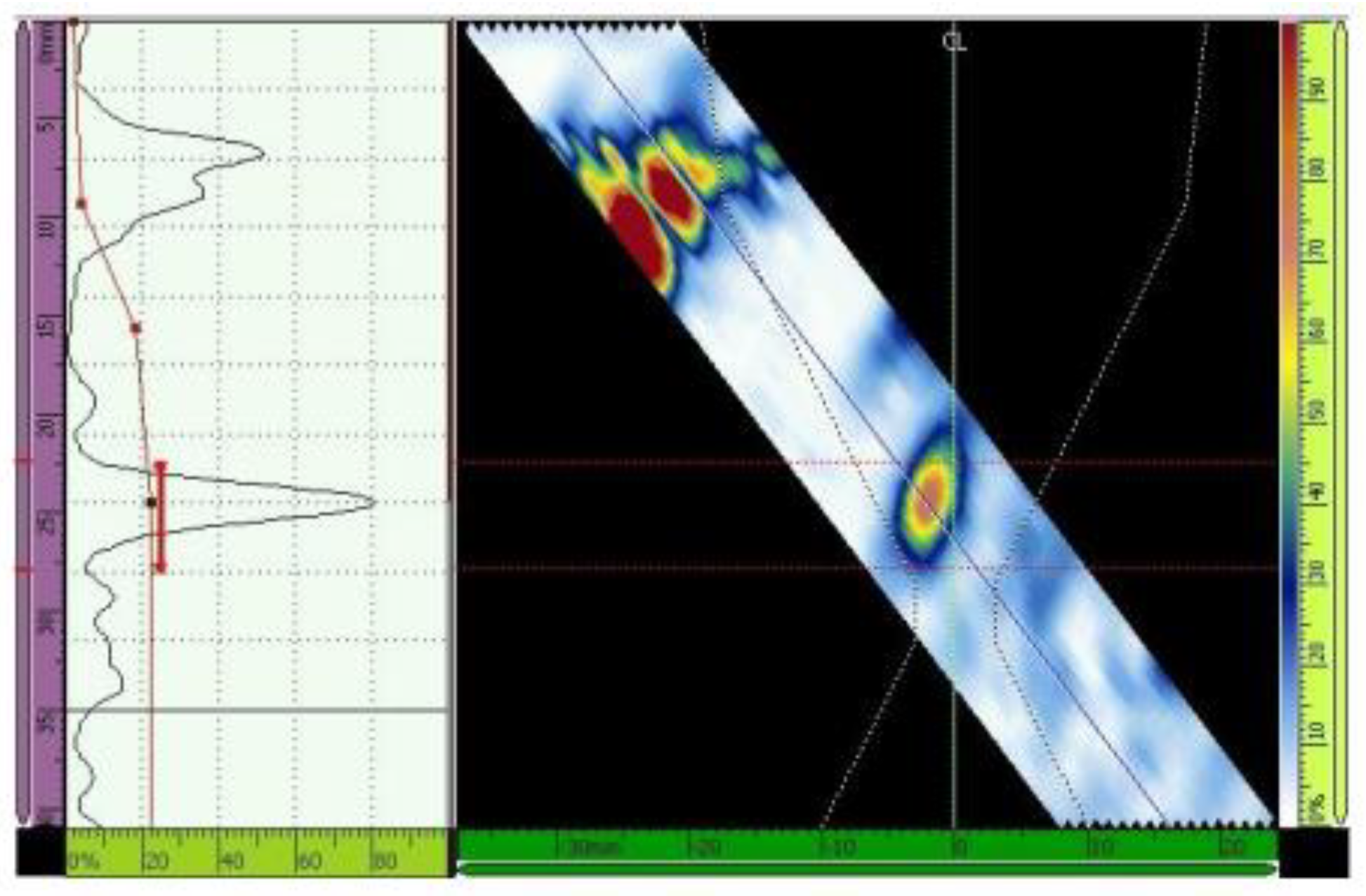
Figure 13.
Echo (maximized to 80% of the screen height) from the third hole. Scanning angle of 45° and 16 active elements. Primary gain = 50 dB.
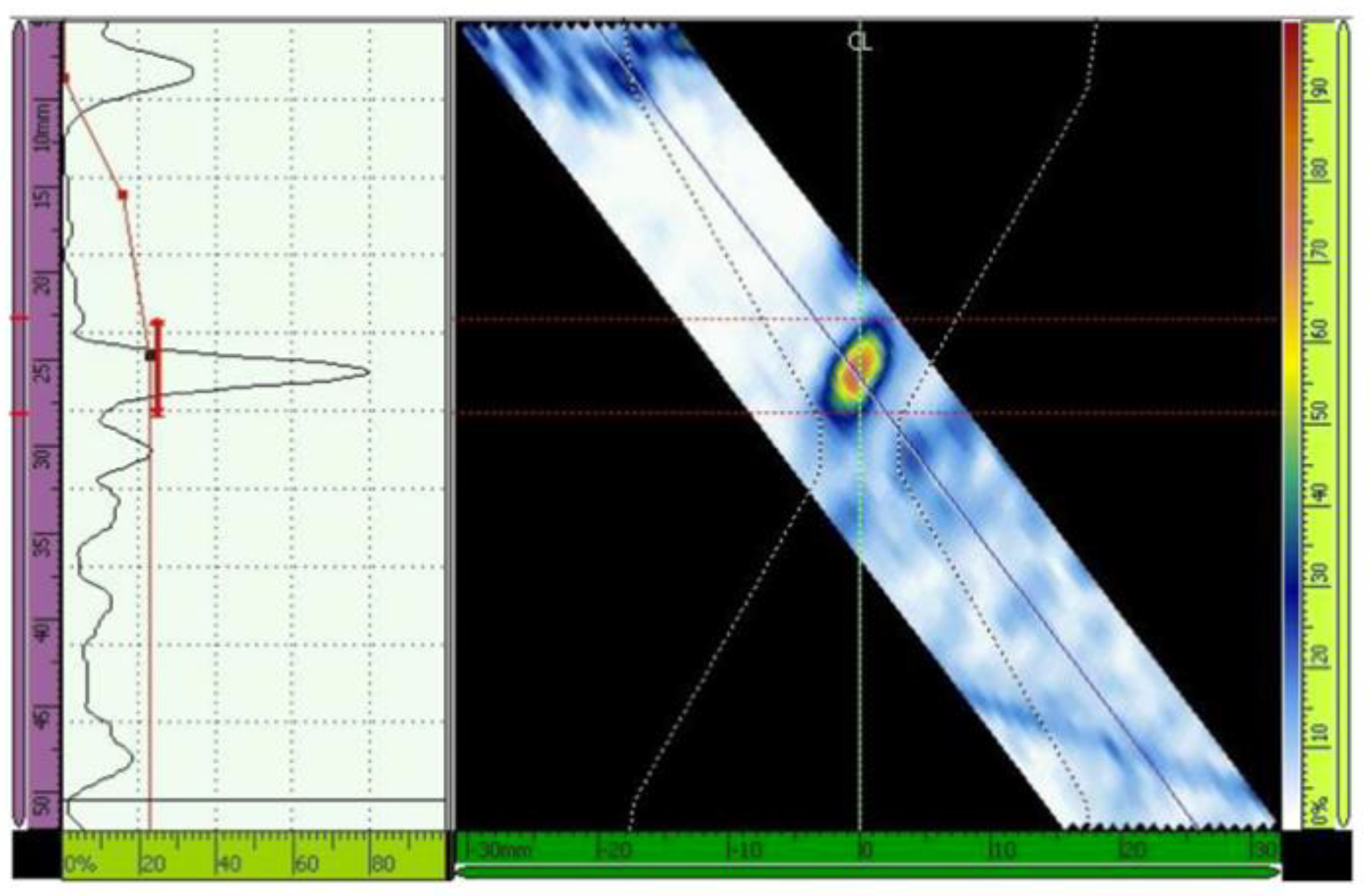
Figure 14.
Time correct gain adjustment. Scanning angle of 45°, 16 active elements. Primary gain = 22.8 dB.
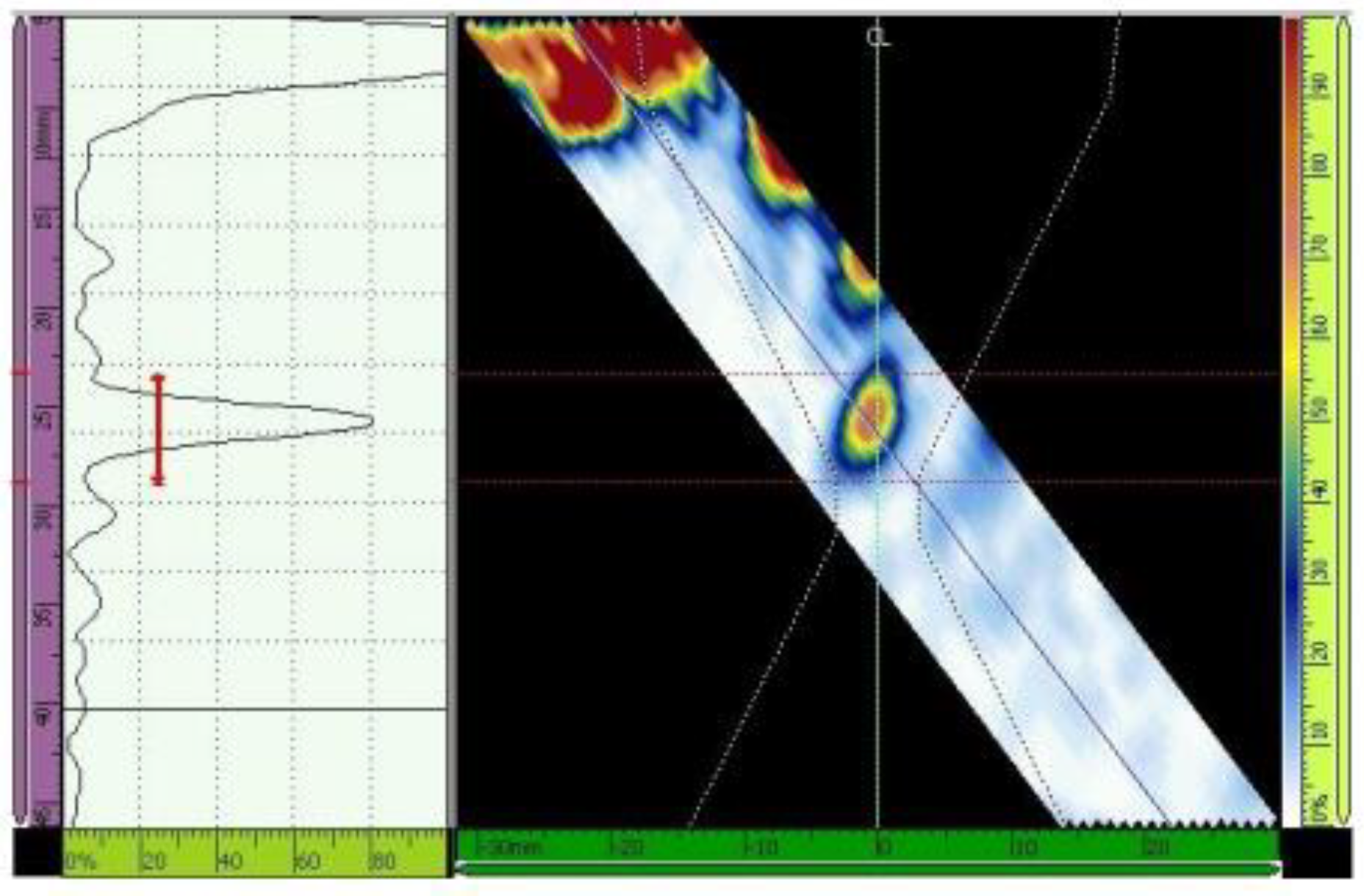
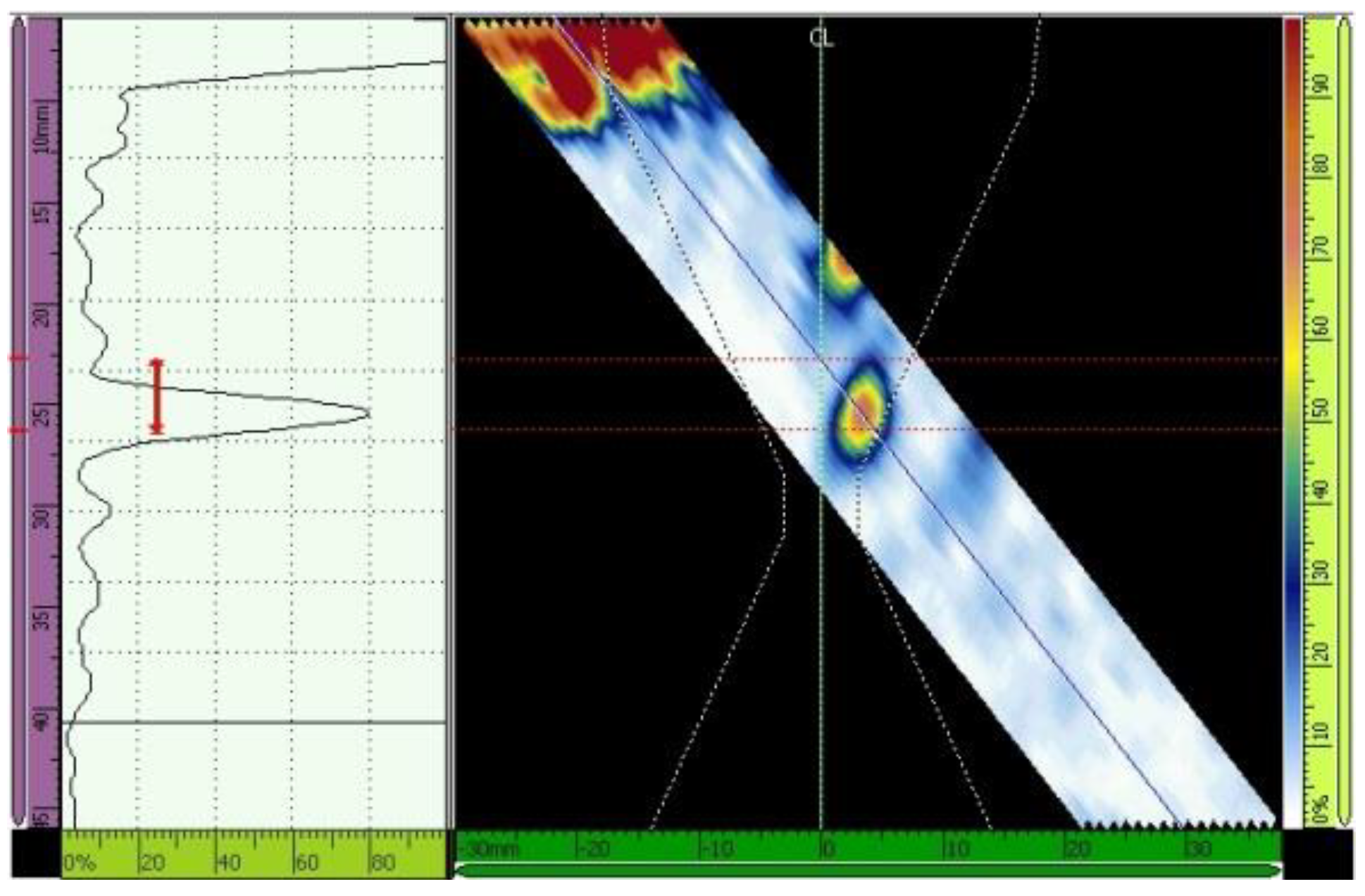
Figure 15.
Echo (maximized to 80% of the screen height) from the third hole. Scanning angle of 48°, 16 active elements. Primary gain = 40.1 dB.
Figure 16.
Time corrected gain adjustment. Scanning angle of 48°, 16 active elements. Primary gain = 22.6 dB.
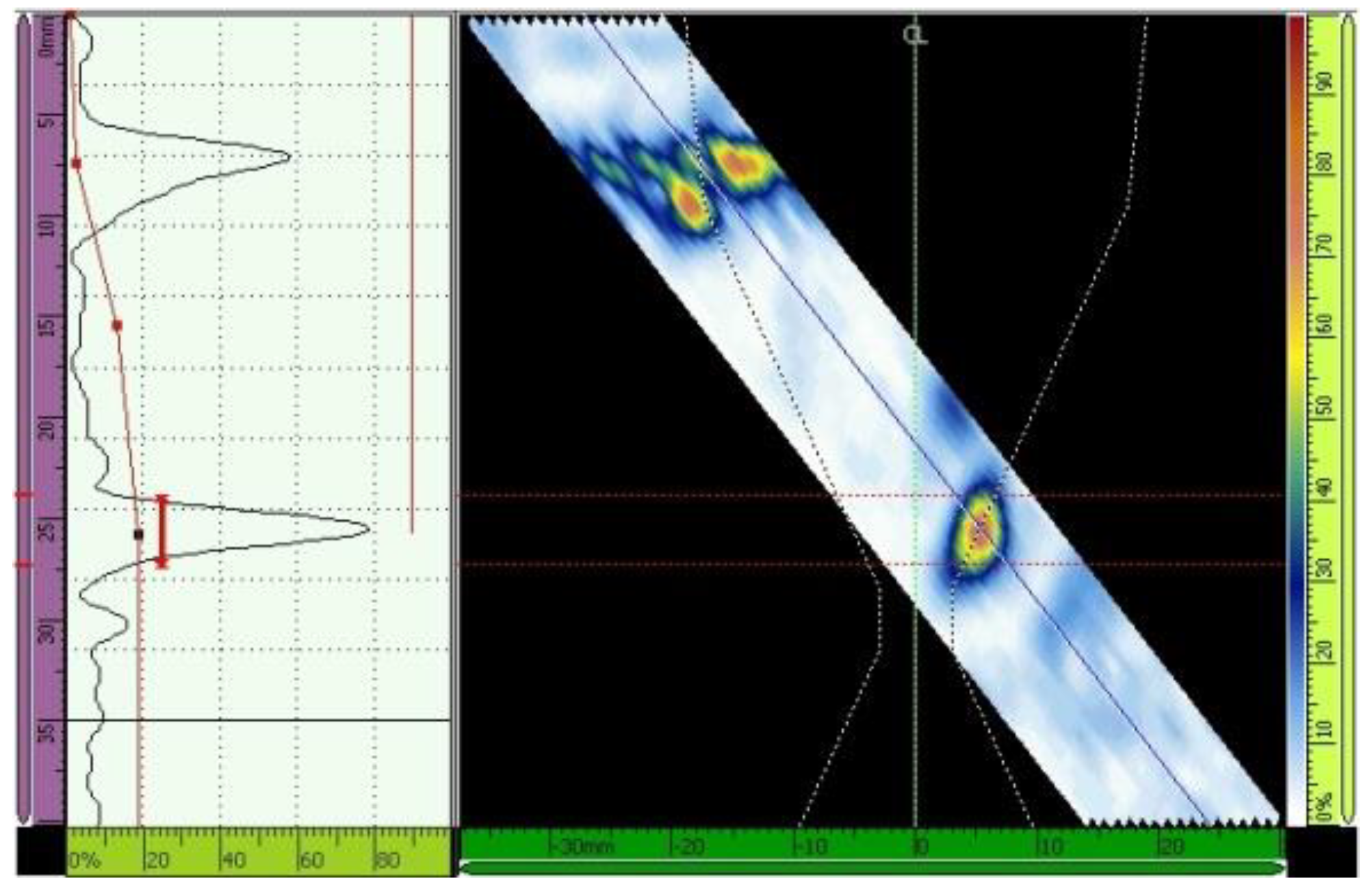
Figure 17.
Echo (maximized to 80% of the screen height) from the third hole. Scanning angle of 52°, 16 active elements. Primary gain = 40.8 dB.
Figure 18.
TCG adjustment. Scanning angle of 52°, 16 active elements. Primary gain = 27.2 dB.
Table 1.
Specified and analyzed mechanical properties-yield strength (YS), ultimate tensile strength (UTS), elongation (El.) and Charpy V energy at −196 °C (CVEn) and lateral expansion (CVEx)-of the base metal and typical values of filler metals mechanical properties.
| Mechanical Properties | Base metal ATSM A333 Gr.8
(9% Ni Steel) | Filler Metal Ni-Based Superalloy 625 |
|---|
| GTAW | SMAW |
|---|
| Specified (min.) [17] | Anal. | Typical Values |
|---|
| YS (MPa) | 515 | 693 | 510 | 530 |
| UTS (MPa) | 690 | 740 | 770 | 770 |
| El. (%) | 22 | 25 | 42 | 30 |
| CVEn (J) | N.A. | 146 | 70 | 45 |
| CVEx (mils/mm) | 14.96/0.38 | 70/1.78 | N.A. | N.A. |
Table 2.
Specified and analyzed chemical compositions (wt.%) of the base, filler and weld metals.
| Element | Chemical Composition (wt.%) |
|---|
| Base Metal (9% Ni) | Filler Metal Ni-Based Superalloy 625 | Weld Metal |
|---|
| GTAW | SMAW |
|---|
| Specified ASTM A333 (max.) [17] | Anal. | Specified AWS A5.14 [18] | Anal. | Specified AWS A5.11 [19] | Anal. | Anal. |
|---|
| C | 0.13 | 0.061 | <0.1 | 0.008 | <0.1 | 0.034 | 0.0326 |
| Mn | 0.9 | 0.607 | <0.5 | 0.02 | <1.0 | 0.68 | 0.887 |
| Si | 0.13/0.32 | 0.279 | <0.5 | 0.05 | <0.75 | 0.35 | 0.494 |
| P | 0.025 | <0.005 | <0.02 | 0.006 | <0.03 | 0.010 | 0.0035 |
| S | 0.025 | <0.005 | <0.015 | 0.000 | <0.02 | 0.003 | 0.0088 |
| Ni | 8.4/9.6 | 9.70 | >58 | 65.10 | >55 | 62.8 | 63.1 |
| Cu | N.A. | <0.005 | <0.5 | 0.03 | <0.5 | 0.00 | 0.0061 |
| Ti | N.A. | 0.0061 | <0.4 | 0.183 | N.A. | 0.05 | 0.0694 |
| Cr | N.A. | 0.0565 | 20/23 | 21.66 | 20/23 | 21.83 | 20 |
| Mo | N.A. | 0.0142 | 8/10 | 8.73 | 8/10 | 8.80 | 8.95 |
| Fe | Balance | 89.200 | <0.5 | 0.430 | <7.0 | 1.84 | 2.49 |
| Pb | N.A. | <0.005 | <0.5 | 0.000 | N.A. | N.A. | 0.0504 |
| Al | N.A. | 0.0218 | <0.4 | 0.140 | N.A. | N.A. | <0.0005 |
| Nb + Ta | N.A. | <0.005 | 3.15/4.15 | 3.66 | 3.15/4.15 | 3.497 | 3.478 |
| Co | N.A. | N.A. | N.A. | N.A. | 0.12 | N.A. | N.A. |
Table 3.
Processes and parameters adopted to girth weld the 9% Ni quenched and tempered steel tubular butt joint with Ni-based superalloy 625 as the filler metal.
| Welding |
|---|
| Parameters | Process |
|---|
| GTAW | SMAW |
|---|
| Root | Hot | Fill | Cap |
|---|
| Amperage (A) | 126 | 126 | 90 | 89 |
| Voltage (V) | 11 | 11 | 26 | 26 |
| Welding speed (cm/min) | 5.6 | 7.3 | 12.6 | 18 |
| Heat input (kJ/mm) | 1.5 | 1.1 | 1.2 | 0.9 |
| Gas type* and flow rate (l/min) | Shield | Ar/12 | Ar/12 | N.A. | N.A. |
| Purge | Ar/25 | Ar/25 | N.A. | N.A. |
Table 4.
Elastic constants (in GPA) for austenitic stainless steel extracted from the CIVA database.
| C11 | C22 | C33 | C23 | C13 | C12 | C44 | C55 | C66 |
|---|
| 250 | 250 | 250 | 138 | 180 | 112 | 117 | 91 | 70 |
Table 5.
Number of active elements, scanning angles and indexes of the CIVA simulation.
| Scanning Angle (°) | No. of Active Elements | Index (mm) |
|---|
| 45 | 16, 24, 32 | 23 |
| 16 | 10, 35, 48 |
| 48 | 16, 24, 32 | 22 |
| 16 | 8, 35, 49 |
| 52 | 16, 24, 32 | 18 |
| 16 | 3, 32, 46 |
Table 6.
Number of active elements, scanning angles and indexes of inspection procedures with an Olympus 2.25L-32-A32 transducer (2.25 MHz).
| Scanning Angle (°) | No. of Active Elements | Index (mm) |
|---|
| 45 | 16 | 10, 23, 35, 48 |
| 48 | 8, 22, 35, 49 |
| 52 | 3, 18, 32, 46 |
Table 7.
Sonic attenuation and sonic speed in the base metal and in the weld metal.
| Wave Type | Base Metal | Weld Metal |
|---|
| Sonic Speed | Attenuation | Sonic Speed | Attenuation |
|---|
| Longitudinal wave | 5820 m/s | 0.098 dB/mm | 5840 m/s | 0.186 dB/mm |
| Transversal wave | 3150 m/s | 0.131 dB/mm | 3075 m/s | 0.220 dB/mm |
Table 8.
Summary of the simulation results.
| Objective | Angle (°) | No. of Active Elements | Index (mm) | Simulation Results |
|---|
| Analyze the influence of varying the number of active elements in the ultrasonic beam propagation through the material. | 45° | 16/24/32 | 23 | Attenuation grows as the number of active elements increases. For all the scanning angles the best results, that is, high coverage and low attenuation were the configuration of 16 elements. |
| 48° | 22 |
| 52° | 18 |
| Analysis of the ultrasonic beam coverage in the welded joint for different scanning indexes. | 45° | 16 | 10/23/35/48 | All indexes showed high coverage and low attenuation on the weld bevel and on the weld metal. |
| 48° | 16 | 8/22/35/49 | All indexes showed low divergence and high coverage on the fusion line and root region. Although, there was excessive beam collimation near the weld cap for the indexes of 22, 35 and 49 mm. |
| 52° | 16 | 3/18/32/46 | Beam divergence was observed in the centerline of the weld for indexes of 3 and 18 mm. For 32 and 46 mm, the attenuation and divergence were low. |
Table 9.
Primary gain from the third hole after TCG adjustment for scanning angles of 45°, 48° and 52°.
| Scanning Angle | Primary Gain from the Third Hole | Primary Gain after Tracing the TCG |
|---|
| 45° | 50.0 dB | 22.8 dB |
| 48° | 40.1 dB | 22.6 dB |
| 52° | 40.8 dB | 27.2 dB |