Determining Material Data for Welding Simulation of Presshardened Steel
Abstract
:1. Introduction
- flow stress ;
- elastic modulus E and Poisson ratio ;
- coefficient of thermal expansion ;
- specific electrical resistance ;
- mass density ;
- specific heat capacity /specific entropy ; and
- specific thermal conductivity .
2. Materials and Methods
2.1. Experimental
2.1.1. Test Procedure
2.1.2. Data Processing
2.2. Numerical Material Simulation
2.3. Resistance Spot Welding Simulation and Welding Experiments
3. Results and Discussion
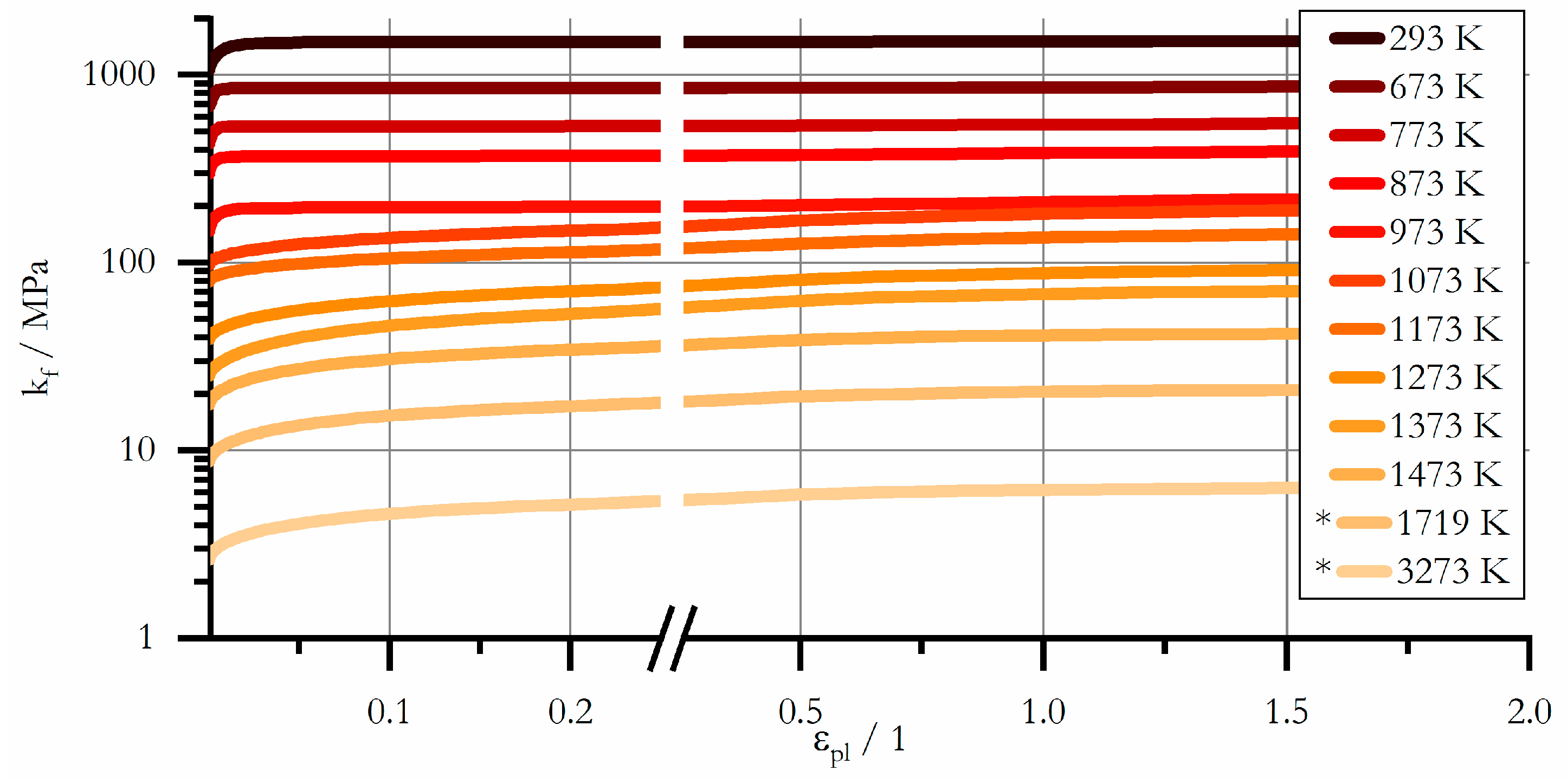
3.1. Flow Stress
3.2. Physical Properties
3.2.1. Elastic Modulus and Poisson Ratio
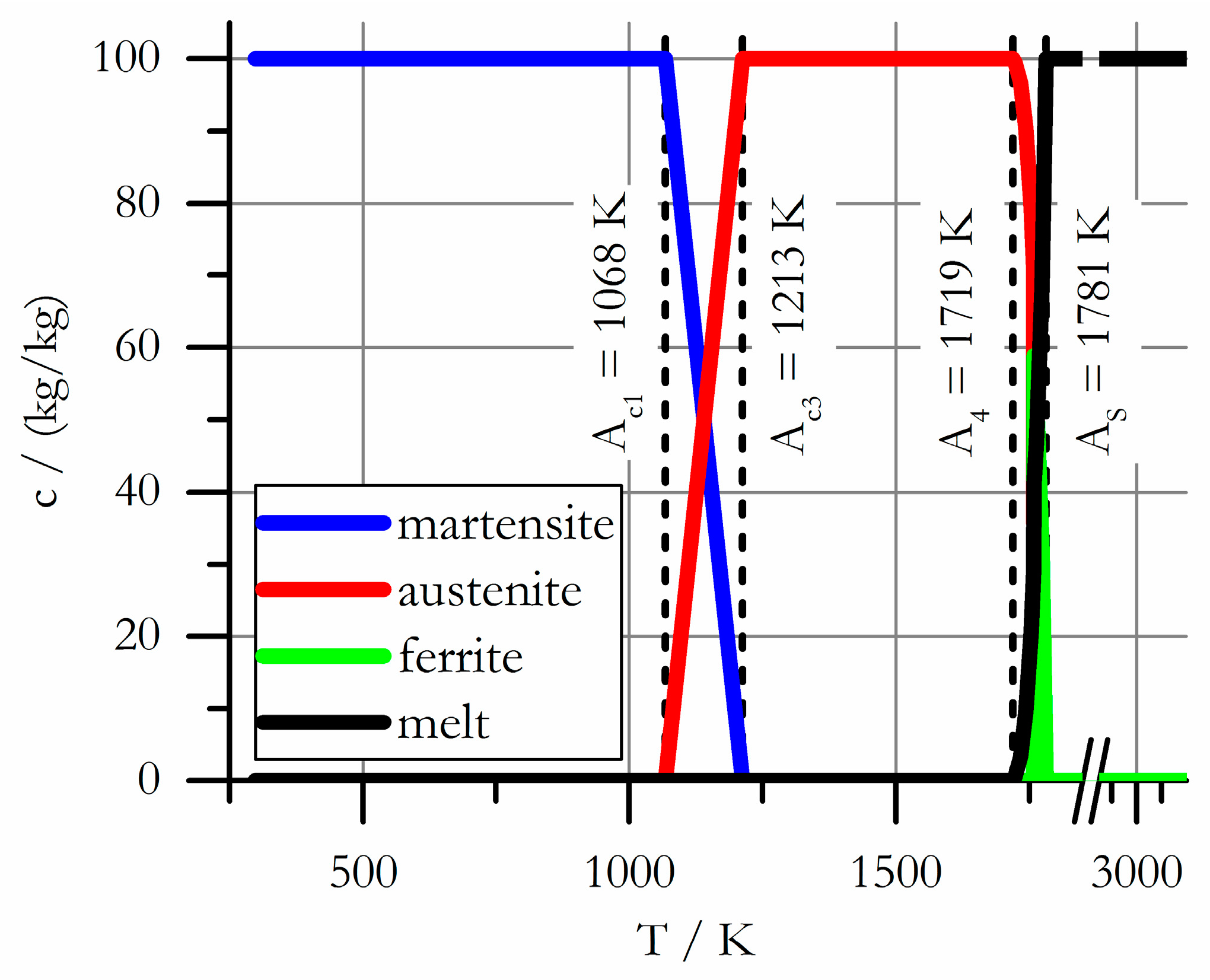
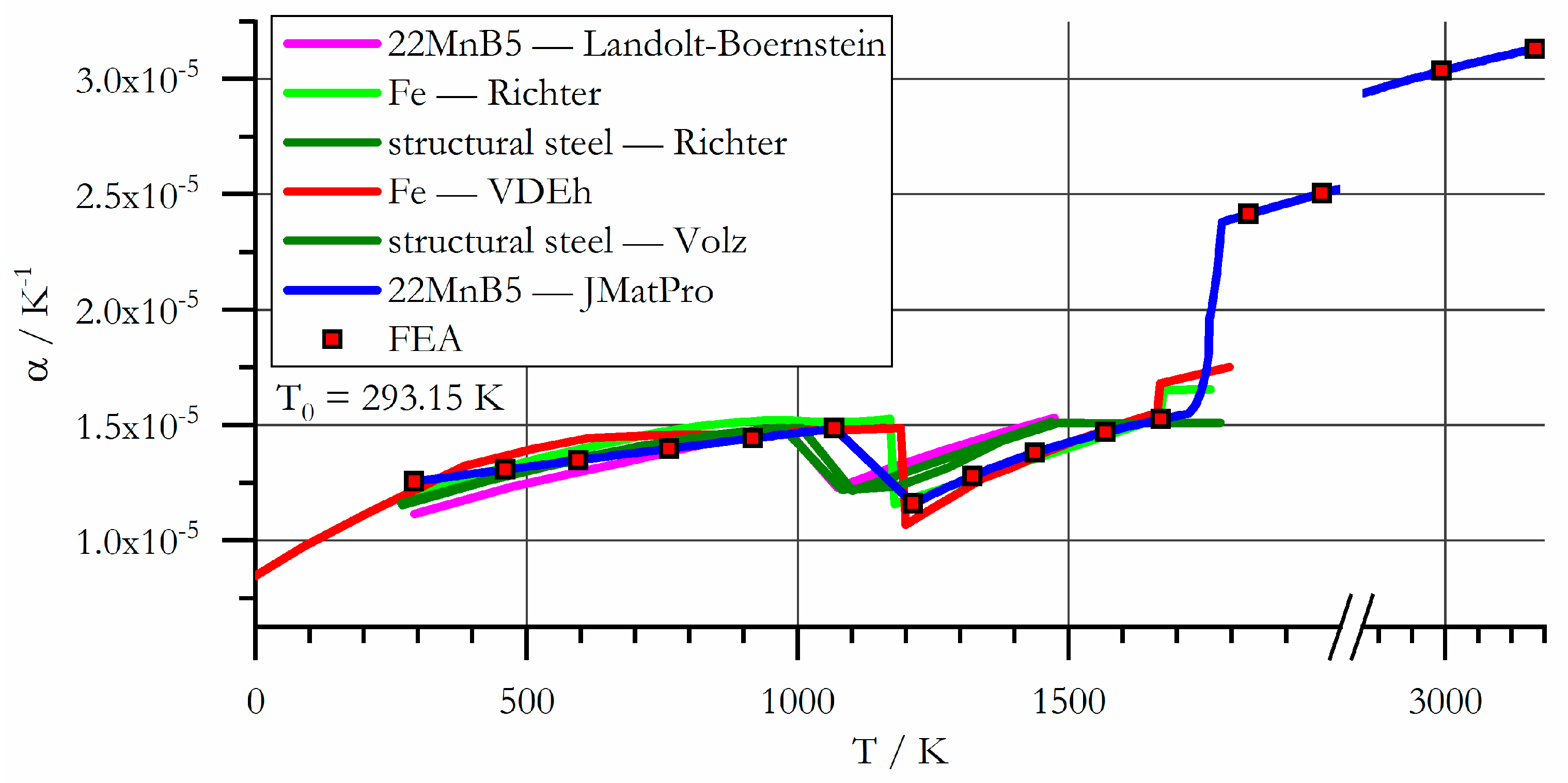
3.2.2. Coefficient of Thermal Expansion
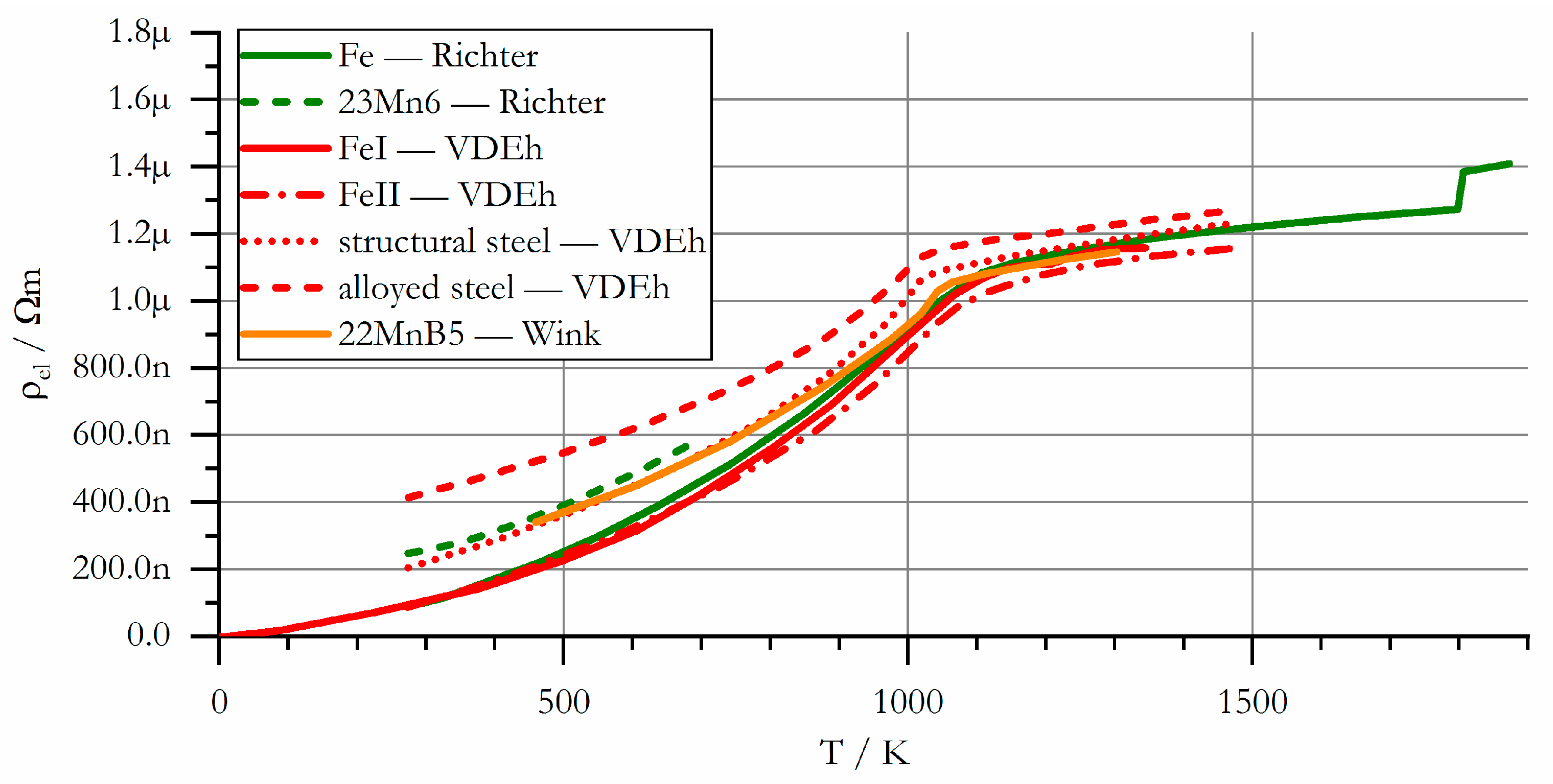
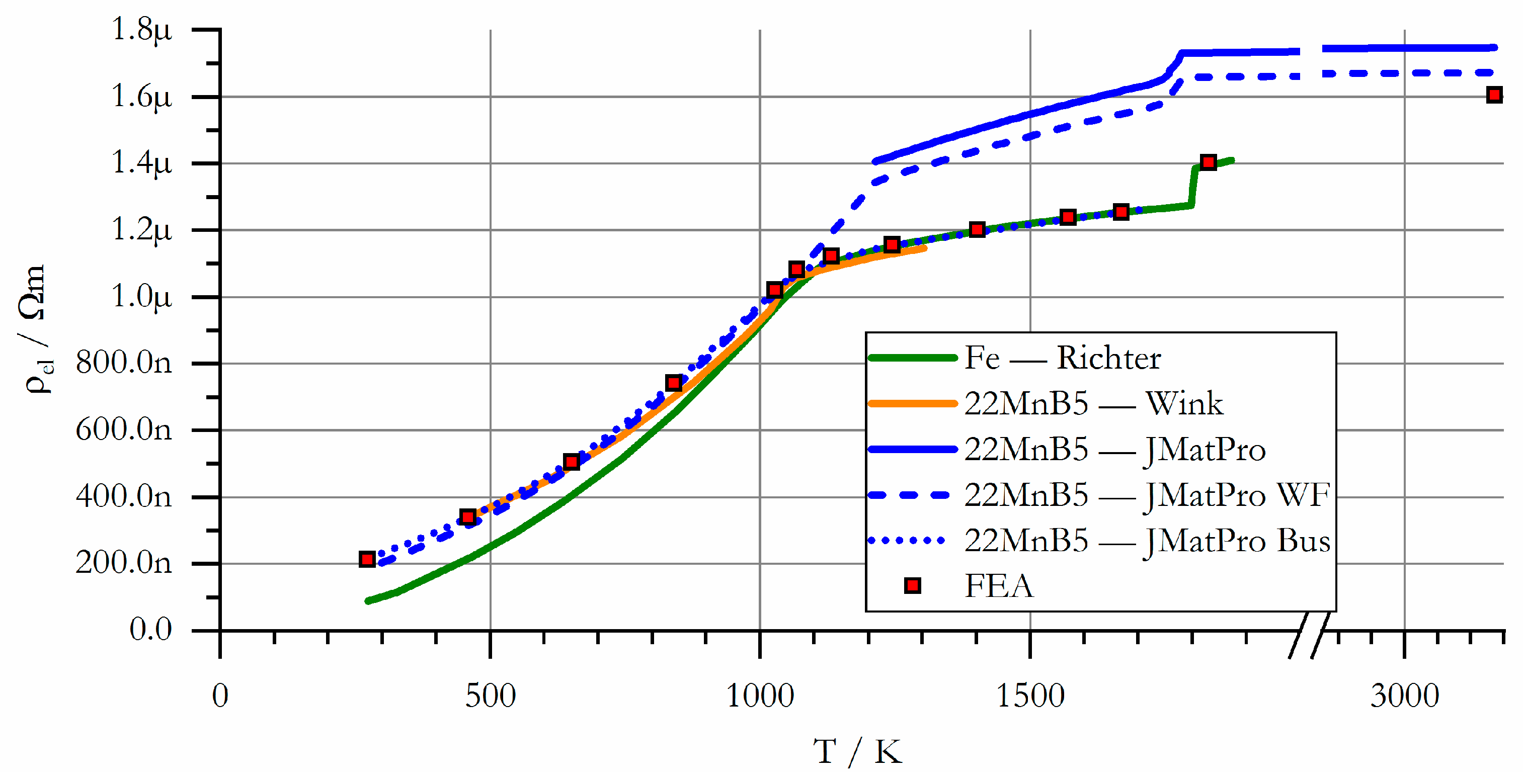
3.2.3. Specific Electric Resistance
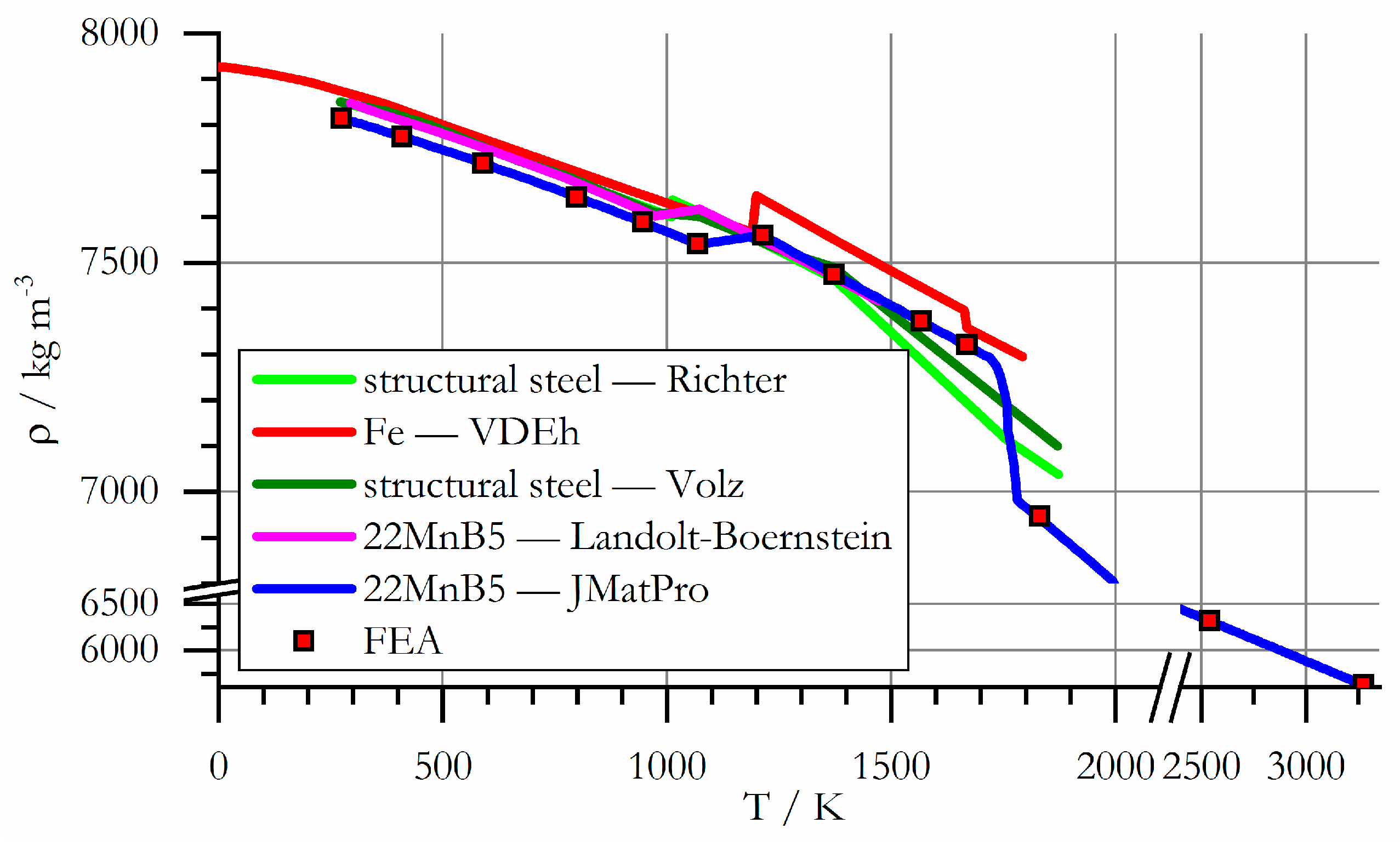
3.2.4. Mass Density
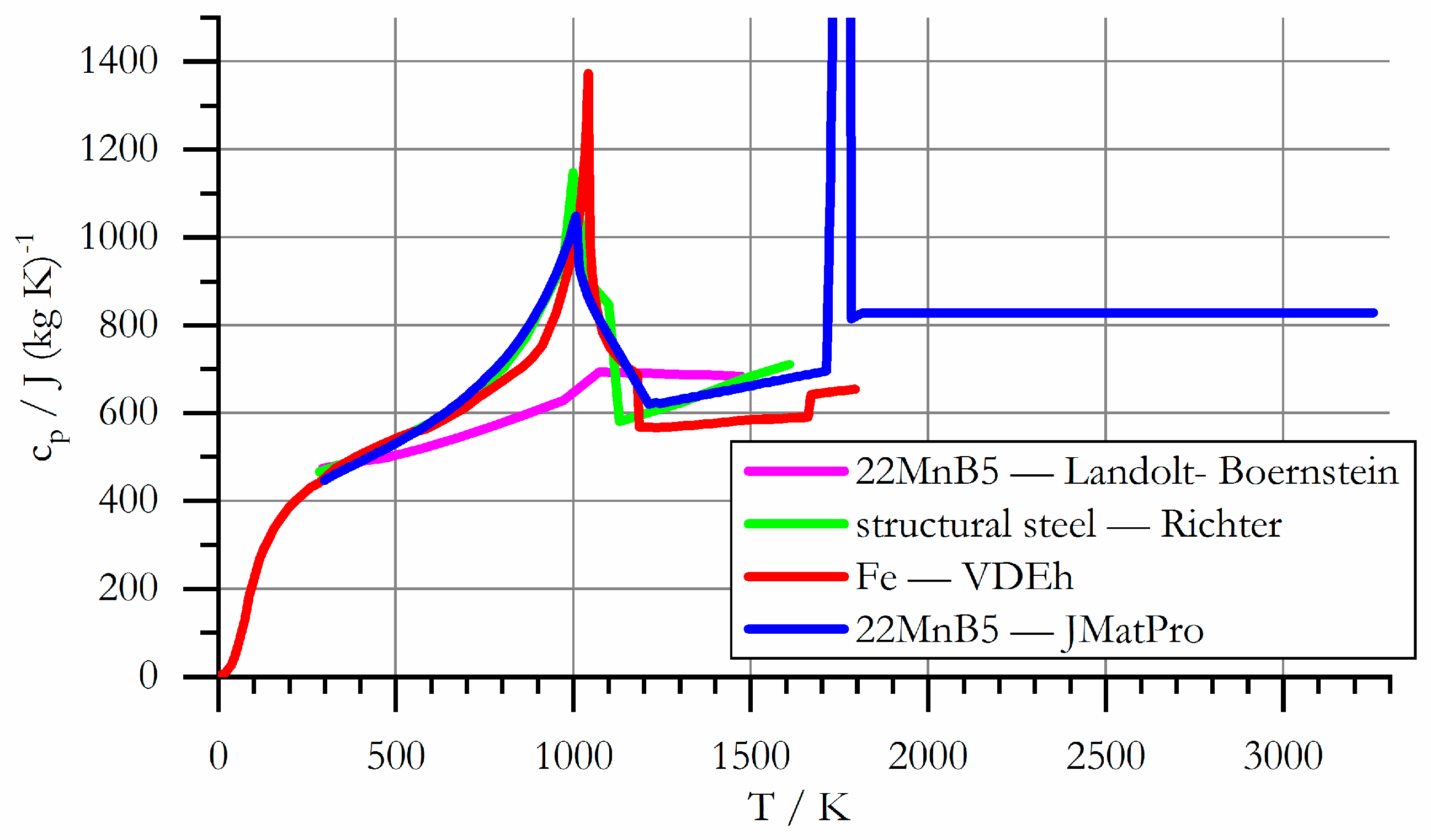
3.2.5. Specific Heat Capacity
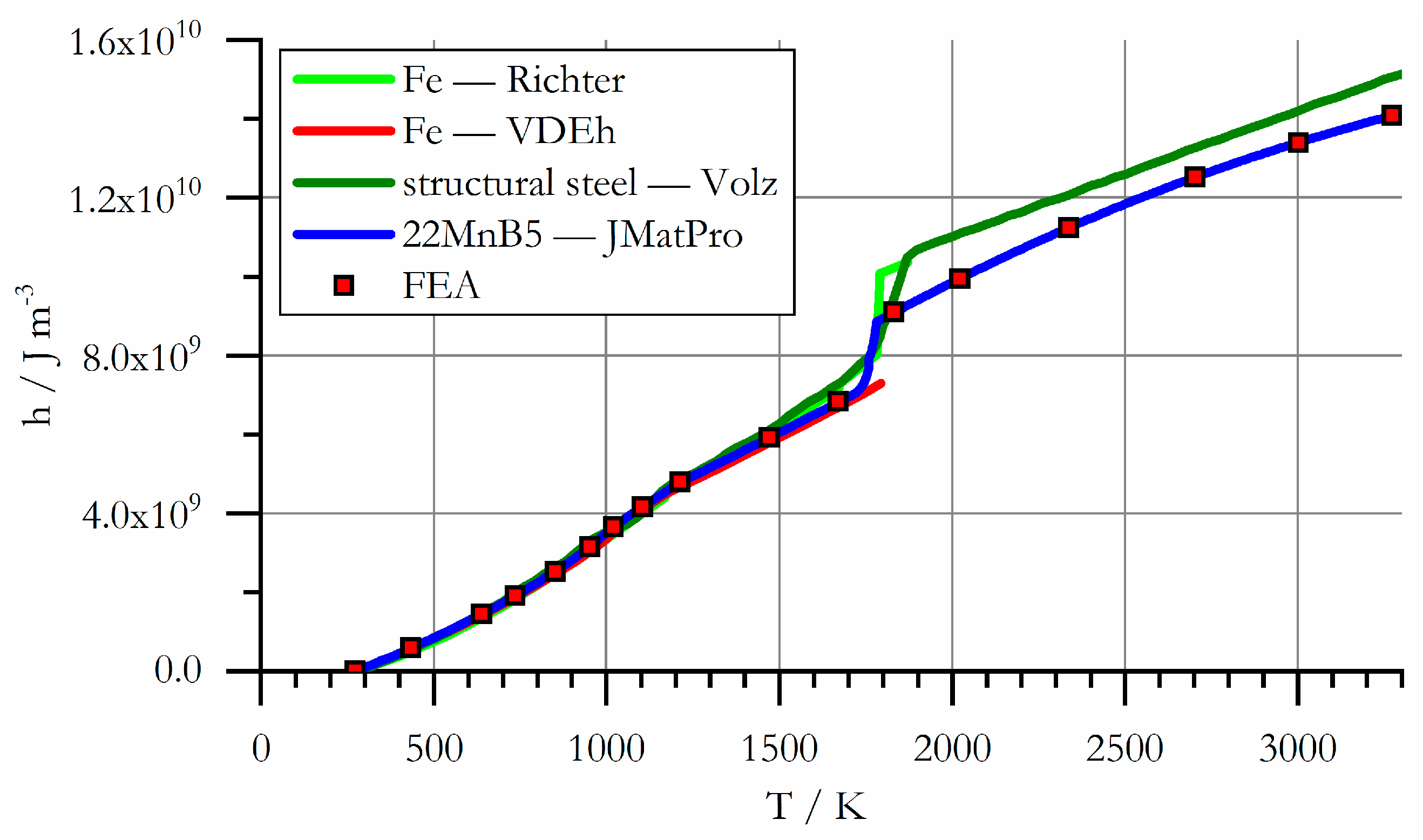
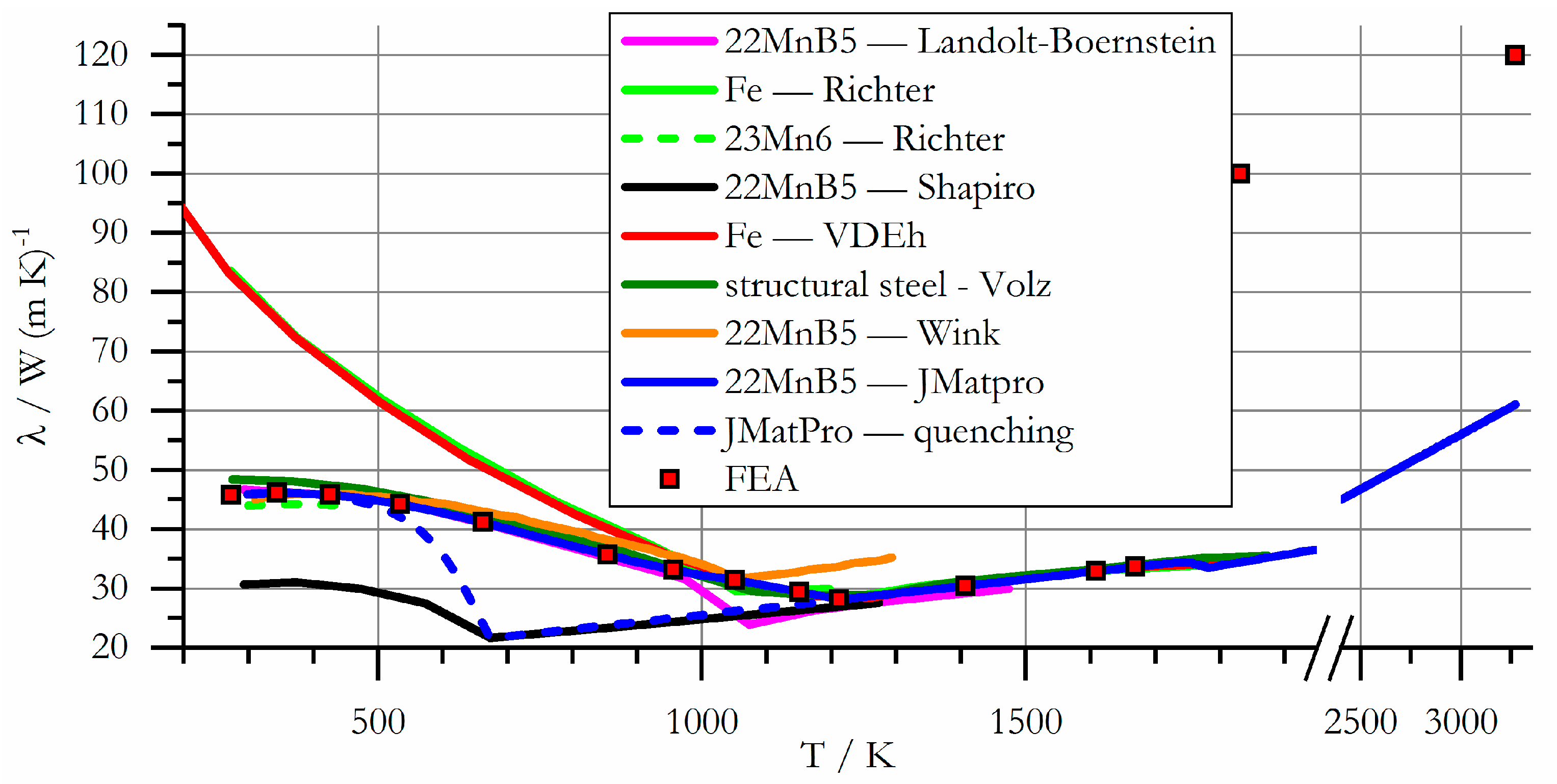
3.2.6. Specific Thermal Conductivity
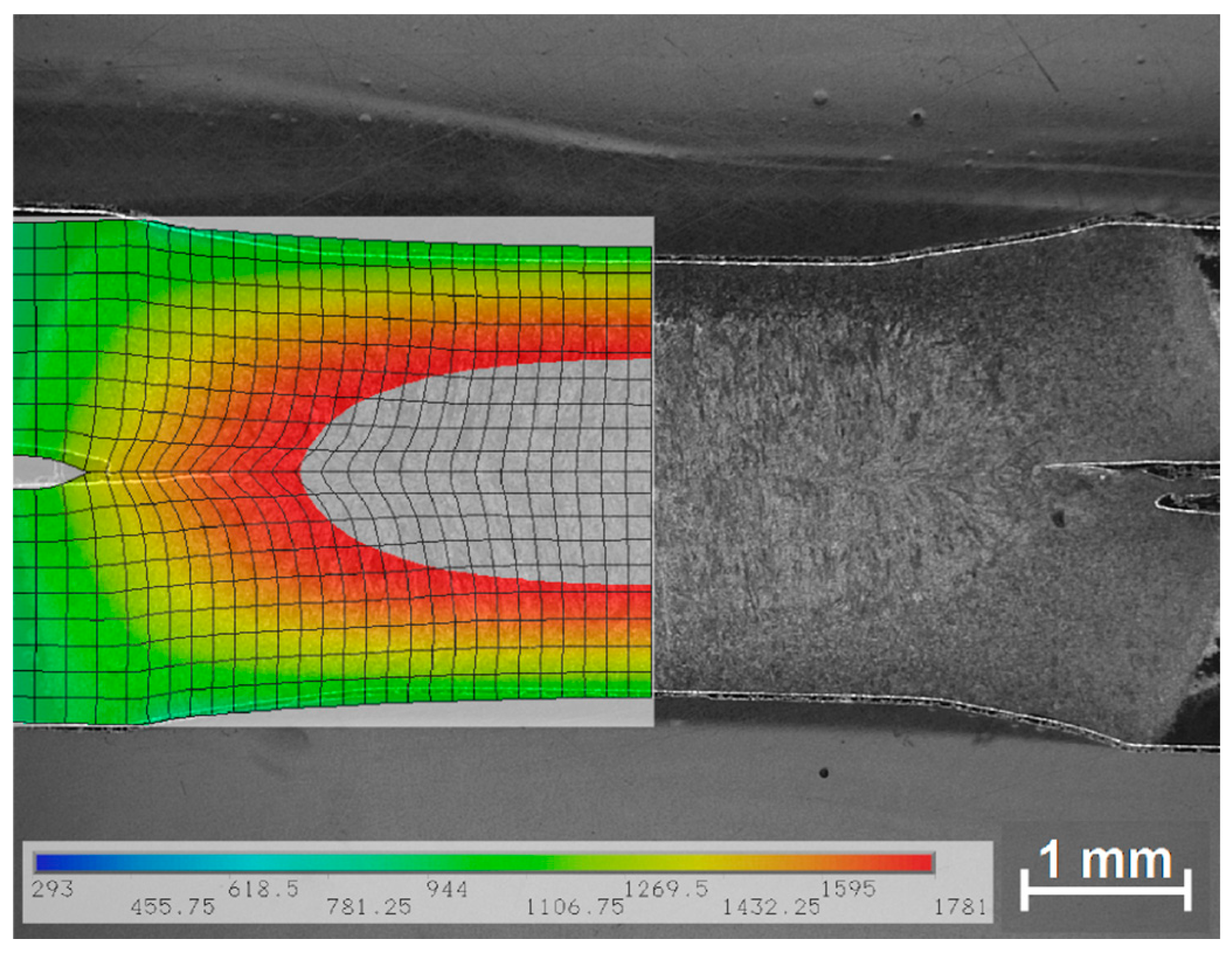
3.3. Data Application in Resistance Spot Welding
3.4. Tabular Data
4. Conclusions
- Data on the flow stress of 22MnB5 was measured and converted to stress–strain data for test temperatures ranging from to .
- Flow stress data is provided by means of flow parameters for the tested temperatures according to the Hockett–Sherby model.
- Physical material property data of 22MnB5 as a function of temperature has been computed using material simulation software. The data was critically reviewed considering literature data.
Author Contributions
Funding
Conflicts of Interest
References
- Podržaj, P.; Jerman, B.; Simončič, S. Poor fit-up condition in resistance spot welding. J. Mater. Process. Technol. 2016, 230, 21–25. [Google Scholar] [CrossRef]
- Schlosser, B.; Jüttner, S. Indikatoren zur Beurteilung der Qualität von MSG-Schweißnähten. In 35. Assistentenseminar Füge- und Schweißtechnik; DVS Media: Magdeburg, Germany, 2016; Volume 314. [Google Scholar]
- Häßler, M.; Füssel, U. Fügen hochbeanspruchter Stähle durch kathodenfokussiertes WIG-Löten (CF-TIG). In 35. Assistentenseminar Füge- und Schweißtechnik; DVS Media: Magdeburg, Germany, 2016; Volume 314. [Google Scholar]
- Brauser, S.; Pepke, L.-A.; Weber, G.; Rethmeier, M. Influence of Production-Related Gaps on Strength Properties and Deformation Behaviour of Spot Welded Trip Steel HCT690T. Weld. World 2012, 56, 115–125. [Google Scholar] [CrossRef]
- Moos, S.; Vezzetti, E. Compliant assembly tolerance analysis: Guidelines to formalize the resistance spot welding plasticity effects. Int. J. Adv. Manuf. Technol. 2012, 61, 503–518. [Google Scholar] [CrossRef]
- Bi, J.; Song, J.; Wei, Q.; Zhang, Y.; Li, Y.; Luo, Z. Characteristics of shunting in resistance spot welding for dissimilar unequal-thickness aluminum alloys under large thickness ratio. Mater. Des. 2016, 101, 226–235. [Google Scholar] [CrossRef]
- Van der Aa, E.; Amirthalingam, M.; Winter, J.; Hanlon, D.N.; Hermans, M.J.M.; Rijnders, M.; Richardson, I.M. Improved Resistance Spot Weldability of 3rd Generation AHHS for Automotive Applications. Math. Model. Weld Phenoma 2016, 11, 175–193. [Google Scholar]
- Raoelison, R.N.; Fuentes, A.; Pouvreau, C.; Rogeon, P.; Carré, P.; Dechalotte, F. Modeling and numerical simulation of the resistance spot welding of zinc coated steel sheets using rounded tip electrode: Analysis of required conditions. Appl. Math. Model. 2014, 38, 2505–2521. [Google Scholar] [CrossRef]
- Schwenk, C.; Rethmeier, M. Material Properties for Welding Simulation—Measurement, Analysis and Exemplary Data. Weld. J. 2011, 90, 220–227. [Google Scholar]
- Karbasian, H.; Tekkaya, A.E. A review on hot stamping. J. Mater. Process. Technol. 2010, 210, 2103–2118. [Google Scholar] [CrossRef]
- Merklein, M.; Johannes, M.; Lechner, M.; Kuppert, A. A review on tailored blanks—Production, applications and evaluation. J. Mater. Process. Technol. 2014, 214, 151–164. [Google Scholar] [CrossRef]
- Geiger, M.; Merklein, M.; Hoff, C. Basic Investigations on the Hot Stamping Steel 22MnB5. Adv. Mater. Res. 2005, 6–8, 795–804. [Google Scholar] [CrossRef]
- Ngyuen, D.-T.; Banh, T.-L.; Jung, D.-W.; Yang, S.-H.; Kim, Y.-S. A Modified Johnson-Cook Model to Predict Stress-Strain Curves of Boron Steel Sheets at Elevated and Cooling Temperatures. High Temp. Mater. Proc. 2012, 31, 37–45. [Google Scholar]
- Merklein, M.; Lechler, J. Investigation of the thermo-mechanical properties of hot stamping steels. J. Mater. Process. Technol. 2006, 177, 452–455. [Google Scholar] [CrossRef]
- Naderi, M. A Numerical and Experimental Investigation into Hot Stamping of Boron Alloyed Heat Treated Steels. Steel Res. Int. 2008, 79, 77–84. [Google Scholar] [CrossRef]
- Gumbsch, P.; Roos, E.; Hahn, O. Charakterisierung und Ersatzmodellierung des Bruchverhaltens von Punktschweißverbindungen an ultrahochfesten Stählen für die Crashsimulation unter Berücksichtigung der Auswirkung der Verbindung auf das Bauteilverhalten; Fraunhofer Institut IWM: Freiburg, Germany; MPA Stuttgart: Stuttgart, Germany; Universität Paderborn: Paderborn, Germany, 2012. [Google Scholar]
- Shapiro, A. Finite Element Modeling of Hot Stamping. Steel Res. Int. 2009, 80, 658–664. [Google Scholar] [CrossRef]
- Spittel, M.; Spittel, T. Steel symbol/number: 22MnB5/1.5528. In Metal Forming Data of Ferrous Alloys—Deformation Behaviour; Warlimont, H., Ed.; Landolt-Börnstein—Group VIII Advanced Materials and Technologies; Springer: Berlin/Heidelberg, Germany, 2009; Volume 2C1. [Google Scholar]
- Wink, H.-J.; Krätschmer, D. Charakterisierung und Modellierung des Bruchverhaltens von Punktschweißverbindungen in pressgehärteten Stählen—Simulation des Schweißprozesses. In Proceedings of the 11. LS-DYNA Forum, Ulm, Germany, 9–10 October 2012. [Google Scholar]
- Hockett, J.E.; Sherby, O.D. Large strain deformation of polycrystalline metals at low homologous temperatures. J. Mech. Phys. Solids 1975, 23, 87–98. [Google Scholar] [CrossRef]
- Kaars, J.; Mayr, P.; Koppe, K. Simple Transition Resistance Model for Spot Welding Simulation of aluminized AHSS. Math. Model. Weld Phenoma 2016, 11, 685–702. [Google Scholar]
- Byl, C.; Bérardan, D.; Dragoe, N. Experimental setup for measurements of transport properties at high temperature and under controlled atmosphere. Meas. Sci. Technol. 2012, 23, 035603. [Google Scholar] [CrossRef]
- Werkstoffkunde Stahl; Eisenhüttenleute, V.D. (Ed.) Springer: Berlin/Heidelberg, Germany, 1984. [Google Scholar]
- Naderi, M.; Saeed-Akbari, A.; Bleck, W. The effects of non-isothermal deformation on martensitic transformation in 22MnB5 steel. Mater. Sci. Eng. A 2008, 487, 445–455. [Google Scholar] [CrossRef]
- Bungardt, K.; Spyra, W. Wärmeleitfähigkeit von Stählen und Legierungen bei Temperaturen Zwischen 20 °C und 700 °C; Verlag Stahleisen: Düsseldorf, Germany, 1965. [Google Scholar]
- Richter, F. Die wichtigsten physikalischen Eigenschaften von 52 Stahlwerkstoffen. Stahleisen Sonderberichte 1973, 8, 1–32. [Google Scholar]
- Richter, F. Physikalische Eigenschaften von Stählen und ihre Temperaturabhängigkeit. In Stahleisen Sonderberichte; Verlag Stahleisen: Düsseldorf, Germany, 1983. [Google Scholar]
- Volz, M. Die Rissentstehung in Statisch Beanspruchten Stahlkonstruktionen unter Berücksichtigung von Schweißeigenspannungen. Ph.D. Thesis, Universität Karlsruhe (TH), Karlsruhe, Germany, 2009. [Google Scholar]
- Kaars, J.; Mayr, P.; Koppe, K. Generalized dynamic transition resistance in spot welding of aluminized 22MnB5. Mater. Des. 2016, 106, 139–145. [Google Scholar] [CrossRef]
- Thermal Conductivity of Pure Metals and Alloys; Madelung, O.; White, G.K. (Eds.) Landolt-Börnstein—Group III Condensed Matter; Springer: Berlin/Heidelberg, Germany, 1991; Volume 15c. [Google Scholar]
- Li, Y.B.; Lin, Z.Q.; Lai, X.M.; Chen, G.L. Electromagnetic Phenomena in Resistance Spot Welding and its Effects on Weld Nugget Formation. In Proceedings of the PIERS Proceedings, Moscow, Russia, 18–21 August 2009. [Google Scholar]
- Na, S.J.; Cheon, J.H.; Kiran, D.V.; Cho, D.W. Heat and Mass Flow in Arc Welding Processes and its Application to Mechanical Analysis of Welded Structures. Math. Model. Weld Phenoma 2016, 11, 5–22. [Google Scholar]





| Quantity | ||
|---|---|---|
| 1153 | 1213 | |
| 993 | 1068 |
| 293 | 1066 | 1488 | 87 | 0.885 |
| 673 | 680 | 844 | 8934 | 1.533 |
| 773 | 432 | 529 | 818 | 1.11 |
| 873 | 298 | 368 | 134.5 | 0.82 |
| 973 | 147 | 196 | 90.5 | 0.83 |
| 1073 | 97 | 248 | 1 | 0.52 |
| 1173 | 79.5 | 180 | 1 | 0.515 |
| 1273 | 39 | 100 | 2 | 0.605 |
| 1373 | 25 | 74.3 | 2.6 | 0.663 |
| 1473 | 17.5 | 43.5 | 3 | 0.615 |
| 273.15 | 211.804 | 0.290 | 293.15 | 1.256 | 273.15 | 0.214 |
| 505.05 | 198.693 | 0.298 | 460.98 | 1.307 | 458.96 | 0.340 |
| 744.51 | 179.279 | 0.307 | 595.73 | 1.348 | 651.12 | 0.506 |
| 935.80 | 151.383 | 0.315 | 762.56 | 1.398 | 840.70 | 0.742 |
| 1068.15 | 128.226 | 0.320 | 917.37 | 1.442 | 1027.97 | 1.020 |
| 1213.15 | 113.060 | 0.347 | 1068.15 | 1.485 | 1068.15 | 1.082 |
| 1426.11 | 91.707 | 0.360 | 1213.15 | 1.160 | 1132.22 | 1.122 |
| 1669.15 | 65.859 | 0.375 | 1322.89 | 1.280 | 1244.72 | 1.156 |
| 1831.15 | 1.470 | 0.450 | 1437.27 | 1.380 | 1402.63 | 1.201 |
| 3273.15 | 1.470 | 0.450 | 1567.51 | 1.469 | 1570.86 | 1.238 |
| 1669.15 | 1.525 | 1669.15 | 1.254 | |||
| 1831.15 | 2.416 | 1831.15 | 1.402 | |||
| 1966.85 | 2.504 | 3273.15 | 1.604 | |||
| 2192.90 | 2.646 | |||||
| 2426.40 | 2.777 | |||||
| 2708.93 | 2.919 | |||||
| 2989.43 | 3.036 | |||||
| 3273.15 | 3.133 |
| 273.15 | 7815 | 273.15 | 0 | 273.15 | 45.738 |
| 408.21 | 7775 | 433.92 | 591 | 343.92 | 46.153 |
| 589.77 | 7717 | 637.68 | 1441 | 425.87 | 45.807 |
| 798.48 | 7643 | 735.55 | 1911 | 534.21 | 44.244 |
| 946.10 | 7588 | 851.72 | 2529 | 662.40 | 41.172 |
| 1068.15 | 7541 | 951.01 | 3150 | 854.26 | 35.678 |
| 1213.15 | 7560 | 1019.39 | 3652 | 956.06 | 33.161 |
| 1372.11 | 7475 | 1103.25 | 4163 | 1051.18 | 31.402 |
| 1566.58 | 7373 | 1213.15 | 4795 | 1150.47 | 29.447 |
| 1669.15 | 7322 | 1470.95 | 5921 | 1211.79 | 28.152 |
| 1831.15 | 6947 | 1669.15 | 6838 | 1407.03 | 30.473 |
| 2092.03 | 6722 | 1831.15 | 9110 | 1608.95 | 32.917 |
| 2539.46 | 6320 | 2022.07 | 9952 | 1669.15 | 33.700 |
| 3273.72 | 5625 | 2336.66 | 11,239 | 1831.15 | 100.000 |
| 2701.79 | 12,521 | 3273.15 | 120.000 | ||
| 3001.71 | 13,405 | ||||
| 3273.15 | 14,090 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kaars, J.; Mayr, P.; Koppe, K. Determining Material Data for Welding Simulation of Presshardened Steel. Metals 2018, 8, 740. https://doi.org/10.3390/met8100740
Kaars J, Mayr P, Koppe K. Determining Material Data for Welding Simulation of Presshardened Steel. Metals. 2018; 8(10):740. https://doi.org/10.3390/met8100740
Chicago/Turabian StyleKaars, Jonny, Peter Mayr, and Kurt Koppe. 2018. "Determining Material Data for Welding Simulation of Presshardened Steel" Metals 8, no. 10: 740. https://doi.org/10.3390/met8100740
APA StyleKaars, J., Mayr, P., & Koppe, K. (2018). Determining Material Data for Welding Simulation of Presshardened Steel. Metals, 8(10), 740. https://doi.org/10.3390/met8100740