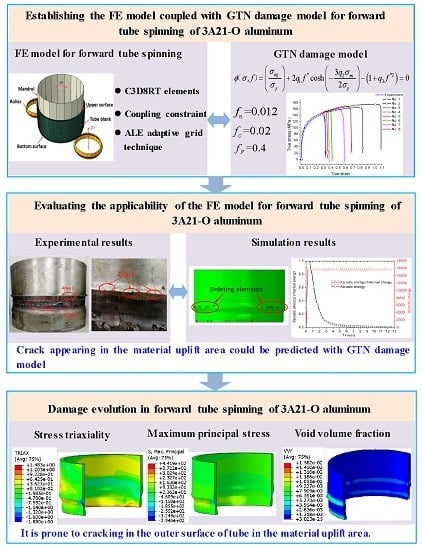
Evaluating the Applicability of GTN Damage Model in Forward Tube Spinning of Aluminum Alloy
Abstract
:1. Introduction
2. Material and Methods
3. Gurson-Tvergaard-Needleman (GTN) Damage Model and Finite Element (FE) Model in Tube Spinning
3.1. GTN Damage Model
3.2. Determination of Parameters in GTN Damage Model
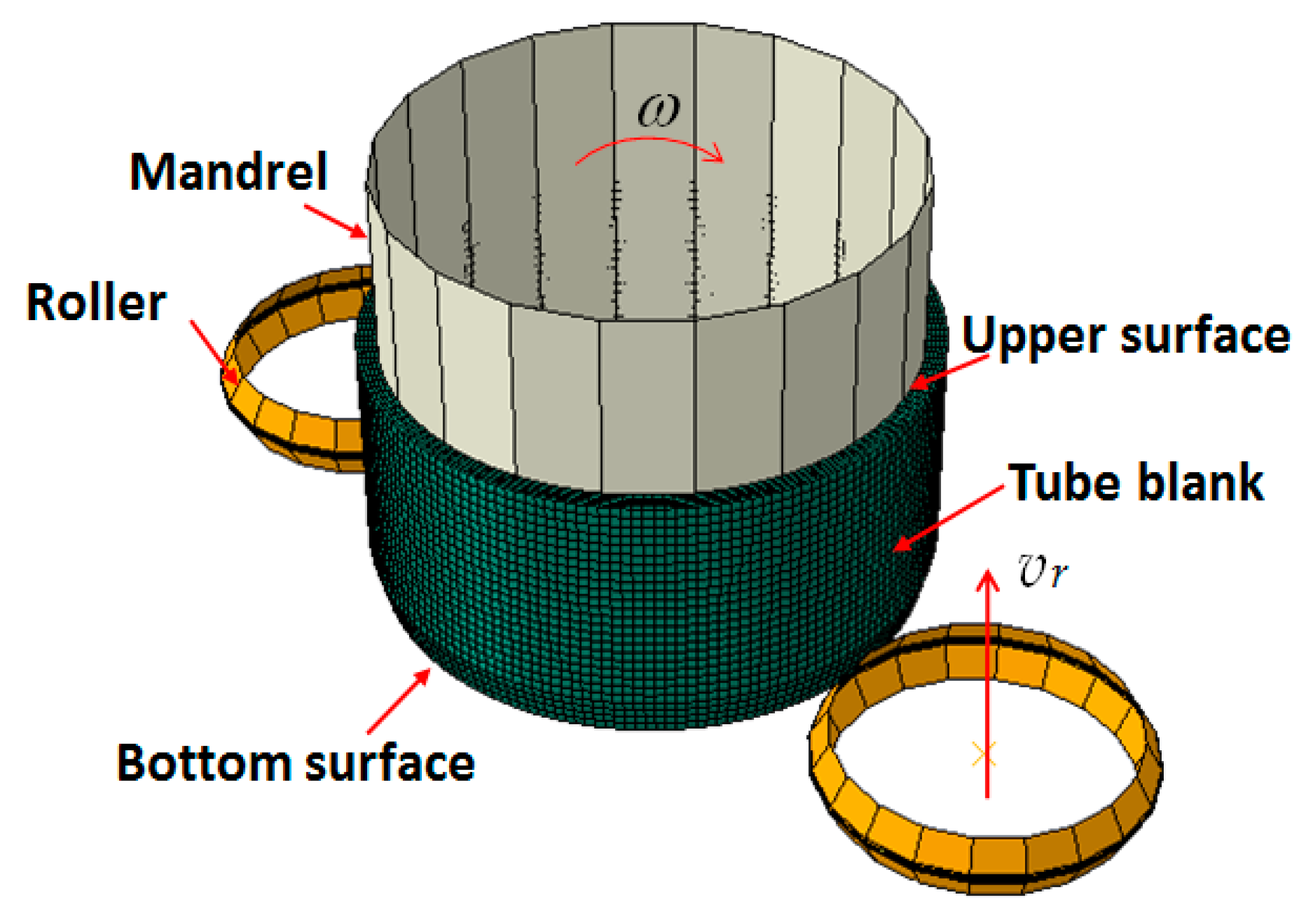
3.3. Establishment of the FE Model for Forward Tube Spinning Coupled with GTN Damage Model
4. Evaluating the Applicability of the FE Model Coupled with GTN Damage
5. Damage Evolution in Forward Tube Spinning
6. Conclusions
Acknowledgements
Author Contribution
Conflicts of Interest
Nomenclature
| Yield function | |
| σeq | Von Mises equivalent stress |
| σy | Mean uniaxial equivalent stress of the matrix material |
| Σm | Macroscopic hydrostatic pressure |
| f | Void volume fraction |
| f* | Modified void volume fraction |
| fc | Critical void volume fraction |
| fF | Void volume fraction at failure |
| Fn | Void volume fraction due to nucleation |
| Fg | Void volume fraction due to growth |
| Sn | Standard deviation of nucleation |
| q1, q2, q3 | Coefficients of the GTN damage model |
References
- Mohebbi, M.S.; Akbarzadeh, A. Experimental study and FEM analysis of redundant strains in tube spinning of tubes. J. Mater. Process. Technol. 2010, 210, 389–395. [Google Scholar] [CrossRef]
- Xia, Q.X.; Xiao, G.F.; Long, H.; Cheng, X.Q.; Sheng, X.F. A review of process advancement of novel metal spinning. Int. J. Mach. Tool. Manuf. 2014, 85, 100–121. [Google Scholar] [CrossRef]
- Music, O.; Allwood, J.M.; Kawai, K. A review of the mechanics of metal spinning. J. Mater. Process. Technol. 2010, 210, 3–23. [Google Scholar] [CrossRef]
- Wong, C.C.; Dean, T.A.; Lin, J. A review of spinning, shear forming and flow forming processes. Int. J. Mach. Tool Manuf. 2003, 431, 1419–1435. [Google Scholar] [CrossRef]
- Gur, M.; Tirosh, J. Plastic flow instability under compressive loading during shear spinning process. Trans. ASME J. Eng. Ind. 1982, 104, 17–22. [Google Scholar] [CrossRef]
- Davis, J.R. Metals Handbook, 2nd ed.; ASM International: Russell, KS, USA, 2001. [Google Scholar]
- Ma, H.; Xu, W.C.; Jin, B.C.; Shan, D.B.; Nutt, S.R. Damage evaluation in tube spinnability test with ductile fracture criteria. Int. J. Mech. Sci. 2015, 100, 99–111. [Google Scholar] [CrossRef]
- Zhan, M.; Zhang, T.; Yang, H.; Li, L.J. Establishment of a thermal damage model for Ti-6Al-2Zr-1Mo-1V titanium alloy and its application in the tube rolling-spinning process. Int. J. Adv. Manuf. Technol. 2016. [Google Scholar] [CrossRef]
- Zhan, M.; Gu, C.J.; Jiang, Z.Q.; Hu, L.J.; Yang, H. Application of ductile fracture criteria in spin-forming and tube-bending processes. Comput. Mater. Sci. 2009, 47, 353–365. [Google Scholar] [CrossRef]
- Gurson, A.L. Continuum theory of ductile rupture by void nucleation and growth. Part I. Yield criteria and flow rules for porous ductile media. J. Eng. Mater. Technol. 1977, 99, 2–15. [Google Scholar] [CrossRef]
- Tvergaard, V.; Needleman, A. Analysis of the cup-cone fracture in a round tensile bar. Acta Metall. 1984, 32, 157–169. [Google Scholar] [CrossRef]
- Chen, Z.Y.; Dong, X.H. The GTN damage model based on Hill’ 48 anisotropic yield criterion and its application in sheet metal forming. Comput. Mater. Sci. 2009, 44, 1013–1021. [Google Scholar] [CrossRef]
- Butcher, C.; Chen, Z.T.; Bardelcik, A.; Worswick, M. Damage-based finite-element modeling of tube hydroforming. Int. J. Fract. 2009, 155, 55–65. [Google Scholar] [CrossRef]
- Sun, Q.; Zan, D.Q.; Chen, J.J.; Pan, H.L. Analysis of edge crack behavior of steel sheet in multi-pass cold rolling based on a shear modified GTN damage model. Theor. Appl. Fract. Mech. 2015, 80, 259–266. [Google Scholar] [CrossRef]
- Nahshon, K.; Hutchinson, J.W. Modification of the Gurson model for shear failure. Eur. J. Mech. A Solid 2008, 27, 1–17. [Google Scholar] [CrossRef]
- Li, H.; Fu, M.W.; Lu, J.; Yang, H. Ductile fracture: Experiments and computations. Int. J. Plast. 2011, 27, 147–180. [Google Scholar] [CrossRef]
- Zhang, J.H.; Zhan, M.; Yang, H.; Jiang, Z.Q.; Han, D. 3D-FE modeling for power spinning of large ellipsoidal heads with variable thicknesses. Compt. Mater. Sci. 2012, 53, 303–313. [Google Scholar] [CrossRef]
- Chu, C.C.; Needleman, A. Void nucleation effects in biaxially stretched sheets. J. Eng. Mater. Technol. 1980, 102, 249–256. [Google Scholar] [CrossRef]
- Vadillo, G.; Fernández-Sáez, J. An analysis of Gurson model with parameters dependent on triaxiality based on unitary cells. Eur. J. Mech. A Solid 2009, 28, 417–427. [Google Scholar] [CrossRef]
- Aravas, N. On the numerical integration of a class of pressure-dependent plasticity models. Int. J. Numer. Methods Eng. 1987, 24, 1395–1416. [Google Scholar] [CrossRef]
- He, M.; Li, F.G.; Wang, Z.G. Forming limit stress diagram prediction of Aluminum alloy 5052 based on GTN model parameters determined by in situ tensile test. Chin. J. Aeronaut. 2011, 24, 378–386. [Google Scholar] [CrossRef]
- Yan, Y.; Sun, Q.; Chen, J.; Pan, H. The initiation and propagation of edge cracks of silicon steel during tandem cold rolling process based on the Gurson-Tvergaard-Needleman damage model. J. Mater. Process. Technol. 2013, 213, 598–605. [Google Scholar] [CrossRef]
- ABQSUS Analysis User’s Manual; Version 6.8; ABAQUS. Inc.: Paris, France, 2008.
- Lou, Y.S.; Huh, H. Prediction of ductile fracture for advanced high strength steel with a new criterion: Experiments and simulation. J. Mater. Process. Technol. 2013, 213, 1284–1302. [Google Scholar] [CrossRef]
- Malcher, L.; Andrade Pires, F.M.; de Sá, J.M.A.C. An extended GTN model for ductile fracture under high and low stress triaxiality. Int. J. Plast. 2014, 54, 193–228. [Google Scholar] [CrossRef]
- Xue, L. Constitutive modeling of void shearing effect in ductile fracture of porous materials. Eng. Fract. Mech. 2008, 75, 3343–3366. [Google Scholar] [CrossRef]
- Chaboche, J.L.; Boudifa, M.; Saanouni, K. A CDM approach of ductile damage with plastic compressibility. Int. J. Fract. 2006, 137, 51–75. [Google Scholar] [CrossRef]
- Kim, J.; Gao, X.S.; Srivatsan, T. Modeling of void growth in ductile solids: Effects of stress triaxiality and initial porosity. Eng. Fract. Mech. 2004, 71, 379–400. [Google Scholar] [CrossRef]












| Position | Si | Fe | Cu | Mn | Mg | Zn | Ti | Al |
|---|---|---|---|---|---|---|---|---|
| Mass fraction (%) | 0.6 | 0.7 | 0.2 | 1.3 | 0.05 | 0.10 | 0.15 | Bal. |
| Parameters | Values |
|---|---|
| Elastic modulus (GPa) | 69.98 |
| Poisson’s ratio | 0.33 |
| Yield strength (MPa) | 52 |
| Strength coefficient (MPa) | 188.76 |
| Hardening exponent | 0.194 |
| Parameters | Experiment | Simulation |
|---|---|---|
| Inner diameter of the tube d (mm) | 320.6 | 80.15 |
| Thickness of the tube t0 (mm) | 12 | 3 |
| Initial height of the tube h (mm) | 150 | 37.5 |
| Roller nose radius r (mm) | 5 | 1.25 |
| Roller feed rate vr (mm/r) | 1.25 | 0.3125 |
| Roller attack angle α (°) | 30 | 30 |
| Mandrel rotational speed ω (r/min) | 100 | 100 |
| Reduction ratio of wall thickness Ψ (%) | 50 | 50 |
| Group | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | Experiment | |
|---|---|---|---|---|---|---|---|---|---|---|
| Values | ||||||||||
| fn | 0.01 | 0.02 | 0.02 | 0.015 | 0.012 | 0.01 | 0.04 | 0.002 | - | |
| fc | 0.05 | 0.05 | 0.02 | 0.02 | 0.02 | 0.01 | 0.05 | 0.005 | - | |
| fF | 0.1 | 0.1 | 0.05 | 0.04 | 0.04 | 0.02 | 0.15 | 0.05 | - | |
| Standard deviation | 1.47 | 1.30 | 1.70 | 1.26 | 1.25 | 1.75 | 1.36 | 1.72 | - | |
| Critical strain | 1.01 | 0.81 | 0.38 | 0.32 | 0.30 | 0.35 | 0.48 | 0.59 | 0.27 | |
| Fracture strain | 1.09 | 0.84 | 0.42 | 0.36 | 0.33 | 0.38 | 0.58 | 0.68 | 0.33 | |
| Simulation results | Mesh Size | ||
|---|---|---|---|
| 2 mm | 1.5 mm | 1 mm | |
| Maximum Mises stress (MPa) | 238.4 | 239.1 | 239.1 |
| Maximum equivalent strain | 2.826 | 3.276 | 3.41 |
| Central processing unit time (h) | 68 | 128 | 244 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Zhan, M.; Guo, J.; Zhao, B. Evaluating the Applicability of GTN Damage Model in Forward Tube Spinning of Aluminum Alloy. Metals 2016, 6, 136. https://doi.org/10.3390/met6060136
Wang X, Zhan M, Guo J, Zhao B. Evaluating the Applicability of GTN Damage Model in Forward Tube Spinning of Aluminum Alloy. Metals. 2016; 6(6):136. https://doi.org/10.3390/met6060136
Chicago/Turabian StyleWang, Xianxian, Mei Zhan, Jing Guo, and Bin Zhao. 2016. "Evaluating the Applicability of GTN Damage Model in Forward Tube Spinning of Aluminum Alloy" Metals 6, no. 6: 136. https://doi.org/10.3390/met6060136
APA StyleWang, X., Zhan, M., Guo, J., & Zhao, B. (2016). Evaluating the Applicability of GTN Damage Model in Forward Tube Spinning of Aluminum Alloy. Metals, 6(6), 136. https://doi.org/10.3390/met6060136