Physics-Informed Decision Framework for Reuse of Reclaimed Steel Members Under Uncertainty
Abstract
1. Introduction
2. Sustainable Steel Design and Reuse as a Decision Problem
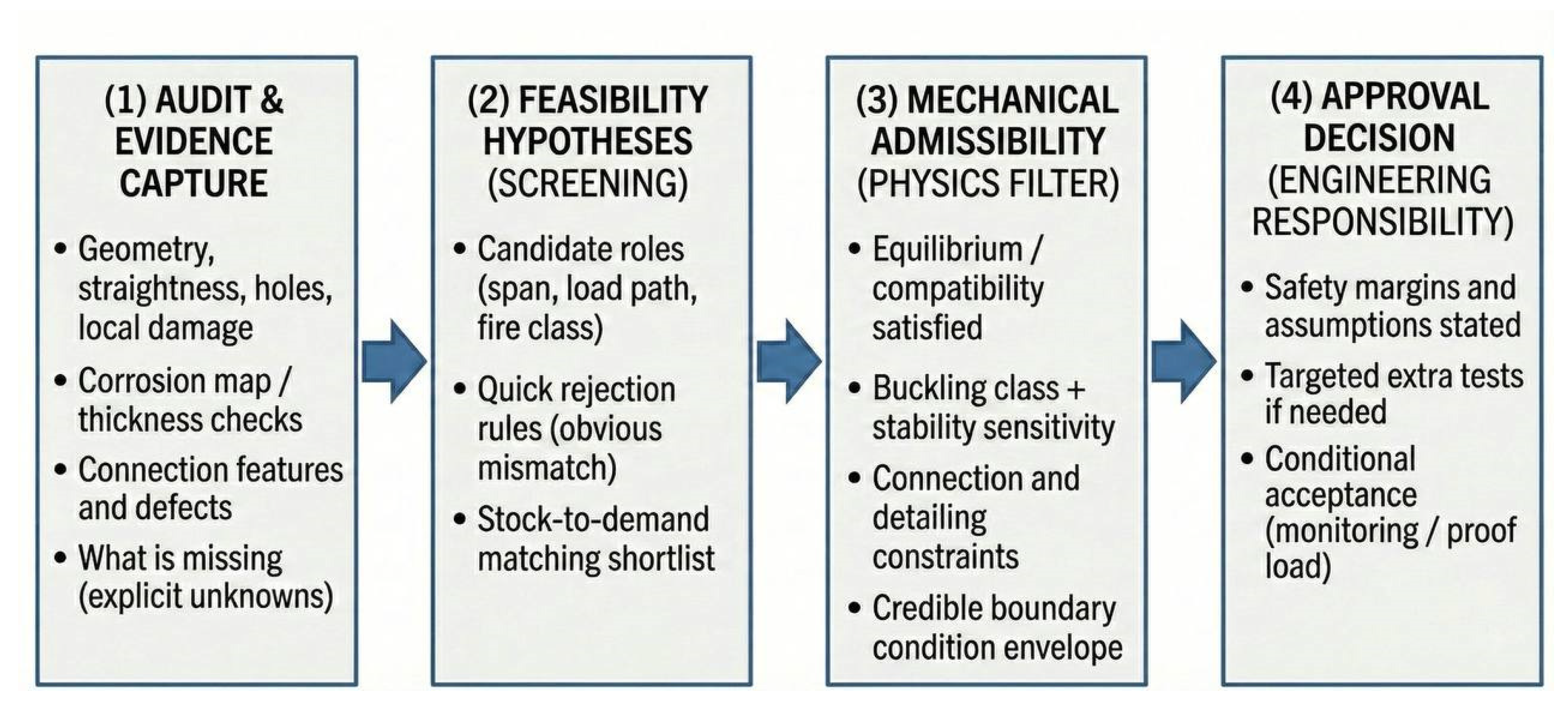
- Evidence collection (audit): Measure geometry, corrosion, straightness, holes, local damage, and connection features; document missing items explicitly;
- Hypothesis generation (feasibility): Identify plausible new roles for the member and screen out incompatible options quickly;
- Mechanical filtering (admissibility): Check that candidates satisfy equilibrium, stability, and detailing constraints under credible boundary conditions;
- Decision and documentation (approval): Select safety margins and any additional tests, proof loads, strengthening, or monitoring required to justify acceptance.
3. Data-Driven and Physics-Informed Methods for Structural Admissibility in Steel Reuse
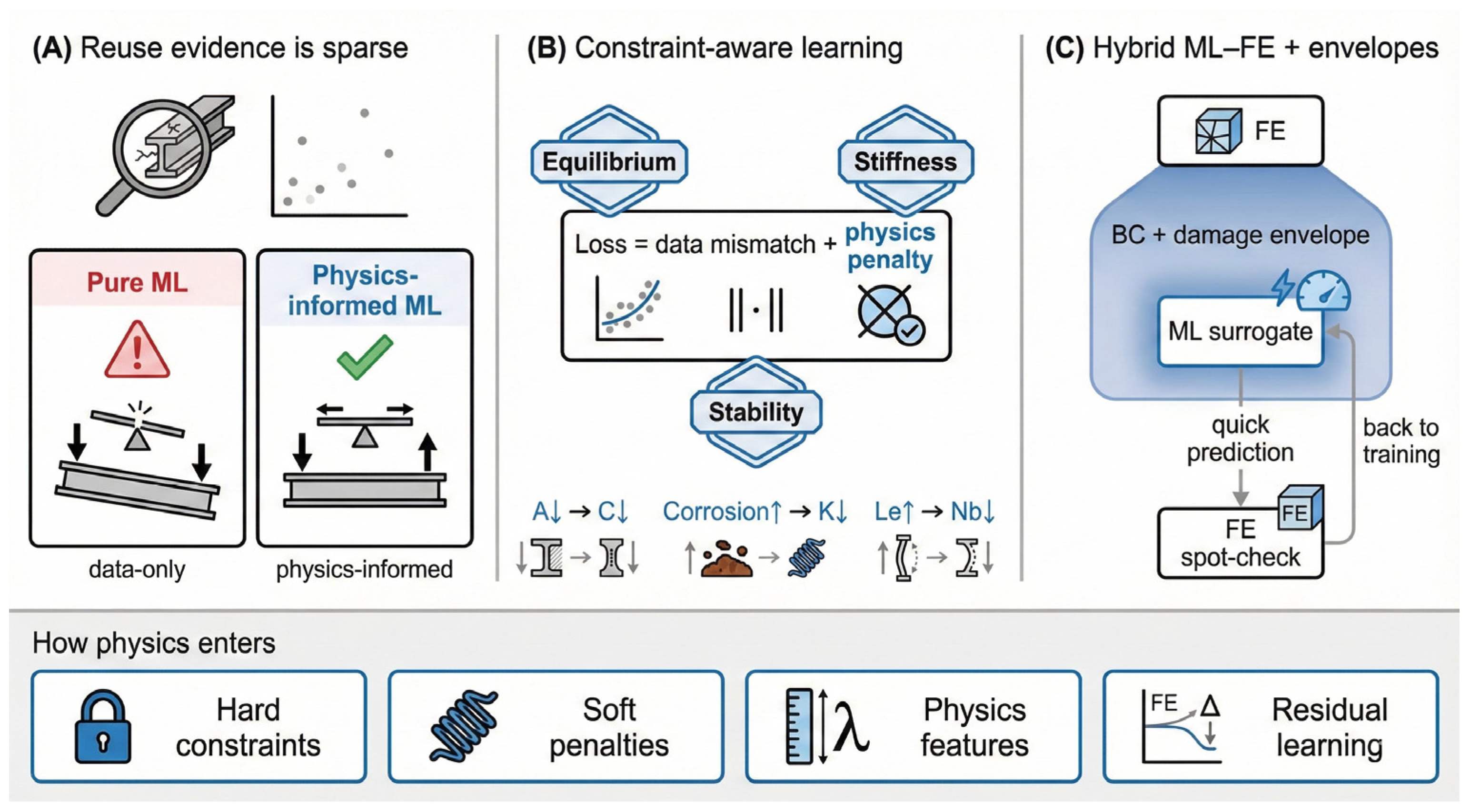
- Hard constraints: The model structure enforces equilibrium or admissibility by construction.
- Soft constraints: Penalties discourage violations, allowing trade-offs when data are noisy.
- Physics-guided features: The model learns from quantities that encode mechanics (slenderness, section class, effective length factors, connection stiffness indicators).
- Residual learning: A mechanics model provides a baseline, and ML learns corrections due to effects that are hard to model directly (damage patterns, uncertain restraint, residual stress proxies).
3.1. Benefits for Steel Reuse Problems
3.2. Practical Challenges
3.3. Applied Studies and Partial Implementations Relevant to Reuse Decisions
3.4. Complete Case Study Examples and Comparison with Standard Reuse Workflows
3.4.1. UK-Style Reuse Pathway with Evidence-Based Certification and Traceability
3.4.2. NDT-Supported Property Recovery Feeding Code Verification
4. Uncertainty and Explainability as Enablers of Reuse Decisions
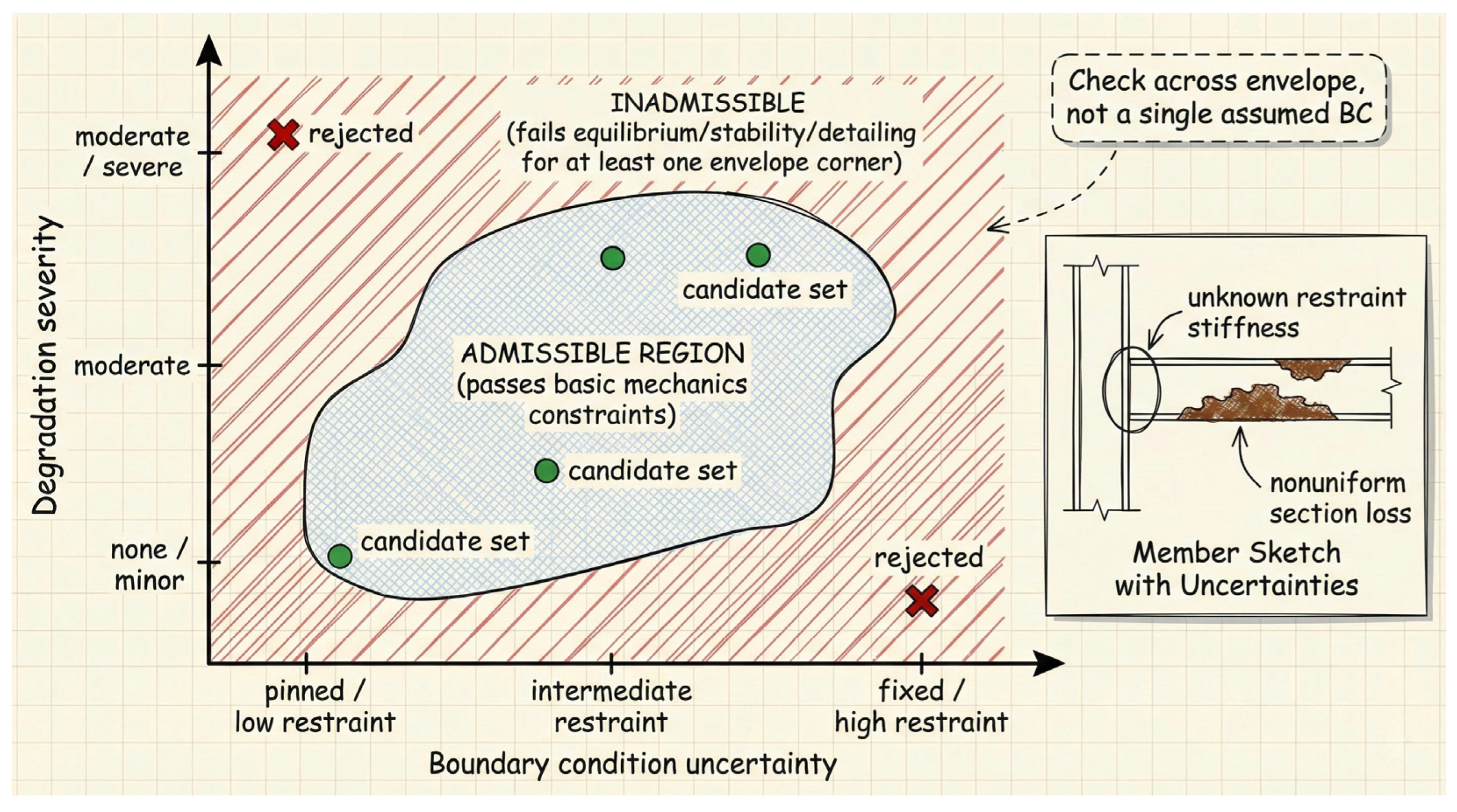
- A conservative resistance bound under a defined envelope of assumptions (not a single scenario);
- A sensitivity ranking showing which unknowns control the decision;
- A low-support indicator when inputs fall outside the model’s reliable domain;
- A recommended evidence action when the decision is borderline (measure/test/assume/reinforce).
4.1. Deployable Uncertainty Quantification and Evidence-Driven Updating for Reuse Approval
4.2. Explainability for Engineering Trust
- (i)
- governing failure mode and check type;
- (ii)
- key evidence used (measurements/tests);
- (iii)
- main assumptions and their ranges (boundary conditions, degradation);
- (iv)
- sensitivity drivers and conservative choices;
- (v)
- decision outcome (accept/conditional accept/reject) and required follow-up actions.
4.3. Design Codes, Standards, and Regulatory Constraints for Steel Reuse
Code-Compliance Mapping for Audit-Ready Approval Packages
- (a)
- Material traceability and grade:
- (b)
- Defect tolerance and section loss:
- (c)
- Connections, restraint, and boundary conditions
- (d)
- Fatigue and repeated loading.
- (e)
- Fire resistance and protection condition.
5. Open Challenges and Research Directions
- Boundary-condition uncertainty as a first-class variable: methods that propagate restraint uncertainty through stability checks and produce admissibility envelopes, not point answers;
- Decision-aware learning objectives: train models to be conservative near acceptance boundaries and to flag low-support cases, rather than optimizing average error;
- Value-of-information planning: methods that recommend the next inspection or test based on pass/fail sensitivity and consequence class;
- Connection-centric reuse modelling: more work is needed on bolts, holes, slip, weld removal, and re-detailing constraints, because connections often control reuse practicality;
- Tracking repeated reuse cycles: methods to update member records after each reuse, including damage accumulation and modifications, to avoid “resetting uncertainty” each time.
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kanyilmaz, A.; Birhane, M.; Fishwick, R.; Del Castillo, C. Reuse of steel in the construction industry: Challenges and opportunities. Int. J. Steel Struct. 2023, 23, 1399–1416. [Google Scholar] [CrossRef]
- Berglund-Brown, J.; Ochsendorf, J. Reusing heavy-section steel in buildings: Carbon reduction potential and material availability. J. Archit. Eng. 2025, 31, 04025020. [Google Scholar] [CrossRef]
- Umaraj, R.R.; Selvaraj, S.K.; Chan, T.M.; Elghazouli, A.Y. Construction sustainability through reusability: Establishing reuse design rules for CFS channel columns subjected to local buckling. Thin-Walled Struct. 2026, 218, 113892. [Google Scholar] [CrossRef]
- Dunant, C.F.; Drewniok, M.P.; Sansom, M.; Corbey, S.; Allwood, J.M.; Cullen, J.M. Real and perceived barriers to steel reuse across the UK construction value chain. Resour. Conserv. Recycl. 2017, 126, 118–131. [Google Scholar] [CrossRef]
- Bartsch, H. Reuse of reclaimed steel components in construction: A systematic review of potential, challenges and future directions. Structures 2025, 80, 110057. [Google Scholar] [CrossRef]
- Sarfarazi, S.; Mascolo, I.; Modano, M.; Guarracino, F. Application of artificial intelligence to support design and analysis of steel structures. Metals 2025, 15, 408. [Google Scholar] [CrossRef]
- Sarfarazi, S.; Modano, M.; Fulgione, M. Artificial intelligence for dynamic characterization of composite panel structures: A structured review. Mech. Res. Commun. 2025, 151, 104607. [Google Scholar] [CrossRef]
- Sarfarazi, S.; Shamass, R.; Rabi, M.; Abarkan, I.; Ferreira, F.P.V.; Tsavdaridis, K.D. Inverse machine learning for the design of perforated beams: Parent section and material prediction. Eng. Appl. Artif. Intell. 2026, 164, 113275. [Google Scholar] [CrossRef]
- De Wolf, C.; Byers, B.S.; Raghu, D.; Gordon, M.; Schwarzkopf, V.; Triantafyllidis, E. D5 digital circular workflow: Five digital steps towards matchmaking for material reuse in construction. npj Mater. Sustain. 2024, 2, 36. [Google Scholar] [CrossRef]
- Selvaraj, S.; Chan, T.M. Recommendations for implementing circular economy in construction: Direct reuse of steel structures. J. Constr. Steel Res. 2024, 214, 108439. [Google Scholar] [CrossRef]
- Xu, X.; Liu, C. Physics-guided deep learning for damage detection in CFRP composite structures. Compos. Struct. 2024, 331, 117889. [Google Scholar] [CrossRef]
- Guo, J.; Baharvand, A.; Tazeddinova, D.; Habibi, M.; Safarpour, H.; Roco-Videla, A.; Selmi, A. An intelligent computer method for vibration responses of the spinning multi-layer symmetric nanosystem using multi-physics modeling. Eng. Comput. 2022, 38, 4217–4238. [Google Scholar] [CrossRef]
- Apalak, M.K.; Karaboga, D.; Akay, B. The artificial bee colony algorithm in layer optimization for the maximum fundamental frequency of symmetrical laminated composite plates. Eng. Optim. 2014, 46, 420–437. [Google Scholar] [CrossRef]
- Thai, C.H.; Tran, T.D.; Phung-Van, P. A size-dependent moving Kriging meshfree model for deformation and free vibration analysis of functionally graded carbon nanotube-reinforced composite nanoplates. Eng. Anal. Bound. Elem. 2020, 115, 52–63. [Google Scholar] [CrossRef]
- Vadyala, S.R.; Betgeri, S.N.; Matthews, J.C.; Matthews, E. A review of physics-based machine learning in civil engineering. Results Eng. 2022, 13, 100316. [Google Scholar] [CrossRef]
- Choudhary, P.K. Optimal design of variable angle tow laminated composite plate for maximum fundamental frequency using genetic algorithm. Mech. Based Des. Struct. Mach. 2025, 53, 7050–7067. [Google Scholar] [CrossRef]
- Li, A.; Ding, Z.; Dieng, A.B.; Beeson, R. Constraint-aware diffusion models for trajectory optimization. In Dynamic Data Driven Applications Systems; International Conference on Dynamic Data Driven Applications Systems; Springer Nature: Cham, Switzerland, 2024; pp. 308–316. [Google Scholar]
- Faruque, M.O.; Hossain, M.A.; Alam, S.M.; Khalid, M. Constraint-aware wind power forecasting with an optimized hybrid machine learning model. Energy Convers. Manag. X 2025, 27, 101026. [Google Scholar] [CrossRef]
- Wang, B.; Zhang, P.; Xiang, Y.; Wang, D.; Wu, B.; Wang, X.; Chen, A. Advancing structural failure analysis with physics-informed machine learning in engineering applications. Engineering 2025, in press. [Google Scholar] [CrossRef]
- Vlasenko, T.; Hutsol, T.; Vlasovets, V.; Glowacki, S.; Nurek, T.; Horetska, I.; Bilovod, O. Ensemble learning-based sustainable approach to rebuilding metal structures prediction. Sci. Rep. 2025, 15, 1210. [Google Scholar] [CrossRef]
- Etim, B.; Al-Ghosoun, A.; Renno, J.; Seaid, M.; Mohamed, M.S. Machine learning-based modeling for structural engineering: A comprehensive survey and applications overview. Buildings 2024, 14, 3515. [Google Scholar] [CrossRef]
- Gharib, S.; Moselhi, O. A conceptual framework for enabling structural steel reuse utilizing circular economy in modular construction. Sustainability 2025, 17, 8945. [Google Scholar] [CrossRef]
- Baniya, S.; Maity, D. A comprehensive review of theoretical concepts and advancements in physics-informed neural networks with applications in structural engineering. Artif. Intell. Rev. 2025, 59, 49. [Google Scholar] [CrossRef]
- Munaro, M.R.; Tavares, S.F. Materials passport review: Challenges and opportunities toward a circular economy building sector. Built Environ. Proj. Asset Manag. 2021, 11, 767–782. [Google Scholar] [CrossRef]
- Byers, B.; De Wolf, C. QR code-based material passports for component reuse across life cycle stages in small-scale construction. Circ. Econ. 2023, 1. [Google Scholar] [CrossRef]
- Elghaish, F.; Hosseini, M.R.; Kocaturk, T.; Arashpour, M.; Ledari, M.B. Digitalised circular construction supply chain: An integrated BIM–blockchain solution. Autom. Constr. 2023, 148, 104746. [Google Scholar] [CrossRef]
- Brown, D.; Pimentel, R.J.; Sansom, M.R. Structural steel reuse: Assessment, testing and design principles. Steel Constr. Inst. 2019, 72. Available online: https://steel-sci.com/assets/downloads/steel-reuse-event-8th-october-2019/SCI_P427.pdf (accessed on 18 January 2026).
- Bartsch, H.; Eyben, F.; Voelkel, J.; Feldmann, M. On the development of regulations for the increased reuse of steel structures. In Life-Cycle of Structures and Infrastructure Systems; CRC Press: Boca Raton, FL, USA, 2023; pp. 1287–1294. [Google Scholar]
- Brütting, J.; Vandervaeren, C.; Senatore, G.; De Temmerman, N.; Fivet, C. Environmental impact minimization of reticular structures made of reused and new elements through life cycle assessment and mixed-integer linear programming. Energy Build. 2020, 215, 109827. [Google Scholar] [CrossRef]
- Minunno, R.; O’Grady, T.; Morrison, G.M.; Gruner, R.L. Exploring environmental benefits of reuse and recycle practices: A circular economy case study of a modular building. Resour. Conserv. Recycl. 2020, 160, 104855. [Google Scholar] [CrossRef]
- Zhuang, G.L.; Shih, S.G.; Wagiri, F. Circular economy and sustainable development goals: Exploring the potentials of reusable modular components in circular economy business model. J. Clean. Prod. 2023, 414, 137503. [Google Scholar] [CrossRef]
- Fujita, M.; Masuda, T. Application of various NDT methods for the evaluation of building steel structures for reuse. Materials 2014, 7, 7130–7144. [Google Scholar] [CrossRef]
- Chen, H.M.; Wang, Y.; Zhou, K.; Lam, D.; Guo, W.; Li, L.; Hopkinson, P. Reclaiming structural steels from end-of-service-life composite structures for reuse: An assessment of the viability of different methods. Dev. Built Environ. 2022, 10, 100077. [Google Scholar] [CrossRef]
- Abbas, M.; Shafiee, M. Structural health monitoring (SHM) and determination of surface defects in large metallic structures using ultrasonic guided waves. Sensors 2018, 18, 3958. [Google Scholar] [CrossRef]
- González, A.; Sendra, C.; Herena, A.; Rosquillas, M.; Vaz, D. Methodology to assess the circularity in building construction and refurbishment activities. Resour. Conserv. Recycl. Adv. 2021, 12, 200051. [Google Scholar] [CrossRef]
- Gordon, M.; Batallé, A.; De Wolf, C.; Sollazzo, A.; Dubor, A.; Wang, T. Automating building element detection for deconstruction planning and material reuse: A case study. Autom. Constr. 2023, 146, 104697. [Google Scholar] [CrossRef]
- City of Amsterdam. Policy: Circular Economy; City of Amsterdam: Amsterdam, The Netherlands, 2022; Available online: https://www.amsterdam.nl/en/policy/sustainability/circular-economy/ (accessed on 18 January 2026).
- Çetin, S.; Raghu, D.; Honic, M.; Straub, A.; Gruis, V. Data requirements and availabilities for material passports: A digitally enabled framework for improving the circularity of existing buildings. Sustain. Prod. Consum. 2023, 40, 422–437. [Google Scholar] [CrossRef]
- Byers, B.; Emmenegger, P.; Hunhevicz, J.; Schumm, D.; Heisel, F.; Hall, D.; De Wolf, C. Decentralized phygital identifiers for circular construction. SSRN Electron. J. 2024, 4946912. [Google Scholar] [CrossRef]
- Rabi, M.; Abarkan, I.; Sarfarazi, S.; Ferreira, F.P.V.; Alkherret, A.J. Automated design and optimization of concrete beams reinforced with stainless steel. Struct. Concr. 2025. early view. [Google Scholar] [CrossRef]
- Despotovic, M.; Glatschke, M. Challenges and opportunities of artificial intelligence and machine learning in circular economy. SocArXiv 2024, 6qmhf_v1. [Google Scholar] [CrossRef]
- Noman, A.A.; Akter, U.H.; Pranto, T.H.; Haque, A.K.M. Machine learning and artificial intelligence in circular economy: A bibliometric analysis and systematic literature review. Ann. Emerg. Technol. Comput. 2022, 6, 13–40. [Google Scholar] [CrossRef]
- Cohen, J.; Huan, X. Uncertainty-aware explainable AI as a foundational paradigm for digital twins. Front. Mech. Eng. 2024, 9, 1329146. [Google Scholar] [CrossRef]
- De Lima, F.A.; Seuring, S.; Genovese, A. How to enhance circular supply chains? Aligning R-imperatives, uncertainty management and sustainability. Int. J. Oper. Prod. Manag. 2024, 44, 836–858. [Google Scholar] [CrossRef]
- Kalakoski, I.K.; Sirén, R.M. Designing with uncertainty—Built heritage in circular economy. In Proceedings of the International Conference CITAA Cities Identity Through Architecture and Arts, Pisa, Italy, 5–7 December 2022; Springer Nature: Cham, Switzerland, 2022; pp. 303–312. [Google Scholar]
- Psarommatis, F.; May, G.; Azamfirei, V. Product reuse and repurpose in circular manufacturing: A critical review of key challenges, shortcomings and future directions. J. Remanufact. 2025, 15, 273–310. [Google Scholar] [CrossRef]
- Fulgione, M.; Palladino, S.; Esposito, L.; Sarfarazi, S.; Modano, M. A multi-stage framework combining experimental testing, numerical calibration, and AI surrogates for composite panel characterization. Buildings 2025, 15, 3900. [Google Scholar] [CrossRef]
- Mascolo, I.; Sarfarazi, S.; Modano, M. Feasible and robust optimisation of cable forces in suspended bridges: A two-stage metaheuristic approach. Mech. Res. Commun. 2025, 150, 104554. [Google Scholar] [CrossRef]
- EN 1990:2023; Eurocode 0: Basis of Structural and Geotechnical Design. European Committee for Standardization (CEN): Brussels, Belgium, 2023.
- EN 1993-1-1:2022; Eurocode 3: Design of Steel Structures—Part 1-1: General Rules and Rules for Buildings. European Committee for Standardization (CEN): Brussels, Belgium, 2022.
- CEN/TS 17440:2020; Assessment and Retrofitting of Existing Structures. European Committee for Standardization (CEN): Brussels, Belgium, 2020.
- EN 1990-2:2026; Eurocode: Basis of Structural and Geotechnical Design—Part 2: Assessment of Existing Structures. European Committee for Standardization (CEN): Brussels, Belgium, 2026.
- EN 1090-2:2018+A1:2024; Execution of Steel Structures and Aluminium Structures—Part 2: Technical Requirements for Steel Structures. European Committee for Standardization (CEN): Brussels, Belgium, 2018 + Amendment 2024.
- ISO 6892-1:2019; Metallic Materials—Tensile Testing—Part 1: Method of Test at Room Temperature. International Organization for Standardization (ISO): Geneva, Switzerland, 2019.
- ISO 18265:2013; Metallic Materials—Conversion of Hardness Values. International Organization for Standardization (ISO): Geneva, Switzerland, 2013.
- EN 10204:2004; Metallic Products—Types of Inspection Documents. European Committee for Standardization (CEN): Brussels, Belgium, 2004.
- CEN/TR 10261:2023; Iron and Steel—European Standards for the Determination of Chemical Composition (Technical Report prepared by ECISS/TC 102). European Committee for Standardization (CEN): Brussels, Belgium, 2023.
- Bartsch, H.; Eyben, F.; Voelkel, J.; Knobloch, M.; Feldmann, M.; Stroetmann, R.; Charlier, M.; Husson, W.; Beyer, A.; Braendstrup, C.; et al. Guidance on establishing European rules for the design of reclaimed steel components for reuse. In JRC Technical Report JRC144410; Publications Office of the European Union: Luxembourg, 2025. [Google Scholar]
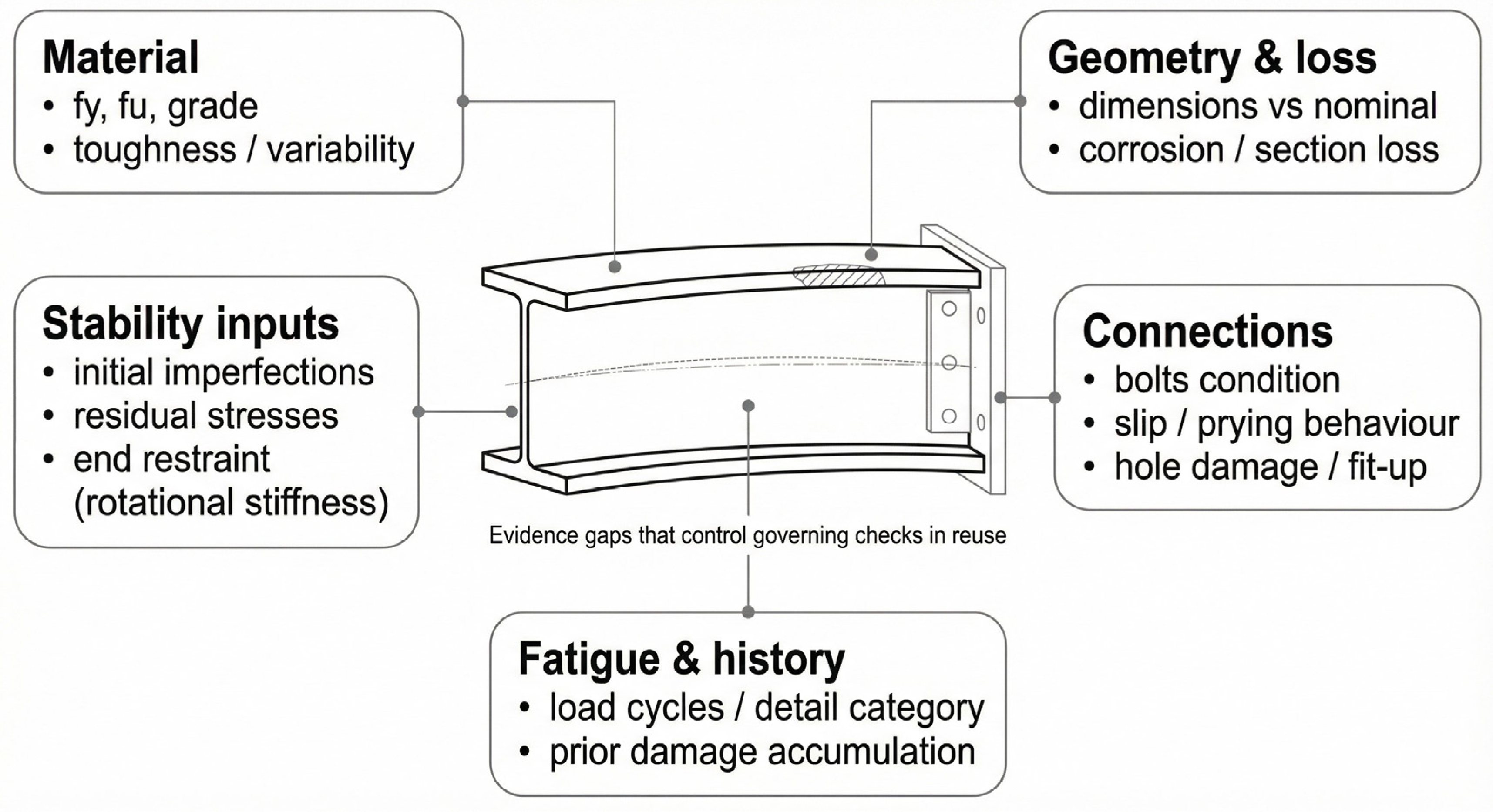
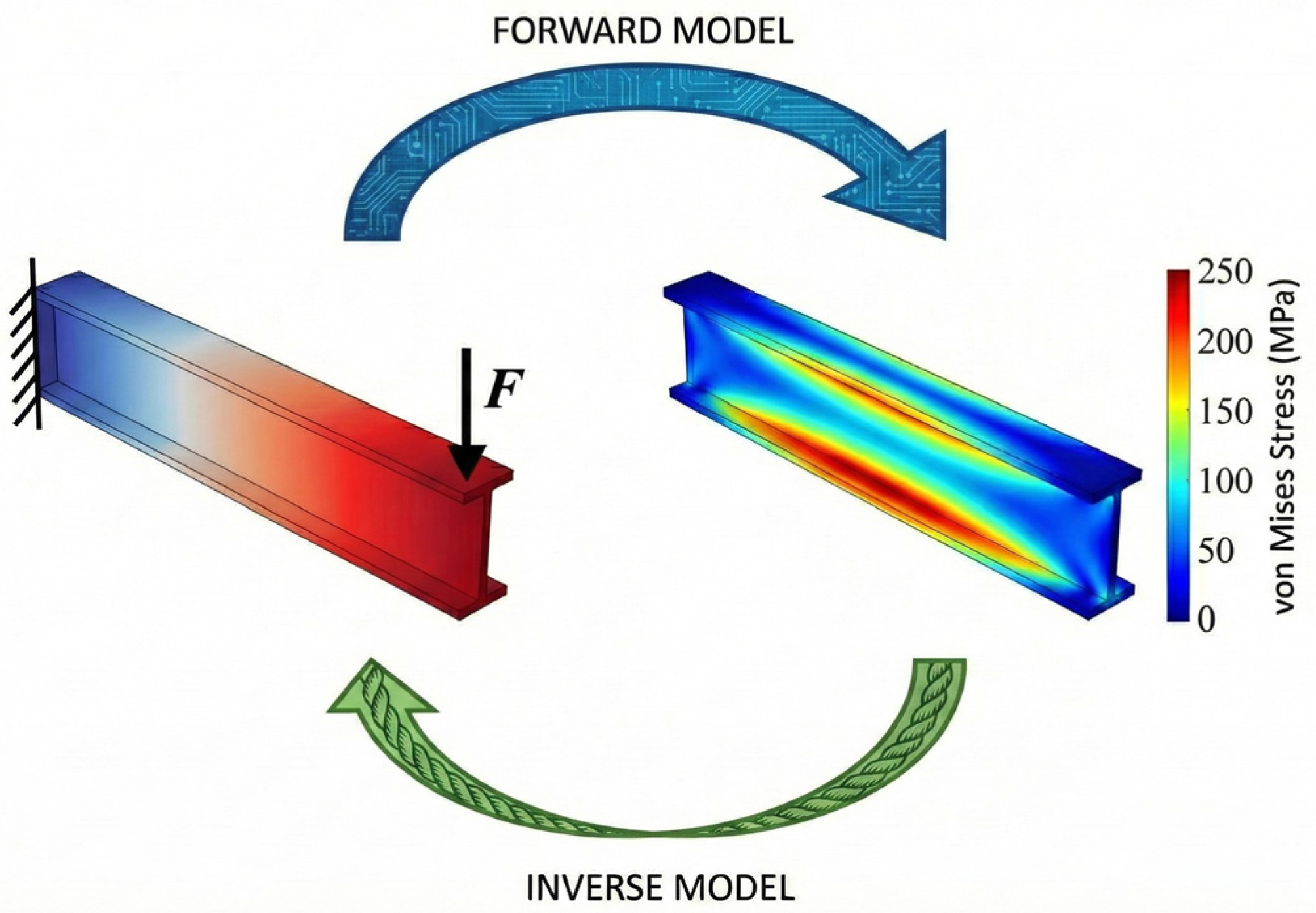
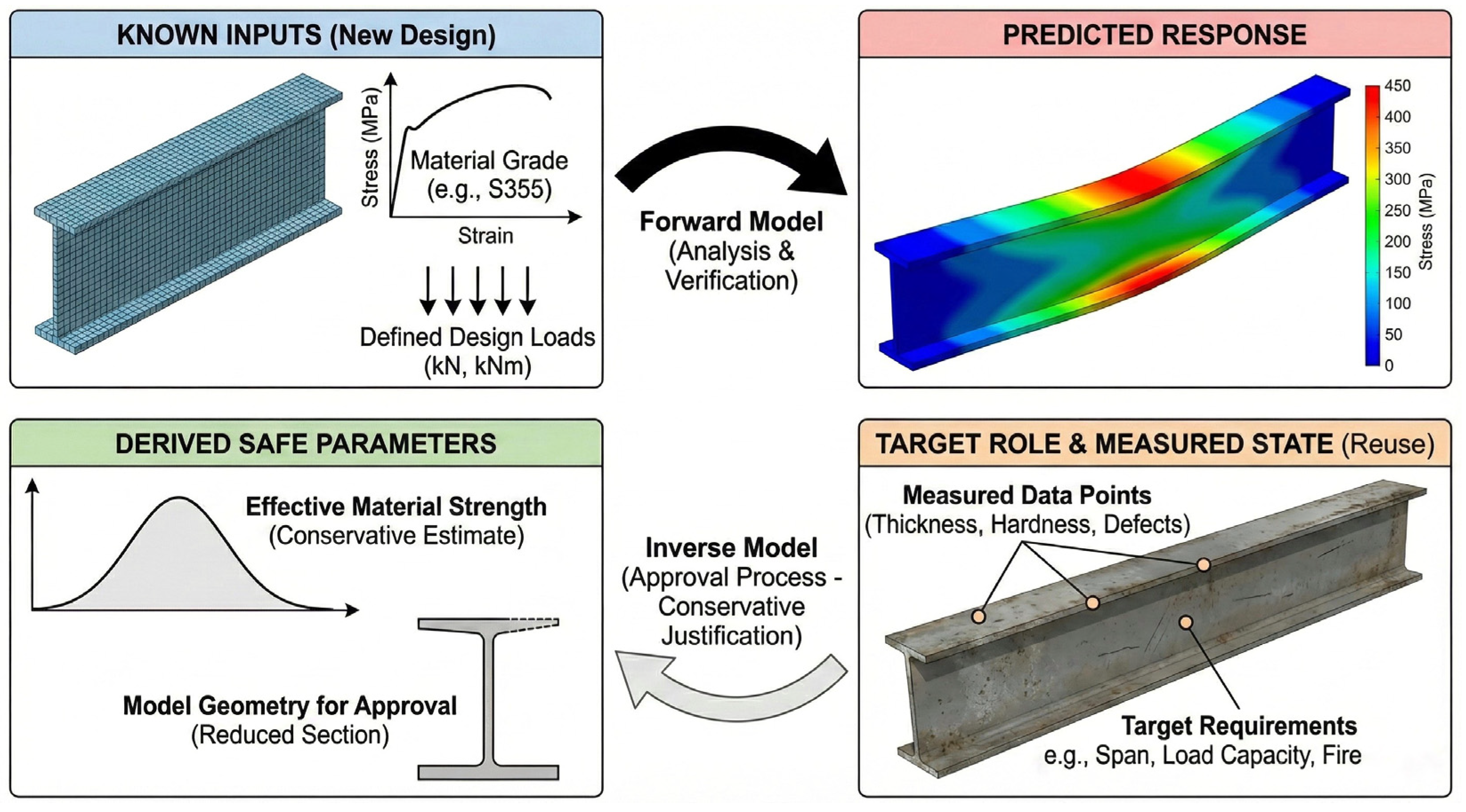
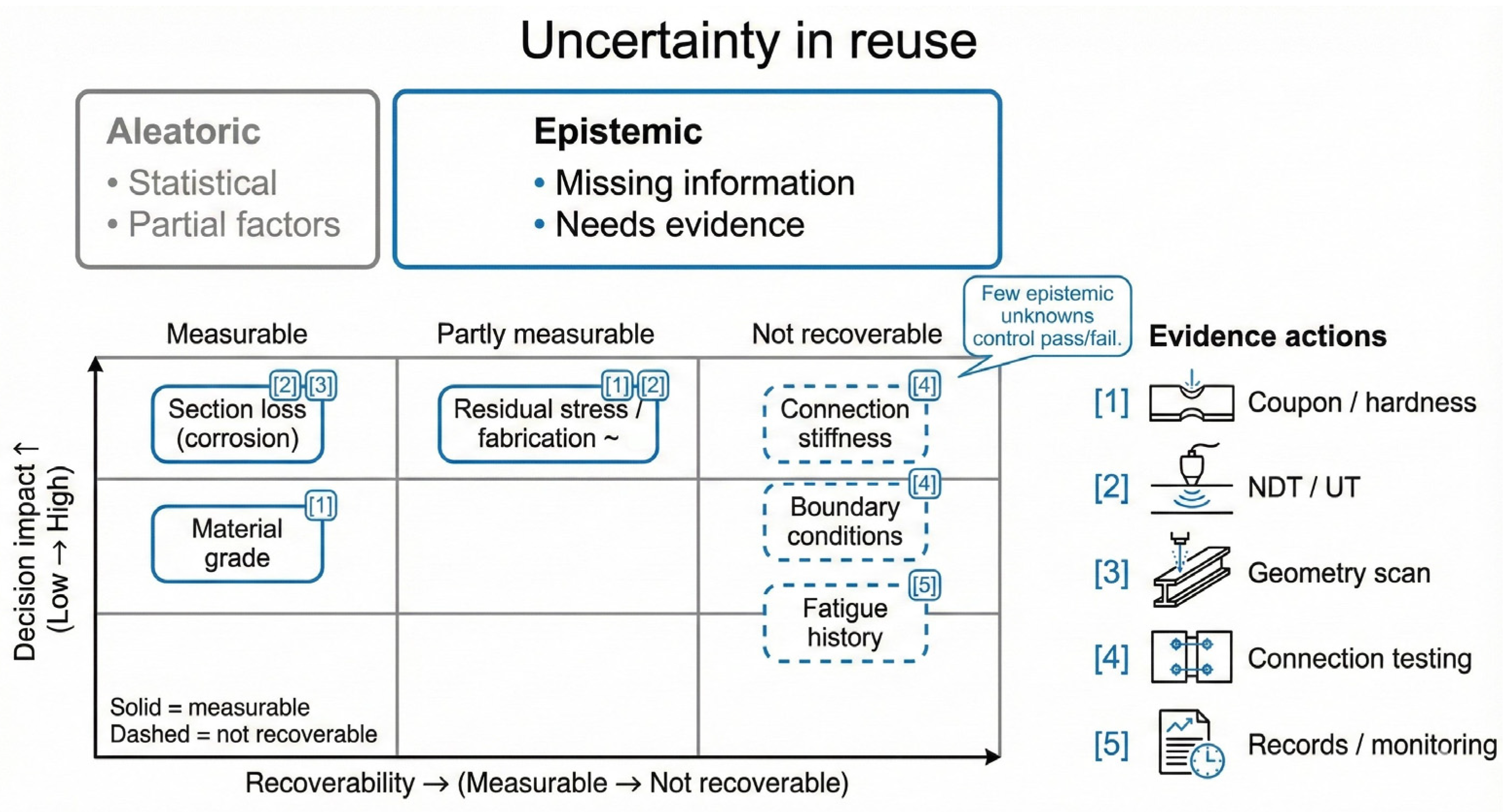
| Stage | Core Question | Typical Outputs | Main Failure Mode in Reuse |
|---|---|---|---|
| Analysis | Given inputs, what is the response? | Demand/capacity ratios, stresses, deflections | Inputs not reliable (grade, BCs, damage) |
| Optimization | What configuration meets targets best? | Best layout/assignment under constraints | Search proposes options that are hard to justify |
| Approval | Can this element be responsibly accepted? | Decision, justification, evidence trail | Cannot defend assumptions and margins |
| Uncertainty Source | Why It Matters Mechanically | Most Sensitive Checks | Evidence Actions (Typical) |
|---|---|---|---|
| Section loss/pitting | Changes area and class locally | Buckling, local capacity, connection region | Thickness mapping, local measurements |
| Imperfections + residual stress | Controls stability reserve | Column buckling, LTB of beams | Straightness survey, conservative imperfection bounds |
| Unknown steel grade | Shifts yield and toughness | Plastic capacity, fracture-sensitive details | Coupons/hardness proxy/conservative grade class |
| Connection condition | BC stiffness and failure modes change | End restraint, slip, prying, bolt shear | Bolt inspection, hole checks, detailing limits |
| Fatigue history | Damage accumulation is path-dependent | Detail categories, welded joints | Service record, conservative fatigue class, NDT |
| Fire protection state | Thermal resistance may be lost | Fire design checks | Inspection, re-protection assumptions |
| ML Method Family (Typical Form) | Typical Reuse Inputs (Examples) | Decision Output That Is Valid in Reuse | Typical Failure Mode in Reuse | Practical Control (How to Use Safely) |
|---|---|---|---|---|
| Evidence-to-property inference (supervised regression; often ensembles) | NDT signals (magnetic, hardness), coupons when available, section ID | Updated resistance-related properties (e.g., yield/tensile proxies) with uncertainty ranges | False confidence when the NDT regime differs from the training | Use as certificate replacement support; require uncertainty bands and “low-support” flag |
| Feasibility ranking/triage (classification or scoring models) | Geometry, damage descriptors, basic loading class, connection tags | ranking of candidates (prioritize inspection/verification effort) | Over-rejection due to biased labels, or unsafe ranking near boundaries | Train/validate on decision labels; report sensitivity drivers, not only score |
| Surrogate response models (regression surrogates; reduced-order ML) | parametric FE data, geometry, restraint envelope assumptions | fast demand/capacity estimates for exploring many assignments | Extrapolation under wrong restraint/degradation assumptions | Restrict to bounded envelopes; use to prune options, then verify with code checks |
| Mechanics-regularized learning (physics-informed/constraint-aware) | same as surrogates, plus explicit constraints and regime boundaries | mechanically admissible trends; conservative resistance bounds under envelopes | Wrong constraints due to incorrect BC or degradation model | Treat BC and degradation as uncertain variables; check admissibility across the envelope |
| Stock-to-demand matching/allocation (combinatorial search; optimization-driven ML) | inventory database, demand set, fabrication constraints (cutting, holes, welding limits) | assignment proposals that minimize waste, modifications, and embodied impact | Solutions that are “optimal” but not approvable due to detailing/BC issues | Couple matching with admissibility filters; reject options that fail governing checks |
| Anomaly/out-of-pattern detection (unsupervised or one-class models) | audit data distributions; NDT feature vectors; geometry families | flag cases that are not comparable to known evidence | False alarms when audit quality varies | Use only as a “caution trigger”; prompts targeted inspection, not rejection |
| Step | Conventional Workflow (Typical) | Decision-Oriented Workflow (This Paper) | Reproducibility Artifact (What Gets Stored) |
|---|---|---|---|
| Audit | Visual inspection and limited notes; unknowns often implicit | Structured audit with explicit unknowns register; focus on decision-critical measurements | Audit sheet, unknowns register, and evidence log |
| Matching | Manual search; often limited to what is available locally | Constraint-based matching supported by structured records and marketplace/platform logic | Candidate list, constraint reasons, and versioned selections |
| Mechanical verification | Code checks with conservative default assumptions | Code checks over an assumption envelope where needed; parameters tightened by evidence and certification routes | Verification report, assumption envelope statement |
| Approval documentation | Capacity value and short justification | Approval package with governing mechanism, evidence inventory, sensitivity drivers, and conditions for acceptance; linked to component identity | Approval template, traceable component record |
| Approval Package Item | What It Should Contain (Practical Definition) | Why Is It Required in Reuse | Typical “Red Flag” If Missing |
|---|---|---|---|
| Decision category | Clear label: Accept/Conditional accept/Reject | Forces a decision framing and prevents “informal optimism” | Only a capacity number is reported, with no decision statement |
| Governing mechanism and check type | Named failure mode and verification family (e.g., member buckling, LTB, net section at connection, fatigue detail, serviceability) | Makes the decision auditable in engineering language and links it to code intent | Generic statements such as “model predicts safe” without stating which check governs |
| Resistance bound under an assumption envelope | A conservative interval or lower bound for resistance under a defined range of boundary conditions and degradation states | Reuse is sensitive to modelling assumptions, especially restraint and stability | Single-value capacity with no statement of boundary condition assumptions |
| Evidence inventory | List of evidence used: measurements, tests, inspection notes, photos, drawings; include dates and responsible party | Reuse decisions depend on evidence quality and traceability | Inputs are treated as “known” but source is unclear or mixed across documents |
| Unknowns register (explicit missing data) | What is unknown: grade, thickness map, straightness, connection condition, fatigue history, fire protection state, etc. | Prevents silent assumptions and hidden uncertainty | Assumptions are implicit and only appear indirectly in the result |
| Sensitivity ranking (decision-critical unknowns) | Top variables that can flip pass/fail, with direction of influence | Focuses inspection/testing where it reduces decision risk most | Extra tests are proposed without showing that they affect the decision |
| Model support/applicability flag | Indication of whether the case is inside the model’s reliable domain (and why), or “low-support” | Reuse often contains out-of-distribution cases; the model must admit limits | The model appears confident even when inputs are missing or atypical |
| Recommended action and rationale | If conditional, what measurement/test/strengthening/monitoring is needed, and how it reduces uncertainty or increases margin | Turns prediction into a controlled engineering plan | Conditional acceptance is stated without specifying the condition in measurable terms |
| Conservatism statement | Where conservatism was introduced (assumption envelope, safety margin, reduction factors) and why | Shows targeted conservatism instead of blanket reductions | Excessively conservative reductions applied with no link to uncertainty drivers |
| Traceability and reproducibility | Version of data/model, key parameters, and a simple record of runs or scenarios considered | Required for review, disputes, and future reuse cycles | Results cannot be reproduced or updated when new evidence arrives |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2026 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license.
Share and Cite
Sarfarazi, S.; Fulgione, M.; Fabbrocino, F. Physics-Informed Decision Framework for Reuse of Reclaimed Steel Members Under Uncertainty. Metals 2026, 16, 171. https://doi.org/10.3390/met16020171
Sarfarazi S, Fulgione M, Fabbrocino F. Physics-Informed Decision Framework for Reuse of Reclaimed Steel Members Under Uncertainty. Metals. 2026; 16(2):171. https://doi.org/10.3390/met16020171
Chicago/Turabian StyleSarfarazi, Sina, Marcello Fulgione, and Francesco Fabbrocino. 2026. "Physics-Informed Decision Framework for Reuse of Reclaimed Steel Members Under Uncertainty" Metals 16, no. 2: 171. https://doi.org/10.3390/met16020171
APA StyleSarfarazi, S., Fulgione, M., & Fabbrocino, F. (2026). Physics-Informed Decision Framework for Reuse of Reclaimed Steel Members Under Uncertainty. Metals, 16(2), 171. https://doi.org/10.3390/met16020171








