Aging Kinetics and Activation Energy-Based Modeling of Electrical Conductivity Evolution in a Cu–4Ti Alloy

Abstract

The aging behavior and electrical performance evolution of Cu–4Ti alloy were systematically investigated through experimental characterization and theoretical modeling. A series of solution and aging treatments were conducted at temperatures ranging from 450 °C to 600 °C for durations of 1–420 min, with and without 50% cold deformation. Based on solid-state diffusion theory, the activation energy of the aging process was determined using the Arrhenius relationship combined with regression analysis. The calculated activation energies were 298.5 kcal·mol⁻¹ for the solution-treated alloy and 136.1 kcal·mol⁻¹ for the cold-deformed alloy, indicating that deformation-induced lattice defects substantially accelerate atomic diffusion and precipitation kinetics. A predictive model was further established to describe electrical conductivity as a function of aging temperature and time, with high correlation coefficients (R² = 0.90 for the non-deformed and R² = 0.89 for the deformed condition). The model accurately captures the conductivity evolution under various heat treatment conditions, demonstrating its strong predictive capability. Moreover, kinetic curves were constructed to intuitively represent the relationship between conductivity, temperature, and time, providing a rapid and visual tool for process optimization.

1. Introduction

Copper alloys are widely employed in electrical and electronic components—such as cables, connectors, and contact wires—owing to their outstanding electrical and thermal conductivities [1,2,3]. With the continuous advancement of performance requirements, achieving higher mechanical strength without sacrificing electrical conductivity has become a critical challenge [4]. Various strengthening strategies, including compositional optimization, precipitation hardening, grain refinement, and thermal treatment, have been developed to enhance the strength of copper alloys [5,6,7]. However, these approaches often compromise conductivity to some extent. Among them, precipitation strengthening has proven to be the most effective route for simultaneously attaining high strength and good electrical performance when the alloy composition is fixed [8,9]. Through appropriate precipitation heat treatment, a desirable balance among mechanical strength, electrical conductivity, and processing cost can be achieved [10].

Among precipitation-strengthened copper alloys, Cu–4Ti has attracted extensive attention due to its superior yield strength, elastic limit, electrical conductivity, ductility, and fatigue resistance [11]. Its mechanical and physical properties can be markedly improved through high-temperature solution treatment followed by aging [12]. A typical heat treatment involves solutionizing at approximately 950 °C for 2 h, rapidly quenching in water, and subsequently aging near 500 °C for a designated period. During solution treatment, Ti atoms dissolve completely into the Cu matrix, and rapid quenching retains them in a supersaturated solid solution, providing the thermodynamic driving force for subsequent precipitation. During aging, Ti atoms precipitate from the Cu lattice to form nanoscale strengthening phases, thereby improving the alloy’s strength while maintaining acceptable electrical conductivity through matrix purification.

Extensive studies have demonstrated that Ti precipitates primarily in the form of β′-Cu₄Ti or β-Cu₄Ti during aging, which reduces the Ti content in the Cu matrix and alleviates lattice distortion [13,14]. This, in turn, decreases electron scattering and enhances electrical conductivity. Cold deformation also plays an important role in tuning the alloy’s properties; however, at higher Ti concentrations, the increased dislocation density and formation of deformation twins during cold working can deteriorate conductivity. In general, the electrical conductivity of Cu–4Ti alloys is primarily governed by the residual Ti content in the Cu matrix, whereas the strength improvement is dominated by the size and distribution of precipitates [15,16,17]. Therefore, aging treatment is the key process for optimizing the overall performance of Cu–4Ti alloys [18,19,20]. Establishing predictive models that correlate aging temperature and duration with the resulting electrical conductivity is essential for process optimization and the accelerated development of high-performance Cu–Ti alloys.

Under specific compositional and solution-treatment conditions, the principal factors controlling the microstructural evolution and property variation of Cu–4Ti alloys are aging temperature and aging time. In essence, the performance of Cu–4Ti alloys after aging can be regarded as a function of these two parameters. The microstructural evolution during aging originates from atomic diffusion under thermally activated conditions, characteristic of a solid-state reaction process that can be quantitatively described by the Arrhenius relationship [21,22,23].

In this study, Cu–4Ti alloy was selected as the model material to establish a predictive model for electrical conductivity during aging, based on the Arrhenius equation. The activation energy associated with the aging process was determined, and the effects of cold deformation on the mechanical and electrical properties were systematically investigated. The outcomes of this work provide theoretical insights and practical guidance for optimizing the performance and designing the aging parameters of high-strength Cu–4Ti alloys.

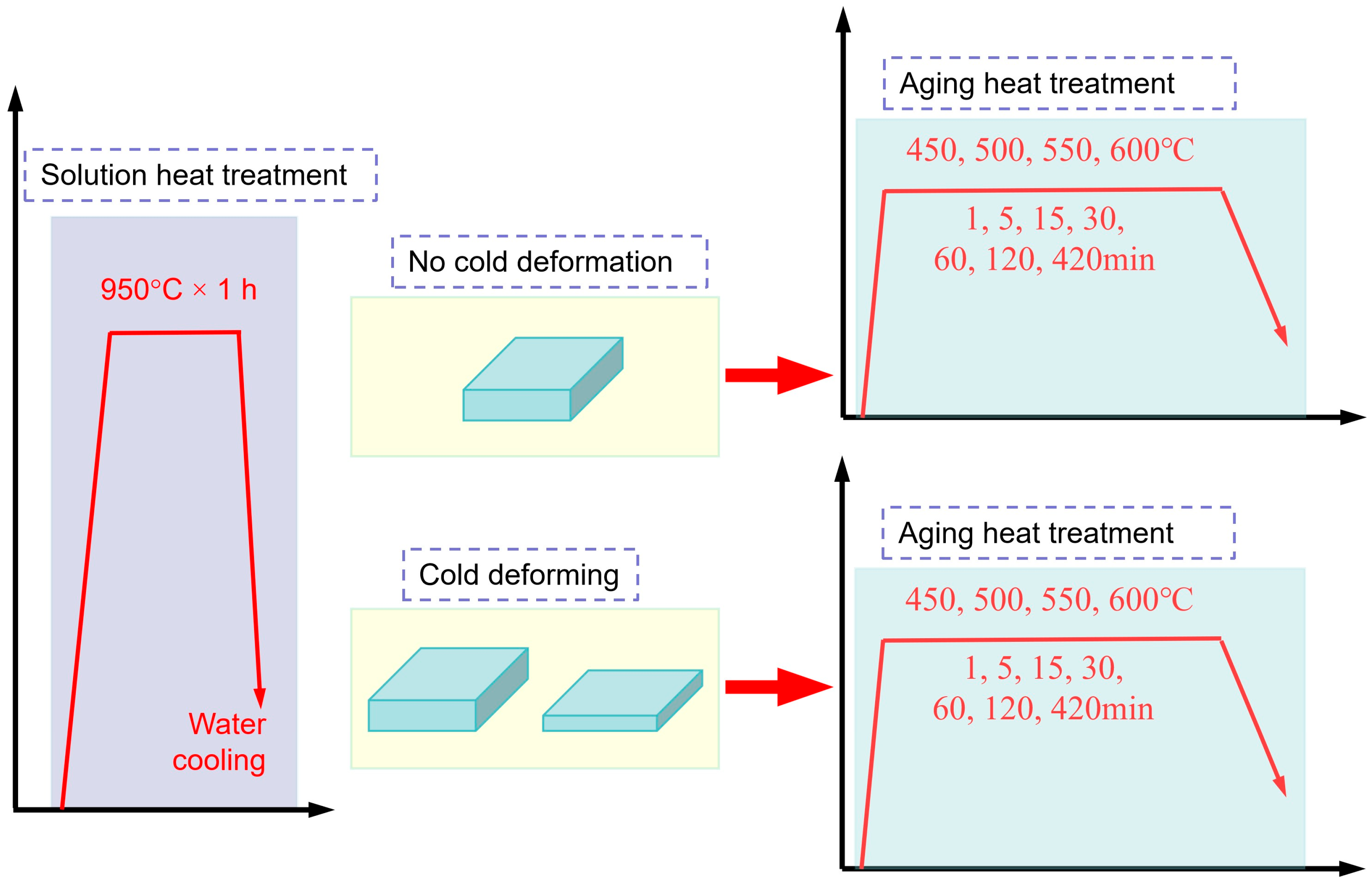
2. Experimental Materials and Methods

The material used in this study was a commercially available Cu–4Ti alloy plate with a thickness of 3 mm under hot-rolled conditions. The nominal chemical composition of the alloy is listed in

Table 1. Chemical composition of Cu–4Ti alloy (wt.%).

Ti	Zn	P	Pb	Mn	Ni	Cu
3.95	0.13	0.065	0.003	0.03	0.01	Bal.

. Following the experimental methodology and processing parameters reported by Konieczny et al. [12], rectangular specimens with dimensions of 3 mm × 20 mm × 20 mm were machined from the plate for subsequent analyses. Prior to heat treatment, all specimens were mechanically ground and ultrasonically cleaned in ethanol to remove surface oxides and contaminants, ensuring consistent surface conditions for all experiments [12].

Solution treatment was carried out in a resistance furnace at 950 °C for 1 h, followed by rapid water quenching within 3 s to ensure complete solid solution of Ti in the Cu matrix. The heat treatment sequence is schematically illustrated in Figure 1.

Aging treatments were then performed at 450, 500, 550, and 600 °C for different durations of 1, 5, 15, 30, 60, 120, and 420 min to investigate the evolution of mechanical and electrical properties. These parameters were selected to establish a predictive model correlating aging temperature and time with electrical conductivity. For comparison, part of the solution-treated specimens were subjected to 50% cold deformation by thickness reduction from 3 mm to 1.5 mm using a laboratory rolling mill. The deformed samples were then aged under the same temperature–time conditions to evaluate the combined effects of aging and deformation on the alloy performance. Electrical conductivity was measured using a calibrated eddy current conductivity meter (e.g., SigmaTest 2.069, Foerster, Germany). Each specimen was measured at least three times, and the average value was reported to ensure accuracy and reproducibility [12].

3. Activation Energy Determination for Aging of Cu–4Ti Alloys

3.1. Rationale and Overview

The activation energy (Q) is the energetic barrier that controls the rate of a thermally activated process [24,25]. For the aging (precipitation) of Cu–4Ti, a larger (Q) means the reaction proceeds more slowly at a given temperature; to obtain the same extent of aging, one must either increase the aging temperature or prolong the aging time [26]. Thus, a reliable estimate of (Q) is of direct practical value for aging process optimization. Microscopically, the aging reaction of Cu–4Ti is driven by atomic diffusion (a thermally activated, solid-state process), and can therefore be treated within the Arrhenius formalism.

3.2. Calculation of Activation Energy During Aging Heat Treatment [27,28,29]

The reaction rate γ of solid-state transformations can be expressed by the Arrhenius equation:

$$\mathsf{\gamma }=Aexp(-{\displaystyle \frac{Q}{RT}}).$$

(1)

where A is the pre-exponential factor, R is the gas constant, T is the absolute temperature, and Q is the activation energy [30,31].

Assuming that after an aging duration of t, the extent of the solid-state reaction is C, Equation (1) can be rewritten as follows:

$$C=\mathsf{\gamma }t=Atexp(-{\displaystyle \frac{Q}{RT}}).$$

(2)

Taking the natural logarithm of both sides yields the following:

$$lnC=lnt-{\displaystyle \frac{Q}{RT}}+lnA.$$

(3)

By converting Equation (3) into the common logarithmic form and rearranging, we obtain the following:

$$logC=logt-({\displaystyle \frac{Q}{2.3R}})(-{\displaystyle \frac{1}{T}})+logA.$$

(4)

where:

A is the pre-exponential factor;

t is the aging (tempering) time (h);

Q is the activation energy associated with the aging process;

R is the ideal gas constant (1.99 cal·mol⁻¹·K⁻¹);

T is the aging (tempering) temperature (K).

Under the above unit system, the activation energy Q is expressed in cal·mol⁻¹, and the unit conversion is given by 1 cal·mol⁻¹ = 4.1868 J·mol⁻¹.

In Equation (4), log A is treated as a constant. To ensure numerical stability and to avoid negative values of log C during the regression analysis, a sufficiently large constant value (log A = 50) is adopted [27,28,29]. This treatment is commonly employed in activation energy-based modeling of solid-state reactions. It should be emphasized that the absolute value of log A does not influence the calculated activation energy Q, which is determined solely by the slope of the regression relationship. The constant log A mainly serves to maintain positive values of the reaction progress parameter λ and to facilitate stable statistical fitting.

Letting log C = λ, we can rewrite the expression as follows:

$$\lambda =logt-{\displaystyle \frac{Q}{2.3R}}(-{\displaystyle \frac{1}{T}})+50.$$

(5)

Obviously, λ (log C) is a physical parameter associated with the extent of the solid-state reaction during aging. The magnitude of λ directly determines the degree of aging and, consequently, the final properties of the alloy. Therefore, the aging property M of the copper alloy can be regarded as a function of λ, that is,

$$M=f(\lambda )=f[logt-({\displaystyle \frac{Q}{2.3R}})(-{\displaystyle \frac{1}{T}})+50].$$

(6)

To establish the functional relationship between M, the aging temperature T, and the aging time t, the activation energy Q must first be determined. In general, it is difficult to measure Q directly. Therefore, Q is typically obtained indirectly based on experimental data and statistical regression analysis.

From Equation (6), it is evident that the post-aging property M is a function of the parameter λ. For convenience, the following can be assumed:

$$M=alogt+b(-{\displaystyle \frac{1}{T}})+c.$$

(7)

Assume that a Cu–4Ti alloy specimen is subjected to n sets of aging treatments under various temperatures (T_i) and durations (t_i), and the corresponding property values (M_i) are experimentally measured, where i = 1, 2, 3, …, n. Substituting these experimental data into Equation (7) yields a set of n linear equations with three unknown parameters (a, b, and c). By applying the least squares method, the numerical values of these parameters can be obtained. To determine the activation energy Q, Equation (7) can be transformed as follows:

$$M=a[logt+({\displaystyle \frac{b}{a}})(-{\displaystyle \frac{1}{T}})+50]-50a+c.$$

(8)

By comparing Equation (8) with Equation (5), the following relationship can be established:

$$b=-{\displaystyle \frac{Q}{2.3R}}.$$

(9)

Thus,

$$Q=-2.3R({\displaystyle \frac{b}{a}}).$$

(10)

By substituting the experimentally derived constants a and b into Equation (10), the activation energy Q of the aging process can be quantitatively determined.

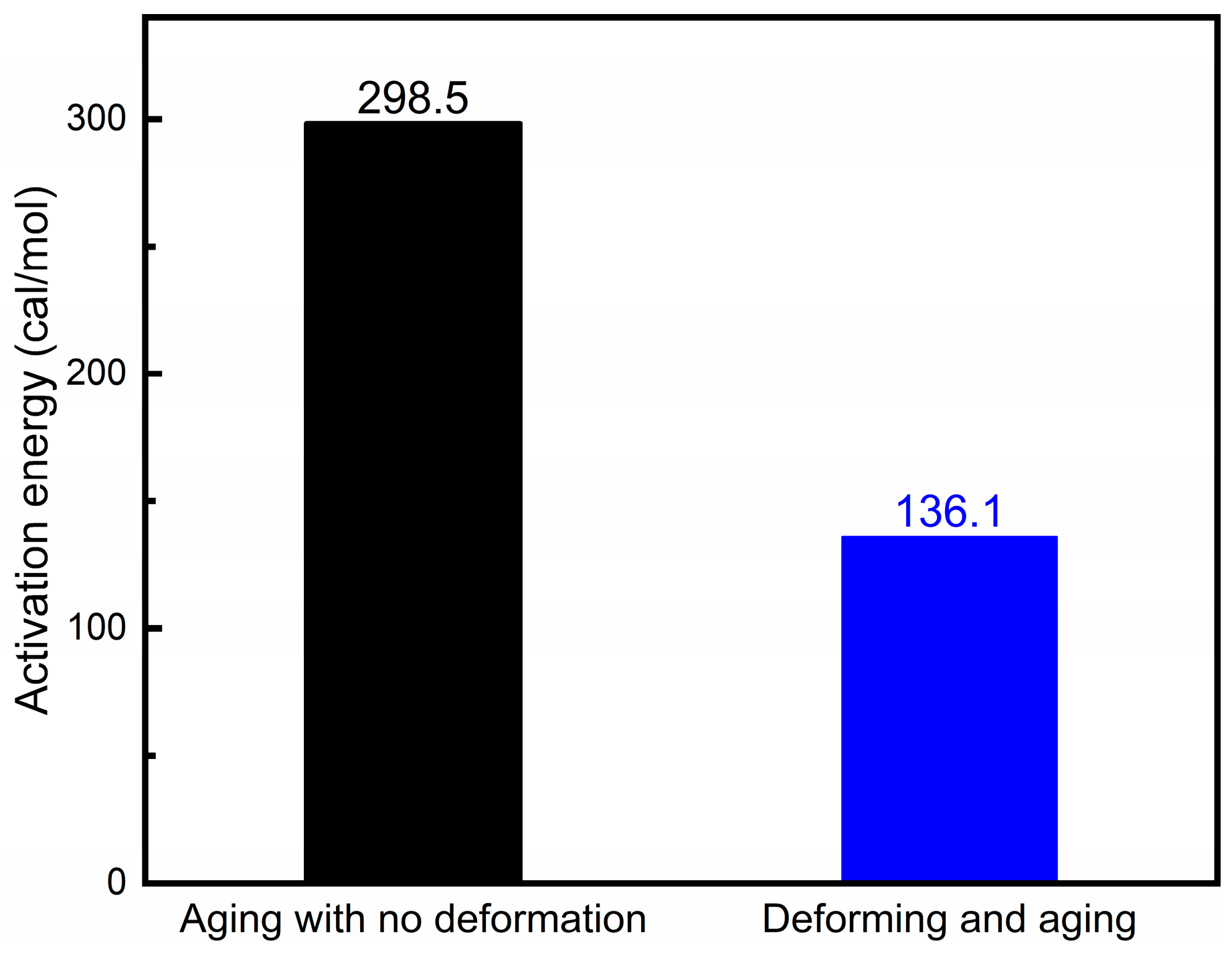
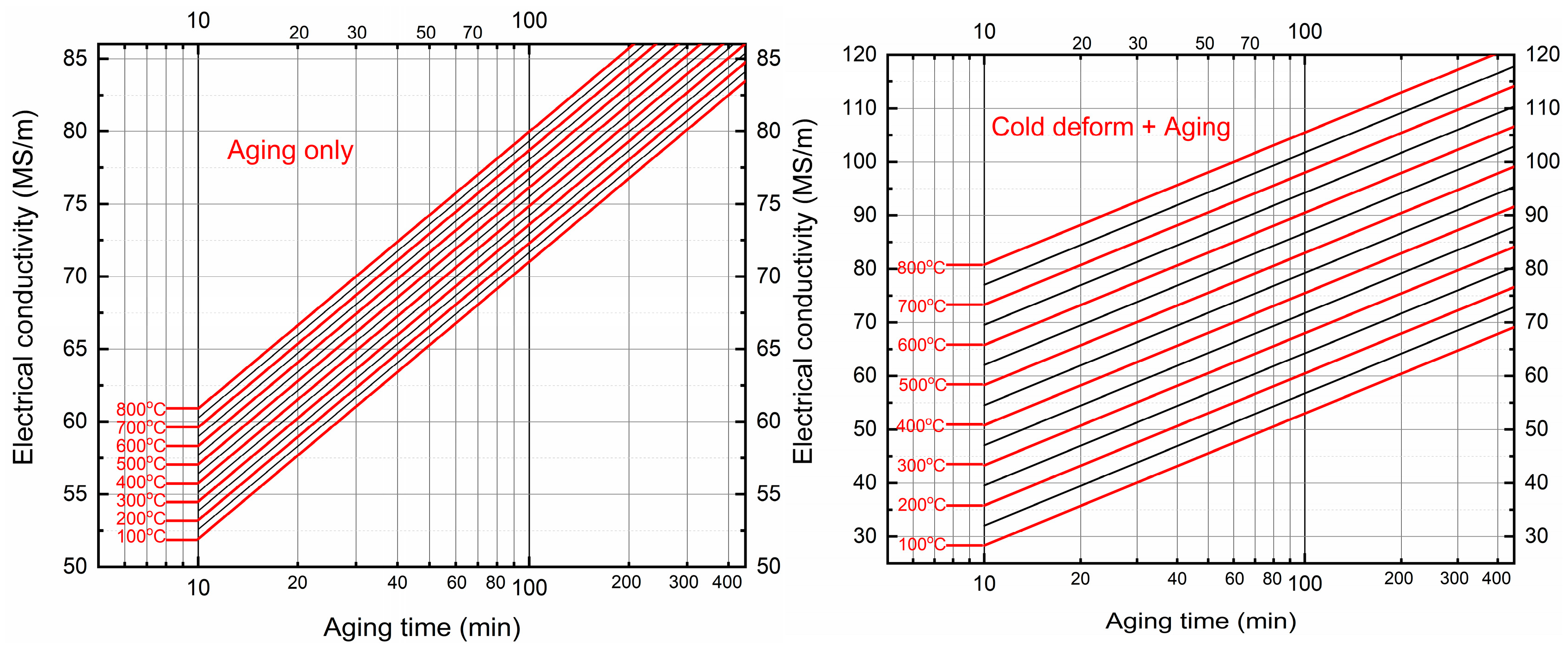
3.3. Statistical Determination of Activation Energy for Cu–4Ti Alloy

To quantitatively determine the activation energy Q, the regression coefficients a, b, and c must first be calculated.

For this purpose, Equation (7) was reformulated by introducing the following variable substitutions:

$$x_0=1, x_1=logt, x_2=-{\displaystyle \frac{1}{T}}, d_0=c, d_1=a, d_2=b, \overline{y}=M.$$

After substitution, the regression equation can be expressed as follows:

$$\overline{y}=d_0{x}_0+d_1{x}_1+d_2{x}_2.$$

(11)

For each experimental group (x₁, x₂), corresponding to a measured value y, the regression equation yields a predicted value $\overline{y}$.

The deviation between the experimental measurement y and the estimated value $\overline{y}$ is defined as follows:

$$y-\overline{y}=y-(d_0{x}_0+d_1{x}_1+d_2{x}_2).$$

(12)

When the sum of squared errors reaches its minimum, the optimal estimates of the unknown parameters (a, b, and c) can be obtained.

According to the least squares method [32,33], the augmented matrix of the error equation system derived from Equation (12) is expressed as follows:

$$\left[\begin{array}{cccc}\sum x_0& \sum x_1& \sum x_2& \sum y\\ \sum x_1& \sum {x_1}^2& \sum x_1{x}_2& \sum x_{1}y\\ \sum x_2& \sum x_1{x}_2& \sum {x_2}^2& \sum x_{2}y\end{array}\right].$$

(13)

By substituting the measured variable values from the regression equation into Equation (13), the parameters a, b, and c can be determined [12]. Subsequently, substituting these parameters into Equation (10) allows for the calculation of the activation energy Q.

For the Cu–4Ti alloy subjected only to aging treatment, the measured conductivity M values under various aging temperatures T and aging times t were used to compute the variables in Equation (11). The calculated results are summarized in

Table 2. Calculated variables in the regression equation for Cu–4Ti alloy.

$\sum {\mathit{x}}_0$	$\sum {\mathit{x}}_1$	$\sum {\mathit{x}}_2$	$\sum \mathit{y}$	$\sum {{\mathit{x}}_1}^2$	$\sum {\mathit{x}}_1{\mathit{x}}_2$	$\sum {\mathit{x}}_1\mathit{y}$	$\sum {{\mathit{x}}_2}^2$	$\sum {\mathit{x}}_2\mathit{y}$
28.00	−9.25	0.04	1846.20	20.10	0.01	−284.91	0.00	2.32

.

By substituting the data from Table 2 into the augmented matrix (Equation (13)), the regression equation for the aging process of Cu–4Ti alloy can be expressed as follows:

$$\overline{y}=48.09x_0-0.2176x_1+1412.67x_2.$$

(14)

The obtained regression coefficients are a = −0.2176 and b = 1412.67. Substituting these values into Equation (10) yields the activation energy:

$$Q=-2.3R({\displaystyle \frac{b}{a}})=298.5 \mathrm{k}\mathrm{c}\mathrm{a}\mathrm{l}/\mathrm{m}\mathrm{o}\mathrm{l}.$$

(15)

For the Cu–4Ti alloy that underwent 50% cold deformation prior to aging treatment, the activation energy was similarly calculated using the same statistical method.

The result is given by the following:

$$Q=-2.3R({\displaystyle \frac{b}{a}})=136.1 \mathrm{k}\mathrm{c}\mathrm{a}\mathrm{l}/\mathrm{m}\mathrm{o}\mathrm{l}.$$

(16)

A comparison of the activation energies for both conditions—without and with prior deformation—is presented in Figure 2.

From Figure 2, it is evident that the activation energy of the purely aged Cu–4Ti alloy is 298.5 cal/mol, whereas that of the cold-deformed and subsequently aged alloy is significantly lower at 136.1 cal/mol. The substantial reduction in activation energy after cold deformation indicates that deformation effectively enhances atomic diffusion during aging. Consequently, comparable aging effects can be achieved at lower temperatures or within shorter durations. This phenomenon arises because cold deformation introduces residual strain energy into the lattice, leading to a locally unstable high-energy state.

During subsequent aging, this stored strain energy facilitates atomic movement and accelerates diffusion, thereby reducing the apparent activation energy required for the aging process.

The activation energy differences obtained for the two processing conditions reflect the underlying precipitation behavior occurring during aging. Although the present study focuses on extracting kinetic parameters through electrical conductivity measurements rather than direct microstructural imaging, the conductivity-based kinetic trends are consistent with the well-established precipitation sequence in Cu–Ti alloys. Numerous TEM, SEM, XRD, and atom-probe investigations have shown that aging within 450–600 °C promotes the formation of metastable β′–Cu₄Ti precipitates, followed by the evolution toward the stable β–Cu₄Ti phase at longer times or higher temperatures [34,35,36,37].

Because electrical conductivity is highly sensitive to the depletion of Ti solute atoms from the Cu matrix, it serves as a quantitative indicator of precipitation progress and has been widely employed in kinetic studies of the Cu–Ti system. In this work, the monotonic increase in conductivity with aging time directly reflects the progress of β′/β precipitation, and the calculated activation energies correspond well to diffusion-controlled precipitation behavior. The significant decrease in activation energy after 50% cold deformation further supports the established mechanism that deformation-induced dislocations act as fast diffusion pathways, thereby accelerating Ti diffusion and precipitation kinetics.

Thus, even in the absence of direct TEM/SEM/XRD evidence, the activation energy values, diffusion behavior, and conductivity-time evolution obtained here align closely with the known precipitation mechanisms of Cu–4Ti alloys. This supports the reliability of the Arrhenius-based kinetic analysis and provides a physically grounded basis for the predictive model established in the following sections.

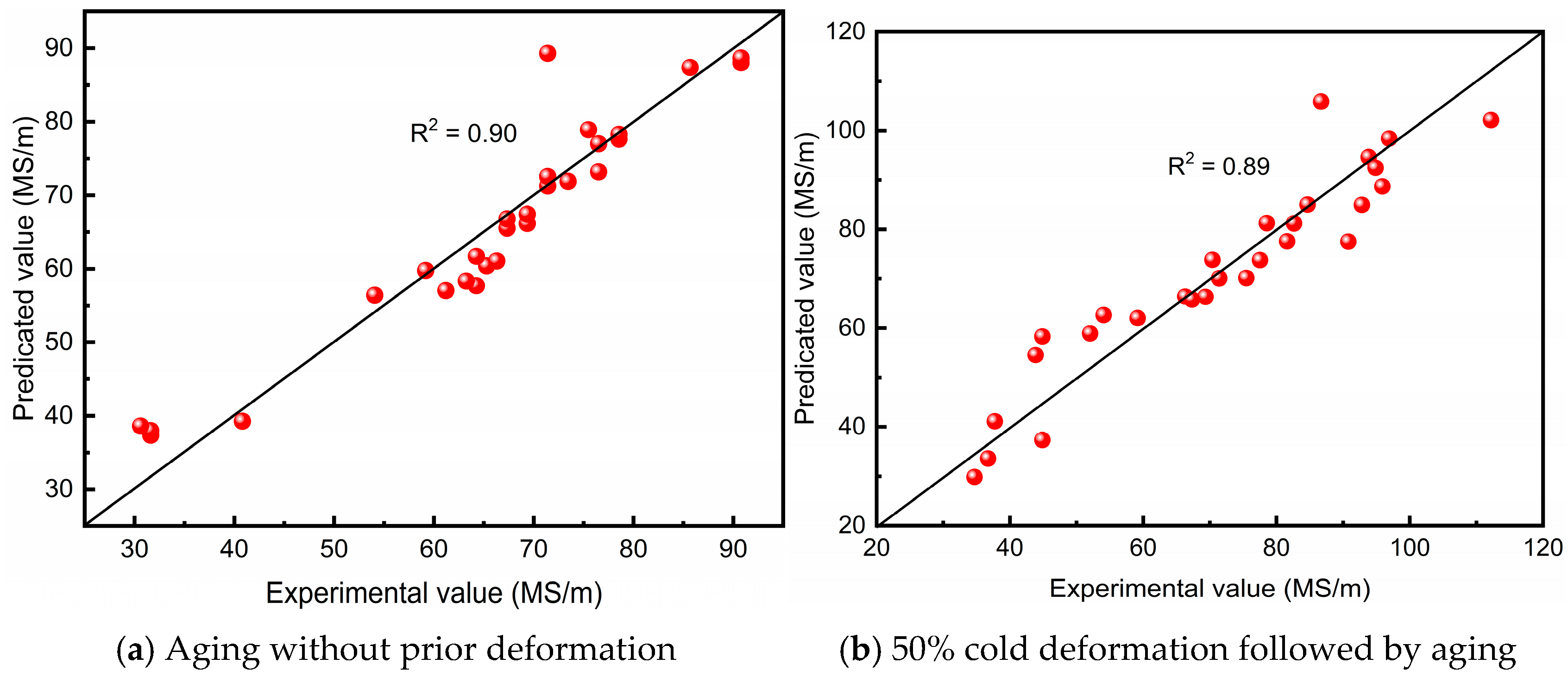
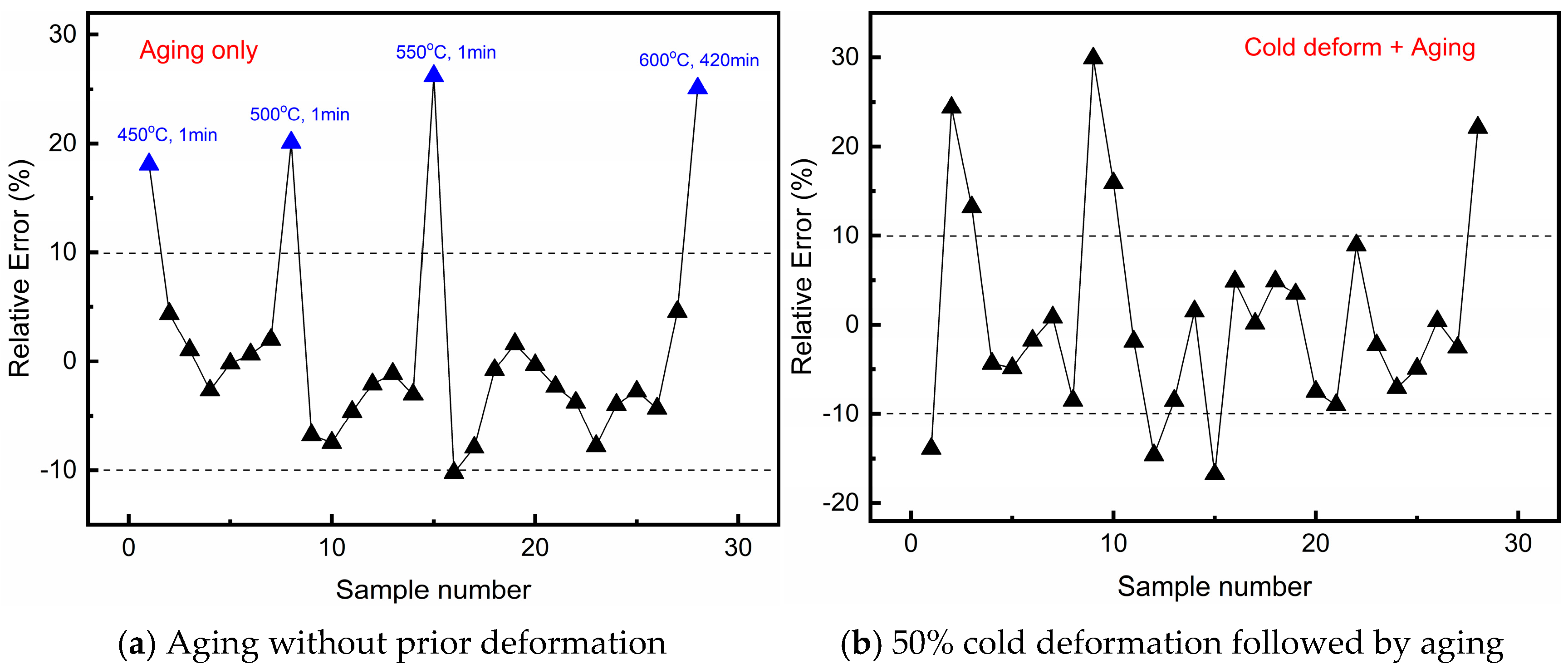
4. Establishment of the Predictive Model for Electrical Conductivity During Aging of Cu–4Ti Alloy

To establish a predictive model for the electrical conductivity of Cu–4Ti alloys subjected to aging heat treatment, the effects of aging temperature and time on electrical conductivity were systematically analyzed. The corresponding experimental results are presented in Figure 3 [12].

As illustrated in Figure 3, the electrical conductivity of the Cu–4Ti alloy exhibits an approximately linear relationship with aging temperature, while showing a logarithmic relationship with aging time. This behavior indicates that temperature serves as a dominant factor accelerating atomic diffusion and phase precipitation, whereas the influence of time follows a diffusion-controlled kinetics pattern.

Based on these observations, a quantitative model describing the dependence of electrical conductivity (σ) on aging temperature (T) and aging time (t) was developed using MATLAB 2025a nonlinear regression analysis.

For the specimens aged without prior deformation, the best-fit empirical relationship is expressed as follows:

$$M=a_{1}T+b_{1}log(t)+c_1 .$$

(17)

where T is the aging temperature (°C), t is the aging time (min), and a₁, b₁, and c₁ are regression coefficients determined by least-squares fitting.

For the specimens subjected to 50% cold deformation prior to aging, the corresponding relationship is given by the following:

$$M=a_{2}T+b_{2}log(t)+c_2 .$$

(18)

where a₂, b₂, and c₂ represent the regression parameters for the deformed condition.

Based on the predictive models established in Equations (17) and (18), the relationship between electrical conductivity, aging temperature, and aging time of the Cu–4Ti alloy was quantitatively fitted using MATLAB 2025a software. For the alloy without prior cold deformation, the functional relationship between electrical conductivity and the aging parameters (temperature and time) can be expressed as follows:

$$M=31.58+0.0128T+19.08logt$$

(19)

For the Cu–4Ti alloy subjected to 50% cold deformation prior to aging, the functional relationship between electrical conductivity, aging temperature, and aging time can be expressed as follows:

$$M=-3.89+0.075T+24.69logt .$$

(20)

The units of temperature and time in Equations (19) and (20) are expressed in degrees Celsius (°C) and minutes (min), respectively.

To evaluate the accuracy of the proposed models, the predicted electrical conductivities were compared with the experimentally measured values under various aging conditions. The comparisons are shown in Figure 4 and Figure 5.

As shown in Figure 4, the predicted values exhibit very good agreement with the experimental data, with coefficients of determination (R²) of 0.90 and 0.89 for the non-deformed and cold-deformed specimens, respectively. This indicates that the established regression models possess high predictive accuracy and statistical significance. Therefore, the proposed models can be reliably employed to predict the electrical conductivity of Cu–4Ti alloys under arbitrary combinations of aging temperature and time, providing valuable guidance for optimizing aging parameters and tailoring the performance of high-strength, high-conductivity Cu–Ti alloys.

As indicated by the relative error results shown in Figure 5, the overall prediction error of the proposed model remains within 30%. The prediction accuracy under the non-deformed condition is noticeably higher than that under the cold-deformed condition, exhibiting smaller relative errors across most aging parameters. This difference can be attributed to the introduction of cold deformation, which significantly increases dislocation density, grain distortion, and residual strain energy in the specimens. These microstructural complexities introduce additional variability into the aging process, thereby reducing the prediction accuracy of the empirical model.

Under the non-deformed condition, larger prediction deviations are observed only under extreme processing parameters, such as very short aging times (e.g., 1 min) or the combined effect of prolonged aging durations and elevated temperatures, for example, aging at 600 °C for 420 min. These conditions lie near the boundaries of the experimental parameter space, where diffusion kinetics and precipitation behavior deviate more strongly from the assumptions underlying the regression model.

5. Physical Basis for the Linear–Logarithmic Temperature–Time Dependencies

The empirical modeling conducted in this study revealed that the electrical conductivity of the Cu–4Ti alloy exhibits an approximately linear dependence on aging temperature, while its evolution with aging time follows a logarithmic trend. This behavior can be physically interpreted by considering the thermally activated nature of diffusion, the precipitation sequence of Cu–Ti alloys, and the strong influence of cold deformation on diffusion pathways.

5.1. Diffusion-Controlled Precipitation and the Linear Temperature Dependence

In Cu–Ti alloys, the strengthening and property evolution during aging are governed by the precipitation of metastable β′–Cu₄Ti and the subsequent formation of stable β–Cu₄Ti phases. These transformations involve long-range diffusion of Ti atoms in the Cu matrix and are therefore controlled by the Arrhenius relation.

Since electrical conductivity is primarily influenced by the decrease in solute Ti atoms in the supersaturated solid solution, the conductivity increase is directly related to the cumulative amount of Ti removed from the matrix by precipitation. For the relatively narrow temperature range used in this study (450–600 °C), the exponential diffusion term can be approximated as quasi-linear with temperature when expressed in Arrhenius coordinates. This leads to an approximately linear dependence of conductivity on aging temperature, as the precipitation rate increases almost proportionally with diffusion coefficient increments within this range.

Thus, the observed linearity with respect to temperature reflects the dominant role of diffusion-controlled solute depletion in the Cu matrix.

5.2. Logarithmic Dependence on Aging Time

The evolution of electrical conductivity with aging time exhibits a logarithmic dependence, which is a characteristic feature of diffusion-controlled precipitation processes. This behavior reflects parabolic kinetic characteristics governed by nucleation-and-growth mechanisms, the progressive depletion of solute Ti atoms in the Cu matrix, and the gradual reduction in thermodynamic driving force as the system approaches equilibrium. In the early stages of aging, the Ti supersaturation level is high, leading to rapid nucleation and growth of precipitates and a sharp increase in electrical conductivity.

As aging proceeds, the number of precipitates acting as diffusion sinks increases, while the concentration gradient driving Ti diffusion continuously decreases. Consequently, the diffusion flux of Ti atoms is progressively reduced, resulting in a marked deceleration of precipitation kinetics at longer aging times. This transition from fast early-stage kinetics to slow late-stage kinetics gives rise to a logarithmic time dependence of conductivity evolution, which effectively captures the underlying diffusion-limited nature of the aging process.

Such logarithmic time-dependent behavior has been widely reported in diffusion-controlled precipitation systems, including Cu–Ti, Cu–Cr, and Cu–Be alloys, and is consistent with the classical Johnson–Mehl–Avrami (JMA) framework describing stage-dependent phase transformation kinetics. The observed log-time dependence therefore has a clear physical basis rooted in solute diffusion, precipitate evolution, and the progressive reduction in driving force during aging.

5.3. Influence of Cold Deformation: Dislocation Density and Accelerated Diffusion Paths

When 50% cold deformation is introduced prior to aging, the evolution of electrical conductivity is markedly accelerated. This behavior originates from the substantial increase in lattice defects induced by plastic deformation, particularly the dramatic rise in dislocation density. Dislocations act as high-diffusivity pathways (pipe diffusion), effective heterogeneous nucleation sites for precipitates, and sources of stored strain energy that promote atomic mobility. Because diffusion along dislocations typically requires a much lower activation energy than lattice diffusion, the effective activation energy governing the aging process is significantly reduced, as evidenced by the decrease from 298.5 to 136.1 kcal·mol⁻¹ observed in this study.

In addition to dislocation-assisted diffusion, cold deformation introduces a variety of deformation-induced defects, including stacking faults, subgrain boundaries, and micro-shear bands. These defects provide short-circuit diffusion paths for Ti atoms, further enhancing long-range atomic transport and accelerating precipitation kinetics. The high density of defects also lowers the nucleation energy barrier for metastable β′–Cu₄Ti precipitates, leading to an earlier onset of precipitation, more rapid depletion of Ti from the Cu matrix, and a correspondingly faster increase in electrical conductivity during aging.

Furthermore, cold deformation may influence precipitate morphology by promoting the formation of finer and more uniformly distributed precipitates rather than coarse plate-like structures. This refinement increases the effective interfacial area available for solute diffusion, thereby enhancing precipitation efficiency. The combined effects of dislocation-assisted diffusion, heterogeneous nucleation, short-circuit diffusion pathways, and precipitate refinement result in a stronger temperature sensitivity and more pronounced nonlinearity in the time-dependent conductivity evolution of the deformed alloy. This physically grounded interpretation explains the observed reduction in activation energy and reinforces both the validity and the mechanistic depth of the proposed conductivity prediction model.

6. Kinetic Curve Construction for the Aging Process of Cu–4Ti Alloy

The kinetic curves of the Cu–4Ti alloy provide an intuitive representation of the quantitative relationship among aging performance (M), aging temperature (T), and aging time (t). Compared with purely analytical expressions, these graphical representations offer a more direct and practical means to interpret the influence of process parameters on the evolution of electrical conductivity during aging.

To visualize the interdependence of these variables, the aging temperature (T) was selected at fixed intervals, while the corresponding aging time (t) and electrical conductivity (M) were plotted along the horizontal and vertical axes, respectively. The resulting kinetic curves are presented in Figure 6.

The mathematical relationships established in the previous section (Equations (19) and (20)) represent the analytical form of these kinetic curves. By substituting the experimental data and fitted parameters into these equations, the corresponding kinetic curves were generated, as illustrated in Figure 6. From the plotted results, it is evident that the electrical conductivity of Cu–4Ti alloy increases monotonically with both aging temperature and aging time. At higher temperatures, the diffusion of Ti atoms and the subsequent precipitation of nanoscale Cu₄Ti phases proceed more rapidly, leading to a faster recovery of conductivity. Conversely, at lower temperatures, the kinetics are sluggish and require extended aging durations to reach comparable conductivity levels.

For the alloy subjected to 50% cold deformation prior to aging, the kinetic curves shift upward, indicating that cold work accelerates the aging response. This enhancement is attributed to the increased density of dislocations and lattice defects introduced during deformation, which serve as preferential diffusion paths and nucleation sites for precipitation, thereby reducing the apparent activation energy and shortening the time required to reach peak conductivity.

Overall, these kinetic curves enable a straightforward and visual prediction of the electrical conductivity of Cu–4Ti alloys under arbitrary combinations of aging temperature and time. Moreover, they provide a practical reference for the optimization and design of aging heat treatment parameters, facilitating the tailored development of high-strength, high-conductivity Cu–Ti alloys for advanced electrical applications.

7. Conclusions

In this study, the aging behavior and electrical performance of Cu–4Ti alloy were systematically investigated through experimental measurements and theoretical modeling. By integrating the Arrhenius-based diffusion theory with regression analysis, a predictive framework for electrical conductivity evolution during aging was established. The key findings are summarized as follows:

(1) The activation energy for the aging process of the solution-treated Cu–4Ti alloy was determined to be 298.5 kcal·mol⁻¹, while that of the 50% cold-deformed alloy decreased significantly to 136.1 kcal·mol⁻¹. The pronounced reduction in activation energy indicates that cold deformation introduces high-density lattice defects and stored strain energy, which effectively lower the diffusion barrier for Ti atoms, thereby accelerating precipitation and aging kinetics.

(2) A quantitative model was developed to describe the dependence of electrical conductivity on aging temperature and time. The model exhibits excellent agreement with experimental measurements, achieving correlation coefficients of R² = 0.90 (non-deformed) and R² = 0.89 (cold-deformed). This strong correlation validates the model’s reliability in predicting the electrical performance of Cu–4Ti alloys under diverse heat treatment conditions.

(3) Based on the established mathematical model, kinetic curves of the aging process were plotted to intuitively represent the evolution of conductivity with time and temperature. These curves enable rapid estimation of optimal aging parameters, offering a practical tool for process design and performance optimization in high-strength, high-conductivity Cu–Ti alloys.

The combination of experimental characterization and kinetic modeling not only provides a deeper understanding of the thermally activated processes governing the Cu–Ti system but also establishes a theoretical basis for tailoring its mechanical–electrical property balance. The proposed methodology can be extended to other precipitation-strengthened copper alloys to accelerate alloy design and heat treatment optimization.