Development of a TaN-Ce Machine Learning Potential and Its Application to Solid–Liquid Interface Simulations
Abstract
1. Introduction
2. Methodologies
2.1. MLP Model and Training Set Preparation
- [1]
- Bulk distortions: Equilibrium and strained configurations of Ce (fcc, bcc, γ-Ce) and δ-TaN (NaCl type) were generated by isotropic scaling (0.78–1.20) combined with random strains up to 3% and random atomic displacements ≤ 0.03 Å.
- [2]
- High-temperature ab initio molecular dynamics (AIMD) sampling: AIMD trajectories for Ce and TaN were collected at 1000–1500 K. Frames were down-selected using SOAP (Smooth Overlap of Atomic Positions) descriptors and farthest-point sampling (FPS) to avoid redundancy.
- [3]
- Surface slabs: TaN(001), (110), and (111) slabs with both Ta- and N-terminations were relaxed and then perturbed as in step (1).
- [4]
- Solid–liquid interfaces: Slabs of TaN in contact with liquid Ce were equilibrated at 1400–1500 K via AIMD. Representative snapshots were again selected via SOAP + FPS.
- [5]
- Substitution configurations: Additional structures were included in which Ce substitutes Ta or N, and vice versa, to enhance coverage of off-stoichiometric and defective environments.
2.2. MD Settings
- [1]
- The initial TaN structure was first relaxed under the NPT ensemble at the target temperature for 500 ps, allowing the system to reach equilibrium lattice parameters and in-plane dimensions.
- [2]
- The liquid Ce phase was simulated under an NPzAT ensemble, enabling free expansion or compression along the z-axis while fixing the x- and y-dimensions to match the in-plane parameters obtained from the first step. This ensured geometric compatibility between the two phases at the interface.
- [3]
- The equilibrated TaN and Ce structures were then joined along the z-direction, leaving a vacuum gap of ~2.0 Å between them to prevent nonphysical initial contacts. The resulting interfacial model was further relaxed using the NPzAT ensemble for 3.0 ns to observe interfacial structural evolution and elemental interdiffusion.
3. Results and Discussions
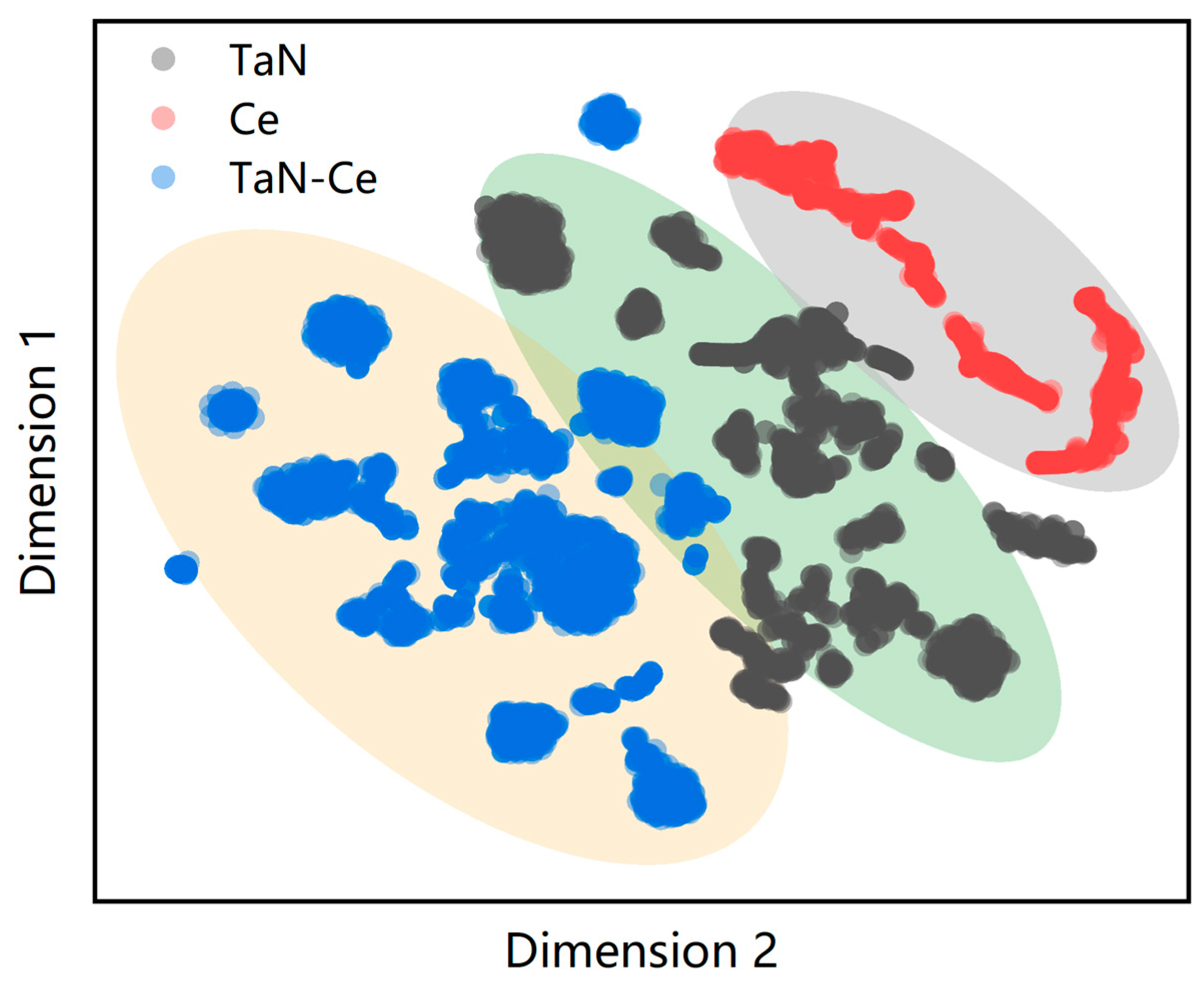
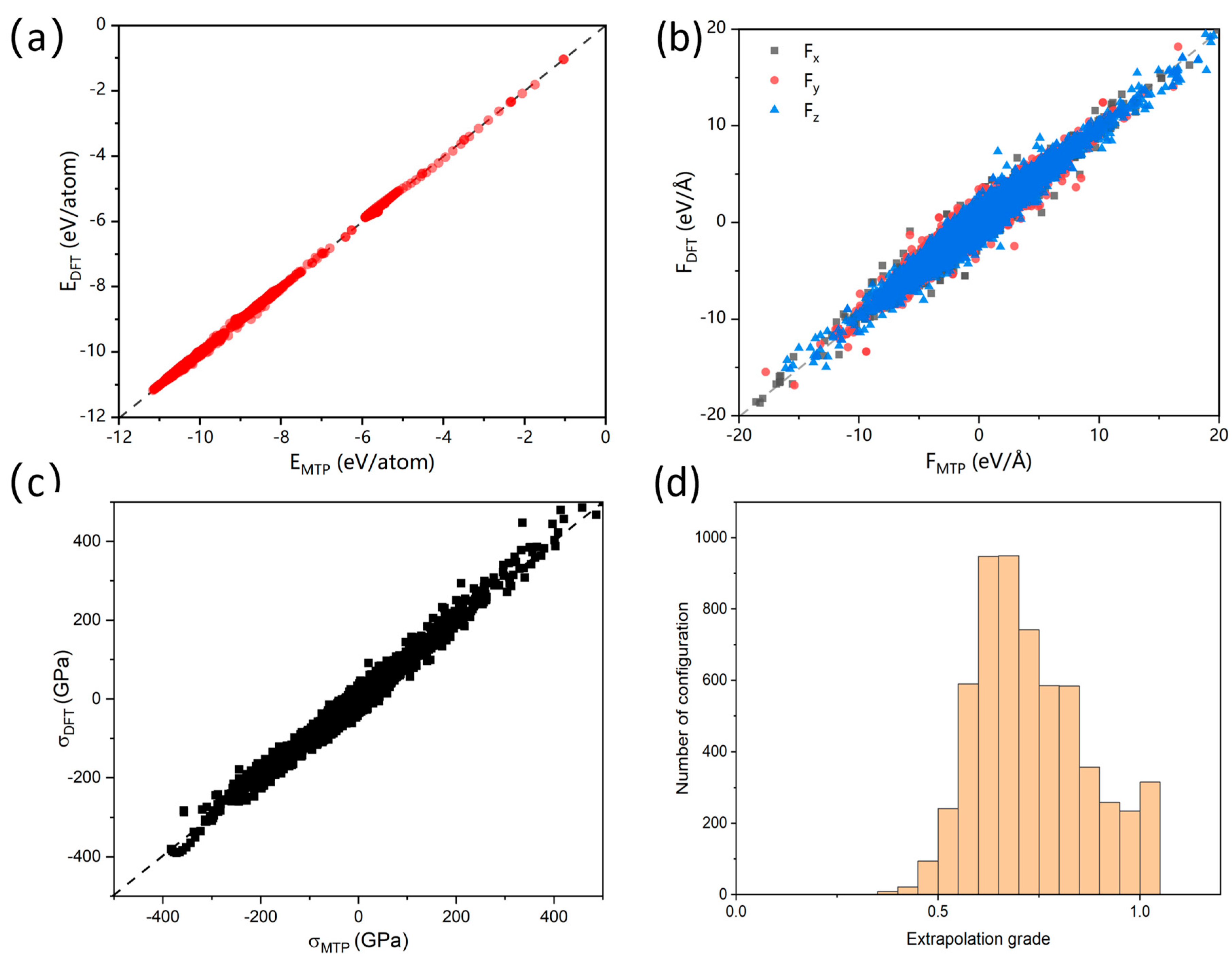
3.1. Accuracy and Error Analysis
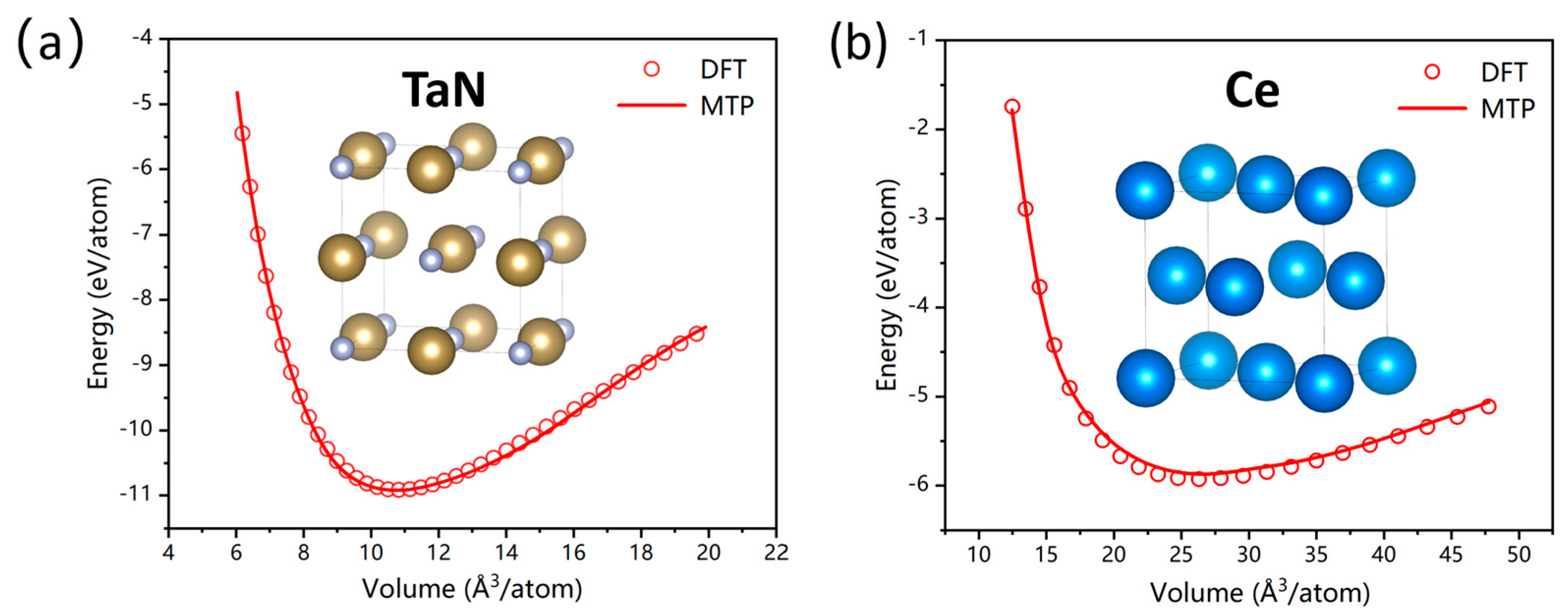
3.2. Validation of Basic Physical Properties
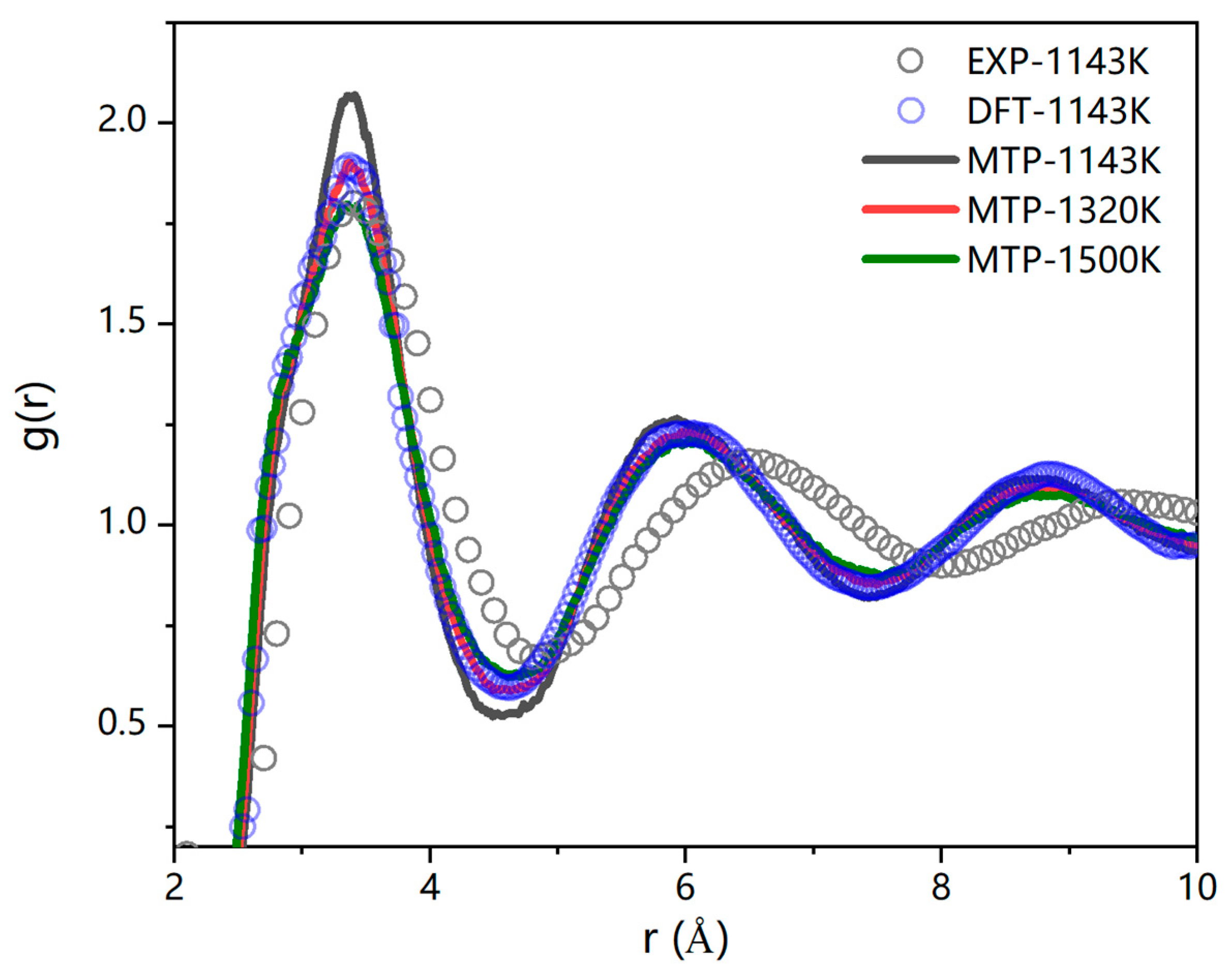
3.3. Simulation of the TaN-Ce Solid–Liquid Interface
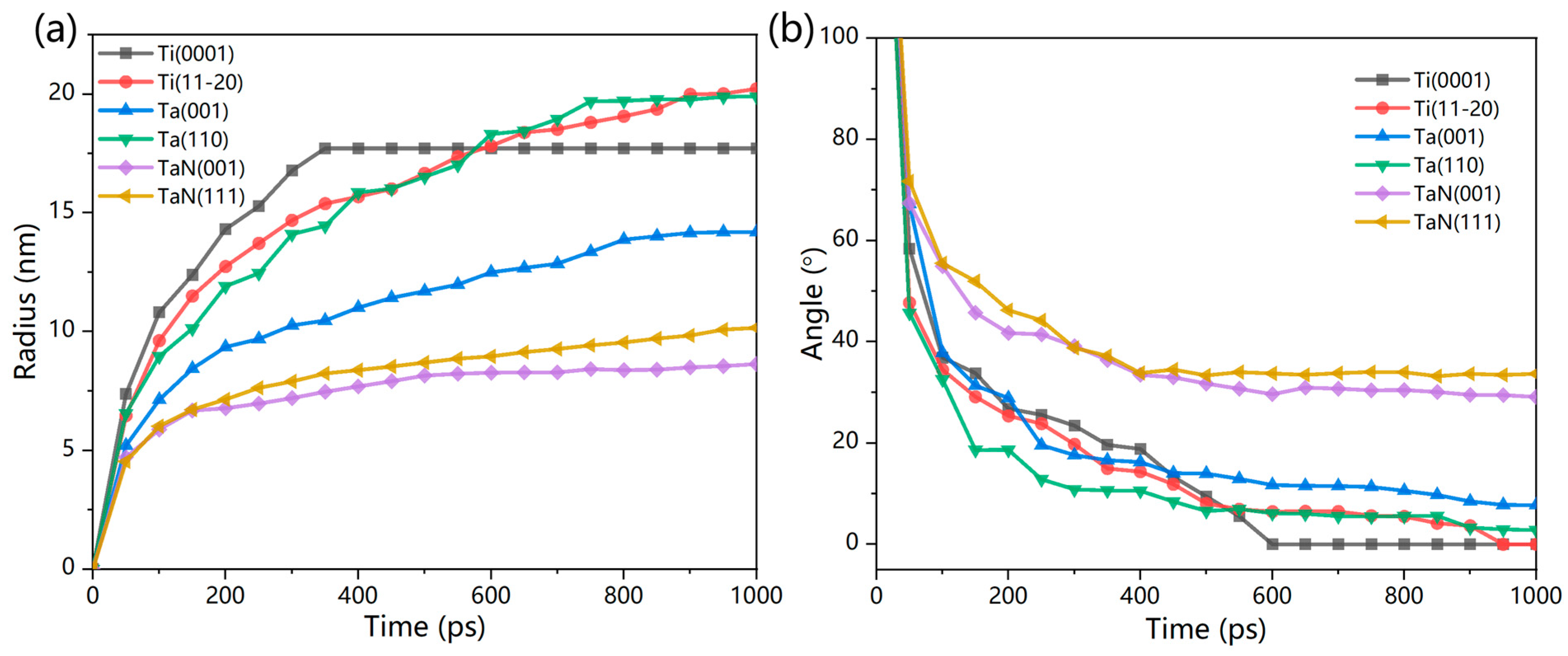
3.4. Wetting Simulation of Liquid Ce Droplets on Ti and Ta Surfaces
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Boring, A.M.; Huang, C.Y.; Gschneidner, K.A., Jr.; McGervey, J.D.; Panigrahi, M.; Usmar, S.G. Study of positron lifetimes in α, β and γ cerium at high pressures. J. Magn. Magn. Mater. 1983, 37, L7–L10. [Google Scholar] [CrossRef]
- Gschneidner, K.A., Jr.; Pecharsky, V.K. The standard state of cerium. J. Phase Equilibria 1999, 20, 612–614. [Google Scholar] [CrossRef]
- Johansson, B.; Luo, W.; Li, S.; Ahuja, R. Cerium: Crystal structure and position in the periodic table. Sci. Rep. 2014, 4, 6398. [Google Scholar] [CrossRef]
- Mimura, K.; Sato, T.; Isshiki, M. Purification of lanthanum and cerium by plasma arc zone melting. J. Mater. Sci. 2008, 43, 2721–2730. [Google Scholar] [CrossRef]
- Balani, K.; Gonzalez, G.; Agarwal, A.; Hickman, R.; O’Dell, J.S.; Seal, S. Synthesis, microstructural characterization, and mechanical property evaluation of vacuum plasma sprayed tantalum carbide. J. Am. Ceram. Soc. 2006, 89, 1419–1425. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, K.; Lyu, X.; Dang, B.; Wei, D.; Zhang, P. Thermal Shock Resistance of Double-glow Plasma Ta/TaC Coating on Graphite Surface. Mater. Rep. 2024, 38, 23080013-9. [Google Scholar]
- Nakamura, D.; Suzumura, A.; Shigetoh, K. Sintered tantalum carbide coatings on graphite substrates: Highly reliable protective coatings for bulk and epitaxial growth. Appl. Appl. Appl. Physics Letters 2015, 106, 082108. [Google Scholar] [CrossRef]
- Hu, X.; Jiang, G.; Fan, P.; Hu, G.; Xu, G.; Wang, W.; Wang, L.; Zhang, H.; Zhong, M. 1000 °C High-Temperature Wetting Behaviors of Molten Metals on Laser-Microstructured Metal Surfaces. Langmuir 2023, 39, 17538–17550. [Google Scholar] [CrossRef] [PubMed]
- Naidich, J.V. The wettability of solids by liquid metals. In Progress in Surface and Membrane Science; Elsevier: Amsterdam, The Netherlands, 1981; Volume 14, pp. 353–484. [Google Scholar]
- Gan, X.; Xiao, S.; Deng, H.; Sun, X.; Li, X.; Hu, W. Atomistic simulations of the Fe (001)–Li solid–liquid interface. Fusion Eng. Des. 2014, 89, 2894–2901. [Google Scholar] [CrossRef]
- Gan, X.; Xiao, S.; Deng, H.; Wang, B.; Sun, X.; Li, X.; Hu, W. Thermodynamic properties of Li, Pb and Li17Pb83 with molecular dynamics simulations. Fusion Eng. Des. 2014, 89, 2946–2952. [Google Scholar] [CrossRef]
- Xu, C.; Meng, X.; Sun, X.; Gan, X.; Li, P.; Xiao, S.; Deng, H.; Li, X.; Hu, W. Atomic scale analysis of the corrosion characteristics of Cu-Li solid-liquid interfaces. J. Alloys Compd. 2018, 763, 1–10. [Google Scholar] [CrossRef]
- Lei, Y.; Zhang, J.; Zhang, Y.; Li, X.; Xu, Y.; Wu, X.; Sun, M.; Liu, C.; Wang, Z. An embedded-atom method potential for studying the properties of Fe-Pb solid-liquid interface. J. Nucl. Mater. 2022, 572, 154041. [Google Scholar] [CrossRef]
- Xu, S.; Fan, X.; Gu, C.; Shi, Y.; Singh, D.J.; Zheng, W. First principles and molecular dynamics study of Li wetting and diffusion on W surfaces. J. Nucl. Mater. 2020, 539, 152345. [Google Scholar] [CrossRef]
- Chen, X.; Sun, X.; Deng, H.; Xiao, S.; Gan, X.; Li, X.; Hu, W. The wetting properties of Li droplet on Cu surfaces: A molecular dynamics study. Comput. Mater. Sci. 2016, 119, 114–119. [Google Scholar] [CrossRef]
- Hashibon, A.; Lozovoi, A.Y.; Mishin, Y.; Elsässer, C.; Gumbsch, P. Interatomic potential for the Cu-Ta system and its application to surface wetting and dewetting. Phys. Rev. B—Condens. Matter Mater. Phys. 2008, 77, 094131. [Google Scholar] [CrossRef]
- Sun, X.; Xiao, S.; Deng, H.; Hu, W. Molecular dynamics simulation of wetting behaviors of Li on W surfaces. Fusion Eng. Des. 2017, 117, 188–193. [Google Scholar] [CrossRef]
- Palafox-Hernandez, J.P.; Laird, B.B.; Asta, M. Atomistic characterization of the Cu–Pb solid–liquid interface. Acta Mater. 2011, 59, 3137–3144. [Google Scholar] [CrossRef]
- Yang, Y.; Olmsted, D.L.; Asta, M.; Laird, B.B. Atomistic characterization of the chemically heterogeneous Al–Pb solid–liquid interface. Acta Mater. 2012, 60, 4960–4971. [Google Scholar] [CrossRef]
- Yang, G.Q.; Li, J.F.; Shi, Q.W.; Kong, L.T. Structural and dynamical properties of heterogeneous solid–liquid Ta–Cu interfaces: A molecular dynamics study. Comput. Mater. Sci. 2014, 86, 64–72. [Google Scholar] [CrossRef]
- Chen, H.; Cai, J.; Zhang, Y.; Lv, X.; Hu, W.; Huang, B. Development of Machine Learning Potentials for Ce-Ti and Ce-Ta Binary Systems and Studies of the Liquid-Solid Interfaces. Corros. Sci. 2025, 246, 112766. [Google Scholar] [CrossRef]
- Novikov, I.S.; Gubaev, K.; Podryabinkin, E.V.; Shapeev, A.V. The MLIP package: Moment tensor potentials with MPI and active learning. Mach. Learn. Sci. Technol. 2020, 2, 025002. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef] [PubMed]
- Plimpton, S. Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Cheng, B.; Griffiths, R.R.; Wengert, S.; Kunkel, C.; Stenczel, T.; Zhu, B.; Deringer, V.L.; Bernstein, N.; Margraf, J.T.; Reuter, K.; et al. Mapping materials and molecules. Acc. Chem. Res. 2020, 53, 1981–1991. [Google Scholar] [CrossRef] [PubMed]
- Mashimo, T.; Tashiro, S.; Toya, T.; Nishida, M.; Yamazaki, H.; Yamaya, S.; Oh-Ishi, K.; Syono, Y. Synthesis of the B1-type tantalum nitride by shock compression. J. Mater. Sci. 1993, 28, 3439–3443. [Google Scholar] [CrossRef]
- Ren, F.; Wang, Y. Pressure-induced phase transition of tantalum mononitride. Thin Solid Films 2011, 519, 3954–3958. [Google Scholar] [CrossRef]
- Liu, C.; Jin, N.; Li, Z.; Liu, X. First-principles calculations on the electronic structure and bonding nature of TaN (111)/TiN (111) interface. J. Alloys Compd. 2017, 717, 326–332. [Google Scholar] [CrossRef]
- Siberchicot, B.; Clerouin, J. Properties of hot liquid cerium by LDA+Umolecular dynamics. J. Phys. Condens. Matter 2012, 24, 455603. [Google Scholar] [CrossRef]
- Dariel, M.P.; Dayan, D.; Languille, A. Self-Diffusion in fcc γ-and bcc δ-Cerium. Phys. Rev. B 1971, 4, 4348. [Google Scholar] [CrossRef]



| Interface | Number of Ta and N Atoms | Number of Ce Atoms | Lx (Å) | Ly (Å) | Lz (Å) |
|---|---|---|---|---|---|
| TaN(001)-Ce | 163,584 | 61,952 | 107.842 | 107.842 | 319.640 |
| TaN(111)-Ce | 161,840 | 61,952 | 109.189 | 108.177 | 315.519 |
| Properties | NaCl-Type TaN | ||
|---|---|---|---|
| Reference | DFT | MTP | |
| a (Å) | 4.336 [28] | 4.442 | 4.442 |
| C11 (GPa) | 772 [29] | 753.0 | 646.4 |
| C12 (GPa) | 132 [29] | 120.2 | 185.8 |
| C44 (GPa) | 65 [29] | 56.5 | 37.7 |
| B (GPa) | 345 [29] | 331.1 | 339.3 |
| Melting point (K) | 3220 | 3193 | |
| (001) (J/m2) | 1.580 | 1.583 | |
| (110) (J/m2) | 2.213 | 2.302 | |
| (111)Ta (J/m2) | 2.422 | 2.525 | |
| (111)N (J/m2) | 1.25 [30] | 1.194 | 1.334 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Cai, J.; Chen, H.; Lv, X.; Huang, B. Development of a TaN-Ce Machine Learning Potential and Its Application to Solid–Liquid Interface Simulations. Metals 2025, 15, 972. https://doi.org/10.3390/met15090972
Zhang Y, Cai J, Chen H, Lv X, Huang B. Development of a TaN-Ce Machine Learning Potential and Its Application to Solid–Liquid Interface Simulations. Metals. 2025; 15(9):972. https://doi.org/10.3390/met15090972
Chicago/Turabian StyleZhang, Yunhan, Jianfeng Cai, Hongjian Chen, Xuming Lv, and Bowen Huang. 2025. "Development of a TaN-Ce Machine Learning Potential and Its Application to Solid–Liquid Interface Simulations" Metals 15, no. 9: 972. https://doi.org/10.3390/met15090972
APA StyleZhang, Y., Cai, J., Chen, H., Lv, X., & Huang, B. (2025). Development of a TaN-Ce Machine Learning Potential and Its Application to Solid–Liquid Interface Simulations. Metals, 15(9), 972. https://doi.org/10.3390/met15090972






