Numerical Simulation of the Solid Particle Entrainment Behavior in Bottom-Blown Ladle
Abstract
1. Introduction
2. Mathematical Modeling
2.1. Assumptions
- Heat transfer among argon gas, molten steel, and refining slag is neglected.
- Both molten steel and refining slag are assumed to be Newtonian fluids, and the turbulence is considered isotropic.
- The three phases coexist stably without any chemical reactions.
- The densities of molten steel, argon gas, and refining slag are constant, and the effects of temperature and hydrostatic pressure on the phase densities are neglected.
- The velocity of bottom-blown gas entering the molten pool is assumed to be constant.
2.2. Hydrodynamic Equation
2.2.1. Continuous Phase Equation
2.2.2. Turbulence Model
2.3. Mesh and Boundary
2.4. Physical Model
2.5. Parameter
2.6. Methodology
3. Results and Analysis
3.1. Verification of Model Correctness
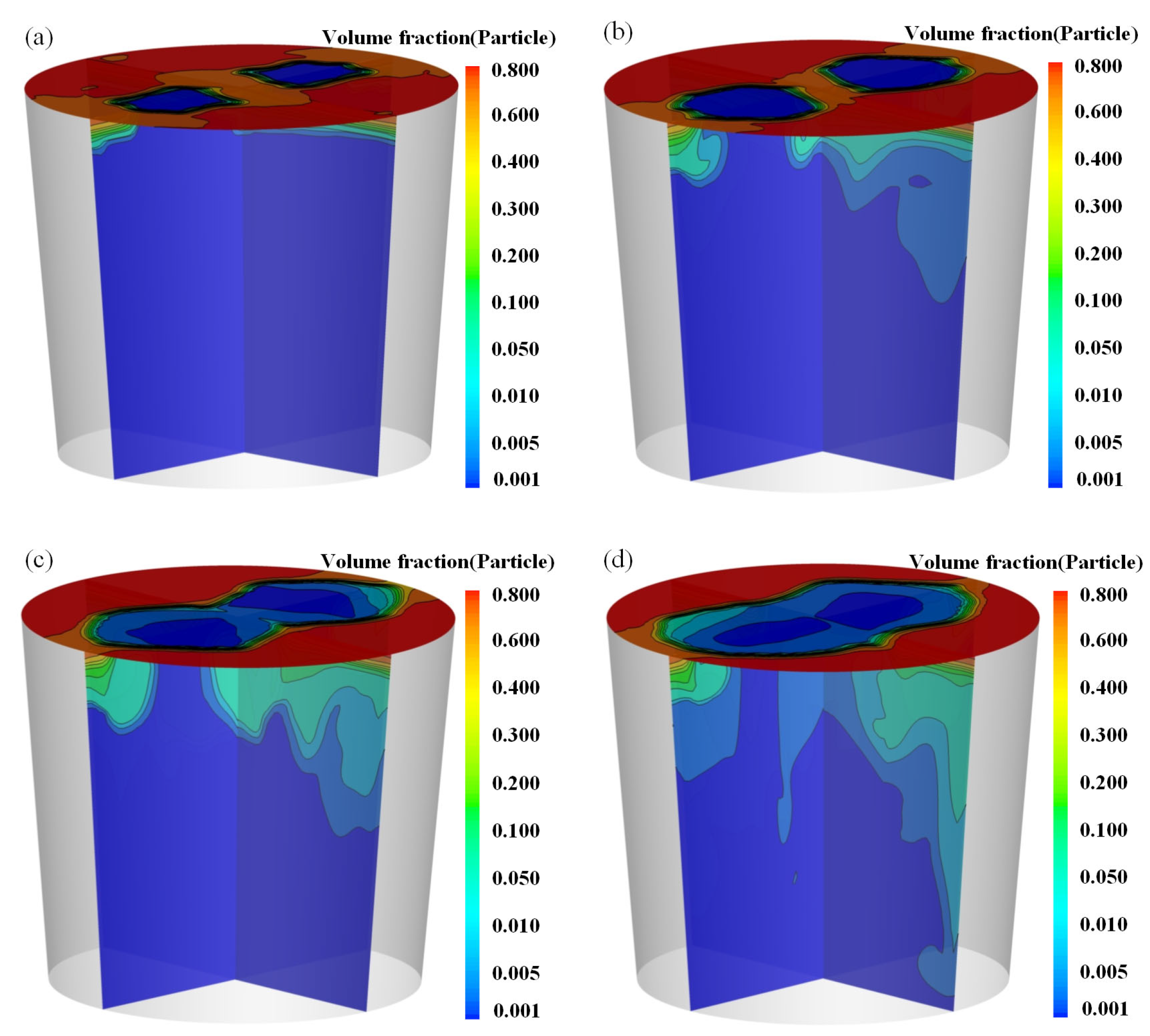
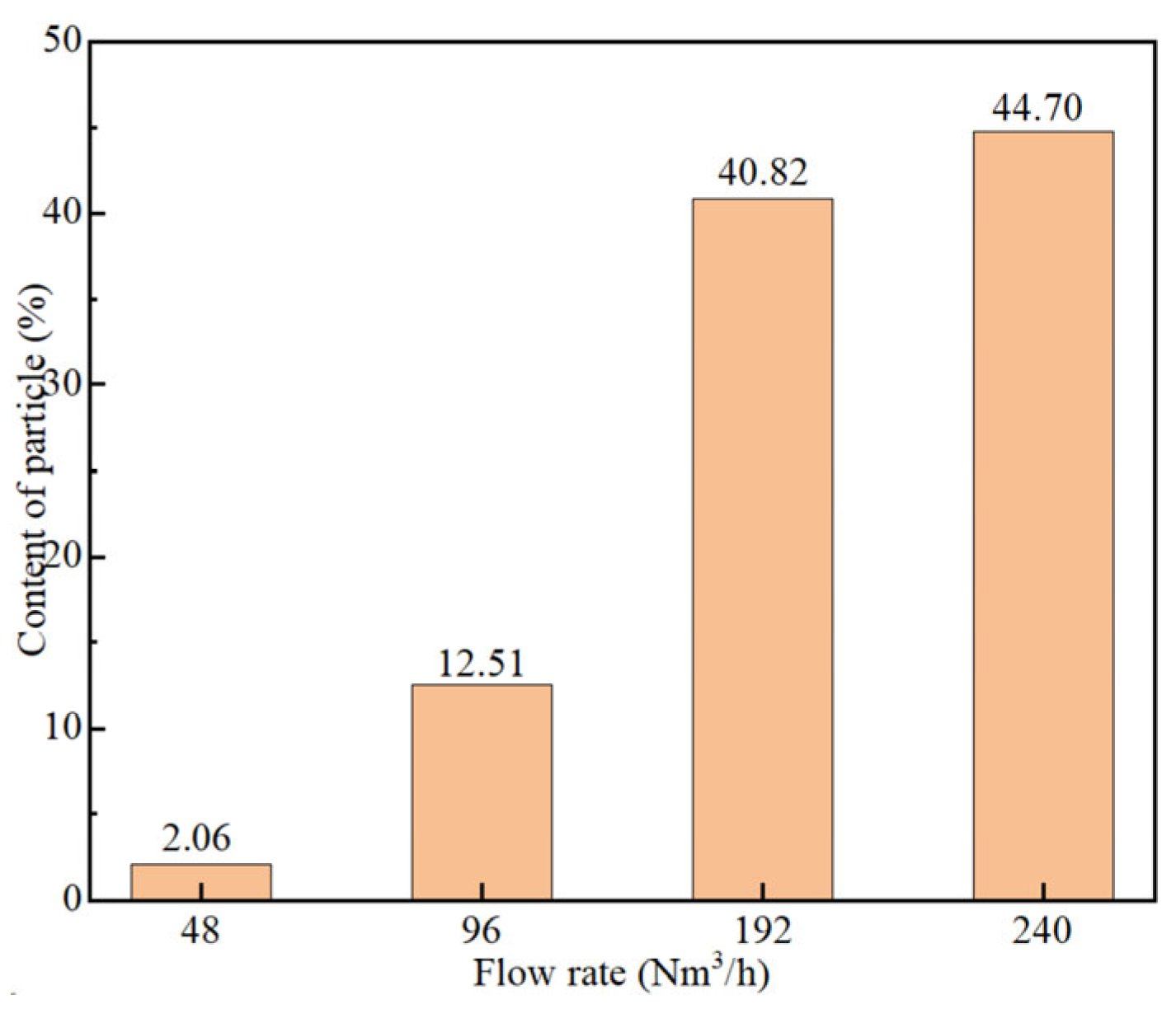
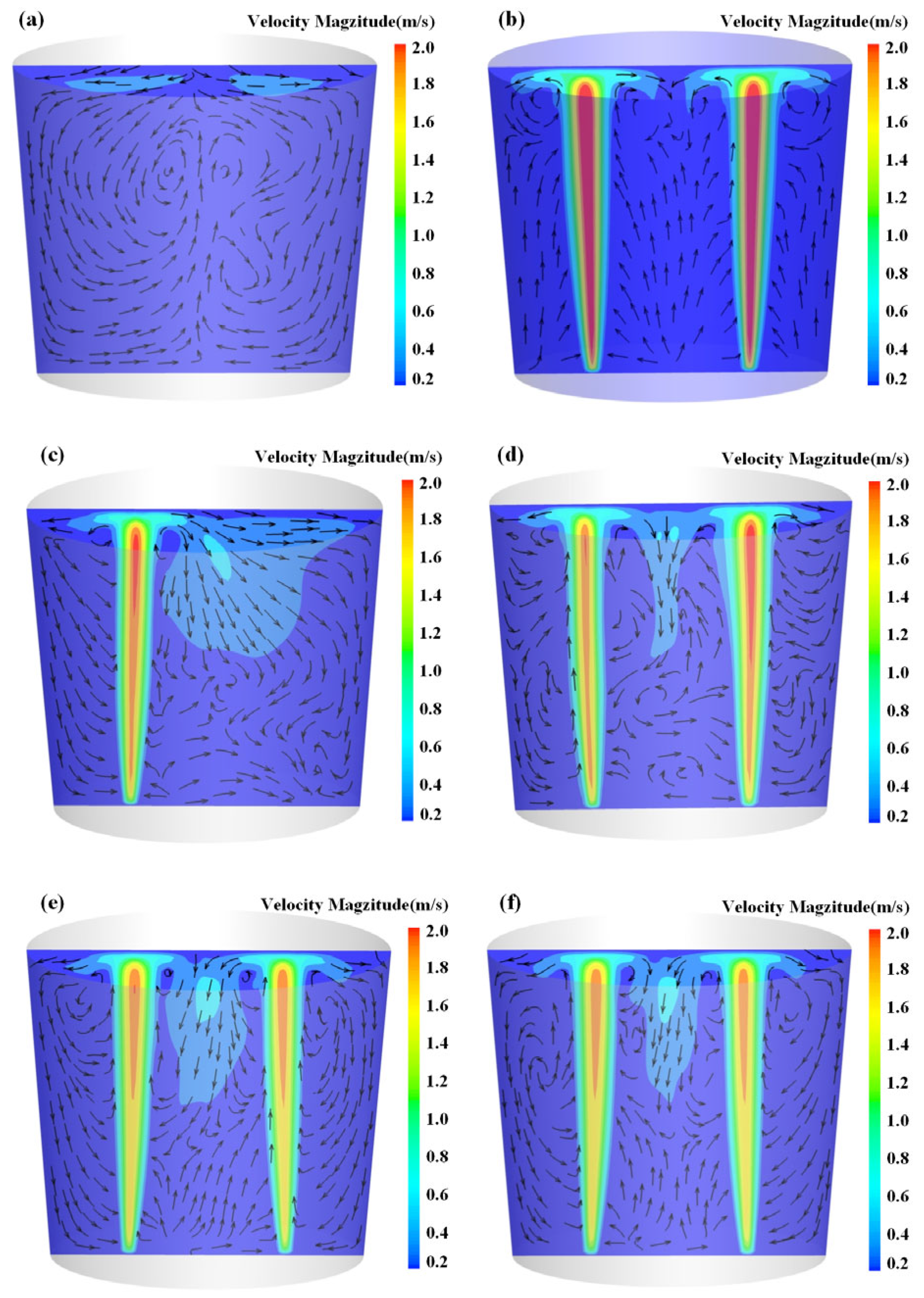
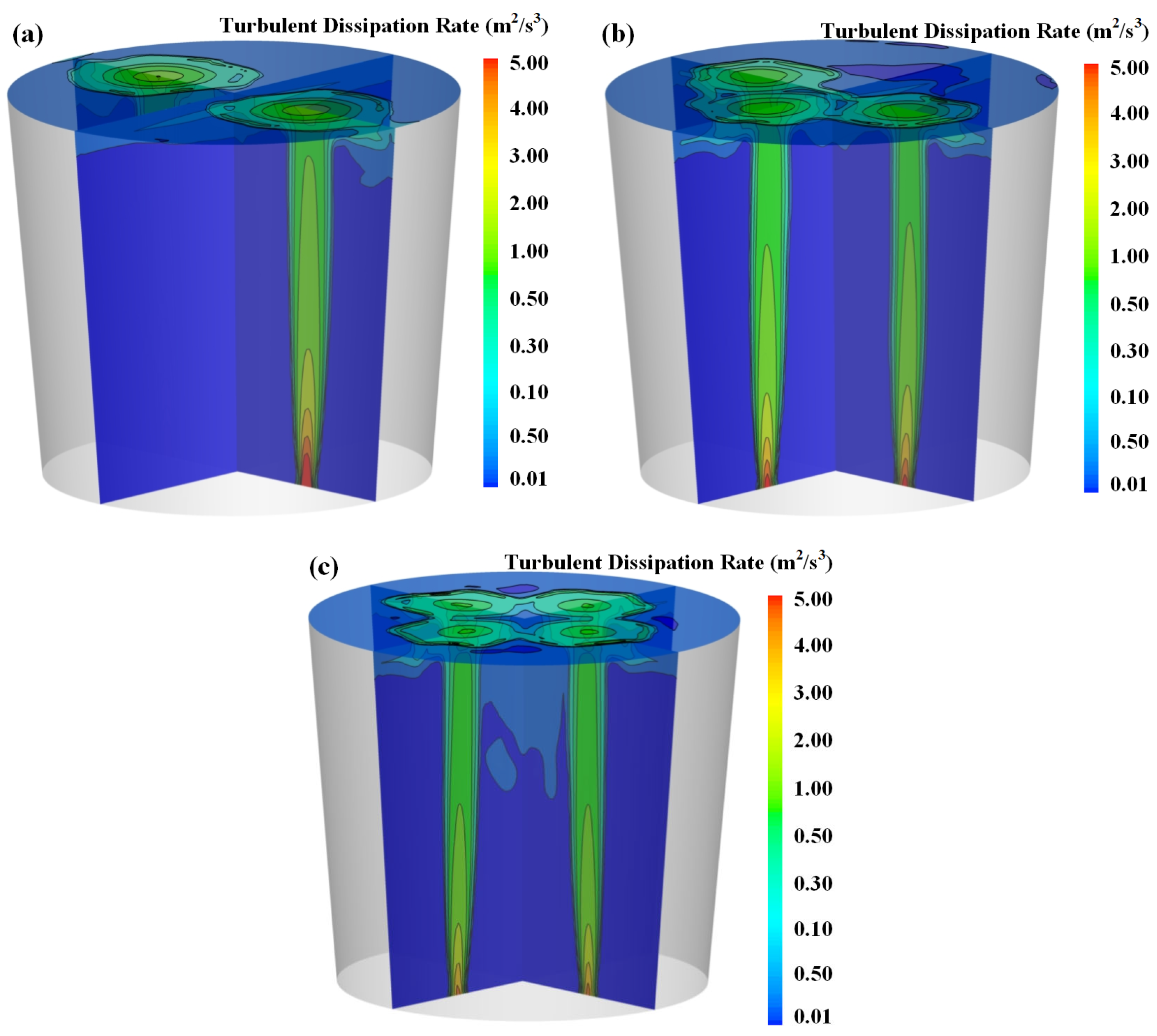
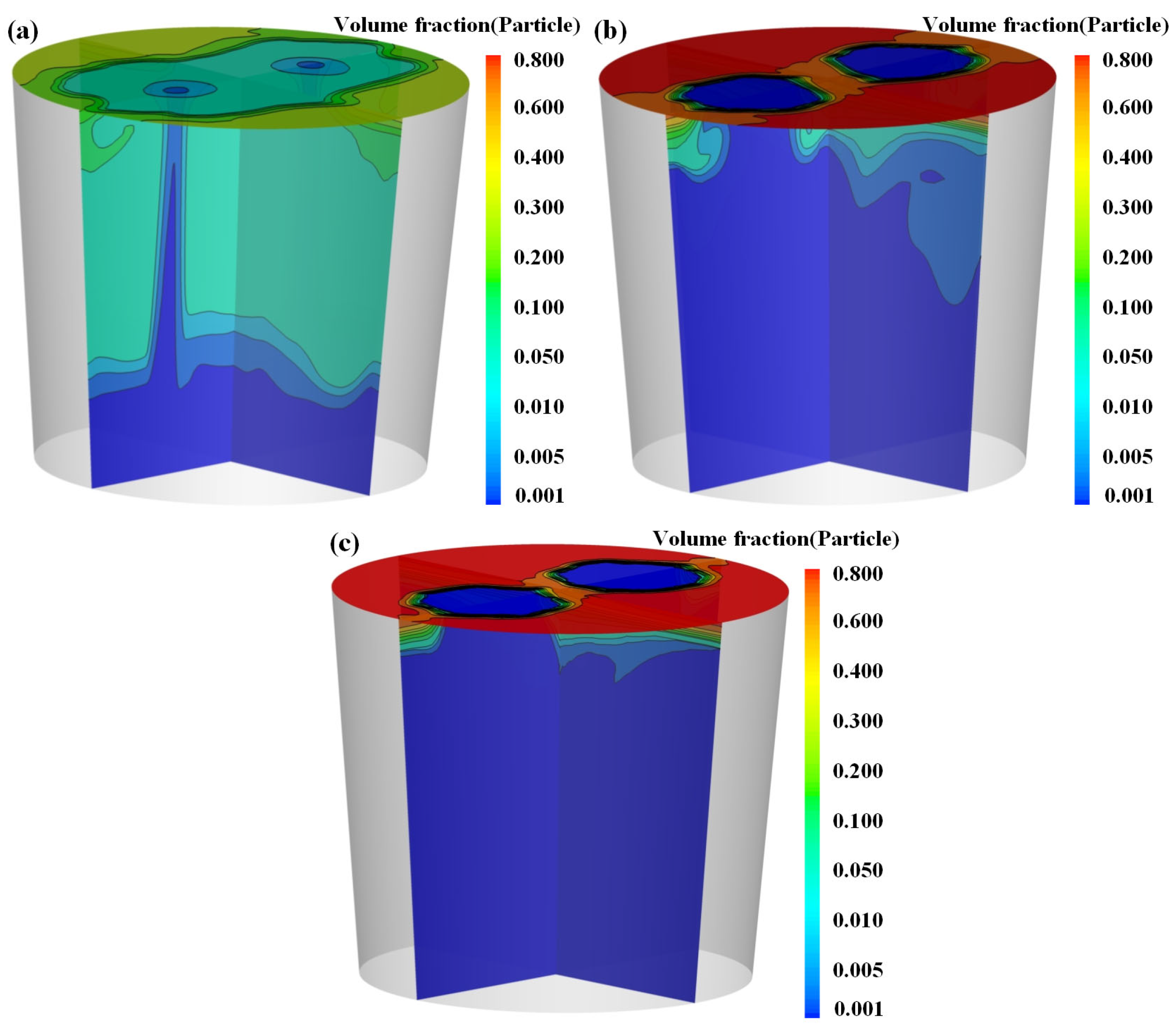
3.2. Effect of Bottom Blowing Flow Rate
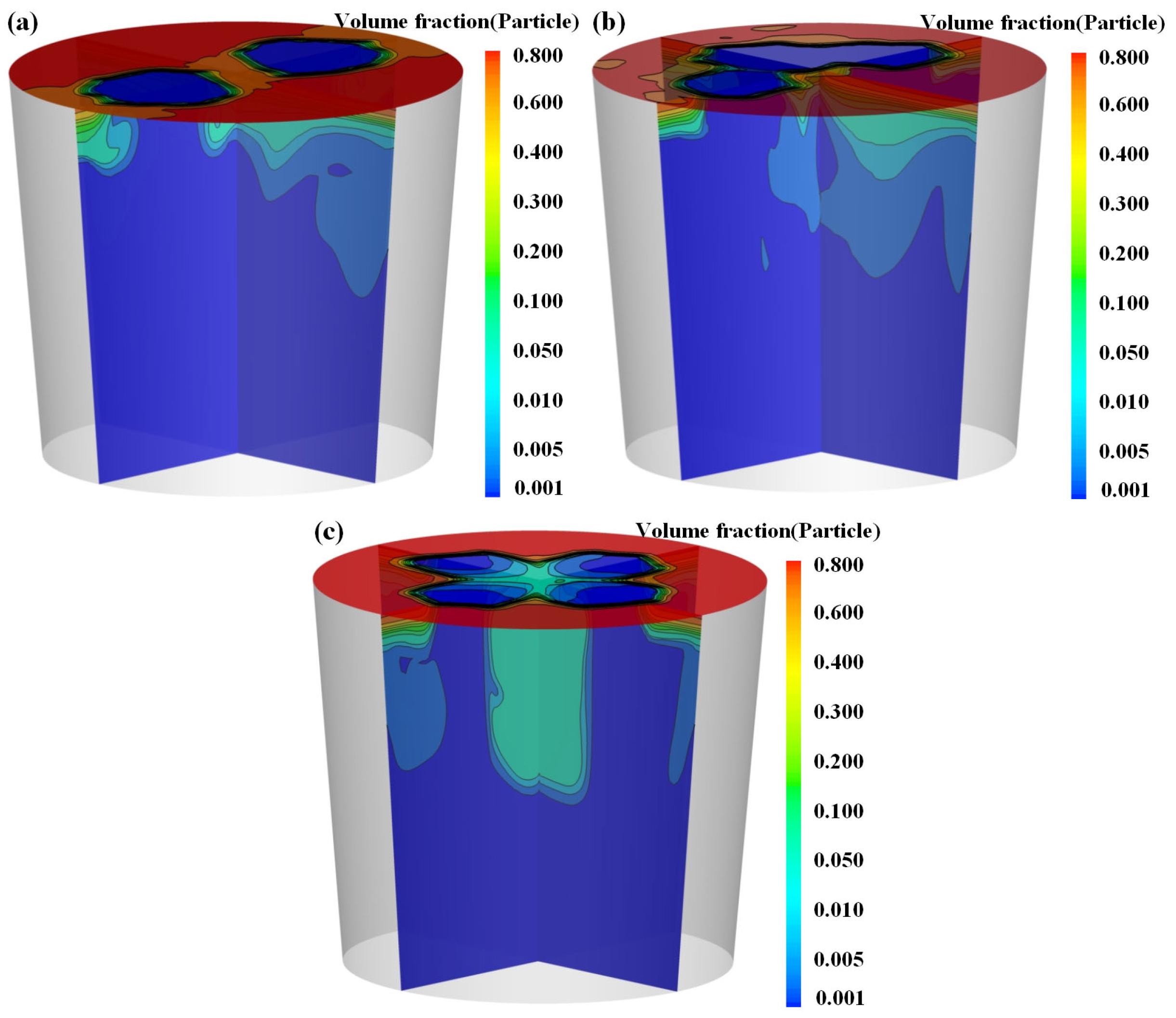
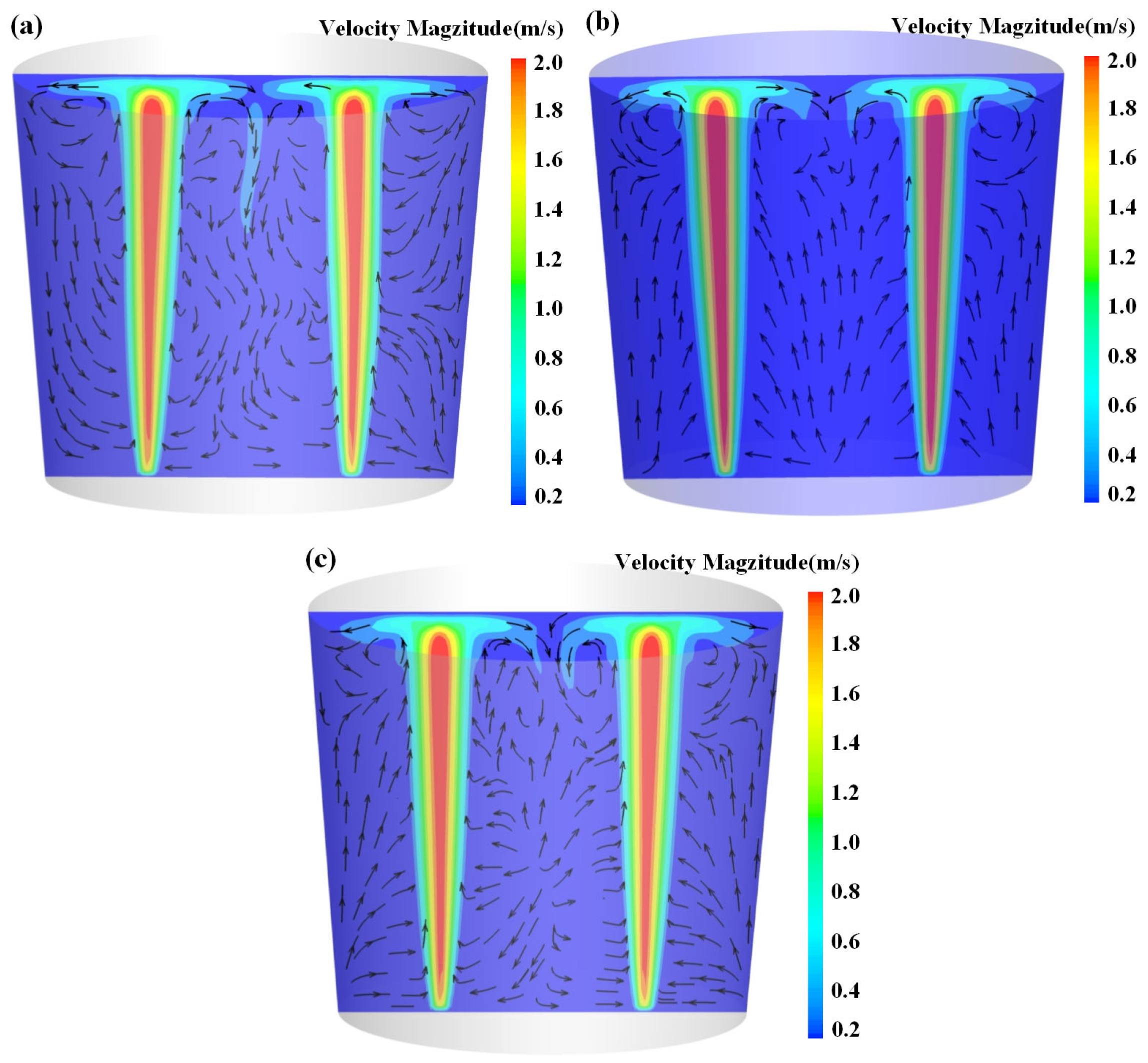
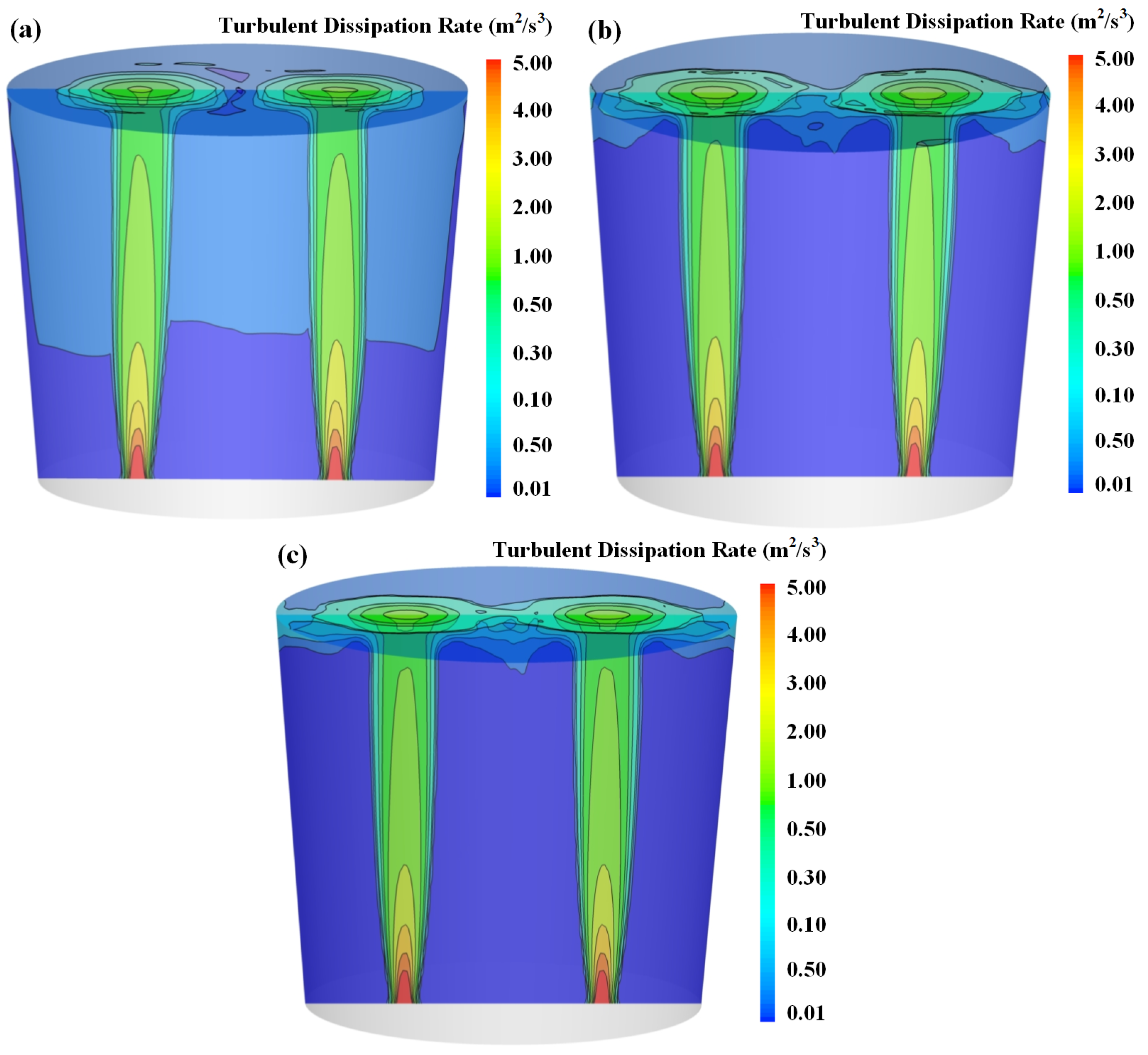
3.3. Effect of Bottom-Blowing Arrangement
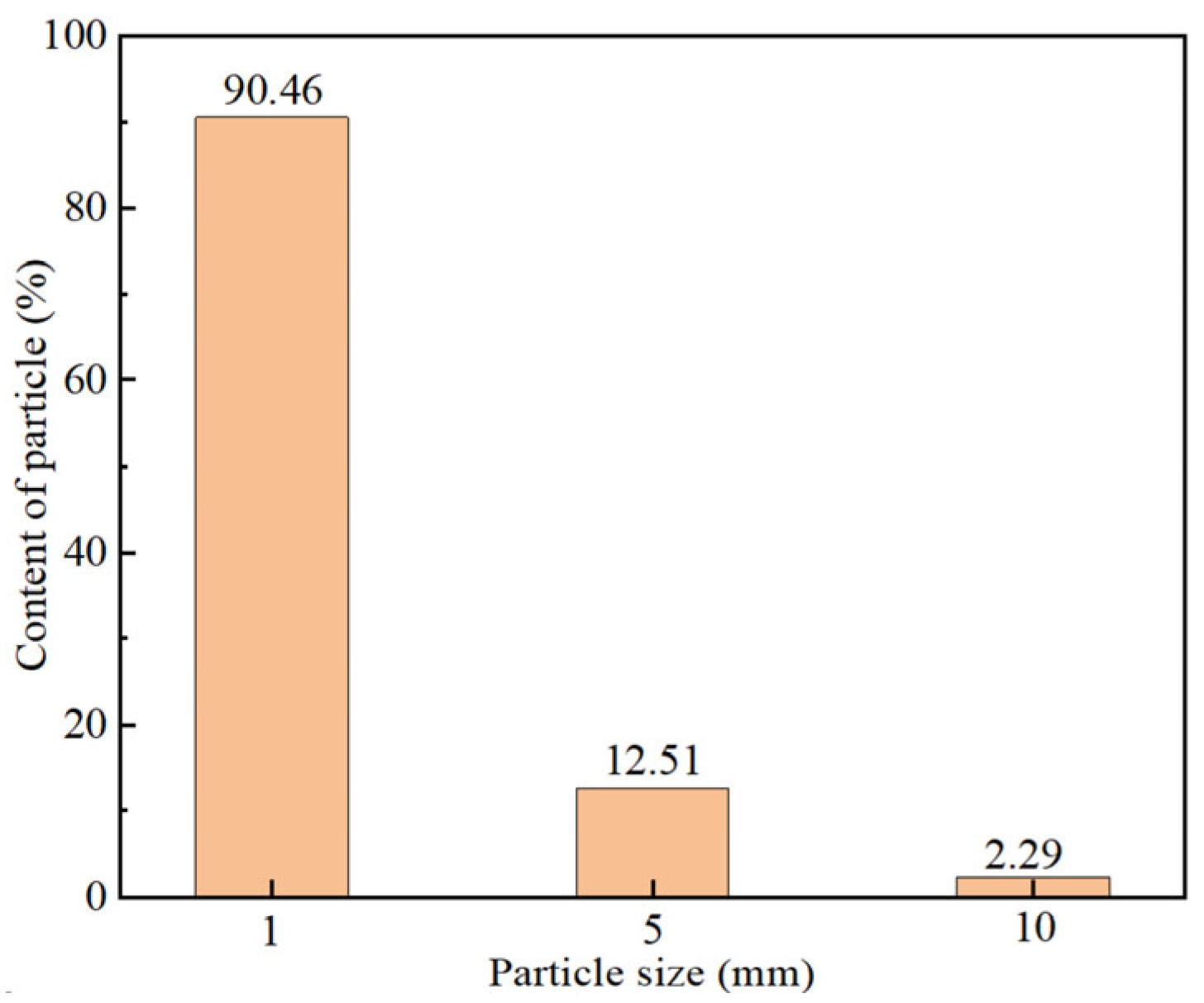
3.4. Effect of Particle Diameter
4. Conclusions
- As the gas flow rate increases, the work imparted by the gas on the molten steel correspondingly rises, resulting in intensified agitation of the liquid phase. This enhanced flow promotes particle entrainment, with the proportion of entrained particles increasing markedly from 2.06% at 48 Nm3/h to 44.7% at 240 Nm3/h, thereby significantly improving the overall mixing efficiency. However, when the gas flow rate exceeds 192 Nm3/h, the incremental enhancement in particle entrainment becomes marginal, suggesting a saturation effect in the entrainment behavior at high flow rates.
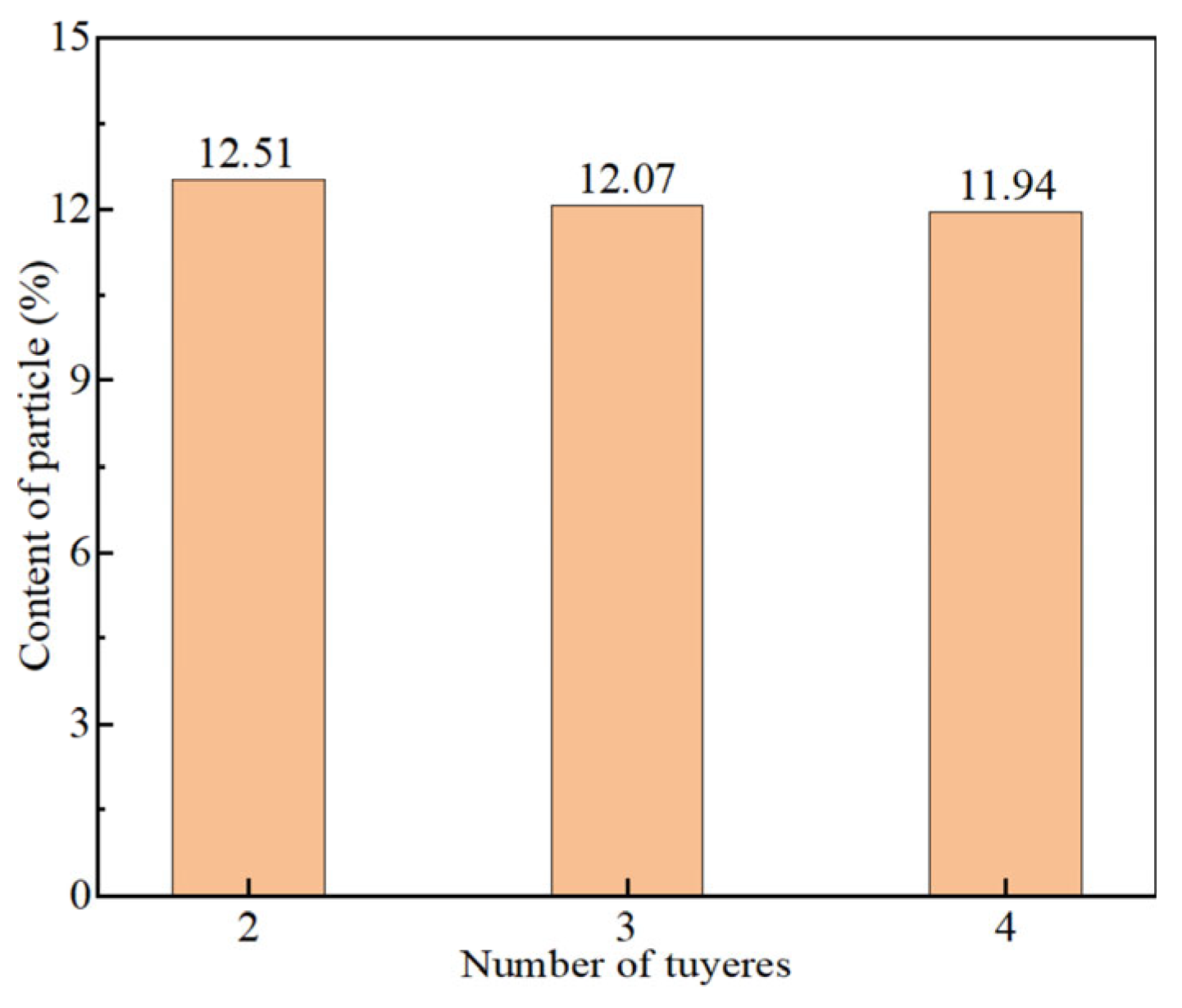
- With an increasing number of tuyeres, the kinetic energy of bottom-blown gas is distributed among multiple gas plumes, thereby weakening the entrainment capacity of each individual plume. Meanwhile, interactions between multiple plumes enhance the turbulence intensity in the free surface region. Quantitative analysis shows that when the number of tuyeres increases from two to four, the total mass of entrained particles decreases by 4.77%, while the area of the “open eyes” expands by 9%.
- The particle size exerts a significant influence on the mixing behavior: as the particle size increases, greater momentum is required to achieve effective entrainment and mixing. Consequently, smaller particles result in higher average particle concentrations under bottom-blowing conditions. However, excessively fine particles can enlarge the “open eyes” area, potentially causing adverse effects such as increased nitrogen absorption and accelerated temperature loss.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| density | volume fraction | ||
| velocity vector | k = l | liquid phase | |
| k = g | gas phase | k = p | particle phase |
| molecular viscosity | turbulent viscosity | ||
| effective viscosity | drag force | ||
| interaction force | turbulent dispersion force | ||
| , | Interphase momentum exchange coefficients | diameters of the bubbles | |
| diameters of the particles | |||
| gas-liquid surface tension coefficient | , | drag force coefficients | |
| dispersion Prandtl number | turbulent dispersion coefficient | ||
| turbulence kinetic energy | turbulence dissipation rate |
References
- Li, X.; Wang, H.; Tian, J.; Wang, D.; Qu, T.; Hou, D.; Hu, S.; Wu, G. Investigation on the Alloy Mixing and Inclusion Removement through Using a New Slot-Porous Matched Tuyeres. Metals 2023, 13, 667. [Google Scholar] [CrossRef]
- Li, X.; Wang, D.; Tian, J.; Wang, H.; Qu, T.; Hou, D.; Hu, S.; Zhang, Z.; Zhou, X.; Wu, G. Modeling of Bubble Transportation, Expansion, as Well as Adhesion of Inclusions in a Ladle With Different Tuyeres. Met. Mater. Trans. B 2024, 55, 14–31. [Google Scholar] [CrossRef]
- Ji, S.; Niu, K.J.; Conejo, A.N. Multiphase Modeling of Steel-slag Mass Transfer through Distorted Interface in Bottom-stirred Ladle. ISIJ Int. 2024, 64, 52–58. [Google Scholar] [CrossRef]
- Xing, L.; Xiao, W.; Bao, Y.; Wang, M.; Ai, X. Process optimization of bottom-blown argon for 130t ladle furnace. Ironmak. Steelmak. 2023, 50, 894–899. [Google Scholar] [CrossRef]
- Lou, W.T.; Zhu, M.Y. A Mathematical Model for the Multiphase Transport and Reaction Kinetics in a Ladle with Bottom Powder Injection. Met. Mater. Trans. B 2017, 48, 3196–3212. [Google Scholar] [CrossRef]
- Guo, X.; Liu, Y.; Jojo-Cunningham, Y.; Silaen, A.; Walla, N.; Zhou, C. Mixing Time Prediction in a Ladle Furnace. Metals 2024, 14, 518. [Google Scholar] [CrossRef]
- Tao, X.; Qi, H.; Guo, Z.; Wang, J.; Wang, X.; Yang, J.; Zhao, Q.; Lin, W.; Yang, K.; Chen, C. Assessment of Measured Mixing Time in a Water Model of Eccentric Gas-Stirred Ladle with a Low Gas Flow Rate: Tendency of Salt Solution Tracer Dispersions. Symmetry 2024, 16, 1241. [Google Scholar] [CrossRef]
- Li, X.; Bao, Y.P.; Lin, L.; Yan, X.; Wang, L. 150 t ladle porous plug bottom argon blowing optimization and industrial tests. Steelmaking 2014, 30, 10–13+17. Available online: https://d.wanfangdata.com.cn/periodical/lg201406003 (accessed on 15 February 2023).
- Irons, G.; Senguttuvan, A.; Krishnapisharody, K. Recent Advances in the Fluid Dynamics of Ladle Metallurgy. Trans. Iron Steel Inst. Jpn. 2015, 55, 1–6. [Google Scholar] [CrossRef][Green Version]
- Senguttuvan, A.; Irons, G.A. Modeling of Slag Entrainment and Interfacial Mass Transfer in Gas Stirred Ladles. ISIJ Int. 2017, 57, 1962–1970. [Google Scholar] [CrossRef]
- Llanos, C.A.; Garcia, S.; Ramos-Banderas, J.A.; Barreto, J.D.J.; Solorio, G. Multiphase Modeling of the Fluidynamics of Bottom Argon Bubbling during Ladle Operations. ISIJ Int. 2010, 50, 396–402. [Google Scholar] [CrossRef]
- Huang, A.; Harmuth, H.; Doletschek, M.; Vollmann, S.; Feng, X. Toward CFD Modeling of Slag Entrainment in Gas Stirred Ladles. Steel Res. Int. 2015, 86, 1447–1454. [Google Scholar] [CrossRef]
- Lou, W.T.; Zhu, M.Y. Numerical Simulations of Inclusion Behaviour and Mixing Phenomena in Gas-stirred Ladles with Different Arrangement of Tuyeres. ISIJ Int. 2014, 54, 9–18. [Google Scholar] [CrossRef]
- Dong, P.L. Physical modeling for optimization of bottom blowing argon process in a 210 t ladle. Iron Steel 2016, 51, 41–44. [Google Scholar] [CrossRef]
- Zhu, M.Y.; Xiao, Z.Q. Mathematical and Physical Simulation of Steel Refining Process; Metallurgical Industry Press: Beijing, China, 1998. [Google Scholar]
- Li, J.; Sun, Y.; Yang, S.; Liu, W. Research Status of Numerical Simulation of Nonmetallic Inclusions Interfacial Removal. Steel Res. Int. 2023, 94, 2200631. [Google Scholar] [CrossRef]
- Tao, X.; Cao, J.; Wang, J.; He, X.; Meng, L.; Guo, Y.; Wang, T.; Li, D.; Fan, J.; Chen, C. Physical Model of Inclusions Removal at Static Steel–Slag Interface. Meterials 2024, 17, 2244. [Google Scholar] [CrossRef]
- Zhang, L.; Taniguchi, S.; Cai, K. Fluid flow and inclusion removal in continuous casting tundish. Met. Mater. Trans. B 2000, 31, 253–266. [Google Scholar] [CrossRef]
- Lei, H.; Nakajima, K.; He, J.C. Mathematical model for nucleation, Ostwald ripening and growth of inclusion in molten steel. ISIJ Int. 2010, 50, 1735–1745. [Google Scholar] [CrossRef]
- Bouris, D.; Bergeles, G. Investigation of inclusion re-entrainment from the steel-slag interface. Met. Mater. Trans. B 1998, 29, 641–649. [Google Scholar] [CrossRef]
- Miki, Y.; Thomas, B.G. Modeling of inclusion removal in a tundish. Met. Mater. Trans. B 2008, 39, 639–654. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, Y.; Zuo, X. Flow transport and inclusion motion in steel continuous-casting mold under submerged entry nozzle clogging condition. Met. Mater. Trans. B 2008, 39, 534–550. [Google Scholar] [CrossRef]
- Zhu, M.; Zheng, S.; Huang, Z.; Gu, W. Numerical simulation of nonmetallic inclusions behaviour in gas-stirred ladles. Steel Res. Int. 2005, 76, 718–722. [Google Scholar] [CrossRef]
- Wang, L.T.; Zhang, Q.Y.; Deng, C.H.; Li, Z.B. Mathematical model for removal of inclusion in molten steel by injecting gas at ladel shroud. ISIJ Int. 2005, 45, 1138–1144. [Google Scholar] [CrossRef]
- Iwamasa, P.K.; Fruehan, R.J. Effect of FeO in the slag and silicon in the metal on the desulfurization of hot metal. Met. Mater. Trans. B 1997, 28, 47–57. [Google Scholar] [CrossRef]
- Roy, D.R.; Pistorius, P.C.; Fruehan, R.J. Effect of silicon on the desulfurization of Al-killed steels: Part II. Experimental results and plant trials. Met. Meter. Trans. B 2013, 44, 1086–1094. [Google Scholar] [CrossRef]
- Roy, D.R.; Pistorius, P.C.; Fruehan, R.J. Effect of silicon on the desulfurization of Al-killed steels: Part I. Mathematical model. Met. Meter. Trans. B 2013, 44, 1095–1104. [Google Scholar] [CrossRef]
- Shibata, E.; Sun, H.; Mori, K. Kinetics of simultaneous reactions between liquid iron-carbon alloys and slags containing MnO. Met. Mater. Trans. B 1999, 30, 279–286. [Google Scholar] [CrossRef]
- Andersson, M.; Hallberg, M.; Jonsson, L.; Jönsson, P. Slag-metal reactions during ladle treatment with focus on desulfurization. Ironmak. Steelmak. 2002, 29, 224–232. [Google Scholar] [CrossRef]

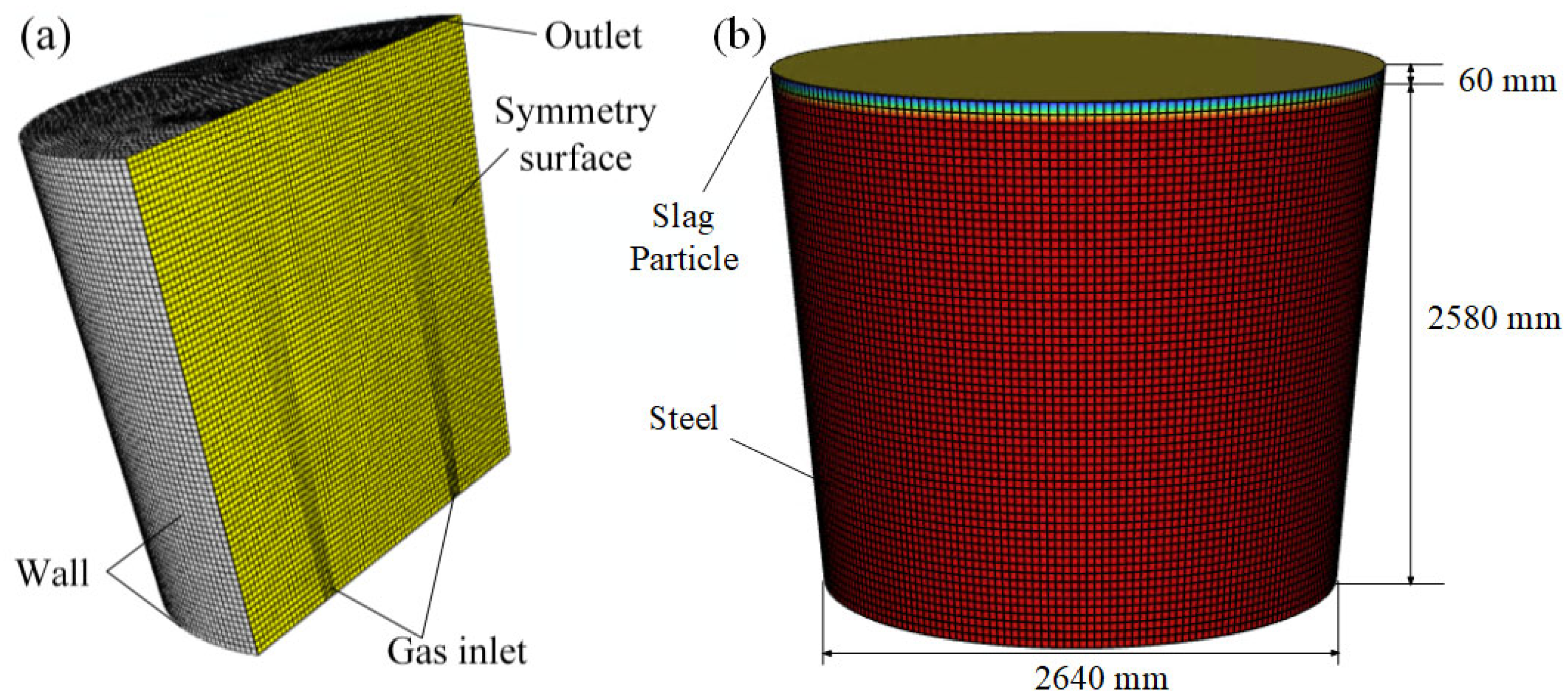
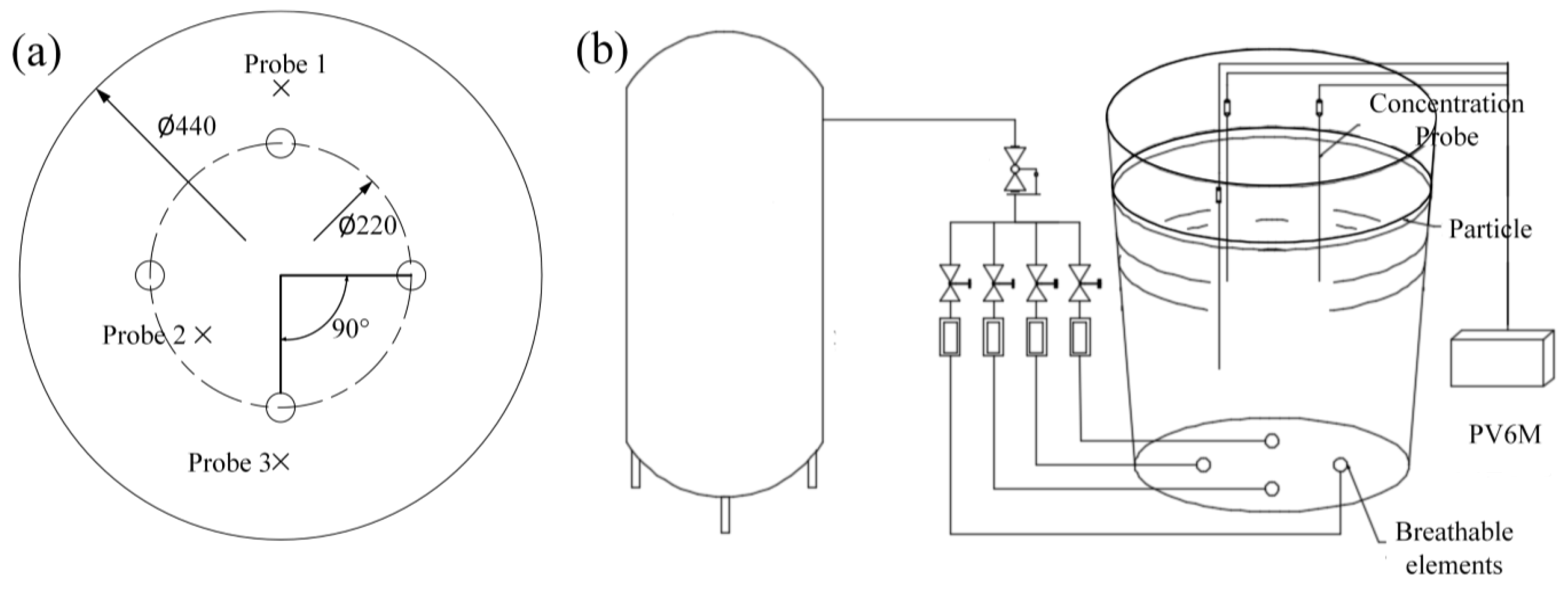

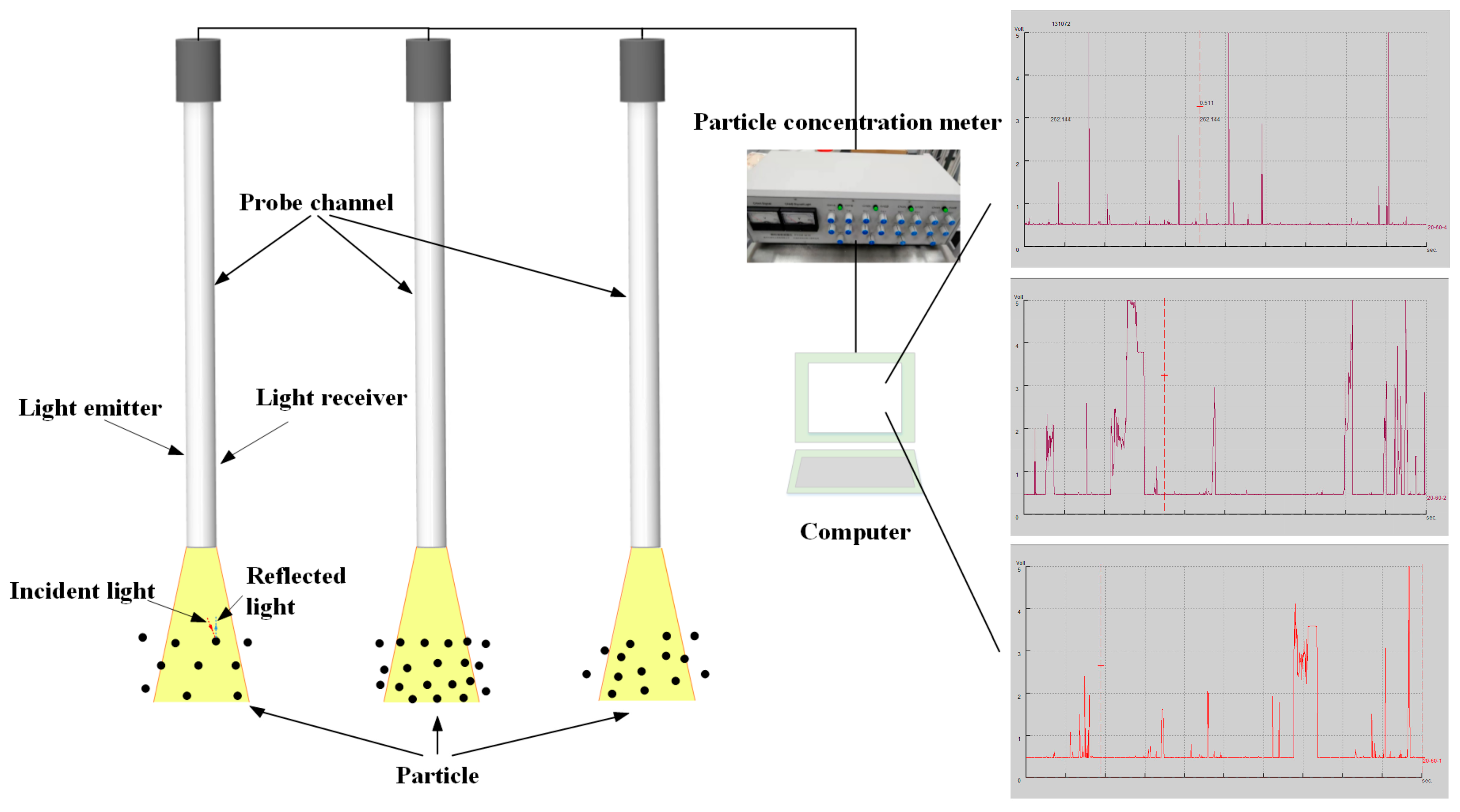
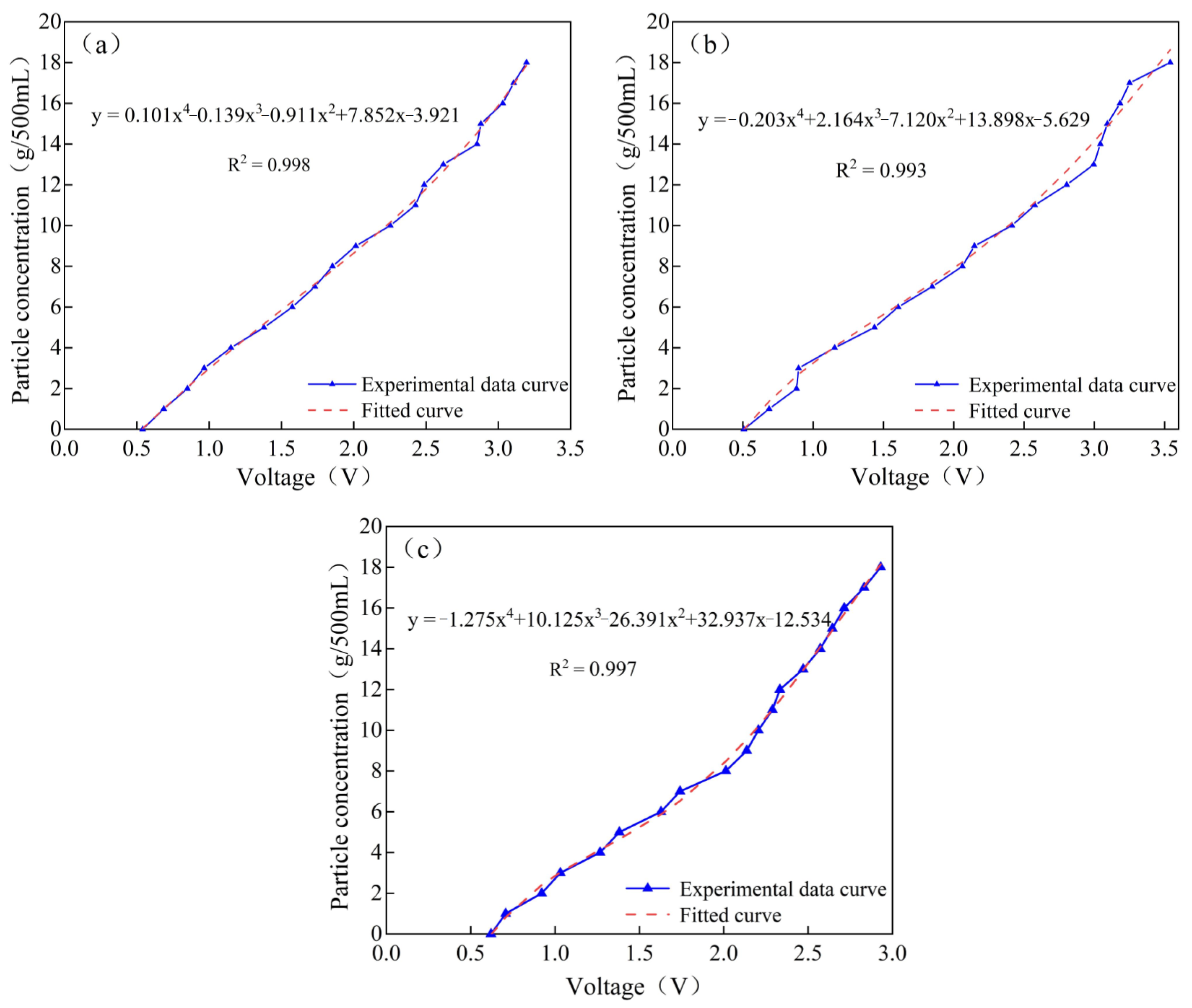
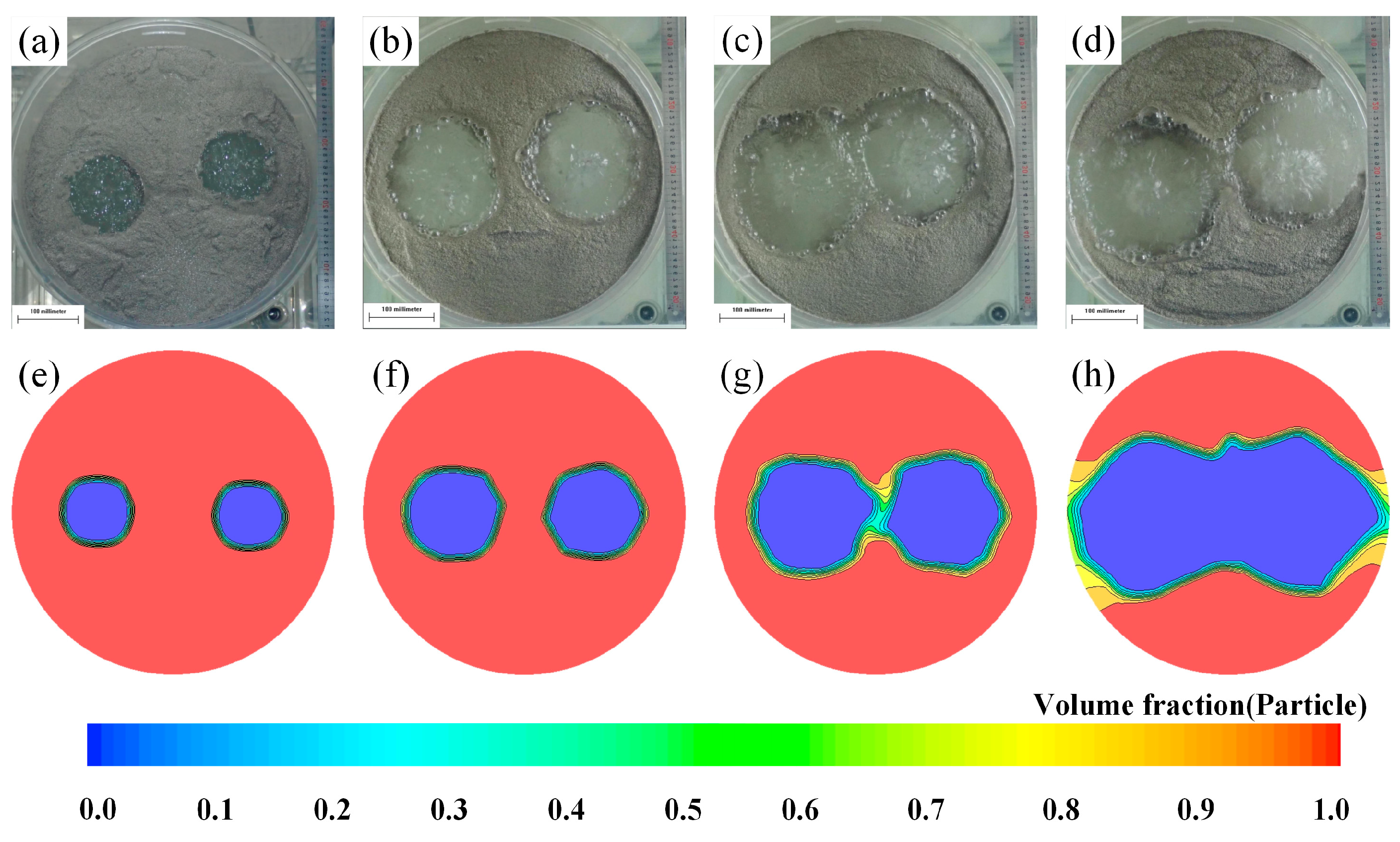

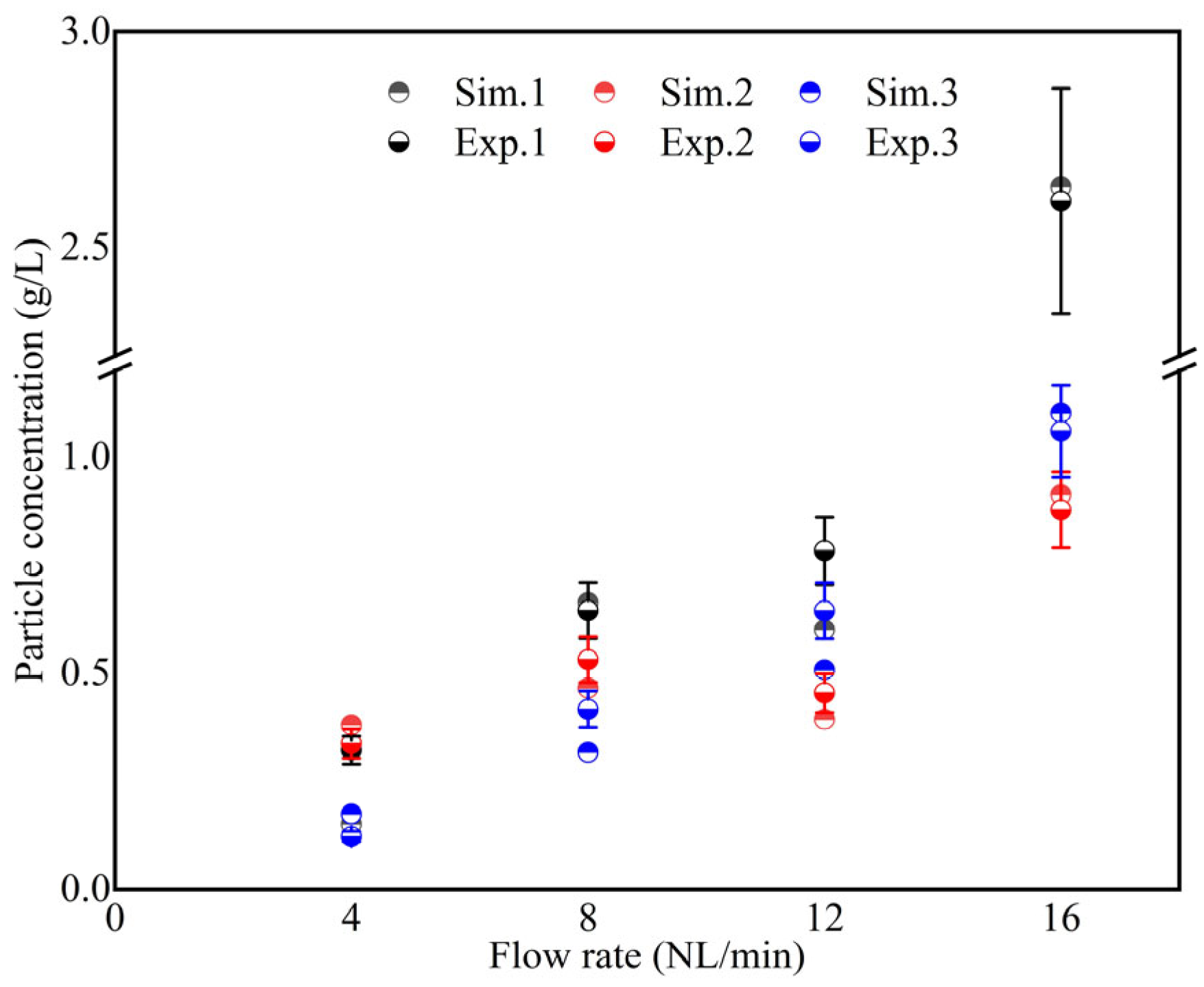

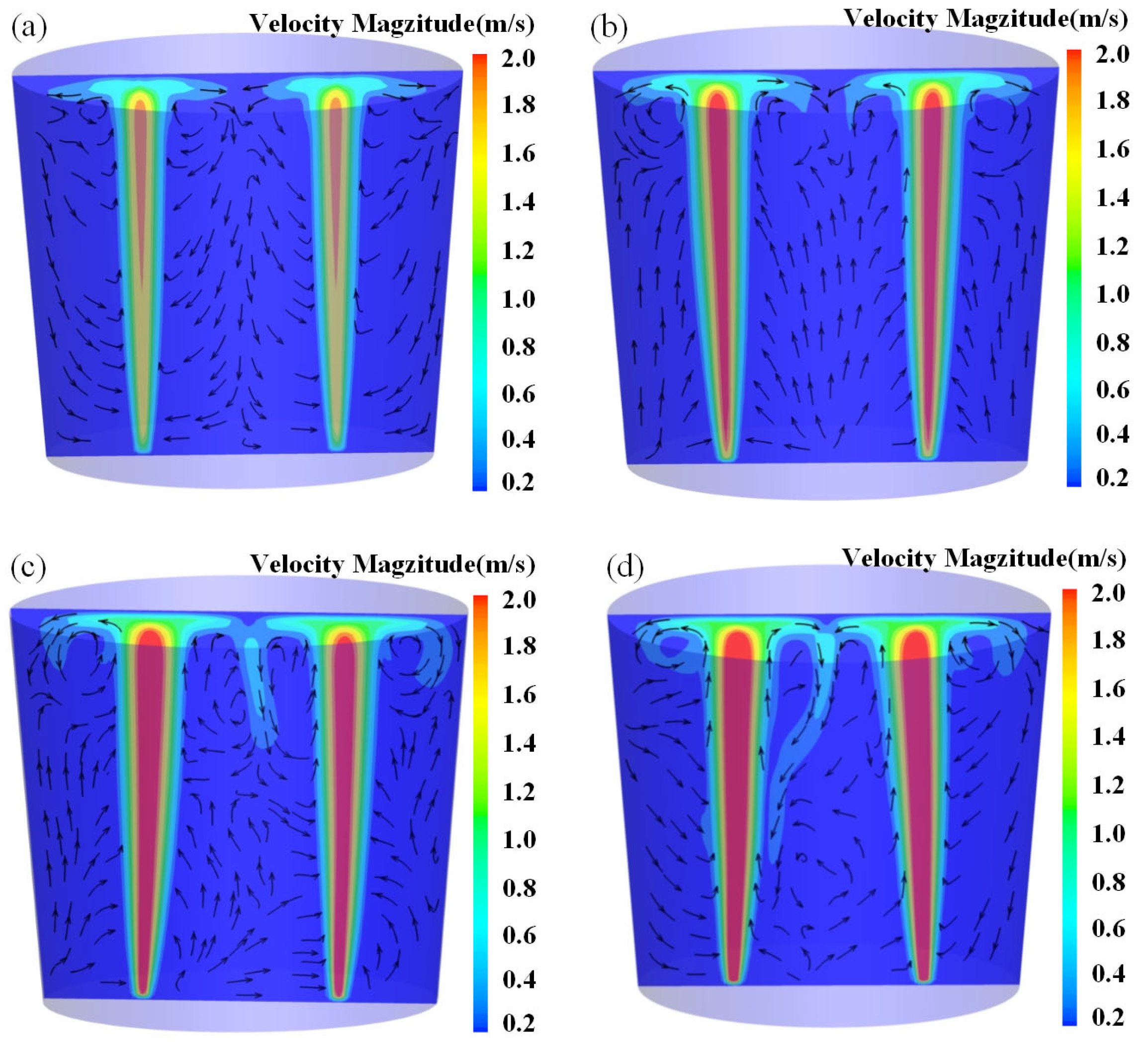
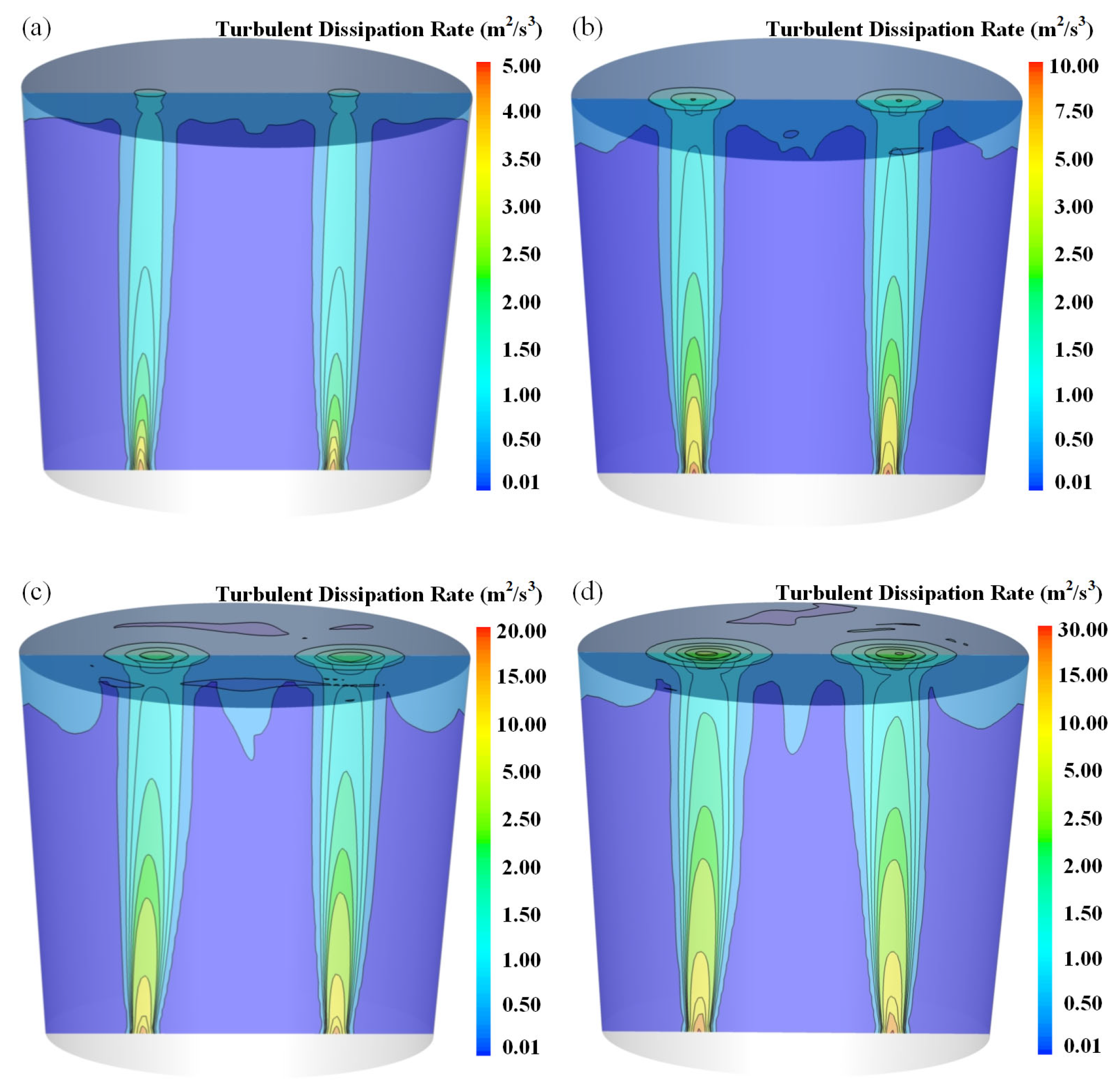



| Parameter | Ladle | Water Model |
|---|---|---|
| Height/mm | 3300 | 550 |
| Top opening dimension/mm | 3180 | 530 |
| Bottom diameter/mm | 2640 | 440 |
| Molten pool height/mm | 2580 | 430 |
| Particle thickness/mm | 60 | 10 |
| Parameter | Value | |
|---|---|---|
| Physical property parameter | ||
| Steel | Density (kg/m3) | 7020 |
| Viscosity (kg/(m s)) | 0.0055 | |
| Particle | Density (kg/m3) | 3400 |
| Viscosity (kg/(m s)) | 0.06 | |
| Argon | Density (kg/m3) | 1.6228 |
| Viscosity (kg/(m s)) | 2.125 × 10−5 | |
| Smelting parameters | ||
| Tapping Temperature (K) | 1873 | |
| Slag Layer Thickness (mm) | 60 | |
| Argon Flow Rate (Nm3/h) | 48, 96, 192, 240 | |
| Composition | C | Si | Mn | P | S | Als | Alt |
|---|---|---|---|---|---|---|---|
| Content (%) | 0.522 | 0.001 | 0.17 | 0.069 | 0.015 | 0.001 | 0.008 |
| Composition | CaO | SiO2 | MgO | Al2O3 | FeO | MnO | R |
|---|---|---|---|---|---|---|---|
| Content (%) | 48.36 | 9.08 | 5.23 | 29.69 | 4.35 | 1.88 | 5.33 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, C.; Lou, W.; Zeng, J.; Wang, Z.; Xie, J. Numerical Simulation of the Solid Particle Entrainment Behavior in Bottom-Blown Ladle. Metals 2025, 15, 963. https://doi.org/10.3390/met15090963
Wang C, Lou W, Zeng J, Wang Z, Xie J. Numerical Simulation of the Solid Particle Entrainment Behavior in Bottom-Blown Ladle. Metals. 2025; 15(9):963. https://doi.org/10.3390/met15090963
Chicago/Turabian StyleWang, Cheng, Wentao Lou, Jie Zeng, Zeyu Wang, and Jianfeng Xie. 2025. "Numerical Simulation of the Solid Particle Entrainment Behavior in Bottom-Blown Ladle" Metals 15, no. 9: 963. https://doi.org/10.3390/met15090963
APA StyleWang, C., Lou, W., Zeng, J., Wang, Z., & Xie, J. (2025). Numerical Simulation of the Solid Particle Entrainment Behavior in Bottom-Blown Ladle. Metals, 15(9), 963. https://doi.org/10.3390/met15090963






