Fatigue Prediction Method of Superalloy Based on the Improved Largest Lyapunov Exponent
Abstract
1. Introduction
2. The Largest Lyapunov Exponent and Prediction
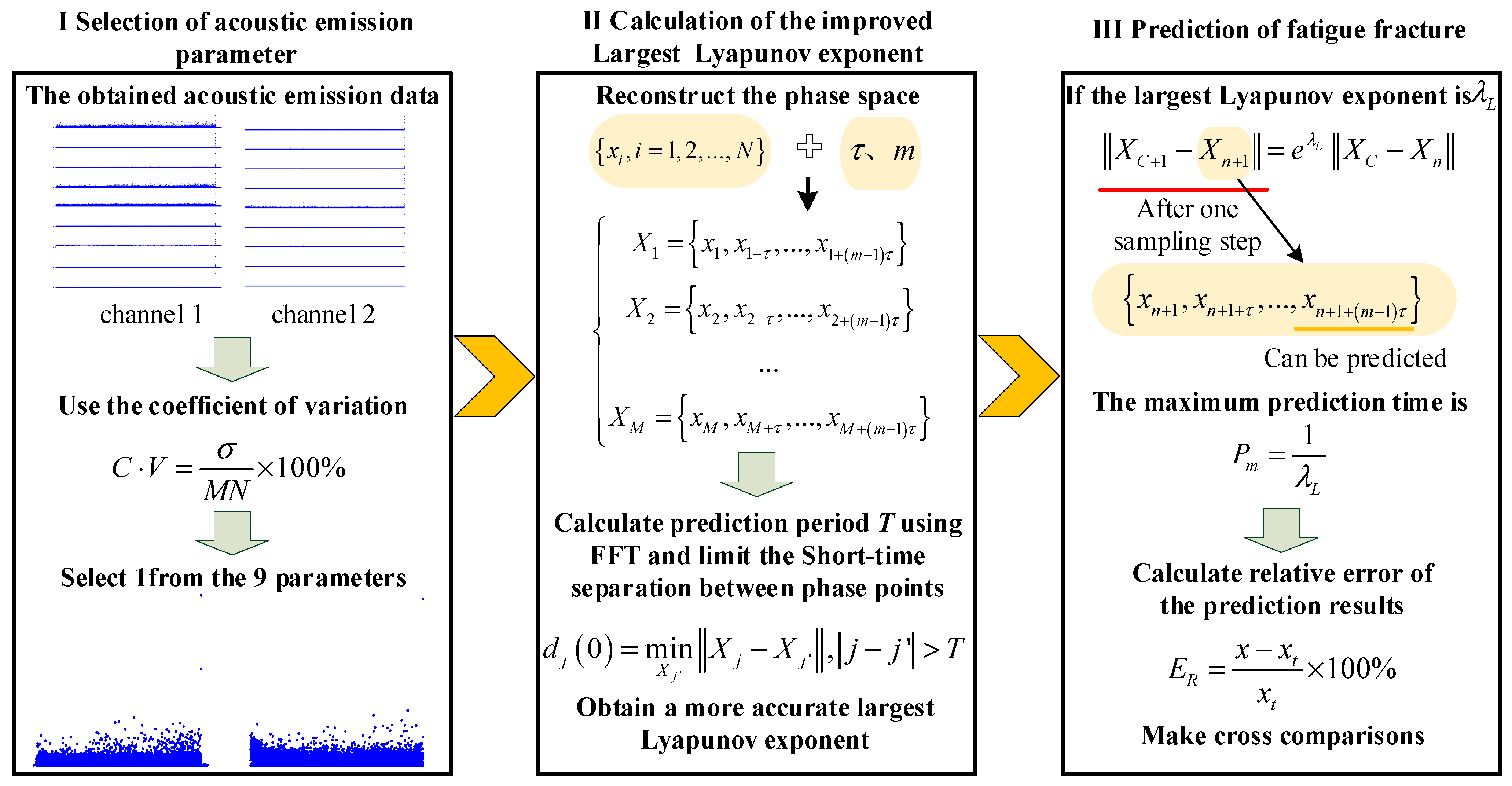
2.1. The Improved Algorithm for the Maximum Lyapunov Exponent
- 1.
- Suppose is a time series whose sampling interval is ;
- 2.
- Time delay τ is determined using the autocorrelation function method, and embedding dimension m is determined using the G-P method [25];
- 3.
- Reconstruct the phase space according to the calculated τ and m to obtain the m-dimensional phase space with M phase points as follows:
- 4.
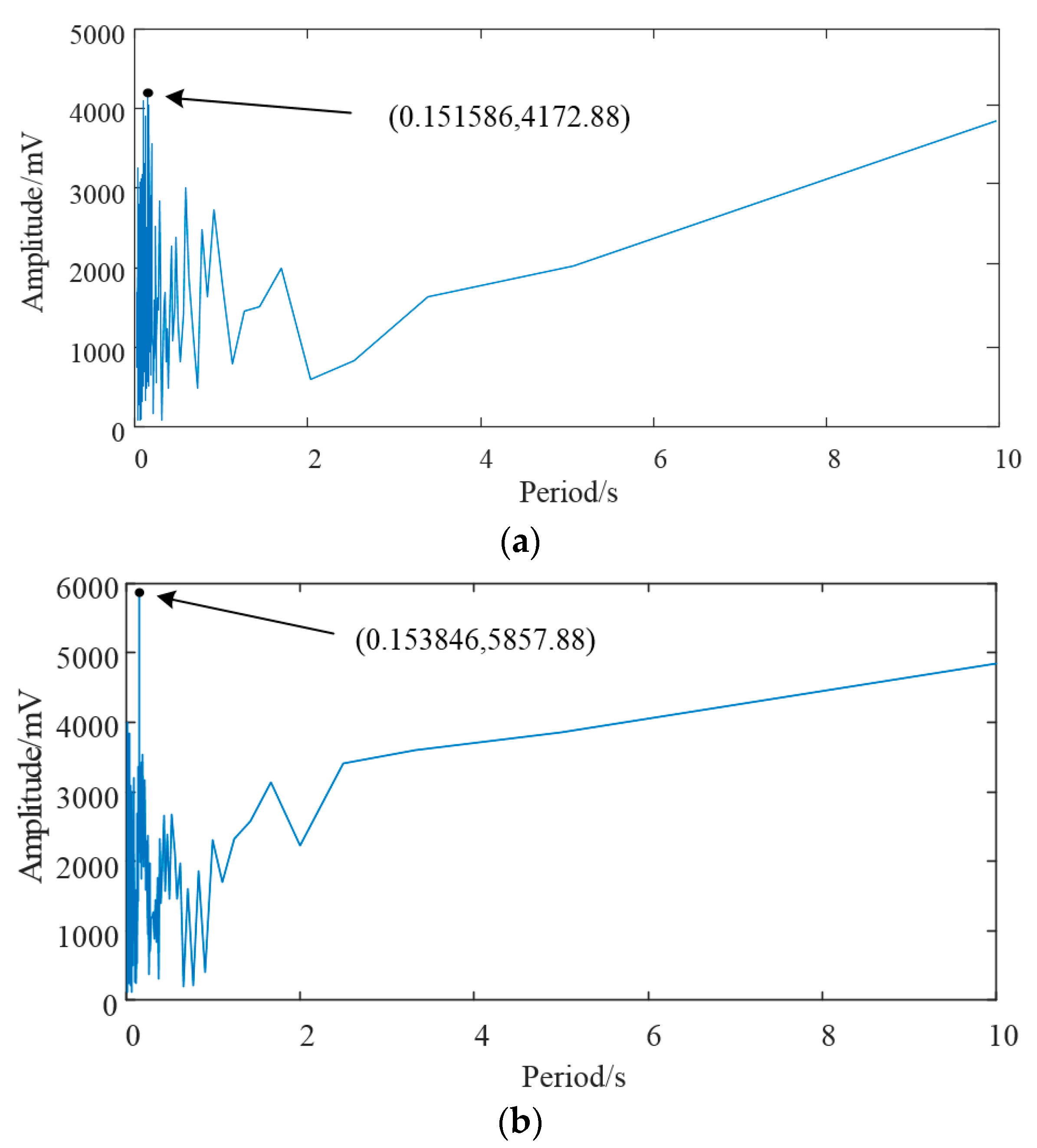
- Find the nearest neighbor points , of each phase point , and limit their short-term separation by the average period T obtained by using FFT to prevent them from being on the same trajectories as follows:
- 5.
- Determine the distance between each phase point and its nearest neighbor point , after the sth discrete-time step, as follows:
- 6.
- Suppose there exists an exponential divergence rate λ between the phase point and its nearest neighbor point , then obtain the following:
- 7.
- For each s, find the average value p(s) of all corresponding to j as follows:
- 8.
- Determine the linear region of curve , and use the least square method to draw a regression line, the slope of which is the largest Lyapunov exponent .
2.2. Prediction Method and the Maximum Prediction Time
3. Results
3.1. Experimental Method
3.2. Experimental Results
4. Discussion
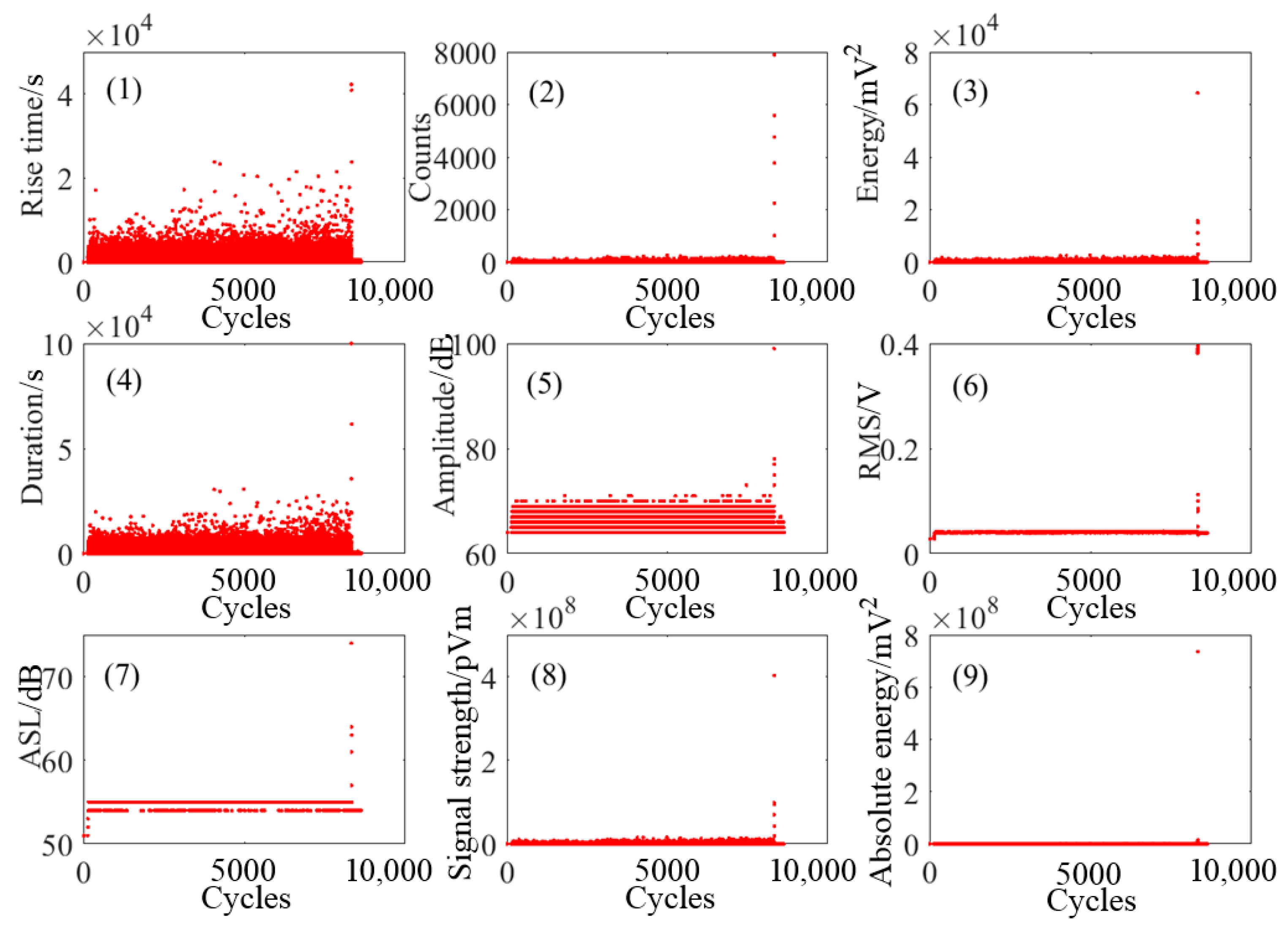
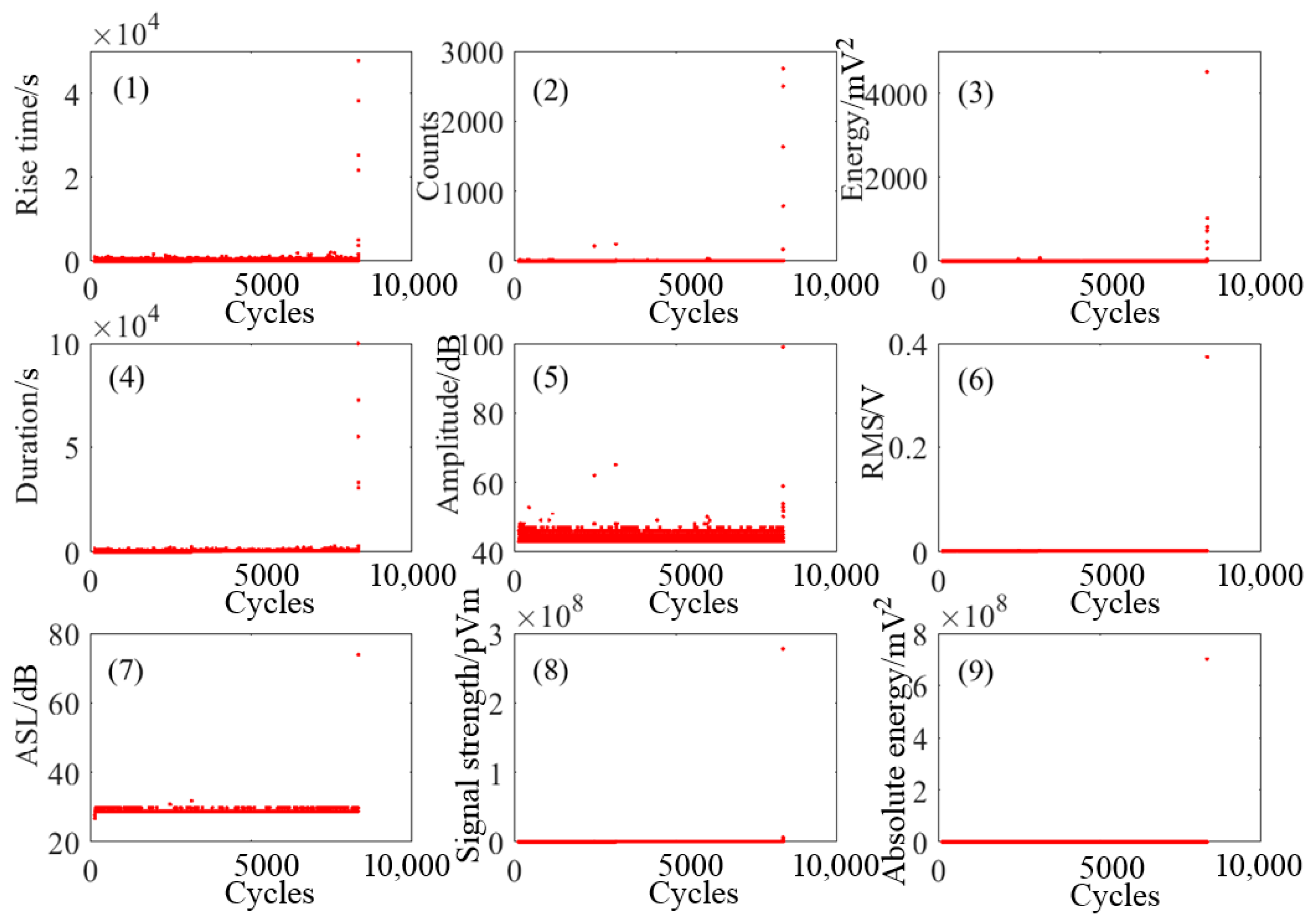
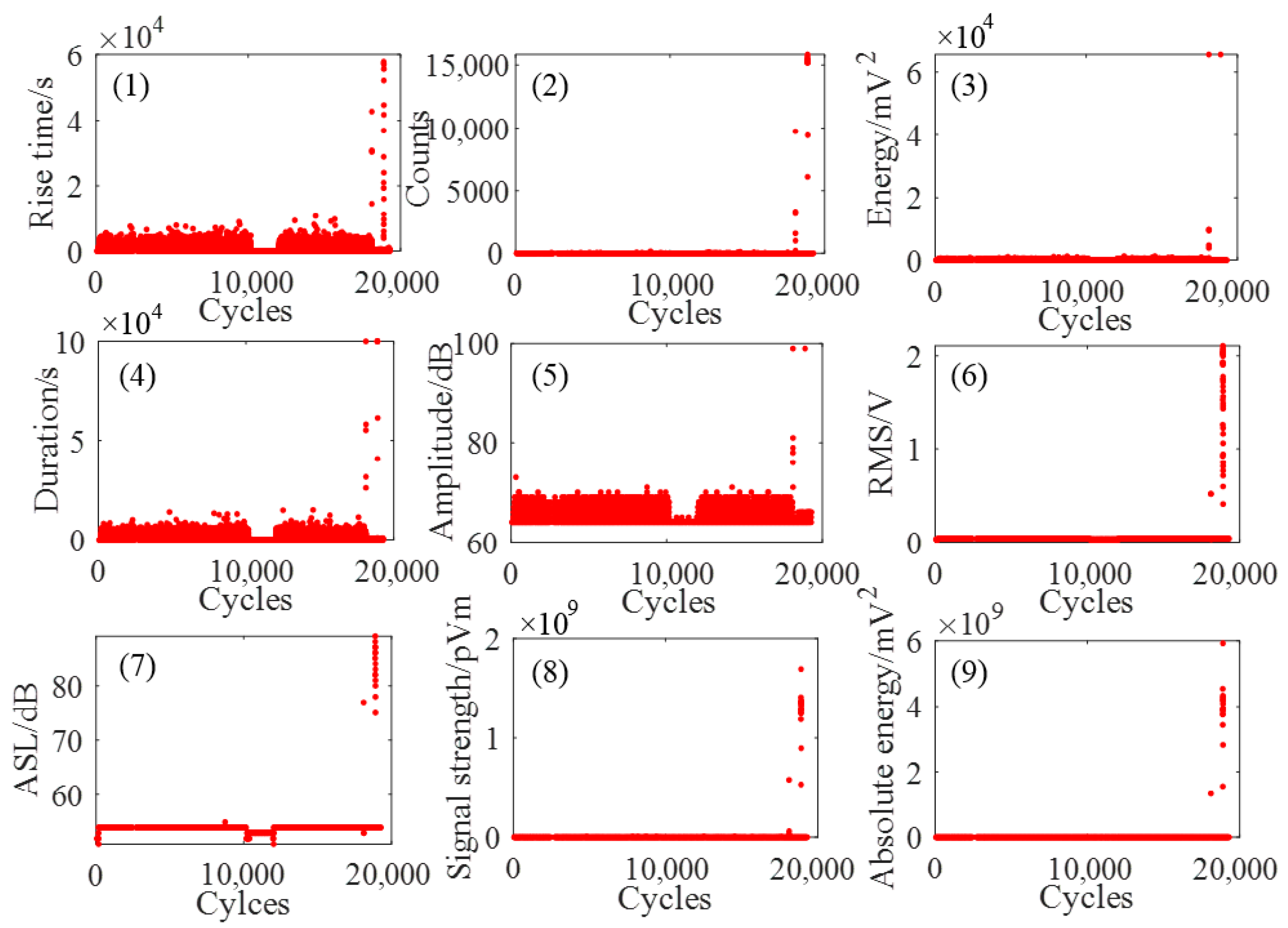
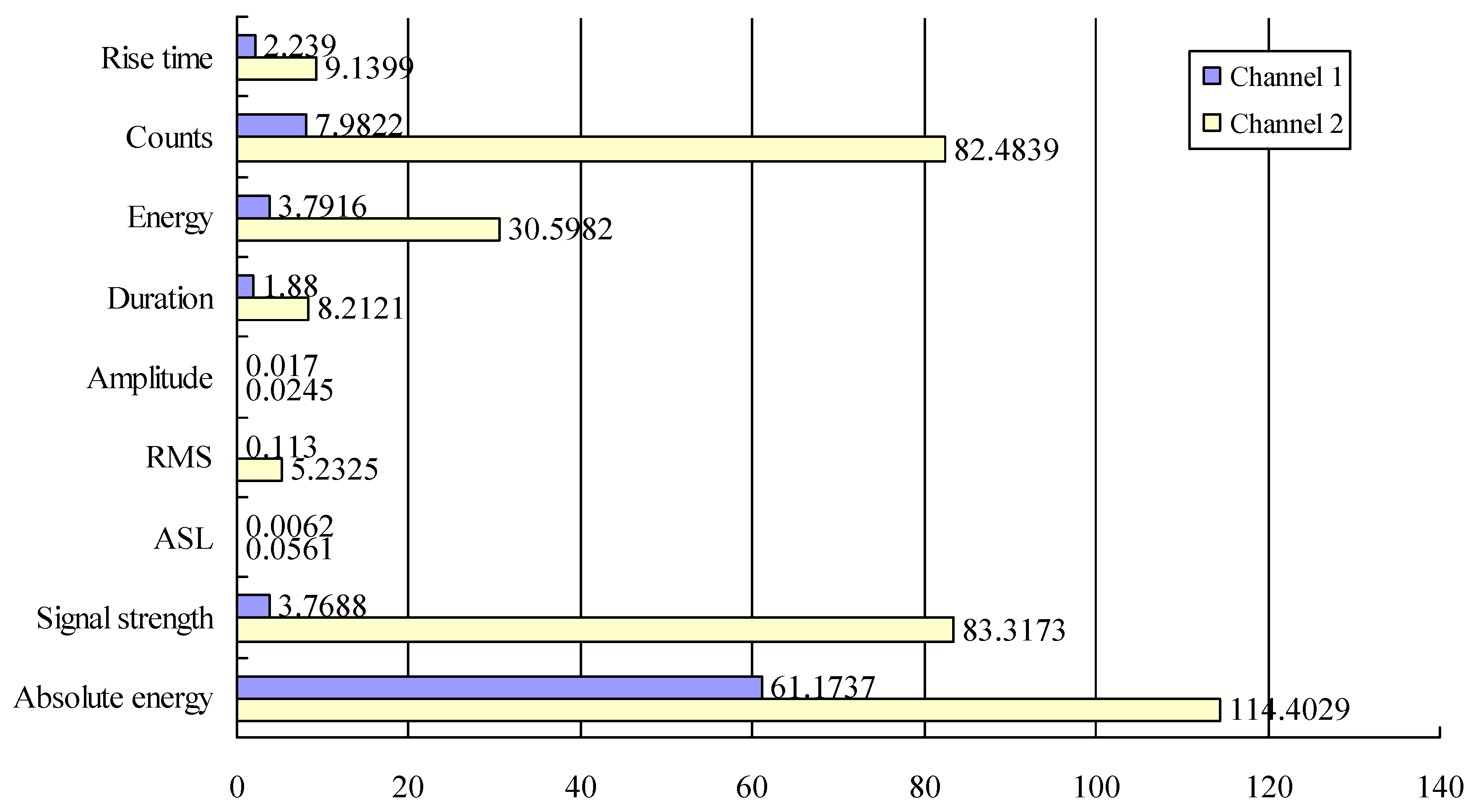
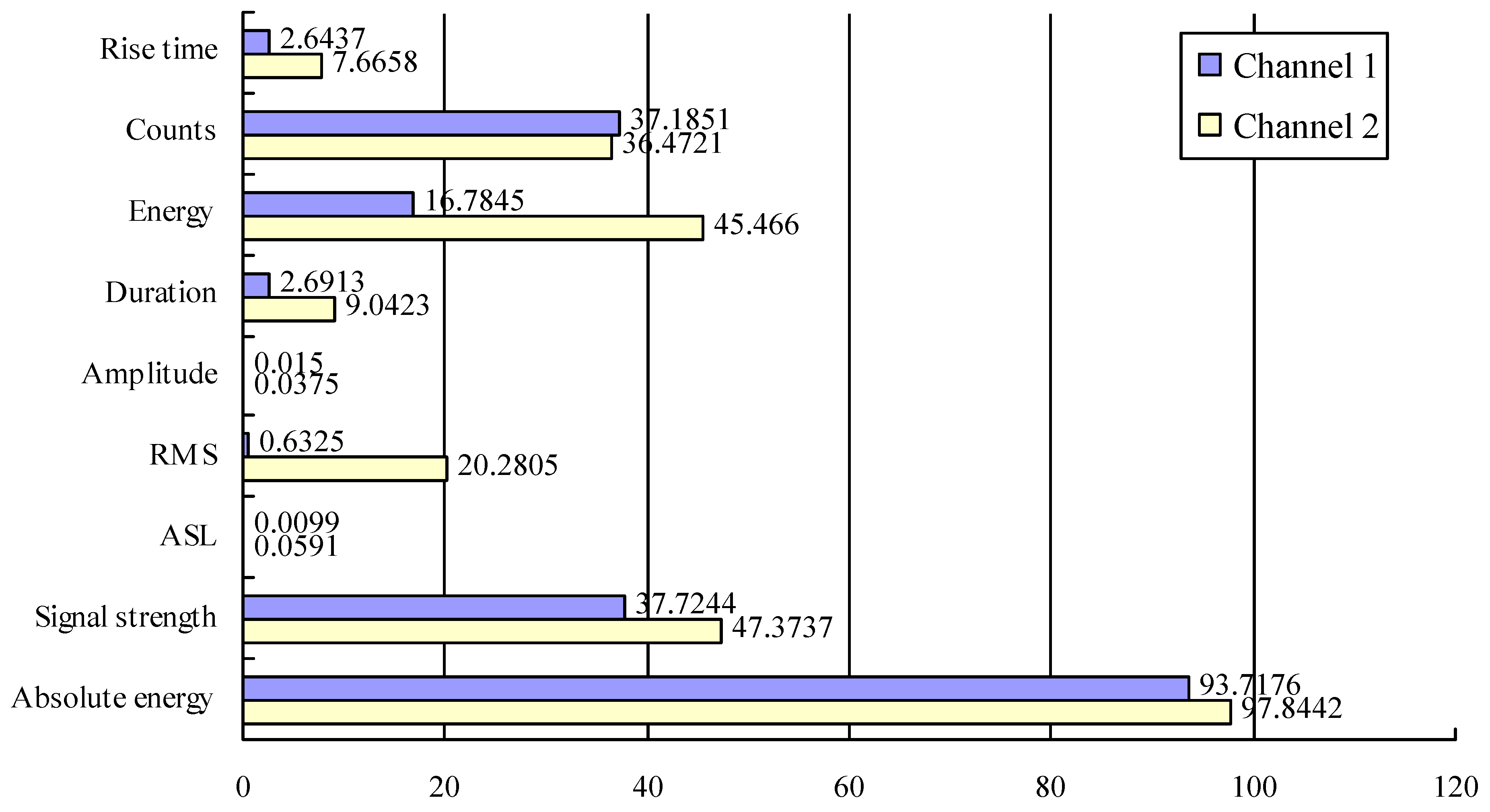
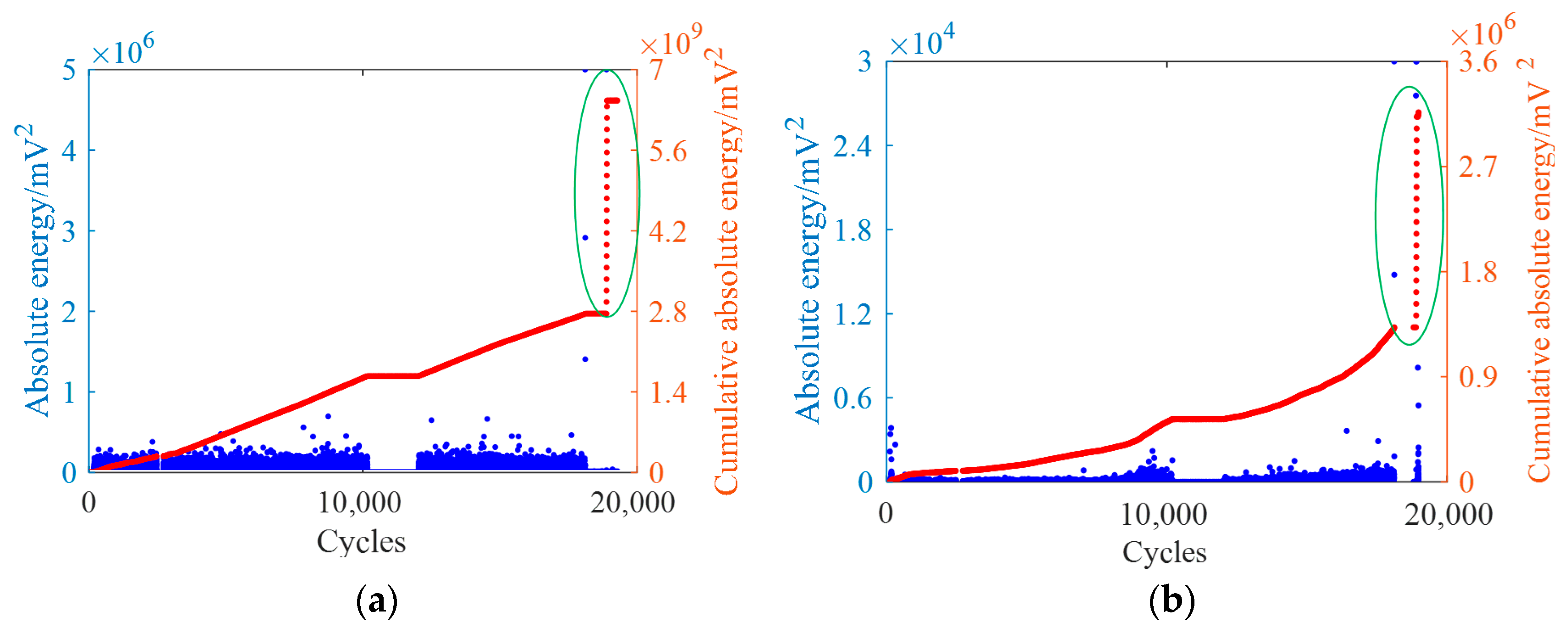
4.1. Selection and Description of AE Parameters
4.2. The Largest Lyapunov Exponent Fatigue Prediction
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ju, J.; Yu, H.; Zhao, Y.; Yang, T.; Xiao, B.; Peng, P.; Wang, R.; Wang, H.; Zeng, X.; Wang, J.; et al. Understanding the oxidation behaviors of a Ni-Co-based superalloy at elevated temperatures through multiscale characterization. Corros. Sci. 2024, 227, 111800. [Google Scholar] [CrossRef]
- Chen, M.; Hua, L.; Hu, Z.; Dong, K.; Qin, X. Cracking and suppression mechanisms of directed energy deposited IN738 superalloy revealed by microstructural characterization, in-situ thermal monitoring, and numerical simulations. J. Alloys Compd. 2025, 1020, 179446. [Google Scholar] [CrossRef]
- Karimian, S.F.; Modarres, M.; Bruck, H.A. A new method for detecting fatigue crack initiation in aluminum alloy using acoustic emission waveform information entropy. Eng. Fract. Mech. 2020, 223, 106771. [Google Scholar] [CrossRef]
- Roberts, T.M.; Talebzadeh, M. Acoustic emission monitoring of fatigue crack propagation. J. Constr. Steel Res. 2003, 59, 695–712. [Google Scholar] [CrossRef]
- Hassan, F.; Mahmood, A.K.B.; Yahya, N.; Saboor, A.; Abbas, M.Z.; Khan, Z.; Rimsan, M. State-of-the-art review on the acoustic emission source localization techniques. IEEE Access 2021, 9, 101246–101266. [Google Scholar] [CrossRef]
- Yu, J.; Ziehl, P.; Zárate, B.; Caicedo, J. Prediction of fatigue crack growth in steel bridge components using acoustic emission. J. Constr. Steel Res. 2011, 67, 1254–1260. [Google Scholar] [CrossRef]
- Chai, M.; Zhang, Z.; Duan, Q.; Song, Y. Assessment of fatigue crack growth in 316LN stainless steel based on acoustic emission entropy. Int. J. Fatigue 2018, 109, 145–156. [Google Scholar] [CrossRef]
- Keshtgar, A.; Sauerbrunn, C.M.; Modarres, M. Structural reliability prediction using acoustic emission-based modeling of fatigue crack growth. Appl. Sci. 2018, 8, 1225. [Google Scholar] [CrossRef]
- Caesarendra, W.; Kosasih, B.; Tieu, A.K.; Zhu, H.; Moodie, C.A.; Zhu, Q. Acoustic emission-based condition monitoring methods: Review and application for low speed slew bearing. Mech. Syst. Signal Process. 2016, 72, 134–159. [Google Scholar] [CrossRef]
- Kishawy, H.A.; Hegab, H.; Umer, U.; Mohany, A. Application of acoustic emissions in machining processes: Analysis and critical review. Int. J. Adv. Manuf. Technol. 2018, 98, 1391–1407. [Google Scholar] [CrossRef]
- Saeedifar, M.; Zarouchas, D. Damage characterization of laminated composites using acoustic emission: A review. Compos. B Eng. 2020, 195, 108039. [Google Scholar] [CrossRef]
- Chai, M.; Zhang, Z.; Duan, Q. A new qualitative acoustic emission parameter based on Shannon’s entropy for damage monitoring. Mech. Syst. Signal Process. 2018, 100, 617–629. [Google Scholar] [CrossRef]
- Chai, M.; Zhang, J.; Zhang, Z.; Duan, Q.; Cheng, G. Acoustic emission studies for characterization of fatigue crack growth in 316LN stainless steel and welds. Appl. Acoust. 2017, 126, 101–113. [Google Scholar] [CrossRef]
- Berkovits, A.; Fang, D. Study of fatigue crack characteristics by acoustic emission. Eng. Fract. Mech. 1995, 51, 401–416. [Google Scholar] [CrossRef]
- Behnia, A.; Chai, H.K.; Shiotani, T. Advanced structural health monitoring of concrete structures with the aid of acoustic emission. Constr. Build. Mater. 2014, 65, 282–302. [Google Scholar] [CrossRef]
- Morton, T.M.; Smith, S.; Harrington, R.M. Effect of loading variables on the acoustic emissions of fatigue-crack growth. Exp. Mech. 1974, 14, 282–302. [Google Scholar] [CrossRef]
- Li, L.; Zhang, Z.; Shen, G. Influence of grain size on fatigue crack propagation and acoustic emission features in commercial-purity zirconium. Mater. Sci. Eng. 2015, 636, 35–42. [Google Scholar] [CrossRef]
- Nemati, N.; Metrovich, B.; Nanni, A. Acoustic emission assessment of through-thickness fatigue crack growth in steel members. Adv. Struct. Eng. 2015, 18, 269–282. [Google Scholar] [CrossRef]
- Gagar, D.; Foote, P.; Irving, P.E. Effects of loading and sample geometry on acoustic emission generation during fatigue crack growth: Implications for structural health monitoring. Int. J. Fatigue 2015, 81, 117–127. [Google Scholar] [CrossRef]
- Keshtgar, A.; Modarres, M. Probabilistic approach for nondestructive detection of fatigue crack initiation and sizing. Int. J. Progn. Health Manag. 2016, 7, 1–10. [Google Scholar] [CrossRef]
- Aggelis, D.G.; Kordatos, E.Z.; Matikas, T.E. Acoustic emission for fatigue damage characterization in metal plates. Mech. Res. Commun. 2011, 38, 106–110. [Google Scholar] [CrossRef]
- Chen, H.L.; Choi, J.H. Acoustic emission study of fatigue cracks in materials used for AVLB. J. Nondestruct. Eval. 2004, 23, 133–151. [Google Scholar] [CrossRef]
- Takens, F. Detecting strange attractors in turbulence. In Dynamical Systems and Turbulence, Warwick 1980; Springer: Berlin/Heidelberg, Germany, 1981; Volume 898, pp. 366–381. [Google Scholar]
- Rosenstein, M.T.; Collins, J.J.; DeLuca, C.J. A Practical Method for calculating Largest Lyapunov Exponents from Small Data Sets. Phys. D Nonlinear Phenom. 1993, 65, 117–134. [Google Scholar] [CrossRef]
- Peter, G.; Itamar, P. Measuring the strangeness of strange attractors. Phys. D Nonlinear Phenom. 1983, 9, 189–208. [Google Scholar]
- Alan, W.; Jack, S.; Harry, L.; Swinney, J.V. Determining Lyapunov exponents from a time series. Phys. D Nonlinear Phenom. 1985, 3, 285–317. [Google Scholar]
- Fraser, A.M. Information and entropy in strange attractors. IEEE Trans. Inf. Theory 1989, 35, 245–262. [Google Scholar] [CrossRef]
- GB/T 15248-2008; The Test Method for Axial Loading Constant-Amplitude Low-Cycle Fatigue of Metallic Materials. General Administration of Quality Supervision, Inspection and Quarantine of the People’s Republic of China, National Standardization Administration: Beijing, China, 2008.







| Set Number | The Largest Lyapunov Exponent in Channel 1 | The Largest Lyapunov Exponent in Channel 2 |
| 1 | 0.00032 | 0.00024 |
| 2 | 0.00152 | 0.00093 |
| 3 | 0.00355 | 0.00278 |
| 4 | 0.00641 | 0.00577 |
| 5 | 0.00428 | 0.00396 |
| Over all | 0.00392 | 0.00251 |
| Set Number | The Largest Lyapunov Exponent in Channel 1 | The Largest Lyapunov Exponent in Channel 2 |
| 1 | 0.00172 | 0.00066 |
| 2 | 0.00671 | 0.00129 |
| 3 | 0.00083 | 0.00311 |
| 4 | 0.00314 | 0.00583 |
| 5 | 0.00422 | 0.00501 |
| Over all | 0.00539 | 0.00324 |
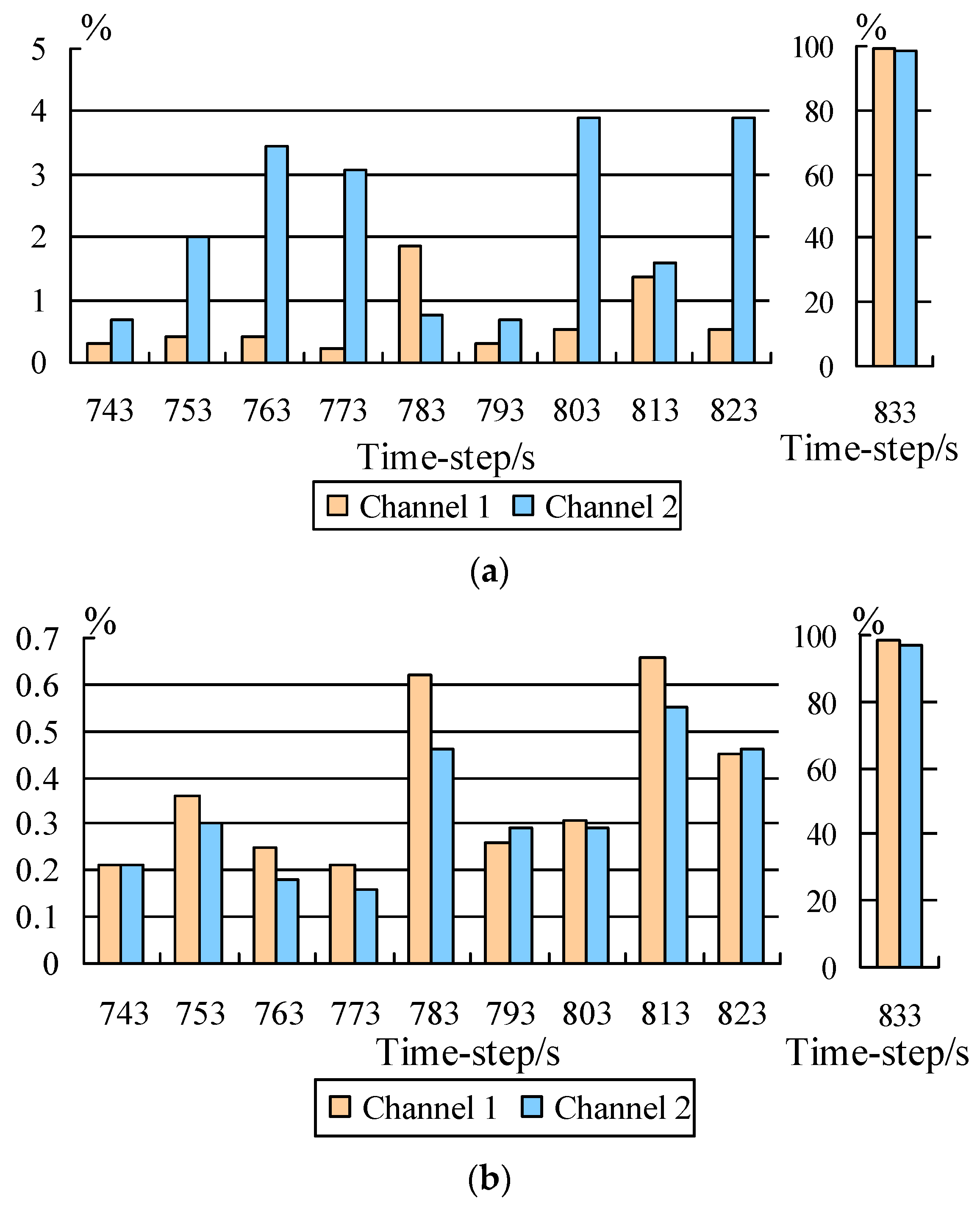
| Prediction Time Step/s | Cycles | Channel 1 | Channel 2 | ||||
| Measured Value | Wolf Method | Small Data Method | Measured Value | Wolf Method | Small Data Method | ||
| 743 | 7430 | 36,655.43 | 36,547.28 | 36,733.75 | 5599.82 | 5638.87 | 5587.92 |
| 753 | 7530 | 29,893.65 | 29,772.42 | 30,001.17 | 2539.42 | 2488.68 | 2546.97 |
| 763 | 7630 | 26,829.72 | 26,945.55 | 26,895.87 | 5628.18 | 5433.40 | 5638.56 |
| 773 | 7730 | 39,033.06 | 38,947.12 | 39,113.89 | 5989.25 | 6173.87 | 5979.88 |
| 783 | 783 | 42,114.50 | 42,887.68 | 42,373.90 | 6826.17 | 6773.33 | 6857.71 |
| 793 | 7930 | 65,863.40 | 65,658.12 | 65,691.57 | 5584.64 | 5621.97 | 5568.72 |
| 803 | 8030 | 41,286.73 | 41,070.82 | 41,416.67 | 1262.39 | 1311.76 | 1266.06 |
| 813 | 830 | 11,464.36 | 11,619.66 | 11,539.97 | 7509.37 | 7390.04 | 7497.85 |
| 823 | 8230 | 45,213.25 | 44,973.31 | 45,417.87 | 4622.99 | 4802.60 | 4644.23 |
| 833 | 8330 | 39,554,569.66 | 400,467.79 | 672,731.97 | 14,963,564.37 | 187,862.23 | 497,662.11 |
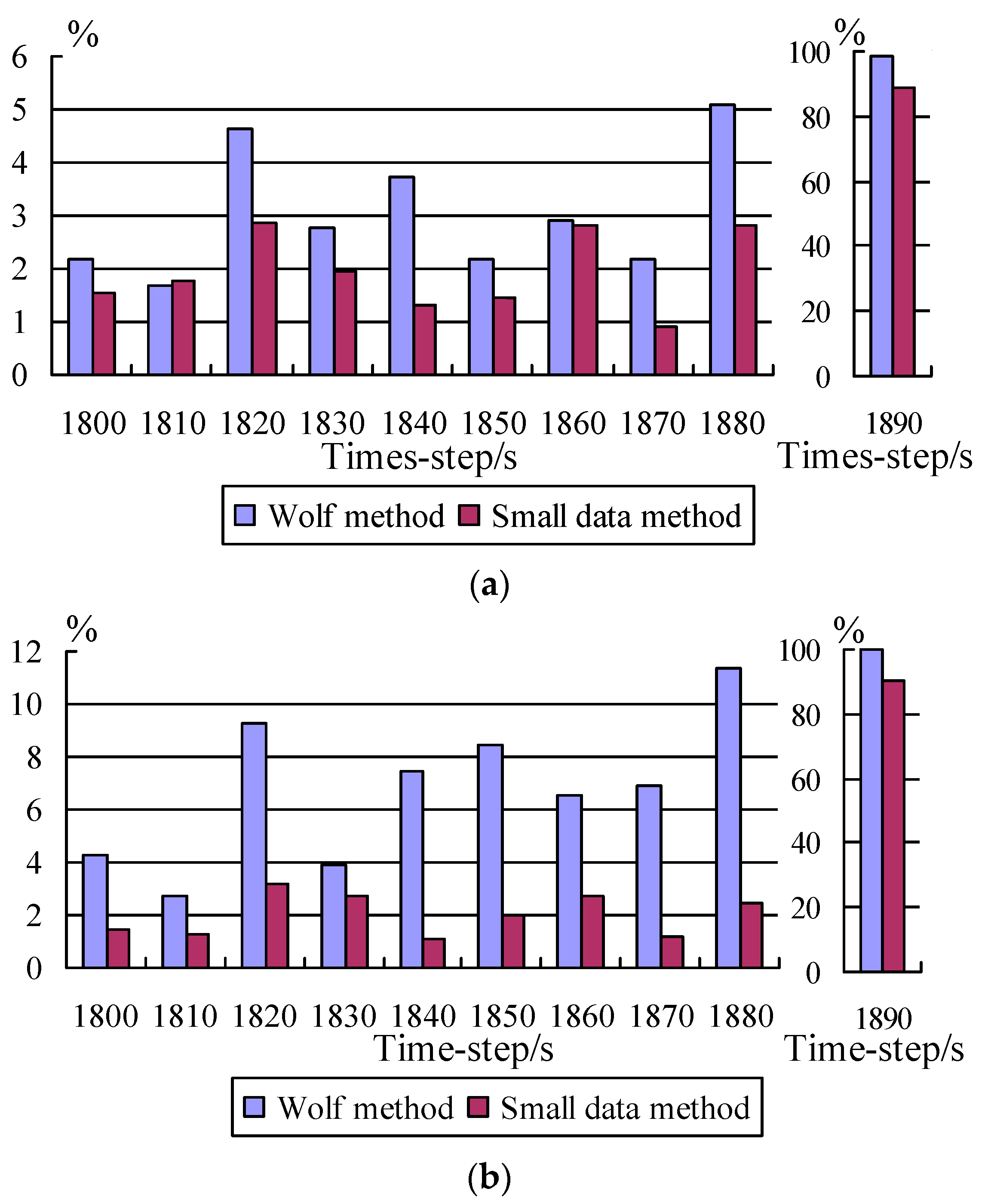
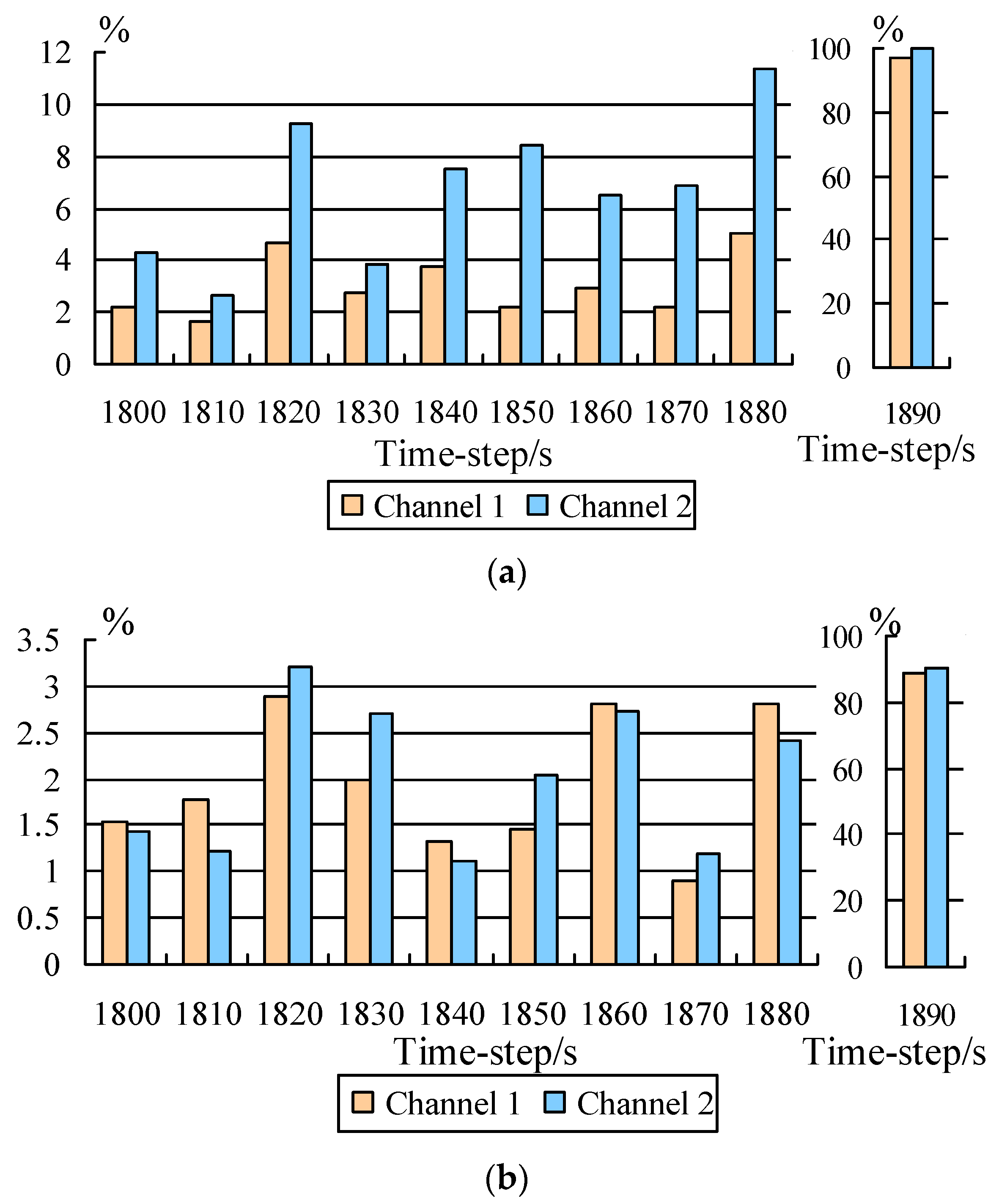
| Prediction Time Step/s | Cycles | Channel 1 | Channel 2 | ||||
| Measured Value | Wolf Method | Small Data Method | Measured Value | Wolf Method | Small Data Method | ||
| 1800 | 18,000 | 14,180.00 | 13,869.03 | 13,962.76 | 527.75 | 550.35 | 535.30 |
| 1810 | 18,100 | 7150.00 | 7031.10 | 7023.73 | 356.25 | 365.84 | 351.88 |
| 1820 | 18,200 | 25.59 | 26.78 | 26.33 | 389.10 | 395.97 | 376.66 |
| 1830 | 18,300 | 6477.00 | 6296.55 | 6349.01 | 163.16 | 156.87 | 158.76 |
| 1840 | 18,400 | 173.87 | 180.35 | 157.81 | 712.99 | 659.64 | 720.96 |
| 1850 | 18,500 | 820.16 | 837.88 | 788.23 | 797.56 | 809.25 | 813.83 |
| 1860 | 18,600 | 691.51 | 717.28 | 710.92 | 430.52 | 458.59 | 442.26 |
| 1870 | 18,700 | 2928.00 | 2864.40 | 2901.65 | 378.19 | 404.25 | 382.71 |
| 1880 | 18,800 | 51.89 | 54.52 | 53.35 | 1822.00 | 1770.77 | 1777.94 |
| 1890 | 18,900 | 4,189,000,000 | 134,885,800.014 | 473,825,575.06 | 11,898,000,000 | 3,530,027.48 | 1,150,536,612.85 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jing, T.; Yu, Y. Fatigue Prediction Method of Superalloy Based on the Improved Largest Lyapunov Exponent. Metals 2025, 15, 945. https://doi.org/10.3390/met15090945
Jing T, Yu Y. Fatigue Prediction Method of Superalloy Based on the Improved Largest Lyapunov Exponent. Metals. 2025; 15(9):945. https://doi.org/10.3390/met15090945
Chicago/Turabian StyleJing, Ting, and Yang Yu. 2025. "Fatigue Prediction Method of Superalloy Based on the Improved Largest Lyapunov Exponent" Metals 15, no. 9: 945. https://doi.org/10.3390/met15090945
APA StyleJing, T., & Yu, Y. (2025). Fatigue Prediction Method of Superalloy Based on the Improved Largest Lyapunov Exponent. Metals, 15(9), 945. https://doi.org/10.3390/met15090945






