Cyclic HCP<->FCC Phase Transformation Crystallography in Pure Cobalt
Abstract
1. Introduction
2. Materials and Methods
3. Results
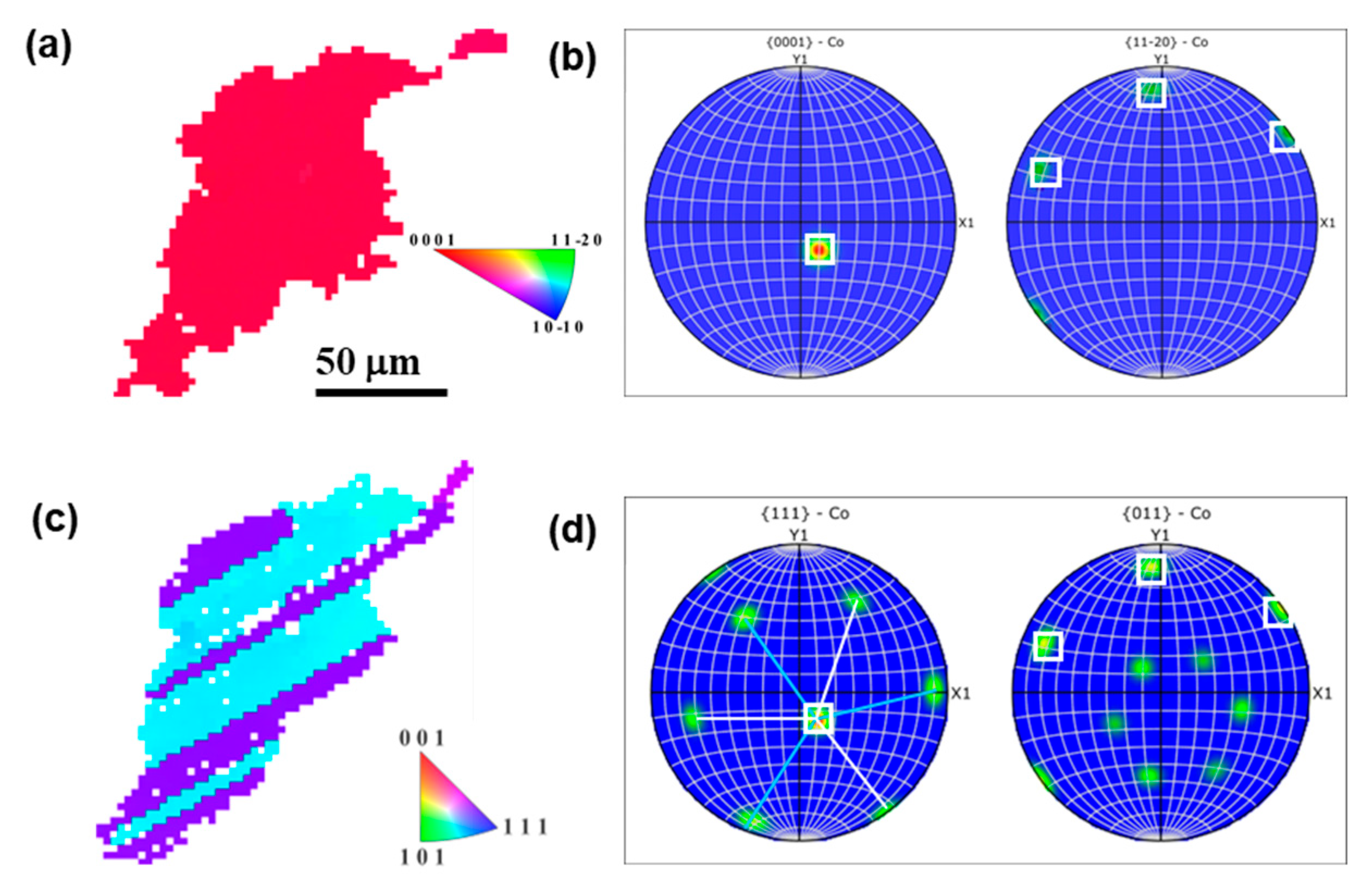
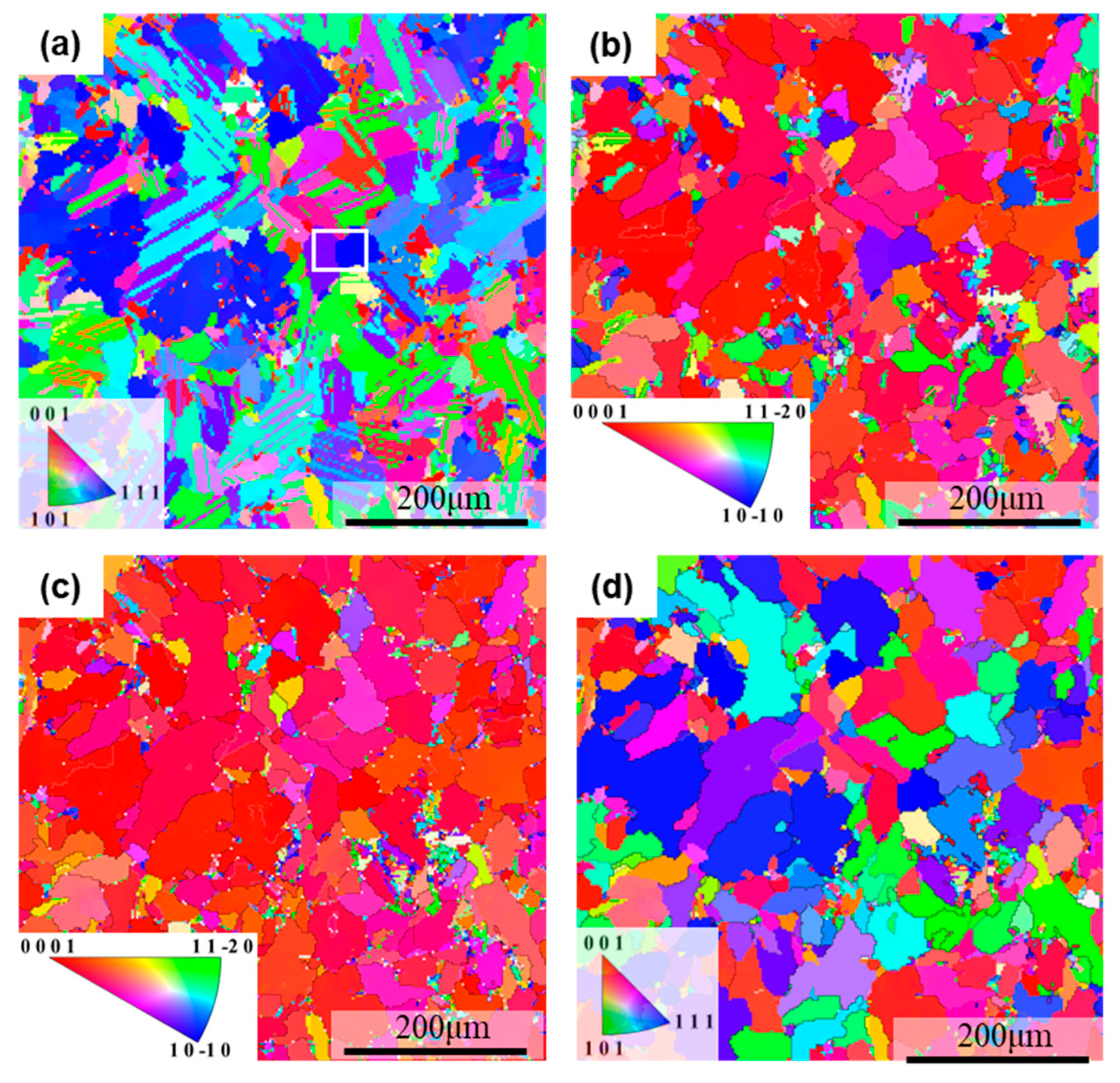
3.1. In Situ Observation
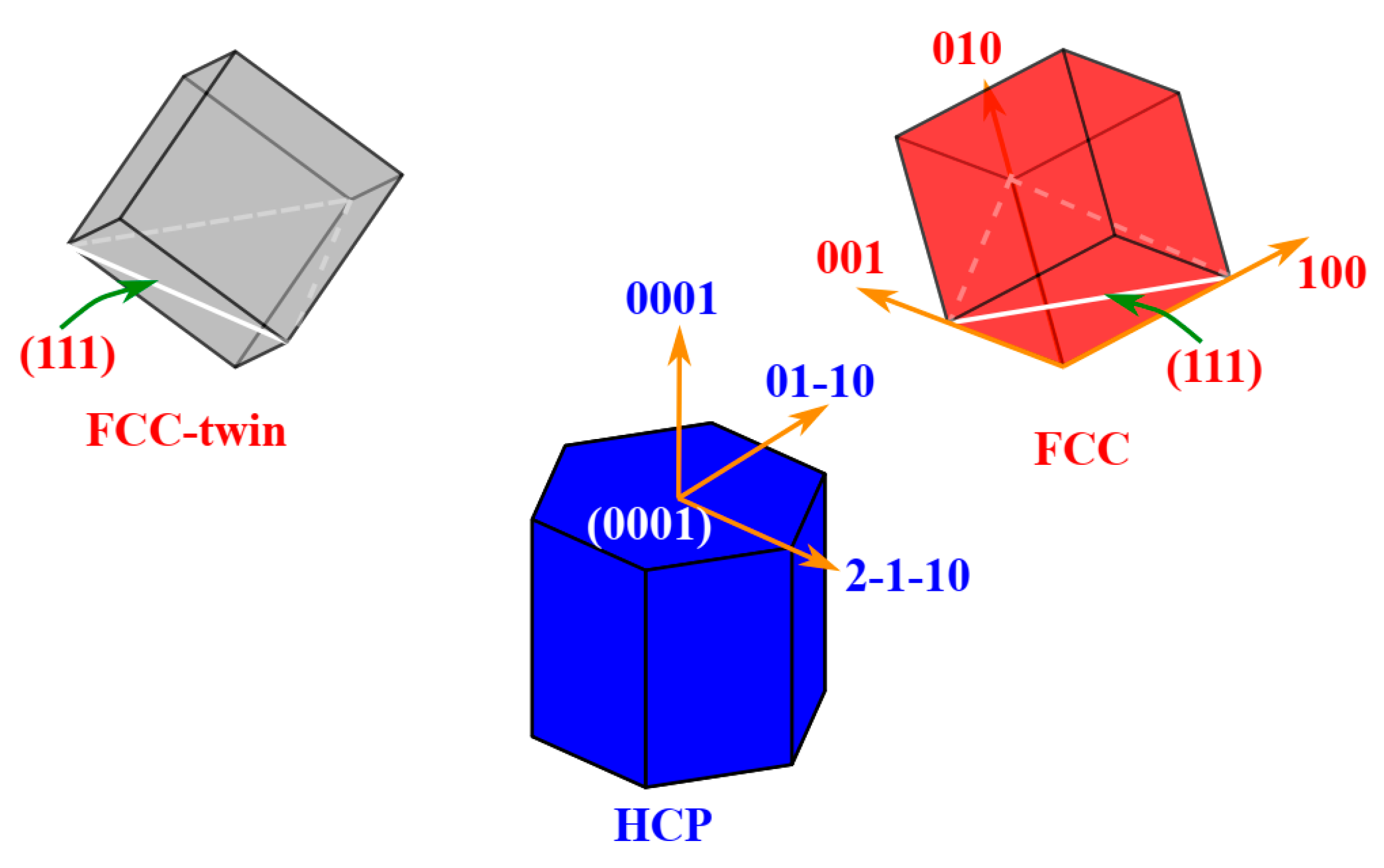
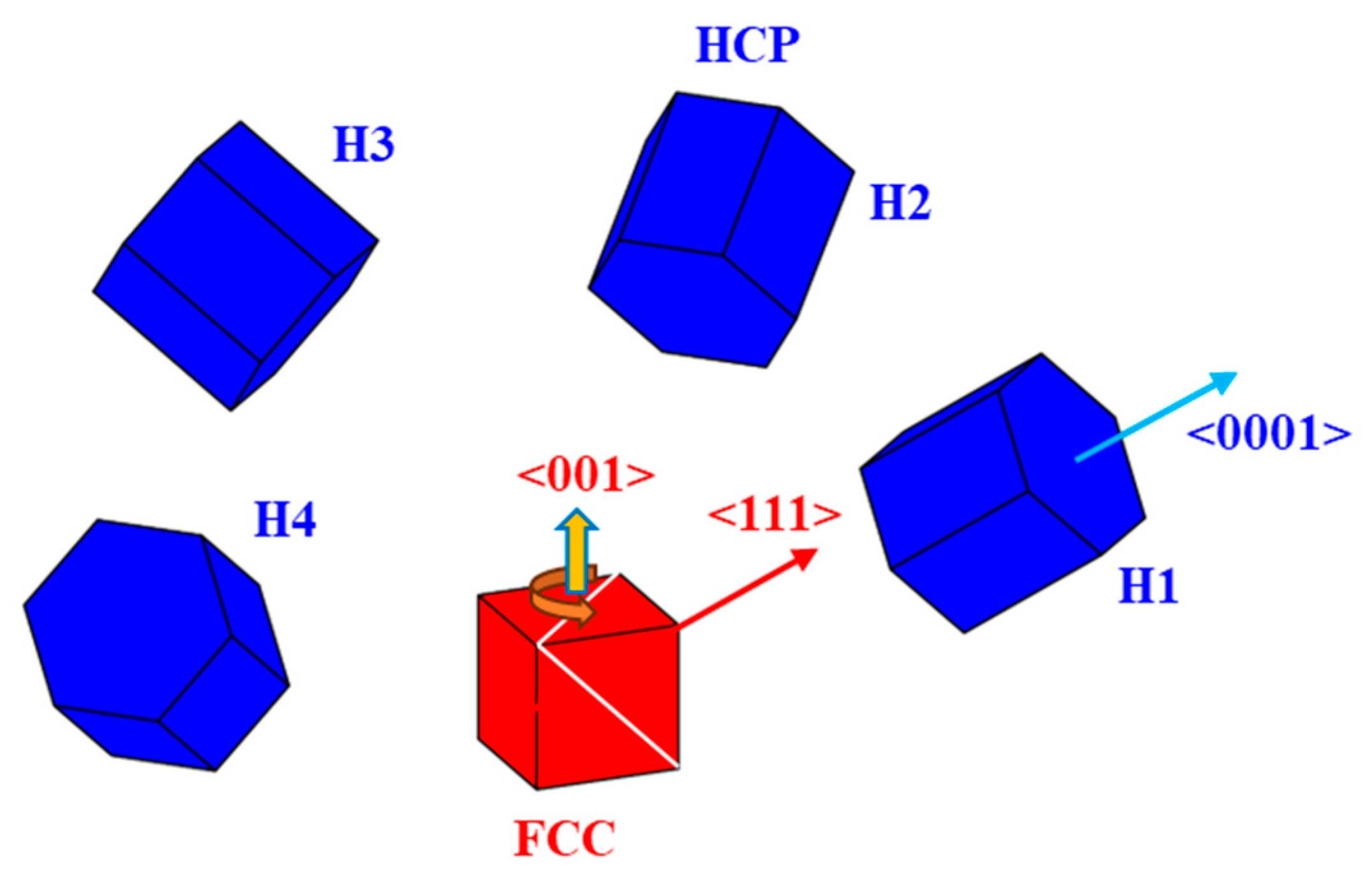
3.2. Orientation Variants
4. Discussion
4.1. Transformation Sequence
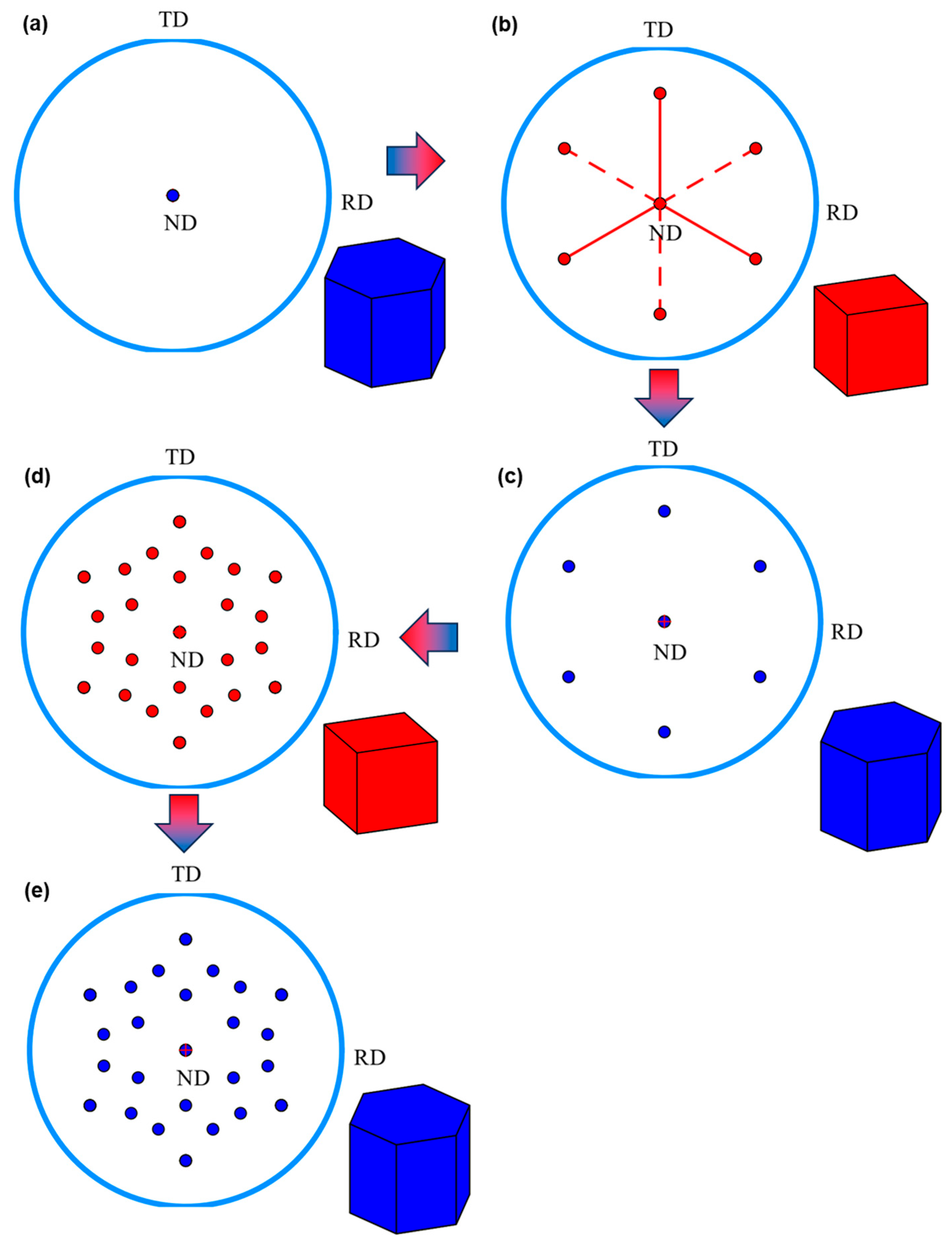
4.2. Variant Selection
4.3. Reconstruction Based on EBSD Scans
4.4. Modification of Texture Memory
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sato, J.; Omori, T.; Oikawa, K.; Ohnuma, I.; Kainuma, R.; Ishida, K. Cobalt-base high-temperature alloys. Science 2006, 312, 90–91. [Google Scholar] [CrossRef]
- Wu, C.; Han, J.-H.; Shi, X.; Koli, D.R.; Penigalapati, D. Cobalt CMP development for 7nm logic device. ECS Trans. 2017, 77, 93. [Google Scholar] [CrossRef]
- Dutta, S.; Beyne, S.; Gupta, A.; Kundu, S.; Van Elshocht, S.; Bender, H.; Jamieson, G.; Vandervorst, W.; Bömmels, J.; Wilson, C.J. Sub-100 nm2 cobalt interconnects. IEEE Electron Device Lett. 2018, 39, 731–734. [Google Scholar] [CrossRef]
- Dee, K.C.; Puleo, D.A.; Bizios, R. An Introduction to Tissue-Biomaterial Interactions; John Wiley & Sons: Hoboken, NJ, USA, 2003. [Google Scholar]
- Ye, X.; Xiang, C.; Nie, H.; Lei, H.; Du, Y.; Xing, W.; Luo, J.; Yu, Z. Facet-dependent interfacial segregation behavior of V-doped WC-Co cemented carbides. Ceram. Int. 2022, 48, 11251–11256. [Google Scholar] [CrossRef]
- Christian, J.W. A theory of the transformation in pure cobalt. Proceedings of the Royal Society of London. Ser. A. Math. Phys. Sci. 1951, 206, 51–64. [Google Scholar] [CrossRef]
- He, J.-J.; Xu, G.-J.; Wang, X.-Q.; Luo, J.-F.; Liu, D.; Li, Y.-J.; Gu, X.-F. Origin of misorientations for fcc→hcp transformation in pure cobalt and its in-situ validation. Trans. Nonferrous Met. Soc. China 2025, 35, 1532–1542. [Google Scholar] [CrossRef]
- Nishiyama, Z. Martensitic Transformation; Elsevier: Amsterdam, The Netherlands, 1978. [Google Scholar]
- Liu, W.; An, X.; Jiang, W.; Ni, S.; Song, M. Microstructural evolution of a polycrystalline cobalt during tensile deformation. Mater. Sci. Eng. A 2021, 826, 141970. [Google Scholar] [CrossRef]
- Zhu, E.; Zhang, J.; Guo, S.; Yang, X.; Zhang, X.; Yang, J. Effect of Co on morphology and preparation of in situ synthesis of WC-Co composite powders. Mater. Res. Express 2019, 6, 086522. [Google Scholar] [CrossRef]
- Kestens, L.A.I.; Pirgazi, H. Texture formation in metal alloys with cubic crystal structures. Mater. Sci. Technol. 2016, 32, 1303–1315. [Google Scholar] [CrossRef]
- Kestens, L.; Jonas, J.J. Transformation and Recrystallization Textures Associated with Steel Processing. Metalwork. Bulk Form. 2005, 14A, 685–700. [Google Scholar] [CrossRef]
- Huang, Y.; Gu, X.; He, J.; Luo, J.; Zhu, Z.; Xu, G. Revealing the Impact of Initial Textures on Orientation Memory Effect During HCP → FCC → HCP Transformation in High-Purity Cobalt. JOM 2025, 77, 2836–2843. [Google Scholar] [CrossRef]
- Furuhara, T.; Maki, T. Variant selection in heterogeneous nucleation on defects in diffusional phase transformation and precipitation. Mater. Sci. Eng. A 2001, 312, 145–154. [Google Scholar] [CrossRef]
- Cayron, C. The transformation matrices (distortion, orientation, correspondence), their continuous forms and their variants. Acta Crystallogr. A 2019, 75, 411–437. [Google Scholar] [CrossRef]
- Wei, Z.; Yang, P.; Gu, X.; Onuki, Y.; Sato, S. Transformation textures in pure titanium: Texture memory vs surface effect. Mater. Charact. 2020, 164, 110359. [Google Scholar] [CrossRef]
- Tomida, T.; Wakita, M.; Yasuyama, M.; Sugaya, S.; Tomota, Y.; Vogel, S.C. Memory effects of transformation textures in steel and its prediction by the double Kurdjumov–Sachs relation. Acta Mater. 2013, 61, 2828–2839. [Google Scholar] [CrossRef]
- Seward, G.G.E.; Celotto, S.; Prior, D.J.; Wheeler, J.; Pond, R.C. In situ SEM-EBSD observations of the hcp to bcc phase transformation in commercially pure titanium. Acta Mater. 2004, 52, 821–832. [Google Scholar] [CrossRef]
- Daymond, M.R.; Holt, R.A.; Cai, S.; Mosbrucker, P.; Vogel, S.C. Texture inheritance and variant selection through an hcp–bcc–hcp phase transformation. Acta Mater. 2010, 58, 4053–4066. [Google Scholar] [CrossRef]
- Lonardelli, I.; Gey, N.; Wenk, H.R.; Humbert, M.; Vogel, S.C.; Lutterotti, L. In situ observation of texture evolution during α → β and β → α phase transformations in titanium alloys investigated by neutron diffraction. Acta Mater. 2007, 55, 5718–5727. [Google Scholar] [CrossRef]
- Gey, N.; Humbert, M. Characterization of the variant selection occurring during the α→β→α phase transformations of a cold rolled titanium sheet. Acta Mater. 2002, 50, 277–287. [Google Scholar] [CrossRef]
- Miyamoto, G.; Iwata, N.; Takayama, N.; Furuhara, T. Mapping the parent austenite orientation reconstructed from the orientation of martensite by EBSD and its application to ausformed martensite. Acta Mater. 2010, 58, 6393–6403. [Google Scholar] [CrossRef]
- Cayron, C. ARPGE: A computer program to automatically reconstruct the parent grains from electron backscatter diffraction data. J. Appl. Crystallogr. 2007, 40, 1183–1188. [Google Scholar] [CrossRef]
- Huang, C.-Y.; Ni, H.-C.; Yen, H.-W. New protocol for orientation reconstruction from martensite to austenite in steels. Materialia 2020, 9, 100554. [Google Scholar] [CrossRef]
- Jourdan, C.; Gastaldi, J.; Grange, G. In situ study of the titanium phase transformation. Phase Transit. 1991, 31, 137–143. [Google Scholar] [CrossRef]
- Ball, J.A.D.; Davis, C.; Slater, C.; Vashishtha, H.; Said, M.; Hébrard, L.; Steinhilber, F.; Wright, J.P.; Connolley, T.; Michalik, S.; et al. Grain-level effects on in-situ deformation-induced phase transformations in a complex-phase steel using 3DXRD and EBSD. Acta Mater. 2024, 265, 119608. [Google Scholar] [CrossRef]
- Guo, J.; Li, M.; Yao, Y.; Jiang, R.; Wang, Z.; Piao, Z.; Li, Y.; Ke, P. In-situ high-temperature scanning electron microscopy study of phase transformation and variant selection phenomena in TC21 titanium alloy. J. Alloys Compd. 2025, 1026, 180386. [Google Scholar] [CrossRef]
- Bondarev, A.; Sreenivasa Rao, P.; Isavand, S.; O’Dowd, N. Revealing the reverse austenite and martensite transformation pathways in P91 steel through in situ MEMS-heating EBSD investigations. Mater. Today Commun. 2025, 43, 111753. [Google Scholar] [CrossRef]
- Zhang, J.-Y.; Zhang, Y.-S.; Mompiou, F.; Zhang, W.-Z. Structures and migrations of interfaces between β precipitates and α′ matrix in a Ti-2.6 wt% Mo alloy. Acta Mater. 2024, 281, 120429. [Google Scholar] [CrossRef]
- Zhou, X.; Kumar, S.; Zhang, S.; Chen, X.; Gault, B.; Dehm, G.; Hickel, T.; Raabe, D. Boron triggers grain boundary structural transformation in steel. Nat. Commun. 2025, 16, 6927. [Google Scholar] [CrossRef] [PubMed]
- Gu, X.-F.; Furuhara, T.; Zhang, W.-Z. PTCLab: Free and open-source software for calculating phase transformation crystallography. J. Appl. Crystallogr. 2016, 49, 1099–1106. [Google Scholar] [CrossRef]
- Christian, J.W. The Theory of Transformation in Metals and Alloys; Pergamon Press: Oxford, UK, 2002. [Google Scholar]
- Farabi, E.; Haghdadi, N.; Czettl, C.; Pachlhofer, J.; Rohrer, G.S.; Ringer, S.P.; Primig, S. On the fcc to hcp transformation in a Co-Ru alloy: Variant selection and intervariant boundary character. Scr. Mater. 2024, 248, 116127. [Google Scholar] [CrossRef]
- Aroyo, M.I. International Tables for Crystallography, Volume A: Space-Group Symmetry, 6th ed.; Springer: Dordrecht, The Netherlands, 2017. [Google Scholar]
- Fekih, M.; Ostormujof, T.M.; Germain, L.; Piette, M.; Sornin, D.; Gey, N. High temperature EBSD experiment versus crystallographic reconstruction to study phase transformation induced microstructures—Application examples for steels. Mater. Charact. 2025, 228, 115427. [Google Scholar] [CrossRef]
- Huang, Y.; He, J.; Gu, X.; Xu, G.; Qi, Q.; Luo, J. In situ EBSD study on the abnormal grain growth phenomenon in high-purity cobalt. J. Mater. Sci. 2024, 59, 18698–18711. [Google Scholar] [CrossRef]



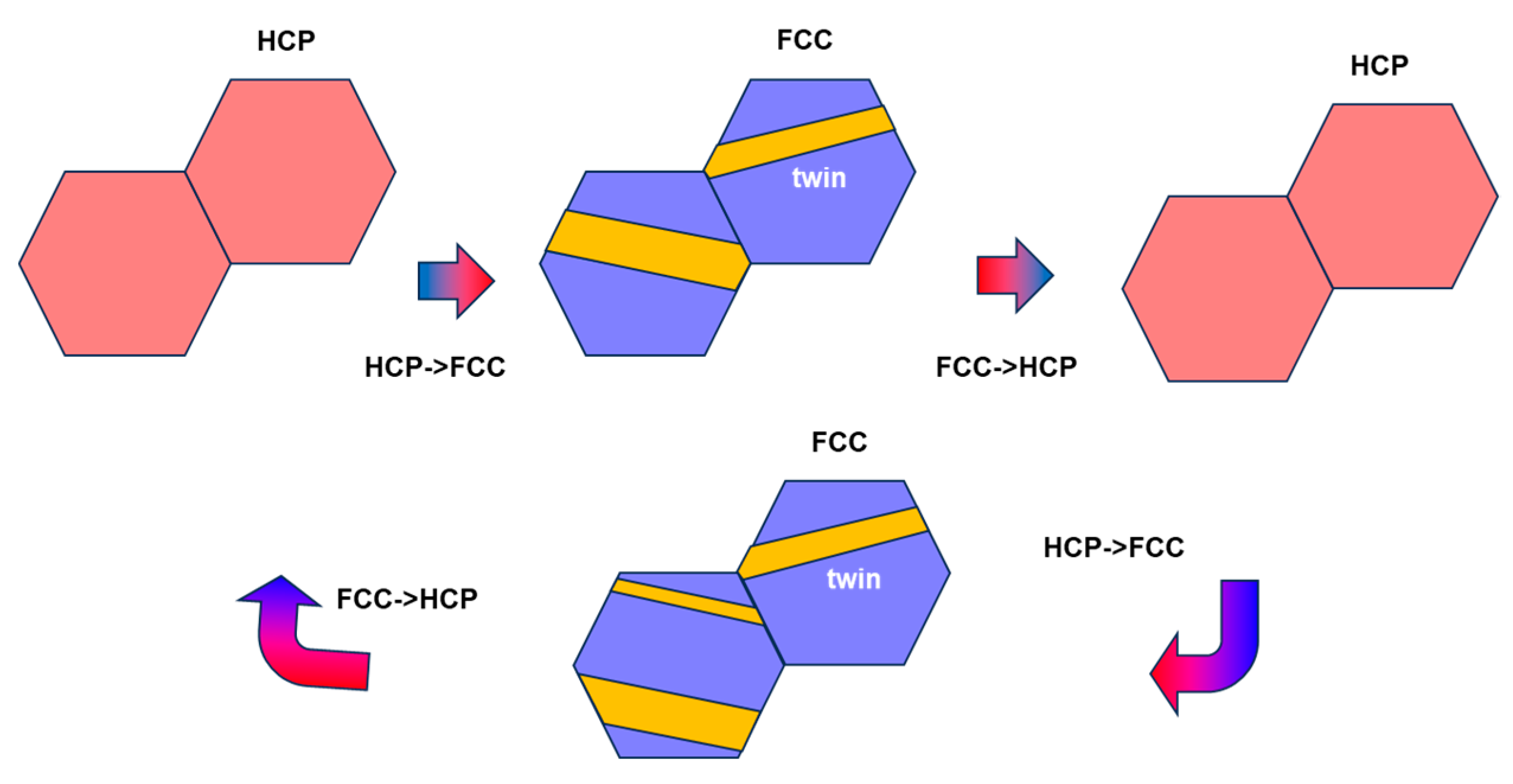
| No. | Close-Packed Planes | Close-Packed Directions | Symmetry Operations in HCP |
|---|---|---|---|
| F1 | (0001)h//(111)f | [2-1-10]h//[−101]f | |
| F2 | (0001)h//(-1-1-1)f | [2-1-10]h//[−101]f |
| No. | Close-Packed Planes | Close-Packed Directions | Symmetry Operations in FCC |
|---|---|---|---|
| H1 | (111)f//(0001)h | [−101]f//[2-1-10]h | |
| H2 | (−111)f//(0001)h | [101]f//[2-1-10]h | |
| H3 | (1-11)f//(0001)h | [011]f//[2-1-10]h | |
| H4 | (11-1)f//(0001)h | [−110]f//[2-1-10]h |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, Y.; He, J.; Zhu, Z.; Xu, G.; Qi, Q.; Luo, J.; Shang, Z.; Gu, X. Cyclic HCP<->FCC Phase Transformation Crystallography in Pure Cobalt. Metals 2025, 15, 947. https://doi.org/10.3390/met15090947
Huang Y, He J, Zhu Z, Xu G, Qi Q, Luo J, Shang Z, Gu X. Cyclic HCP<->FCC Phase Transformation Crystallography in Pure Cobalt. Metals. 2025; 15(9):947. https://doi.org/10.3390/met15090947
Chicago/Turabian StyleHuang, Yuhang, Jinjiang He, Zhiyi Zhu, Guojin Xu, Qiqi Qi, Junfeng Luo, Zaiyan Shang, and Xinfu Gu. 2025. "Cyclic HCP<->FCC Phase Transformation Crystallography in Pure Cobalt" Metals 15, no. 9: 947. https://doi.org/10.3390/met15090947
APA StyleHuang, Y., He, J., Zhu, Z., Xu, G., Qi, Q., Luo, J., Shang, Z., & Gu, X. (2025). Cyclic HCP<->FCC Phase Transformation Crystallography in Pure Cobalt. Metals, 15(9), 947. https://doi.org/10.3390/met15090947







