A Simulation-Based Comparative Analysis of Physics and Data-Driven Models for Temperature Prediction in Steel Coil Annealing
Abstract
1. Introduction
2. Review of the Related Literature
2.1. Physics-Based Modeling Approaches
2.2. Machine Learning and Data-Driven Methods
2.3. Trends and Synthesis
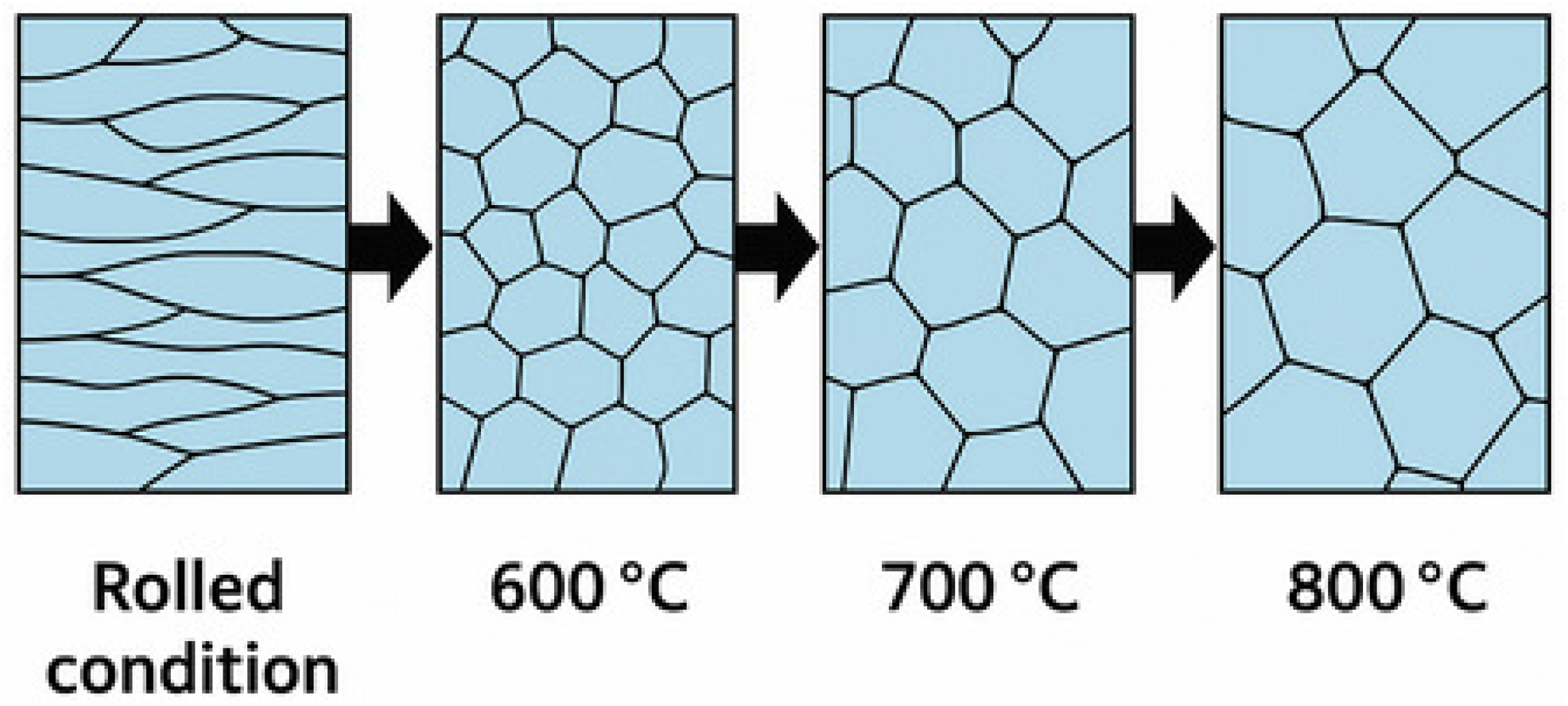
3. Understanding Steel Coil Annealing
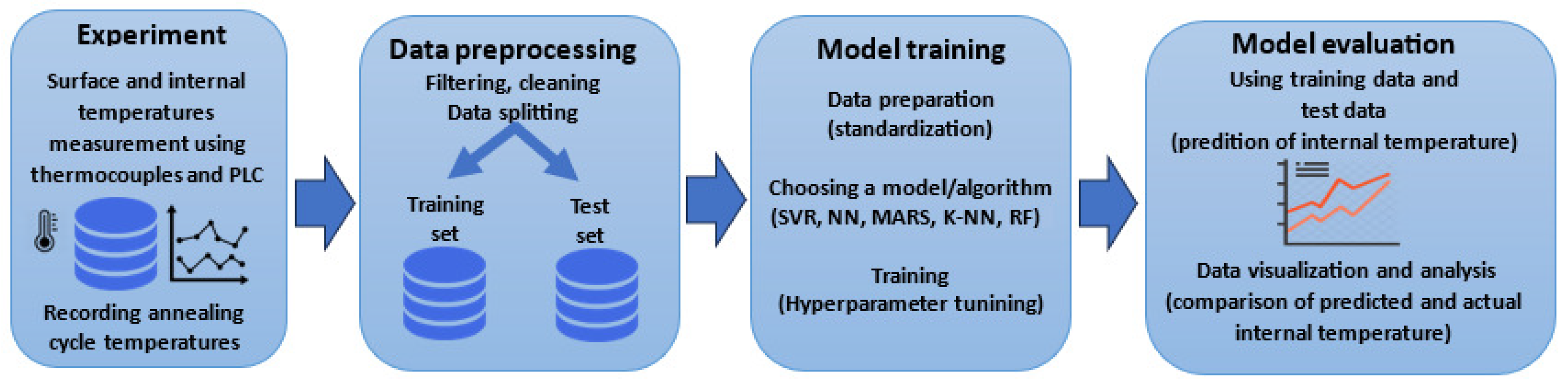
4. Materials and Methods
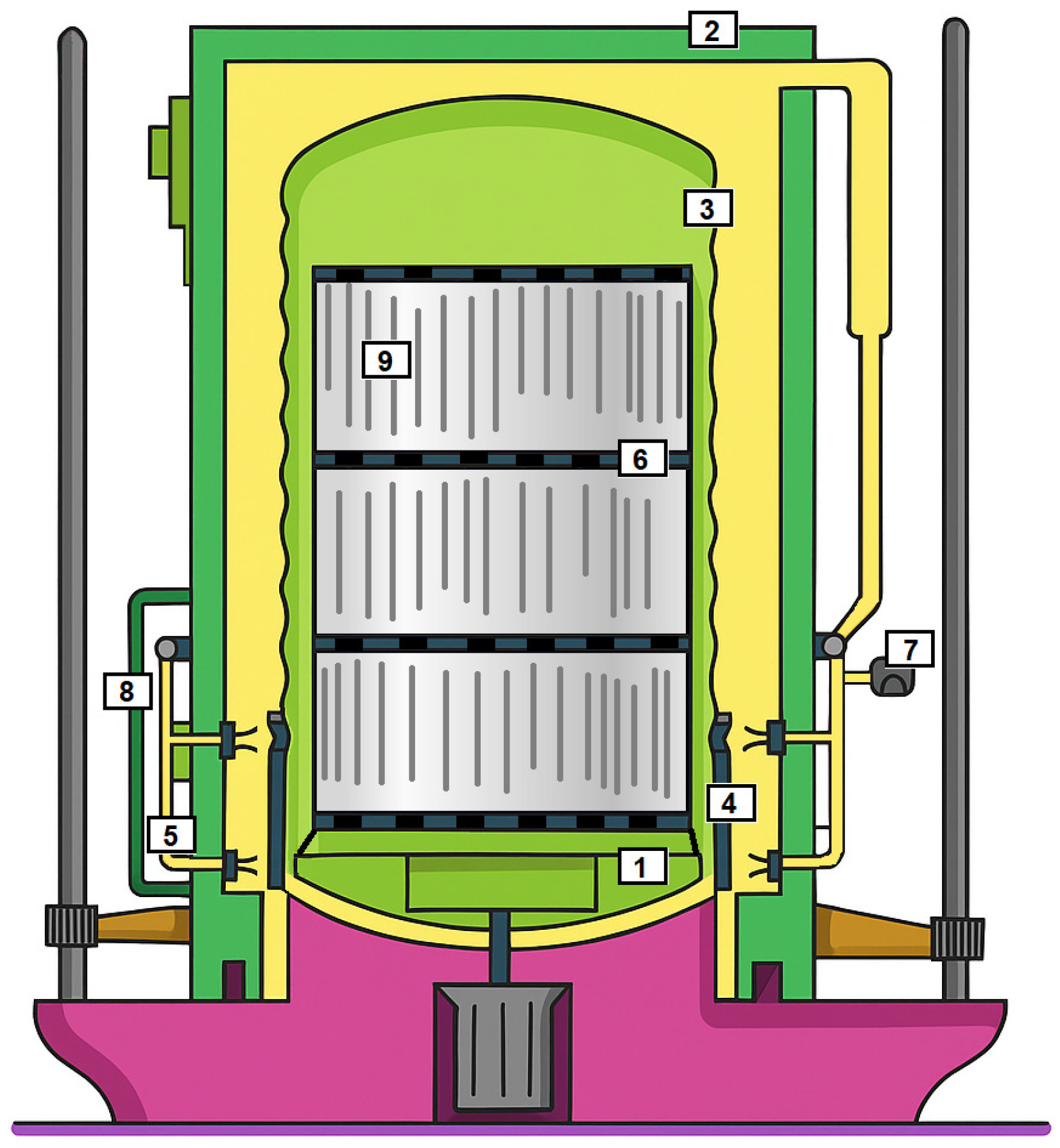
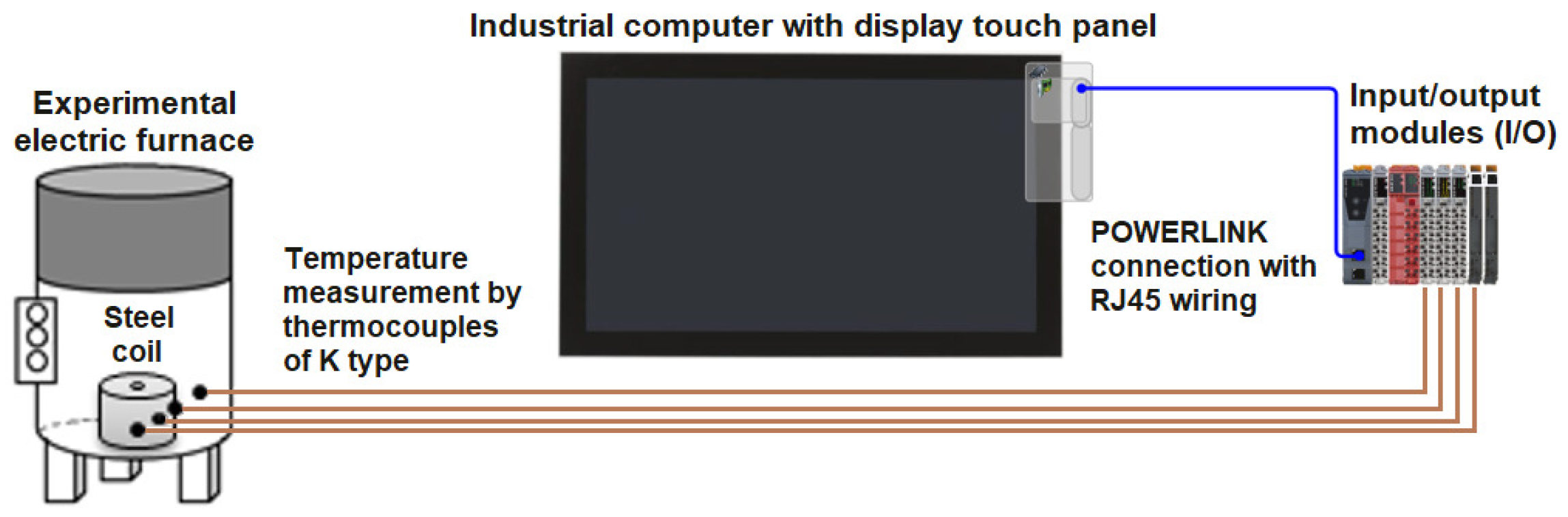
4.1. Experimental Annealing Furnace
4.2. Modeling Methods for Modeling Internal Temperatures
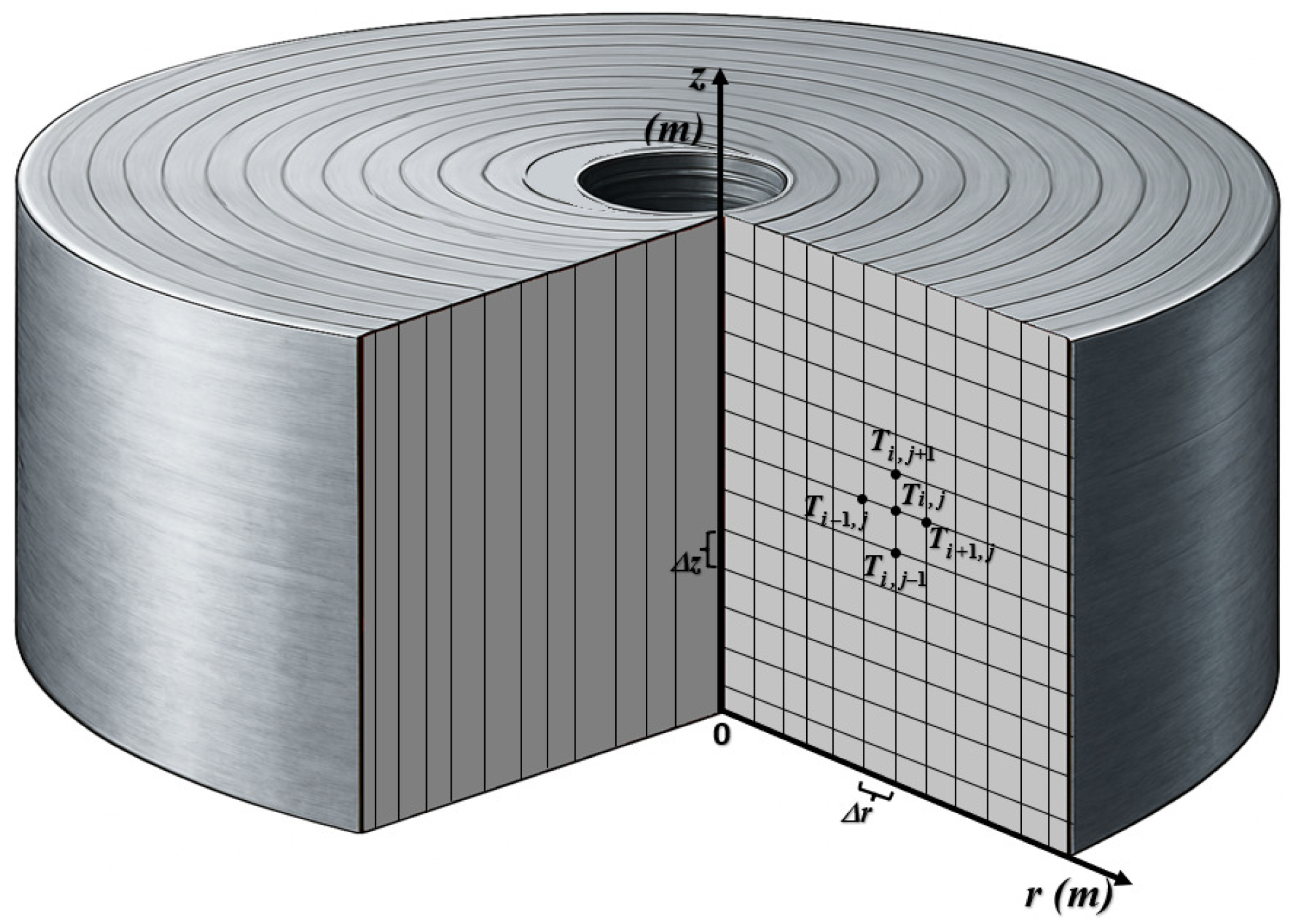
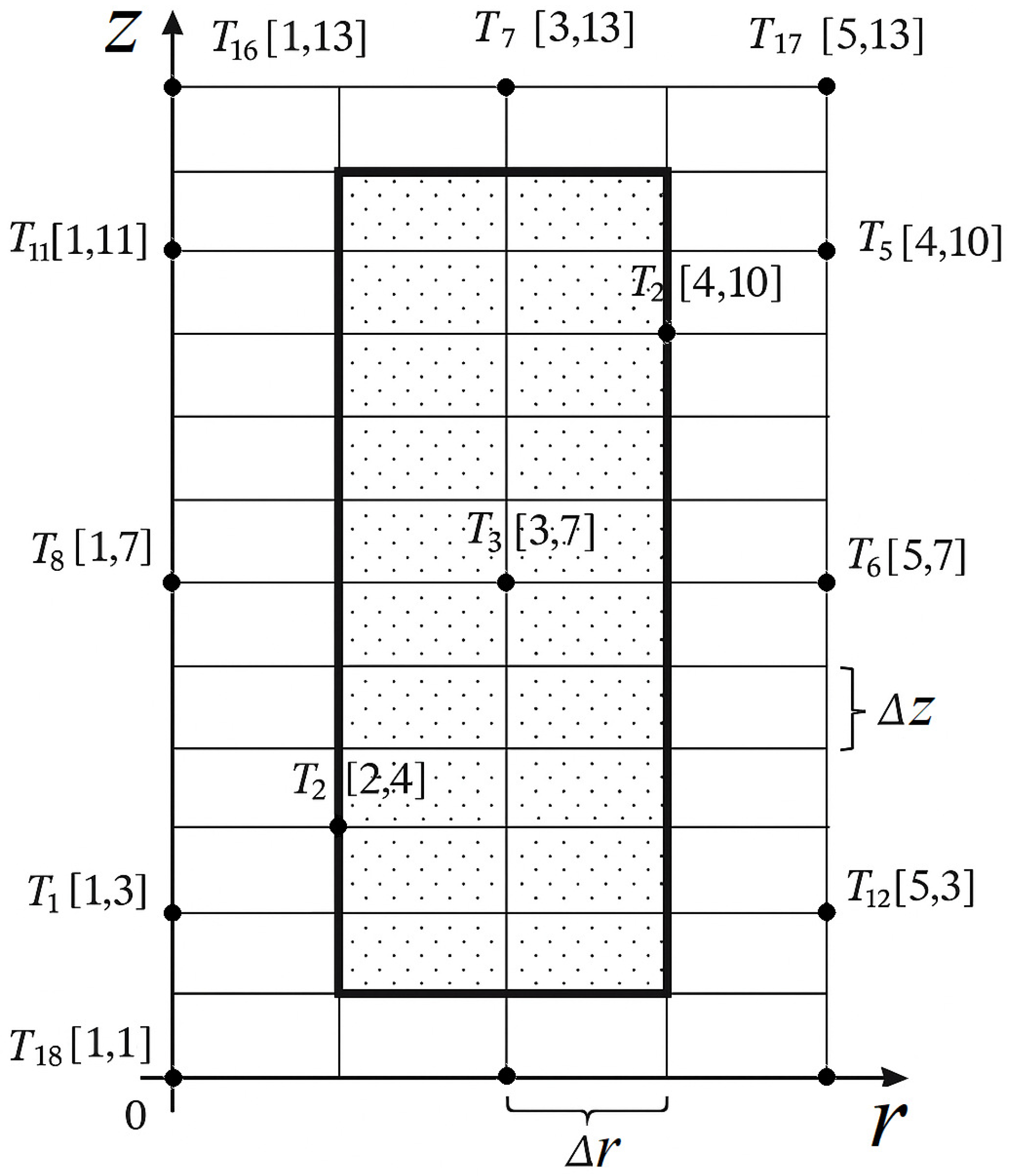
4.2.1. Modeling Basedd on Finite Difference Method
4.2.2. Modeling Based on Machine Learning (ML)
- Linear kernel:
- Gaussian kernel:where is the kernel width parameter.
- Polynomial kernel:where d is an integer.
- For each ,
- –
- generate and by sampling n instances with a replacement from the original dataset;
- –
- train a regression tree on this sample.
4.2.3. Pros and Cons of Applied Methods
- Finite Difference Method (FDM) for Heat Conduction Modeling
- –
- Advantages: Based on first principles and physical laws; provides interpretable results; suitable for extrapolation beyond training data; does not require data-driven learning; useful for simulating spatial and temporal temperature evolution in solid materials.
- –
- Disadvantages: Requires precise knowledge of material properties and boundary conditions; limited adaptability to unknown dynamics; sensitive to discretization errors; may become computationally intensive for fine grids or 3D simulations.
- Support Vector Regression (SVR)
- –
- Advantages: Strong capability for modeling nonlinear relationships; robust against overfitting and noisy inputs; exhibits low generalization errors.
- –
- Disadvantages: Requires careful kernel selection; needs input normalization; harder to interpret.
- Neural Networks (NN)
- –
- Advantages: Powerful for nonlinear problems; flexible architecture; robust to noise and missing data.
- –
- Disadvantages: Computationally expensive; sensitive to hyperparameters; prone to overfitting; difficult to interpret; requires large datasets.
- Multivariate Adaptive Regression Splines (MARS)
- –
- Advantages: Handles both linear and nonlinear relationships; automatically detects interactions; works with mixed data types.
- –
- Disadvantages: Susceptible to overfitting; slower training on large datasets; complex interpretation.
- k-Nearest Neighbors (k-NN)
- –
- Advantages: Simple and intuitive; no training phase; non-parametric and adaptable.
- –
- Disadvantages: Memory-intensive; prediction can be slow; sensitive to choice of k and distance metric.
- Random Forests (RF)
- –
- Advantages: High accuracy; handles missing data; robust to noise; suitable for both classification and regression.
- –
- Disadvantages: Computationally demanding; potentially complex models; slower training with large datasets.
4.2.4. Evaluation of Model Performance
- The correlation coefficient (), which quantifies the linear association between predicted (simulated, Y) and measured values (y).
- The coefficient of determination (), representing the proportion of variance in the measured data explained by the model. An value of 1 indicates a perfect fit.
- The mean squared error (MSE), which reflects the average squared difference between predicted (simulated) and actual values.
- The root mean squared error (RMSE) and its normalized form, relative RMSE (RRMSE), which measure average prediction error in absolute and relative terms.
- The mean absolute percentage error (MAPE), a scale-independent indicator commonly used in regression tasks. Although some studies refer to the mean of relative errors as the mean relative error (MRE) and others as the mean absolute percentage error (MAPE), both metrics are mathematically equivalent when expressed as a percentage. Therefore, results reported using either term can be directly compared in terms of model prediction accuracy.
5. Results and Discussion
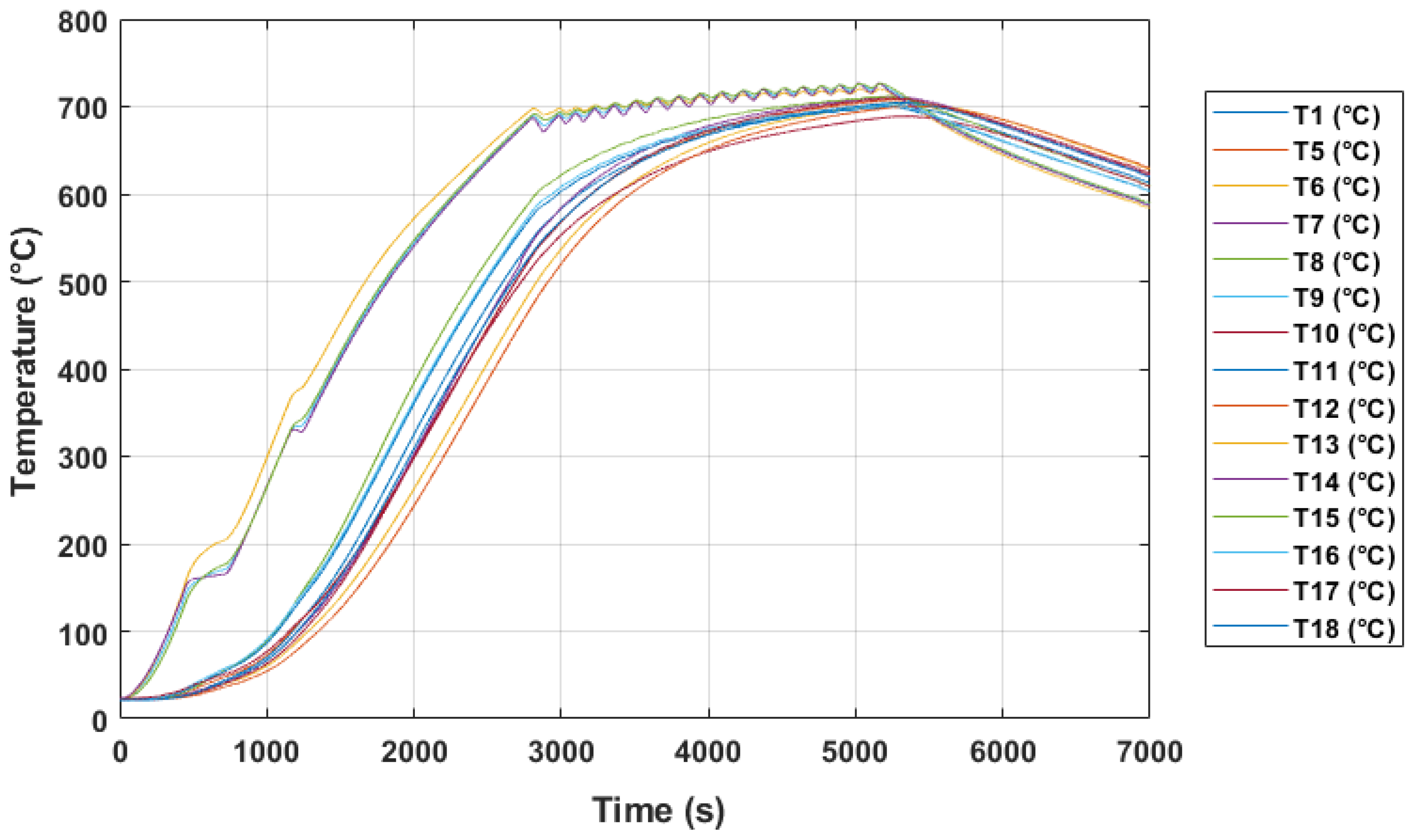
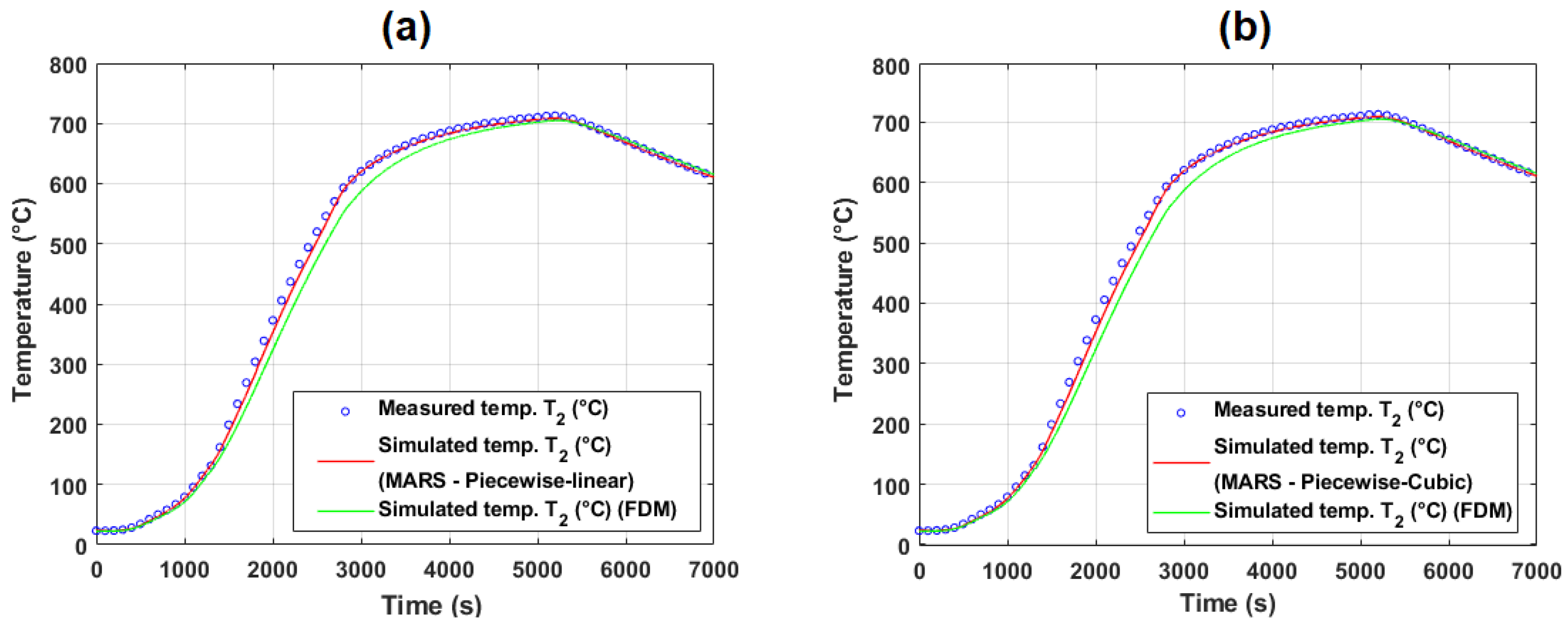
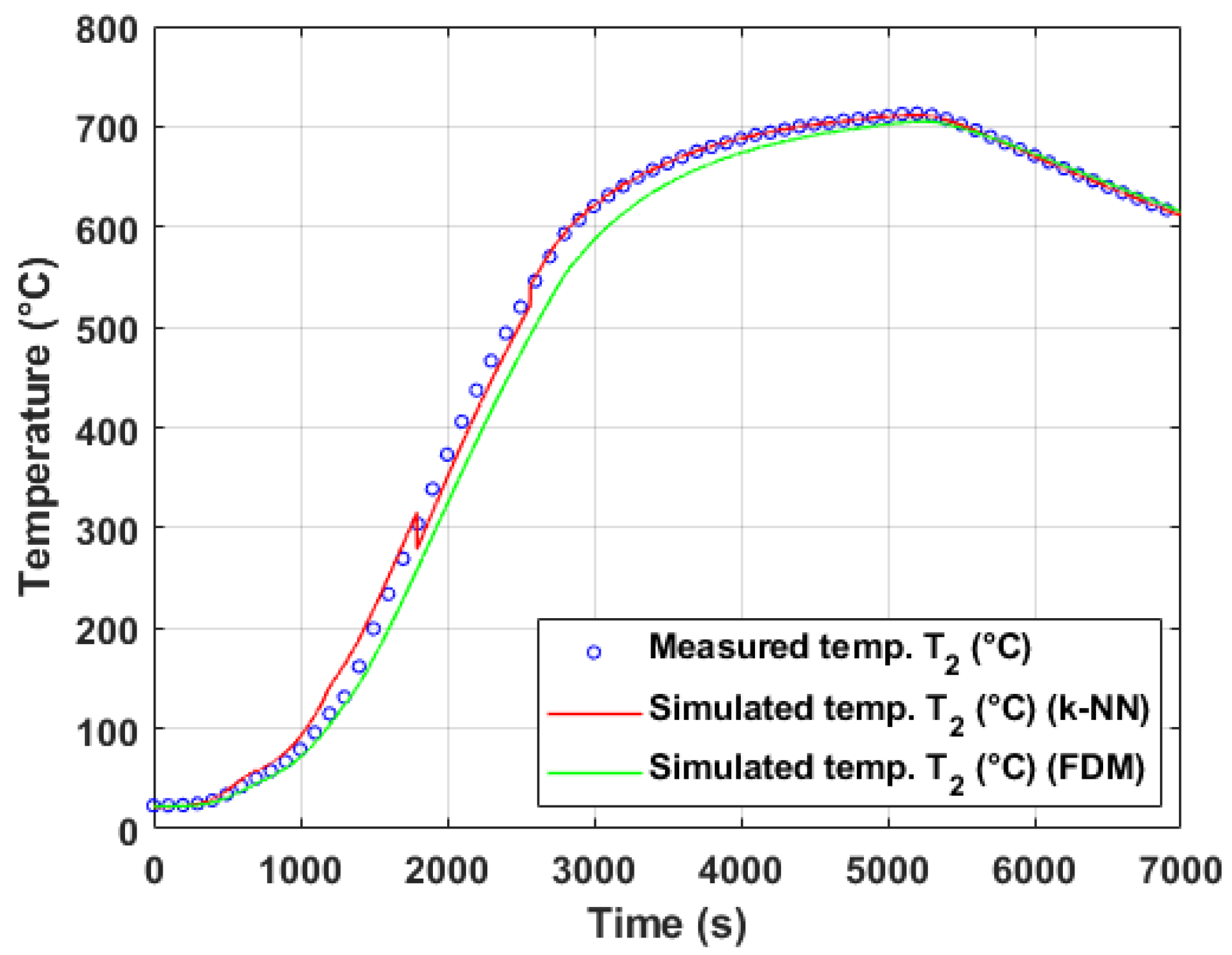
5.1. Temperature Modeling Based on Lab-Scale Measurement
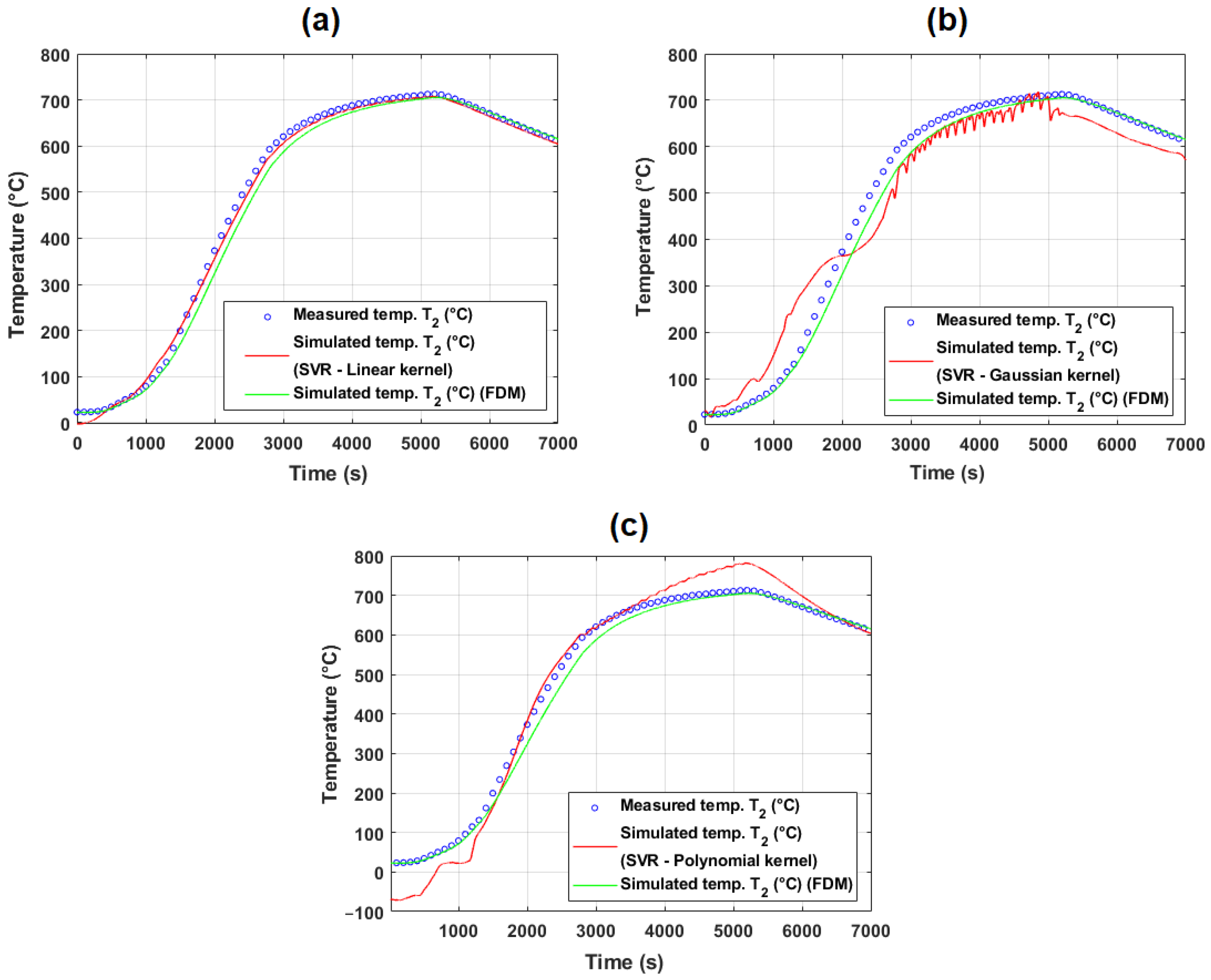
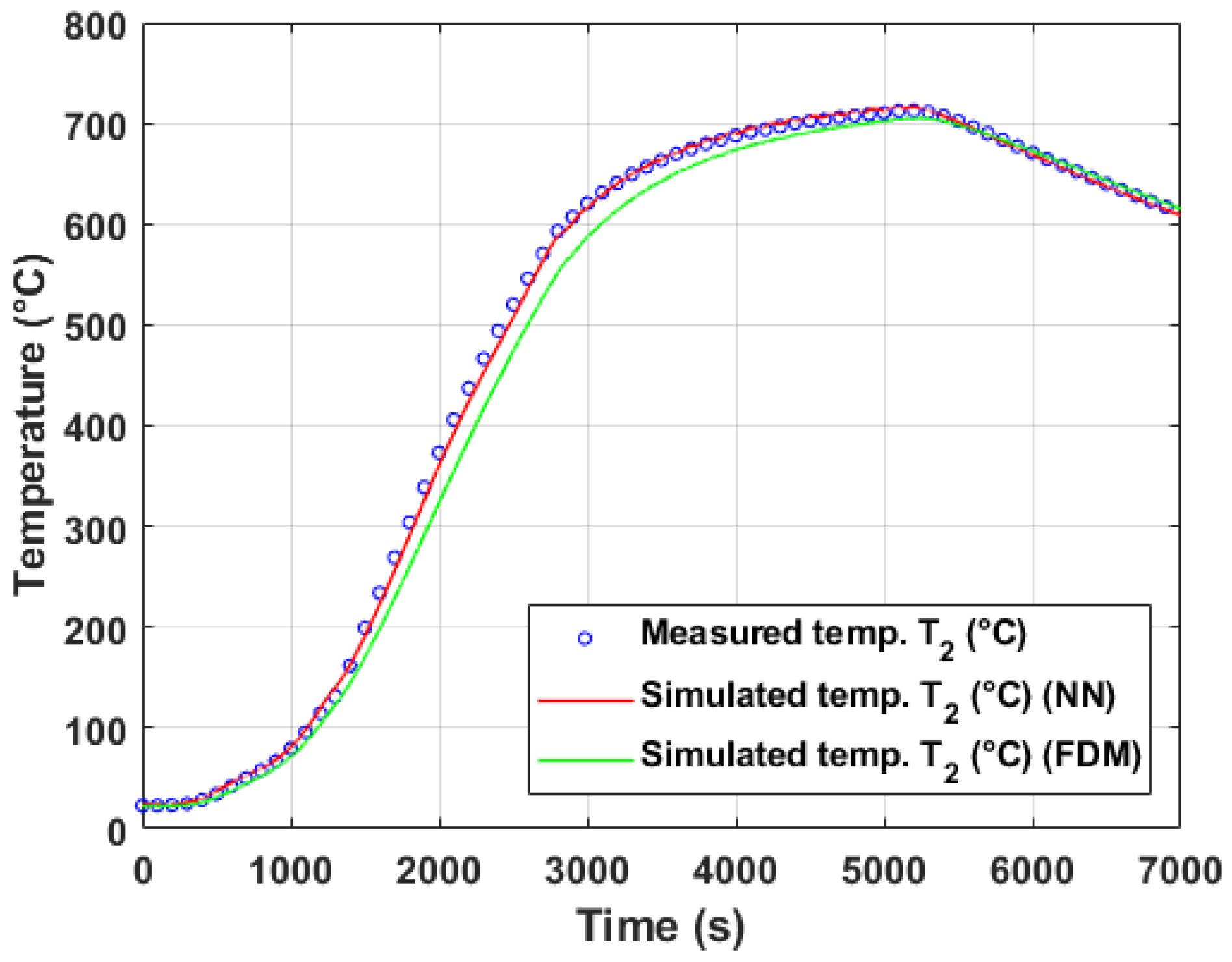
5.1.1. Evaluation of Model Performance on Training and Test Data (Experiment #2)
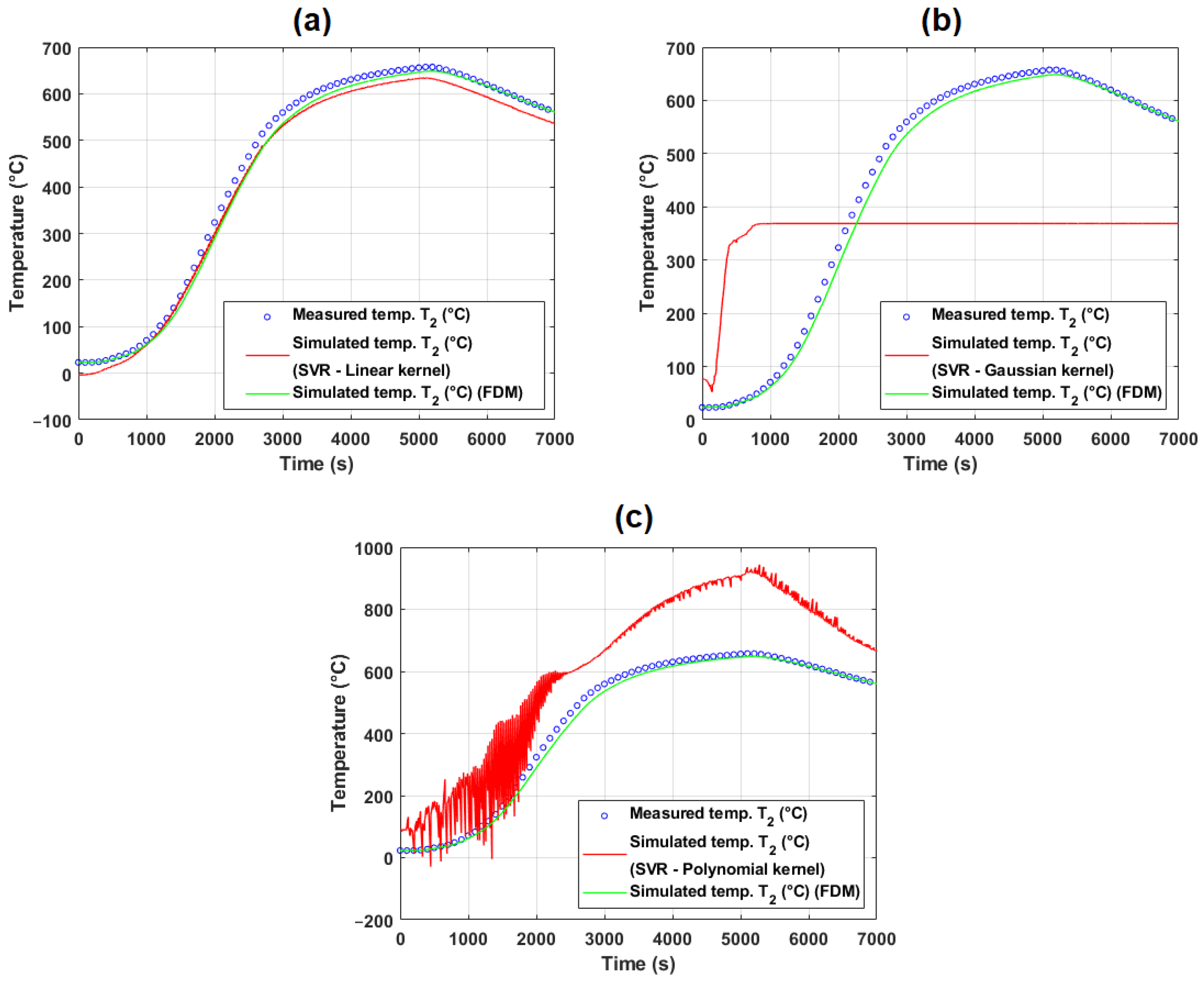
5.1.2. Evaluation of Model Performance on Training and Test Data (Experiment #4)
5.1.3. Discussion of Model Generalization and Experimental Variability
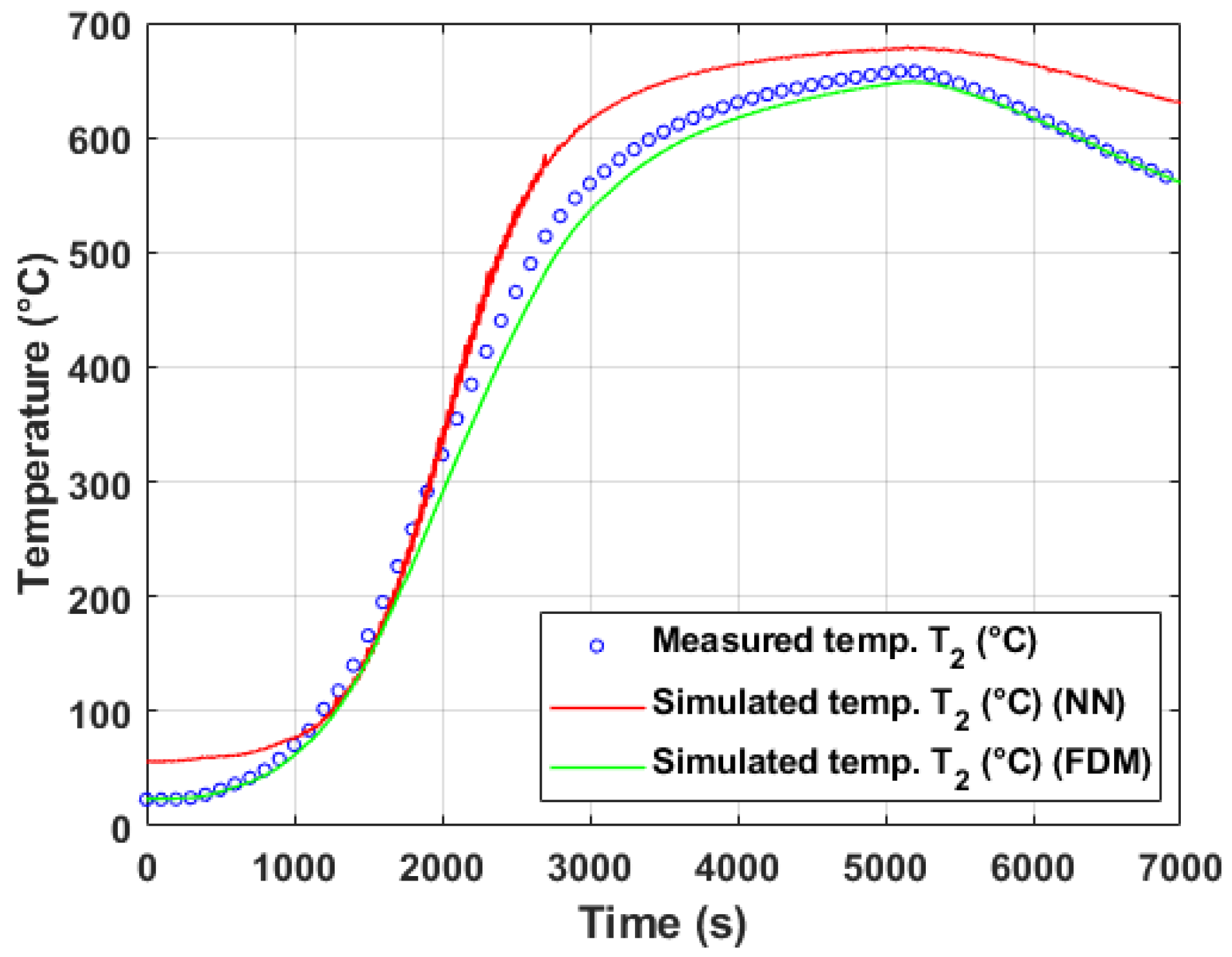
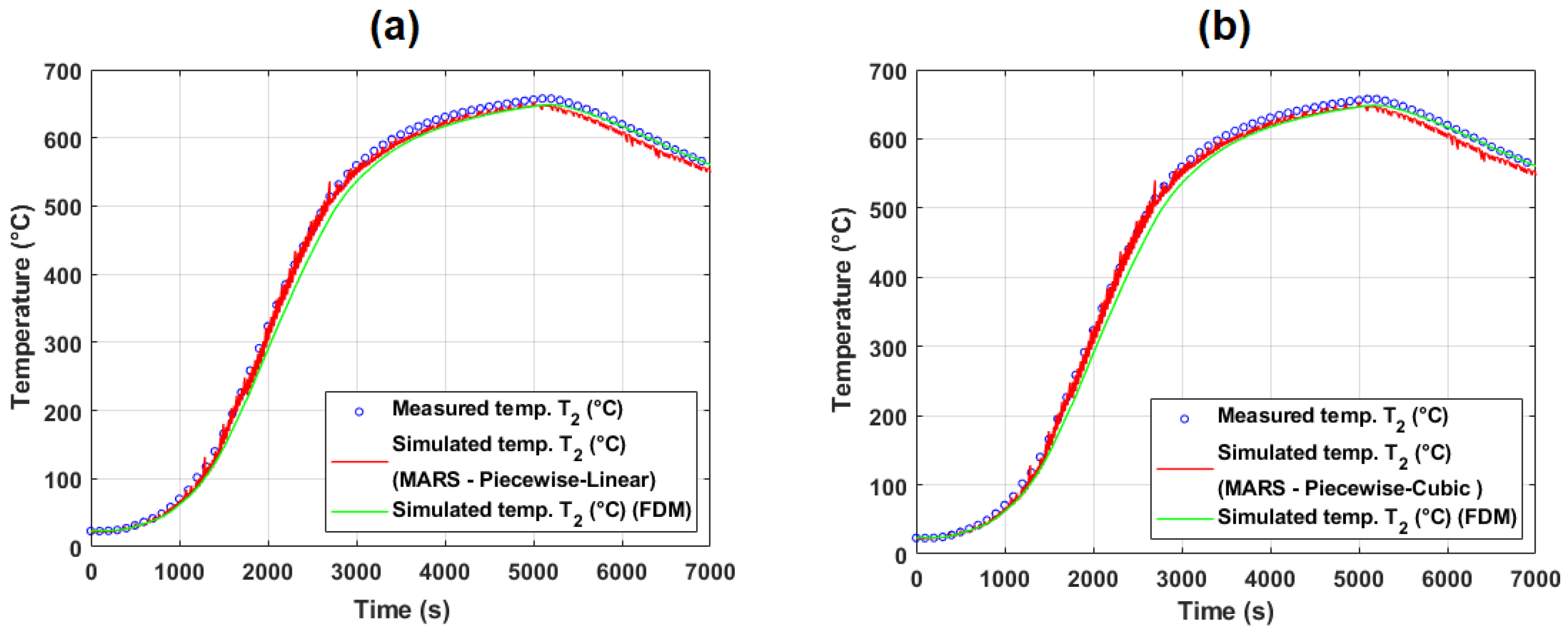
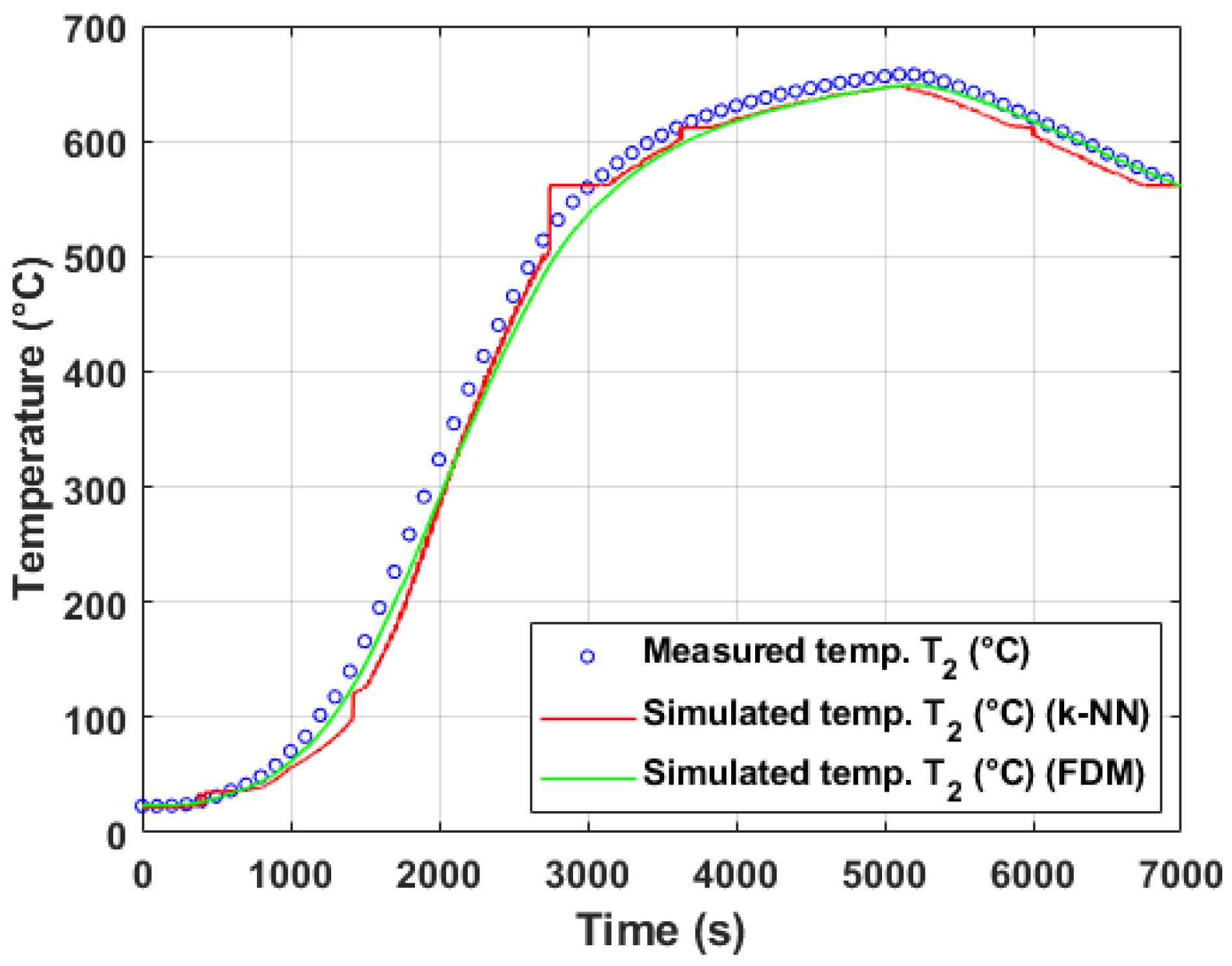
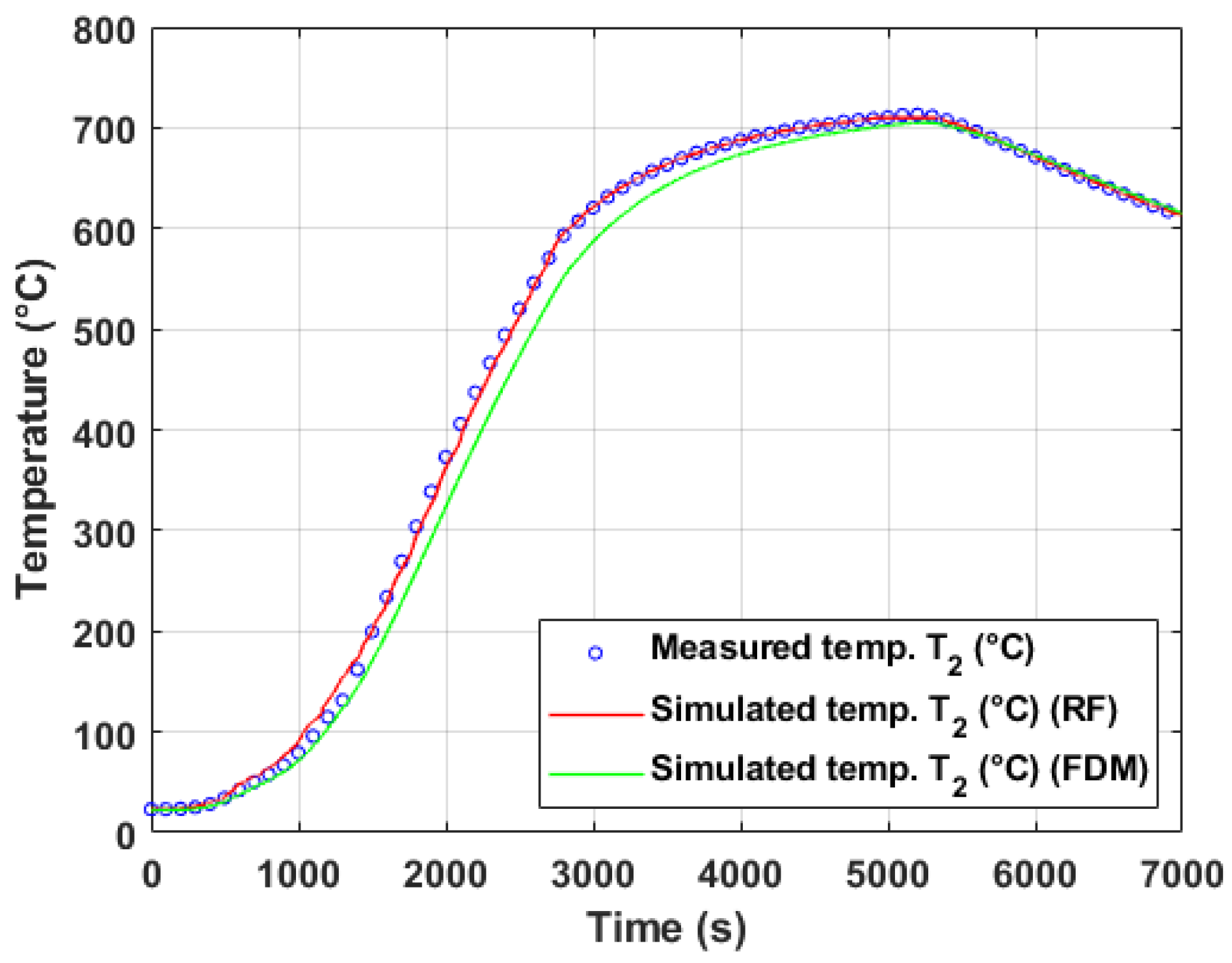
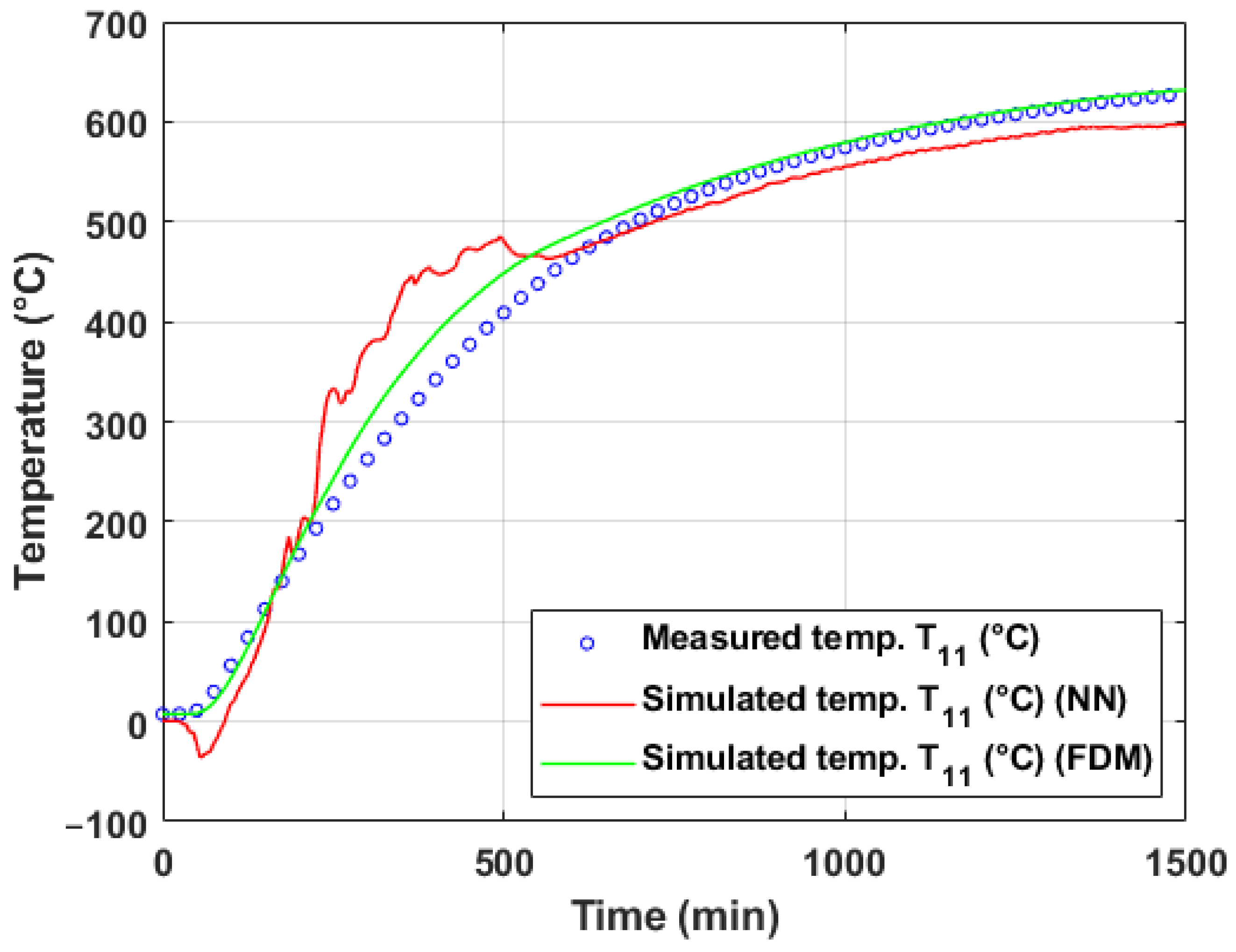
5.2. Temperature Modeling Based on Operational Measurement
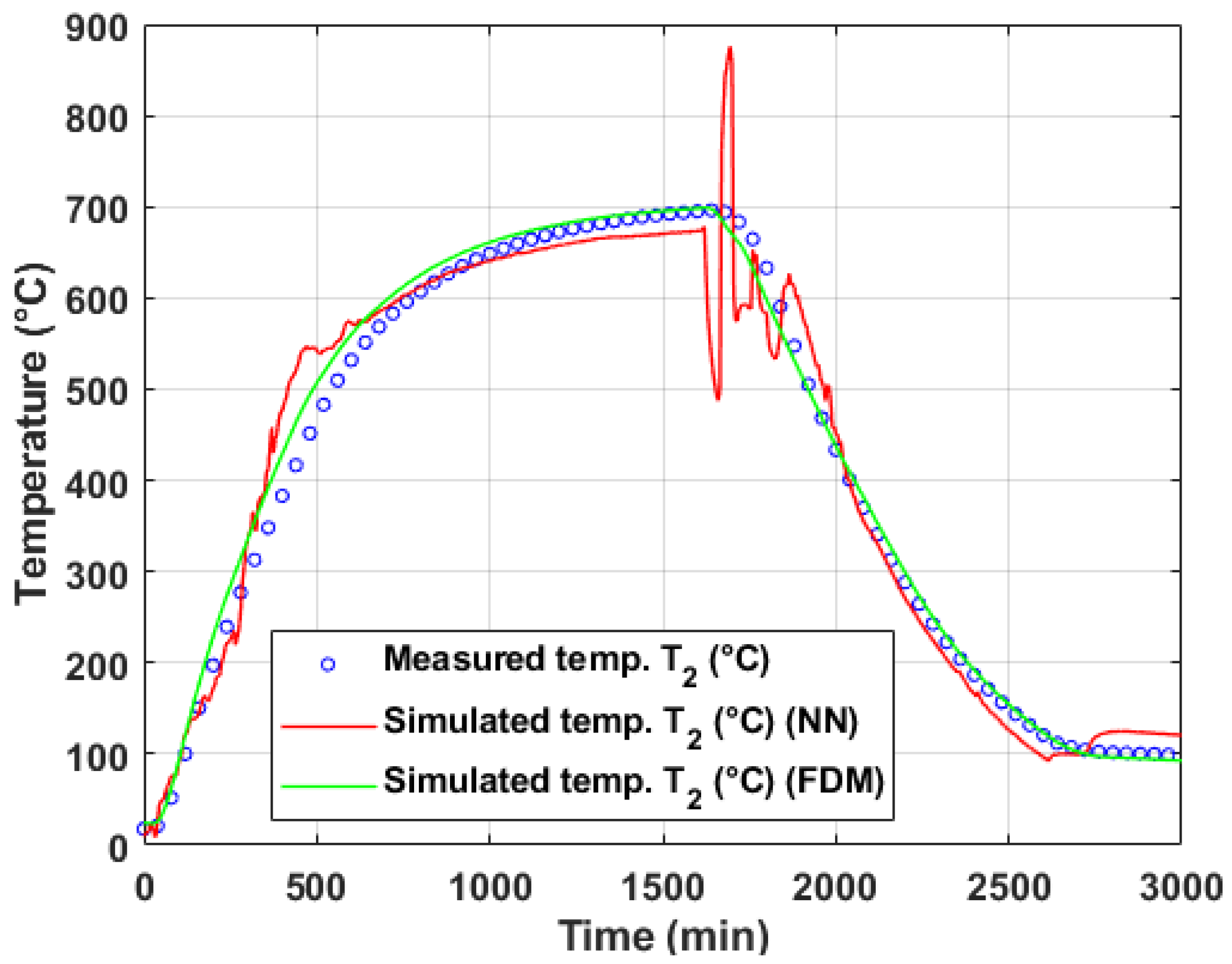
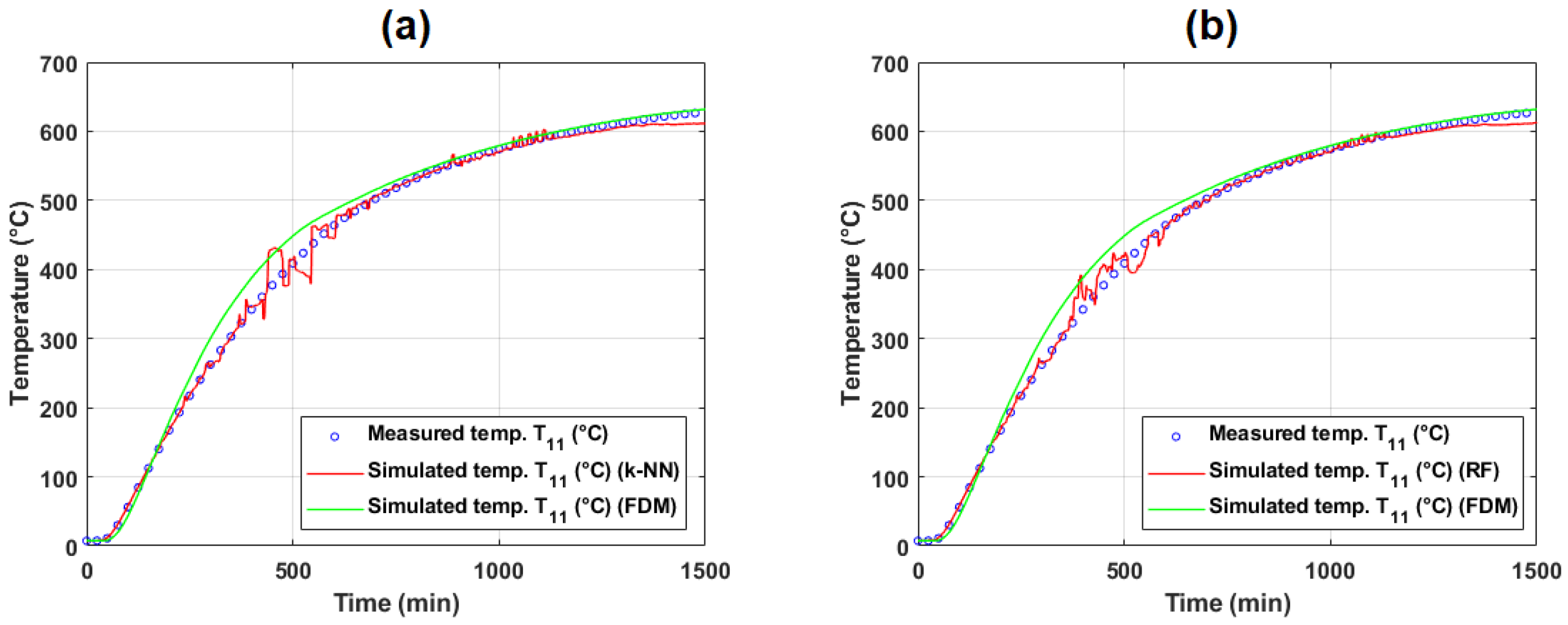
5.2.1. Evaluation of Model Performance on Training and Test Data (Operational Experiment #1)
| Temperature | Method | MSE | MAPE (%) | RMSE | RRMSE (%) | PI | Max. Deviation (°C) | ||
|---|---|---|---|---|---|---|---|---|---|
| FDM | 0.9966 | 0.9933 | 415.2310 | 5.4459 | 20.3772 | 4.6286 | 2.3182 | 45.8609 | |
| SVR (linear kernel) | 0.9862 | 0.9727 | 1001.9793 | 25.1101 | 31.6541 | 7.1901 | 3.6199 | 111.7091 | |
| SVR (Gaussian kernel) | 0.9685 | 0.9379 | 2870.5070 | 16.7263 | 53.5771 | 12.1698 | 6.1824 | 311.7023 | |
| SVR (polynomial kernel) | 0.5719 | 0.3270 | 118,449,324.5368 | 19,275.1619 | 10,883.4427 | 2472.1307 | 1572.7473 | 45,295.0617 | |
| Feed-forward NN | 0.9664 | 0.9340 | 2419.8762 | 21.6994 | 49.1922 | 11.1738 | 5.6823 | 131.7777 | |
| MARS (piecewise-linear) | 0.9989 | 0.9979 | 76.2742 | 3.9521 | 8.7335 | 1.9838 | 0.9924 | 49.1798 | |
| MARS (piecewise-cubic) | 0.9990 | 0.9980 | 69.7127 | 3.3933 | 8.3494 | 1.8965 | 0.9487 | 43.7511 | |
| k-NN regression | 0.9982 | 0.9965 | 130.7727 | 1.7991 | 11.4356 | 2.5975 | 1.2999 | 55.2761 | |
| RF | 0.9988 | 0.9977 | 92.3713 | 1.8243 | 9.6110 | 2.1831 | 1.0922 | 53.9474 |
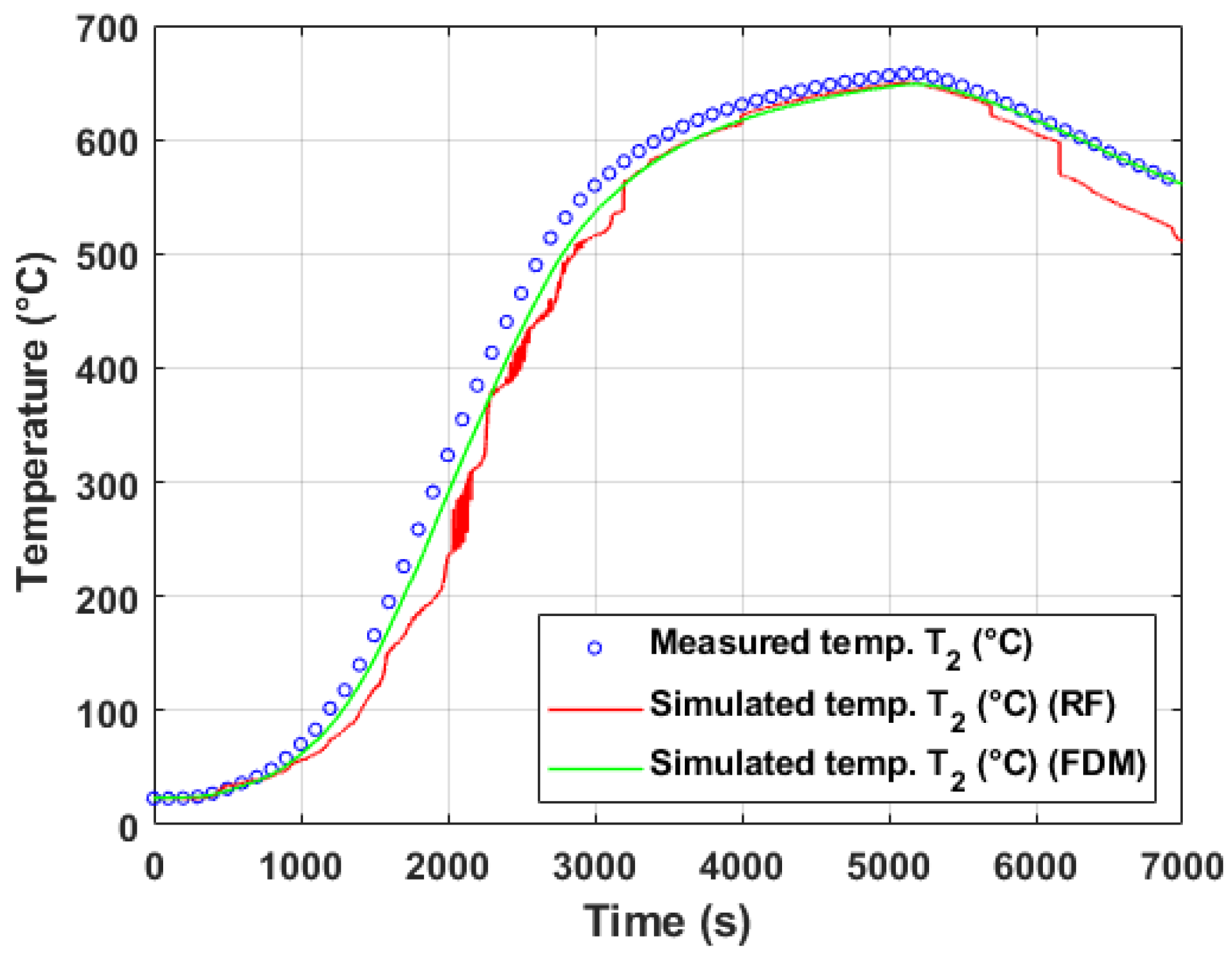
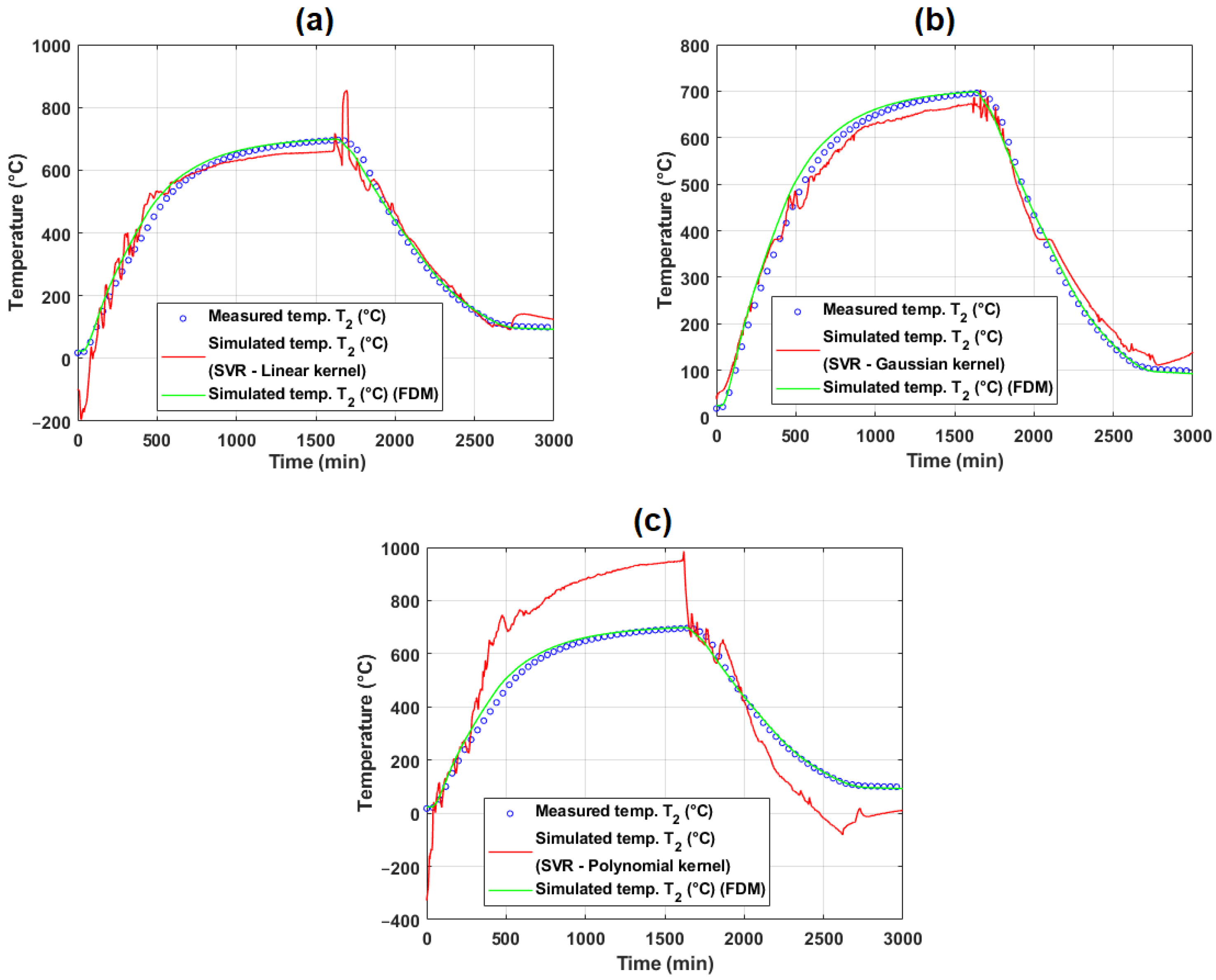
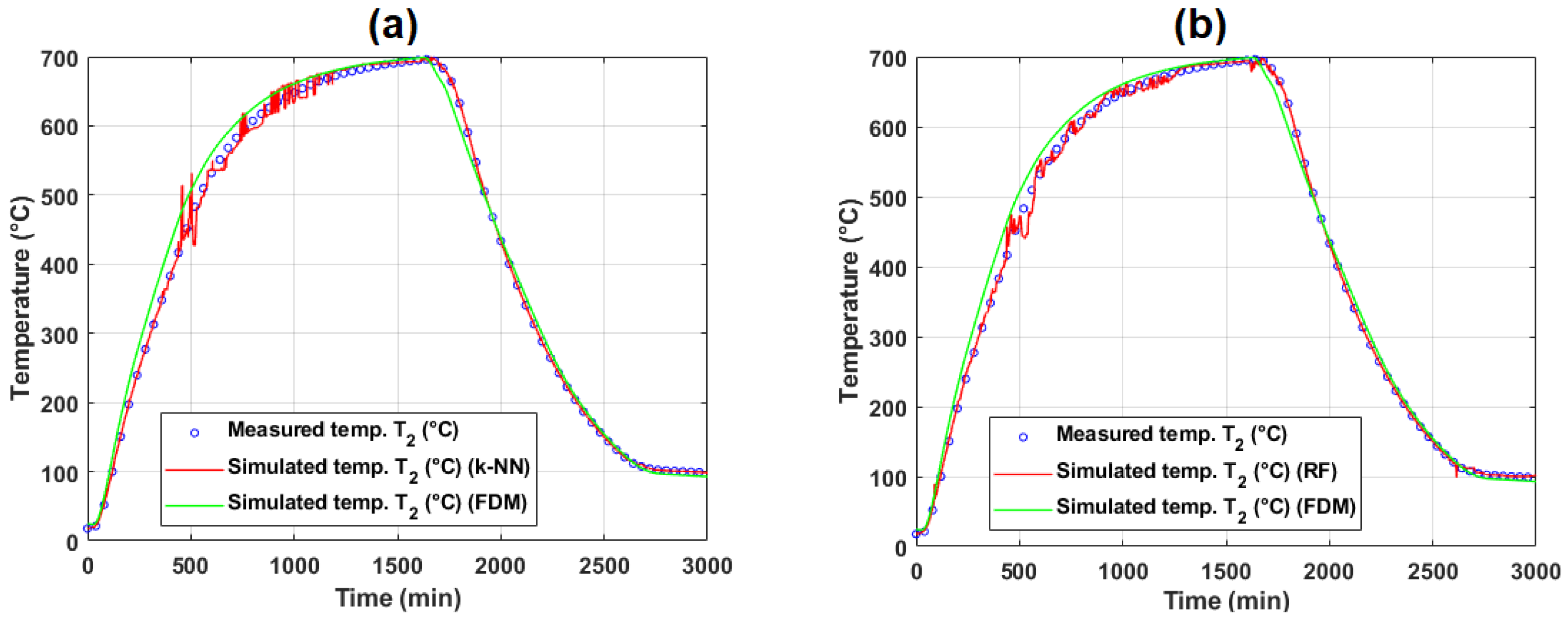
5.2.2. Evaluation of Model Performance on Training and Test Data (Operational Experiment #2)
| Temperature | Method | MSE | MAPE (%) | RMSE | RRMSE (%) | PI | Max. Deviation (°C) | ||
|---|---|---|---|---|---|---|---|---|---|
| FDM | 0.9974 | 0.9948 | 359.6462 | 5.0291 | 18.9643 | 4.5607 | 2.2833 | 47.0768 | |
| SVR (linear kernel) | 0.9814 | 0.9632 | 1980.1651 | 28.2223 | 44.4990 | 10.7015 | 5.4009 | 212.8222 | |
| SVR (Gaussian kernel) | 0.9979 | 0.9957 | 773.1371 | 13.7086 | 27.8053 | 6.6869 | 3.3470 | 53.4657 | |
| SVR (polynomial kernel) | 0.9649 | 0.9311 | 30,436.9398 | 64.0292 | 174.4619 | 41.9562 | 21.3525 | 346.2543 | |
| Feed-forward NN | 0.9829 | 0.9661 | 1823.3756 | 10.2402 | 42.7010 | 10.2691 | 5.1789 | 209.2889 | |
| MARS (piecewise-linear) | 0.9988 | 0.9975 | 135.7857 | 3.7704 | 11.6527 | 2.8024 | 1.4020 | 84.7990 | |
| MARS (piecewise-cubic) | 0.9984 | 0.9969 | 170.1303 | 3.9005 | 13.0434 | 3.1368 | 1.5696 | 97.9619 | |
| k-NN regression | 0.9994 | 0.9988 | 65.8502 | 0.8771 | 8.1148 | 1.9515 | 0.9761 | 82.5804 | |
| RF | 0.9995 | 0.9990 | 56.2155 | 1.1998 | 7.4977 | 1.8031 | 0.9018 | 50.8717 | |
| FDM | 0.9994 | 0.9987 | 77.0031 | 2.1911 | 8.7751 | 2.0683 | 1.0345 | 23.8051 | |
| SVR (linear kernel) | 0.9842 | 0.9686 | 1513.8770 | 26.1283 | 38.9086 | 9.1709 | 4.6220 | 195.2460 | |
| SVR (Gaussian kernel) | 0.9979 | 0.9958 | 640.3879 | 11.8434 | 25.3059 | 5.9647 | 2.9855 | 47.1678 | |
| SVR (polynomial kernel) | 0.9627 | 0.9268 | 3936.6021 | 29.7861 | 62.7423 | 14.7886 | 7.5349 | 155.9811 | |
| Feed-forward NN | 0.6925 | 0.4796 | 24,952.9029 | 77.2680 | 157.9649 | 37.2330 | 21.9985 | 385.5039 | |
| MARS (piecewise-linear) | 0.9984 | 0.9968 | 157.3074 | 4.1271 | 12.5422 | 2.9563 | 1.4793 | 62.6750 | |
| MARS (piecewise-cubic) | 0.9978 | 0.9956 | 211.9201 | 5.1786 | 14.5575 | 3.4313 | 1.7175 | 77.9930 | |
| k-NN regression | 0.9993 | 0.9987 | 62.7630 | 0.9031 | 7.9223 | 1.8673 | 0.9340 | 81.5399 | |
| RF | 0.9994 | 0.9988 | 58.9727 | 1.2171 | 7.6794 | 1.8101 | 0.9053 | 51.5673 |
5.2.3. Discussion of Model Generalization and Experimental Variability
- Differences in experimental conditions: The two experiments featured distinct coil geometries, stacking configurations (four coils in experiment #1 vs. three in experiment #2), and convective ring placements, which likely altered heat transfer patterns within the stacks. Since ML models learn from data patterns rather than physical laws, they may struggle to extrapolate beyond the training domain if these operational variations are not adequately represented in the training set.
- Limited number of input observations: Compared to laboratory experiments, operational measurements included fewer surface thermocouples. The reduced spatial resolution of inputs could limit the ML models’ ability to infer the thermal behavior deep within the coil stack, particularly for internal thermocouples such as .
- Dataset imbalance and covariate shift: The training datasets were derived from specific annealing cycles. If the test dataset exhibits different dynamics or operating regimes (e.g., heating/cooling rates, atmospheric control), data-driven models may encounter covariate shift, leading to degraded predictive performance.
- Hybrid modeling approaches, combining physics-based models with ML techniques (e.g., physics-informed neural networks or residual learning), to integrate domain knowledge with data-driven flexibility.
- Data augmentation and inclusion of synthetic datasets generated by physical simulations to enrich the diversity of ML training data and improve extrapolation capabilities.
- Feature engineering, incorporating additional process parameters (e.g., coil weight, convective ring properties, or atmosphere flow rates) as inputs to the ML models.
- Cross-validation across different operational datasets to systematically assess model robustness and reduce overfitting.
5.3. Discussion on Laboratory and Operational Measurements
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| PLC | Programmable Logic Controller |
| OPC | Open Platform Communications |
| PWM | Pulse-Width modulation |
| SMC | Sliding Mode Control |
| PID | Proportional–Integral–Derivative |
| PDE | Partial Differential Equation |
| ML | Machine Learning |
| ANN | Artificial Neural Network |
| FDM | Finite Difference Method |
| FEM | Finite Element Method |
| RF | Random Forest |
| k-NN | k-Nearest Neighbors |
| MAPE | Mean Absolute Percentage Error |
| MARS | Multivariate Adaptive Regression Splines |
| BF | Basis Function |
| PC | Personal Computer |
| NN | Neural Network |
| PI | Performance Index |
| RMSE | Root Mean Squared Error |
| RRMSE | Relative RMSE |
| GCV | Generalized Cross-Validation |
| SVM | Support Vector Machines |
| SVR | Support Vector Regression |
| PINNs | Physics-Informed Neural Networks |
| ELM | Extreme Learning Machines |
| CBR | Case-Based Reasoning |
| RBFNN | Radial Basis Function Neural Networks |
| Coil’s surface temperature as input observations | |
| y, | Target variable (predicted temperature) (°C) |
| Correlation coefficient | |
| Coefficient of determination | |
| Temperature at spatial grid node and time step k (in FDM) (K) | |
| Measured temperature at index j (K) | |
| Simulated (predicted) temperature by FDM at index j (K) | |
| t | Time (s) |
| Time step (s) | |
| Thermal conductivity (in FDM context) | |
| Thermal diffusivity | |
| c | Specific heat capacity |
| Material density | |
| Kernel matrix | |
| Prediction function |
Appendix A. Main Approaches for Temperature Modeling in Steel Coil Annealing
| Approach | Type | Accuracy | Computational Demand | Real-Time Capable | Interpretability | Data Requirements | Strengths | Weaknesses | Key References |
|---|---|---|---|---|---|---|---|---|---|
| Finite Difference/ Element (FD/FEM) | Physics-based | High | High | Feasible (optimized) | High | Low/ Medium | Detailed, spatially resolved, process simulation | Detailed data and tuning, slower (for large system sizes) | [7,8,9,81], [1,2,10,14] |
| Lumped Parameter Models | Physics-based | Moderate | Low | Yes | Moderate | Low | Fast, applicable to real-time control, compact | Misses spatial gradients, idealizations | [8] |
| Analytical/Hybrid Physics | Physics-based | Low–Mod | Very Low | Yes | High | Low | Simple, transparent | Oversimplified; poor under industrial variability | [8,11,12,13] |
| Artificial Neural Networks (ANN, ELM, RBFNN, GRNN) | ML | Moderate–High | Moderate | Yes | Low | High | Captures nonlinearity, adaptive, incremental learning possible | Opacity, needs extensive and curated process data | [18,19,20,35,82], [28,29,30], [21,22,23], [24,25,26,27] |
| Ensemble/ Incremental ML Models | ML | High | Moderate | Yes | Low | High | Robustness to outliers, adapts over time | Complexity, model management | [19,35] |
| Support Vector Regression (SVR) | ML | Moderate | Moderate | Yes | Moderate | Medium | Effective with small-to-midsize, nonlinear datasets | Parameter tuning, not yet dominant in this domain | [31,32,33] |
| Bayesian Belief Network + CBR | ML/ Probabilistic | Moderate–High | Moderate | Yes | Moderate–High | High | Probabilistic predictions, reliability estimation | Integration complexity, data intensive | [34] |
| System Identification + Physics | Hybrid | High | Low–Moderate | Yes | Moderate | Medium | Combines best of both—realistic, adaptive | Model structure design can be tricky | [8] |
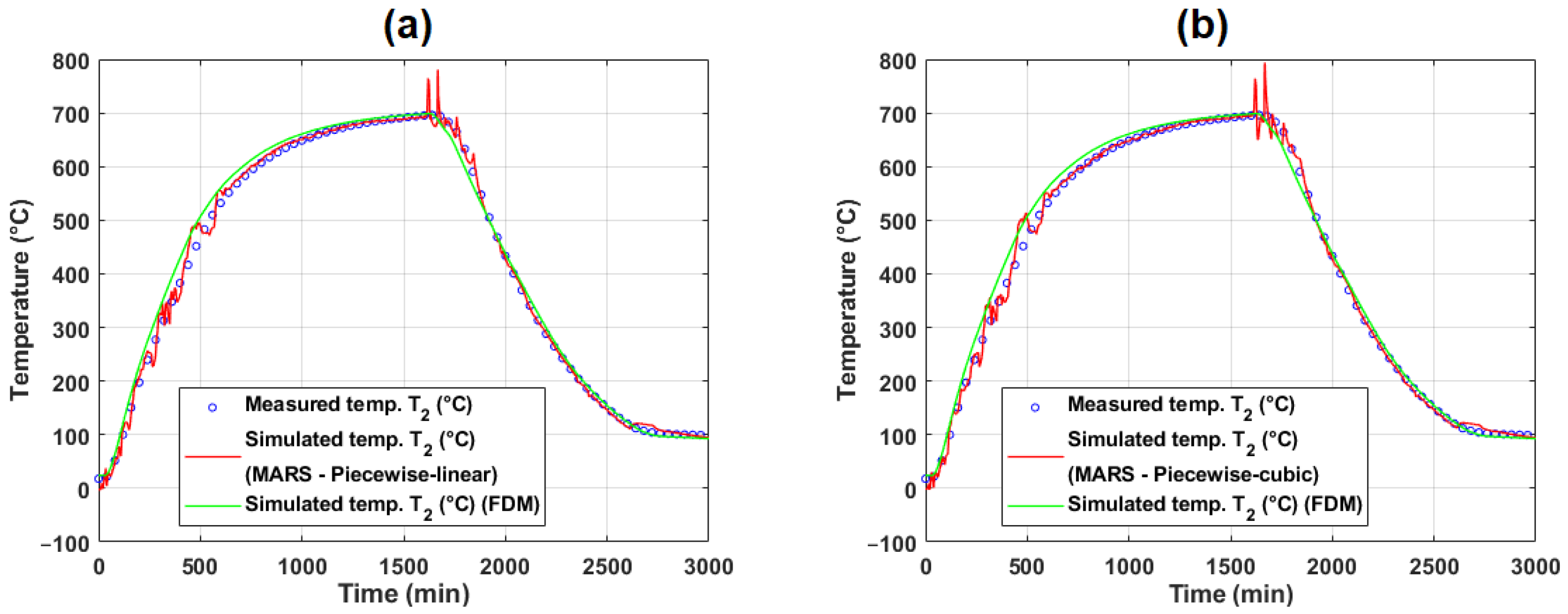
Appendix B. Examples of MARS Models for Temperature Prediction
Appendix B.1. Examples of MARS Models Tested on Laboratory Experiment #2
Appendix B.2. Examples of MARS Models Tested on Laboratory Experiment #4
Appendix B.3. Examples of MARS Models Tested on Operational Experiment #1
Appendix B.4. Examples of MARS Models Tested on Operational Experiment #2
Appendix C. Performance of Prediction Models
Appendix C.1. Performance of Prediction Models Based on Laboratory Measurements
| Temperature | Method | MSE | MAPE (%) | RMSE | RRMSE (%) | PI | Max. Deviation (°C) | Training Time (s) | ||
|---|---|---|---|---|---|---|---|---|---|---|
| SVR (linear kernel) | 0.9991 | 0.9982 | 206.3542 | 8.4739 | 14.3650 | 2.9776 | 1.4895 | 26.7858 | 0.5078 | |
| SVR (Gaussian kernel) | 0.9988 | 0.9976 | 493.0208 | 12.6531 | 22.2041 | 4.6025 | 2.3026 | 26.8894 | 2.7228 | |
| SVR (polynomial kernel) | 0.9960 | 0.9920 | 1255.0118 | 27.0391 | 35.4261 | 7.3431 | 3.6790 | 91.2727 | 204.8109 | |
| Feed-forward NN | 0.9991 | 0.9983 | 97.8152 | 3.0665 | 9.8902 | 2.0500 | 1.0255 | 27.3036 | 2.3030 | |
| MARS (piecewise-linear) | 0.9999 | 0.9999 | 8.4439 | 1.0752 | 2.9058 | 0.6023 | 0.3012 | 18.5558 | 277.0577 | |
| MARS (piecewise-cubic) | 0.9999 | 0.9999 | 7.6207 | 1.0613 | 2.7606 | 0.5722 | 0.2861 | 14.4765 | 277.2751 | |
| k-NN regression | 1.0000 | 1.0000 | 0.0059 | 0.0211 | 0.0769 | 0.0159 | 0.0080 | 0.8420 | 0.0005 | |
| RF | 1.0000 | 1.0000 | 0.2364 | 0.3185 | 0.4862 | 0.1008 | 0.0504 | 3.7641 | 408.6441 | |
| SVR (linear kernel) | 0.9996 | 0.9991 | 327.1397 | 10.7956 | 18.0870 | 3.7341 | 1.8675 | 27.7161 | 0.5069 | |
| SVR (Gaussian kernel) | 0.9988 | 0.9975 | 513.9495 | 13.0350 | 22.6705 | 4.6804 | 2.3417 | 27.3927 | 1.8591 | |
| SVR (polynomial kernel) | 0.9950 | 0.9901 | 2681.7040 | 47.7559 | 51.7852 | 10.6912 | 5.3589 | 148.3949 | 206.2741 | |
| Feed-forward NN | 0.9992 | 0.9984 | 89.0672 | 3.6682 | 9.4375 | 1.9484 | 0.9746 | 32.4508 | 2.4091 | |
| MARS (piecewise-linear) | 0.9999 | 0.9998 | 10.9923 | 1.5093 | 3.3155 | 0.6845 | 0.3423 | 21.8608 | 172.7441 | |
| MARS (piecewise-cubic) | 0.9999 | 0.9998 | 13.4625 | 1.6948 | 3.6691 | 0.7575 | 0.3788 | 25.5280 | 175.0099 | |
| k-NN regression | 1.0000 | 1.0000 | 0.0060 | 0.0211 | 0.0773 | 0.0160 | 0.0080 | 0.8480 | 0.0005 | |
| RF | 1.0000 | 1.0000 | 0.3645 | 0.3167 | 0.6038 | 0.1246 | 0.0623 | 7.4659 | 412.1197 | |
| SVR (linear kernel) | 0.9987 | 0.9973 | 293.5400 | 6.2609 | 17.1330 | 3.5741 | 1.7882 | 29.6053 | 0.5071 | |
| SVR (Gaussian kernel) | 0.9986 | 0.9971 | 606.6613 | 14.9653 | 24.6305 | 5.1381 | 2.5709 | 29.6704 | 3.1536 | |
| SVR (polynomial kernel) | 0.9805 | 0.9614 | 9683.2636 | 92.9081 | 98.4036 | 20.5277 | 10.3649 | 237.4634 | 204.4006 | |
| Feed-forward NN | 0.9990 | 0.9980 | 115.8309 | 4.1185 | 10.7625 | 2.2451 | 1.1231 | 44.4325 | 2.5095 | |
| MARS (piecewise-linear) | 0.9999 | 0.9998 | 13.7911 | 1.3112 | 3.7136 | 0.7747 | 0.3874 | 17.8987 | 109.6908 | |
| MARS (piecewise-cubic) | 0.9999 | 0.9998 | 13.7823 | 1.2872 | 3.7125 | 0.7744 | 0.3872 | 17.7504 | 107.7261 | |
| k-NN regression | 1.0000 | 1.0000 | 0.0058 | 0.0221 | 0.0764 | 0.0159 | 0.0080 | 0.8080 | 0.0005 | |
| RF | 1.0000 | 1.0000 | 0.4620 | 0.3626 | 0.6797 | 0.1418 | 0.0709 | 5.9890 | 418.2398 |
| Temperature | Method | MSE | MAPE (%) | RMSE | RRMSE (%) | PI | Max. Deviation (°C) | Training Time (s) | ||
|---|---|---|---|---|---|---|---|---|---|---|
| SVR (linear kernel) | 0.9992 | 0.9984 | 210.8758 | 7.6106 | 14.5216 | 2.9248 | 1.4630 | 27.4629 | 0.5500 | |
| SVR (Gaussian kernel) | 0.9983 | 0.9966 | 541.7956 | 13.2073 | 23.2765 | 4.6882 | 2.3461 | 27.4989 | 4.3830 | |
| SVR (polynomial kernel) | 0.9943 | 0.9886 | 4297.1065 | 22.8259 | 65.5523 | 13.2030 | 6.6204 | 125.2540 | 210.6607 | |
| Feed-forward NN | 0.9953 | 0.9905 | 555.4765 | 11.7858 | 23.5685 | 4.7470 | 2.3791 | 66.3279 | 2.2936 | |
| MARS (piecewise-linear) | 1.0000 | 0.9999 | 3.1617 | 0.8351 | 1.7781 | 0.3581 | 0.1791 | 6.9960 | 164.8469 | |
| MARS (piecewise-cubic) | 1.0000 | 1.0000 | 2.6542 | 0.7931 | 1.6292 | 0.3281 | 0.1641 | 6.6689 | 164.9850 | |
| k-NN regression | 1.0000 | 1.0000 | 0.0054 | 0.0252 | 0.0732 | 0.0147 | 0.0074 | 0.6400 | 0.0007 | |
| RF | 1.0000 | 1.0000 | 0.4019 | 0.3495 | 0.6339 | 0.1277 | 0.0638 | 2.3455 | 502.0956 | |
| SVR (linear kernel) | 0.9997 | 0.9993 | 454.0943 | 10.1622 | 21.3095 | 4.3106 | 2.1556 | 28.6731 | 0.5874 | |
| SVR (Gaussian kernel) | 0.9983 | 0.9966 | 590.7974 | 13.5822 | 24.3063 | 4.9168 | 2.4605 | 28.7169 | 2.9958 | |
| SVR (polynomial kernel) | 0.9744 | 0.9494 | 118,618.1770 | 158.3507 | 344.4099 | 69.6688 | 35.2868 | 449.8708 | 236.9107 | |
| Feed-forward NN | 0.9995 | 0.9989 | 65.0840 | 3.8738 | 8.0675 | 1.6319 | 0.8162 | 33.2073 | 2.3110 | |
| MARS (piecewise-linear) | 1.0000 | 0.9999 | 5.2053 | 0.9543 | 2.2815 | 0.4615 | 0.2308 | 19.1786 | 96.7913 | |
| MARS (piecewise-cubic) | 1.0000 | 0.9999 | 5.7526 | 1.0714 | 2.3985 | 0.4852 | 0.2426 | 20.2650 | 94.9964 | |
| k-NN regression | 1.0000 | 1.0000 | 0.0052 | 0.0252 | 0.0719 | 0.0146 | 0.0073 | 0.5600 | 0.0008 | |
| RF | 1.0000 | 1.0000 | 0.3166 | 0.3352 | 0.5626 | 0.1138 | 0.0569 | 3.0145 | 410.0908 | |
| SVR (linear kernel) | 0.9985 | 0.9970 | 392.7063 | 8.1388 | 19.8168 | 4.0506 | 2.0268 | 30.6820 | 538.9285 | |
| SVR (Gaussian kernel) | 0.9981 | 0.9963 | 695.1388 | 16.2762 | 26.3655 | 5.3891 | 2.6971 | 30.7138 | 5.8669 | |
| SVR (polynomial kernel) | 0.9946 | 0.9892 | 9786.0766 | 29.4302 | 98.9246 | 20.2203 | 10.1376 | 174.3081 | 248.8493 | |
| Feed-forward NN | 0.9801 | 0.9605 | 2445.7820 | 45.7249 | 49.4548 | 10.1086 | 5.1052 | 188.1040 | 1.6127 | |
| MARS (piecewise-linear) | 0.9999 | 0.9998 | 10.1456 | 1.2863 | 3.1852 | 0.6511 | 0.3255 | 9.7176 | 94.2215 | |
| MARS (piecewise-cubic) | 0.9999 | 0.9998 | 10.1422 | 1.2889 | 3.1847 | 0.6510 | 0.3255 | 9.3297 | 94.3742 | |
| k-NN regression | 1.0000 | 1.0000 | 0.0050 | 0.0261 | 0.0709 | 0.0145 | 0.0072 | 0.3600 | 0.0009 | |
| RF | 1.0000 | 1.0000 | 0.2290 | 0.2999 | 0.4785 | 0.0978 | 0.0489 | 2.6471 | 413.7298 |
Appendix C.2. Performance of Prediction Models Based on Operational Measurements
| Temperature | Method | MSE | MAPE (%) | RMSE | RRMSE (%) | PI | Max. Deviation (°C) | Training Time (s) | ||
|---|---|---|---|---|---|---|---|---|---|---|
| SVR (linear kernel) | 0.9867 | 0.9735 | 979.3091 | 24.1428 | 31.2939 | 7.1281 | 3.5880 | 111.9911 | 1.1883 | |
| SVR (Gaussian kernel) | 0.9977 | 0.9954 | 188.7308 | 13.7114 | 13.7379 | 3.1292 | 1.5664 | 36.7733 | 0.4382 | |
| SVR (polynomial kernel) | 0.5753 | 0.3309 | 119,880,717.7171 | 18,858.8490 | 10,949.0053 | 2493.9446 | 1583.1882 | 45,321.8804 | 55.9787 | |
| Feed-forward NN | 0.9684 | 0.9378 | 2272.6891 | 21.2996 | 47.6727 | 10.8588 | 5.5165 | 134.9683 | 1.6135 | |
| MARS (piecewise-linear) | 0.9991 | 0.9982 | 64.4111 | 3.6631 | 8.0257 | 1.8281 | 0.9144 | 51.4917 | 18.5185 | |
| MARS (piecewise-cubic) | 0.9991 | 0.9981 | 67.5497 | 3.3056 | 8.2189 | 1.8721 | 0.9365 | 47.5348 | 18.4478 | |
| k-NN regression | 1.0000 | 1.0000 | 1.1567 | 0.4367 | 1.0755 | 0.2450 | 0.1225 | 16.8735 | 0.0006 | |
| RF | 1.0000 | 0.9999 | 2.6662 | 0.7120 | 1.6329 | 0.3719 | 0.1860 | 18.4848 | 97.7661 |
| Temperature | Method | MSE | MAPE (%) | RMSE | RRMSE (%) | PI | Max. Deviation (°C) | Training Time (s) | ||
|---|---|---|---|---|---|---|---|---|---|---|
| SVR (linear kernel) | 0.9814 | 0.9631 | 1962.2975 | 28.0743 | 44.2978 | 10.6929 | 5.3967 | 212.8389 | 4.9031 | |
| SVR (Gaussian kernel) | 0.9978 | 0.9957 | 795.8607 | 13.7621 | 28.2110 | 6.8097 | 3.4085 | 35.2121 | 1.0933 | |
| SVR (polynomial kernel) | 0.9658 | 0.9328 | 27,545.3331 | 62.3341 | 165.9679 | 40.0623 | 20.3795 | 350.0137 | 92.7547 | |
| Feed-forward NN | 0.9833 | 0.9668 | 1762.2903 | 10.2336 | 41.9796 | 10.1333 | 5.1094 | 209.9725 | 1.4795 | |
| MARS (piecewise-linear) | 0.9986 | 0.9973 | 142.8723 | 3.8249 | 11.9529 | 2.8853 | 1.4436 | 91.5833 | 59.0619 | |
| MARS (piecewise-cubic) | 0.9985 | 0.9970 | 161.4353 | 3.9386 | 12.7057 | 3.0670 | 1.5347 | 104.9361 | 59.2119 | |
| k-NN regression | 1.0000 | 1.0000 | 1.3221 | 0.1945 | 1.1498 | 0.2776 | 0.1388 | 12.3883 | 0.0005 | |
| RF | 1.0000 | 0.9999 | 5.0337 | 0.5131 | 2.2436 | 0.5416 | 0.2708 | 51.0764 | 167.8558 | |
| SVR (linear kernel) | 0.9842 | 0.9687 | 1494.4749 | 25.8540 | 38.6584 | 9.1448 | 4.6088 | 195.2825 | 3.5057 | |
| SVR (Gaussian kernel) | 0.9958 | 0.9979 | 651.8275 | 11.9016 | 25.5309 | 6.0394 | 3.0229 | 32.5504 | 0.9362 | |
| SVR (polynomial kernel) | 0.9617 | 0.9248 | 4125.7109 | 29.8540 | 64.2317 | 15.1942 | 7.7456 | 159.4703 | 93.7252 | |
| Feed-forward NN | 0.6925 | 0.4796 | 24,661.5245 | 76.8499 | 157.0399 | 37.1484 | 21.9483 | 389.5280 | 0.7673 | |
| MARS (piecewise-linear) | 0.9982 | 0.9964 | 169.8030 | 4.3422 | 13.0308 | 3.0825 | 1.5426 | 79.9006 | 48.1415 | |
| MARS (piecewise-cubic) | 0.9978 | 0.9955 | 211.6325 | 5.2211 | 14.5476 | 3.4413 | 1.7226 | 79.0734 | 47.7717 | |
| k-NN regression | 1.0000 | 1.0000 | 1.2695 | 0.2156 | 1.1267 | 0.2665 | 0.1333 | 12.2896 | 0.0005 | |
| RF | 0.9999 | 0.9999 | 5.7414 | 0.5681 | 2.3961 | 0.5668 | 0.2834 | 65.3652 | 171.1530 |
References
- Durdán, M.; Kačur, J. System for indirect measurement of the heat flows at annealing of the steel coils. Acta Metall. Slovaca 2013, 19, 112–121. [Google Scholar] [CrossRef]
- Durdán, M.; Mojžišová, A.; Laciak, M.; Kačur, J. System for indirect temperature measurement in annealing process. Measurement 2014, 47, 911–918. [Google Scholar] [CrossRef]
- Kačur, J.; Durdán, M.; Laciak, M.; Flegner, P. Soft-Sensing in Batch Annealing Based on Finite Differential Method and Support Vector Regression. Adv. Sci. Technol. Res. J. 2019, 13, 70–86. [Google Scholar] [CrossRef]
- Couchet, C.; Bonnet, F.; Teixeira, J.; Allain, S.Y.P. Numerical Investigations of Phase Transformations Controlled by Interface Thermodynamic Conditions during Intercritical Annealing of Steels. Metals 2023, 13, 1288. [Google Scholar] [CrossRef]
- Yang, Y.; Ma, X.; Lu, H.; Zhao, Z. Effect of Annealing Temperature on Microstructure and Properties of DH Steel and Optimization of Hole Expansion Property. Metals 2024, 14, 791. [Google Scholar] [CrossRef]
- Chu, X.; Zhou, F.; Liu, L.; Xu, X.; Ma, X.; Li, W.; Zhao, Z. Evolution of Microstructure, Properties, and Fracture Behavior with Annealing Temperature in Complex Phase Steel with High Formability. Metals 2024, 14, 380. [Google Scholar] [CrossRef]
- Sahay, S.S.; Kumar, A.M. Applications of Integrated Batch Annealing Furnace Simulation. Mater. Manuf. Process. 2002, 17, 439–453. [Google Scholar] [CrossRef]
- Tian, Y.; Hou, C.; Gao, F. Mathematical Model of a Continuous Galvanizing Annealing Furnace. Dev. Chem. Eng. Miner. Process. 2000, 8, 359–374. [Google Scholar] [CrossRef]
- Kostúr, K.; Laciak, M.; Truchlý, M. Systémy Nepriameho Merania; TU: Košice, Slovakia, 2005. [Google Scholar]
- Haouam, A.; Bigerelle, M.; Merzoug, B. Simplex Enhanced Numerical Modeling of the Temperature Distribution in a Hydrogen Cooled Steel Coil Annealing Process. Procedia Eng. 2016, 157, 50–57. [Google Scholar] [CrossRef]
- Durdán, M.; Stehlíková, B.; Pástor, M.; Kačur, J.; Laciak, M.; Flegner, P. Research of annealing process in laboratory conditions. Measurement 2015, 73, 607–618. [Google Scholar] [CrossRef]
- Yang, X.J.; Dai, F.X.; Bao, X.J.; Chen, G.; Zhang, L.; Li, Y.R. Study of heat transfer model and buried thermocouple test of bell-type annealing furnace based on thermal equilibrium. Sci. Rep. 2025, 15, 13362. [Google Scholar] [CrossRef]
- Liao, S.; Xue, T.; Jeong, J.; Webster, S.; Ehmann, K.; Cao, J. Hybrid thermal modeling of additive manufacturing processes using physics-informed neural networks for temperature prediction and parameter identification. Comput. Mech. 2023, 72, 499–512. [Google Scholar] [CrossRef]
- Kostúr, K. Process check of annealing process of coiled sheets by indirect measurement. Metalurgija 2017, 56, 229–232. [Google Scholar]
- Zhou, X.; Xu, J.; Meng, L.; Wang, W.; Zhang, N.; Jiang, L. Machine-Learning-Assisted Composition Design for High-Yield-Strength TWIP Steel. Metals 2024, 14, 952. [Google Scholar] [CrossRef]
- Bachmann, B.I.; Müller, M.; Britz, D.; Staudt, T.; Mücklich, F. Reproducible Quantification of the Microstructure of Complex Quenched and Quenched and Tempered Steels Using Modern Methods of Machine Learning. Metals 2023, 13, 1395. [Google Scholar] [CrossRef]
- Tiwari, S.; Heo, S.; Park, N.; Reddy, N.G.S. Modeling Mechanical Properties of Industrial C-Mn Cast Steels Using Artificial Neural Networks. Metals 2025, 15, 790. [Google Scholar] [CrossRef]
- Pernía-Espinoza, A.; Castejón-Limas, M.; González-Marcos, A.; Lobato-Rubio, V. Steel annealing furnace robust neural network model. Ironmak. Steelmak. 2005, 32, 418–426. [Google Scholar] [CrossRef]
- Tian, H.X.; Mao, Z.Z. An Ensemble ELM Based on Modified AdaBoost.RT Algorithm for Predicting the Temperature of Molten Steel in Ladle Furnace. IEEE Trans. Autom. Sci. Eng. 2010, 7, 73–80. [Google Scholar] [CrossRef]
- Qiao, L.; Zhu, J.; Wang, Y. Machine Learning-Aided Process Design: Modeling and Prediction of Transformation Temperature for Pearlitic Steel. Steel Res. Int. 2021, 93, 1–10. [Google Scholar] [CrossRef]
- Bhadeshia, H.K.D.H. Neural Networks in Materials Science. ISIJ Int. 1999, 39, 966–979. [Google Scholar] [CrossRef]
- Çöl, M.; Ertunç, H.M.; Yılmaz, M. An artificial neural network model for toughness properties in microalloyed steel in consideration of industrial production conditions. Mater. Des. 2007, 28, 488–495. [Google Scholar] [CrossRef]
- Dehghani, K.; Shafiei, A. Predicting the bake hardenability of steels using neural network modeling. Mater. Lett. 2008, 62, 173–178. [Google Scholar] [CrossRef]
- Garrett, P.H. Neural network directed steel annealing. In High Performance Instrumentation and Automation; CRC Press: Boca Raton, FL, USA, 2018; pp. 209–216. [Google Scholar] [CrossRef]
- Chen, M.Y.; Linkens, D.A. A systematic neuro-fuzzy modeling framework with application to material property prediction. IEEE Trans. Syst. Man Cybern. Part B (Cybern.) 2001, 31, 781–790. [Google Scholar] [CrossRef]
- Chen, M.Y.; Linkens, D.A.; Bannister, A. Numerical analysis of factors influencing Charpy impact properties of TMCR structural steels using fuzzy modelling. Mater. Sci. Technol. 2004, 20, 627–633. [Google Scholar] [CrossRef]
- Jones, D.M. The Modelling of Mechanical Properties of Steel from Processing Parameters at the Port Talbot Hot Strip Mill. Engineering Doctorate Thesis, Cardiff University, Engineering Department, Cardiff, UK, 2006. [Google Scholar]
- Mojžišová, A.; Kostúr, K. Model of indirect temperature measurement by neural network. Acta Montan. Slovaca 2008, 13, 105–110. [Google Scholar]
- Wigley, N.R. Property Prediction of Continuous Annealed Steels. Engineering Doctorate Thesis, Cardiff University, Cardiff, UK, 2012. [Google Scholar]
- Saraee, M.; Moghimi, M.; Bagheri, A. Modeling batch annealing process using data mining techniques for cold rolled steel sheets. In Proceedings of the 17th Annual ACM SIGKDD Conference on Knowledge Discovery and Data Mining (KDD ’11), San Diego, CA, USA, 21–24 August 2011; ACM: New York, NY, USA, 2011; pp. 18–22. [Google Scholar] [CrossRef]
- Kačur, J.; Laciak, M.; Durdán, M.; Flegner, P. Utilization of Machine Learning method in prediction of UCG data. In Proceedings of the 2017 18th International Carpathian Control Conference (ICCC), Sinaia, Romania, 28–31 May 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 278–283. [Google Scholar] [CrossRef]
- Kačur, J.; Laciak, M.; Flegner, P.; Terpák, J.; Durdán, M.; Tréfa, G. Application of Support Vector Regression for Data-Driven Modeling of Melt Temperature and Carbon Content in LD Converter. In Proceedings of the 2019 20th International Carpathian Control Conference (ICCC), Krakow-Wieliczka, Poland, 26–29 May 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Zhang, Y.; Cao, W.; Qu, Q. Multi-Objective Optimization for Gas Distribution in Continuous Annealing Process. J. Adv. Comput. Intell. Intell. Inform. 2019, 23, 229–235. [Google Scholar] [CrossRef]
- Feng, K.; He, D.; Xu, A.; Wang, H. End Temperature Prediction of Molten Steel in LF based on CBR–BBN. Steel Res. Int. 2015, 87, 79–86. [Google Scholar] [CrossRef]
- Tian, H.; Mao, Z.; Wang, A. A New Incremental Learning Modeling Method Based on Multiple Models for Temperature Prediction of Molten Steel in LF. ISIJ Int. 2009, 49, 58–63. [Google Scholar] [CrossRef]
- Smith, C.A.; Yates, C.A. Spatially extended hybrid methods: A review. J. R. Soc. Interface 2018, 15, 20170931. [Google Scholar] [CrossRef]
- Łach, Ł.; Svyetlichnyy, D. Advances in Numerical Modeling for Heat Transfer and Thermal Management: A Review of Computational Approaches and Environmental Impacts. Energies 2025, 18, 1302. [Google Scholar] [CrossRef]
- Peng, X.; Zuo, S.; Fan, G.; Qin, X.; Yu, H.; Zhou, Y.; Qin, C.; Hu, S. Temperature Uniformity Measurement and Temperature Field Simulation Analysis of Bell-Type Furnace for High-Temperature Annealing Process of Grain-Oriented Silicon Steel. J. Mater. Sci. Mater. Eng. 2025, 20, 81. [Google Scholar] [CrossRef]
- Van Vlack, L.H. Elements of Materials Science and Engineering, 6th ed.; Pearson: London, UK, 1989; p. 624. [Google Scholar]
- Van, V.; Lawrence, H.; Balise, P.L. Elements of Materials Science. Phys. Today 1959, 12, 52–53. [Google Scholar] [CrossRef]
- Das, S.; Singh, S.B.; Mohanty, O.N.; Bhadeshia, H.K.D.H. Understanding the complexities of bake hardening. Mater. Sci. Technol. 2008, 24, 107–111. [Google Scholar] [CrossRef]
- Humphreys, F. Modelling microstructural evolution during annealing. Model. Simul. Mater. Sci. Eng. 2000, 8, 893–910. [Google Scholar] [CrossRef]
- Takahashi, M.; Okamoto, A. Effect of Nitrogen on Recrystallization Textures of Extra Low Carbon Steel Sheet. Trans. Iron Steel Inst. Jpn. 1979, 19, 391–400. [Google Scholar] [CrossRef]
- Schoina, L.; Jones, R.; Burgess, S.; Vaughan, D.; Andrews, L.; Foley, A.; Valera Medina, A. Numerical and Techno-Economic Analysis of Batch Annealing Performance Improvements in Tinplate Manufacturing. Energies 2023, 16, 7040. [Google Scholar] [CrossRef]
- Llewellyn, D.T.; Hudd, R. Steels: Metallurgy and Applications, 3rd ed.; Butterworth-Heinemann Ltd.: Oxford, UK, 1998. [Google Scholar]
- Szala, M.; Winiarski, G.; Wójcik, Ł.; Bulzak, T. Effect of Annealing Time and Temperature Parameters on the Microstructure, Hardness, and Strain-Hardening Coefficients of 42CrMo4 Steel. Materials 2020, 13, 2022. [Google Scholar] [CrossRef] [PubMed]
- Zheng, Z.; Ren, J.; Zhang, L.; Guan, L.; Liu, C.; Liu, Y.; Cheng, S.; Su, Z.; Yang, F. Effects of normalizing and tempering temperature on the bainite microstructure and properties of low alloy fire-resistant steel bars. High Temp. Mater. Process. 2024, 43, 1–6. [Google Scholar] [CrossRef]
- Bultel, H.; Vogt, J.B. Influence of heat treatment on fatigue behaviour of 4130 AISI steel. Procedia Eng. 2010, 2, 917–924. [Google Scholar] [CrossRef]
- Park, M.; Kang, M.S.; Park, G.W.; Choi, E.Y.; Kim, H.C.; Moon, H.S.; Jeon, J.B.; Kim, H.; Kwon, S.H.; Kim, B.J. The Effects of Recrystallization on Strength and Impact Toughness of Cold-Worked High-Mn Austenitic Steels. Metals 2019, 9, 948. [Google Scholar] [CrossRef]
- Li, B.; Liu, Y.; Chen, Y.; Li, N.; Zhao, X.; Li, J.; Wang, M. Effect of Batch-Annealing Temperature on Oxidation of 22MnB5 Steel during Austenitizing. Metals 2023, 13, 1011. [Google Scholar] [CrossRef]
- Durdán, M.; Kačur, J.; Laciak, M.; Flegner, P. Thermophysical Properties Estimation in Annealing Process Using the Iterative Dynamic Programming Method and Gradient Method. Energies 2019, 12, 3267. [Google Scholar] [CrossRef]
- Kačur, J.; Durdán, M.; Flegner, P.; Laciak, M.; Bogdanovská, G. Pulse-width modulation control of experimental bell furnace. In Proceedings of the International Multidisciplinary Scientific GeoConference Surveying Geology and Mining Ecology Management, SGEM 2018, Section Informatics, Albena, Bulgaria, 2–8 July 2018; STEF92 Technology: Sofia, Bulgaria, 2018; Volume 18, pp. 649–656. [Google Scholar] [CrossRef]
- Terpák, J.; Dorčák, Ľ. Procesy Prenosu; TU Košice, Faculty BERG: Košice, Slovakia, 2001. [Google Scholar]
- Patankar, S.V. Numerical Heat Transfer and Fluid Flow; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar] [CrossRef]
- Kostúr, K. Simulačné Modely Tepelných Agregátov; Štroffek: Košice, Slovakia, 1997. [Google Scholar]
- Touloukian, Y.S.; Powell, R.W.; Ho, C.Y.; Klemens, P.G. Thermophysical Properties of Matter—The TPRC Data Series. Volume 1. Thermal Conductivity-Metallic Elements and Alloys; IFI Plenum: New York, NY, USA; Washington, DC, USA; Purdue Research Foundation: West Lafayette, IN, USA, 1970; pp. 1–1595. [Google Scholar]
- Durdán, M.; Laciak, M.; Kačur, J.; Flegner, P.; Terpák, J.; Hobľáková, K. Nonlinear Programming Methods Application in the Annealing Process. In Proceedings of the 2025 26th International Carpathian Control Conference (ICCC), Starý Smokovec, Slovakia, 19–21 May 2025; IEEE: Piscataway, NJ, USA, 2025; pp. 1–6. [Google Scholar] [CrossRef]
- Vapnik, V.N. Constructing Learning Algorithms. In The Nature of Statistical Learning Theory; Springer: New York, NY, USA, 1995; pp. 119–166. [Google Scholar] [CrossRef]
- Smola, A.; Schölkopf, B.; Müller, K.R. General cost functions for support vector regression. In Proceedings of the 9th Australian Conference on Neural Networks, Brisbane, QLD, Australia, 18–23 June 2023; Downs, T., Frean, M., Gallagher, M., Eds.; University of Queensland: St. Lucia, QLD, Australia, 1999; pp. 79–83. [Google Scholar]
- Müller, K.R.; Smola, A.J.; Rätsch, G.; Schölkopf, B.; Kohlmorgen, J.; Vapnik, V. Predicting time series with support vector machines. In Artificial Neural Networks—ICANN’97; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 1997; pp. 999–1004. [Google Scholar] [CrossRef]
- Burges, C.J.C.; Schölkopf, B. Improving the accuracy and speed of support vector learning machines. In Advances in Neural Information Processing Systems 9; Mozer, M., Jordan, M., Petsche, T., Eds.; MIT Press: Cambridge, MA, USA, 1997; pp. 375–381. [Google Scholar]
- MathWorks. Statistics and Machine Learning Toolbox (R2025a). 2025. Available online: https://www.mathworks.com/products/statistics.html (accessed on 24 July 2025).
- MathWorks. Understanding Support Vector Machine Regression, Statistics and Machine Learning Toolbox User’s Guide (R2025a). 2025. Available online: https://www.mathworks.com/help/stats/understanding-support-vector-machine-regression.html (accessed on 24 July 2025).
- Smola, A.J.; Schölkopf, B. On a Kernel-Based Method for Pattern Recognition, Regression, Approximation, and Operator Inversion. Algorithmica 1998, 22, 211–231. [Google Scholar] [CrossRef]
- Kvasnička, V.; Beňušková, Ľ.; Pospíchal, J.; Farkaš, I.; Tiňo, P.; Kráľ, A. Úvod do Teórie Neurónových Sietí; IRIS: Bratislava, Slovakia, 1997. [Google Scholar]
- MathWorks. Deep Learning Toolbox: Design, Train, Analyze, and Simulate Deep Learning Networks; MathWorks: Natick, MA, USA, 2025. [Google Scholar]
- Friedman, J.H. Multivariate Adaptive Regression Splines. Ann. Stat. 1991, 19, 1–67. [Google Scholar] [CrossRef]
- Díaz, J.; Fernández, F.J.; Prieto, M.M. Hot Metal Temperature Forecasting at Steel Plant Using Multivariate Adaptive Regression Splines. Metals 2019, 10, 41. [Google Scholar] [CrossRef]
- Kačur, J.; Durdán, M.; Laciak, M.; Flegner, P. A Comparative Study of Data-Driven Modeling Methods for Soft-Sensing in Underground Coal Gasification. Acta Polytech. 2019, 59, 322–351. [Google Scholar] [CrossRef]
- Jekabsons, G. ARESLab: Adaptive Regression Splines Toolbox for Matlab/Octave. 2022. Available online: http://www.cs.rtu.lv/jekabsons/regression.html (accessed on 24 February 2022).
- Fix, E.; Hodges, J.L. Discriminatory Analysis: Nonparametric Discrimination: Consistency Properties (Report); USAF School of Aviation Medicine: Randolph Field, TX, USA, 1951. [Google Scholar] [CrossRef]
- Altman, N.S. An Introduction to Kernel and Nearest-Neighbor Nonparametric Regression. Am. Stat. 1992, 46, 175–185. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning—Data Mining, Inference, and Prediction, 2nd ed.; Springer: New York, NY, USA, 2009. [Google Scholar] [CrossRef]
- Piryonesi, S.M.; El-Diraby, T.E. Role of Data Analytics in Infrastructure Asset Management: Overcoming Data Size and Quality Problems. J. Transp. Eng. Part B Pavements 2020, 146, 04020022. [Google Scholar] [CrossRef]
- Ferreira, D. k-Nearest Neighbors (kNN) Regressor. 2025. Available online: https://www.mathworks.com/matlabcentral/fileexchange/81893-k-nearest-neighbors-knn-regressor (accessed on 24 July 2025).
- Ho, T.K. Random decision forests. In Proceedings of the 3rd International Conference on Document Analysis and Recognition, Montreal, QC, Canada, 14–16 August 1995; IEEE Computer Society Press: Piscataway, NJ, USA, 1995; pp. 278–282. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Banerjee, S. Generic eXample Code and Generic Function for Random Forests. 2025. Available online: https://www.mathworks.com/matlabcentral/fileexchange/51985-simple-example-code-and-generic-function-for-random-forests (accessed on 24 July 2025).
- Gandomi, A.H.; Roke, D.A. Assessment of artificial neural network and genetic programming as predictive tools. Adv. Eng. Softw. 2015, 88, 63–72. [Google Scholar] [CrossRef]
- Kačur, J.; Flegner, P.; Durdán, M.; Laciak, M. Prediction of Temperature and Carbon Concentration in Oxygen Steelmaking by Machine Learning: A Comparative Study. Appl. Sci. 2022, 12, 7757. [Google Scholar] [CrossRef]
- Bi, C.C.; Li, N.; Huang, D. Study on Billet Temperature Prediction and Furnace Temperature Optimal Setting of Regenerative Reheating Furnace. Acta Autom. Sin. 2004, 30, 1–5. [Google Scholar]
- Jiménez, J.; Mochón, J.; de Ayala, J.S.; Obeso, F. Blast Furnace Hot Metal Temperature Prediction through Neural Networks-Based Models. ISIJ Int. 2004, 44, 573–580. [Google Scholar] [CrossRef]






| Condition/Property | Description/Value |
|---|---|
| Initial condition | Uniform initial temperature across the domain |
| Radial outer boundary () | Dirichlet: measured surface temperature from thermocouples |
| Axial boundaries ( and ) | Neumann: insulated boundary () or measured temperature if available |
| Thermal conductivity | 50–80 (20–700 °C) |
| Density | 7800–7850 |
| Specific heat | 460–600 (20–700 °C) |
| Thermal diffusivity | Calculated as |
| Temperature | Method | MSE | MAPE (%) | RMSE | RRMSE (%) | PI | Max. Deviation (°C) | ||
|---|---|---|---|---|---|---|---|---|---|
| FDM | 0.9977 | 0.9953 | 540.4461 | 5.0330 | 23.2475 | 4.7007 | 2.3531 | 51.4602 | |
| SVR (linear kernel) | 0.9994 | 0.9987 | 138.0414 | 7.3626 | 11.7491 | 2.3757 | 1.1882 | 25.9277 | |
| SVR (Gaussian kernel) | 0.9861 | 0.9724 | 2767.9616 | 22.4897 | 52.6114 | 10.6382 | 5.3564 | 126.5662 | |
| SVR (polynomial kernel) | 0.9977 | 0.9954 | 1864.6749 | 39.3406 | 43.1819 | 8.7316 | 4.3708 | 95.0755 | |
| Feed-forward NN | 0.9991 | 0.9983 | 97.8152 | 3.0665 | 9.8902 | 2.0500 | 1.0255 | 27.3036 | |
| MARS (piecewise-linear) | 0.9997 | 0.9994 | 65.7732 | 1.8219 | 8.1101 | 1.6399 | 0.8201 | 21.2783 | |
| MARS (piecewise-cubic) | 0.9997 | 0.9994 | 67.2075 | 1.9637 | 8.1980 | 1.6577 | 0.8290 | 21.6922 | |
| k-NN regression | 0.9992 | 0.9984 | 109.8672 | 3.5877 | 10.4818 | 2.1195 | 1.0602 | 32.7000 | |
| RF | 0.9997 | 0.9994 | 37.8436 | 2.3402 | 6.1517 | 1.2439 | 0.6220 | 23.3970 | |
| FDM | 0.9995 | 0.9990 | 170.0699 | 3.8654 | 13.0411 | 2.6541 | 1.3274 | 26.9984 | |
| SVR (linear kernel) | 0.9999 | 0.9998 | 392.3905 | 11.7515 | 19.8088 | 4.0315 | 2.0158 | 27.1880 | |
| SVR (Gaussian kernel) | 0.9957 | 0.9913 | 1199.4459 | 14.7148 | 34.6330 | 7.0485 | 3.5319 | 66.1461 | |
| SVR (polynomial kernel) | 0.9965 | 0.9929 | 3601.1432 | 57.8792 | 60.0095 | 12.2131 | 6.1174 | 146.4095 | |
| Feed-forward NN | 0.9996 | 0.9991 | 57.3574 | 2.4260 | 7.5735 | 1.5414 | 0.7708 | 18.3408 | |
| MARS (piecewise-linear) | 0.9999 | 0.9998 | 18.1366 | 2.0005 | 4.2587 | 0.8667 | 0.4334 | 15.5551 | |
| MARS (piecewise-cubic) | 0.9999 | 0.9997 | 20.1640 | 2.4694 | 4.4904 | 0.9139 | 0.4570 | 8.7338 | |
| k-NN regression | 1.0000 | 0.9999 | 5.9435 | 0.9553 | 2.4379 | 0.4962 | 0.2481 | 8.8200 | |
| RF | 0.9999 | 0.9999 | 13.2493 | 0.9593 | 3.6400 | 0.7408 | 0.3704 | 12.4364 | |
| FDM | 0.9999 | 0.9997 | 58.0273 | 2.3171 | 7.6176 | 1.5668 | 0.7834 | 13.8095 | |
| SVR (linear kernel) | 0.9994 | 0.9989 | 148.0223 | 6.0519 | 12.1664 | 2.5024 | 1.2516 | 24.4570 | |
| SVR (Gaussian kernel) | 0.9832 | 0.9667 | 3521.3349 | 27.6762 | 59.3408 | 12.2054 | 6.1543 | 136.3094 | |
| SVR (polynomial kernel) | 0.9873 | 0.9747 | 10,211.8079 | 101.8807 | 101.0535 | 20.7849 | 10.4590 | 232.3988 | |
| Feed-forward NN | 0.9995 | 0.9991 | 62.0696 | 3.5665 | 7.8784 | 1.6205 | 0.8104 | 20.4360 | |
| MARS (piecewise-linear) | 0.9999 | 0.9998 | 18.1366 | 2.0005 | 4.2587 | 0.8667 | 0.4334 | 15.5551 | |
| MARS (piecewise-cubic) | 1.0000 | 0.9999 | 10.4490 | 1.6268 | 3.2325 | 0.6649 | 0.3324 | 11.4345 | |
| k-NN regression | 0.9999 | 0.9998 | 15.8717 | 1.0035 | 3.9839 | 0.8194 | 0.4097 | 13.6000 | |
| RF | 1.0000 | 0.9999 | 5.3910 | 0.7655 | 2.3218 | 0.4776 | 0.2388 | 9.7072 |
| Temperature | Method | MSE | MAPE (%) | RMSE | RRMSE (%) | PI | Max. Deviation (°C) | ||
|---|---|---|---|---|---|---|---|---|---|
| FDM | 0.9989 | 0.9977 | 294.9576 | 4.4690 | 17.1743 | 3.8133 | 1.9077 | 35.8958 | |
| SVR (linear kernel) | 0.9998 | 0.9996 | 574.1722 | 13.1395 | 23.9619 | 5.3204 | 2.6605 | 32.5186 | |
| SVR (Gaussian kernel) | 0.4583 | 0.2101 | 54,047.2024 | 140.2450 | 232.4805 | 51.6190 | 35.3957 | 319.8229 | |
| SVR (polynomial kernel) | 0.9819 | 0.9641 | 29,834.8118 | 74.6854 | 172.7276 | 38.3517 | 19.3509 | 288.4810 | |
| Feed-forward NN | 0.9968 | 0.9935 | 1539.8026 | 19.0351 | 39.2403 | 8.7128 | 4.3635 | 73.9665 | |
| MARS (piecewise-linear) | 0.9998 | 0.9995 | 107.7784 | 3.0365 | 10.3816 | 2.3051 | 1.1527 | 29.2249 | |
| MARS (piecewise-cubic) | 0.9997 | 0.9994 | 116.6417 | 3.1239 | 10.8001 | 2.3980 | 1.1992 | 27.8945 | |
| k-NN regression | 0.9983 | 0.9966 | 407.9437 | 6.7567 | 20.1976 | 4.4846 | 2.2442 | 55.2871 | |
| RF | 0.9948 | 0.9897 | 1279.2204 | 8.6428 | 35.7662 | 7.9414 | 3.9810 | 108.9974 | |
| FDM | 0.9968 | 0.9937 | 763.2908 | 6.9172 | 27.6277 | 6.0063 | 3.0079 | 60.6107 | |
| SVR (linear kernel) | 0.9992 | 0.9984 | 1709.8916 | 19.4145 | 41.3508 | 8.9898 | 4.4967 | 62.6530 | |
| SVR (Gaussian kernel) | 0.5340 | 0.2852 | 56,215.3635 | 120.7524 | 237.0978 | 51.5456 | 33.6021 | 304.7536 | |
| SVR (polynomial kernel) | 0.9775 | 0.9555 | 131,518.5861 | 249.6136 | 362.6549 | 78.8420 | 39.8697 | 612.8103 | |
| Feed-forward NN | 0.9955 | 0.9909 | 754.1794 | 7.5140 | 27.4623 | 5.9704 | 2.9920 | 73.8377 | |
| MARS (piecewise-linear) | 0.9990 | 0.9980 | 180.0890 | 3.1270 | 13.4197 | 2.9175 | 1.4595 | 41.2451 | |
| MARS (piecewise-cubic) | 0.9987 | 0.9975 | 222.1936 | 3.0374 | 14.9062 | 3.2406 | 1.6213 | 40.1436 | |
| k-NN regression | 0.9972 | 0.9944 | 772.4119 | 8.5757 | 27.7923 | 6.0421 | 3.0253 | 71.6013 | |
| RF | 0.9939 | 0.9878 | 1237.6149 | 8.6225 | 35.1798 | 7.6482 | 3.8358 | 105.7638 | |
| FDM | 0.9993 | 0.9986 | 315.4478 | 4.4041 | 17.7609 | 3.9019 | 1.9516 | 31.4712 | |
| SVR (linear kernel) | 0.9998 | 0.9996 | 1090.5491 | 12.4810 | 33.0235 | 7.2550 | 3.6278 | 43.3134 | |
| SVR (Gaussian kernel) | 0.4097 | 0.1679 | 62,362.6146 | 148.8183 | 249.7251 | 54.8623 | 38.9173 | 316.9154 | |
| SVR (polynomial kernel) | 0.9505 | 0.9035 | 55,356.7333 | 118.8545 | 235.2801 | 51.6880 | 26.5003 | 796.2979 | |
| Feed-forward NN | 0.9805 | 0.9613 | 5101.2201 | 72.5726 | 71.4228 | 15.6909 | 7.9229 | 183.1845 | |
| MARS (piecewise-linear) | 0.9996 | 0.9993 | 129.3436 | 4.3369 | 11.3729 | 2.4985 | 1.2495 | 24.3075 | |
| MARS (piecewise-cubic) | 0.9996 | 0.9993 | 129.9495 | 4.3847 | 11.3995 | 2.5044 | 1.2524 | 25.3766 | |
| k-NN regression | 0.9970 | 0.9941 | 671.0097 | 7.5791 | 25.9039 | 5.6908 | 2.8497 | 61.5594 | |
| RF | 0.9935 | 0.9871 | 1249.5063 | 7.1061 | 35.3484 | 7.7657 | 3.8954 | 109.3951 |
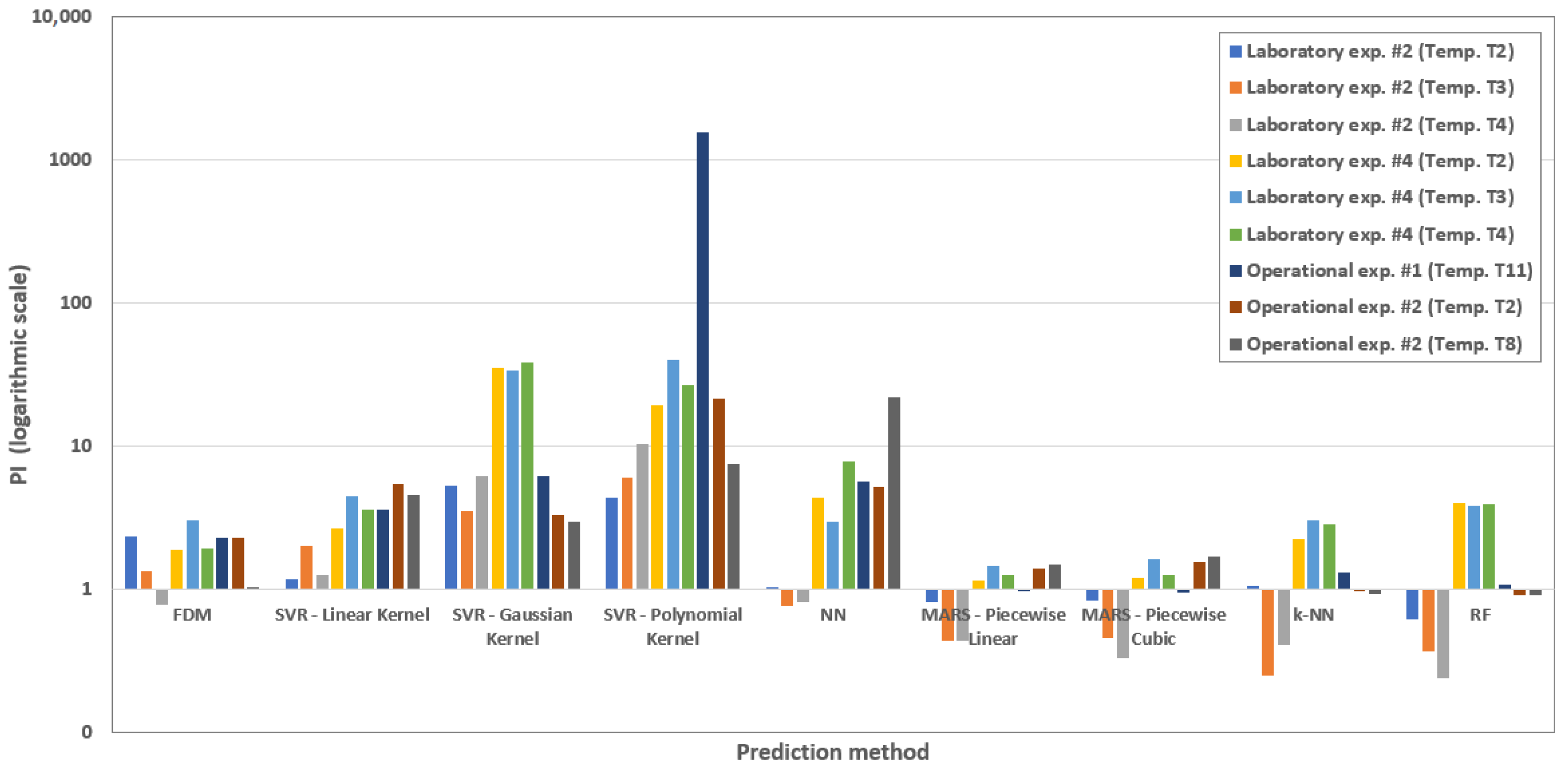
| Scenario | FDM | SVR Linear Kernel | SVR Gaussian Kernel | SVR Polynomial Kernel | NN | MARS Piecewise Linear | MARS Piecewise Cubic | k-NN | RF |
|---|---|---|---|---|---|---|---|---|---|
| Laboratory exp. #2 (Temp. T2) | 2.3531 | 1.1882 | 5.3564 | 4.3708 | 1.0255 | 0.8201 | 0.8290 | 1.0602 | 0.6220 |
| Laboratory exp. #2 (Temp. T3) | 1.3274 | 2.0158 | 3.5319 | 6.1174 | 0.7708 | 0.4334 | 0.4570 | 0.2481 | 0.3704 |
| Laboratory exp. #2 (Temp. T4) | 0.7834 | 1.2516 | 6.1543 | 10.4590 | 0.8104 | 0.4334 | 0.3324 | 0.4097 | 0.2388 |
| Laboratory exp. #4 (Temp. T2) | 1.9077 | 2.6605 | 35.3957 | 19.3509 | 4.3635 | 1.1527 | 1.1992 | 2.2442 | 3.9810 |
| Laboratory exp. #4 (Temp. T3) | 3.0079 | 4.4967 | 33.6021 | 39.8697 | 2.9920 | 1.4595 | 1.6213 | 3.0253 | 3.8358 |
| Laboratory exp. #4 (Temp. T4) | 1.9516 | 3.6278 | 38.9173 | 26.5003 | 7.9229 | 1.2495 | 1.2524 | 2.8497 | 3.8954 |
| Operational exp. #1 (Temp. T11) | 2.3182 | 3.6199 | 6.1824 | 1572.7473 | 5.6823 | 0.9924 | 0.9487 | 1.2999 | 1.0922 |
| Operational exp. #2 (Temp. T2) | 2.2833 | 5.4009 | 3.3470 | 21.3525 | 5.1789 | 1.4020 | 1.5696 | 0.9761 | 0.9018 |
| Operational exp. #2 (Temp. T8) | 1.0345 | 4.6220 | 2.9855 | 7.5349 | 21.9985 | 1.4793 | 1.7175 | 0.9340 | 0.9053 |
| Model | Approach | Prediction Accuracy | Notes | Reference |
|---|---|---|---|---|
| Finite Difference Model (FDM) | Physics-based (heat conduction) | Max deviation: 11.2 °C, RMSE: 5.8 °C (test data) | Robust, requires material properties and boundary conditions | This study |
| Multivariate Adaptive Regression Splines (MARS) | Data-driven (ML) | Max deviation: 8.9 °C, RMSE: 4.7 °C (test data) | Good generalization, interpretable basis functions | This study |
| Random Forest (RF) | Data-driven (ML) | Max deviation: 9.3 °C, RMSE: 5.1 °C (test data) | Robust to noise and overfitting, handles large datasets | This study |
| Physics-informed Neural Networks (PINNs) | Hybrid (Physics + ML) | MAE: 7.2 °C (additive manufacturing data) | Combines PDE constraints with data-driven learning | [13] |
| Analytical thermal model for bell-type annealing | Physics-based (analytical) | Relative error: <0.5% at cold spot, <5% at hot spot | Simplified analytical formulation | [12] |
| Neural Network model for annealing furnaces | Data-driven (ML) | RMSE: 8.7 °C | Trained on noisy industrial data | [18] |
| Finite Difference Model (hydrogen annealing) | Physics-based (FDM) | Max deviation: 12.4 °C (core temperatures) | Calibrated with industrial data | [10] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kačur, J.; Flegner, P.; Durdán, M.; Laciak, M. A Simulation-Based Comparative Analysis of Physics and Data-Driven Models for Temperature Prediction in Steel Coil Annealing. Metals 2025, 15, 932. https://doi.org/10.3390/met15090932
Kačur J, Flegner P, Durdán M, Laciak M. A Simulation-Based Comparative Analysis of Physics and Data-Driven Models for Temperature Prediction in Steel Coil Annealing. Metals. 2025; 15(9):932. https://doi.org/10.3390/met15090932
Chicago/Turabian StyleKačur, Ján, Patrik Flegner, Milan Durdán, and Marek Laciak. 2025. "A Simulation-Based Comparative Analysis of Physics and Data-Driven Models for Temperature Prediction in Steel Coil Annealing" Metals 15, no. 9: 932. https://doi.org/10.3390/met15090932
APA StyleKačur, J., Flegner, P., Durdán, M., & Laciak, M. (2025). A Simulation-Based Comparative Analysis of Physics and Data-Driven Models for Temperature Prediction in Steel Coil Annealing. Metals, 15(9), 932. https://doi.org/10.3390/met15090932









