Quantifying Latent Heat in AlSi5Cu Alloys (with 1, 2, and 4% of Cu by Mass) via DSC, Thermal Analysis, and Commercial Software

Abstract

This study comprehensively evaluates the latent heat of hypoeutectic AlSi5Cu alloys with 1, 2, and 4% of Cu by mass, investigating their solidification behavior under controlled cooling conditions. Latent heat, a critical thermophysical property, significantly influences solidification and microstructural formation in casting processes. The evaluation employed an integrated approach, combining experimental measurements from Differential Scanning Calorimetry (DSC) and thermal analysis (TA-Newtonian method) with computational assessments performed using JMatPro and Thermo-Calc software packages. The findings reveal a reasonable agreement between the measured and calculated latent heat values, suggesting that methods beyond DSC, such as commercial software and thermal analysis techniques, offer acceptable and viable alternatives for determining latent heat in AlSiCu alloys. While DSC served as the experimental reference, providing particularly consistent lowest values for AlSi5Cu1 and AlSi5Cu2, relative error analysis indicated that JMatPro generally yielded results closest to DSC, especially for AlSi5Cu2 (0.245% relative error), and the TA-Newtonian method also showed strong agreement, particularly for AlSi5Cu1 (0.356% relative error) and AlSi5Cu4 (0.787% relative error). Maximum deviation was observed with Thermo-Calc for AlSi5Cu1 (7.474%). These discrepancies are primarily attributed to inherent differences in the underlying thermodynamic databases for computational tools and the sensitivity of experimental techniques to specific material properties and solidification behaviors.

1. Introduction

Hypoeutectic AlSi5Cu alloys (with 1, 2, and 4% of Cu by mass) are of significant industrial importance due to their exceptional combination of mechanical properties, excellent castability, corrosion resistance, high thermal conductivity, machinability, and cost effectiveness [1,2,3,4]. These alloys find widespread applications in critical sectors such as automotive, aerospace, electronics, marine, and other industries, primarily due to the tailored microstructures and properties resulting from their principal alloying elements: [5] silicon and copper. A fundamental thermophysical property crucial for understanding and optimizing casting processes is latent heat. Latent heat represents the energy absorbed or released during a material’s phase transition, specifically from liquid to solid, without a corresponding change in temperature. Accurate determination of latent heat is paramount for effective casting process simulation, as it directly influences solidification behavior, microstructure formation, and, consequently, the overall quality of the cast product [5,6,7]. The precise prediction of thermal behavior during casting relies heavily on this property.

This study systematically evaluates the latent heat of cast AlSi5Cu (w_Cu = 1, 2, and 4%) alloys, investigating their solidification behavior under controlled cooling conditions of 6 °C/min. To ensure strong comparison and validate results across diverse methodologies, an integrated approach combining experimental measurements with computational and analytical methods has been employed.

2. Materials and Methods

Experimental measurements were performed using DSC for latent heat determination [6,8]. While DSC offers high sensitivity and versatility, it requires specific sample preparation (typically 10–20 mg) and precise calibration, which can be particularly challenging for inhomogeneous alloys.

Completing the experimental investigations, two prominent commercial thermodynamic software packages, JMatPro v15.1 and Thermo-Calc version 2025.2.174669-233, were employed for computational analysis [9,10]. Both software packages utilize the Scheil–Gulliver (SG) model, which, despite its simplifying assumptions regarding solute diffusion (negligible in the solid state and complete in the liquid state), has demonstrated remarkable accuracy in simulating non-equilibrium solidification in aluminum alloys, aligning well with experimental observations [7,11]. A key difference between these software packages lies in their respective thermodynamic databases.

Beyond calorimetric and computational methods, thermal analysis, specifically cooling curve analysis, offers another valuable approach for determining latent heat in cast aluminum alloys [6,12,13]. This method involves monitoring temperature changes during the solidification of molten metal poured into a small thermal analysis cup. The cooling curve method is favored in commercial applications due to its simplicity, cost effectiveness, minimal sample preparation requirements, consistency, and applicability directly on foundry floors [6,12]. It has been a cornerstone in the casting industry for centuries, employed in fundamental metallurgical studies, and phase diagram determination [14]. Numerous studies have successfully utilized thermal analysis techniques based on Newtonian, Fourier, and Energy Balance methods to calculate the fraction solid and latent heat of various cast aluminum alloys [15,16,17,18,19,20]. The integration of these diverse techniques aims to provide a comprehensive and highly accurate assessment of latent heat in the AlSi5Cu (w_Cu = 1, 2, and 4%) alloys studied. In this paper, the Newtonian method will be specifically employed for further analysis of the cooling curves, with detailed fundamental information provided in following sections.

Newtonian Method

In this study, the solidification paths of AlSi5Cu (w_Cu = 1, 2, and 4%) alloys were analyzed using cooling curve analysis combined with the Newtonian method, which utilizes temperature data from a single thermocouple positioned at the center of the thermal analysis cup [18,21,22]. This method operates under three key assumptions: (i) the alloy test sample exhibits a negligible thermal gradient, effectively behaving as a “lumped thermal system” where temperature is uniformly distributed (Biot number < 0.1); (ii) the sensible specific heat of the alloy remains constant and temperature independent within the freezing range; and (iii) the heat transfer coefficient from the surroundings to the sample and vice versa for the given experimental conditions can be characterized by a single, unique temperature function [21].

The core of the Newtonian analysis is the heat balance equation for the solidifying sample/mold system, which can be expressed as follows:

$${\displaystyle \frac{{\displaystyle dQ}}{dt}}-M\cdot C_p{\displaystyle \frac{dT}{dt}}=U\cdot A\cdot \left(T-T_0\right)$$

(1)

where M is the sample’s mass, C_p is specific heat of the metal, T is the metal temperature, t is time, U is overall heat transfer coefficient, A is sample surface area, T₀ is ambient temperature, and Q is latent heat of solidification. When no phase transformation occurs (i.e., dQ/dt = 0), then the cooling rate of the sample, represented by the first derivative of the cooling curve, can be defined as follows:

$${\displaystyle \frac{dT}{dt}}=-{\displaystyle \frac{U\cdot A\cdot \left(T-T_0\right)}{M{C}_p}}=Z_N$$

(2)

As presented in Figure 1, this forms the “Newtonian baseline” (BLN or Z_N).

The analysis begins by fitting a polynomial (typically of the third order or higher) to the first derivative of the cooling curve, plotted against recorded temperature, in the single-phase regions (above the liquidus temperature (T_LIQ) and below the solidus temperature (T_SOL)). The total latent heat (L) can then be calculated as follows:

$$L={\displaystyle \frac{{\displaystyle Q}}{M}}={{\displaystyle C}}_P{\displaystyle \underset{t_{\mathrm{s}}}{\overset{t_{\mathrm{e}}}{\int }}\left[{\left(\frac{dT}{dt}\right)}_{cc}-Z_N\right]}dt$$

(3)

By integrating the difference between the first derivative curve (FD) and the baseline (BLN/Z_N) over the solidification duration, from the start (t_s) to the end (t_e) of solidification. This allows for the calculation of the solid fraction at any given time during solidification by determining the cumulative area between the first derivative curve and the baseline as a fraction of the total area between these two curves. Ultimately, the latent heat of solidification can be determined from Equation (4) that relates it to the specific heat (CP) and the area between the derived cooling curve and the zero curve.

$$L=C_P\cdot x \left(\mathrm{area} \mathrm{between} \mathrm{derived} \mathrm{cooling} \mathrm{curve} \mathrm{and} \mathrm{zero} \mathrm{curve}\right)$$

(4)

The average specific heat capacities (C_p) for the AlSi5Cu (w_Cu = 1, 2, and 4%) alloys were determined using the Kopp–Neumann rule [23]. The calculation is performed according to Equation (5):

$$C_p\left[{\displaystyle \frac{\mathrm{J}}{\mathrm{kgK}}}\right]=0.01\cdot \left(w_{\mathrm{Al}}\cdot C_{p\mathrm{Al}}+...+w_{\mathrm{ElementX}}\cdot C_{p\mathrm{ElementX}}\right)$$

(5)

The average specific heat capacity at constant pressure of a solid substance established by empirical Formula (5) can be approximated as a weighted sum of the specific heat capacities at constant pressure of the elements constituting this substance.

3. Results

The experimental procedure involved hypoeutectic AlSi5Cu(1, 2, 4) alloys, the composition of which is listed in

Table 1. Chemical composition of the investigated alloy.

Alloy	w [%]
	Si	Cu	Fe	Mg	Mn	Zn	Ti	Sr	Ni	Al
AlSi5Cu1	4.85	1.03	0.09	0.14	0.01	0.01	0.058	0.000	0.000	93.812
AlSi5Cu2	5.01	2.06	0.10	0.15	0.01	0.01	0.062	0.000	0.000	92.598
AlSi5Cu4	4.89	3.85	0.09	0.16	0.01	0.01	0.057	0.000	0.000	90.933

.

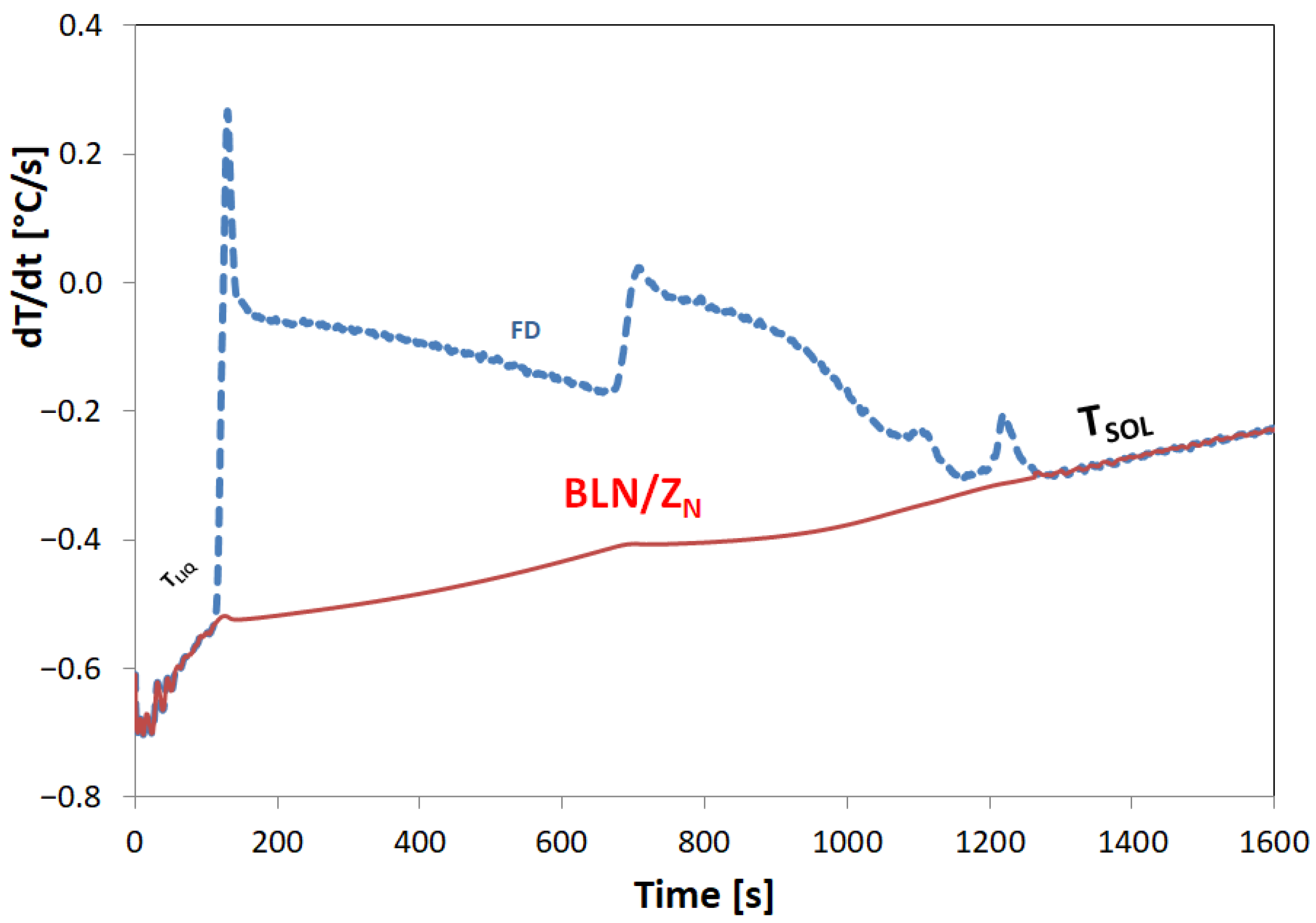
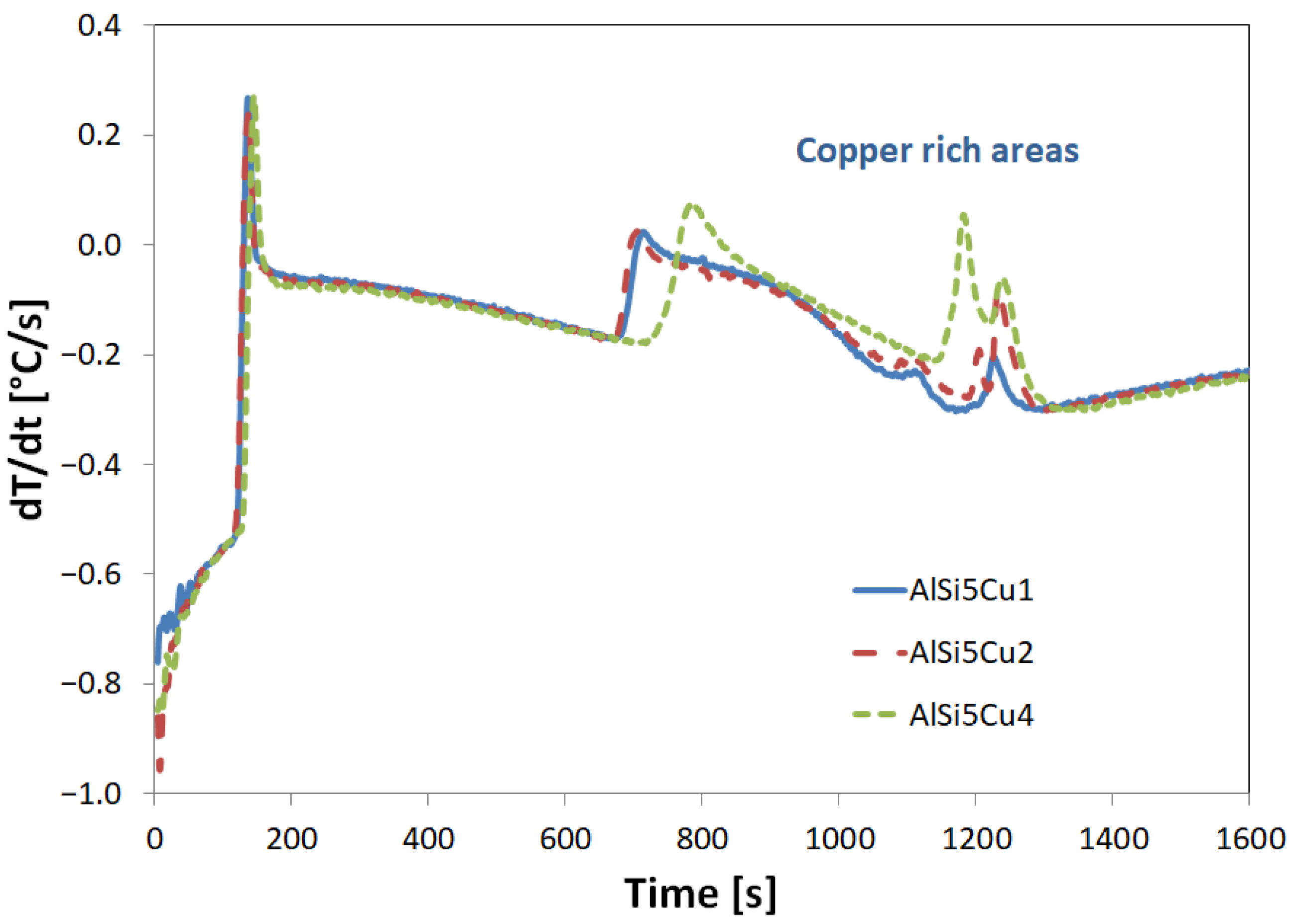
3.1. Melting Procedure

The selected hypoeutectic AlSi5Cu (w_Cu = 1, 2, and 4%) alloys were melted in an electric resistance furnace, in a protective nitrogen gas atmosphere to prevent contamination with hydrogen and oxygen. During the melting process, no modifier or grain refiner were added to the melt. All experiments were performed at the same melting temperature of 730 °C. For the TA procedure, four test samples weighing approximately 200 ± 10 g were charged into TA steel cups and melted down. The steel cup, of a 50 mm diameter and height of 60 mm, was insulated both at the top and the bottom. The steel cup weighed 60 g. For recording temperatures ranging from 700 to 400 °C, calibrated K-type thermocouple, with an accuracy of ±0.5 °C, was inserted into the melt. To provide representative temperature, the thermocouple’s tip was consistently maintained a height of 20 mm from the bottom of the crucible. A high-speed National Instruments data acquisition system (NI cDAQ-9171, Austin, TX, USA) connected to a personal computer was used for collection of TA. Five data points (temperature/time) per second were recorded during all experiments by the acquisition system. The acquisition process included smoothing, curve fitting, calculation of the first derivatives, identification of the start (liquidus temperature) and end of solidification (solidus temperature), determination of the zero curves (baseline), and computation of latent heat according to three different methods: Newtonian, Fourier, and Energy balance method. For all experiments, cooling conditions were constant, maintaining an average cooling rate of 5.88 °C/min (0.098 °C/s) for all cooling curves. Based on these data, the cooling rate was calculated as the ratio of the temperature difference between the liquidus and solidus temperatures to the total solidification time within this temperature range.

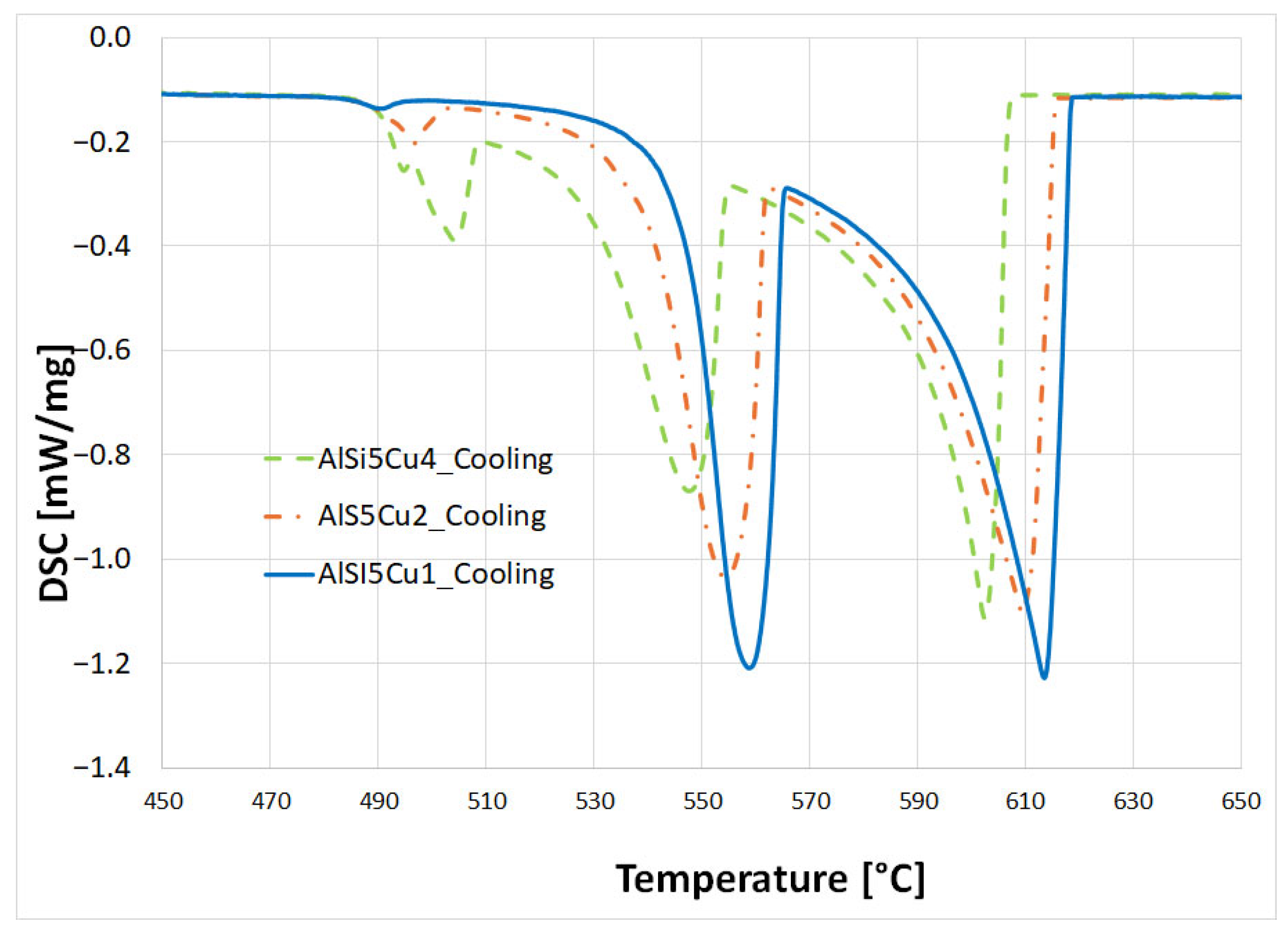
3.2. DSC Procedure

To obtain an unbiased microstructure and repeatable results, the DSC specimens were “rapidly quenched” by a massive copper chill and machined to a thickness of 0.5 mm and a diameter of 5 mm (average mass was ~20 mg) by the standard DSC procedure, as detailed in the literature [6]. After reaching the desired dimensions, they were cleaned and placed into an alumina crucible. The DSC experiments were performed at the same heating and cooling rates of 6, 10, and 50 °C/min. Argon, as a protective gas, was used during the experiments. The DSC equipment was calibrated using a sapphire standard test sample.

Table 2. The DSC thermal process cycles for the AlSI5Cu (w_Cu = 1, 2, and 4%) aluminum alloy.

Temperature Segment	Temperature [°C]	Heating/Cooling Rate [6 °C/min]
Isothermal	25	0
Dynamic	800	6
Isothermal	800	0
Dynamic	25	−6

lists the thermal process cycles used for testing the AlSi5Cu (w_Cu = 1, 2, and 4%) aluminum alloy. Each thermal cycle included a heating and cooling process: (1) isothermal maintenance for 10 min to 25 °C; (2) heating to 800 °C with heating rate, 6 °C/min; (3) isothermal maintenance for 10 min to 800 °C; and (4) cooling to 25 °C with cooling rate, 6°C/min. Each DSC experiment was repeated twice, and an average value for latent heat was taken for further consideration. The transformation energy for all tested DSC specimens was measured using a NETZSCH DSC 404 C Pegasus Differential Scanning Calorimeter, operating between 25 and 1500 °C.

Analysis of the solidification path for AlSi5Cu (w_Cu = 1, 2, and 4%) alloys, whether determined by cooling curve analysis (Figure 2) or DSC analysis (Figure 3), consistently reveals the presence of at least three characteristic reactions, regardless of the technique employed.

The solidification process for the AlSi5Cu (1-4) alloy series can be described as follows:

• Primary α-aluminum dendrite formation: The initial reaction marks the precipitation of primary α-aluminum dendrites, occurring between approximately 617 °C (for AlSi5Cu4) and 629 °C (for AlSi5Cu1). This temperature is primarily influenced by the copper content of the alloy. As these dendrites form, the concentration of both silicon and copper increases in the remaining liquid. Initially, these dendritic crystals are separate and freely moving within the melt. However, as cooling progresses, the tips of the growing dendrites begin to impinge upon one another, eventually forming a coherent dendritic network.
• Al-Si eutectic precipitation: Further cooling leads to the onset of primary Al-Si eutectic structure precipitation, observed between 574 °C (AlSi5Cu1) and 562 °C (AlSi5Cu4). This reaction involves the formation of a eutectic mixture of silicon and α-aluminum, which in turn causes a further localized increase in the copper content of the remaining liquid.
• Copper-rich eutectic formation: The final significant reaction involves the formation of copper-rich eutectic structures, which precipitate in the temperature range of 513 °C (AlSi5Cu1) to 507 °C (AlSi5Cu4).

The solidified microstructure of AlSi5Cu (w_Cu = 1, 2, and 4%) alloys is consequently characterized by the presence of two distinct eutectics (Al-Si and Al-Si-Cu) alongside the precipitated primary α-aluminum phase. These three phases collectively dictate the total amount of latent heat released during the solidification of these alloys.

The latent heat properties of AlSi5Cu (w_Cu = 1, 2, and 4%) alloys were comprehensively evaluated using both experimental and computational approaches. Experimentally, DSC and TA were employed. For computational assessments, the advanced software packages JMatPro and Thermo-Calc were utilized.

Table 3. Measured latent heat values for AlSi5Cu (wCu = 1, 2, and 4%) alloys by applying DSC, software Thermo Calc and JMatPro packages and TA techniques.

Alloy	Latent Heat, kJ/kg
	DSC Method	Thermo-Calc	JMatPro	TA-Newtonian
AlSi5Cu1	424.10	455.80	432.06	422.59
AlSi5Cu2	429.40	447.39	430.45	423.28
AlSI5Cu4	437.60	433.78	428.97	434.15

documents the complete set of latent heat values obtained from these diverse methodologies, along with their comparisons across different methods.

A complete overview of the latent heat values (in kJ/kg) for AlSi5Cu alloys with varying copper content (w_Cu = 1, 2, and 4%), obtained through diverse methodologies, DSC, Thermo-Calc, JMatPro, and TA-Newtonian, is given in Table 3. A preliminary inspection of the results reveals variations in the latent heat values across the different techniques for each alloy composition. For AlSi5Cu1, the DSC method yielded 424.10 kJ/kg, while Thermo-Calc produced a notably higher value of 455.80 kJ/kg, JMatPro 432.06 kJ/kg, and TA-Newtonian 422.59 kJ/kg. Similar discrepancies are observed for AlSi5Cu2 and AlSi5Cu4. Notably, the DSC method consistently provides the lowest latent heat values for AlSi5Cu1 and AlSi5Cu2. In contrast, for AlSi5Cu4, the DSC value (437.60 kJ/kg) is higher than those from Thermo-Calc (433.78 kJ/kg) and JMatPro (428.97 kJ/kg), but still lower than the TA-Newtonian result (434.15 kJ/kg). These initial observations suggest that the computational methods (Thermo-Calc and JMatPro) and the TA-Newtonian method produce values that can deviate from the experimentally determined DSC results, with the extent and direction of this deviation being alloy dependent.

4. Discussion

The diverse methodologies employed for latent heat determination in AlSi5Cu alloys experimental Differential Scanning Calorimetry (DSC) and thermal analysis (TA-Newtonian method), alongside computational JMatPro and Thermo-Calc software each present inherent strengths and limitations, contributing to the observed variations in reported values. DSC, while directly measuring heat flow, is particularly susceptible to the representativeness of small, inhomogeneous alloy samples and the precision of baseline definition during data integration, where complex solidification pathways can introduce inaccuracies. Furthermore, precise instrument calibration and control over experimental parameters like heating rates and purge gas flow are paramount, as even sensitive deviations can influence the measured heat exchange [6,8]. Conversely, the accuracy of computational tools like JMatPro and Thermo-Calc is fundamentally tied to the comprehensiveness and quality of their underlying thermodynamic databases, with any gaps or inaccuracies directly propagating to the calculated latent heat. These software packages often rely on simplified models such as the Scheil–Gulliver, which, despite its utility for aluminum alloys, assumes ideal conditions like infinite liquid diffusion and negligible solid diffusion, thereby potentially deviating from actual non-equilibrium solidification [7]. The TA-Newtonian method, while practical for foundry applications, faces challenges in precisely defining the sensible heat baseline from cooling curves and accurately characterizing the complex, temperature-dependent overall heat transfer coefficient. Moreover, its assumption of a uniform temperature distribution within the sample (lumped thermal system) might not hold true for all conditions, especially in larger castings or alloys with lower thermal conductivity [18,21]. Cooling curve analysis applied for the calculations of latent heat severely depends on several key factors. First of all, it is essential to precisely identify liquidus and solidus temperatures from the first derivative curves. The methodology’s precision was enhanced through polynomial fitting techniques applied to the first derivative curve before liquidus and after solidus temperatures, utilizing the Newtonian method. A crucial parameter in these calculations is the specific heat capacity of the investigated alloys, determined to be 1.112, 1.103, and 1.093 kJ/kgK for AlSi5Cu1, AlSi5Cu2, and AlSi5Cu4 alloys using the Kopp–Neumann rule [22]. This empirical approach calculates the average specific heat capacity as a weighted sum of the constituent elements’ specific heat capacities. Ultimately, these disparities underscore that no single method offers a reliable determination of latent heat; rather, the discrepancies highlight the complex relationship of experimental precision, modeling assumptions, and material characteristics, emphasizing the value of a multi-methodological approach for robust thermophysical property characterization. A more detailed quantitative comparison, specifically through the calculation of relative errors against the DSC values, will be essential to precisely assess the agreement and reliability of each method.

To quantify the precision of each method, relative error calculations were performed using Equation (6), with results presented in

Table 4. Values of the latent heat of hypoeutectic AlSi5Cu (wCu = 1, 2, and 4%) alloys calculated by various methods and their relative errors.

Relative Error [%]
Alloy	Thermo-Calc	JMatPro	TA-Newtonian
AlSi5Cu1	−7.474	−1.877	0.356
AlSi5Cu2	−4.188	−0.245	1.424
ALSi5Cu4	0.873	1.972	0.787

. These calculations used the average of two DSC measurements as a reference value, providing a statistical foundation for comparing methodological accuracy. This comprehensive evaluation validates the reliability of various approaches while acknowledging their inherent variations, offering valuable insights for material processing optimization and thermal property prediction.

$$\mathrm{Relative}\mathrm{error}=\frac{L_{\mathrm{DSC}(6 °C/\min )}-L_{\mathrm{Calculated}}}{L_{\mathrm{DSC}(6 °C/\min )}}\cdot 100$$

(6)

where L_DSC (6 °C/min) is the latent heat measured by DSC (for AlSi5Cu (w_Cu = 1, 2, and 4%) alloys and L_Calculated is the latent heat calculated by the Newtonian method or calculated using various commercial software (Thermo-Calc and JMatPro).

The relative errors in latent heat predictions, calculated using Equation (6), for all performed measurements, i.e., calculations, are given in Table 4.

Table 4 presents the relative error, quantifying the deviation of latent heat values obtained from Thermo-Calc, JMatPro, and TA-Newtonian methods when compared to the DSC method, which serves as experimental reference. An analysis of this table reveals varying degrees of agreement across the different methods and alloy compositions. For AlSi5Cu1, Thermo-Calc exhibits a notable negative relative error of 7.474%, indicating that its calculated latent heat is significantly lower than the DSC measurement. JMatPro, in contrast, shows a much smaller negative error of −1.877%, while TA-Newtonian demonstrates remarkably close agreement with DSC, presenting a positive error of only 0.356%. For AlSi5Cu2, the trend continues with Thermo-Calc showing a negative deviation (−4.188%), although less pronounced than for AlSi5Cu1. JMatPro maintains a very low error of 0.245%, suggesting excellent consistency with DSC for this alloy. The TA-Newtonian method for AlSi5Cu2 shows a positive error of 1.424%. For the alloy AlSi5Cu4, the pattern shifts, with Thermo-Calc now showing a positive relative error of 0.873%, and JMatPro a larger positive error of 1.972%. TA-Newtonian for AlSi5Cu4 also presents a positive error of 0.787%.

Overall, Table 4 highlights that JMatPro generally provides results closer to the DSC measurements, especially for AlSi5Cu2. The TA-Newtonian method also demonstrates good agreement, particularly for AlSi5Cu1 and AlSi5Cu4. Thermo-Calc, while exhibiting the largest negative errors for AlSi5Cu1 and AlSi5Cu2, shows improved agreement for AlSi5Cu4. These variations underline the influence of specific alloy composition on the accuracy of each method, likely due to characteristic differences in the underlying thermodynamic databases for computational tools and the sensitivity of experimental techniques to material properties and solidification behaviors.

Analyzing the results given in Table 4, it can be concluded that the latent heat of solidification for the investigated alloys AlSi5Cu (w_Cu = 1, 2, and 4%) can be accurately predicted by various methods. The maximum average relative error was −7.474% when using the Thermo-Calc method. Generally, the consistent small relative errors across the different methods indicate that the calculated latent heat values matched the measured reference values with high accuracy. This small discrepancy can be attributed to factors previously discussed, such as specific sample characteristics, baseline definitions, and inherent model assumptions.

As shown in Table 3, increasing copper content from 1% to 4% by mass in Al-5Si-Cu alloys does not significantly increase their latent heat, despite influencing solidification behavior. Previous studies [23,24] have shown that higher copper content impacts the quantity and morphology of Cu-rich phases. Light optical microscopy (LOM) observations, combined with image analysis (IA), confirm this, revealing an increase in the area fraction of Cu-enriched phases from approximately 0.55% to 2.42% when copper content rises from 1% to 4% [24]. These studies also indicate a noticeable extension of the total solidification time and a broadening of the solidification temperature range for these phases. Specifically, raising the copper content from 1 to 4% by mass prolongs the solidification time from 1167 s to 1211 s and expands the precipitation interval of Cu-rich phases from 31.4 °C to 65.4 °C [24]. While this extended transformation behavior might partially explain the experimentally observed, although minor, increase in latent heat with higher copper content (as more energy is released over a prolonged solidification period), this increase is ultimately not particularly significant. This is primarily because the latent heat of pure copper (around 200 kJ/kg) is relatively low compared to silicon (∼1800 kJ/kg) and aluminum (∼390 kJ/kg), leading to a less pronounced effect of copper on the overall latent heat changes in these alloys.

The recognized disagreement between our experimental results and the computational predictions from Thermo-Calc and JMatPro, as presented in Table 3, requires a more detailed commentary. Specifically, our experimental data show an increase in latent heat with rising Cu concentration, while the computational predictions show the opposite trend. This “diametrically opposite effect” is a critical point that requires rationalization, as it highlights the limitations of equilibrium modeling when applied to real world solidification processes.

This deviation can be primarily attributed to the non-equilibrium nature of our experiments. While commercial software like Thermo-Calc and JMatPro perform calculations based on equilibrium phase diagrams, assuming infinitely slow cooling rates, our samples were subjected to controlled cooling, which is a non-equilibrium process. This faster cooling may lead to the formation of metastable phases or a different solidification path, where the precipitation of specific copper-containing phases, such as the Al2Cu phase, releases additional latent heat that is not fully captured by the equilibrium models.

Furthermore, the thermodynamic databases used in these software packages, while comprehensive, may not perfectly account for the complex interactions and kinetic effects that occur in multi-component systems like the AlSi5Cu alloys. For instance, the formation and growth of the Al2Cu phase may release a different amount of heat under non-equilibrium conditions than what is predicted at equilibrium. Therefore, this qualitative discrepancy highlights a crucial point: experimental analysis remains essential for understanding the true thermophysical behavior of alloys, particularly when complex kinetics are at play. This is a significant finding that adds substantial value to this study, providing a valuable point of reference for other researchers who rely on computational methods for predicting alloy behavior.

This study highlights the strengths and versatility of the TA technique and software packages for accurately determining the latent heat of solidification in aluminum–silicon-copper hypoeutectic alloys. Several key advantages are offered by the TA method, including its user friendliness, cost effectiveness, and gathering experimental data under various process parameters, making it a practical and reliable option for foundries and materials researchers. Additionally, the TA technique does not require specialized sample preparation or highly trained personnel for result interpretation, further enhancing its applicability in industrial and research settings. At the same time, this study acknowledges that the accuracy of the TA method’s baseline curve and heat transfer coefficient determination can significantly influence the precision of the calculated latent heat values. Employing higher order polynomial fitting for these critical parameters could further enhance the accuracy of latent heat predictions across a broader range of metallic materials. Alongside the TA technique, the study also demonstrated the suitability of commercially available software packages, such as Thermo-Calc and JMatPro, for accurately calculating thermodynamic properties, including the latent heat of solidification, for the AlSi5Cu (w_Cu = 1, 2, and 4%) alloys. These software tools complement the TA method, offering the convenience of computational modeling and access to comprehensive thermodynamic databases. However, the generic data within these software packages may not fully capture the distinctions of specific alloy compositions, solid fractions, and heat capacities, potentially leading to small discrepancies in the calculated latent heat values. Overall, the study underscores the strengths of both the TA technique and commercial software tools in predicting solidification’s latent heat while highlighting opportunities for further refinement and optimization of these analytical approaches to achieve even greater accuracy and reliability.

5. Conclusions

This study comprehensively evaluated the latent heat properties of AlSi5Cu (w_Cu = 1, 2, and 4%) alloys using a multi-methodological approach, involving experimental Differential Scanning Calorimetry (DSC) and Thermal Analysis (TA) techniques, alongside computational assessments with JMatPro and Thermo-Calc software packages. The complete set of latent heat values and their comparisons are documented, providing a comprehensive overview. Analysis of the relative errors, calculated against the DSC measurements as reference, indicates that the latent heat of solidification for the investigated alloys can be accurately predicted by various methods. JMatPro generally demonstrated results closer to the DSC values, particularly for AlSi5Cu2, while the TA-Newtonian method also showed good agreement, especially for AlSi5Cu1 and AlSi5Cu4. The maximum average relative error was observed with the Thermo-Calc method for AlSi5Cu1. The observed discrepancies between methods are attributable to several factors. DSC measurements, while direct, are susceptible to the representativeness of small, inhomogeneous alloy samples and the precision of baseline definition and calibration. Computational tools like JMatPro and Thermo-Calc are fundamentally limited by the completeness and accuracy of their thermodynamic databases and rely on simplifying models such as the Scheil–Gulliver, which can deviate from actual non-equilibrium solidification. The TA-Newtonian method, favored for its simplicity and applicability in foundries, depends on the accurate definition of the sensible heat baseline from cooling curves and precise characterization of the complex, temperature-depending overall heat transfer coefficient. Its assumption of a uniform temperature distribution within the sample might not hold true under all conditions, particularly for larger castings. The accuracy of TA calculations was enhanced by precise identification of liquidus and solidus temperatures and polynomial fitting techniques. A crucial parameter in these calculations was the specific heat capacity, which was determined using the Kopp–Neumann rule for the investigated alloys. Ultimately, these disparities underscore that no single method offers an exclusively reliable determination of latent heat; rather, the discrepancies highlight the complex interplay of experimental precision, modeling assumptions, and material characteristics. Therefore, this study emphasizes the value of a multi-methodological approach for robust thermophysical property characterization. The TA technique stands out for its user friendliness, cost effectiveness, and flexibility in data gathering. Similarly, commercially available software packages like Thermo-Calc and JMatPro are valuable for their computational convenience and access to thermodynamic databases. While acknowledging that generic software data may not fully capture specific alloy distinctions, the study validates the reliability of various approaches for predicting solidification’s latent heat and suggests that employing higher order polynomial fitting can further improve the accuracy of TA predictions of latent heat across a broader range of metallic materials.