On the Solidification and Phase Stability of Re-Bearing High-Entropy Superalloys with Hierarchical Microstructures
Abstract
1. Introduction
2. Materials and Method
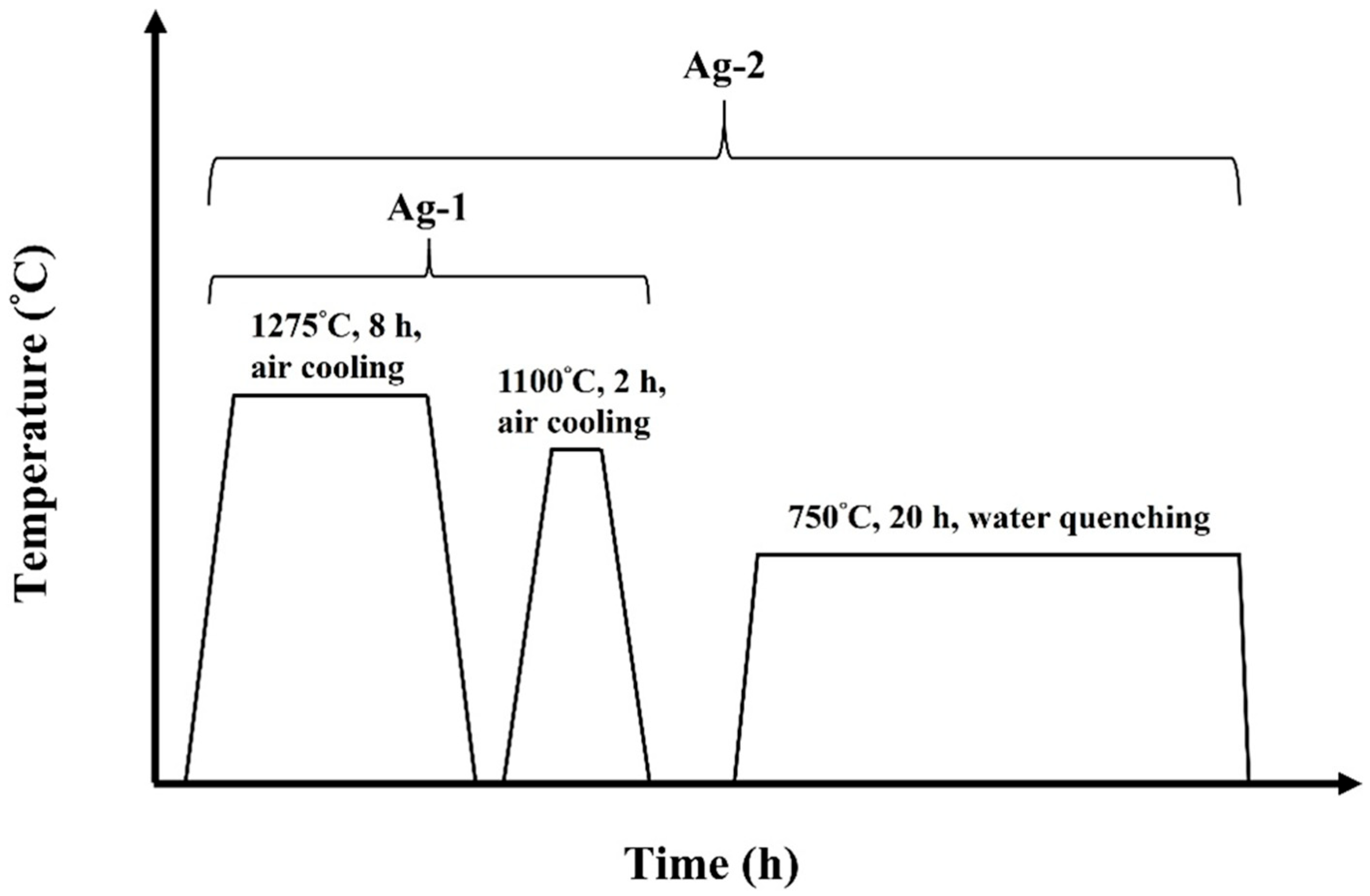
2.1. Materials and Processing
2.2. Microstructural Observations and Calculations
2.3. Mechanical Tests
3. Results and Discussion
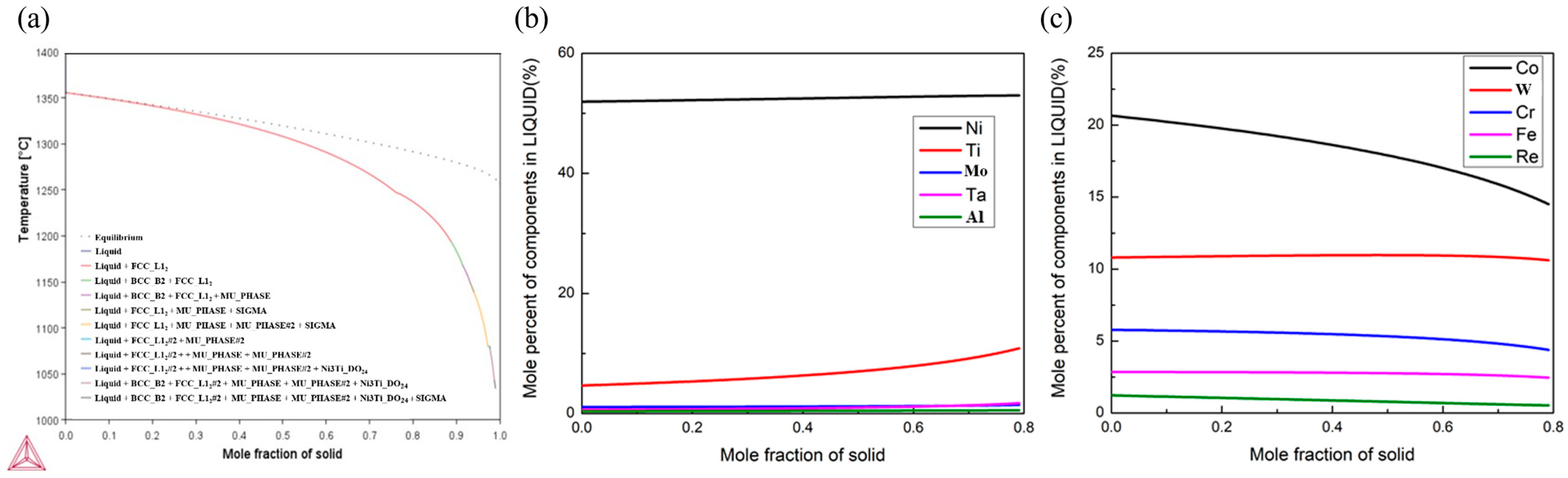
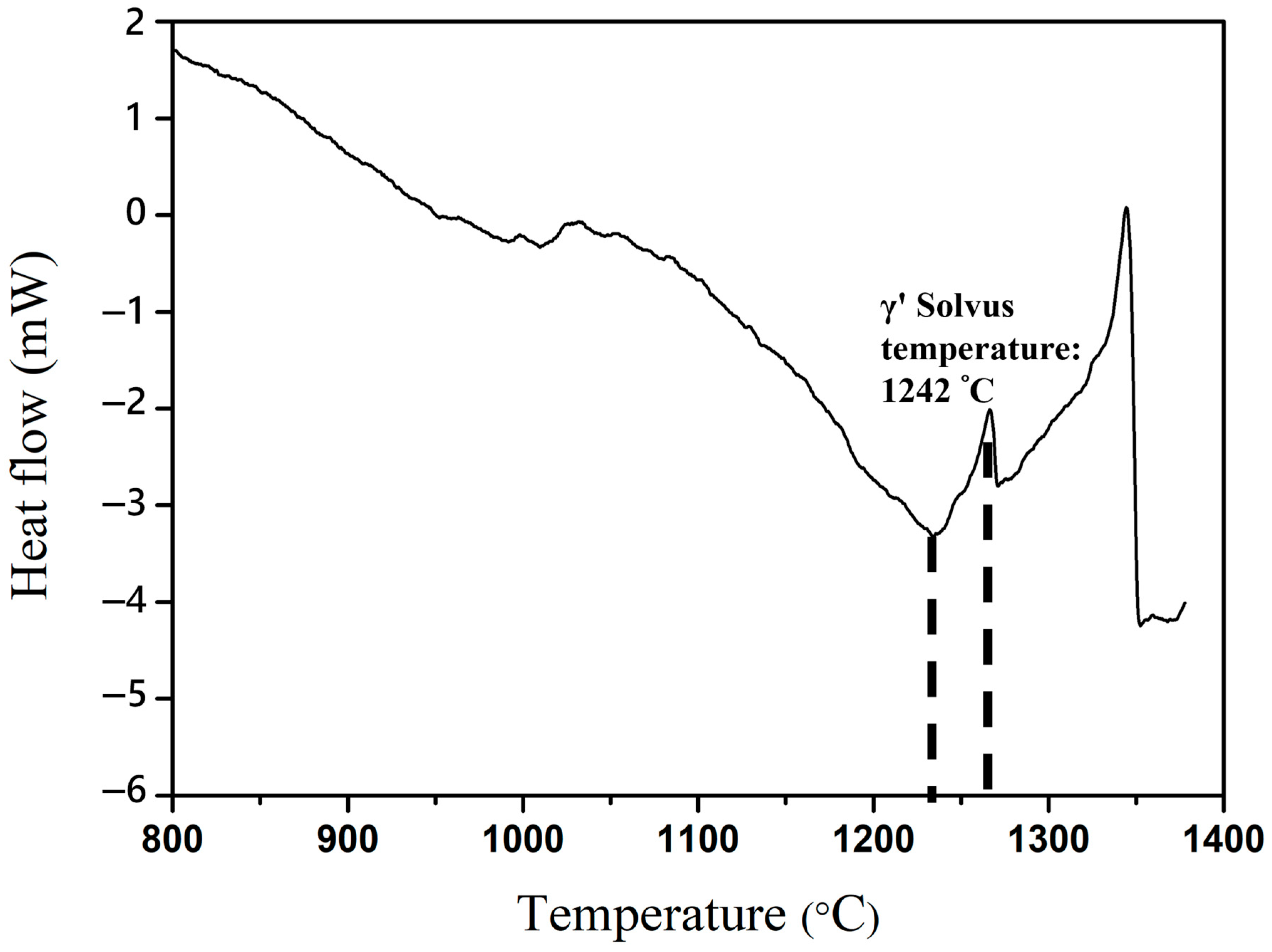
3.1. Solidification Process
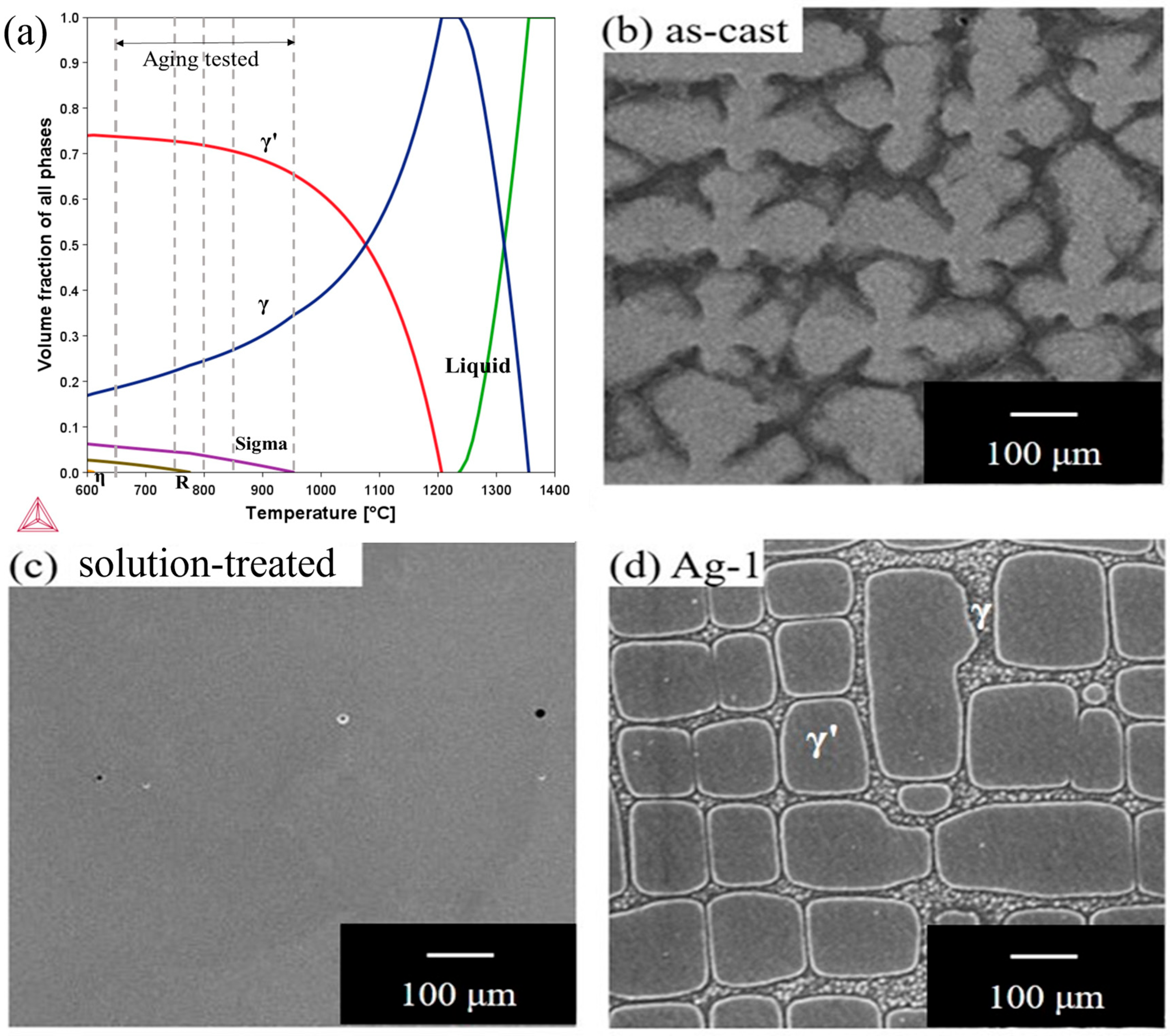
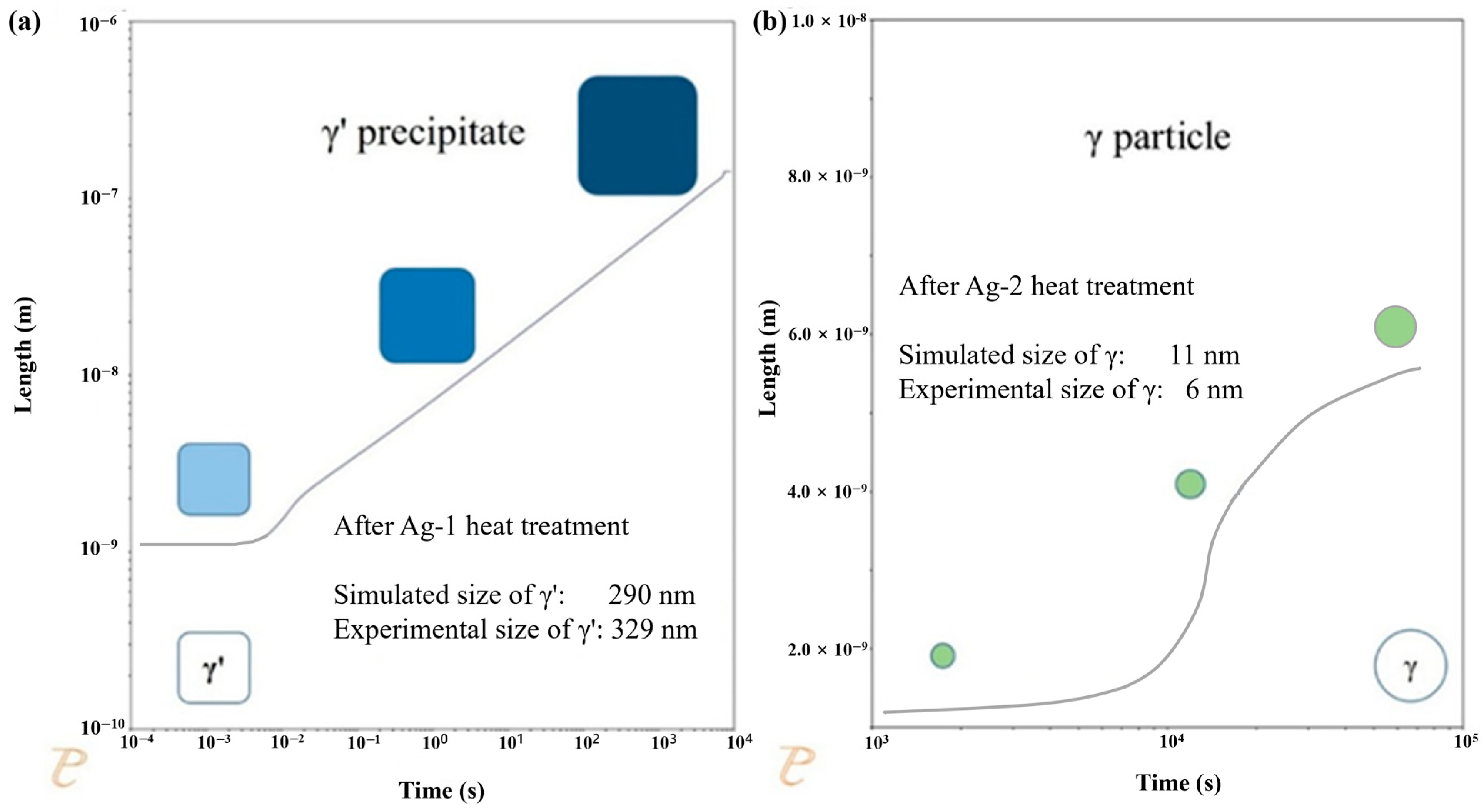
3.2. Producing a Hierarchical Microstructure
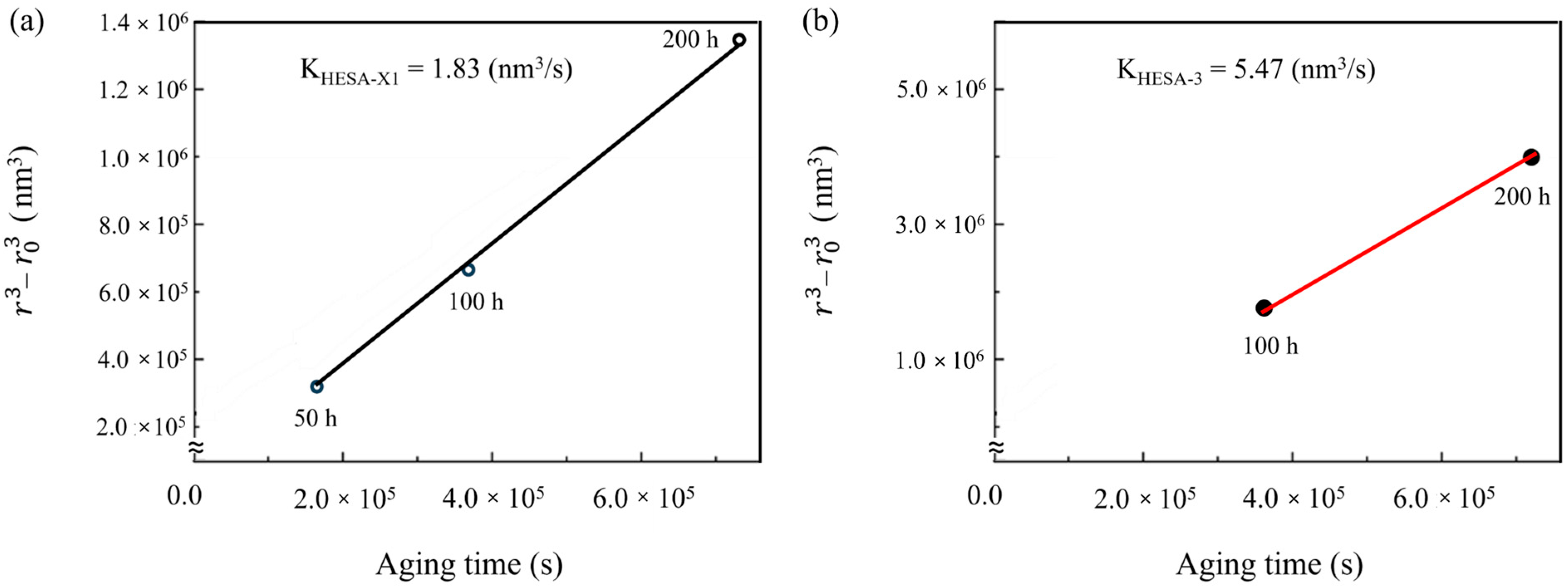
3.3. Stability of the Microstructure
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yeh, J.-W.; Chen, S.K.; Lin, S.-J.; Gan, J.-Y.; Chin, T.-S.; Shun, T.-T.; Tsau, C.-H.; Chang, S.-Y. Nanostructured high-entropy alloys with multiple principal elements: Novel alloy design concepts and outcomes. Adv. Eng. Mater. 2004, 6, 299–303. [Google Scholar] [CrossRef]
- Qian, X.; Han, D.; Zheng, L.; Chen, J.; Tyagi, M.; Li, Q.; Du, F.; Zheng, S.; Huang, X.; Zhang, S.; et al. High-entropy polymer produces a giant electrocaloric effect at low fields. Nature 2021, 600, 664–669. [Google Scholar] [CrossRef] [PubMed]
- Hsu, W.-L.; Tsai, C.-W.; Yeh, A.-C.; Yeh, J.-W. Clarifying the four core effects of high-entropy materials. Nat. Rev. Chem. 2024, 8, 471–485. [Google Scholar] [CrossRef] [PubMed]
- Raza, H.; Cheng, J.; Wang, J.; Kandasamy, S.; Zheng, G.; Chen, G. Titanium-containing high entropy oxide (Ti-HEO): A redox expediting electrocatalyst towards lithium polysulfides for high performance Li-S batteries. Nano Res. Energy 2024, 3, e9120116. [Google Scholar] [CrossRef]
- Li, L.; Zhang, M.; Jiang, M.; Gao, L.; Ma, Z.; Cao, M. High entropy ceramics for electromagnetic functional materials. Adv. Funct. Mater. 2024, 35, 2416673. [Google Scholar] [CrossRef]
- Tung, C.-C.; Yeh, J.-W.; Shun, T.-T.; Chen, S.-K.; Huang, Y.-S.; Chen, H.-C. On the elemental effect of AlCoCrCuFeNi high-entropy alloy system. Mater. Lett. 2007, 61, 1–5. [Google Scholar] [CrossRef]
- He, J.Y.; Liu, W.H.; Wang, H.; Wu, Y.; Liu, X.J.; Nieh, T.G.; Lu, Z.P. Effects of Al addition on structural evolution and tensile properties of the FeCoNiCrMn high-entropy alloy system. Acta Mater. 2014, 62, 105–113. [Google Scholar] [CrossRef]
- Hsu, C.Y.; Yeh, J.W.; Chen, S.K.; Shun, T.T. Wear resistance and high-temperature compression strength of Fcc CuCoNiCrAl0. 5Fe alloy with boron addition. Metall. Mater. Trans. A 2004, 35, 1465–1469. [Google Scholar] [CrossRef]
- Chuang, M.-H.; Tsai, M.-H.; Wang, W.-R.; Lin, S.-J.; Yeh, J.-W. Microstructure and wear behavior of AlxCo1. 5CrFeNi1. 5Tiy high-entropy alloys. Acta Mater. 2011, 59, 6308–6317. [Google Scholar] [CrossRef]
- Lee, C.; Chang, C.; Chen, Y.; Yeh, J.; Shih, H. Effect of the aluminium content of AlxCrFe1. 5MnNi0. 5 high-entropy alloys on the corrosion behaviour in aqueous environments. Corros. Sci. 2008, 50, 2053–2060. [Google Scholar] [CrossRef]
- Chou, Y.; Wang, Y.; Yeh, J.; Shih, H. Pitting corrosion of the high-entropy alloy Co1. 5CrFeNi1. 5Ti0. 5Mo0. 1 in chloride-containing sulphate solutions. Corros. Sci. 2010, 52, 3481–3491. [Google Scholar] [CrossRef]
- He, J.Y.; Wang, H.; Huang, H.L.; Xu, X.D.; Chen, M.W.; Wu, Y.; Liu, X.J.; Nieh, T.G.; An, K.; Lu, Z.P. A precipitation-hardened high-entropy alloy with outstanding tensile properties. Acta Mater. 2016, 102, 187–196. [Google Scholar] [CrossRef]
- Tong, Y.; Chen, D.; Han, B.; Wang, J.; Feng, R.; Yang, T.; Zhao, C.; Zhao, Y.L.; Guo, W.; Shimizu, Y. Outstanding tensile properties of a precipitation-strengthened FeCoNiCrTi0. 2 high-entropy alloy at room and cryogenic temperatures. Acta Mater. 2019, 165, 228–240. [Google Scholar] [CrossRef]
- Zhang, W.; Chabok, A.; Wang, H.; Shen, J.; Oliveira, J.P.; Feng, S.; Schell, N.; Kooi, B.J.; Pei, Y. Ultra-strong and ductile precipitation-strengthened high entropy alloy with 0.5% Nb addition produced by laser additive manufacturing. J. Mater. Sci. Technol. 2024, 187, 195–211. [Google Scholar] [CrossRef]
- Włoczewski, M.; Jasiewicz, K.; Jenczyk, P.; Gadalińska, E.; Kulikowski, K.; Zhang, Y.; Li, R.X.; Jarząbek, D.M. AlCoCrFeNiTi0. 2 High-Entropy Alloy Under Plasma Nitriding: Complex Microstructure Transformation, Mechanical and Tribological Enhancement. Met. Mater. Trans. A 2025, 56, 2040–2056. [Google Scholar] [CrossRef]
- Alvi, S.; Milczarek, M.; Jarzabek, D.M.; Hedman, D.; Kohan, M.G.; Levintant-Zayonts, N.; Vomiero, A.; Akhtar, F. Enhanced mechanical, thermal and electrical properties of high-entropy HfMoNbTaTiVWZr thin film metallic glass and its nitrides. Adv. Eng. Mater. 2022, 24, 2101626. [Google Scholar] [CrossRef]
- Martin, P.; Aguilar, C.; Cabrera, J. A review on mechanical alloying and spark plasma sintering of refractory high-entropy alloys: Challenges, microstructures, and mechanical behavior. J. Mater. Res. Technol. 2024, 30, 1900–1928. [Google Scholar] [CrossRef]
- Shen, X.; Guo, Z.; Liu, F.; Dong, F.; Zhang, Y.; Liu, C.; Wang, B.; Luo, L.; Su, Y.; Cheng, J.; et al. Microstructural evolution and mechanical behavior of novel TiZrTaxNbMo refractory high-entropy alloys. J. Alloys Compd. 2024, 990, 174459. [Google Scholar] [CrossRef]
- Manzoni, A.M.; Glatzel, U. New multiphase compositionally complex alloys driven by the high entropy alloy approach. Mater. Charact. 2019, 147, 512–532. [Google Scholar] [CrossRef]
- Sahragard-Monfared, G.; Belcher, C.H.; Bajpai, S.; Wirth, M.; Devaraj, A.; Apelian, D.; Lavernia, E.J.; Ritchie, R.O.; Minor, A.M.; Gibeling, J.C.; et al. Tensile creep behavior of the Nb45Ta25Ti15Hf15 refractory high entropy alloy. Acta Mater. 2024, 272, 119940. [Google Scholar] [CrossRef]
- Sengupta, A.; Putatunda, S.K.; Bartosiewicz, L.; Hangas, J.; Nailos, P.J.; Peputapeck, M.; Alberts, F.E. Tensile behavior of a new single-crystal nickel-based superalloy (CMSX-4) at room and elevated temperatures. J. Mater. Eng. Perform. 1994, 3, 73–81. [Google Scholar] [CrossRef]
- Reed, R.C. The Superalloys: Fundamentals and Applications; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar]
- Long, H.; Mao, S.; Liu, Y.; Zhang, Z.; Han, X. Microstructural and compositional design of Ni-based single crystalline superalloys—A review. J. Alloys Compd. 2018, 743, 203–220. [Google Scholar] [CrossRef]
- Yeh, A.C.; Tsao, T.K.; Chang, Y.J.; Chang, K.C.; Yeh, J.W.; Chiou, M.S.; Jian, S.R.; Kuo, C.M.; Wang, W.R.; Murakami, H. Developing new type of high temperature alloys–high entropy superalloys. Int. J. Metall. Mater. Eng. 2015, 1, 1–4. [Google Scholar]
- Detrois, M.; Jablonski, P.D.; Antonov, S.; Li, S.; Ren, Y.; Tin, S.; Hawk, J.A. Design and thermomechanical properties of a γʹ precipitate-strengthened Ni-based superalloy with high entropy γ matrix. J. Alloys Compd. 2019, 792, 550–560. [Google Scholar] [CrossRef]
- Chen, Y.-T.; Chang, Y.-J.; Murakami, H.; Gorsse, S.; Yeh, A.-C. Designing high entropy superalloys for elevated temperature application. Scr. Mater. 2020, 187, 177–182. [Google Scholar] [CrossRef]
- Tsao, T.; Yeh, A.; Kuo, C.; Murakami, H. On The Superior High Temperature Hardness of Precipitation Strengthened High Entropy Ni-Based Alloys. Adv. Eng. Mater. 2016, 19, 1600475. [Google Scholar] [CrossRef]
- Tsao, T.-K.; Yeh, A.-C.; Kuo, C.-M.; Kakehi, K.; Murakami, H.; Yeh, J.-W.; Jian, S.-R. The high temperature tensile and creep behaviors of high entropy superalloy. Sci. Rep. 2017, 7, 12658. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.-T.; Chang, Y.-J.; Murakami, H.; Sasaki, T.; Hono, K.; Li, C.-W.; Kakehi, K.; Yeh, J.-W.; Yeh, A.-C. Hierarchical microstructure strengthening in a single crystal high entropy superalloy. Sci. Rep. 2020, 10, 12163. [Google Scholar] [CrossRef] [PubMed]
- Antonov, S.; Detrois, M.; Isheim, D.; Seidman, D.; Helmink, R.C.; Goetz, R.L.; Sun, E.; Tin, S. Comparison of thermodynamic database models and APT data for strength modeling in high Nb content γ–γ′ Ni-base superalloys. Mater. Des. 2015, 86, 649–655. [Google Scholar] [CrossRef]
- Sulzer, S.; Hasselqvist, M.; Murakami, H.; Bagot, P.; Moody, M.; Reed, R. The effects of chemistry variations in new nickel-based superalloys for industrial gas turbine applications. Met. Mater. Trans. A 2020, 51, 4902–4921. [Google Scholar] [CrossRef]
- Giraud, R.; Cormier, J.; Hervier, Z.; Bertheau, D.; Harris, K.; Wahl, J.; Milhet, X.; Mendez, J.; Organista, A. Effect of the prior microstructure degradation on the high temperature/low stress non-isothermal creep behavior of cmsx-4® Ni-based single crystal superalloy. Superalloys 2012, 2012, 265–274. [Google Scholar]
- Cormier, J. Thermal cycling creep resistance of Ni-based single crystal superalloys. Superalloys 2016, 2016, 385–394. [Google Scholar]
- Lifshitz, I.; Slyozov, V. The kinetics of precipitation from supersaturated solid solutions. J. Phys. Chem. Solids 1961, 19, 35–50. [Google Scholar] [CrossRef]
- Wagner, C. Theorie der alterung von niederschlägen durch umlösen (Ostwald-reifung). Z. Elektrochem. Berichte Bunsenges. Phys. Chem. 1961, 65, 581–591. [Google Scholar] [CrossRef]
- Wang, Y.; Tang, J.; Fujihara, H.; Adachi, N.; Todaka, Y.; Xu, Y.; Saha, M.; Sasaki, T.; Shimizu, K.; Hirayama, K.; et al. Advancing the hydrogen tolerance of ultrastrong aluminum alloys via nanoprecipitate modification. Corros. Sci. 2024, 240, 112471. [Google Scholar] [CrossRef]
- Wang, B.; Zhang, J.; Huang, T.; Su, H.; Li, Z.; Liu, L.; Fu, H. Influence of W, Re, Cr, and Mo on microstructural stability of the third generation Ni-based single crystal superalloys. J. Mater. Res. 2016, 31, 3381–3389. [Google Scholar] [CrossRef]
- Uddagiri, M.; Shchyglo, O.; Steinbach, I.; Tegeler, M. Solidification of the Ni-based superalloy CMSX-4 simulated with full complexity in 3-dimensions. Prog. Addit. Manuf. 2024, 9, 1185–1196. [Google Scholar] [CrossRef]
- Jablonski, P.D.; Cowen, C.J. Homogenizing a nickel-based superalloy: Thermodynamic and kinetic simulation and experimental results. Met. Mater. Trans. B 2009, 40, 182–186. [Google Scholar] [CrossRef]
- Xinxu, L.; Chonglin, J.; Yong, Z.; Shaomin, L.; Zhouhua, J. Segregation and homogenization for a new nickel-based superalloy. Vacuum 2020, 177, 109379. [Google Scholar] [CrossRef]
- Okugawa, M.; Izumikawa, D.; Koizumi, Y. Simulations of non-equilibrium and equilibrium segregation in nickel-based superalloy using modified Scheil-Gulliver and phase-field methods. Mater. Trans. 2020, 61, 2072–2078. [Google Scholar] [CrossRef]
- Paraschiv, A.; Matache, G.; Puscasu, C. The effect of heat treatment on the homogenization of CMSX-4 Single-Crystal Ni-Based Superalloy. Transp. Res. Procedia 2018, 29, 303–311. [Google Scholar] [CrossRef]
- Tai, W.; Zhang, R.; Cui, C.; Zhou, Z.; Zhou, Y.; Sun, X. Solidification segregation behavior and homogenization process of a difficult-to-deform superalloy used at 850° C. Crystals 2023, 13, 1582. [Google Scholar] [CrossRef]
- Matache, G.; Stefanescu, D.M.; Puscasu, C.; Alexandrescu, E. An Investigation of dendritic segregation in directionally solidified CMSX-4 superalloy. In Advances in the Science and Engineering of Casting Solidification: An MPMD Symposium Honoring Doru Michael Stefanescu; Springer: Cham, Switzerland, 2016; pp. 223–230. [Google Scholar]
- Xu, Q.; Zhang, Y. Precipitation and growth simulation of γ′ phase in single crystal superalloy DD6 with multiphase-field method and explicit nucleation algorithm. Metals 2020, 10, 1346. [Google Scholar] [CrossRef]
- Schleifer, F.; Fleck, M.; Holzinger, M.; Lin, Y.-Y.; Glatzel, U. Phase-field modeling of γ′ and γ″ precipitate size evolution during heat treatment of Ni-based superalloys. In Proceedings of the Superalloys 2020: Proceedings of the 14th International Symposium on Superalloys, Seven Springs, PA, USA, 13–17 September 2020; Springer: Cham, Switzerland, 2020; pp. 500–508. [Google Scholar]
- Nathal, M.V.; MacKay, R.A.; Miner, R.V. Influence of precipitate morphology on intermediate temperature creep properties of a nickel-base superalloy single crystal. Met. Trans. A 1989, 20, 133–141. [Google Scholar] [CrossRef]
- Murakumo, T.; Kobayashi, T.; Koizumi, Y.; Harada, H. Creep behaviour of Ni-base single-crystal superalloys with various γ′ volume fraction. Acta Mater. 2004, 52, 3737–3744. [Google Scholar] [CrossRef]
- Saito, T.; Ishida, A.; Yuyama, M.; Takata, Y.; Kawagishi, K.; Yeh, A.-C.; Murakami, H. Tensile creep behavior of single-crystal high-entropy superalloy at intermediate temperature. Crystals 2020, 11, 28. [Google Scholar] [CrossRef]
- Sugui, T.; Minggang, W.; Tang, L.; Benjiang, Q.; Jun, X. Influence of TCP phase and its morphology on creep properties of single crystal nickel-based superalloys. Mater. Sci. Eng. A 2010, 527, 5444–5451. [Google Scholar] [CrossRef]
- Rakoczy, Ł.; Grudzień-Rakoczy, M.; Cygan, R.; Kargul, T.; Maj, Ł.; Zielińska-Lipiec, A. Analysis of the as-cast microstructure and properties of the Ni-based superalloy MAR-M247® produced via directional solidification. Met. Mater. Trans. A 2023, 54, 3630–3652. [Google Scholar] [CrossRef]
- Zhao, Y.; Xiong, W. Influence of Homogenization on Phase Transformations during Isothermal Aging of Inconel 718 Superalloys Fabricated by Additive Manufacturing and Suction Casting. Materials 2023, 16, 4968. [Google Scholar] [CrossRef] [PubMed]
- Meher, S.; Aagesen, L.K.; Carroll, M.C.; Pollock, T.M.; Carroll, L.J. The origin and stability of nanostructural hierarchy in crystalline solids. Sci. Adv. 2018, 4, eaao6051. [Google Scholar] [CrossRef] [PubMed]
- Smith, T.; Rao, Y.; Wang, Y.; Ghazisaeidi, M.; Mills, M. Diffusion processes during creep at intermediate temperatures in a Ni-based superalloy. Acta Mater. 2017, 141, 261–272. [Google Scholar] [CrossRef]
- Gorsse, S.; Chen, Y.-T.; Hsu, W.-C.; Murakami, H.; Yeh, A.-C. Modeling the precipitation processes and the formation of hierarchical microstructures in a single crystal high entropy superalloy. Scr. Mater. 2021, 193, 147–152. [Google Scholar] [CrossRef]
- Giamei, A.F.; Anton, D.L. Rhenium additions to a Ni-base superalloy: Effects on microstructure. Met. Trans. A 1985, 16, 1997–2005. [Google Scholar] [CrossRef]
- Fährmann, M.; Wolf, J.; Pollock, T. The influence of microstructure on the measurement of γ-γ′ lattice mismatch in single-crystal Ni-base superalloys. Mater. Sci. Eng. A 1996, 210, 8–15. [Google Scholar] [CrossRef]
- Harada, H.; Murakami, H. Design of Ni-base superalloys. In Computational Materials Design; Springer: Berlin/Heidelberg, Germany, 1999; pp. 39–70. [Google Scholar]
- Giese, S.; Bezold, A.; Pröbstle, M.; Heckl, A.; Neumeier, S.; Göken, M. The importance of diffusivity and partitioning behavior of solid solution strengthening elements for the high temperature creep strength of Ni-base superalloys. Met. Mater. Trans. A 2020, 51, 6195–6206. [Google Scholar] [CrossRef]
- Zhang, J.; Huang, T.; Lu, F.; Cao, K.; Wang, D.; Zhang, J.; Zhang, J.; Su, H.; Liu, L. The effect of rhenium on the microstructure stability and γ/γ′ interfacial characteristics of Ni-based single crystal superalloys during long-term aging. J. Alloys Compd. 2021, 876, 160114. [Google Scholar] [CrossRef]
- Durst, K.; Göken, M. Micromechanical characterisation of the influence of rhenium on the mechanical properties in nickel-base superalloys. Mater. Sci. Eng. A 2004, 387-389, 312–316. [Google Scholar] [CrossRef]
- Neumeier, S.; Pyczak, F.; Göken, M. The influence of Ruthenium and Rhenium on the local properties of the γ-and γ′-phase in Nickel-base superalloys and their consequences for alloy behavior. Superalloys 2008, 2008, 109–119. [Google Scholar]
- Caron, P.; Khan, T. Evolution of Ni-based superalloys for single crystal gas turbine blade applications. Aerosp. Sci. Technol. 1999, 3, 513–523. [Google Scholar] [CrossRef]
- Caron, P.; Khan, T. Improvement of creep strength in a nickel-base single-crystal superalloy by heat treatment. Mater. Sci. Eng. 1983, 61, 173–184. [Google Scholar] [CrossRef]
- Nathal, M.V. Effect of initial gamma prime size on the elevated temperature creep properties of single crystal nickel base superalloys. Met. Trans. A 1987, 18, 1961–1970. [Google Scholar] [CrossRef]
- Xia, P.; Yu, J.; Sun, X.; Guan, H.; Hu, Z. Influence of γ′ precipitate morphology on the creep property of a directionally solidified nickel-base superalloy. Mater. Sci. Eng. A 2008, 476, 39–45. [Google Scholar] [CrossRef]
- Huang, Y.; Wang, X.; Cui, C.; Li, J.; Ye, L.; Hou, G.; Yang, Y.; Liu, J.; Liu, J.; Zhou, Y.; et al. The effect of coarsening of γ′ precipitate on creep properties of Ni-based single crystal superalloys during long-term aging. Mater. Sci. Eng. A 2020, 773, 138886. [Google Scholar] [CrossRef]
- Baldan, A. Review progress in Ostwald ripening theories and their applications to nickel-base superalloys Part I: Ostwald ripening theories. J. Mater. Sci. 2002, 37, 2171–2202. [Google Scholar] [CrossRef]
- Baldan, A. Review Progress in Ostwald ripening theories and their applications to the γ′-precipitates in nickel-base superalloys Part II Nickel-base superalloys. J. Mater. Sci. 2002, 37, 2379–2405. [Google Scholar] [CrossRef]
- Yoon, K.E.; Noebe, R.D.; Seidman, D.N. Effects of rhenium addition on the temporal evolution of the nanostructure and chemistry of a model Ni–Cr–Al superalloy. I: Experimental observations. Acta Mater. 2007, 55, 1145–1157. [Google Scholar] [CrossRef]
- Tiley, J.; Viswanathan, G.; Srinivasan, R.; Banerjee, R.; Dimiduk, D.; Fraser, H. Coarsening kinetics of γ′ precipitates in the commercial nickel base Superalloy René 88 DT. Acta Mater. 2009, 57, 2538–2549. [Google Scholar] [CrossRef]
- Karunaratne, M.; Carter, P.; Reed, R. Interdiffusion in the face-centred cubic phase of the Ni–Re, Ni–Ta and Ni–W systems between 900 and 1300 C. Mater. Sci. Eng. A 2000, 281, 229–233. [Google Scholar] [CrossRef]
- Campbell, C.; Boettinger, W.; Kattner, U. Development of a diffusion mobility database for Ni-base superalloys. Acta Mater. 2002, 50, 775–792. [Google Scholar] [CrossRef]
- Ardell, A.J.; Ozolins, V. Trans-interface diffusion-controlled coarsening. Nat. Mater. 2005, 4, 309–316. [Google Scholar] [CrossRef] [PubMed]
- Ardell, A.J. Trans-interface-diffusion-controlled coarsening of γ′ precipitates in ternary Ni–Al–Cr alloys. Acta Mater. 2013, 61, 7828–7840. [Google Scholar] [CrossRef]
- Ardell, A.J. Quantitative predictions of the trans-interface diffusion-controlled theory of particle coarsening. Acta Mater. 2010, 58, 4325–4331. [Google Scholar] [CrossRef]
- Pandey, P.; Sawant, A.; Nithin, B.; Peng, Z.; Makineni, S.; Gault, B.; Chattopadhyay, K. On the effect of Re addition on microstructural evolution of a CoNi-based superalloy. Acta Mater. 2019, 168, 37–51. [Google Scholar] [CrossRef]



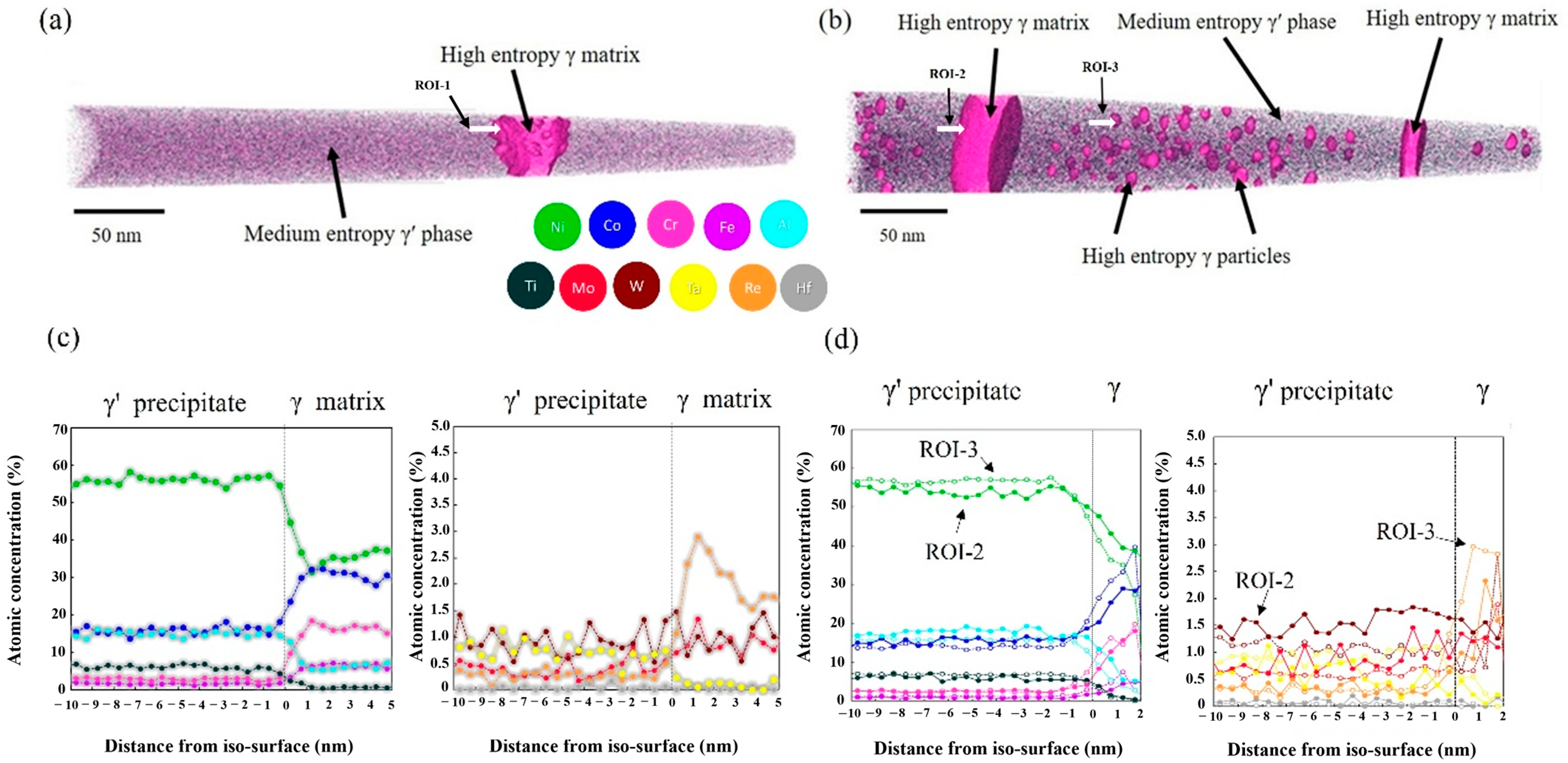
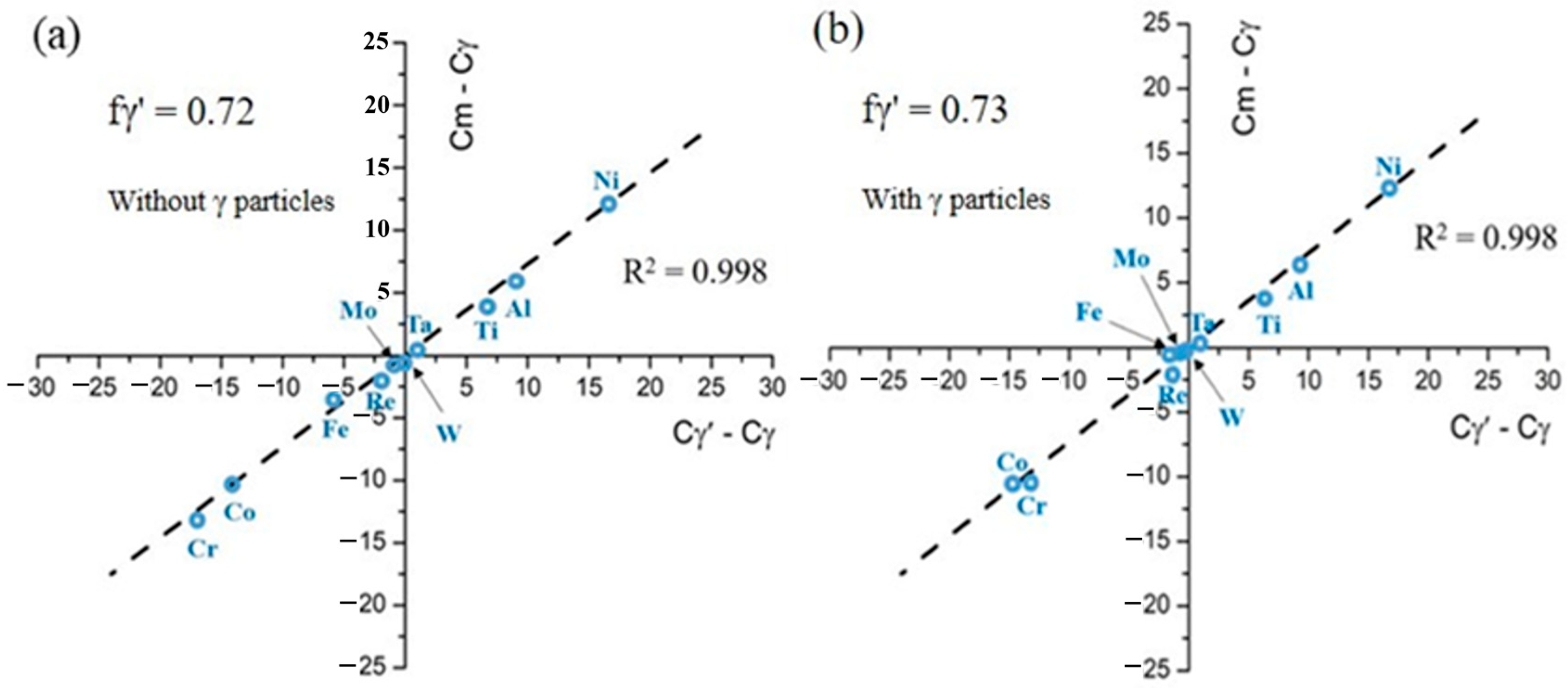
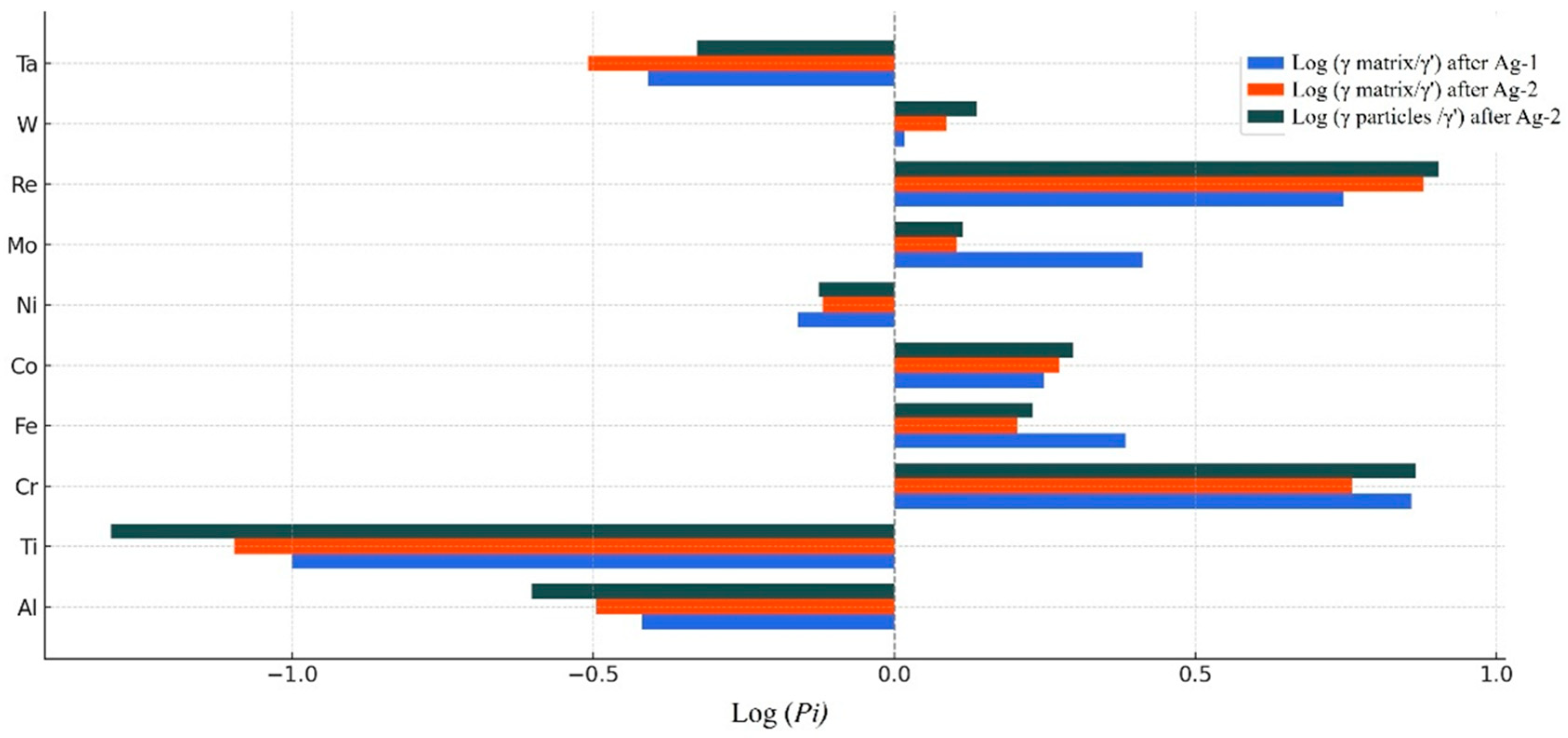

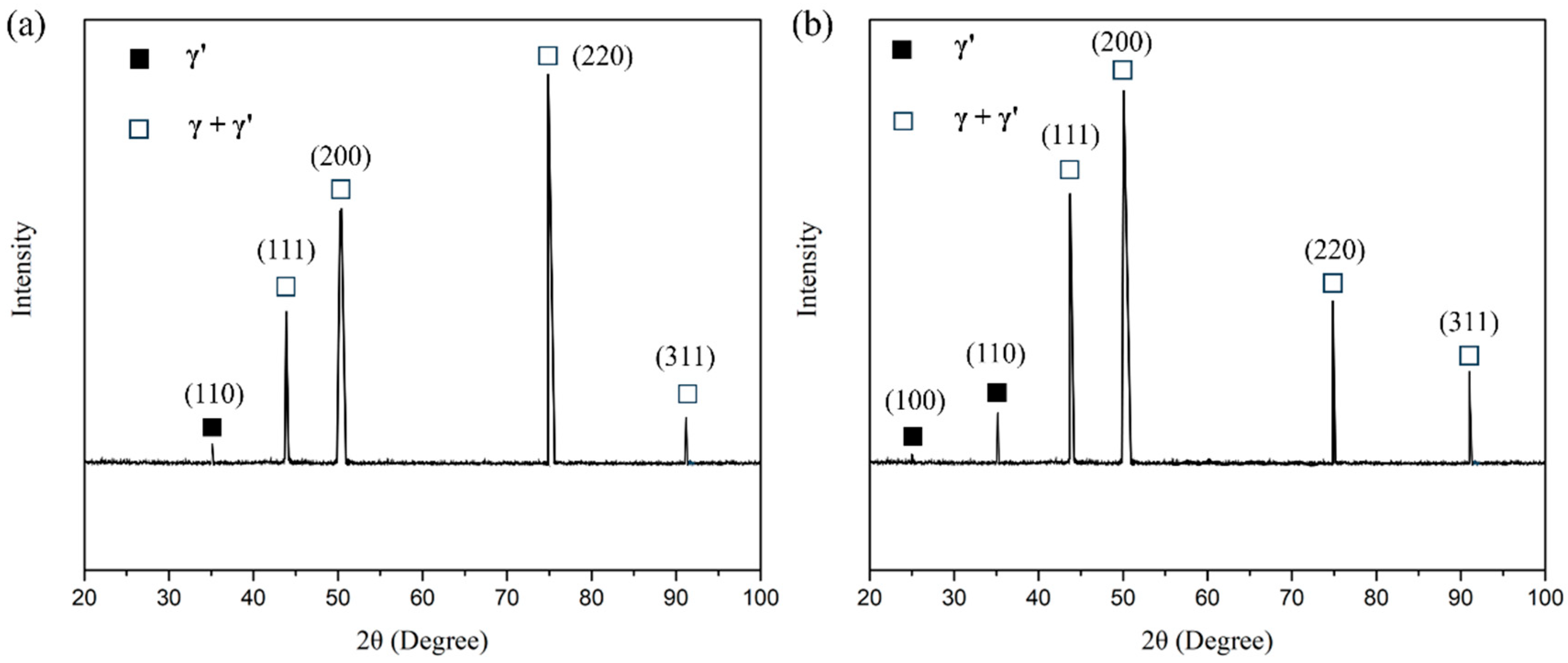


| Ni | Co | Fe | Cr | Al | Ti | Mo | W | Re | Ta | Hf | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| HESA-X1 | 50.87 | 20 | 3 | 6 | 12 | 5 | 0.5 | 1 | 1 | 0.6 | 0.03 |
| HESA-X1 (at.%) | Al | Ti | Cr | Fe | Co | Ni | Mo | Re | W | Ta | Hf |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Nominal | 12 | 5 | 6 | 3 | 20 | 50.87 | 0.5 | 1 | 1 | 0.6 | 0.03 |
| FCC γ matrix | 5.7 | 0.77 | 15.9 | 5.2 | 31.2 | 36.6 | 0.98 | 2.34 | 1.02 | 0.29 | 0 |
| L12 γ′ precipitate | 15.1 | 7.73 | 2.2 | 2.15 | 17.6 | 52.7 | 0.38 | 0.42 | 0.98 | 0.74 | 0 |
| Pi (γ matrix/γ′) | 0.38 | 0.1 | 7.22 | 2.42 | 1.77 | 0.69 | 2.58 | 5.57 | 1.04 | 0.39 | - |
| HESA-X1 (at.%) | Al | Ti | Cr | Fe | Co | Ni | Mo | Re | W | Ta | Hf |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Nominal | 12 | 5 | 6 | 3 | 20 | 50.87 | 0.5 | 1 | 1 | 0.6 | 0.03 |
| FCC γ matrix | 5.5 | 0.59 | 16.7 | 3.3 | 30.3 | 38.28 | 1.08 | 2.58 | 1.44 | 0.23 | 0 |
| FCC γ particles | 4.3 | 0.41 | 16.89 | 3.58 | 31.83 | 38.01 | 0.83 | 2.75 | 1.05 | 0.35 | 0 |
| L12 γ′ precipitate | 17.3 | 7.46 | 2.9 | 2.1 | 16.1 | 51.02 | 0.85 | 0.34 | 1.18 | 0.75 | 0 |
| Pi (γ matrix/γ′) | 0.32 | 0.08 | 5.76 | 1.6 | 1.88 | 0.76 | 1.27 | 7.56 | 1.22 | 0.31 | - |
| Pi (γ particles/γ′) | 0.25 | 0.05 | 7.34 | 1.7 | 1.98 | 0.75 | 1.3 | 8.01 | 1.37 | 0.47 | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hsu, W.-C.; Saito, T.; Saha, M.; Murakami, H.; Sasaki, T.; Yeh, A.-C. On the Solidification and Phase Stability of Re-Bearing High-Entropy Superalloys with Hierarchical Microstructures. Metals 2025, 15, 820. https://doi.org/10.3390/met15080820
Hsu W-C, Saito T, Saha M, Murakami H, Sasaki T, Yeh A-C. On the Solidification and Phase Stability of Re-Bearing High-Entropy Superalloys with Hierarchical Microstructures. Metals. 2025; 15(8):820. https://doi.org/10.3390/met15080820
Chicago/Turabian StyleHsu, Wei-Che, Takuma Saito, Mainak Saha, Hideyuki Murakami, Taisuke Sasaki, and An-Chou Yeh. 2025. "On the Solidification and Phase Stability of Re-Bearing High-Entropy Superalloys with Hierarchical Microstructures" Metals 15, no. 8: 820. https://doi.org/10.3390/met15080820
APA StyleHsu, W.-C., Saito, T., Saha, M., Murakami, H., Sasaki, T., & Yeh, A.-C. (2025). On the Solidification and Phase Stability of Re-Bearing High-Entropy Superalloys with Hierarchical Microstructures. Metals, 15(8), 820. https://doi.org/10.3390/met15080820







