A Method for Determining Twins and Corresponding Schmid Factors Based on Electron Diffraction
Abstract
1. Introduction
2. Calculation Method
3. Materials
4. Results and Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Britton, T.B.; Jiang, J.; Guo, Y.; Vilalta-Clemente, A.; Wallis, D.; Hansen, L.N.; Winkelmann, A.; Wilkinson, A.J. Tutorial: Crystal orientations and EBSD—Or which way is up? Mater. Charact. 2016, 117, 113–126. [Google Scholar] [CrossRef]
- Wei, S.; Zhu, G.; Tasan, C.C. Slip-twinning interdependent activation across phase boundaries: An in-situ investigation of a Ti-Al-V-Fe (α + β) alloy. Acta Mater. 2021, 206, 116520. [Google Scholar] [CrossRef]
- Xu, S.; Wang, J. Deformation twins stimulated by {112¯2} twinning in adjacent grain in titanium. Acta Mater. 2022, 229, 117805. [Google Scholar] [CrossRef]
- Zhang, M.; Li, J.; Tang, B.; Wang, W.Y.; Li, K.; Zhang, T.; Wang, D.; Kou, H. Quantification of α phase strengthening in titanium alloys: Crystal plasticity model incorporating α/β heterointerfaces. Int. J. Plast. 2022, 158, 103444. [Google Scholar] [CrossRef]
- Fidder, H.; Basu, I.; DeHosson, J.T.M. Twinning induced spatial stress gradients: Local versus global stress states in hexagonal close-packed materials. Acta Mater. 2023, 256, 119142. [Google Scholar] [CrossRef]
- Zeng, X.; Liu, C.; Zhao, C.; Dong, J.; Roters, F.; Guan, D. Three-dimensional study of grain scale tensile twinning activity in magnesium: A combination of microstructure characterization and mechanical modeling. Acta Mater. 2023, 255, 119043. [Google Scholar] [CrossRef]
- Zhang, R.; Zhao, Q.; Guo, D.; Du, Y.; Zou, L.; Ying, Y.; Zhang, B.; Zhao, Y. New findings on the cryogenic TWIP effect in Ti-3Al-2Zr-1.5Mo alloy with lamellar microstructure. Scr. Mater. 2023, 229, 115385. [Google Scholar] [CrossRef]
- Sohrabi, M.J.; Mirzadeh, H.; Sadeghpour, S.; Mahmudi, R. Grain size dependent mechanical behavior and TRIP effect in a metastable austenitic stainless steel. Int. J. Plast. 2023, 160, 103502. [Google Scholar] [CrossRef]
- Wang, Z.; Shi, S.; Yu, J.; Li, B.; Li, Y.; Chen, X. Combining multiscale structure and TRIP effect to enhance room temperature tensile properties of 304 stainless steel by cryogenic cyclic plastic strengthening. Scr. Mater. 2023, 234, 115581. [Google Scholar] [CrossRef]
- Zhang, J.X.; Zhang, J.Y.; Xiao, W.C.; Hou, J.X.; Li, Q.; Xiao, B.; Yang, S.Y.; Wu, J.L.; Zhang, T.L.; Yang, T. Grain refinement induced unusually large shape memory effect in lightweight titanium alloy. Acta Mater. 2024, 272, 119936. [Google Scholar] [CrossRef]
- He, X.; Deng, Y.; Guo, X. In-situ EBSD tensile revealing the evolution mechanism of high angle grain boundaries in Al–Zn–Mg alloy profile with heterogeneous structures. Mater. Sci. Eng. A 2024, 901, 146539. [Google Scholar] [CrossRef]
- Yang, B.; Wang, J.; Ferdowsi, M.R.G.; Chao, Q.; Gao, X.; Li, Y.; Zhu, Y.; Barnett, M.; Llorca, J. Effect of precipitates on the dominant active slip systems in Mg-4.5Zn (wt.%) alloy. Acta Mater. 2024, 278, 120231. [Google Scholar] [CrossRef]
- Xiao, J.F.; Cayron, C.; Van der Meer, M.; Logé, R.E. EBSD study of variant reorientation, texture, and twin formation in a martensitic NiTi alloy deformed in compression. Acta Mater. 2024, 264, 119553. [Google Scholar] [CrossRef]
- Ruggles, T.J.; Bomarito, G.F.; Qiu, R.L.; Hochhalter, J.D. New levels of high angular resolution EBSD performance via inverse compositional Gauss–Newton based digital image correlation. Ultramicroscopy 2018, 195, 85–92. [Google Scholar] [CrossRef] [PubMed]
- Brodu, E.; Bouzy, E.; Fundenberger, J.-J.; Guyon, J.; Guitton, A.; Zhang, Y. On-axis TKD for orientation mapping of nanocrystalline materials in SEM. Mater. Charact. 2017, 130, 92–96. [Google Scholar] [CrossRef]
- Cao, Y.; Ni, S.; Liao, X.; Song, M.; Zhu, Y. Structural evolutions of metallic materials processed by severe plastic deformation. Mater. Sci. Eng. R 2018, 133, 1–59. [Google Scholar] [CrossRef]
- Ovid’ko, I.A.; Valiev, R.Z.; Zhu, Y.T. Review on superior strength and enhanced ductility of metallic nanomaterials. Prog. Mater. Sci. 2018, 94, 462–540. [Google Scholar] [CrossRef]
- Ji, W.; Zhou, R.; Vivegananthan, P.; Wu, M.S.; Gao, H.; Zhou, K. Recent progress in gradient-structured metals and alloys. Prog. Mater. Sci. 2023, 140, 101194. [Google Scholar] [CrossRef]
- Zhang, Y.; Cheng, Z.; Zhu, T.; Lu, L. Mechanics of gradient nanostructured metals. J. Mech. Phys. Solids 2024, 189, 105719. [Google Scholar] [CrossRef]
- Lu, L.; Sui, M.L.; Lu, K. Superplastic extensibility of nanocrystalline copper at room temperature. Science 2000, 287, 1463–1466. [Google Scholar] [CrossRef]
- Zhao, S.; Zhang, R.; Yu, Q.; Ell, J.; Ritchie, R.O.; Minor, A.M. Cryoforged nanotwinned titanium with ultrahigh strength and ductility. Science 2021, 373, 1363–1368. [Google Scholar] [CrossRef] [PubMed]
- Guan, X.R.; Chen, Q.; Qu, S.J.; Cao, G.J.; Wang, H.; Ran, X.D.; Feng, A.H.; Chen, D.L. High-strain-rate deformation: Stress-induced phase transformation and nanostructures in a titanium alloy. Int. J. Plast. 2023, 169, 103707. [Google Scholar] [CrossRef]
- Xiong, F.; Wu, Y.; Liu, X.; Wang, H.; Jiang, S.; Zhang, X.; Lu, Z. Enhancing cryogenic yield strength and ductility of the Al0.1CoCrFeNi high-entropy alloy by synergistic effect of nanotwins and dislocations. Scr. Mater. 2023, 232, 115495. [Google Scholar] [CrossRef]
- Molnárová, O.; Klinger, M.; Duchoň, J.; Seiner, H.; Šittner, P. Plastic deformation of B19’ monoclinic martensite in NiTi shape memory alloys: HRTEM analysis of interfaces in martensite variant microstructures. Acta Mater. 2023, 258, 119242. [Google Scholar] [CrossRef]
- Banerjee, A.; He, M.-R.; Chávez, F.A.; Krogstad, J.A.; Hemker, K.J. Tailoring the nanotwin spacing of Ni-Mo-W alloys via composition and substrate temperature control. Scr. Mater. 2024, 243, 115979. [Google Scholar] [CrossRef]
- Li, K.; Zhao, D.; Xing, Y.; Chen, W.; Zhang, J.; Sun, J. Kink-mediated high strength and large ductility via nanocrystallization in a tough titanium alloy. Acta Mater. 2024, 273, 119963. [Google Scholar] [CrossRef]
- Ke, J.G.; Liu, R.; Xie, Z.M.; Zhang, L.C.; Wang, X.P.; Fang, Q.F.; Liu, C.S.; Wu, X.B. Ultrahigh strength, thermal stability and high thermal conductivity in hierarchical nanostructured Cu-W alloy. Acta Mater. 2024, 264, 119547. [Google Scholar] [CrossRef]
- Wang, Y.; Yan, F.; Lai, M.; Li, X. Formation of nanocrystalline and nanolaminate structures in a twinning induced plasticity Ti-12Mo alloy: The role played by {332} <113> twinning. Acta Mater. 2024, 276, 120078. [Google Scholar] [CrossRef]
- Wang, S.; Wu, M.; Shu, D.; Zhu, G.; Wang, D.; Sun, B. Mechanical instability and tensile properties of TiZrHfNbTa high entropy alloy at cryogenic temperatures. Acta Mater. 2020, 201, 517–527. [Google Scholar] [CrossRef]
- Fu, R.; Feng, Z.; Huang, X. Orientation distribution and deviation behaviors of dislocation loops in a quenched Al-Cu alloy. Acta Mater. 2024, 270, 119837. [Google Scholar] [CrossRef]
- Zhang, L.X.; Liu, L.; Guo, S.; Pan, Q.S.; Lu, L. Microstructure and evolution of gradient dislocation cells in multi-principal element alloy subjected to cyclic torsion. Acta Mater. 2024, 275, 120059. [Google Scholar] [CrossRef]
- Yu, H.; Dong, Q.; Yao, Z.; Daymond, M.R. Stacking faults observed in {101−2} extension twins in a compressed high Sn content Zr alloy. Scr. Mater. 2017, 141, 72–75. [Google Scholar] [CrossRef]
- Chen, Y.; Guo, T.; Pang, X.; Qiao, L. Formation of high-density stacking faults in ceramic films induced by Ti transition layer. Scr. Mater. 2022, 211, 114496. [Google Scholar] [CrossRef]
- Laird, C.; Eichen, E.; Bitler, W.R. Accuracy in the use of electron-diffraction spot patterns for determining crystal orientations. J. Appl. Phys. 1966, 37, 2225–2231. [Google Scholar] [CrossRef]
- Pumphrey, P.H.; Bowkett, K.M. An accurate method for determining crystallographic orientations by electron diffraction. Phys. Status Solidi A 1970, 2, 339–346. [Google Scholar] [CrossRef]
- Pumphrey, P.H.; Bowkett, K.M. On the resolution of the 180° uncertainty in indexing electron diffraction spot patterns. Phys. Status Solidi A 1971, 5, K155–K157. [Google Scholar] [CrossRef]
- Liu, Q. A simple method for determining orientation and misorientation of the cubic crystal specimen. J. Appl. Crystallogr. 1994, 27, 755–761. [Google Scholar] [CrossRef]
- Liu, Q. A simple and rapid method for determining orientations and misorientations of crystalline specimens in TEM. Ultramicroscopy 1995, 60, 81–89. [Google Scholar] [CrossRef]
- Zhang, Z.; Huang, J.; Guo, P.; Peng, J.; Wang, S.; Chen, C. A method for measuring the micro-texture information based on transmission electron microscopy. J. Mater. Res. Technol. 2020, 9, 6916–6921. [Google Scholar] [CrossRef]
- Zaefferer, S. New developments of computer-aided crystallographic analysis in transmission electron microscopy. J. Appl. Crystallogr. 2000, 33, 10–25. [Google Scholar] [CrossRef]
- Fundenberger, J.J.; Morawiec, A.; Bouzy, E.; Lecomte, J.S. System for creating orientation maps using TEM. Mater. Chem. Phys. 2003, 81, 535–537. [Google Scholar] [CrossRef]
- Wu, G.; Zaefferer, S. Advances in TEM orientation microscopy by combination of dark-field conical scanning and improved image matching. Ultramicroscopy 2009, 109, 1317–1325. [Google Scholar] [CrossRef] [PubMed]
- Liu, H.H.; Schmidt, S.; Poulsen, H.F.; Godfrey, A.; Liu, Z.Q.; Sharon, J.A.; Huang, X. Three-dimensional orientation mapping in the transmission electron microscope. Science 2011, 332, 833–834. [Google Scholar] [CrossRef]
- Rauch, E.F.; Véron, M. Automated crystal orientation and phase mapping in TEM. Mater. Charact. 2014, 98, 1–9. [Google Scholar] [CrossRef]
- Kobler, A.; Kübel, C. Challenges in quantitative crystallographic characterization of 3D thin films by ACOM-TEM. Ultramicroscopy 2017, 173, 84–94. [Google Scholar] [CrossRef]
- Baral, P.; Kashiwar, A.; Coulombier, M.; Delannay, L.; Hoummada, K.; Raskin, J.P.; Idrissi, H.; Pardoen, T. Grain boundary-mediated plasticity in aluminum films unraveled by a statistical approach combining nano-DIC and ACOM-TEM. Acta Mater. 2024, 276, 120081. [Google Scholar] [CrossRef]
- ASTM E9-19; Standard Test Methods of Compression Testing of Metallic Materials at Room Temperature. ASTM International: West Conshohocken, PA, USA, 2019.
- Lilensten, L.; Sun, F.; Hocini, A.; Dirras, G.; Vermaut, P.; Prima, F. {332} <113> mechanical detwinning as a deformation mechanism in the β-metastable Ti-15Mo alloy during cyclic loading. Scr. Mater. 2023, 232, 115503. [Google Scholar]
- Zhang, F.; Xu, S.; Pan, S.; Qian, F.; Fan, Q.; Cheng, X. Subsequent growth and sequential twinning induced by the interaction of {332} twins in Ti15Mo alloy. Mater. Charact. 2024, 208, 113621. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, X.; Xin, R.; Xin, S.; Liu, Q. Understanding cross boundary {332} <113> twins in a Ti-15Mo alloy by composite Schmid factor. Mater. Charact. 2022, 193, 112310. [Google Scholar] [CrossRef]
- Ren, L.; Xiao, W.; Ma, C.; Zheng, R.; Zhou, L. Development of a high strength and high ductility near β-Ti alloy with twinning induced plasticity effect. Scr. Mater. 2018, 156, 47–50. [Google Scholar] [CrossRef]
- Tian, Y.; Zhang, L.; Wu, D.; Xue, R.; Deng, Z.; Zhang, T.; Liu, L. Achieving stable ultra-low elastic modulus in near-β titanium alloys through cold rolling and pre-strain. Acta Mater. 2025, 286, 120726. [Google Scholar] [CrossRef]

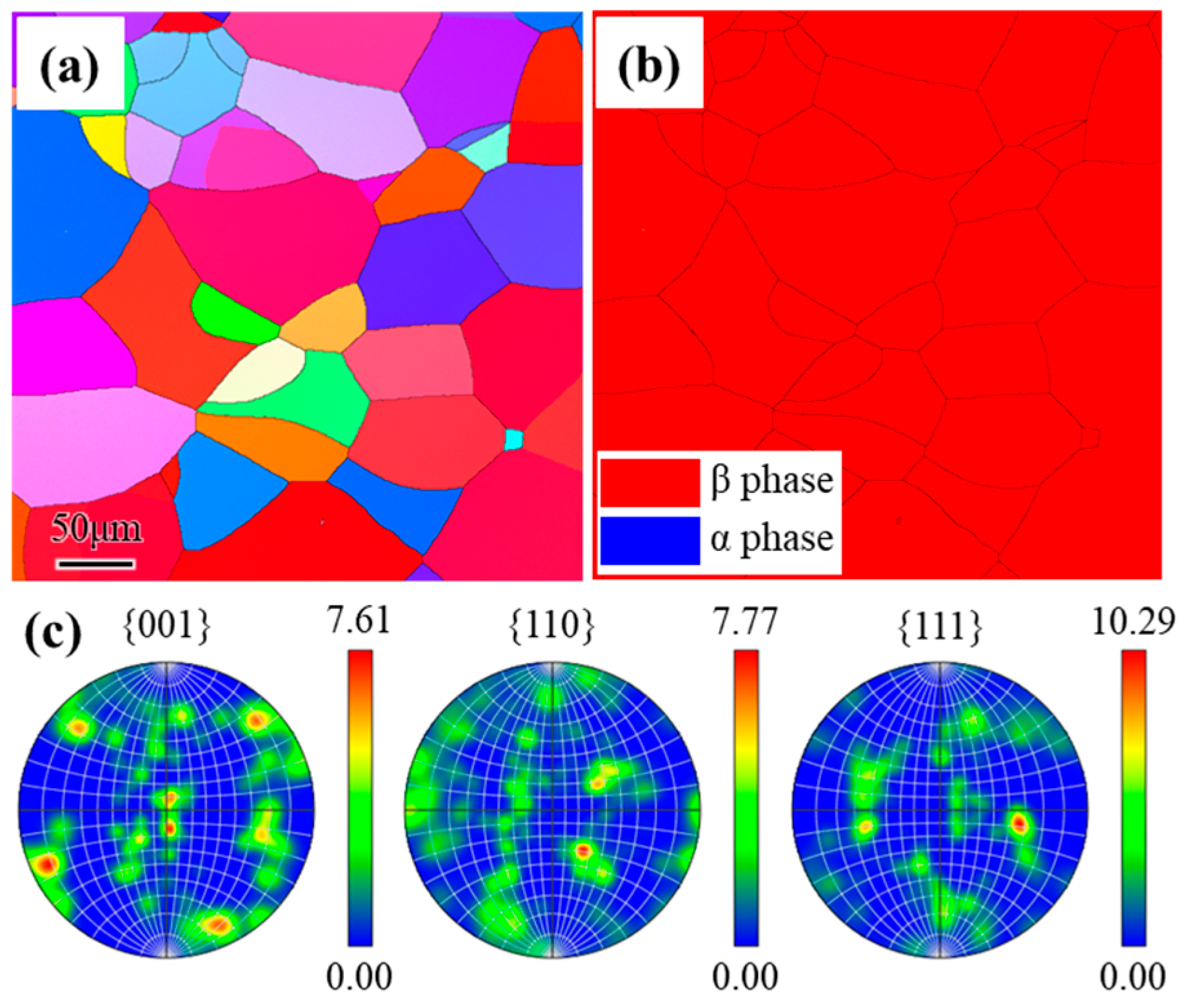
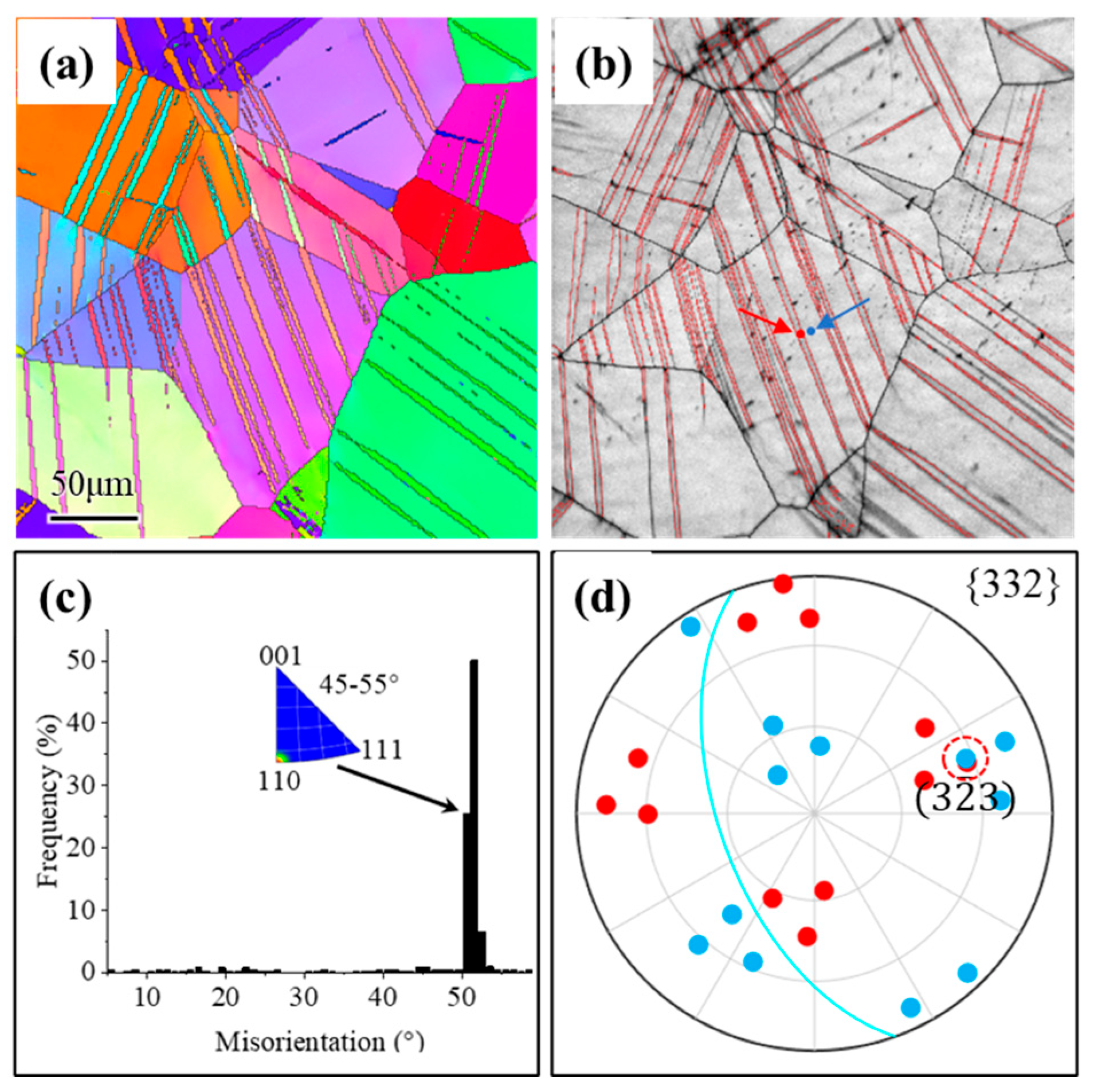
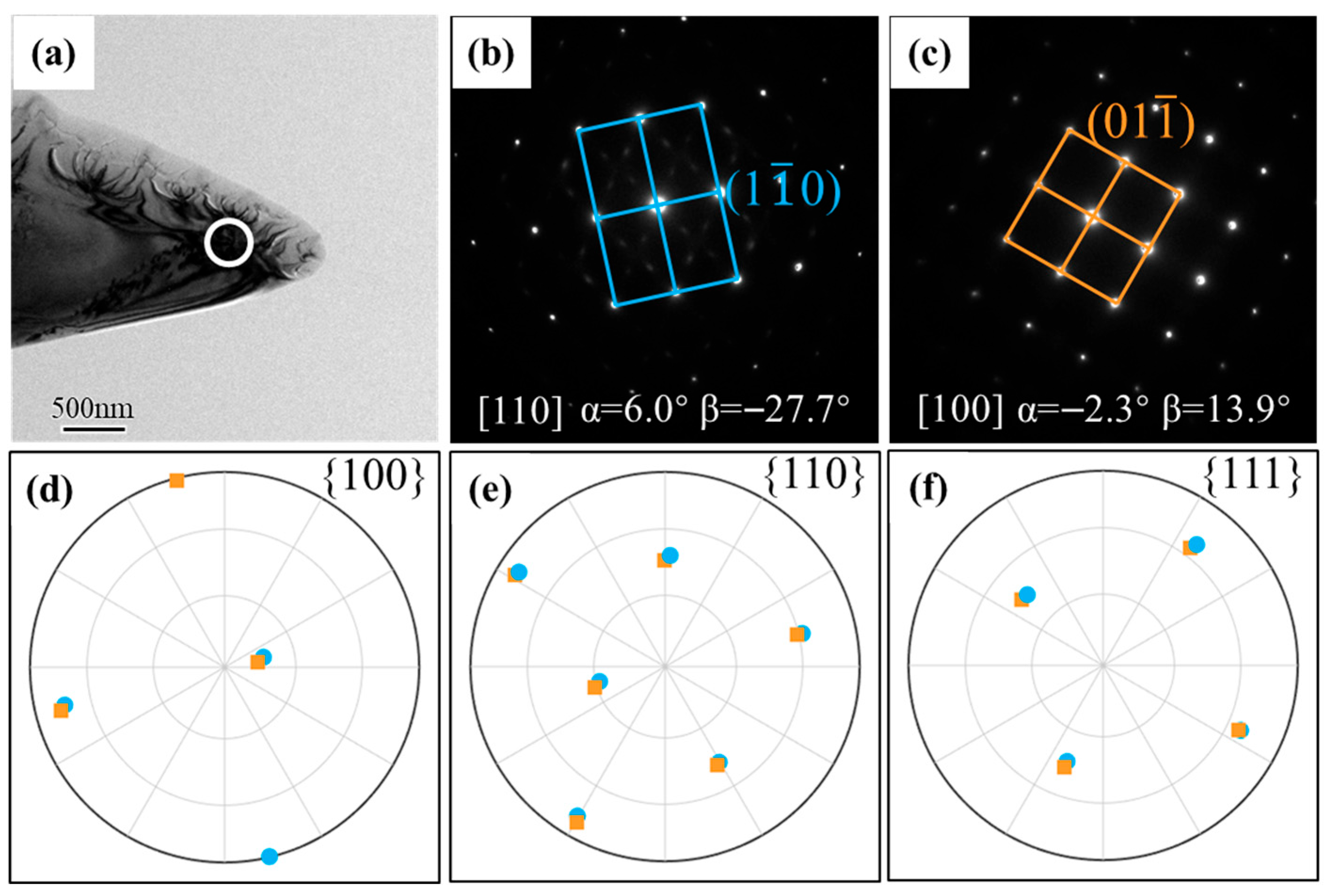

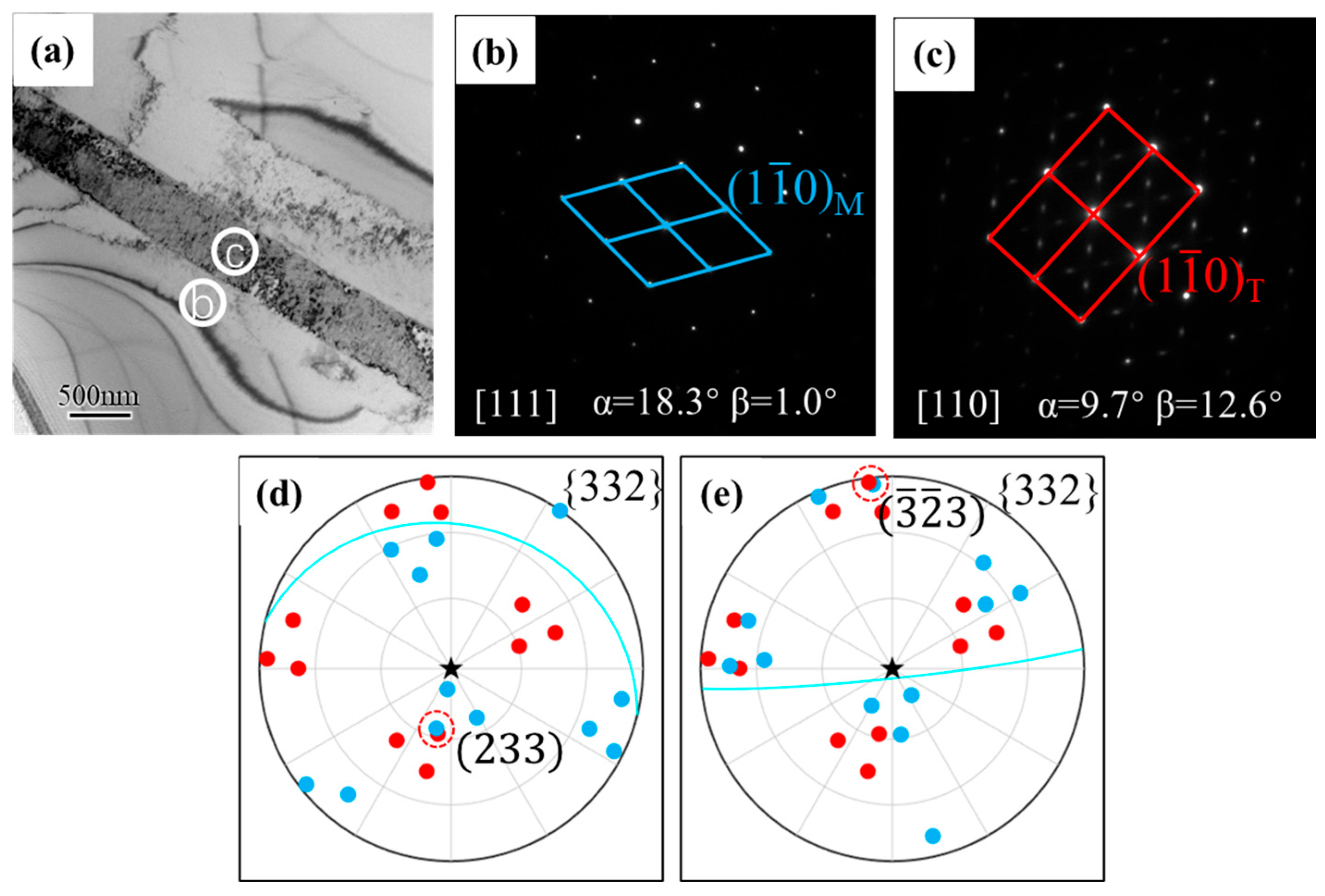

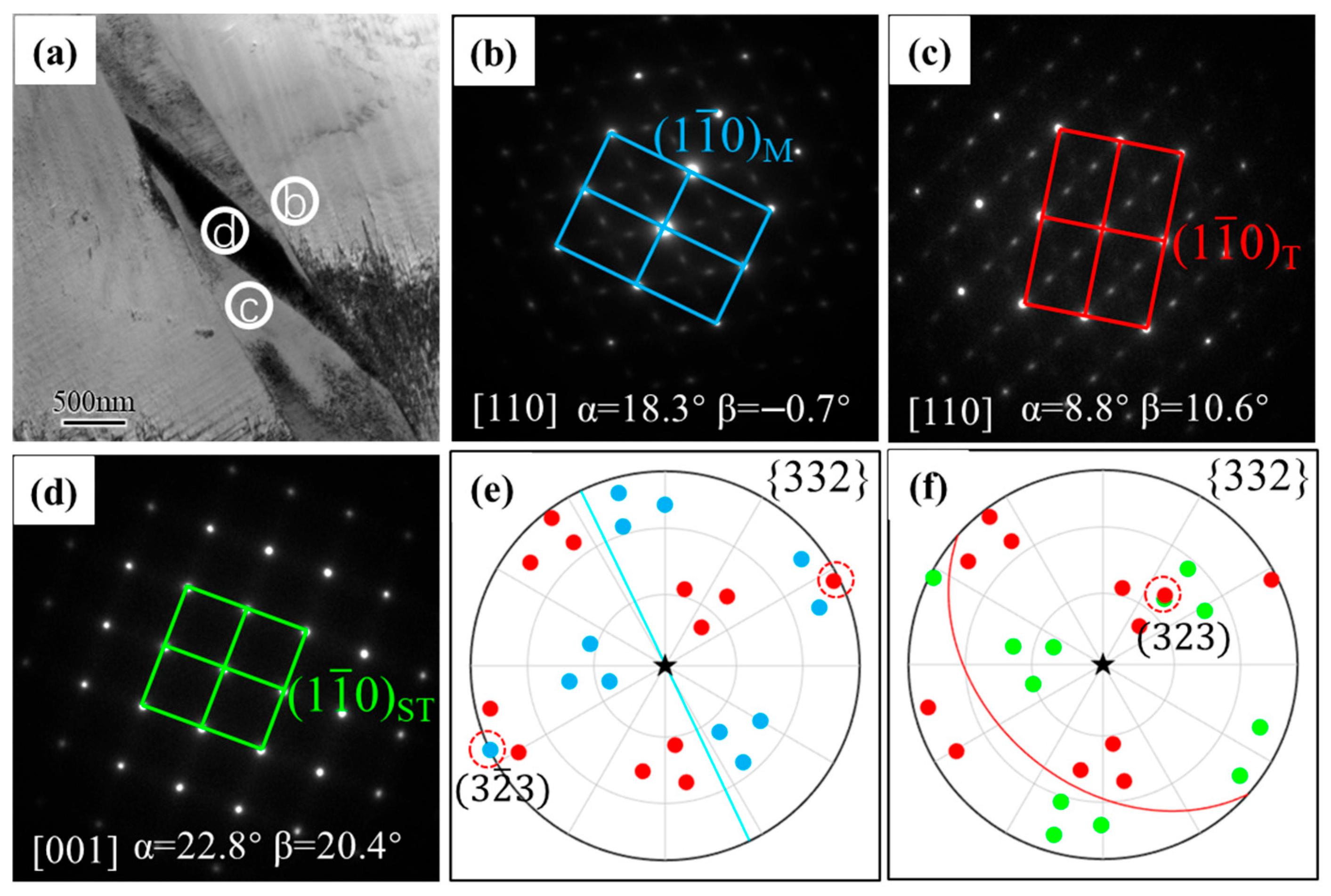
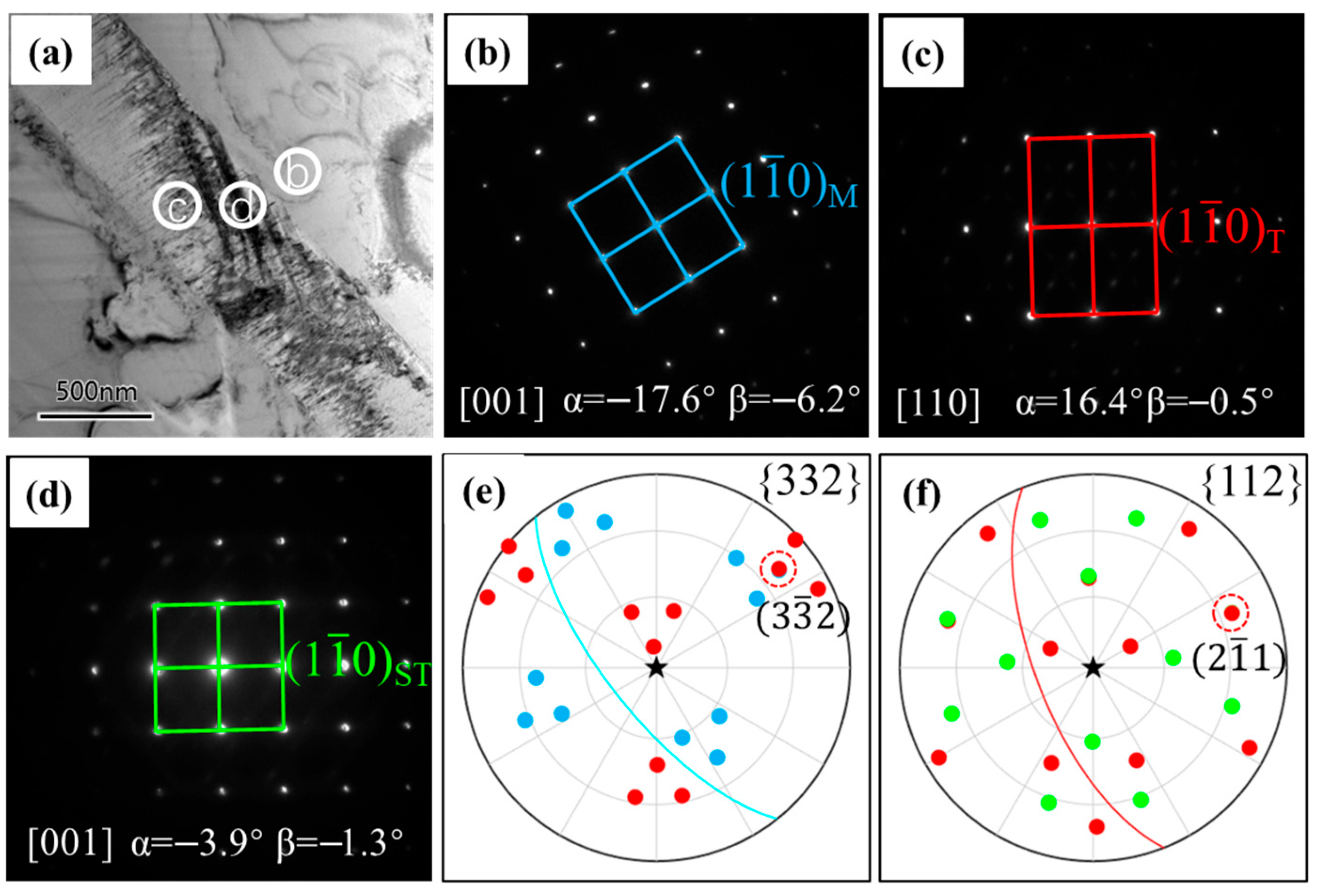
| Twin Variants | Twinning Systems | SF | Twin Variants | Twinning Systems | SF |
|---|---|---|---|---|---|
| V1 | −0.02 | V7 | −0.41 | ||
| V2 | 0.32 | V8 | 0.06 | ||
| V3 | 0.30 | V9 | −0.11 | ||
| V4 | 0.49 | V10 | −0.09 | ||
| V5 | −0.12 | V11 | −0.42 | ||
| V6 | −0.06 | V12 | 0.05 |
| Twin Variants | Twinning Systems | SF | Twin Variants | Twinning Systems | SF |
|---|---|---|---|---|---|
| V1 | −0.14 | V7 | 0.00 | ||
| V2 | 0.04 | V8 | −0.33 | ||
| V3 | 0.02 | V9 | 0.33 | ||
| V4 | −0.50 | V10 | 0.29 | ||
| V5 | 0.24 | V11 | 0.07 | ||
| V6 | 0.24 | V12 | −0.26 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Xin, R.; Wen, X.; Wang, J. A Method for Determining Twins and Corresponding Schmid Factors Based on Electron Diffraction. Metals 2025, 15, 920. https://doi.org/10.3390/met15080920
Li Z, Xin R, Wen X, Wang J. A Method for Determining Twins and Corresponding Schmid Factors Based on Electron Diffraction. Metals. 2025; 15(8):920. https://doi.org/10.3390/met15080920
Chicago/Turabian StyleLi, Zhirui, Renlong Xin, Xin Wen, and Jian Wang. 2025. "A Method for Determining Twins and Corresponding Schmid Factors Based on Electron Diffraction" Metals 15, no. 8: 920. https://doi.org/10.3390/met15080920
APA StyleLi, Z., Xin, R., Wen, X., & Wang, J. (2025). A Method for Determining Twins and Corresponding Schmid Factors Based on Electron Diffraction. Metals, 15(8), 920. https://doi.org/10.3390/met15080920







