Understanding Room-Temperature Ductility of Bcc Refractory Alloys from Their Atomistic-Level Features

Abstract

Many bcc refractory alloys show excellent high-temperature mechanical properties, while their fabricability can be limited by brittleness near room temperature. For the purpose of predicting ductile alloys, a number of ductility metrics based on atomic structures and crystal properties, ranging from mechanistic to empirical, have been proposed. In this work, we propose an “average bond stiffness” as a new ductility metric that is also convenient to obtain from first-principles calculations, in addition to using the average magnitude of static displacements of atoms. The usefulness of average bond stiffness is validated by comparing first-principles calculation results to experimental data on the “rhenium effect” in Mo/W-base and V/Nb/Ta-base binary alloys. The average bond stiffness also correlates well with the room-temperature ductility of refractory high-entropy alloys, with a better performance than some ductility metrics previously reported. While in reality the ductility of an alloy can be influenced by many factors, from processing and microstructure, the average magnitude of static displacements and the average bond stiffness are atomistic-level features useful for design of alloy composition towards a desired level of ductility.

1. Introduction

Body-centered cubic (bcc) refractory alloys, especially high-entropy alloys (HEAs), receive significant research attention for their high-temperature load-bearing capabilities [1,2]. However, an outstanding problem for almost all bcc alloys is their low-temperature brittleness. As temperature decreases, the ductility of bcc alloys can drop abruptly, exhibiting the so-called ductile–brittle transition (DBT) phenomenon [3]. Low-temperature brittleness limits fabricability near room temperature and reduces defect tolerance when the material is in use near or below room temperature. For practical reasons, it is desirable to let the alloy maintain some room-temperature ductility, or let the ductile–brittle transition temperature (DBTT) be sufficiently low [4,5].

However, ductility itself is a quantity involving complex microstructural processes, making it difficult to mechanistically model or predict ductility. There are various methods of measuring ductility, including elongation or reduction in area under uniaxial tension, strain at fracture under uniaxial compression, angle or radius of curvature under bending conditions, etc. [6]. It is difficult to compare or convert results obtained using different methods. For a ductile metallic material, plastic deformation occurs first, and then damage accumulates typically in the form of nucleation, growth, and coalescence of microvoids [7]. Currently, there are already micromechanical models that enable simulations of the processes to reflect deformation and damage until fracture [8], which makes it possible to determine the ductility of the material measured in different types of tests. However, this kind of model usually requires a large number of material parameters, which, in most cases, are determined by fitting to known mechanical behaviors of the material. It means this approach, though mechanistic, is less predictive but more explanatory in linking alloy composition to ductility.

Due to the formidable complexity of the microprocesses behind ductility, researchers have been trying to devise “ductility metrics” for bcc metals and alloys, based on properties that are convenient to calculate or measure. Some commonly used metrics include the valence-electron concentration (VEC), Pugh’s ratio (ratio of shear modulus to bulk modulus), local lattice distortion (“LLD”), and the D parameter [9,10,11]. In some publications, electronic structure [12,13] and enthalpy of mixing [14] are also considered to correlate with ductility. Machine learning models are also implemented to predict ductility [5,15]. Among the aforementioned metrics, except for the D parameter, all the other ductility metrics are based on perfect-crystal properties of pure elements or alloys. Usually, perfect-crystal properties are less costly to compute but also mechanistically less relevant to ductility, due to a lack of consideration of crystal defects (dislocations or microvoids) essential to fracture and ductility. It is of practical interest to exploit the usefulness of perfect-crystal properties with some more physical significance, for the purpose of understanding or even predicting ductility, while maintaining a relatively low computational cost.

In this work, we present our findings on how to relate atomistic features of perfect-crystal solid-solution alloys to ductility. The basic idea is to examine not only the lattice distortion but also a kind of “average bond stiffness” relevant to the energetics associated with the lattice distortion. We then validate our approach using some experimental ductility data of refractory bcc alloys, including some binary alloys and equiatomic high-entropy alloys (HEA). A significant role of bond stiffness in determining ductility is revealed and discussed.

2. Methods

For a good representation of disordered, random bcc solid solutions using supercells, we use a Monte Carlo code “spcm” to generate bcc supercells where atomic configurations are randomized. The generated supercells used in this work include 4 × 4 × 4 bcc unit cells (128 atoms) for binary alloys and quaternary equiatomic HEAs, and 5 × 5 × 5 bcc primitive cells (125 atoms) for quinary equiatomic HEAs. For binary alloys A_1−cB_c, 128-atom supercells with compositions c = 0.0625, 0.125, 0.25, 0.375, 0.5 (atomic fraction) are generated. The generated atomic configurations exhibit Warren–Cowley short-range order parameters being zero or close to zero within the first eight coordinate shells.

To investigate atomic structures and energetics of the alloys, we use the software VASP (Vienna Ab initio Simulation Package, version 6.4.2) [16,17] for density-functional theory (DFT) [18] calculations. Projector-augmented wave (PAW) potentials [19,20] and PBEsol exchange-correlation [21] are adopted. The plane-wave cutoff energy is set to 500 eV. The k-mesh used for all supercells is a 4 × 4 × 4 Monkhorst–Pack [22]-type mesh. Smearing of partial occupancies is the Methfessel–Paxton type [23] with a width of 0.2 eV. To obtain equilibrium atomic structures and energy, atomic coordinates are relaxed until all force components are below 0.01 eV/Å in magnitude. The relaxations are performed without altering the overall shapes of the supercells.

We compare the atomic positions and total energies before and after relaxation. From the atomic positions in the relaxed, equilibrium configuration and the ideal bcc configuration, we extract the average magnitude of static displacements $\overline{\Delta r}$:

$$\overline{\Delta r}={\displaystyle \frac{1}{N}}\sum _{i=1}^N\sqrt{{\left(x_{i,eq}-x_{i,0}\right)}^2+{\left(y_{i,eq}-y_{i,0}\right)}^2+{\left(z_{i,eq}-z_{i,0}\right)}^2}$$

(1)

where $N$ is the number of atoms in the supercell, $\left(x_{i,eq},y_{i,eq},z_{i,eq}\right)$ and $\left(x_{i,0},y_{i,0},z_{i,0}\right)$ are, respectively, Cartesian coordinates of the relaxed (equilibrium) position and the unrelaxed bcc lattice position of atom $i$. The average magnitude of static displacements is also called “local lattice distortion” (LLD) by some researchers [24]. We also extract an “average bond stiffness” $\overline{k}$ defined as

$$\begin{array}{c}\overline{k}={\displaystyle \frac{2\left(E_{bcc}-E_{rel}\right)}{N\overline{\Delta r^2}}}\\ \overline{\Delta r^2}={\displaystyle \frac{1}{N}}{\displaystyle \sum _{i=1}^N}\left[{\left(x_{i,eq}-x_{i,0}\right)}^2+{\left(y_{i,eq}-y_{i,0}\right)}^2+{\left(z_{i,eq}-z_{i,0}\right)}^2\right]\end{array}$$

(2)

where $E_{bcc}$ and $E_{rel}$ are, respectively, the supercell total energies before and after relaxation. The average bond stiffness can be regarded as an effective stiffness for a hypothetical process of restoring the ideal bcc structure from the equilibrium configuration. $\overline{\Delta r}$ and $\overline{k}$ are computationally convenient to obtain, because a common procedure to obtain the equilibrium configuration is to relax the atoms from ideal lattice positions.

The roles of $\overline{\Delta r}$ and $\overline{k}$ in affecting alloy ductility can be rationalized as follows: Presumably, the perfect bcc structure has the highest symmetry and the lowest resistance to dislocation motion. If other conditions are kept constant, then larger static displacements (large $\overline{\Delta r}$) are expected to create higher resistance against dislocation motion. However, LLD only contains information about atomic positions, without having any information on force or energy. This is supplemented by the average bond stiffness $\overline{k}$. If interatomic bonds are stiff (high $\overline{k}$), then the energy cost to restore the perfect bcc structure from the relaxed, equilibrium configuration is expected to be high, which is unfavorable for dislocation mobility.

The reasoning can be summarized as two rules:

• Rule 1: Under constant $\overline{k}$, the alloy with lower $\overline{\Delta r}$ should exhibit higher ductility;
• Rule 2: Under constant $\overline{\Delta r}$, the alloy with lower $\overline{k}$ should exhibit higher ductility.

In Section 3, we use some refractory binary alloys and HEAs to showcase the usefulness of $\overline{\Delta r}$ and $\overline{k}$ in analyzing room-temperature ductility.

3. Results

Using the first-principles methods, we have calculated the atomic displacements and the associated total-energy change before and after relaxation, for binary alloys and HEAs. $\overline{\Delta r}$ and $\overline{k}$ are extracted and used to analyze the effects of alloying elements on ductility in some alloy systems.

3.1. The “Rhenium Effect”

It is well known that alloying Re in Mo or W enhances room-temperature ductility and lowers DBTT [6]. The unique ductility-enhancing effect of Re is named “the rhenium effect”. However, the rhenium effect is not universal: it is effective in Group VIB elements (Cr, Mo, W), but not in Group VB elements (V, Nb, Ta) [6,25]. By calculating $\overline{\Delta r}$ and $\overline{k}$ of Re-containing alloys using DFT, and then comparing the results from the V/Nb/Ta–Re systems and the Mo/W–Re systems (Figure 1), the selectiveness of the “rhenium effect” can be rationalized by the distinct behaviors of how Re affects the alloy bond stiffness $\overline{k}$: while Re can significantly reduce bond stiffness in Mo–Re and W–Re alloys, it does the opposite in V–Re, Nb–Re, and Ta–Re alloys, raising the average bond stiffness $\overline{k}$. The effect of Re on $\overline{\Delta r}$ is relatively weak, but a low-level $\overline{\Delta r}$ is maintained, which is a favorable feature for ductility.

For example, Buckman [25] has reported (citing Begley [26]) how alloying elements in Nb-alloys raise DBTT. Their efficiency in raising DBTT is ranked as Re > W > Mo > Zr > Ti. The rank in $\overline{k}$ from DFT calculations almost coincides with the rank in the experimentally measured efficiency in raising DBTT (Re > W > Mo > (Zr, Ti)). Re, W, and Mo raise the average bond stiffness $\overline{k}$, while Zr and Ti lower it. The $\overline{k}\mathrm{s}$ for Zr and Ti are very close, so then the $\overline{\Delta r}$ criterion (Rule 1) can be invoked to explain the experimental result that Ti is less embrittling, for Ti causes smaller $\overline{\Delta r}$ than Zr. The results for Nb-alloys are shown in Figure 2.

The analysis of experimental and DFT results shows that the rhenium effect can be regarded as a bond-stiffness effect to a large extent: In Mo and W, Re addition softens the bonds and promotes ductility, whereas in Nb, Re addition stiffens the bonds and reduces ductility. The role of $\overline{k}$ appears to be dominant over that of $\overline{\Delta r}$ in affecting alloy ductility.

3.2. Bcc Refractory HEAs

Bcc refractory HEAs attract significant research interest, one of the reasons being that they can exhibit high-temperature strength superior to the mainstream superalloys. However, usually, an outstanding problem is the insufficient room-temperature ductility or high DBTT. As discussed in the Introduction, researchers have developed and tested various kinds of “ductility metrics” (for example, [10,27,28]), and attempted to use them to guide alloy design in the vast space of chemical composition of HEAs. Singh et al. [9] compiled ductility data of 56 HEAs, and examined four ductility metrics in terms of the goodness of linear fitting to compression fracture strain (${\epsilon }_f$). Here, we also use the calculated $\overline{k}$ from the DFT and available experimental fracture strain data to analyze the usefulness of $\overline{k}$ being a ductility metric for RHEA.

Using the DFT, we have calculated $\overline{\Delta r}$ and $\overline{k}$ for 21 equiatomic HEAs whose data on compression fracture strain ${\epsilon }_f$ have been reported in the literature, as tabulated in

Table 1. Ductility of HEAs (in compressive fracture strain) from the literature, and their $\overline{k}$ and $\overline{\Delta r}$ from DFT. All alloys appear in Figure 3 while only those with an asterisk (*) appear in Figure 4.

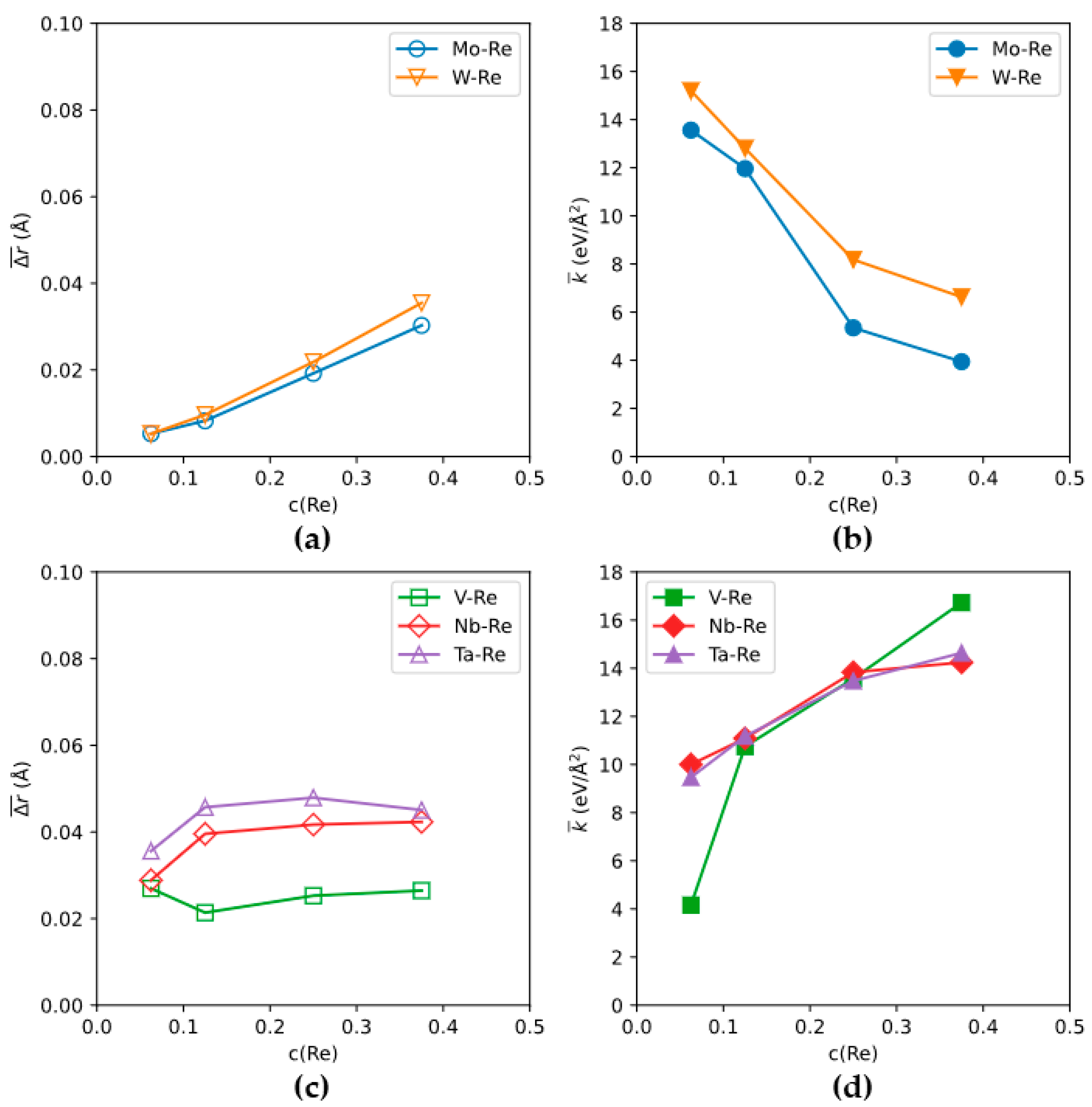
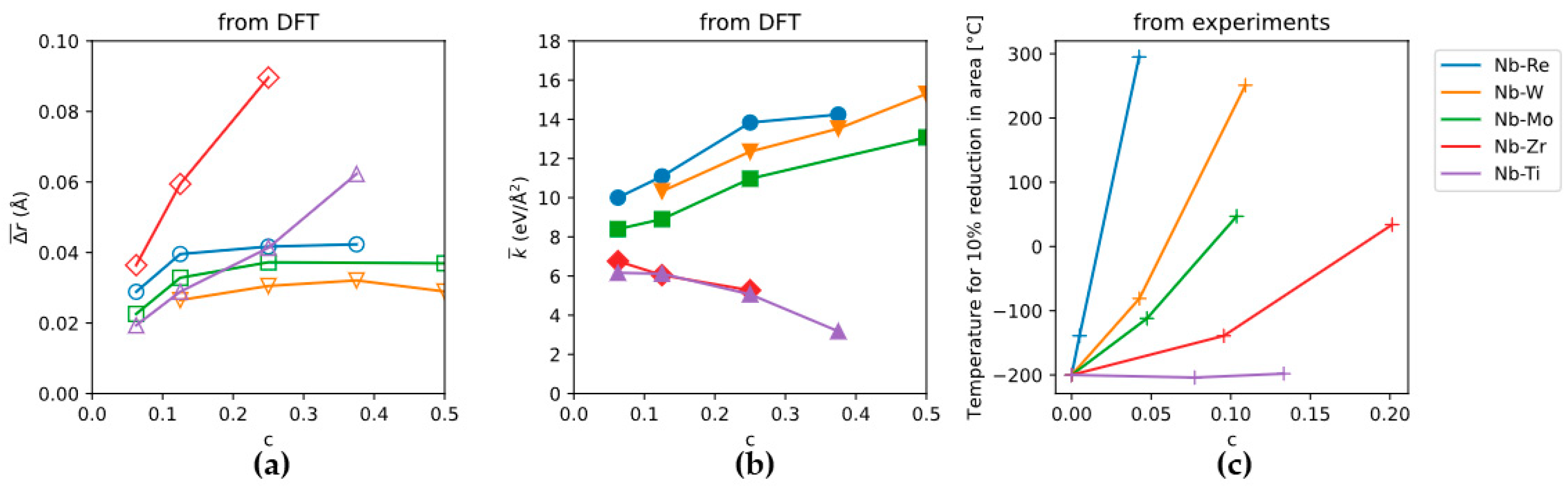
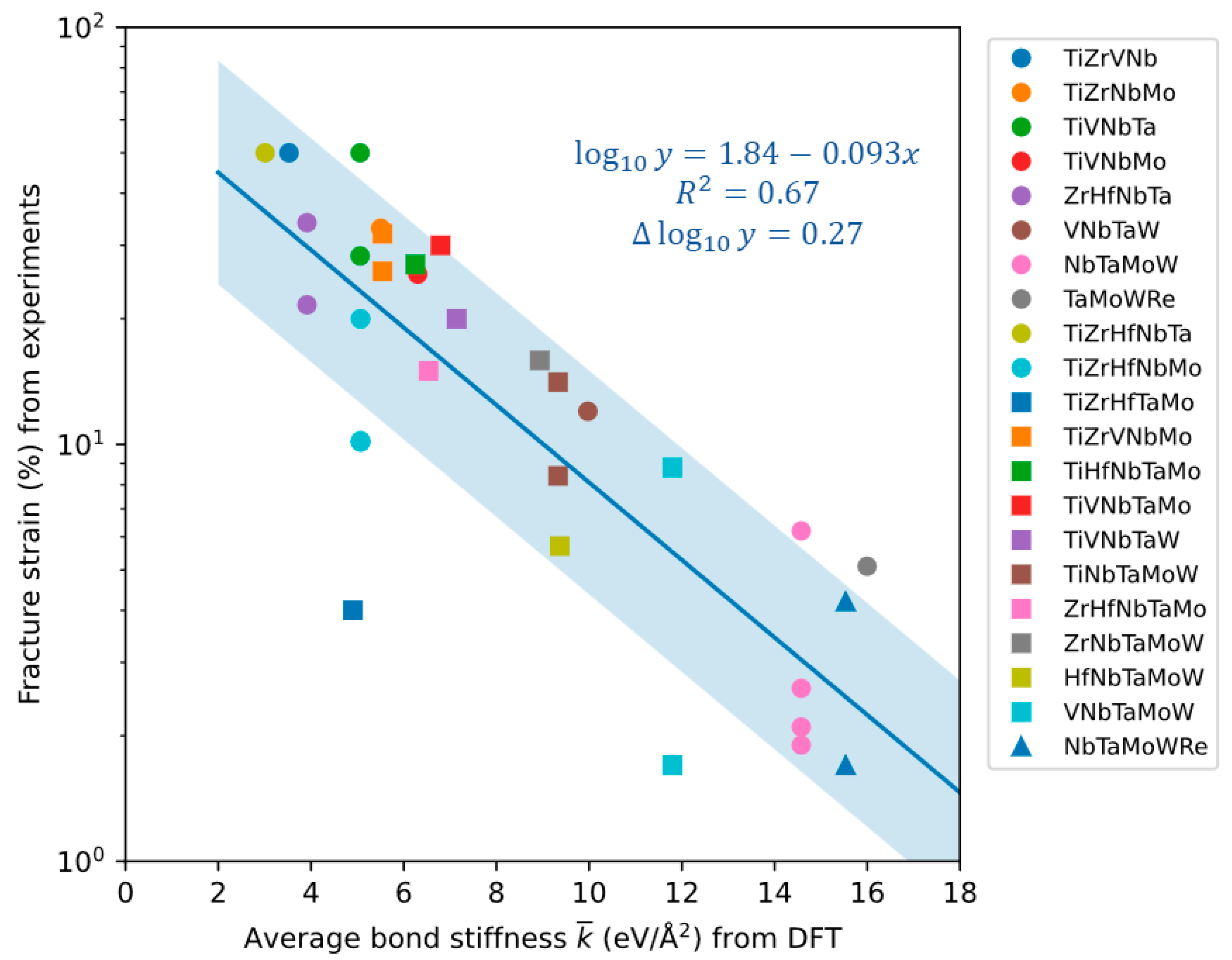
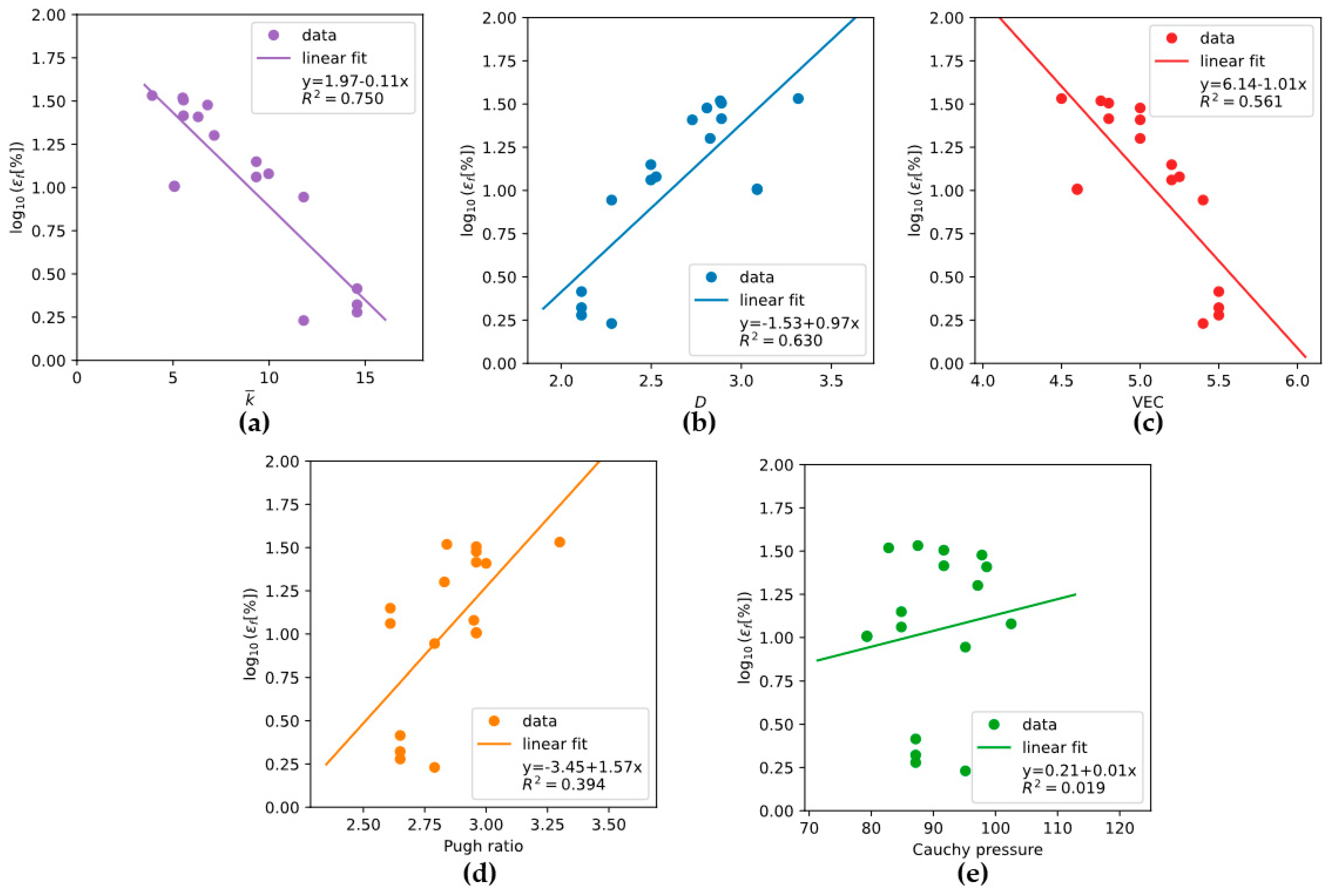
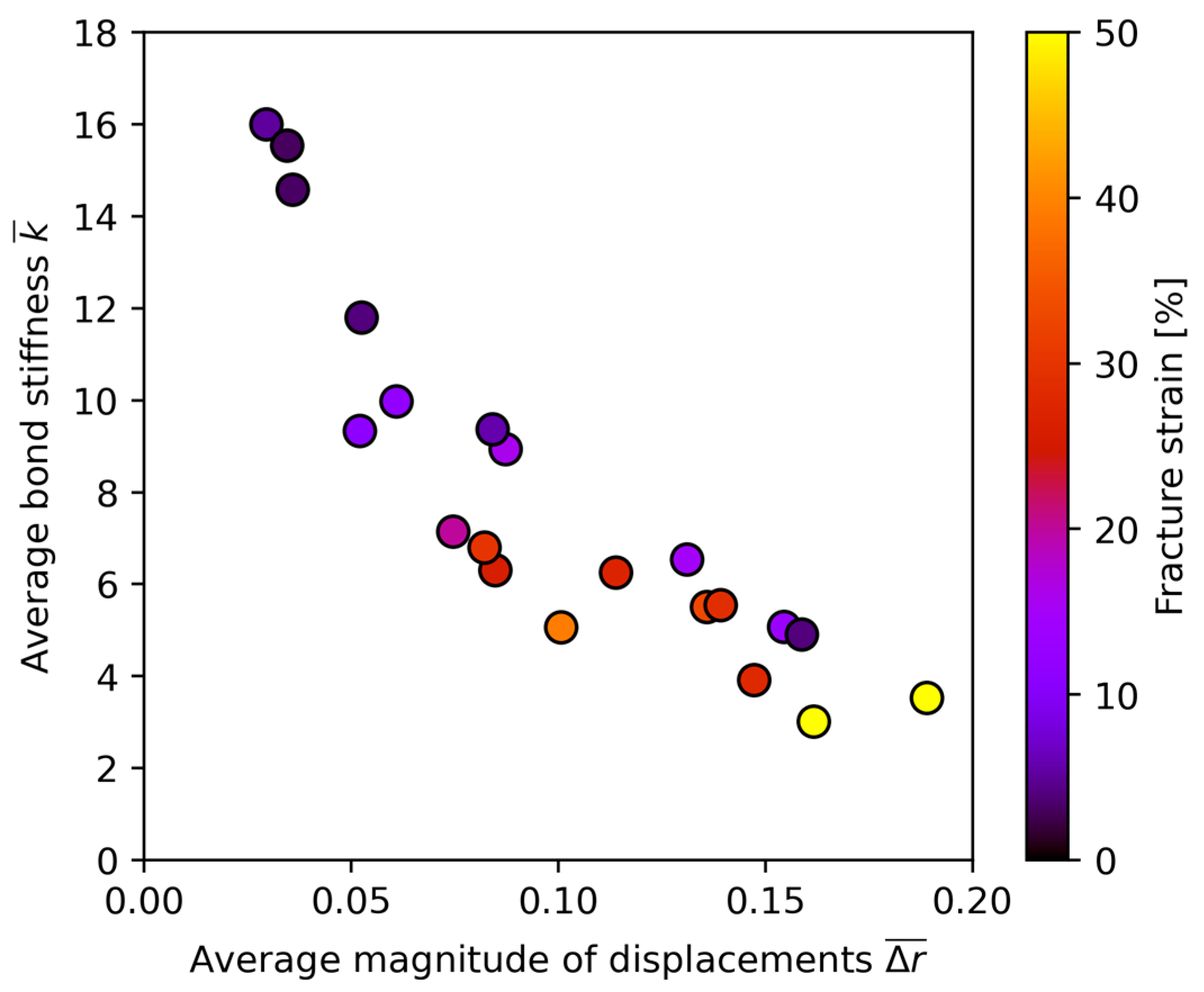
Alloy	${\mathit{\epsilon }}_{\mathit{f}}$ (%) Experimental	$\overline{\mathit{k}}$ (eV/Å2) from DFT	$\overline{\Delta \mathit{r}}$ (Å) from DFT
TiZrVNb	>50 [29], 50 [30]	3.53	0.189
TiZrNbMo *	33 [31]	5.50	0.136
TiVNbTa	>50 [32], 28.3 [33]	5.06	0.101
TiVNbMo *	25.6 [34]	6.30	0.085
ZrHfNbTa *	34 [35]	3.91	0.147
VNbTaW *	12 [32]	9.97	0.061
NbTaMoW *	2.1 [36], 2.6 [37], 1.9 [38], 6.2 [39]	14.58	0.036
TaMoWRe	5.1 [40]	16.00	0.029
TiZrHfNbTa	>50 [41,42]	3.01	0.162
TiZrHfNbMo *	10.12 [43], 10.2 [44], 20 [45]	5.07	0.155
TiZrHfTaMo	4 [45]	4.91	0.159
TiZrVNbMo *	26 [31], 32 [30]	5.54	0.139
TiHfNbTaMo	27 [45]	6.25	0.114
TiVNbTaMo *	30 [46]	6.80	0.082
TiVNbTaW *	20 [32], 14.1 [37]	7.14	0.075
TiNbTaMoW *	8.4 [38]	9.33	0.052
ZrHfNbTaMo	15 [45]	6.54	0.131
ZrNbTaMoW	15.9 [45]	8.93	0.087
HfNbTaMoW	5.7 [47]	9.37	0.084
VNbTaMoW *	1.7 [36], 8.8 [37], 1.7 [47]	11.80	0.052
NbTaMoWRe	4.2 [39], 1.7 [48]	15.53	0.035

and plotted in Figure 3. Figure 3 shows a generally clear linear relationship between ${\log }_{10}{\epsilon }_f$ and $\overline{k}$, apart from a few outliers. Linear fitting to ${\log }_{10}{\epsilon }_f$ instead of ${\epsilon }_f$ can also avoid the possibility of predicting negative ${\epsilon }_f$.

To compare $\overline{k}$ with other ductility metrics, we use the data of 11 equiatomic HEAs (marked with an asterisk in Table 1), of which ${\log }_{10}{\epsilon }_f$, $\overline{k}$, valence-electron concentration (VEC), Cauchy pressure, Pugh’s ratio, and the D parameter are all available. Linear regression results (Figure 4) show that $\overline{k}$ fits to ${\log }_{10}{\epsilon }_f$ better (in terms of $R^2$) than the other four metrics.

For the 21 HEAs, the $\overline{\Delta r}-\overline{k}$ correlation is shown in Figure 5. Generally, $\overline{k}$ and $\overline{\Delta r}$ data tend to cluster in a band showing a genuine trade-off between the two variables. However, as we have shown, for ductility, the average bond stiffness $\overline{k}$ plays a more dominant role than $\overline{\Delta r}$, which is clear from Figure 5 also.

4. Discussion

This work is unique in proposing an “average bond stiffness” that is convenient to obtain and relevant to the structures of solid solutions. The average bond stiffness in this work is representative of the whole supercell of solid solution, and is simple because it requires only atomic relaxation calculations with no extra calculations needed. Pant and Aidhy [24] have also proposed a “bond stiffness” and correlated it to a number of other alloy properties. The “average bond stiffness” we propose is different from theirs, in that ours requires only the total-energy difference in the supercell and static displacements of individual atoms, without the need to make assumptions and approximations for modes of atomic displacements or number of nearest neighbors, etc.

It is obvious that in this work we do not consider numerous other factors that affect alloy ductility: impurity level, degrees of deformation and recrystallization, grain size, inhomogeneity (due to nonequilibrium solidification or phase separation), etc. In fact, the data we have adopted to support the analysis are not always strictly comparable, because the alloys are often different in terms of the factors listed above. Presumably, this is part of the reason for the scatter in Figure 3 and Figure 4. It may be possible in the future to make the ductility model more comprehensive, and not only based on the average bond stiffness.

Also, in this work, due to limitations on supercell size and randomness, we restricted the calculations and analysis to a few special compositions for binary alloys and equiatomic compositions of HEAs. Extension to general compositions will presumably require theoretical advances in better understanding the structure and energetics of solid solutions, including interstitial solutions [49]. The DFT results are invariably affected by the qualities of pseudopotentials and the exchange-correlation potential. Their influences on the atomic displacements and bond stiffness used in this work will require further investigation in order to remove any significant computational artifacts.

5. Conclusions

In this work, we analyze the ductility of bcc refractory alloys from atomistic-level features, namely, the average magnitude of static displacement $\overline{\Delta r}$ and a newly proposed “average bond stiffness” $\overline{k}$. The motivation is to extract parameters useful for ductility, while keeping the low computing cost of first-principles calculations of defect-free crystal structures. From the perspective of solid solution structure and energetics, we hypothesize that decreasing $\overline{\Delta r}$ and decreasing $\overline{k}$ can be favorable for improving ductility.

For bcc Re-containing binary alloys, we show that the “rhenium effect” (Re enhancing the ductility of Mo or W) can be understood as essentially a bond stiffness effect. In Mo/W–Re alloys, adding Re within its solubility limit reduces $\overline{k}$ significantly. On the contrary, in V/Nb/Ta–Re alloys, adding Re significantly raises $\overline{k}$. The results of the two cases are consistent with the experimental findings that Re enhances the ductility of Mo or W, but embrittles V, Nb, and Ta. In both cases, $\overline{\Delta r}$ is kept to a relatively low level. The rank of embrittling efficiency of Re, W, Mo, Zr, and Ti in Nb-base binary alloys can also be explained by the $\overline{k}$ (primarily) and $\overline{\Delta r}$ from DFT calculations.

For bcc refractory HEAs, we also show that $\overline{k}$ is a useful ductility metric. Using the experimental data of compressive fracture strain from 21 equiatomic HEAs, we show that the logarithm of fracture strain follows a linear relationship to $\overline{k}$ reasonably well. Data support the conclusion that $\overline{k}$ works better than other ductility metrics (the D parameter, Pugh ratio, Cauchy pressure, valence electron concentration) in terms of the goodness of a linear fitting to the logarithm of fracture strain.

In summary, our findings reveal the significance of the “average bond stiffness”, together with the average magnitude of static displacements, in understanding the ductility of bcc refractory alloys. In spite of many other factors, from the processing and microstructure that influence ductility, our work provides a new “ductility metric” that is convenient and useful. More work in the future is required to generalize $\overline{\Delta r}$ and $\overline{k}$ for more complex compositions, beyond the special compositions considered in this work.