Abstract
The structural, elastic, electronic, magnetic, and half-metallic properties of full-Heusler LiSi and LiGe compounds were investigated using first-principles calculations. Among the studied configurations, the cubic XA structures in the ferromagnetic state for both compounds are the most stable. They exhibit mechanical stability, elastic anisotropy, and ductility. Compared to LiGe, LiSi demonstrates higher stability, stronger anisotropy, greater brittleness, higher Debye and melting temperatures, and a smaller Grüneisen parameter. Both compounds exhibit metallic majority-spin channels and semiconducting minority-spin channels. At the equilibrium lattice constant, LiSi and LiGe exhibit half-metallic gaps of 0.141 eV and 0.179 eV, respectively. Both compounds exhibit 100% spin-polarization ratio in specific lattice constant ranges. The total magnetic moment per formula unit (3.000 ) follows the generalized Slater–Pauling rule and depends on Fe atomic magnetic moments. These properties indicate that LiSi and LiGe hold promise for spintronic applications.
1. Introduction
Half-metallic materials possess a distinctive electronic structure characterized by one spin channel being metallic and the other semiconducting, resulting in an energy gap. This configuration enables these materials to achieve complete spin polarization at the Fermi level (), rendering them highly appealing for spintronic applications [1]. The half-metallic ferromagnetic properties of NiMnSb and PtMnSb were first identified by de Groot et al. through first-principles electronic structure calculations [2]. Since then, a variety of materials, including Heusler compounds [3,4,5], oxides [6,7,8], pnictides [9,10], and chalcogenides [11,12], have been discovered to exhibit half-metallic characteristics. Among these, Heusler compounds stand out for their high Curie temperatures and structural resemblance to widely utilized binary semiconductors with a zinc-blende crystal structure, making them particularly valuable for technological applications [1].
Full-Heusler compounds are a category of ternary intermetallic compounds characterized by the formula YZ, where X and Y are transition metals and Z is a main group element [1]. The crystalline structure of these compounds depends on the relative valences of X and Y. Specifically, when X exhibits a higher valence than Y, the compounds adopt the L structure, which is associated with the space group Fmm, with MnAl serving as the prototype. In this configuration, X, Y, and Z occupy the Wyckoff positions 8c (1/4, 1/4, 1/4), 4a (0, 0, 0), and 4b (1/2, 1/2, 1/2), respectively [1]. On the other hand, when Y has a higher valence than X, the compounds form the XA structure, corresponding to the space group F3M, with CuTi as the prototype. Within this structure, X atoms occupy the distinct positions 4a (0, 0, 0) and 4c (1/4, 1/4, 1/4), while Y and Z are situated at 4b (1/2, 1/2, 1/2) and 4d (3/4, 3/4, 3/4), respectively [1].
-based Heusler compounds represent a significant family of Heusler materials, with their half-metallic properties thoroughly examined through computational studies. Notable instances include MnZ (Z = Si, Ge, and Sn) [13], NiZ (Z = Al, Ga, Si, Ge) [14], CoAl [15], XY (X = V, Nb; Y = Al, Ga) [16], CrSb [17], YAl (Y = Cr, Mo, and W) [18], RhZ (Z = Al, Si, Ga, Ge, In, Sn) [19], CrTe [20], CoSi (x = 0 to 1) [21], CoS [22], MnAs [23], ZrAs [24], CrX (X = Si, Ge) [25], and others. Recent research by Jiang et al. revealed that LiAs is a half-metallic ferromagnet with a total magnetic moment per formula of 4 and a band gap of 0.34 eV [26], where the Y atom is Li, an alkaline metal, unlike typical transition metals. In pursuit of new candidates for spintronic applications, we concentrate on LiSi and LiGe, full-Heusler compounds that have not been studied experimentally or theoretically. This study presents the first comprehensive analysis of the structural, elastic, electronic, magnetic, and half-metallic properties of LiSi and LiGe using first-principles calculations.
2. Computational Details
The computational framework for this study was based on the projector augmented wave (PAW) method [27,28], implemented within the Vienna Ab initio Simulation Package (VASP) using density functional theory (DFT) [29,30]. The exchange-correlation energy was modeled using the generalized gradient approximation (GGA) with the Perdew–Burke–Ernzerhof (PBE) functional [31]. Calculations employed the standard VASP potentials for Fe, Li, Si, and Ge. A plane-wave basis set with a cutoff energy of 600 eV was utilized, and the total energy convergence criterion was set to eV per atom. Brillouin zone integration was performed using a Monkhorst–Pack k-point grid [32] for the primitive cell shown in Figure 1a, and a Monkhorst–Pack k-point grid [32] for the unit cell shown in Figure 1b. For each deformed configuration, only atomic positions were relaxed until the residual forces on all atoms were reduced to below 0.01 eV/Å. For the precise determination of the elastic constants, the final energy calculations were performed using the linear tetrahedron method with Blöchl corrections.
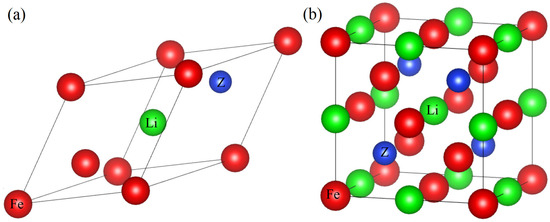
Figure 1.
The primitive cell (a) and the unit cell (b) of Fe2LiZ with the XA structure.
3. Results and Discussion
3.1. Structural and Elastic Properties
The total energy () of the primitive cell for the nonmagnetic (NM) and ferromagnetic (FM) LiSi (Fe2LiGe) Heusler compound with L21 and XA structures as a function of the lattice constant (a) is shown in Figure 2a,b. From Figure 2a, it is clearly observed that the XA structure in the FM state is the most energetically stable for Fe2LiSi, followed by the L21 structure in the FM and NM states, and the XA structure in the NM state is the least energetically stable. Similarly, Figure 2b shows that, for Fe2LiGe, the XA structure in the FM state is the most energetically favorable, followed by the L21 structure in the FM state and the XA structure in the NM state, and the L21 structure in the NM state is the least energetically favorable. Consequently, the XA structures in the FM state of both Fe2LiSi and Fe2LiGe are energetically favorable. The total energy–lattice constant data of the FM Fe2LiSi and Fe2LiGe with the XA structure were fitted using the Birch–Murnaghan equation of state [33], and the equilibrium lattice constant (), bulk modulus (B), and first pressure derivative of bulk modulus () of both compounds are listed in Table 1. According to the Open Quantum Materials Database (OQMD) [34] (http://www.oqmd.org), Fe2LiSi in XA configuration has a lattice constant of 5.561 Å and Fe2LiGe has 5.684 Å, both in reasonable agreement with our theoretical values. To the best of our knowledge, no experiments have reported these properties of Fe2LiSi and Fe2LiGe compounds.
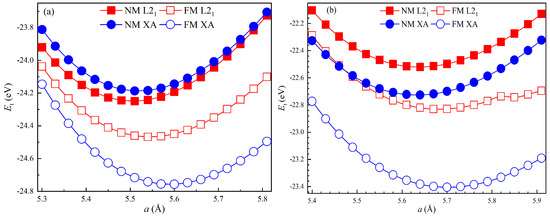
Figure 2.
Dependence of the total energy () of the primitive cell on the lattice constant (a) of (a) Fe2LiSi and (b) Fe2LiGe.

Table 1.
Equilibrium lattice constant (, Å), bulk modulus (B, GPa), and the first pressure derivative of bulk modulus (), and elastic constants (, , and , GPa) of Fe2LiSi and Fe2LiGe.
Understanding the stability of a material is essential for both fundamental research and practical applications. A crystal structure cannot exist in a stable or metastable phase unless its elastic constants () satisfy specific conditions. For a cubic crystal, the three mechanical stability criteria are well-established: , , and [1,26]. As described in the literature [35], the bulk modulus B of an isotropic cubic crystal is expressed in terms of the elastic constants and as . The elastic constants () and are determined through total energy calculations involving volume-conserving orthorhombic () and monoclinic () strains, respectively. Both strains are defined as [35]
The total energy is an even function of the strain parameters and , and the change is given by
Here, represents the volume of the unit cell in the equilibrium state. In this study, both and vary from to in increments of 0.003. For each deformed configuration, the total energy is calculated using the first-principles method. After fitting the energy–strain data with a second-order polynomial function, as shown in Figure 3, the constants () and are extracted directly from the equations. The fitted functions for Fe2LiSi are as follows:
and for Fe2LiGe are as follows:
Here, all correlation coefficients () are very close to 1. The elastic constants for FM Fe2LiSi and Fe2LiGe with the XA structure are listed in Table 1. As shown in Table 1, the elastic constants of both compounds satisfy the three mechanical stability criteria of the cubic system, confirming their mechanical stability. The elastic anisotropy () is defined as [35]. Crystals exhibiting large values may exhibit a tendency to deviate from the cubic structure. As shown in Table 1, the anisotropy values are 2.803 for Fe2LiSi and 2.667 for Fe2LiGe, indicating that Fe2LiSi has a slightly higher elastic anisotropy than Fe2LiGe.
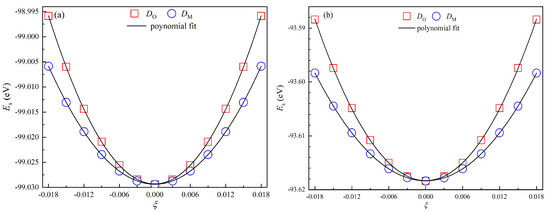
Figure 3.
Total energy of the strained unit cell () as a function of strain parameter () for (a) Fe2LiSi and (b) Fe2LiGe. The solid lines denote the results from second-order polynomial fitting.
For Fe2LiSi and Fe2LiGe, the elastic constant , representing stiffness against principal strains, exceeds the single-crystal shear modulus for the (100) plane along the [010] direction. The tetragonal shear modulus (), defined as [35], describes the shear deformation along the (110) plane in the [110] direction. Large values of indicate a higher stability of the crystal against tetragonal shear deformation. The tetragonal shear modulus is calculated as 47.43 GPa for Fe2LiSi and 40.02 GPa for Fe2LiGe, demonstrating that Fe2LiSi exhibits greater stability than Fe2LiGe. In the bond-orbital model, Kleinman’s internal displacement parameter () is defined as [35]. This parameter describes the relative positions of atoms in different sublattices under volume-conserving strain distortions, where symmetry no longer fixes their positions. The parameter vanishes when no internal displacements occur. Specifically, when bond lengths remain unchanged, and when bond angles remain unchanged, both under linear strain. Kleinman’s parameter is calculated as 0.68 for Fe2LiSi and 0.70 for Fe2LiGe, indicating that both compounds exhibit relatively rigid atomic positions against lattice distortions.
Additionally, the elastic constants govern the response of the crystal to external forces, as characterized by the bulk modulus B, shear modulus (G), Young’s modulus (E), and Poisson’s ratio (). Based on the Voigt–Reuss–Hill scheme [36,37,38], the shear modulus G of the isotropic cubic crystal is given by
The Young’s modulus E and Poisson’s ratio of the isotropic cubic crystal are related to the bulk modulus B and shear modulus G through the following relation:
The calculated values of G, E, and are listed in Table 2. From Table 2, it is evident that the moduli B, G, and E for Fe2LiSi are larger than those for Fe2LiGe. The elastic moduli of Fe2LiSi and Fe2LiGe follow the general inequality . Therefore, the tetragonal shear modulus , rather than isotropic shear modulus G, is the primary factor influencing the stability of the cubic XA structure for both compounds. According to Frantsevich’s rule [39], brittle materials exhibit Poisson’s ratio below 0.26, while values above this threshold indicate ductile behavior. The Poisson’s ratios for Fe2LiSi and Fe2LiGe are calculated as 0.2629 and 0.2822, respectively, further confirming their ductile behavior. A smaller Poisson’s ratio suggests that Fe2LiGe exhibits better ductility compared to Fe2LiSi.

Table 2.
Polycrystalline bulk modulus (B, GPa), shear modulus (G, GPa), Young’s modulus (E, GPa), and Poisson’s ratio () of Fe2LiSi and Fe2LiGe.
As an extension of this study, the thermal properties of a crystal determine the suitable conditions for initiating and maintaining the quality of crystal growth. We computed the Debye temperature (), an important fundamental parameter for the thermodynamic properties of a solid, closely related to physical properties such as elastic constants, specific heat, and melting point. The Debye temperature is used to distinguish between high- and low-temperature regions in solids. Generally speaking, a higher implies a higher thermal conductivity and melting temperature. At low temperatures, vibrational excitations arise solely from acoustic vibrations and the Debye temperature calculated from elastic constants is the same as that determined from experimental measurements. A widely used method for calculating involves elastic constant data, allowing to be estimated from the mean sound velocity () via the classical relation [40]
Here, h and represent Plank’s and Boltzmann’s constants, respectively; n is the number of atoms per formula unit; is Avogadro’s number; is the mass density; M is the molecular mass per formula unit; and , are longitudinal and transverse elastic wave velocities, respectively, derived from Navier’s equations [41]:
The Grüneisen parameter () is related to sound velocities. Specifically, the acoustical Grüüneisen parameter is defined as [42]
The melting temperature () is calculated from the elastic constant via the following expression [43]:
The calculated mass densities, acoustic velocities, Debye temperatures, Grüneisen parameter, and melting points are listed in Table 3. As shown in Table 3, the density and Grüneisen parameter of Fe2LiSi are smaller than those of Fe2LiGe, while its other physical quantities are larger. To the best of our knowledge, no experimental and theoretical data are available for meaningful comparison. Therefore, the present results serve as a prediction for future experimental studies.

Table 3.
Mass density (, g/cm3), polycrystalline longitudinal (), transverse () and mean () sound velocities (m/s), Debye temperature (, K), Grüneisen parameter (), and melting temperature (, K) of Fe2LiSi and Fe2LiGe.
Electronic, Magnetic, and Half-Metallic Properties
The spin-polarized band structures of Fe2LiSi and Fe2LiGe compounds in the XA structure at equilibrium are shown in Figure 4a,b for Fe2LiSi and Figure 4c,d for Fe2LiGe. As shown in Figure 4a,c, the valence and conduction bands overlap in the majority-spin band structure for both compounds, with the intersecting the overlapping regions. Consequently, the majority-spin channel exhibits metallic characteristics. In contrast, Figure 4b,d reveal a semiconducting band gap near the in the minority-spin band structures of both compounds. The band structure shows that the conduction band minimum (CBM) is at the X point, while the valence band maximum (VBM) is at the L point for both Fe2LiSi and Fe2LiGe, indicating an indirect band gap. The energy gaps are 0.141 eV for Fe2LiSi and 0.179 eV for Fe2LiGe. As is known, the half-metallicity is characterized by the coexistence of a metallic state for one spin orientation and an insulating state for the opposite spin orientation. These findings confirm that Fe2LiSi and Fe2LiGe are half-metallic FM compounds in the equilibrium state.
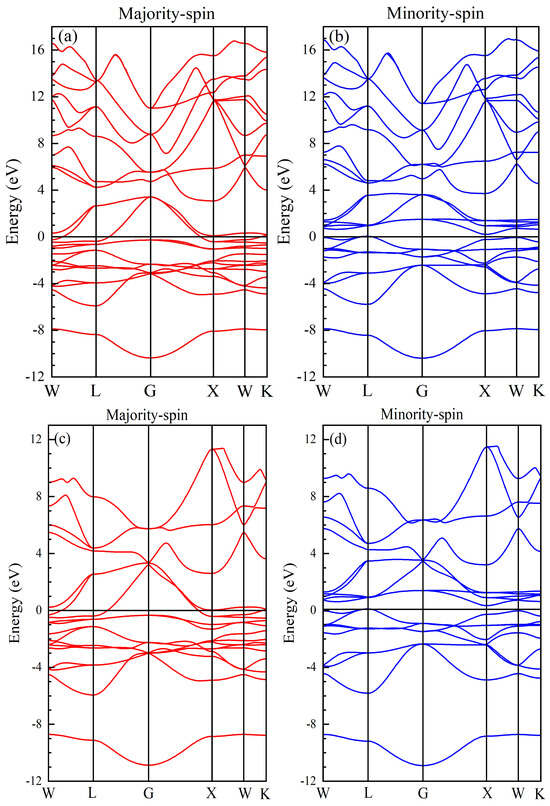
Figure 4.
Band structures of (a,b) Fe2LiSi and (c,d) Fe2LiGe. The Fermi level is shifted to 0 eV.
Figure 5a,b presents the calculated total and projected density of states (DOS) for Fe2LiSi and Fe2LiGe, respectively. The positive and negative DOS values correspond to the majority-spin and minority-spin channels, respectively. As shown in Figure 5a, the total DOS of Fe2LiSi is divided into two distinct energy regions: to eV and to 16 eV. In the deep energy regions, between and eV, the majority-spin and minority-spin DOS are nearly identical. Compared to the majority-spin channel, the minority-spin states in the energy region between and 16 eV shift toward higher energy region. The majority-spin states are present at the , whereas the minority-spin states exhibit an energy gap around the . Therefore, Fe2LiSi exhibits half-metallic behavior. Comparing the total DOS with the projected DOS of various atoms reveals that the majority-spin and minority-spin total DOS below eV originate primarily from Si s states, while those between and eV are dominated by Fe(A) and Fe(B) d states and Si p states. In the energy range from to 3.9 eV, the total DOS in both spin directions is primarily attributed to Fe d states, while, beyond 3.9 eV, it is influenced by various states of all atoms. Notably, Li atoms contribute negligibly to the total DOS across the entire studied energy range. As shown in Figure 5b, the total DOS of Fe2LiGe is also divided into two distinct energy regions: to eV and to 11 eV, similar to Fe2LiSi. Comparing the total DOS with the projected DOS of different atoms shows that the total DOS below eV is dominated by the Ge s states, between and eV by Ge p and Fe d states, between and 3.6 eV by the Fe d states, and above 3.6 eV by the Fe d and Ge p states. Additionally, Li atoms contribute minimally to the total DOS across the studied energy range.

Figure 5.
Total and projected density of states (DOS) of (a) Fe2LiSi and (b) Fe2LiGe. The Fermi level is shifted to 0 eV.
Furthermore, analyzing the projected DOS reveals strong d–d orbital hybridization between Fe atoms in Fe2LiSi and Fe2LiGe, alongside p–d hybridization involving Fe, Li, and Z (Si or Ge) atoms. It is established that covalent and d–d hybridizations among transition metals serve as two primary mechanisms for forming half-metallic band gaps in the XA structure. Additionally, p–d hybridizations between transition metals and Z atoms influence both the formation and width of the bandgap [1,26]. The d–d hybridization between Fe atoms is the primary cause of the minority-spin band gap in the XA Fe2LiSi and Fe2LiGe, as these compounds exclusively contain the transition metal Fe. Furthermore, p–d hybridization between Fe and Z atoms significantly impacts both the formation and width of the band gap.
Further investigation into half-metallicity involved calculating the minority-spin band gaps of Fe2LiSi and Fe2LiGe at varying lattice constants. Fe2LiSi exhibits half-metallic behavior within a lattice constant range of 5.57–5.84 Å, with a nonlinear variation in its half-metallic band gap. Similarly, Fe2LiGe exhibits half-metallic behavior within a lattice constant range of 5.52–5.73 Å. Notably, its half-metallic band gap remains constant across this range. The spin-polarization ratio (), a key parameter for half-metallic materials, is defined as , where and denote the majority-spin and minority-spin DOS at the , respectively. Notably, both compounds exhibit SPR values exceeding 93% across the studied lattice constant range. Remarkably, the reaches 100% for Fe2LiSi in the range of 5.59–5.81 Å and for Fe2LiGe in the range of 5.55–5.702 Å.
As a key characteristic of half-metallic materials, the total magnetic moment per formula unit () must be an integer value. For XA-structured half-metallic full-Heusler compounds, follows the generalized Slater–Pauling rule: , where represents the total number of valence electrons in the molecular formula [1,26]. Consequently, we calculated the total and atomic magnetic moments of Fe2LiSi and Fe2LiGe at different lattice constants. The magnetic moments of both compounds at their equilibrium lattice constants are summarized in Table 4. Notably, both compounds exhibit an integer of 3 . It is well-known that Fe contributes 8 valence electrons, Li contributes 1, and both Si and Ge contribute 4 each. Consequently, for both Fe2LiSi and Fe2LiGe is 21. Clearly, the total magnetic moments of both compounds adhere perfectly to the Slater–Pauling rule, confirming the stability of their half-metallic behavior at the equilibrium lattice constant. Additionally, the total magnetic moments of both compounds are predominantly determined by the atomic magnetic moment of Fe(A) and Fe(B) atoms.

Table 4.
Total and atomic magnetic moments () of Fe2LiSi and Fe2LiGe in equilibrium state.
The dependencies of the magnetic moments on the lattice constant are shown in Figure 6a for Fe2LiSi and Figure 6b for Fe2LiGe. These figures clearly show that the total magnetic moment remains at 3 within lattice constant ranges of 5.57–5.84 Å for Fe2LiSi and 5.52–5.73 Å for Fe2LiGe. For both compounds, the atomic magnetic moments of Fe(A) and Fe(B) linearly decrease and increase, respectively, with increasing lattice constant. Meanwhile, the Li atoms exhibit nearly constant magnetic moment across the lattice constant range, while the Z atoms’ moments slightly decrease with increasing lattice constant. The linear fitting of the atomic magnetic moments of Fe(A) and Fe(B) yields the following relations for Fe2LiSi:
and for Fe2LiGe:
Here, represents the atomic magnetic moment, and all linear correlation coefficients () are close to 1. Clearly, the decrease rate of Fe(A)’s magnetic moment is smaller than the increase rate of Fe(B)’s for both compounds.
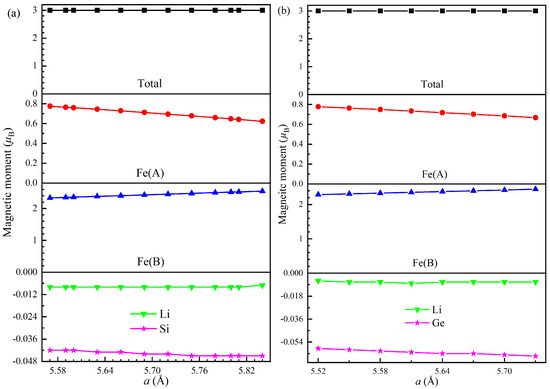
Figure 6.
Total and atomic magnetic moments of (a) Fe2LiSi and (b) Fe2LiGe at different lattice constants.
4. Conclusions
The structural, elastic, electronic, magnetic, and half-metallic properties of full-Heusler Fe2LiSi and Fe2LiGe compounds in their ground-state have been predicted by first-principles calculations. Among the four distinct combinations of crystal structure and magnetic state, the XA structures in the FM state of both compounds are the energetically most favorable. The elastic properties of Fe2LiSi and Fe2LiGe compounds in the most energetically favorable FM XA structure have been predicted. Both compounds exhibit mechanical stability, elastic anisotropy, and ductility. Compared to Fe2LiGe, the full-Heusler compound Fe2LiSi exhibits higher stability, stronger elastic anisotropy, greater brittleness, higher Debye and melting temperatures, and a smaller Grüneisen parameter. Furthermore, the electronic, magnetic, and half-metallic properties of Fe2LiSi and Fe2LiGe compounds have been predicted. The majority-spin channels of both compounds exhibit metallic behavior, whereas their minority-spin channels display semiconducting properties. The half-metallic gaps of Fe2LiSi and Fe2LiGe in their equilibrium states are 0.141 and 0.179 eV, respectively. The full-Heusler compounds Fe2LiSi and Fe2LiGe exhibit an SPR of 100% within the lattice constant range of 5.59–5.81 Å and 5.55–5.702 Å, respectively. The total magnetic moment per formula for Fe2LiSi and Fe2LiGe in their equilibrium state is 3.000 , which obeys the generalized Slater–Pauling rule (), and primarily depends on the magnetic moment of Fe atoms at different Wyckoff positions. Over the entire studied lattice constant range, the total magnetic moment remains constant, while the atomic magnetic moments of Fe(A) linearly decrease, Fe(B) linearly increase, Li atoms remain nearly unchanged, and Z (Si or Ge) atoms slightly decrease with increasing lattice constant. These findings indicate that both compounds hold promise as materials for spintronic applications.
Author Contributions
Conceptualization, Y.W. and X.Z.; methodology, Y.W., Y.Y. and X.Z.; validation, Y.Y. and Z.L.; formal analysis, Y.Y., Z.L. and X.Z.; investigation, Y.W. and X.Z.; data curation, Y.W., Z.L. and X.Z.; writing—original draft preparation, Y.W.; writing—review and editing, Y.Y., Z.L. and X.Z.; visualization, Y.Y. and Z.L.; funding acquisition, Y.W. and Y.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Specialized fund for the Doctoral of Kaili University (grant number BS202502013), Guizhou Provincial Basic Research Program (Natural Science) of Youth Guidance (Qian Ke He Jichu-[2024]Qingnian 024), and the National Natural Science Foundation of China (grant number 12064019).
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Tavares, S.; Yang, K.; Meyers, M.A. Heusler alloys: Past, properties, new alloys, and prospects. Prog. Mater. Sci. 2023, 132, 101017. [Google Scholar] [CrossRef]
- de Groot, R.A.; Mueller, F.M.; van Engen, P.G.; Buschow, K.H.J. New class of materials: Half-metallic ferromagnets. Phys. Rev. Lett. 1983, 50, 2024. [Google Scholar] [CrossRef]
- Li, G.; Li, Z.; Liu, Z. Study on the phase stability, mechanical and half-metallic properties of half-Heusler alloys FeMnZ (Z = Si, Ge, and Sn). J. Magn. Magn. Mater. 2025, 614, 172742. [Google Scholar] [CrossRef]
- Rachida, T.; Yahia, B.; Hichem, B.; Tayeb, B.E.; Said, M.; Ayoub, B.; Youcef, R.; Mohammed, R. Half-metallic ferromagnetism and thermoelectric performance of PdFeCrZ (Z = Al, Si, Sb, Ge) quaternary Heusler alloys for thermos-spintronic applications. J. Magn. Magn. Mater. 2025, 624, 173072. [Google Scholar] [CrossRef]
- Faid, F.; Mebarki, H.; Mokadem, K.; Abdalilah, F.M.; Benmakhlouf, A.; Khatiri, M.; Helaimia, T. Systematic study of structural, elastic, electronic, magnetism and half-metallic properties for the quaternary alloys: Heusler type VZrReZ (Z = Si, Ge and Sn). J. Magn. Magn. Mater. 2024, 605, 172345. [Google Scholar] [CrossRef]
- Mahmood, Q. Study of half metallic ferromagnetism, Curie temperature, and thermoelectric aspects of double perovskite oxides Ba2XMoO6 (X = Cr, Mn, Fe, Co) for spintronic applications. Mater. Sci. Semicon. Proc. 2025, 193, 109519. [Google Scholar] [CrossRef]
- Zhang, J.; Temnikov, F.; Ye, X.; Wang, X.; Pan, Z.; Liu, Z.; Pi, Z.; Tang, S.; Chen, C.; Pao, C. Large manipulation of ferrimagnetic curie temperature by A-site chemical substitution in ACu3Fe2Re2O12 (A = Na, Ca, and La) half metals. Inorg. Chem. 2025, 64, 472–478. [Google Scholar] [CrossRef] [PubMed]
- Zhang, R.; Fu, J.; Xiang, Y.; Li, L.; Wu, X.; Wu, S. V doped orth-Ga2O3: Half-metallic ferromagnetism, large magnetic anisotropy energy and high curie temperature. J. Alloys Compd. 2025, 1010, 177301. [Google Scholar] [CrossRef]
- Mogulkoc, A.; Modarresi, M.; Rudenko, A.N. Two-dimensional chromium pnictides CrX (X = P, As, Sb): Half-metallic ferromagnets with high curie temperature. Phys. Rev. B 2020, 102, 024441. [Google Scholar] [CrossRef]
- Charifi, Z.; Guendouz, D.; Baaziz, H.; Soyalp, F.; Hamad, B. Ab-initio investigations of the structural, electronic, magnetic and mechanical properties of CrX (X = As, Sb, Se, and Te) transition metal pnictides and chalcogenides. Phys. Scr. 2019, 94, 14. [Google Scholar] [CrossRef]
- Kattan, N.A.; Ayyaz, A.; Alkhaldi, H.D.; Alkhaldi, N.D.; Bouzgarrou, S.; Boukhris, I.; Albalawi, H.; Mahmood, Q.; Al-Buriahi, M.S. First principles investigations of electronic, ferromagnetic, and thermoelectric aspects of chalcogenides BeCe2X4 (X = S, Se, Te) for spintronics. J. Phys. Chem. Solids 2025, 206, 112843. [Google Scholar] [CrossRef]
- Sohail, S.; Irfan, M.; Ain, Q.; Ibrahim, F.A.; Hamdy, M.; Issa, S.A.M.; Zakaly, H.M.H. First principles computation of exchange mechanism, radiation shielding, and physical properties of FeCu2SnX4 (X = S, Se, Te): Transitions metal based chalcogenides for spintronic and energy storage system applications. Mater. Sci. Semicon. Proc. 2025, 190, 109303. [Google Scholar] [CrossRef]
- Jain, V.K.; Lakshmi, N.; Jain, R.; Chandra, A.R. Electronic structure, elastic, magnetic, and optical Properties of Fe2MnZ (Z = Si, Ge, and Sn) full Heusler alloys: First-principle calculations. J. Supercond. Nov. Magn. 2019, 32, 739–749. [Google Scholar] [CrossRef]
- Ganai, Z.S.; Yousuf, S.; Batoo, K.M.; Khan, M.; Gupta, D.C. Half-metallicity and onsite Hubbard interaction on d-electronic states: A case study of Fe2NiZ (Z = Al, Ga, Si, Ge) Heusler systems. Philos. Mag. 2019, 99, 1551–1562. [Google Scholar] [CrossRef]
- Rai, D.P.; Rinkima, L.; Zuala, L.; Fomin, L.A.; Malikov, I.V.; Sayede, A.; Ghimire, M.P.; Thapa, R.K.; Zadeng, L. Pressure dependent half-metallic ferromagnetism in inverse Heusler alloy Fe2CoAl: DFT+U calculation. RSC Adv. 2020, 10, 44633–44640. [Google Scholar] [CrossRef] [PubMed]
- Lee, H.-W.; Hsing, C.-R.; Chang, C.-M.; Wei, C.-M. Electronic structures of 24-valence-electron full Heusler compounds investigated by density functional and GW calculations. J. Phys. Condens. Mat. 2020, 32, 175501. [Google Scholar] [CrossRef] [PubMed]
- Mansour, B.; Zoubir, A.; Ahmad, K.S.; Sabria, T.; Aftab, A.M.; Bouabdellah, B.; Abderrahim, B.M.; Amel, L. Electronic structure, thermoelectric, mechanical and phonon properties of full-Heusler alloy (Fe2CrSb): A first-principles study. Bull. Mater. Sci. 2021, 44, 221. [Google Scholar]
- Wang, L.; Cao, Y.; Zhang, C.; Xu, Y.; Zhou, S. Theoretical study of structural, mechanical, electronic, magnetic and thermodynamic properties of Cu2MnAl-type Fe2YAl (Y = Cr, Mo and W) full-Heusler alloys. Mater. Sci. Eng. B 2022, 278, 115639. [Google Scholar] [CrossRef]
- Erager, K.R.; Baigutlin, D.; Sokolovskiy, V.; Buchelnikov, V. On the possible half-metallic properties of Fe2RhZ (Z = Al, Si, Ga, Ge, In, Sn) ferromagnetic Husler alloys. J. Commun. Technol. Electron. 2023, 68, 389–399. [Google Scholar] [CrossRef]
- Bhattacharya, J.; Dutt, R.; Chakrabarti, A. Ab-initio predictions of mechanical, electronic, magnetic, and transport properties of bulk and heterostructure of a novel Fe-Cr based full Heusler chalcogenide. J. Phys. Chem. Solids 2023, 178, 111307. [Google Scholar] [CrossRef]
- Biswas, S.; Alagarsamy, P.; Srinivasan, A. Influence of atomic substitution on the structural stability and half-metallicity of Fe2-xCrxCoSi (x = 0 to 1) alloys. J. Magn. Magn. Mater. 2024, 612, 172648. [Google Scholar] [CrossRef]
- Hariharan, M.; Eithiraj, R.D. Structural, electronic, magnetic, and thermoelectric properties of newly predicted Fe2CoS and Ni2CoS alloys for spintronics applications: A DFT study. J. Magn. Magn. Mater. 2024, 589, 171553. [Google Scholar] [CrossRef]
- Pérez, C.A.S.; de Marchi, A.F. DFT calculations for electronic and magnetic properties of full Heusler Fe2MnAs alloy in perfect and defect structures. J. Magn. Magn. Mater. 2024, 589, 171541. [Google Scholar] [CrossRef]
- Iram, N.; Sharma, R.; Ahmed, J.; Almeer, R.; Kumar, A.; Abbas, Z. Exploring the physical, magnetic, opto-spintronics and thermoelectric properties of Fe2ZrAs Heusler alloy through DFT study. J. Phys. Chem. Solids 2025, 196, 112368. [Google Scholar] [CrossRef]
- Zaoui, Y.; Beldi, L.; Bouhafs, B.; Kanoun, M.B.; Goumri-Said, S. Dynamic stability, half-metallicity, and optical properties of Fe2CrX (X = Si, Ge) full-heusler alloys: Competition between L21 and XA ordering. Mater. Sci. Eng. B 2025, 317, 118168. [Google Scholar] [CrossRef]
- Jiang, D.; Ye, Y.; Gou, Q.; Wu, D.; Wen, Y. First-principles predictions on structural, elastic and half-metallic properties Fe2LiAs Heusler compound. J. Mag. Mag. Mater. 2018, 458, 235–240. [Google Scholar] [CrossRef]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Kresse, G.; Fürthmller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
- Kresse, G.; Fürthmller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
- Francis, B. Finite elastic strain of cubic crystals. Phys. Rev. 1947, 71, 809–824. [Google Scholar]
- Kirklin, S.; Thompson, A.; Doak, J.W.; Aykol, M.; Rühl, S.; Wolverton, C. The Open Quantum Materials Database (OQMD): Assessing the accuracy of DFT formation energies. Npj Comput. Mater. 2015, 1, 15010. [Google Scholar] [CrossRef]
- Wu, S.-C.; Fecher, C.H.; Naghavi, S.S.; Felser, C. Elastic properties and stability of Heusler compounds: Cubic Co2YZ compounds with L21 structure. J. Appl. Phys. 2019, 125, 082523. [Google Scholar] [CrossRef]
- Hill, R. The elastic behaviour of a crystalline aggregate. Proc. Phys. Soc. A 1952, 65, 349–354. [Google Scholar] [CrossRef]
- Voigt, W. Lehrbuch der Kristallphysik; Taubner: Leipzig, Germany, 1928. [Google Scholar]
- Reuss, A. Calculation of the flow limits of mixed crystals on the basis of the plasticity of monocrystals. Z. Angew. Math. Mech. 1929, 9, 49–58. [Google Scholar] [CrossRef]
- Frantsevich, I.N.; Voronov, F.F.; Bokuta, S.A. Elastic Constants and Elastic Moduli of Metals and Insulators Handbook; Naukova Dumka: Kiev, Ukraine, 1983; pp. 60–180. [Google Scholar]
- Anderson, O.L. A simplified method for calculating the debye temperature from elastic constants. J. Phys. Chem. Solids 1963, 24, 909–917. [Google Scholar] [CrossRef]
- Schreiber, E.; Anderson, O.L.; Soga, N. Elastic Constants and Their Measurements; McGraw: New York, NY, USA, 1973. [Google Scholar]
- Belomestnykh, V.N. The acoustical Grüneisen constants of solids. Tech. Phys. Lett. 2004, 30, 91–93. [Google Scholar] [CrossRef]
- Fine, M.E.; Brown, L.D.; Marcus, H.L. Elastic constants versus melting temperature in metals. Scr. Metall. 1984, 18, 951. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).