Hot Tensile Behavior of 05Cr17Ni4Cu4Nb Stainless Steel: Damage Model and Fracture Characteristics
Abstract
1. Introduction
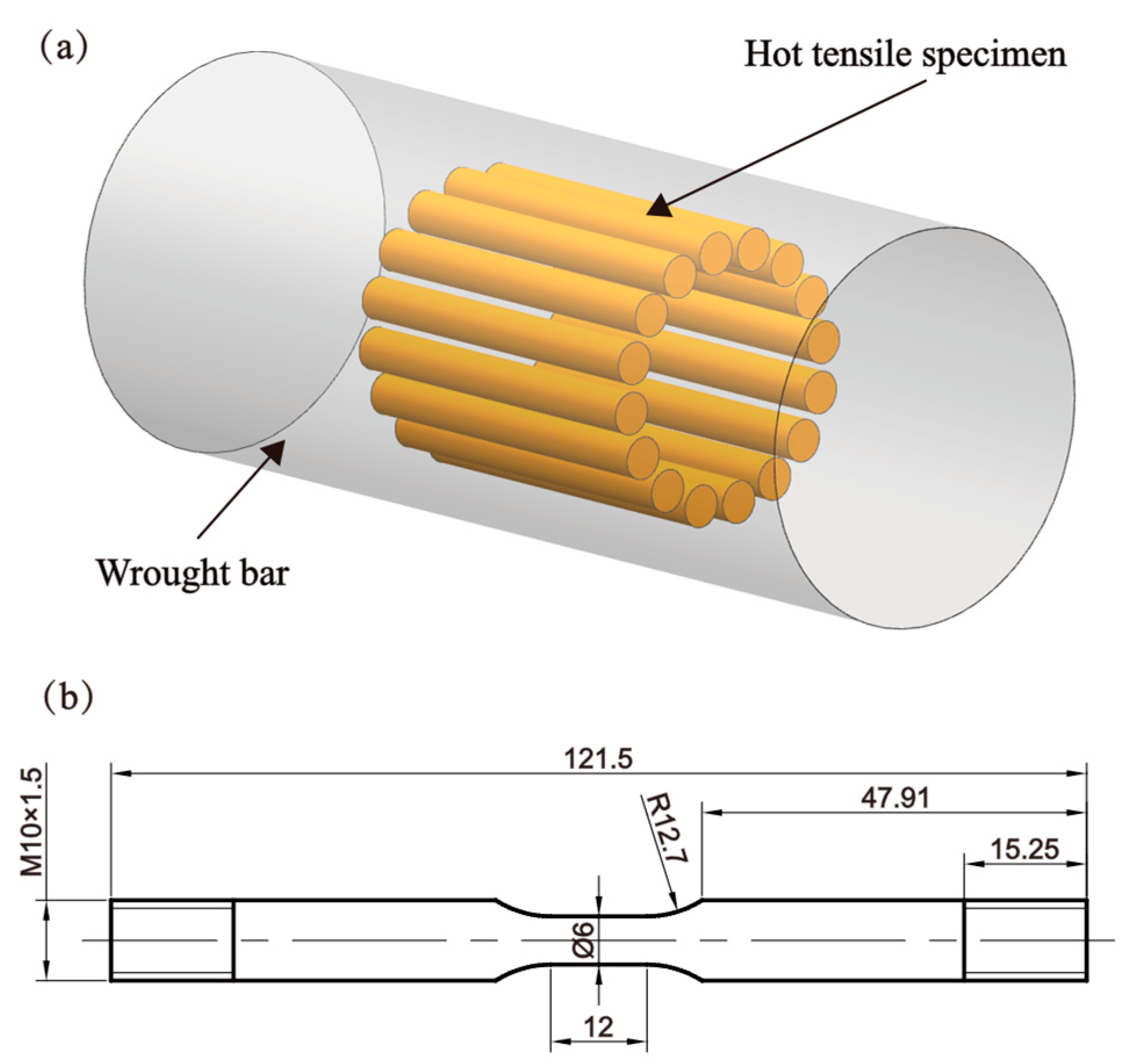
2. Experimental Procedure
3. Result and Discussion
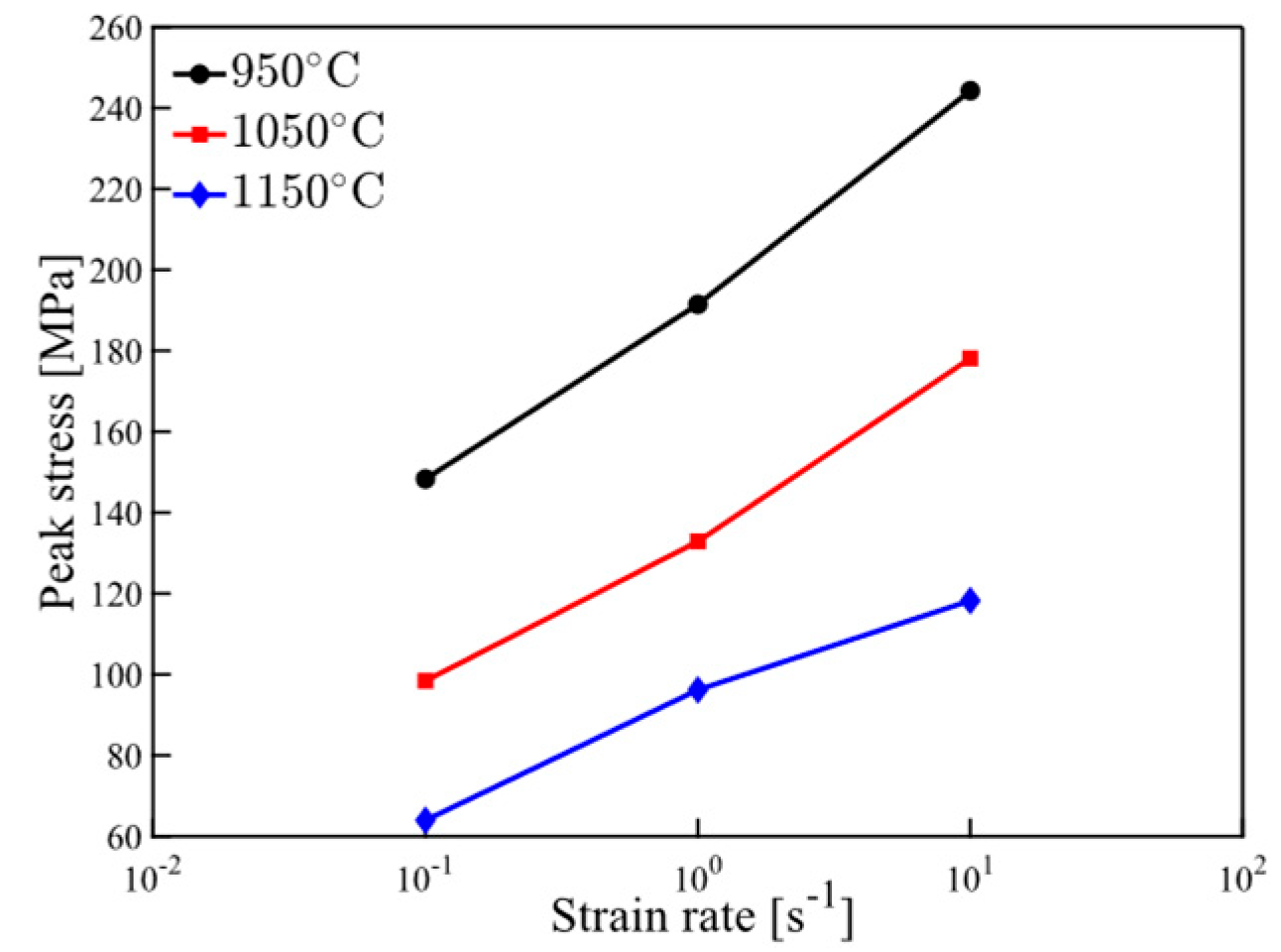
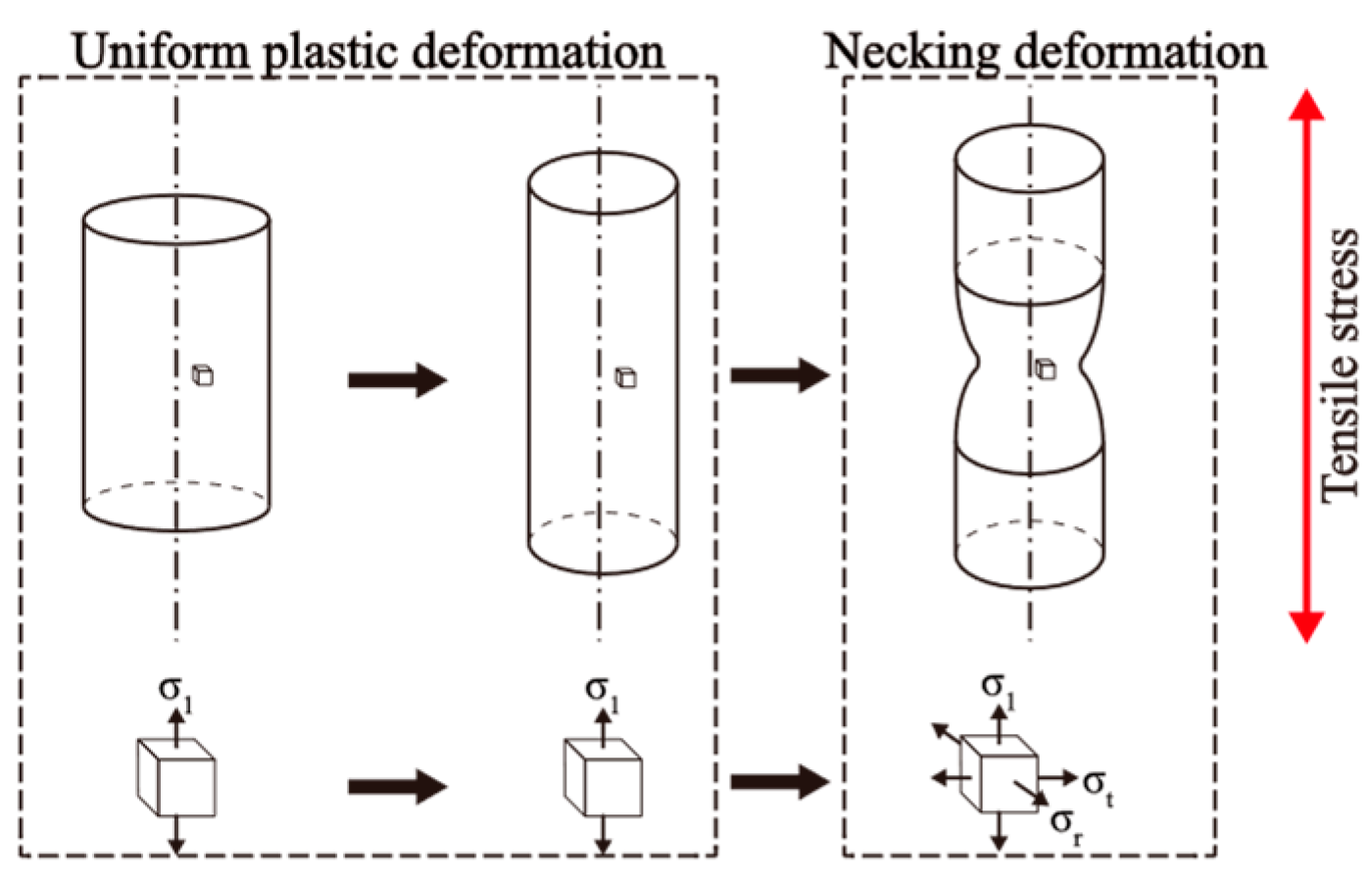
3.1. Mechanical Response
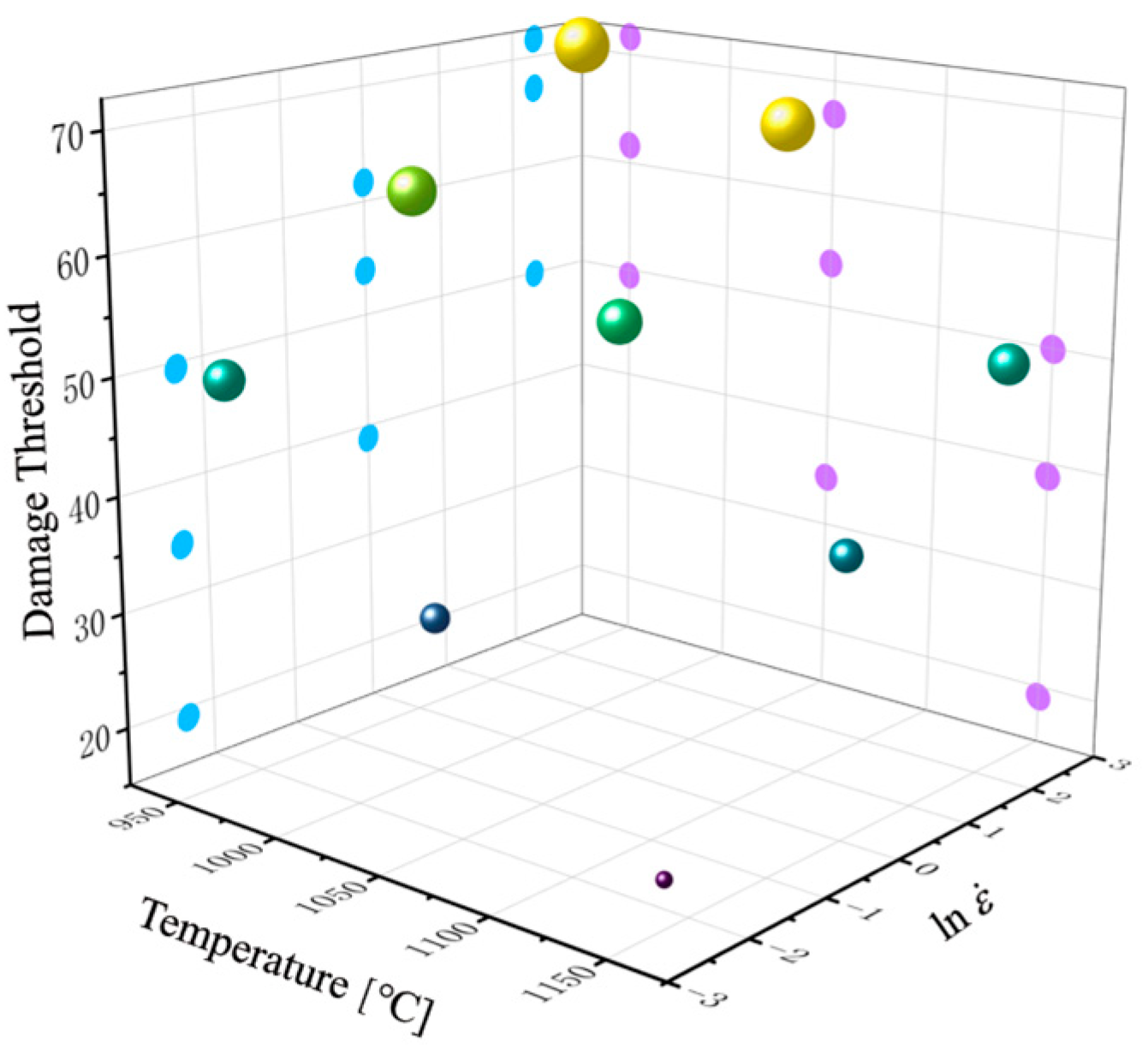
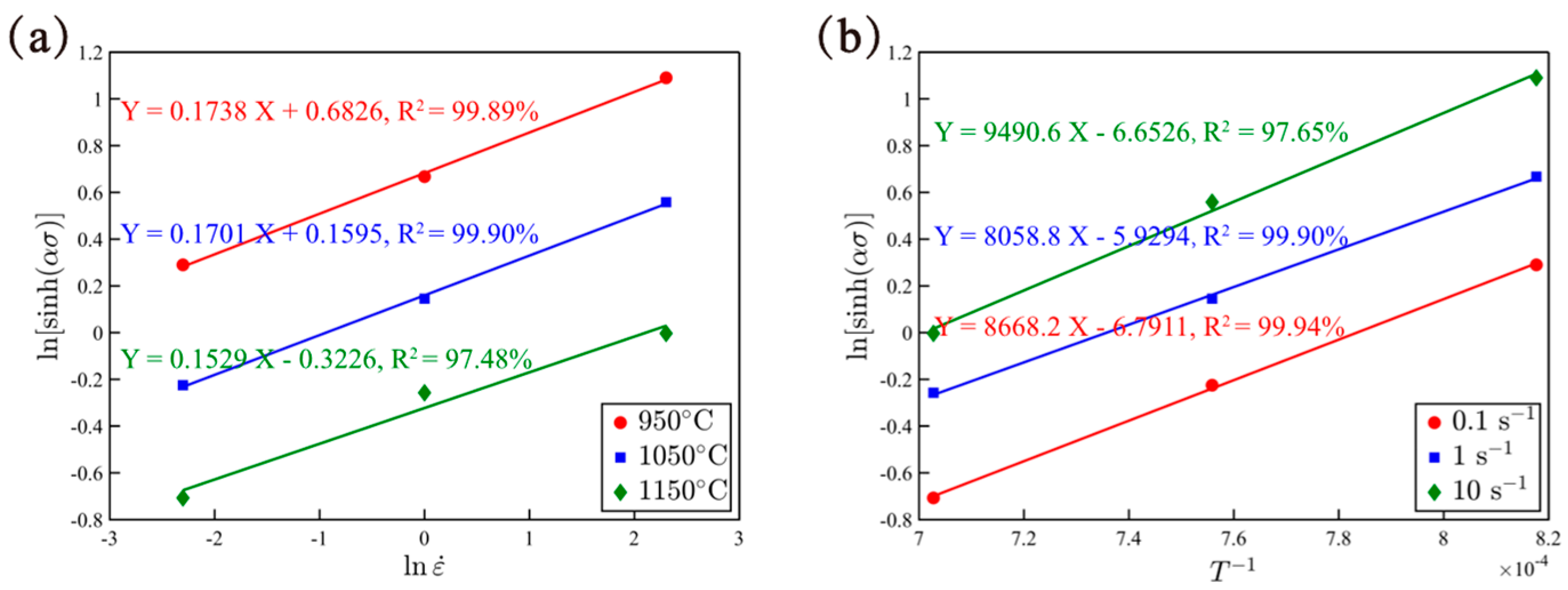
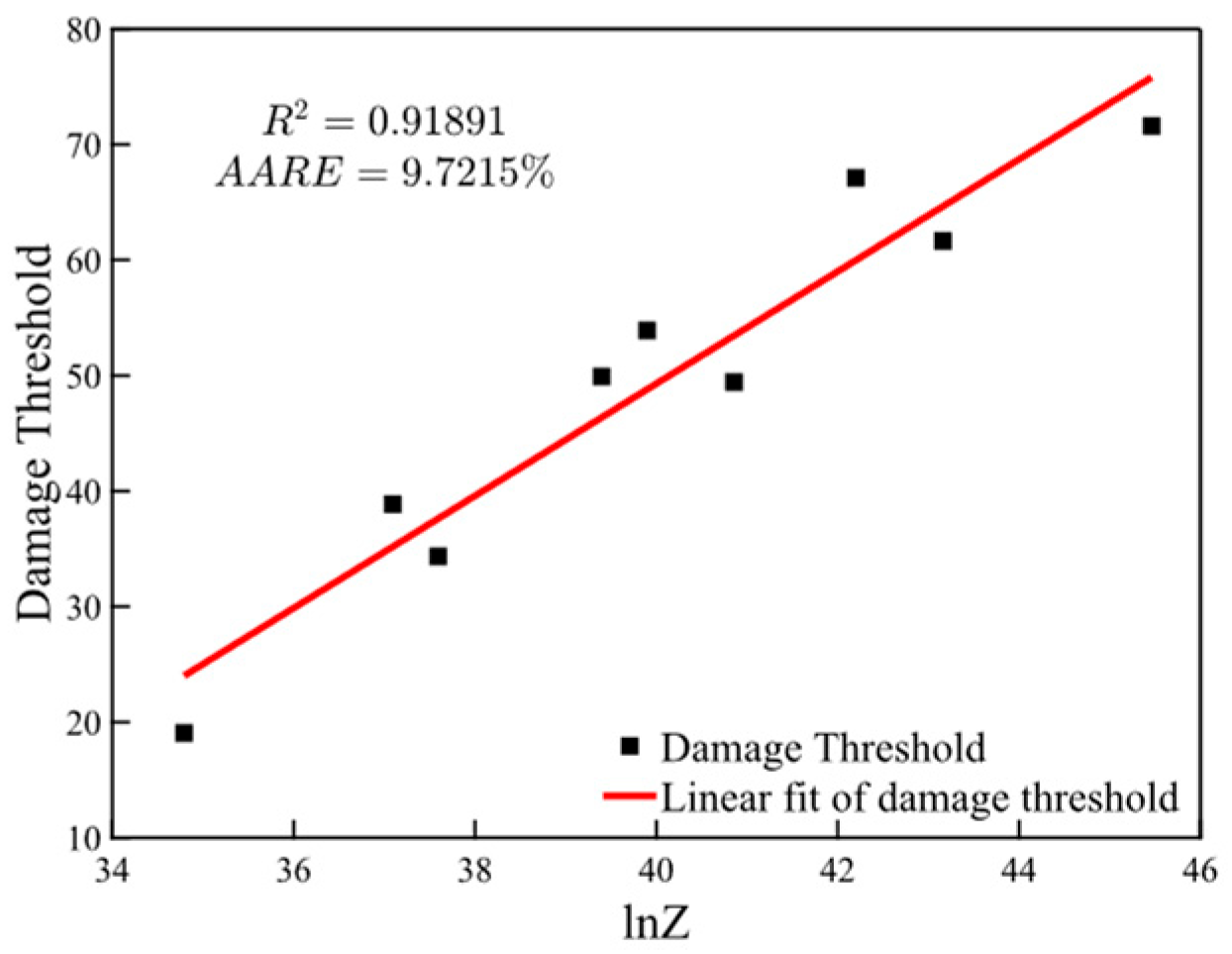
3.2. Damage Model
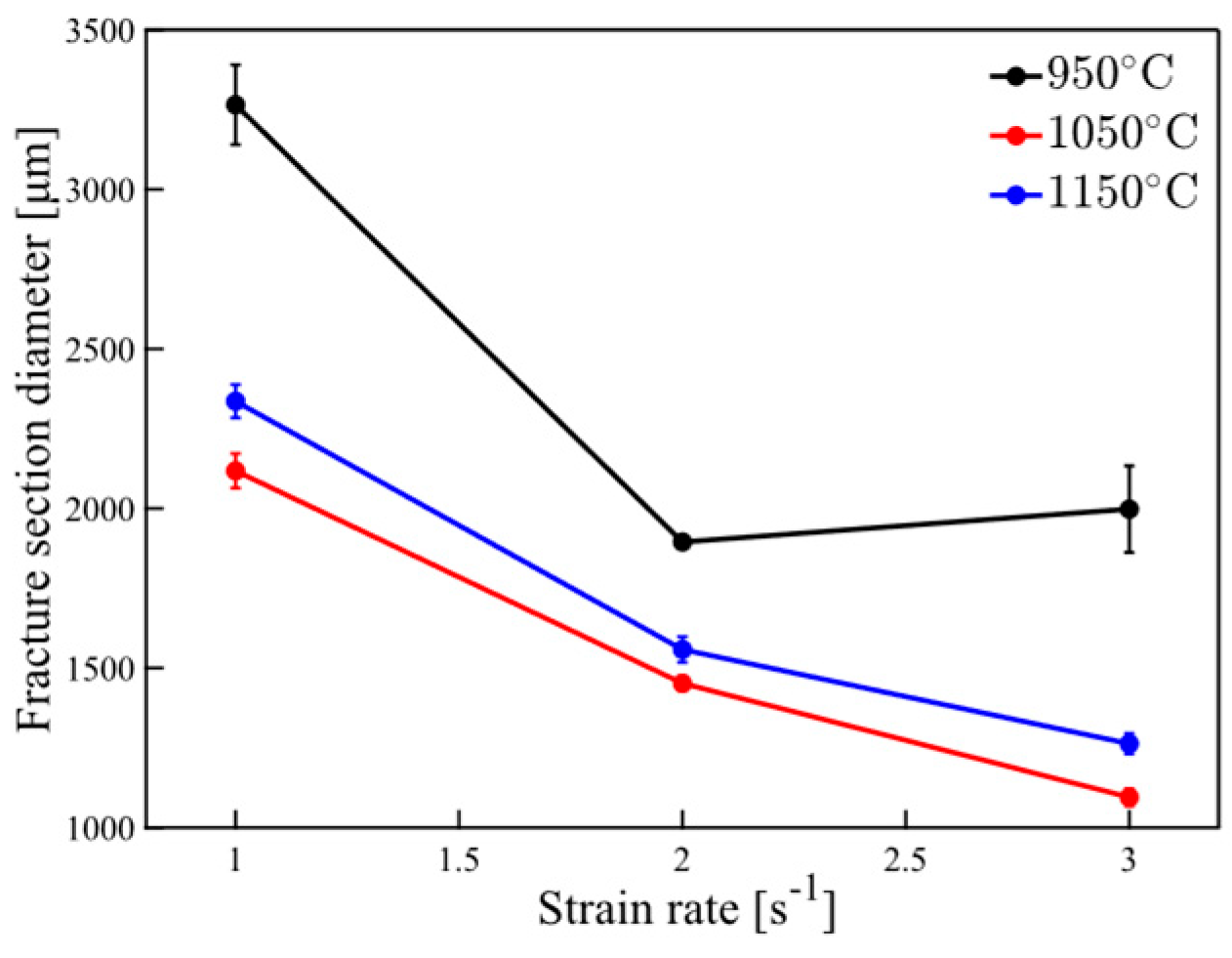
3.3. Fracture Characteristics
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Strain | |
| Strain rate | |
| εf | Fracture strain |
| Peak strain | |
| Stress | |
| σ1 | Maximum principal stress |
| Peak stress | |
| T | Temperature |
| Actual length of the gauge section | |
| Elongation of the gauge section | |
| A | Actual cross-sectional area of the parallel section |
| Ao | Original cross-sectional area of the parallel section |
| F | Tensile load |
| Damage value | |
| Damage threshold | |
| Constant determined through Arrhenius equation fitting | |
| A1 | Constant determined through Arrhenius equation fitting |
| n | Constant determined through Arrhenius equation fitting |
| R | Gas constant, 8.314 J/(mol · K) |
| Q | Activation energy |
| Z | Strain rate factor compensated by temperature |
| R2 | Linear correlation coefficient |
| AARE | Average absolute relative error |
| X | Independent variable |
| Y | Dependent variable |
References
- Wang, L.; Hu, H.; Wang, W.; He, P.; Li, Z.; Xu, G. Analysis on the Key Parameters to Predict Flow Stress during Ausforming in a High-Carbon Bainitic Steel. Metals 2023, 13, 1526. [Google Scholar] [CrossRef]
- Wu, S.; Qu, R.; Zhu, Z.; Zhang, H.; Zhang, Z. Deformation Map of Metallic Glass: Normal Stress Effect. Sci. China Mater. 2020, 63, 2620–2626. [Google Scholar] [CrossRef]
- Mahnken, R.; Stein, E. Parameter Identification for Finite Deformation Elasto-Plasticity in Principal Directions. Comput. Methods Appl. Mech. Eng. 1997, 147, 17–39. [Google Scholar] [CrossRef]
- Melzer, D.; Smirnov, I.; Lukáš, O.; Dlouhý, J.; Evstifeev, A.; Džugan, J.; Valiev, R. Fracture Locus Characteristics of Al Alloy 5083 Processed by Equal Channel Angular Pressing Using Miniaturized Specimens. J. Alloys Compd. 2021, 889, 161675. [Google Scholar] [CrossRef]
- Brünig, M.; Albrecht, D.; Gerke, S. Numerical Analyses of Stress-Triaxiality-Dependent Inelastic Deformation Behavior of Aluminum Alloys. Int. J. Damage Mech. 2011, 20, 299–317. [Google Scholar] [CrossRef]
- Wei, X.; Zhang, X.; Cai, M.; Peng, Z.; Liu, Y.; Lian, C.; Peng, H.; Hodgson, P. Stress-State-Dependent Deformation and Fracture Behaviors in a Cold-Rolled 7Mn Steel. Mater. Sci. Eng. A 2022, 831, 142102. [Google Scholar] [CrossRef]
- McQueen, H.J.; Imbert, C.A.C. Dynamic Recrystallization: Plasticity Enhancing Structural Development. J. Alloys Compd. 2004, 378, 35–43. [Google Scholar] [CrossRef]
- Abedi, H.R.; Zarei Hanzaki, A.; Liu, Z.; Xin, R.; Haghdadi, N.; Hodgson, P.D. Continuous Dynamic Recrystallization in Low Density Steel. Mater. Des. 2017, 114, 55–64. [Google Scholar] [CrossRef]
- Huang, S.H.; Chen, T.; Chen, Q.; Zhao, Z.D.; Xia, X.S.; Wu, Y. Verification of Dislocation Density and Dynamic Recrystallization in Deformed Pure Copper. Strength Mater 2020, 52, 16–23. [Google Scholar] [CrossRef]
- Peng, Y.; Liang, S.; Liu, C.; Barella, S.; Guo, S.; Gruttadauria, A.; Belfi, M.; Liu, Y.; Qu, X.; Mapelli, C. Dynamic Recrystallization Behavior Under Inhomogeneous Thermomechanical Deformation State. Steel Res. Int. 2023, 94, 2200574. [Google Scholar] [CrossRef]
- Mi, G.; Zhang, J.; Xu, B.; Sun, M. Surface Stress Evolution and Cracks Prevention of Ingots during the Upsetting Process. Eng. Rev. 2019, 39, 292–301. [Google Scholar] [CrossRef]
- Lezhnev, S.; Naizabekov, A.; Panin, E.; Tolkushkin, A.; Kuis, D.; Kasperovich, A.; Yordanova, R. Development and Computer Simulation of the New Combined Process for Producing a Rebar Profile. Model. Simul. Eng. 2023, 2023, 7348592. [Google Scholar] [CrossRef]
- Krishna, R.H.; Jena, D.P. Analytical and Numerical Modelling of Open-Die Forging Process for Elliptical Cross-Section of Billet. Measurement 2019, 134, 855–865. [Google Scholar] [CrossRef]
- Fanini, S.; Ghiotti, A.; Bruschi, S. Prediction Of The Fracture Due To Mannesmann Effect In Tube Piercing. AIP Conf. Proc. 2007, 908, 1407–1412. [Google Scholar] [CrossRef]
- Ghiotti, A.; Fanini, S.; Bruschi, S.; Bariani, P.F. Modelling of the Mannesmann Effect. CIRP Ann. 2009, 58, 255–258. [Google Scholar] [CrossRef]
- Fernandes, M.; Marouf, N.; Montmitonnet, P.; Mocellin, K. Impact of the Different Friction Coefficients on the Tools on the Mechanics of the Mannesmann 2-Roll Tube Piercing. ISIJ Int. 2020, 60, 2917–2926. [Google Scholar] [CrossRef]
- Zhang, Z.; Liu, D.; Man, T.; Li, N.; Yang, Y.; Pang, Y.; Wang, J. Numerical and Experimental Investigations on Mannesmann Effect of Nickel-Based Superalloy. Arch. Civ. Mech. Eng. 2022, 22, 133. [Google Scholar] [CrossRef]
- Mackenzie, A.C.; Hancock, J.W.; Brown, D.K. On the Influence of State of Stress on Ductile Failure Initiation in High Strength Steels. Eng. Fract. Mech. 1977, 9, 167–188. [Google Scholar] [CrossRef]
- Meade, E.D.; Sun, F.; Tiernan, P.; O’Dowd, N.P. A Multiscale Experimentally-Based Finite Element Model to Predict Microstructure and Damage Evolution in Martensitic Steels. Int. J. Plast. 2021, 139, 102966. [Google Scholar] [CrossRef]
- Hu, P.; Liu, Y.; Zhu, Y.; Ying, L. Crystal Plasticity Extended Models Based on Thermal Mechanism and Damage Functions: Application to Multiscale Modeling of Aluminum Alloy Tensile Behavior. Int. J. Plast. 2016, 86, 1–25. [Google Scholar] [CrossRef]
- Wang, C.; Liu, X.; Gui, J.; Du, Z.; Xu, Z.; Guo, B. Effect of MnS Inclusions on Plastic Deformation and Fracture Behavior of the Steel Matrix at High Temperature. Vacuum 2020, 174, 109209. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, J.; He, Y. Formation Mechanism and Evolution of Plastic Damage in Billet during Reduction Pretreatment. Metals 2023, 13, 747. [Google Scholar] [CrossRef]
- Chen, X.; Lu, Y.; Ning, M.; Zhou, X.; Chen, J. Tailoring Microstructural Evolution and Fracture Damage Behavior of a Mg–Y–Zn Alloy during Hot Tensile Deformation. Mater. Sci. Eng. A 2023, 871, 144857. [Google Scholar] [CrossRef]
- Wu, H.; Qian, Q.; Xu, W.; Liu, C.; Xu, J.; Shan, D.; Guo, B. A Thermal Damage-Coupled Constitutive Model for Predicting Fracture and Microstructure Evolution and Its Application in the Hot Spinnability Process. J. Mater. Res. Technol. 2024, 30, 1594–1610. [Google Scholar] [CrossRef]
- Xu, W.; Wu, H.; Ma, H.; Shan, D. Damage Evolution and Ductile Fracture Prediction during Tube Spinning of Titanium Alloy. Int. J. Mech. Sci. 2018, 135, 226–239. [Google Scholar] [CrossRef]
- Xiao, Y.; Cui, Z.; Yin, H.; Guo, C. High Temperature Deformation Behavior and Constitutive Modelling for 05Cr17Ni4Cu4Nb Stainless Steel. Procedia Eng. 2014, 81, 1277–1282. [Google Scholar] [CrossRef][Green Version]
- Zhang, J.-L.; Jia, H.-S.; Yi, X.-B.; Xu, C.-W.; Luo, W.-C.; Tang, L.-H.; Shen, J.-C.; Li, X. Dynamic Mechanical Properties and Comparison of Two Constitutive Models for Martensitic Stainless Steel 0Cr17Ni4Cu4Nb. Mater. Res. Express 2021, 8, 106501. [Google Scholar] [CrossRef]
- Zhu, L.; Huang, X.; Liu, H. Study on Constitutive Model of 05Cr17Ni4Cu4Nb Stainless Steel Based on Quasi-Static Tensile Test. J. Mech. Sci. Technol. 2022, 36, 2871–2878. [Google Scholar] [CrossRef]
- Guo, J.; Wu, L.; Yang, X.; Zhong, S. Elastic-Plastic Endochronic Constitutive Model of 0Crl7Ni4Cu4Nb Stainless Steels. Math. Probl. Eng. 2016, 2016, 4396296. [Google Scholar] [CrossRef]
- Li, J.; Wang, B.; Huang, H.; Fang, S.; Chen, P.; Zhao, J.; Qin, Y. Behaviour and Constitutive Modelling of Ductile Damage of Ti-6Al-1.5Cr-2.5Mo-0.5Fe-0.3Si Alloy under Hot Tensile Deformation. J. Alloys Compd. 2019, 780, 284–292. [Google Scholar] [CrossRef]
- Sakai, T.; Belyakov, A.; Kaibyshev, R.; Miura, H.; Jonas, J.J. Dynamic and Post-Dynamic Recrystallization under Hot, Cold and Severe Plastic Deformation Conditions. Prog. Mater. Sci. 2014, 60, 130–207. [Google Scholar] [CrossRef]
- Noell, P.J.; Sills, R.B.; Boyce, B.L. Suppression of Void Nucleation in High-Purity Aluminum via Dynamic Recrystallization. Metall. Mater. Trans. A 2020, 51, 154–166. [Google Scholar] [CrossRef]
- Mirsayar, M.M. Maximum Principal Strain Criterion for Fracture in Orthotropic Composites under Combined Tensile/Shear Loading. Theor. Appl. Fract. Mech. 2022, 118, 103291. [Google Scholar] [CrossRef]
- Cao, T.; Gong, Y.; Zhao, L.; Wang, L.; Hu, N. Stress Based Fracture Criteria for Mixed-Mode I/II Delamination of Unidirectional Composite Laminates. Compos. Struct. 2024, 344, 118325. [Google Scholar] [CrossRef]
- Gerke, S.; Valencia, F.R.; Norz, R.; Volk, W.; Brünig, M. Damage and Fracture in Thin Metal Sheets: New Biaxial Experiments. Adv. Ind. Manuf. Eng. 2023, 7, 100129. [Google Scholar] [CrossRef]
- Abdolvand, H. Development of Microstructure-Sensitive Damage Models for Zirconium Polycrystals. Int. J. Plast. 2022, 149, 103156. [Google Scholar] [CrossRef]
- Zhu, Y.; Zeng, W.; Zhang, F.; Zhao, Y.; Zhang, X.; Wang, K. A New Methodology for Prediction of Fracture Initiation in Hot Compression of Ti40 Titanium Alloy. Mater. Sci. Eng. A 2012, 553, 112–118. [Google Scholar] [CrossRef]
- Sellars, C.M.; Whiteman, J.A. Recrystallization and Grain Growth in Hot Rolling. Met. Sci. 1979, 13, 187–194. [Google Scholar] [CrossRef]
- Maire, E.; Bouaziz, O.; Di Michiel, M.; Verdu, C. Initiation and Growth of Damage in a Dual-Phase Steel Observed by X-Ray Microtomography. Acta Mater. 2008, 56, 4954–4964. [Google Scholar] [CrossRef]
- Huang, K.; Logé, R.E.; Marthinsen, K. On the Sluggish Recrystallization of a Cold-Rolled Al–Mn–Fe–Si Alloy. J. Mater. Sci. 2016, 51, 1632–1643. [Google Scholar] [CrossRef]
- Luton, M.J.; Sellars, C.M. Dynamic Recrystallization in Nickel and Nickel-Iron Alloys during High Temperature Deformation. Acta Metall. 1969, 17, 1033–1043. [Google Scholar] [CrossRef]
- Wilkerson, J.W.; Ramesh, K.T. A Dynamic Void Growth Model Governed by Dislocation Kinetics. J. Mech. Phys. Solids 2014, 70, 262–280. [Google Scholar] [CrossRef]
- Chen, W.; Zeng, X.; Chen, L.; Yang, X.; Wang, F. Competition between Plasticity- and Void-Based Dynamic Damage Behaviors of Single Crystal HCP-Zr by Considering the High Strain Rate and Temperature. Mech. Mater. 2020, 141, 103261. [Google Scholar] [CrossRef]
- Derazkola, H.A.; Gil, E.G.; Murillo-Marrodan, A. Analysis of Super Cr13 Stainless-Steel Internal Fracture Growth Effects during Skew Mill Piercing Process. Results Eng. 2024, 21, 101682. [Google Scholar] [CrossRef]







| Element | Cr | Ni | Cu | Nb | C | Si | Mn | Fe |
| Ingredient | 16.75 | 3.90 | 3.52 | 0.25 | 0.06 | 0.70 | 0.42 | Bal. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yuan, J.; Jiang, H.; Zheng, L.; Zhang, K. Hot Tensile Behavior of 05Cr17Ni4Cu4Nb Stainless Steel: Damage Model and Fracture Characteristics. Metals 2025, 15, 776. https://doi.org/10.3390/met15070776
Yuan J, Jiang H, Zheng L, Zhang K. Hot Tensile Behavior of 05Cr17Ni4Cu4Nb Stainless Steel: Damage Model and Fracture Characteristics. Metals. 2025; 15(7):776. https://doi.org/10.3390/met15070776
Chicago/Turabian StyleYuan, Jing, Hongjun Jiang, Liwei Zheng, and Kuangyu Zhang. 2025. "Hot Tensile Behavior of 05Cr17Ni4Cu4Nb Stainless Steel: Damage Model and Fracture Characteristics" Metals 15, no. 7: 776. https://doi.org/10.3390/met15070776
APA StyleYuan, J., Jiang, H., Zheng, L., & Zhang, K. (2025). Hot Tensile Behavior of 05Cr17Ni4Cu4Nb Stainless Steel: Damage Model and Fracture Characteristics. Metals, 15(7), 776. https://doi.org/10.3390/met15070776





