Machine Learning-Driven Prediction of Glass-Forming Ability in Fe-Based Bulk Metallic Glasses Using Thermophysical Features and Data Augmentation
Abstract
1. Introduction
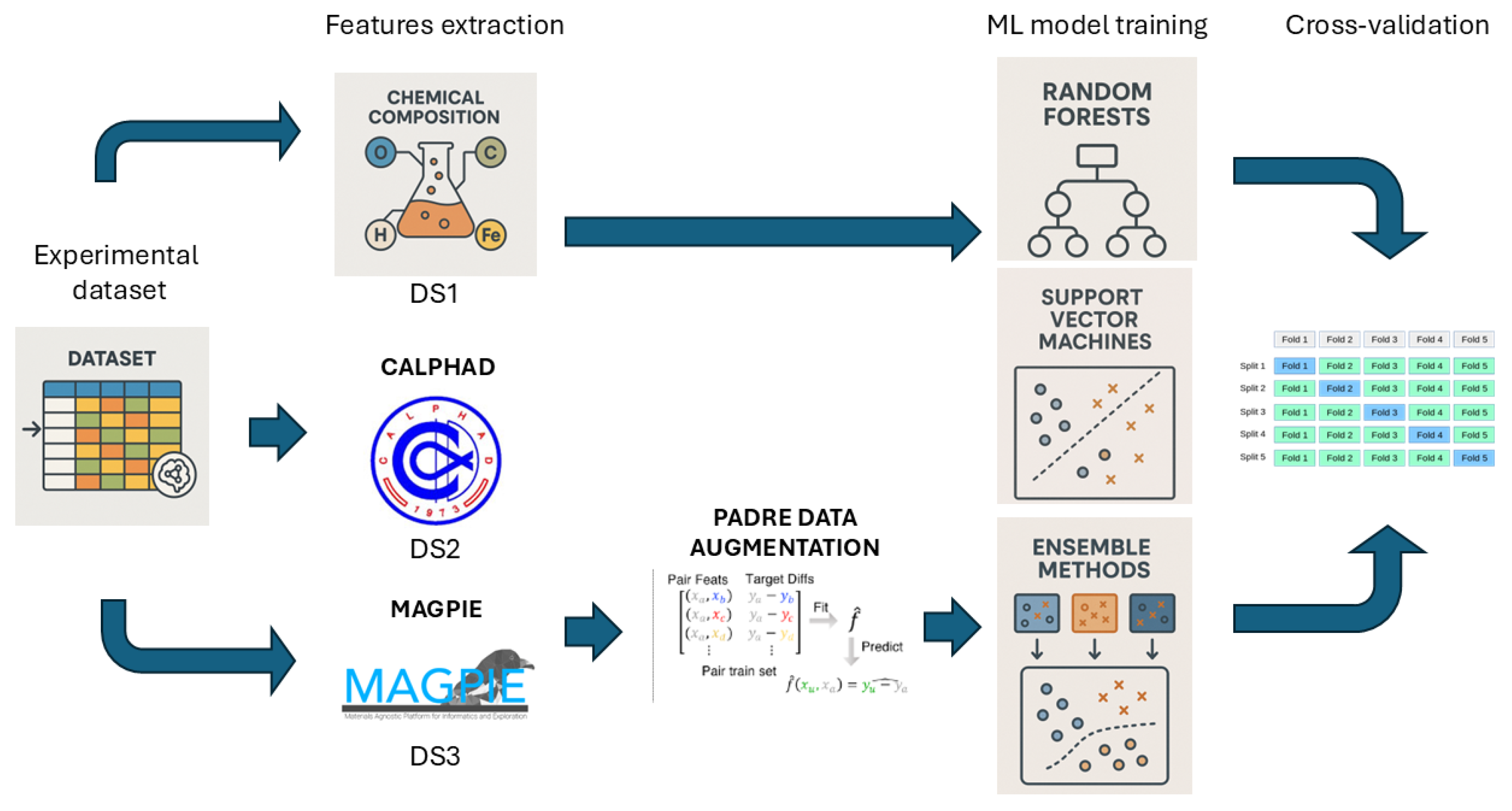
2. Methodology
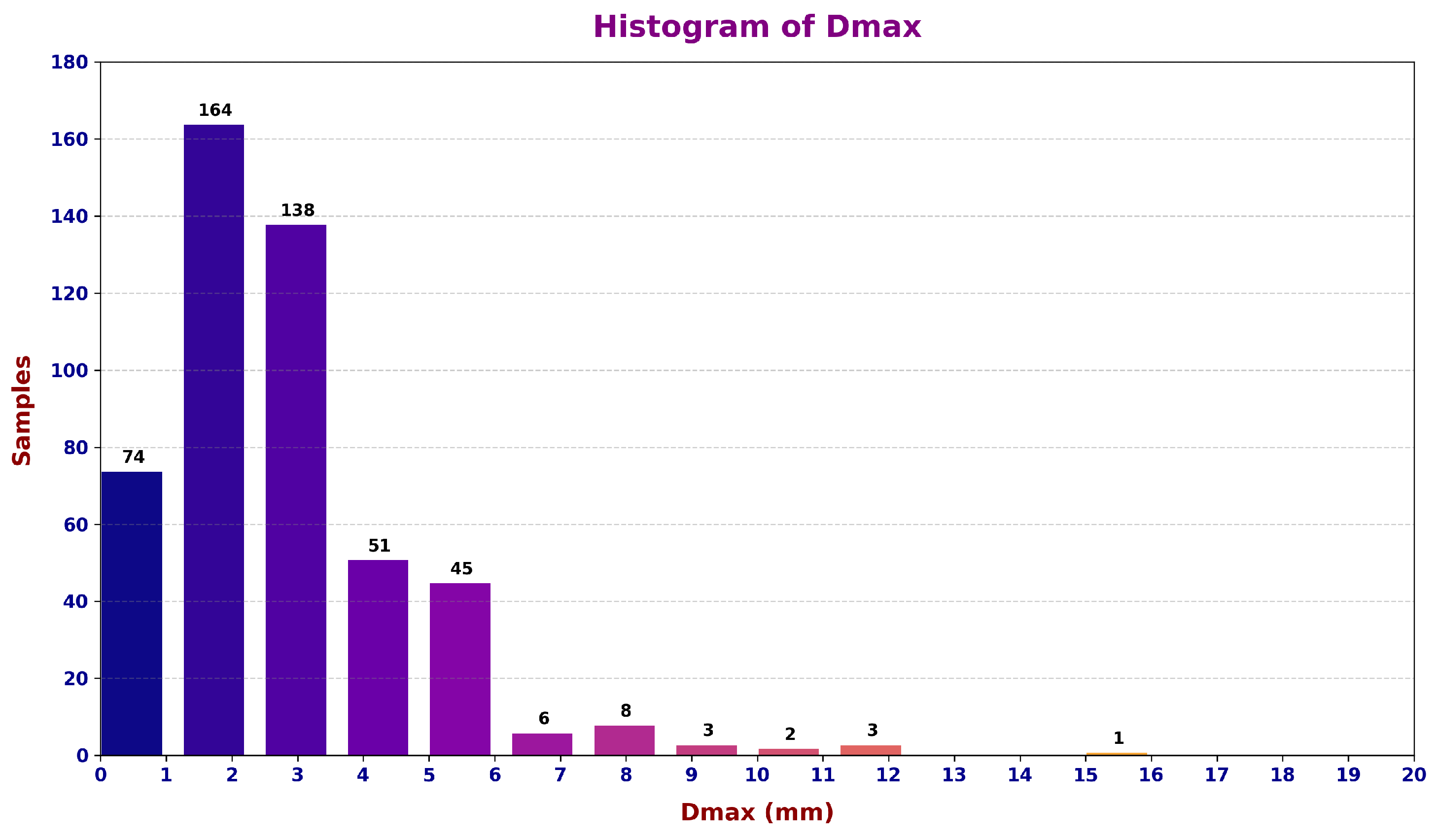
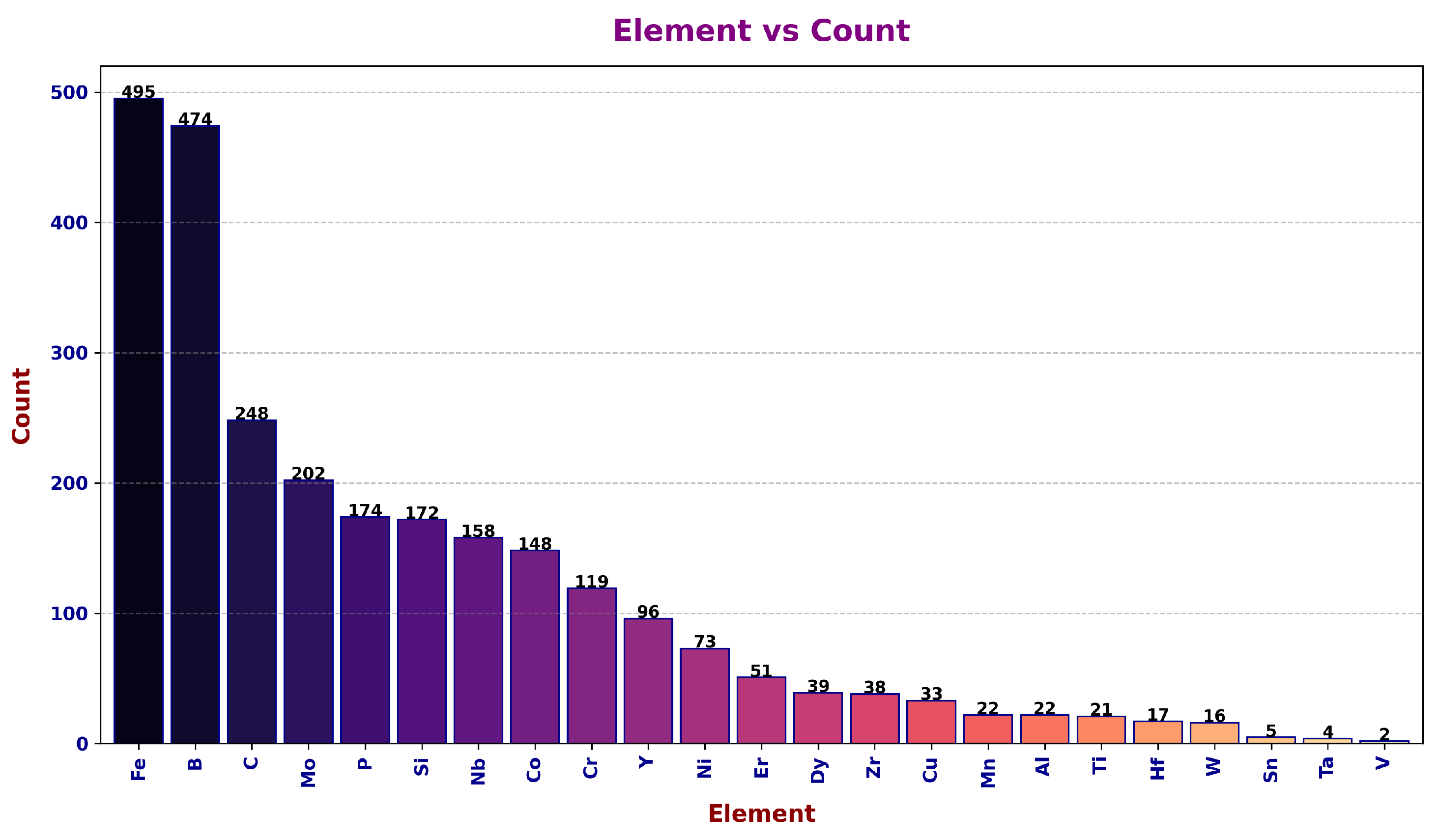
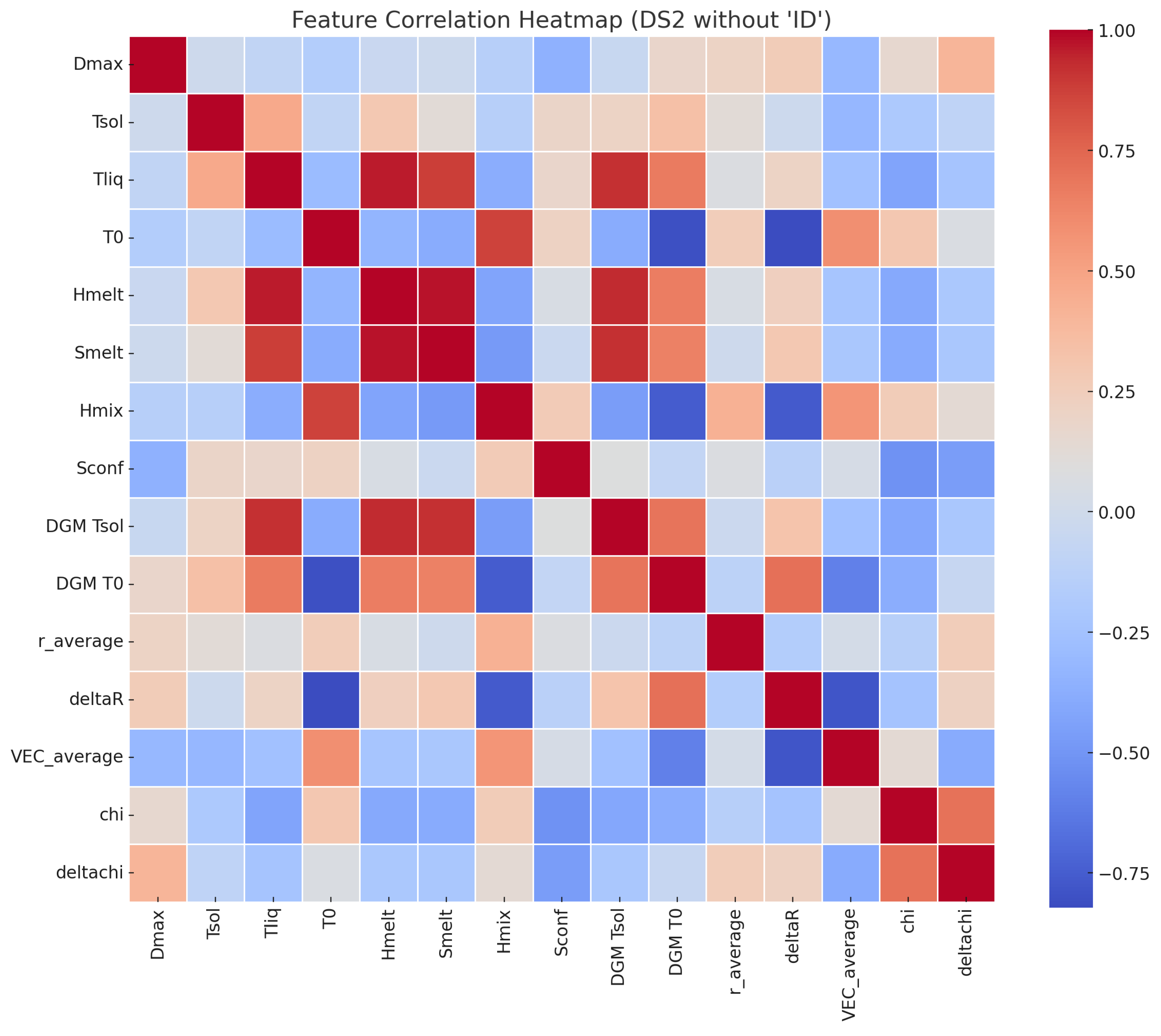
2.1. Datasets
2.2. Machine Learning
3. Results and Discussion
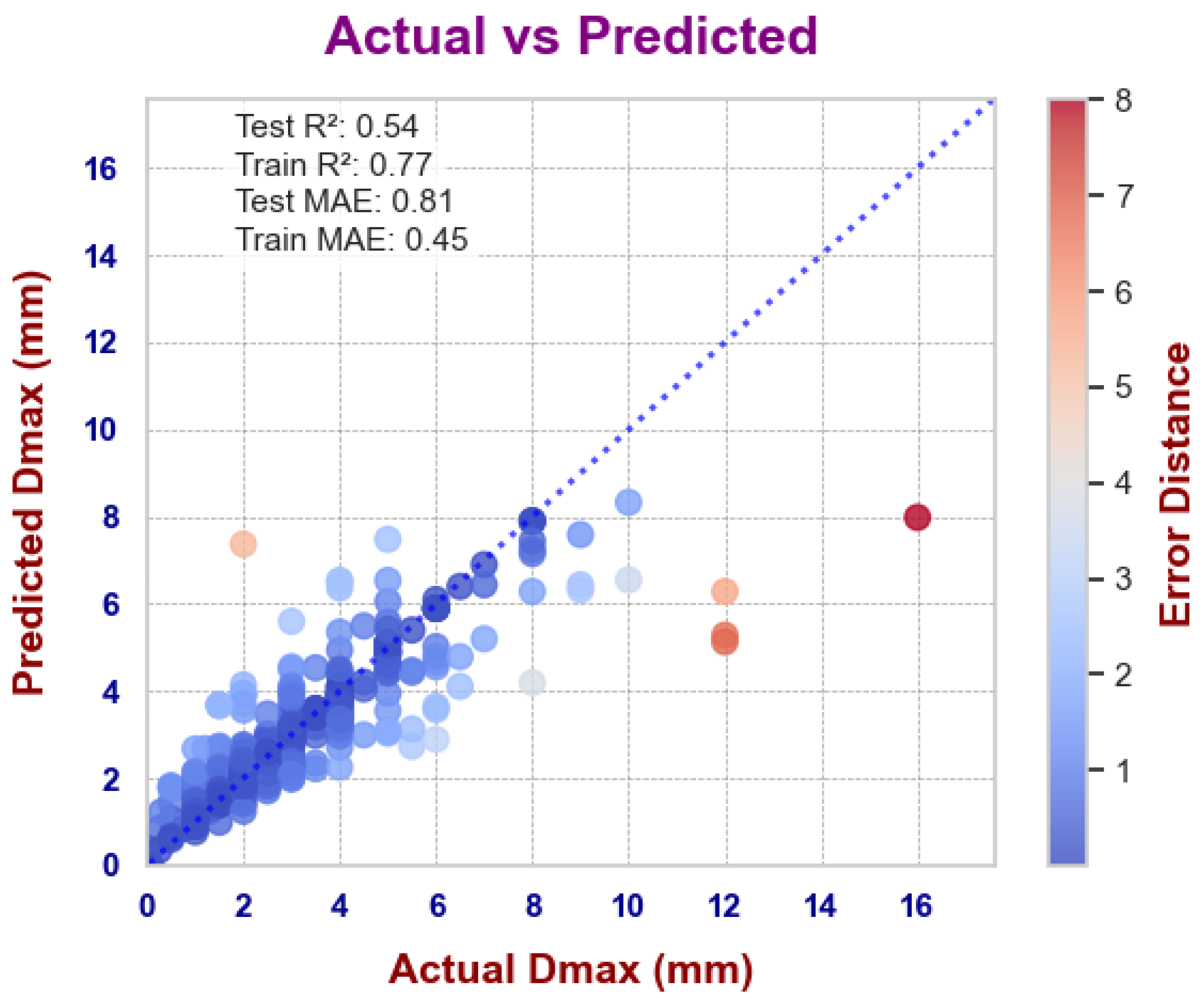
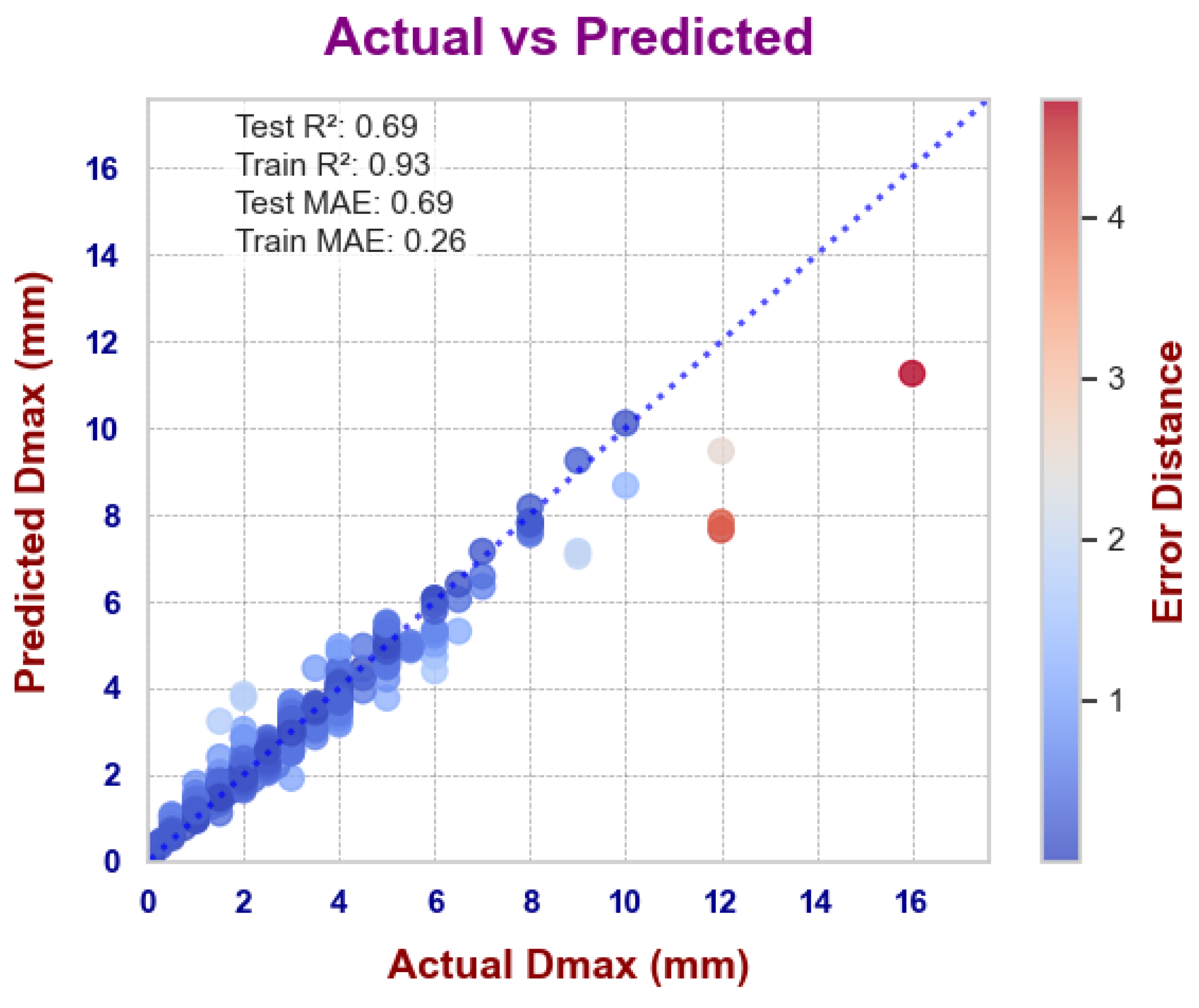
3.1. ML Models on Composition and Thermophysical Datasets
3.2. ML Models on Magpie Dataset
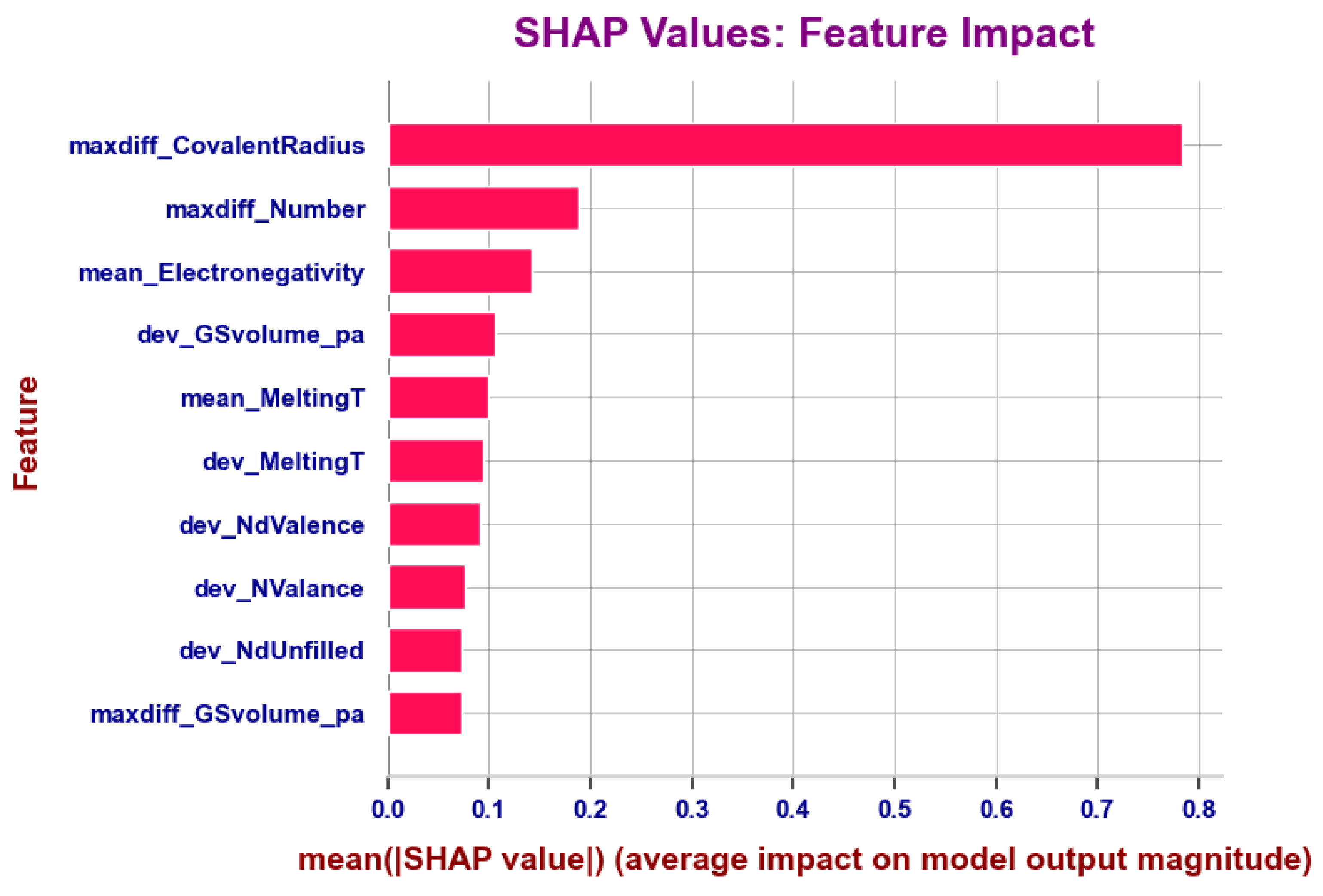
3.3. Features Importance
4. Ensemble Methods
PADRE Data Augmentation
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Klement, W.; Willens, R.; Duwez, P. Non-crystalline structure in solidified gold–silicon alloys. Nature 1960, 187, 869–870. [Google Scholar] [CrossRef]
- Greer, A. 4—Metallic Glasses. In Physical Metallurgy, 5th ed.; Laughlin, D.E., Hono, K., Eds.; Elsevier: Oxford, UK, 2014; pp. 305–385. [Google Scholar] [CrossRef]
- Khanolkar, G.R.; Rauls, M.B.; Kelly, J.P.; Graeve, O.A.; Eliasson, A.M.H.; Eliasson, V. Shock Wave Response of Iron-based In Situ Metallic Glass Matrix Composites. Sci. Rep. 2016, 6, 22568. [Google Scholar] [CrossRef] [PubMed]
- Hashimoto, K. What we have learned from studies on chemical properties of amorphous alloys? Appl. Surf. Sci. 2011, 257, 8141–8150. [Google Scholar] [CrossRef]
- Sparks, T.D.; Kauwe, S.K.; Parry, M.E.; Tehrani, A.M.; Brgoch, J. Machine Learning for Structural Materials. Annu. Rev. Mater. Res. 2020, 50, 27–48. [Google Scholar] [CrossRef]
- Greer, A.L. Confusion by design. Nature 1993, 366, 303–304. [Google Scholar] [CrossRef]
- Inoue, A. Stabilization of metallic supercooled liquid and bulk amorphous alloys. Acta Mater. 2000, 48, 279–306. [Google Scholar] [CrossRef]
- Palumbo, M.; Battezzati, L. Thermodynamics and kinetics of metallic amorphous phases in the framework of the CALPHAD approach. Calphad 2008, 32, 295–314. [Google Scholar] [CrossRef]
- Miracle, D.B.; Sanders, W.S.; Senkov, O.N. The influence of efficient atomic packing on the constitution of metallic glasses. Philos. Mag. 2003, 83, 2409–2428. [Google Scholar] [CrossRef]
- Graeve, O.A.; García-Vázquez, M.S.; Ramírez-Acosta, A.A.; Cadieux, Z. Latest Advances in Manufacturing and Machine Learning of Bulk Metallic Glasses. Adv. Eng. Mater. 2023, 25, 2201493. [Google Scholar] [CrossRef]
- Schmidt, J.; Marques, M.; Botti, S.; Marques, M. Recent advances and applications of machine learning in solid-state materials science. npj Comput. Mater. 2019, 5, 83. [Google Scholar] [CrossRef]
- Ward, L.; O’Keeffe, S.C.; Stevick, J.; Jelbert, G.R.; Aykol, M.; Wolverton, C. A machine learning approach for engineering bulk metallic glass alloys. Acta Mater. 2018, 159, 102–111. [Google Scholar] [CrossRef]
- Ren, B.; Long, Z.; Deng, R. A new criterion for predicting the glass-forming ability of alloys based on machine learning. Comput. Mater. Sci. 2021, 189, 110259. [Google Scholar] [CrossRef]
- Deng, B.; Zhang, Y. Critical feature space for predicting the glass forming ability of metallic alloys revealed by machine learning. Chem. Phys. 2020, 538, 110898. [Google Scholar] [CrossRef]
- Ghorbani, A.; Askari, A.; Malekan, M.; Nili-Ahmadabadi, M. Thermodynamically-guided machine learning modelling for predicting the glass-forming ability of bulk metallic glasses. Sci. Rep. 2022, 12, 11754. [Google Scholar] [CrossRef]
- Long, T.; Long, Z.; Pang, B.; Li, Z.; Liu, X. Overcoming the challenge of the data imbalance for prediction of the glass forming ability in bulk metallic glasses. Mater. Today Commun. 2023, 35, 105610. [Google Scholar] [CrossRef]
- Mastropietro, D.G.; Moya, J.A. Design of Fe-based bulk metallic glasses for maximum amorphous diameter (Dmax) using machine learning models. Comput. Mater. Sci. 2021, 188, 110230. [Google Scholar] [CrossRef]
- Xiong, J.; Shi, S.Q.; Zhang, T.Y. Machine learning prediction of glass-forming ability in bulk metallic glasses. Comput. Mater. Sci. 2021, 192, 110362. [Google Scholar] [CrossRef]
- Xiong, J.; Shi, S.Q.; Zhang, T.Y. A machine-learning approach to predicting and understanding the properties of amorphous metallic alloys. Mater. Des. 2020, 187, 108378. [Google Scholar] [CrossRef]
- Xiong, J.; Zhang, T.Y. Data-driven glass-forming ability criterion for bulk amorphous metals with data augmentation. J. Mater. Sci. Technol. 2022, 121, 99–104. [Google Scholar] [CrossRef]
- Dasgupta, A.; Broderick, S.; Mack, C.; Urala Kota, B.; Subramanian, R.; Setlur, S.; Govindaraju, V.; Rajan, K. Probabilistic Assessment of Glass Forming Ability Rules for Metallic Glasses Aided by Automated Analysis of Phase Diagrams. Sci. Rep. 2019, 9, 357. [Google Scholar] [CrossRef]
- Lukas, H.; Fries, S.G.; Sundman, B. Computational Thermodynamics: The Calphad Method; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- ThermoCalc. ThermoCalc Website. 2023. Available online: https://thermocalc.com/ (accessed on 25 November 2024).
- Tynes, M.; Gao, W.; Burrill, D.J.; Batista, E.R.; Perez, D.; Yang, P.; Lubbers, N. Pairwise Difference Regression: A Machine Learning Meta-algorithm for Improved Prediction and Uncertainty Quantification in Chemical Search. J. Chem. Inf. Model. 2021, 61, 3846–3857. [Google Scholar] [CrossRef] [PubMed]
- Andersson, J.O.; Helander, T.; Höglund, L.; Shi, P.; Sundman, B. Thermo-Calc & DICTRA, computational tools for materials science. Calphad 2002, 26, 273–312. [Google Scholar] [CrossRef]
- Bocklund, B.; Otis, R.; Egorov, A.; Obaied, A.; Roslyakova, I.; Liu, Z. ESPEI for efficient thermodynamic database development, modification, and uncertainty quantification: Application to Cu–Mg. MRS Commun. 2019, 9, 618–627. [Google Scholar] [CrossRef]
- Ward, L.; Agrawal, A.; Choudhary, A.; Wolverton, C. A General-Purpose Machine Learning Framework for Predicting Properties of Inorganic Materials. npj Comput. Mater. 2016, 2, 16028. [Google Scholar] [CrossRef]
- James, G.; Witten, D.; Hastie, T.; Tibshirani, R.; Taylor, J. Classification, Regression. In An Introduction to Statistical Learning: With Applications in Python; Springer: Berlin/Heidelberg, Germany, 2023. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Müller, A.; Nothman, J.; Louppe, G.; et al. Scikit-learn: Machine Learning in Python. arXiv 2018, arXiv:1201.0490. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, KDD ’16, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar] [CrossRef]
- Lundberg, S.M.; Lee, S.I. A Unified Approach to Interpreting Model Predictions. In Advances in Neural Information Processing Systems 30; Guyon, I., Luxburg, U.V., Bengio, S., Wallach, H., Fergus, R., Vishwanathan, S., Garnett, R., Eds.; Curran Associates Inc.: New York, NY, USA, 2017; pp. 4765–4774. [Google Scholar]
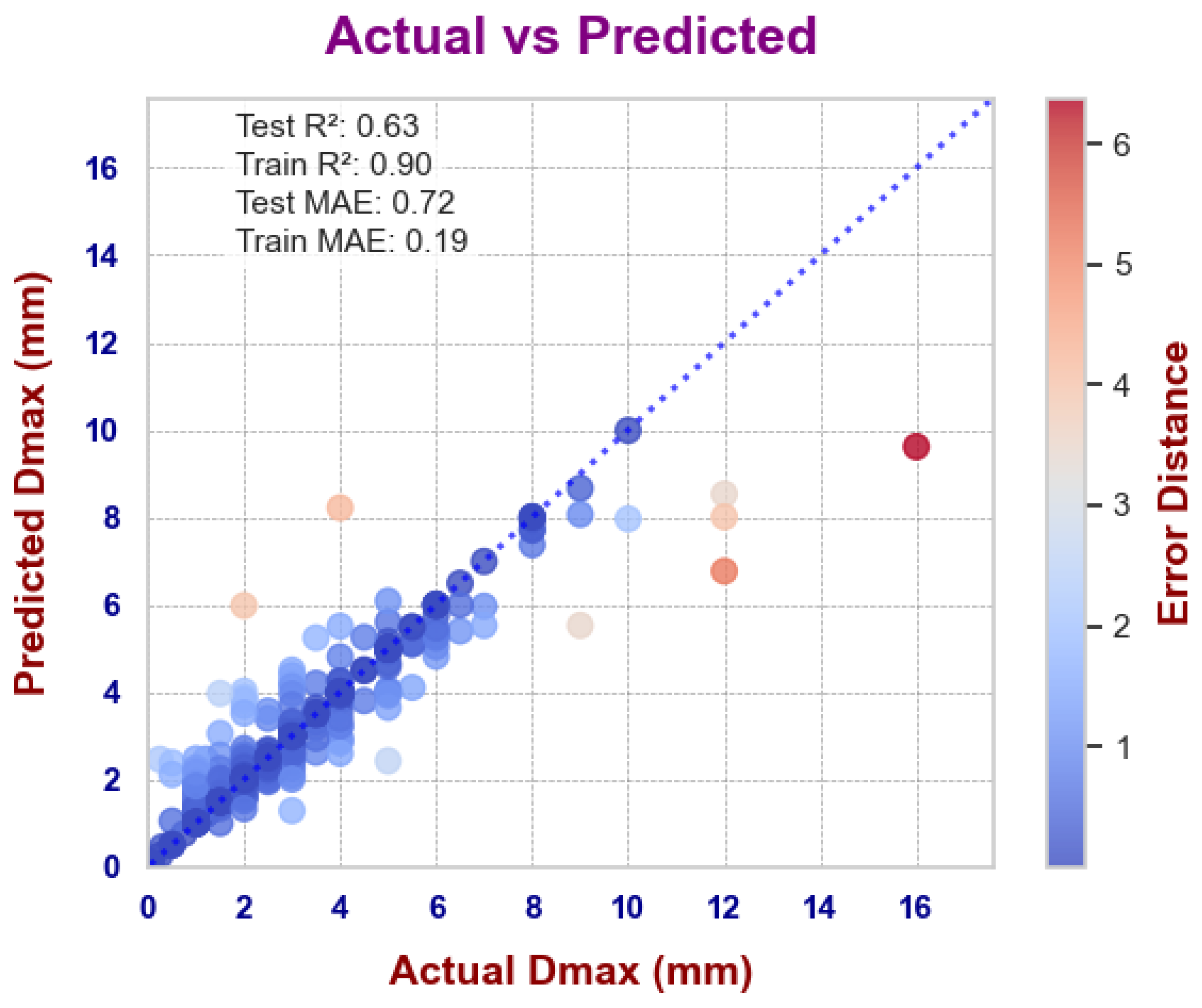
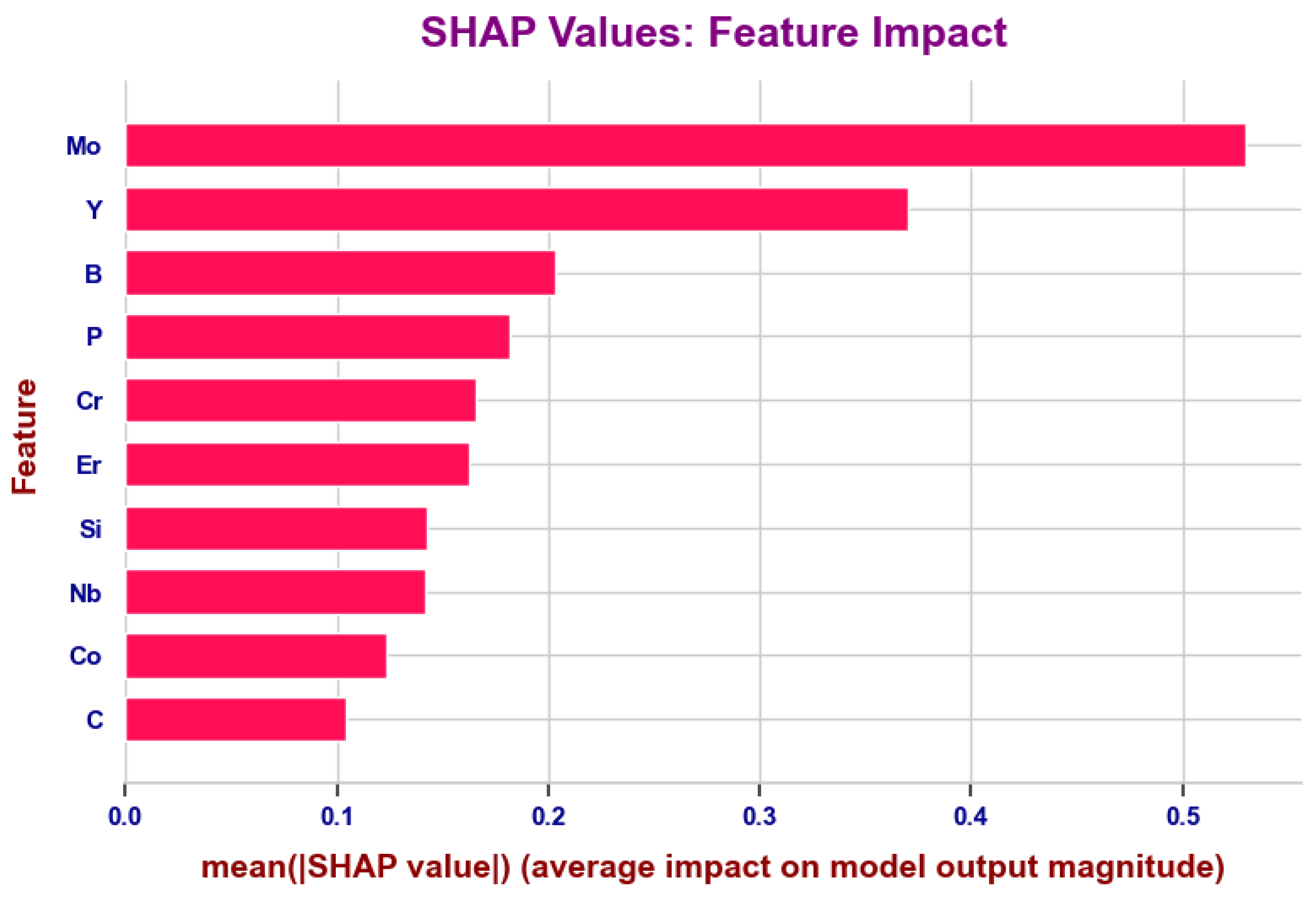
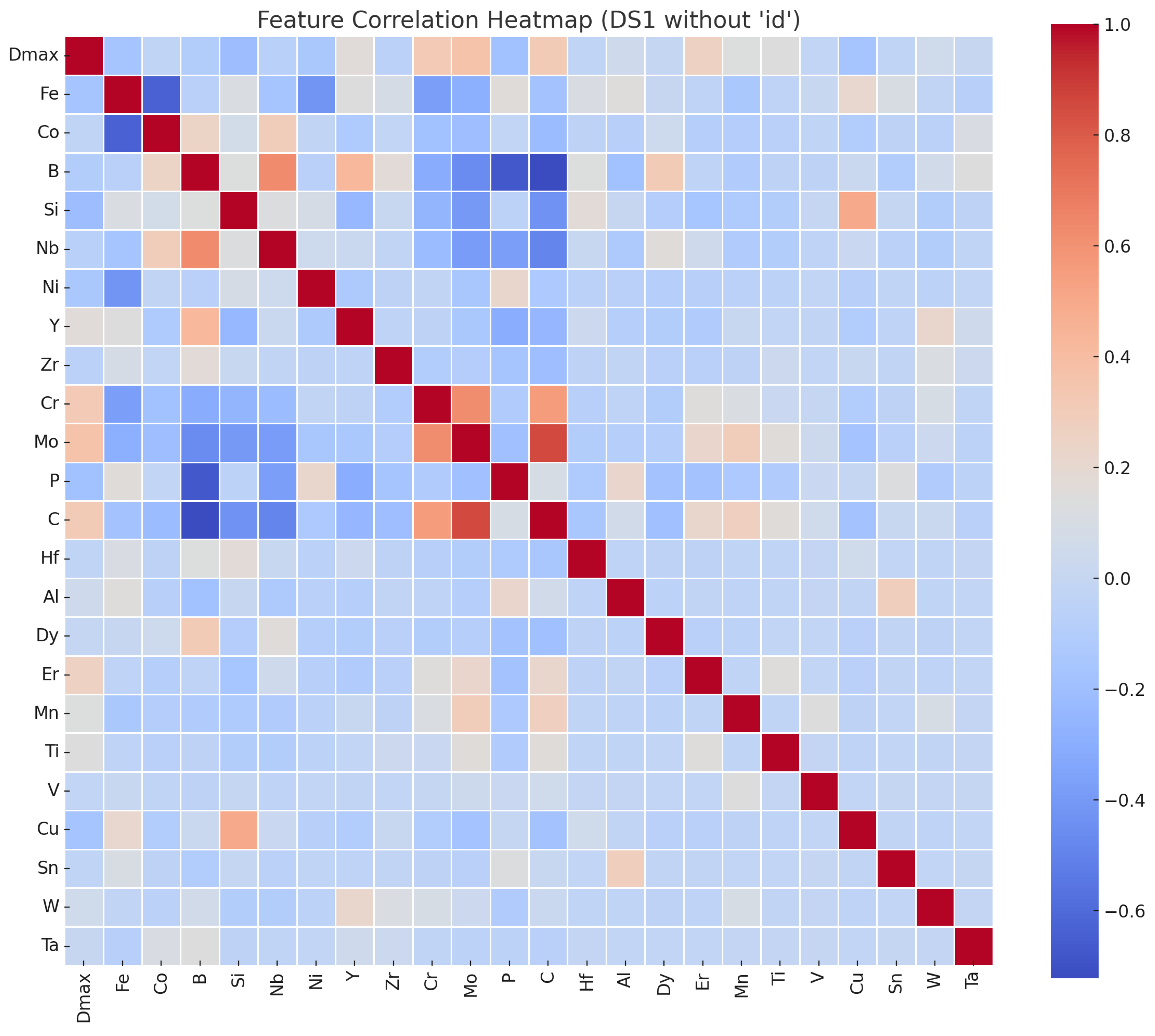
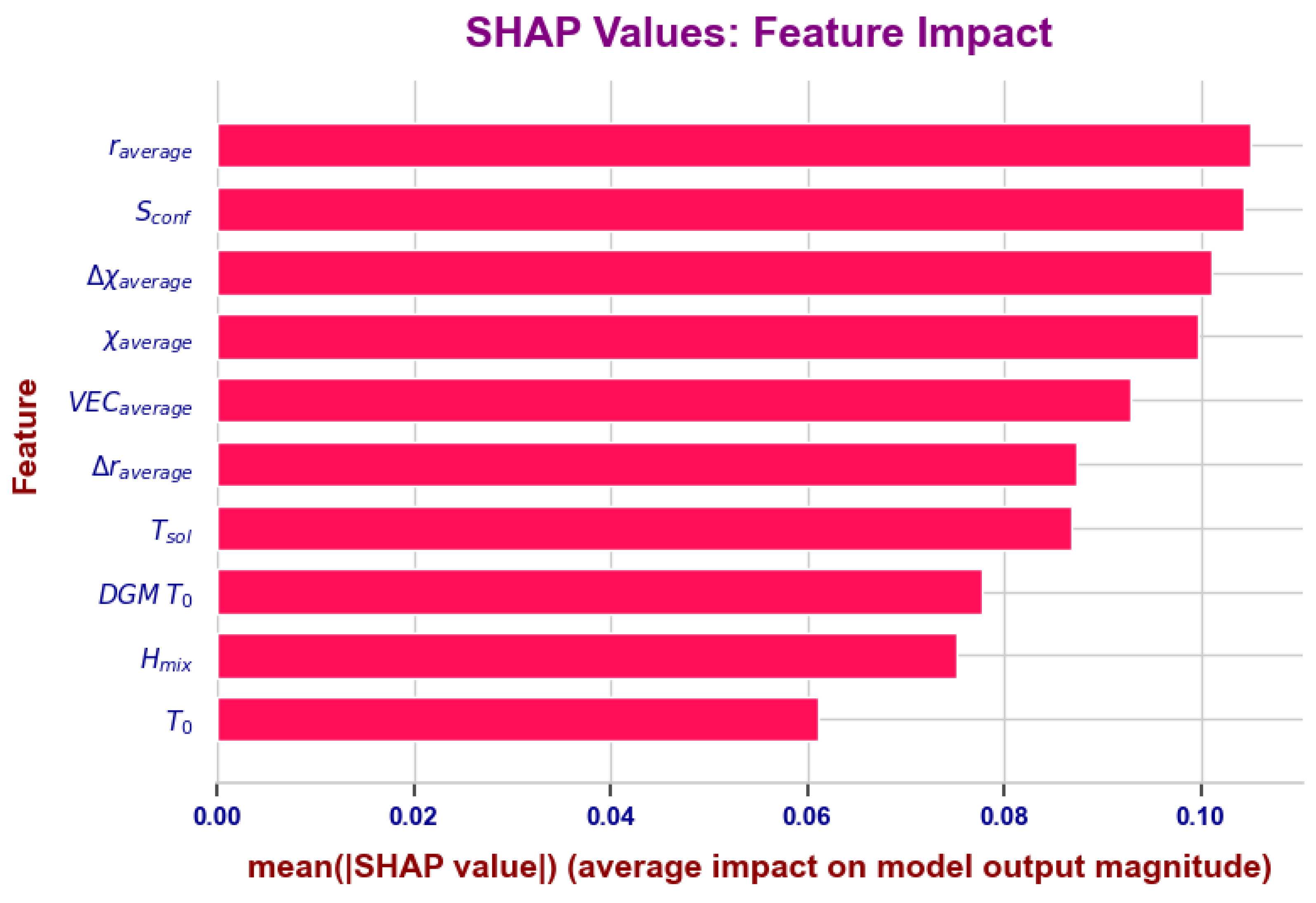
| ML Model | Test Score | Test Score |
|---|---|---|
| Multiple Linear Regressor (DS1) | 0.18 | 1.18 |
| Multiple Linear Regressor (DS2) | 0.24 | 1.13 |
| Support Vector Regressor (DS1) | 0.54 | 0.81 |
| Support Vector Regressor (DS2) | 0.63 | 0.72 |
| XGBoost (DS1) | 0.54 | 0.85 |
| XGBoost (DS2) | 0.60 | 0.77 |
| Model | Test Score | Test Score |
|---|---|---|
| RF | 0.61 | 0.79 |
| GBRF | 0.62 | 0.76 |
| XGBoost | 0.65 | 0.73 |
| Support Vector Regressor | 0.58 | 0.79 |
| Ensemble Models Results | ||
|---|---|---|
| Ensemble | Test Score | Test Score |
| MLR(DS1) + XGB(DS1) | 0.52 | 0.89 |
| MLR(DS2) + XGB(DS2) | 0.52 | 0.88 |
| SVR(DS1) + XGB(DS1) | 0.62 | 0.75 |
| SVR(DS2) + XGB(DS2) | 0.67 | 0.70 |
| XGB(DS1) + XGB(DS2) | 0.65 | 0.75 |
| SVR(DS1) + XGB(DS1) + | ||
| SVR(DS2) + XGB(DS2) | 0.68 | 0.69 |
| SVR(DS3) + XGB(DS3) + | ||
| SVR(DS2) + XGB(DS2) | 0.69 | 0.69 |
| Test Score | Notes | Source |
|---|---|---|
| 0.79 | a posteriori approach, including ribbon samples, large dataset | [12] |
| 0.64 | a posteriori approach, only BMGs samples, large dataset | [12] |
| 0.64 | a posteriori approach | [14] |
| 0.95 | a posteriori approach | [15] |
| 0.68 | a priori approach, best ensemble method | this work |
| 0.63 | a priori approach, best single model | this work |
| 0.64 | a priori approach | [19] |
| 0.71 | a priori approach, ensemble method | [17] |
| 0.76 | a priori approach, data augmentation | [20] |
| Dataset | Test Score | Test Score |
|---|---|---|
| DSA1 | 0.54 | 0.85 |
| DSA2 | 0.59 | 0.78 |
| DSA1-2 | 0.58 | 0.76 |
| DSA2-2 | 0.66 | 0.72 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bobadilla, R.D.B.; Baricco, M.; Palumbo, M. Machine Learning-Driven Prediction of Glass-Forming Ability in Fe-Based Bulk Metallic Glasses Using Thermophysical Features and Data Augmentation. Metals 2025, 15, 763. https://doi.org/10.3390/met15070763
Bobadilla RDB, Baricco M, Palumbo M. Machine Learning-Driven Prediction of Glass-Forming Ability in Fe-Based Bulk Metallic Glasses Using Thermophysical Features and Data Augmentation. Metals. 2025; 15(7):763. https://doi.org/10.3390/met15070763
Chicago/Turabian StyleBobadilla, Renato Dario Bashualdo, Marcello Baricco, and Mauro Palumbo. 2025. "Machine Learning-Driven Prediction of Glass-Forming Ability in Fe-Based Bulk Metallic Glasses Using Thermophysical Features and Data Augmentation" Metals 15, no. 7: 763. https://doi.org/10.3390/met15070763
APA StyleBobadilla, R. D. B., Baricco, M., & Palumbo, M. (2025). Machine Learning-Driven Prediction of Glass-Forming Ability in Fe-Based Bulk Metallic Glasses Using Thermophysical Features and Data Augmentation. Metals, 15(7), 763. https://doi.org/10.3390/met15070763






