Numerical Simulation of Fluid Flow, Heat Transfer, and Solidification in AISI 304 Stainless Steel Twin-Roll Strip Casting

Abstract

The production of AISI 304 stainless steel (a corrosion-resistant alloy prone to solidification defects from high alloy content) particularly benefits from twin-roll strip casting—a short-process green technology enabling sub-rapid solidification (the maximum cooling rate exceeds 1000 °C/s) control for high-performance steels. However, the internal phenomena within its molten pool remain exceptionally challenging to monitor. This study developed a multiscale numerical model to simulate coupled fluid flow, heat transfer, and solidification in AISI 304 stainless steel twin-roll strip casting. A quarter-symmetry 3D model captured macroscopic transport phenomena, while a slice model resolved mesoscopic solidification structure. Laboratory experiments had verified that the deviation between the predicted temperature field and the measured average value (1384.3 °C) was less than 5%, and the error between the solidification structure simulation and the electron backscatter diffraction (EBSD) data was within 5%. The flow field and flow trajectory showed obvious recirculation zones: the center area was mainly composed of large recirculation zones, and many small recirculation zones appeared at the edges. Parameter studies showed that, compared with the high superheat (110 °C), the low superheat (30 °C) increased the total solid fraction by 63% (from 8.3% to 13.6%) and increased the distance between the kiss point and the bottom of the molten pool by 154% (from 6.2 to 15.8 mm). The location of the kiss point is a key industrial indicator for assessing solidification integrity and the risk of strip fracture. In terms of mesoscopic solidification structure, low superheat promoted the formation of coarse columnar crystals (equiaxed crystals accounted for 8.9%), while high superheat promoted the formation of equiaxed nucleation (26.5%). The model can be used to assist in the setting of process parameters and process optimization for twin-roll strip casting.

1. Introduction

AISI 304 stainless steel dominates >50% of global corrosion-resistant steel demand (food/chemical/medical industries), yet its wide solidification range and low thermal conductivity exacerbate segregation and surface cracking risks during thin-strip casting, demanding targeted process optimization to replace costly post-casting treatments [1]. While advanced deposition techniques like directed energy deposition (DED) and laser metal deposition (LMD) have enabled refined microstructures and enhanced mechanical properties in additively manufactured AISI 304 stainless steel, these methods remain constrained by low throughput and high cost for large-scale strip production [2,3].

Twin-roll strip casting is a transformative near-net-shape manufacturing technology in which molten metal is directly solidified into thin strips (typically 1–5 mm thick) through rapid thermal extraction between reverse-rotating water-cooled copper rollers [4,5]. This innovative process has significant sustainability advantages [6,7]: compared with traditional continuous casting and multi-pass hot rolling, it eliminates the energy-intensive reheating stage, greatly reducing the requirements for rolling deformation, thereby reducing energy consumption and carbon dioxide emissions by 30–50% throughout the production chain [8]. This efficiency advantage makes strip casting an environmentally friendly strategic technology for manufacturing advanced steel grades [9,10], especially stainless steel—a material that requires fine control of the solidification structure to optimize its strength-ductility synergy characteristics [11,12]. At present, neither industrial practice nor laboratory experiments can observe and measure in real time key phenomena such as the fluctuation of the molten pool, heat transfer at the interface between the steel and the rollers, and early grain nucleation [13,14]. However, heat transfer and dynamic solidification have significant influences on the edge cracking and microstructure inhomogeneity of the steel strip [15]. Therefore, industrial deployment is constantly challenged by the complexity of multiple physical fields within a closed molten pool [16].

To address the current difficulties in the application of this technology, numerical simulation has become a key tool for detecting the TRSC mechanism, considering the infeasibility of experimental measurement and observation of high-temperature molten pools [17]. The CFD method is widely used in the calculation of the physical field of molten pools. Liu et al. [18] employed commercial CFD software (ProCAST) to simulate transient multiphysics phenomena—fluid flow, heat transfer, and solidification—during twin-roll strip casting using diverse delivery systems. The 3D model coupled Volume of Fluid (VOF) free-surface tracking, k-ε turbulence modeling, and enthalpy-based phase change. Mahmoudi et al. [19] employed 3D k-ε CFD simulations to demonstrate that nozzle design (free/submerged jets, slot/slot-submerged inlets) critically governs flow patterns and heat flux distribution in the upper mold region of continuous strip casting, with slot-type inlets significantly reducing turbulence and average flow velocities. Similarly, the finite element method is also widely applied. Wang et al. [20] employed a 3D CAFE model incorporating Gaussian nucleation and KGT dendrite kinetics to demonstrate that pouring temperature dominantly controls grain density and microstructure evolution in twin-roll strip casting, while roll-strip heat transfer exhibits negligible influence under examined cooling conditions. Zhang et al. [21] simulated stress evolution in 304 stainless steel during twin-roll casting by a finite element model, identifying maximum tensile stress at subsurface regions 5–10° from the nip point. Jiang et al. [22] developed a 3D thermo-fluid FEM model incorporating inverse boundary condition determination at roll-pool interfaces, revealing how pouring temperature and liquid level height govern flow-thermal behavior in twin-roll stainless steel casting, with simulated surface temperatures validated against experimental measurements. Zhang et al. [23] employed a 2D thermal model of top-side-pouring twin-roll casting to obtain the double-peak heat flux/temperature profiles at high speeds, demonstrating that cooling water flux outweighs rolling speed in controlling roll surface temperature, with optimized fluxes of 4 m³/h (upper) and 6 m³/h (bottom roll) achieving thermal balance.

Despite the progress made, there is still a serious gap in the simulation of twin-roll strip casting. Firstly, the models adopted in the research are somewhat different from those in actual industry, and some approximations and simplifications have been adopted [24]. Secondly, most studies adopt simplified thermal boundaries and ignore the experimentally verified values at the roller/steel interface. Furthermore, many studies have not linked flow, heat transfer, and solidification structures. They have only studied flow coupled with heat transfer or heat transfer coupled with solidification, either due to the limitations of the calculation methods/software or for the consideration of balancing the amount of calculation and accuracy.

To address these gaps, this study establishes a multi-scale numerical model to simulate the fluid flow, heat transfer, and solidification in the twin-roll strip casting process of AISI 304 stainless steel. The one quarter 3D model is used to simulate macroscopic transport phenomena, while the slice model simulates mesoscopic solidification structures. Meanwhile, the initial/boundary conditions used in the simulation are all derived from experiments, and the model verification is also accomplished through temperature measurement during the experimental process and electron back-scattered diffraction (EBSD) of the cast strip. The mesoscopic solidification structures of stainless steel strips under varying superheat levels were compared by this model, and their practical implications for industrial production were analyzed, thus providing a basis for process optimization.

2. Experimental Methods

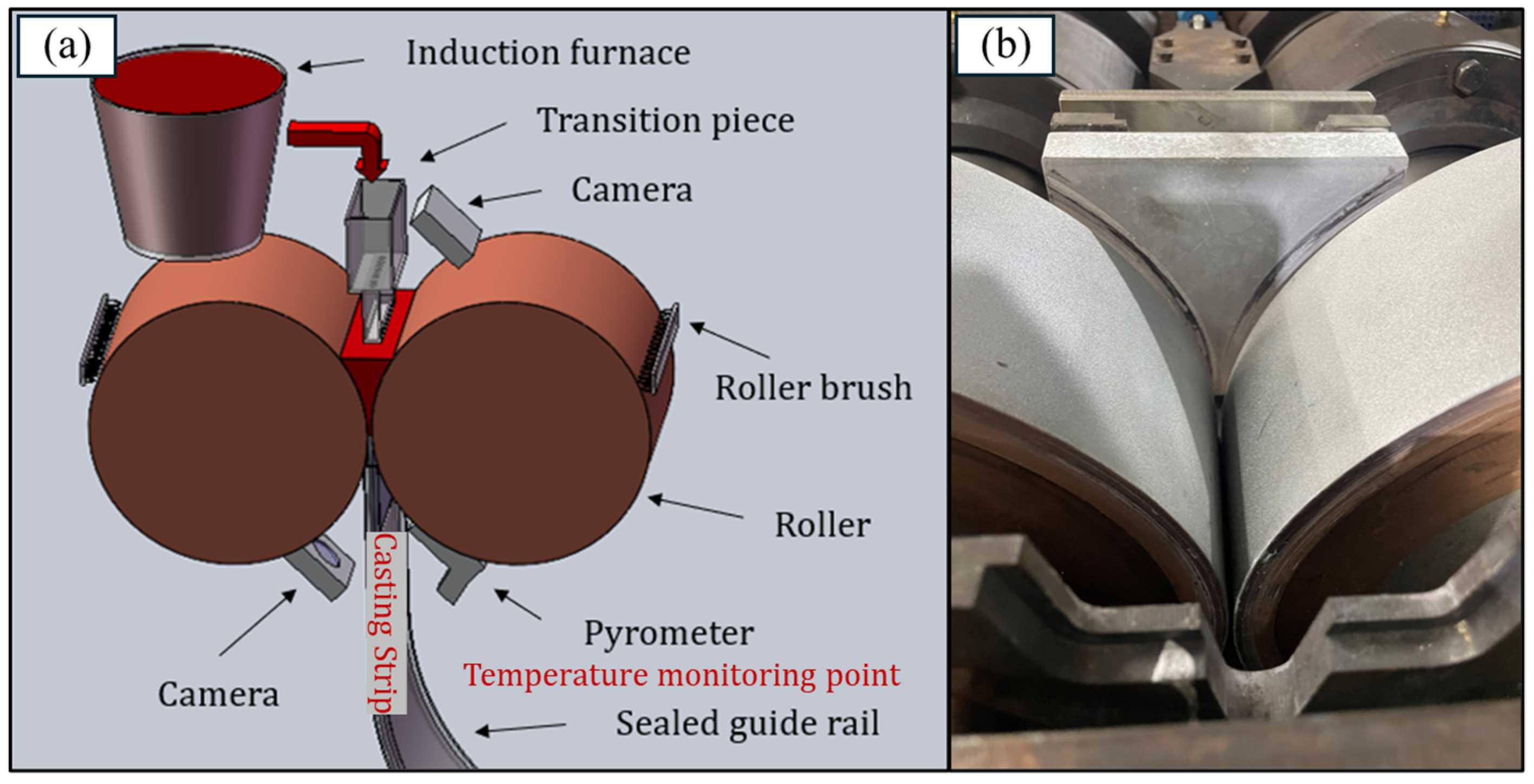
2.1. Casting Procedure and Material

Laboratory-scale twin-roll strip casting equipment was constructed to replicate industrial-scale equipment (Figure 1a). The equipment consists of several components: a melting system (medium-frequency induction furnace), a flow control device (transition piece), a pair of water-cooled copper rollers, side dams, and data/image acquisition systems. The diameter of the casting roller is 300 mm, and the rotational speed is 17.0 rpm. Figure 1b shows the actual molten pool formed between the rollers and side dams. In the casting experiment, raw metal materials were first melted in the induction furnace and superheated to a predetermined temperature. The molten metal was then poured into the transition piece, which directed the liquid metal into the molten pool, forming a certain height of the molten pool liquid level. Due to the cooling effect of the copper rollers, solidification initiated upon contact, forming a thin solidified shell. As the rollers rotated at high speed, the solidified shells grew continuously and merged at the roll nip, ultimately producing a 2~3 mm thick strip. The data acquisition system records the real-time temperature of the casting strip, images during the casting process, and other data for subsequent analysis. Key process parameters, including superheat, casting speed, and cooling water flow rate, were carefully controlled to match industrial operating conditions.

The molten pool in the numerical model was defined as AISI 304 stainless steel, with its chemical composition provided in

Table 1. Main composition of AISI 304 stainless steel.

Element	C	Cr	Ni	Mn	Si
wt.%	0.045	18.25	8.1	1.25	0.45

. To support the simulations, thermo-physical parameters of the AISI 304 stainless steel were calculated using the Fe database in ProCAST 2018.0, and the results are shown in Figure 2, including thermal conductivity, density, enthalpy, and solid fraction. The enthalpy-temperature relationship and solid fraction curve were determined using the Scheil–Gulliver model to account for non-equilibrium solidification characteristics. These parameters critically govern the heat transfer and phase transition behaviors during the strip casting process. Under non-equilibrium solidification conditions, the melting point temperature and solidification temperature of AISI 304 stainless steel are 1462 °C and 1208 °C, respectively. The significant variation in the thermal conductivity of stainless steel between 1000 and 1500 °C is mainly caused by the lattice thermal vibration and phase transformation effect of the material itself.

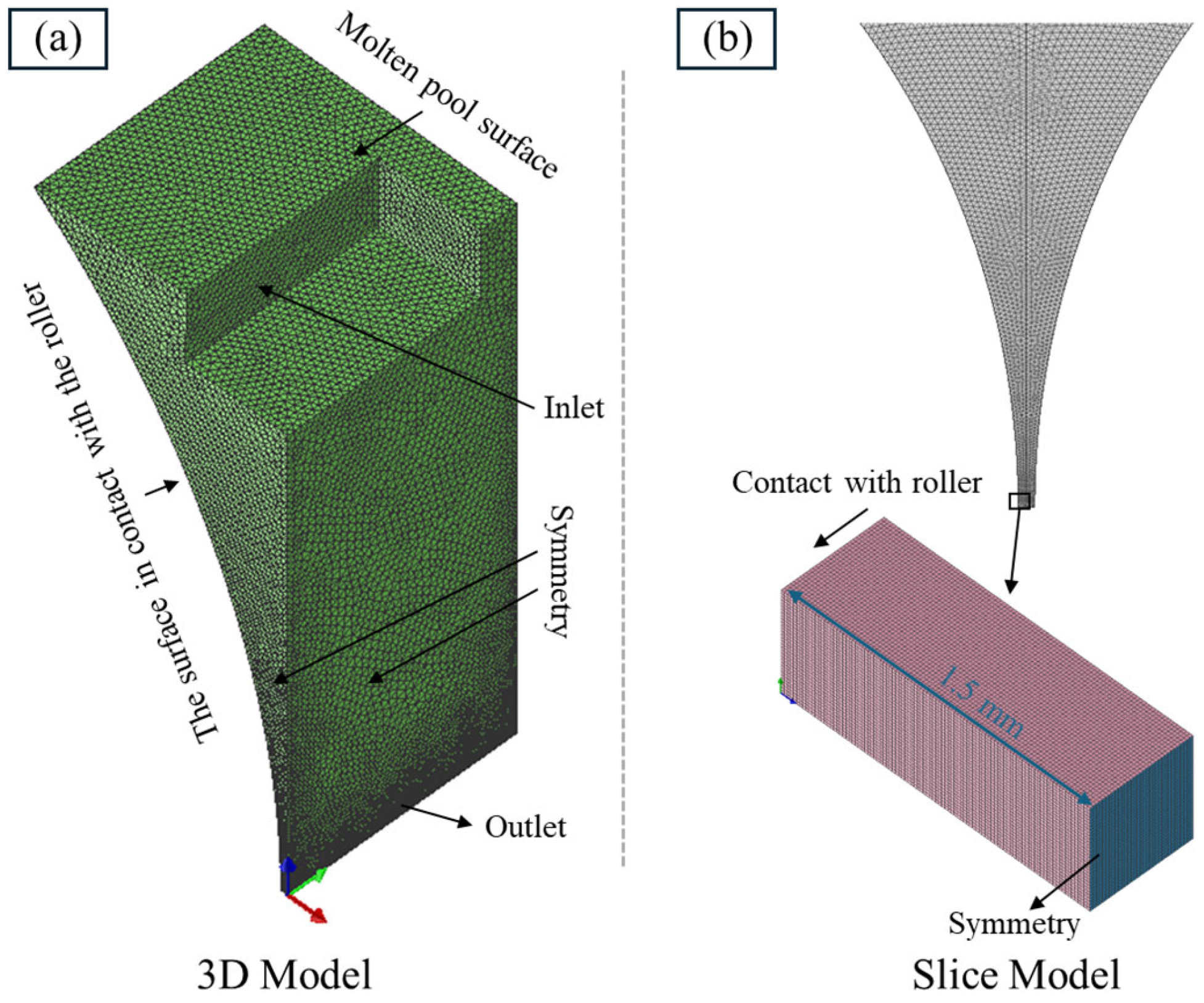
2.2. Modeling

Based on the experimental twin-roll strip casting equipment in the laboratory, two computational models were established for numerical simulation: a three-dimensional (3D) quarter-symmetry model of the molten pool (Figure 3a) and a slice model (Figure 3b). Both models were subsequently imported into ProCAST software (version 2018, ESI, Paris, France) for numerical computations.

The 3D model included five boundary surfaces: the upper free surface of the molten pool, the roller–contact surface, the steel inlet/outlet, and two symmetrical surfaces. Considering the geometric complexity of the molten pool, an unstructured tetrahedral mesh scheme was adopted with a nominal element size of 1.5 mm. To enhance numerical accuracy in the outlet region, local mesh refinement was implemented with element size reduced to 0.4 mm. This meshing strategy resulted in a total of 267,797 finite volume elements. The slice model was specifically developed for resolving mesoscopic-scale solidification structure development. Its total length is one-half of the thickness of the cast strip (1.5 mm), and the left side is the roller–contact surface, with the right side being a symmetrical surface. The calculation for the slice model can clarify the solidification process that the molten steel undergoes in the molten pool from the moment it first contacts the casting rollers until it flows to the meshing point of the two rollers. Since the shape of the model is cuboid, a hexahedral mesh was used with a mesh size of 0.015 mm, and 369,034 micro-elements were divided. Both meshing schemes underwent quality verification, satisfying the convergence criteria of ProCAST’s finite volume solver.

2.3. Assumptions and Governing Equations

The flow, heat transfer, and solidification processes in twin-roll strip casting are a complex phenomenon. To enable efficient numerical analysis without compromising accuracy, the following assumptions were adopted:

• A quarter-symmetry geometry was constructed based on the symmetrical distribution of flow and temperature fields in the molten pool.
• The casting process was treated as a steady-state process.
• The influence of segregation behavior on heat transfer and fluid flow was neglected.
• Except for the roller/steel interface, heat transfer on the other surfaces had a very minor influence on the results and was ignored in the calculation process.
• Free surface fluctuations were not incorporated in the model.

The governing equations included (Figure 4): flow governing equations (continuity and momentum conservation); heat transfer governing equations (energy conservation); and a grain nucleation and growth model for solidification simulation.

2.4. Initial/Boundary Conditions

The numerical model was established with initial and boundary conditions assigned based on experimental data from the laboratory twin-roll strip casting. The initial molten steel temperature was set to 1532 °C (a superheat of 70 °C), with a casting speed of 16 m/min and a strip thickness of 3 mm. The inlet velocity was calculated through mass conservation principles, while the solid transport rate matched the casting speed. The volume flow rate through the cross-section of the roller gap is 8 × 10⁻⁵ m³/s. Thermal boundary conditions were defined using experimental measurements. In the experiment, the heat dissipation of the cast strip can be calculated based on the casting temperature and the strip temperature. The heat passing through the interface is equal to this value, so the average heat flux at the interface can also be calculated. The roller/steel interface was assigned a heat flux boundary condition with an average value of 6.7868 MW/m², distributed as a gradient to reflect actual heat transfer patterns, while other surfaces were treated as adiabatic [25]. Considering the heat loss due to the contact side seal plate and the air, the heat transfer coefficients were set at 30 and 20 W/m²/K, respectively [17].

For solidification modeling, dendrite tip growth parameters were specified as a₂ = 0.005 and a₃ = 0.09, with a Gibbs–Thomson coefficient of 3 × 10⁻⁷ K·m. Surface nucleation parameters included a mean undercooling of 0.5 K (standard deviation 0.1 K) and maximum nucleation density of 7.7 × 10¹¹ m⁻². Volume nucleation was characterized by a higher mean undercooling of 1.5 K (standard deviation 0.75 K) with a maximum nucleation density of 1.5 × 10¹³ m⁻². These parameters were adjusted based on the previous research [26] and the actual solidification conditions during the experimental process, and finally the solidification parameters suitable for the AISI 304 strip casting solidification process were determined.

3. Results and Discussion

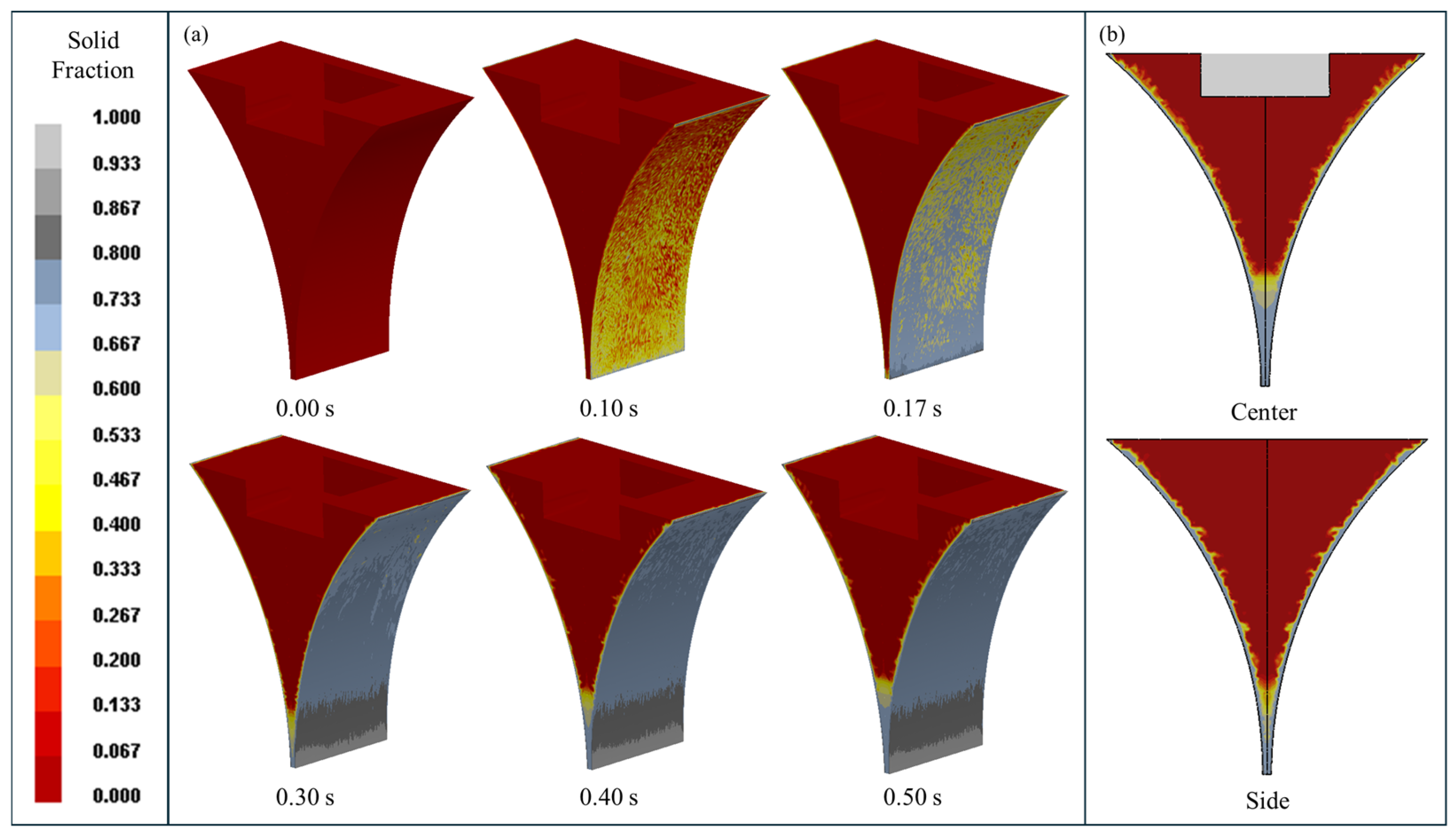
3.1. Evolutions of Macroscopic Physical Field for Twin-Roll Strip Casting

To better visualize the computational results, the quarter-pool simulation was symmetrically mirrored to generate and present half-pool results. Figure 5a shows the overall flow field distribution. The flow velocity is significant near the casting roller and the inlet of the molten steel, while the flow velocity is relatively low in other areas. This phenomenon is caused by the combined effect of the pressure of molten steel and the tangential velocity applied by the rotating rollers. The high-speed flow (Center: about 0.2 m/s; Edge: over 0.25 m/s) near the rollers is crucial for maintaining sufficient momentum to overcome viscous resistance and ensure the continuous formation of the strip.

To investigate the spatial variations in flow behavior, cross-sectional slices of the molten pool have been analyzed (Figure 5b–d). In the center region (away from the side dams), the molten steel enters through the inlet, impinges on the roller surface, and subsequently accelerates downward due to the tangential velocity transferred by the rotating rollers (Figure 5c). A similar flow pattern is observed in the edge region (close to the side dams), where the steel flows rapidly along the roller surface (Figure 5d).

Figure 6 presents the simulated flow trajectories in both the center and edge regions of the molten pool. The simulation results indicate that multiple recirculation zones exist in the center region, including numerous small recirculation zones distributed along the rollers and 2~3 larger recirculation zones within the molten pool, which are similar to those observed in conventional continuous casting processes. In contrast, the edge region exhibits only small recirculation zones along the rollers, along with significant reverse flow in the lower portion of the molten pool. This phenomenon is attributed to the weak solidification conditions at the edge compared to the center region. Under high flow velocities (about 0.28 m/s), a small portion of unsolidified liquid steel flows back from areas with thinner solidified shells (i.e., the edge region) into the molten pool. This also explains the phenomenon that the flow velocity in the lower half area of the molten pool edge is very fast.

The temperature field calculation results exhibit consistency with the flow field results, as illustrated in Figure 7. In the center of the molten pool, areas with higher flow velocities correspond to lower temperatures. The area near the roller is subjected to a strong cooling effect, resulting in a significant temperature drop, while the center area experiences relatively weak cooling. The edge of the molten pool is similar to the center. It is subjected to strong cooling near the casting roller, generating a large temperature drop and continuous solidification. It descends along the casting roller until it reaches the outlet. The observed temperature distribution conforms to the fluid-driven heat transport mechanism, and the rapid renewal of the fluid in the high-speed zone alleviates the local heat accumulation.

The results of the solid fraction in the molten pool are shown in Figure 8. Figure 8a shows the variation of the solid fraction during the simulation process, which also reflects the change of the solid fraction from the start of casting to the steady-state situation during the casting process. At 0.00 s, the molten steel has filled the molten pool area, but the cooling and solidification process has not yet begun. By 0.10 s, the molten steel has begun to solidify from the top and is continuously flowing down along the casting roller. At 0.17 s, the molten steel has solidified to form a strip of a certain thickness. By 0.30 s, the surface near the casting roller has basically solidified completely. After this, the solidification situation basically does not change much. It can be considered that the casting solidification process reached a steady state. Figure 8b shows the solid fraction at the center and edge of the molten pool. Apart from the fact that the amount of solidified shell at the lower part of the molten pool is greater at the center, there are basically no other differences, and the solidification modes are relatively similar.

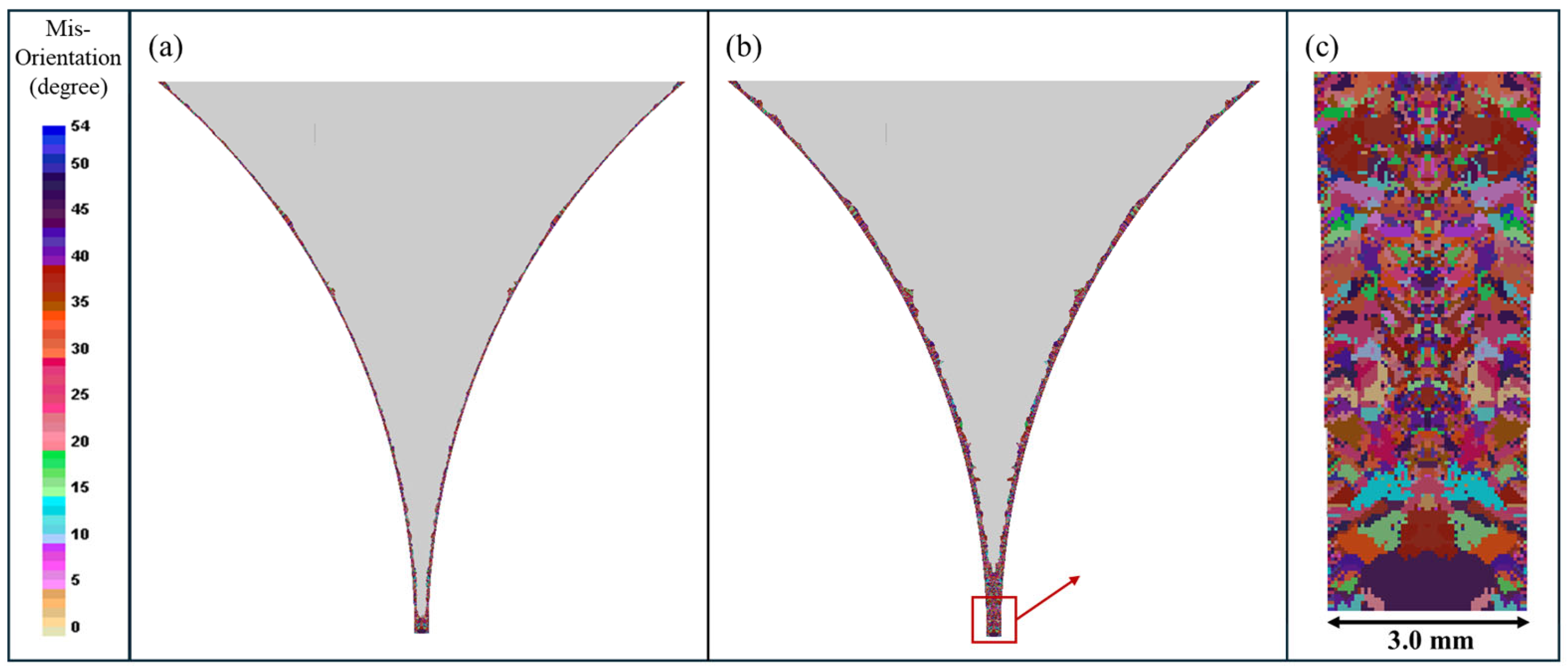
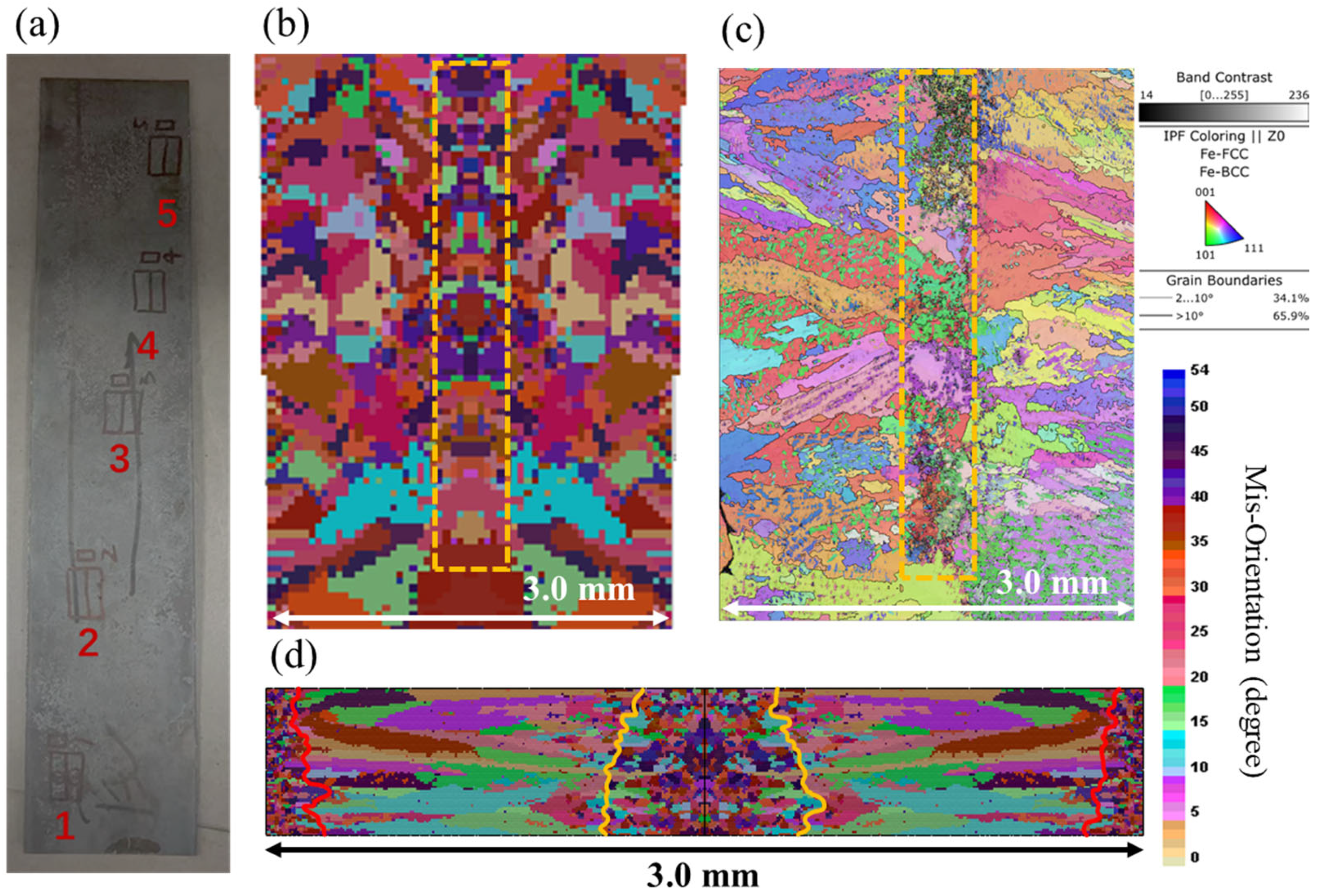
3.2. Evolutions of Solidification Structure for Twin-Roll Strip Casting

Figure 9 shows the mesoscopic solidification structure results of the 3D model. Among them, Figure 9a shows the early solidification structure, where a relatively thin layer of solidification structure grows along the roller surface and the solidification structures on both sides are coupled at the meshing point of the casting roller. Figure 9b shows the situation at the end of solidification, at which point the solidification structure has grown relatively thick and the solidification structure is coupled at a higher place. Figure 9c is an enlarged view of the mesoscopic structure at the end of solidification. From it, the columnar crystals on both sides and the fine equiaxed crystals in the middle can be clearly observed. However, due to the insufficiently fine mesh division, there is a slight distortion in the mesoscopic structure results, and the columnar crystals are relatively coarse. Therefore, a slice model is needed to assist in numerical simulation.

Figure 10 presents the simulated mesoscopic solidification structure from the slice model. The left side (strip center) exhibits a fine equiaxed grain structure, resulting from lower cooling intensity in this region. Nucleation occurred due to undercooling, followed by the formation of fine equiaxed grains during solidification. Close to the copper roller on the right side (strip edge), a surface chill layer with refined grains is observed due to rapid cooling. Between these two zones, columnar grains grow opposite to the direction of heat flow. The strong cooling conditions promote a distinct orientation in the columnar grains. This microstructure represents a typical sub-rapid solidification structure in twin-roll strip casting.

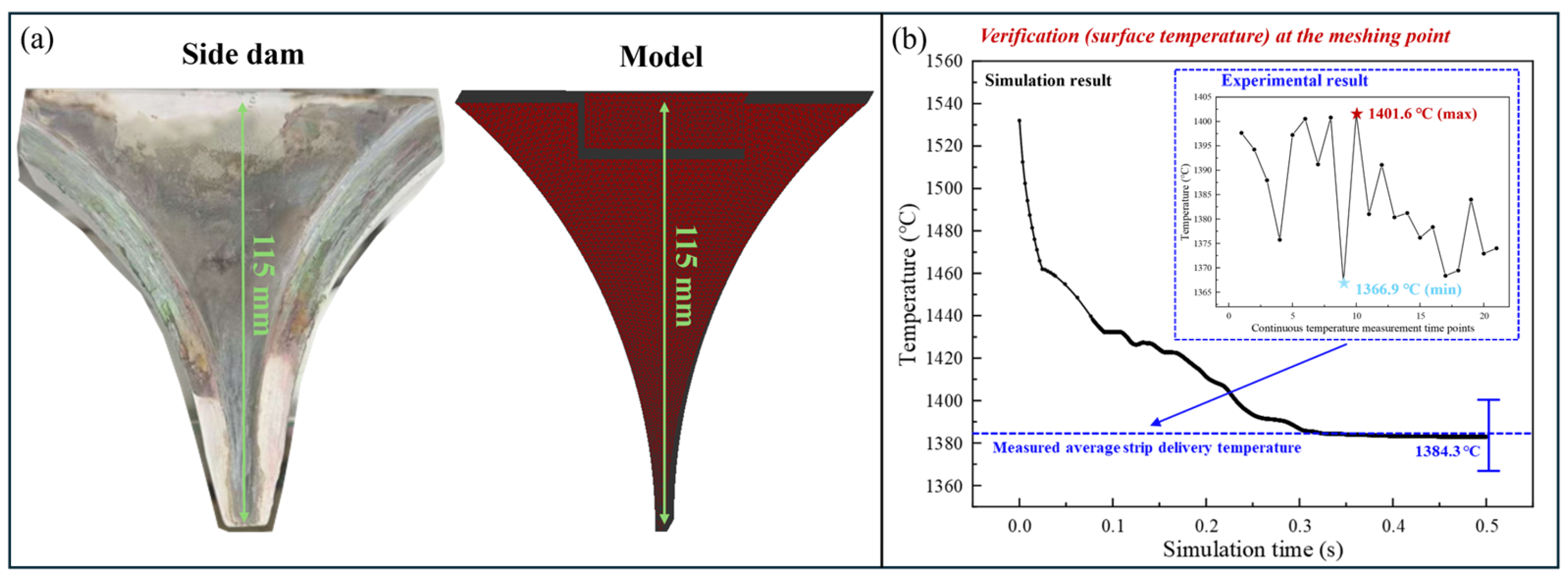
3.3. Comparisons Between Modeling and Experiment

Casting experiments were conducted under identical conditions to validate the numerical model. First, the side dams in the experiments were examined (Figure 11a), confirming that the modeled molten pool geometry (115 mm height) closely matched the actual pool dimensions and shape. For temperature field validation (Figure 11b), surface temperatures of the cast strip were measured during the experiment, with recorded values ranging from 1366.9 °C (minimum) to 1401.6 °C (maximum) and an average of approximately 1384.3 °C. Simulated temperature variations at the strip surface stabilized after 0.3 s, exhibiting negligible fluctuations. The simulated temperatures in the steady state aligned closely with the experimental average, demonstrating the model’s accuracy in predicting molten pool thermal behavior.

The mesoscopic solidification structure was validated with the experimental results, as shown in Figure 12. Samples obtained from the twin-roll strip casting experiment were sampled at different positions, and the sample size was 6 mm × 10 mm (Figure 12a). The sample was polished after sandpaper grinding, followed by vibration polishing to relieve stress. Electron backscatter diffraction (EBSD) mapping was performed on the thickness surface of the cast strip with a voltage of 20 kV and a scanning step size of 2 μm. The results at different positions are basically consistent. The specific grain orientations and grain boundary superpositions are shown in Figure 12c. It can be clearly observed that there were columnar crystal regions with relatively consistent directionality and a small equiaxed crystal region at the center. Among them, the equiaxed crystal region accounted for approximately 17.8% (the area proportion is counted through image processing software). The yellow line area represents the central equiaxed crystal.

Comparatively, the 3D simulation results (Figure 12b) exhibited similar microstructural morphology to the EBSD data, with an equiaxed grain fraction of 17.2%. The slice model results (Figure 12d) replicated the experimental structure of surface chill layer–columnar grains–central equiaxed grains. The equiaxed grain fraction in this model reached 18.7%. All simulated results fell within a 5% error margin relative to experimental measurements, confirming model accuracy.

In conclusion, the verification of the temperature field and solidification structure indicates that this model can simulate the casting process of twin-roll strips quite well, providing a good tool for optimizing industrial process parameters.

3.4. Influence of Superheat on Solidification and Macrostructure Formation for Twin-Roll Strip Casting

The validated model was applied to simulate the casting process under varying superheat conditions (Figure 13), specifically investigating superheat levels of 30 °C, 70 °C, and 110 °C. Under the condition of higher superheat, the viscosity of steel decreased, and the fluidity of the molten pool increased, thereby enhancing the convective heat transfer within the molten pool. Conversely, lower superheat increased viscosity and restricted fluid motion. Temperature data monitored at two critical locations—Point 1 (edge) and Point 2 (center) near the pool bottom—exhibited consistent trends across all conditions: the overall temperature of the molten pool under high superheat conditions was higher than that under low superheat conditions. The temperature difference at the outlet of the molten pool under different superheats continuously decreased as the casting proceeded. The reason was that the solidified shells reaching this position were all strongly cooled. At such a high cooling rate, the difference in superheats had little influence, so the final temperature tended to be consistent.

Figure 14 presented the simulated solid fraction distributions under different superheat conditions. The total solid fraction within the molten pool and the vertical distance from the kiss point—defined as the position where solid fraction exceeded 70%—to the pool bottom were quantified. At 30 °C superheat, the total solid fraction reached 13.6%, with the kiss point positioned 15.8 mm above the bottom. When superheat increased to 70 °C, the total solid fraction decreased to 11.3% and the kiss point lowered to 11.8 mm above the bottom. Under 110 °C superheat, these parameters further declined to 8.3% and 6.2 mm, respectively. This relationship confirms that the amount of molten steel solidified is greater and the kiss point is higher under lower superheat conditions.

In industrial practice, the position of the kiss point served as a critical indicator for solidification, casting/rolling forces, and strip breakage risk assessment. Monitoring this parameter provided significant operational guidance for process stability and product quality control.

Similarly, the solidification structure under different superheats was calculated using the slice model, as shown in Figure 15. At a superheat of 30 °C, the columnar crystals are coarse and large, while the central equiaxed crystal region is relatively small, accounting for approximately 8.9% of the area. At a superheat of 70 °C, the columnar crystals were refined somewhat, and the central equiaxed crystal region increased, accounting for approximately 18.7% of the area. At a superheat of 110 °C, the columnar crystals are finer, and the central equiaxed crystal region is larger, accounting for approximately 26.5% of the area.

The reason is that under high superheat, the overall temperature of the molten pool is relatively high, and the temperature gradient at the solidification front decreases, which is conducive to the nucleation of equiaxed crystals. High superheat leads to a decrease in the degree of solidification supercooling, a decline in the nucleation driving force, and a reduction in the number of grains. Under low superheat, the temperature gradient at the solidification front is steep, and columnar crystal growth is dominant, which will inhibit the formation of equiaxed crystals. Grain refinement, an increase in the number of grains, and a rise in the proportion of equiaxed grains. The increase of nucleation rate and the increase of solidification subcooling degree promote non-uniform nucleation.

For AISI 304 stainless steel, superior equiaxed grains can provide good elongation performance, and the fine grains in the middle can offer certain fine-grain strengthening and enhance strength. Therefore, by reasonably controlling the proportion of the solidification structure, the solidification conditions can be controlled as required to achieve the desired performance.

4. Conclusions

This study established a validated multiscale numerical framework for simulating coupled flow, heat transfer, and solidification phenomena in AISI 304 stainless steel twin-roll strip casting. The key conclusions are as follows:

• The model demonstrated high accuracy through temperature field predictions deviating less than 5% from experimental measurements (average 1384.3 °C) and solidification structure simulations matching EBSD-observed equiaxed grain fractions within 5% error.
• The flow field and flow trajectory showed obvious recirculation zones: the center area was mainly composed of large recirculation zones, and many small recirculation zones appeared at the edges. The position of the kiss point becomes a key process indicator, and its distance from the bottom of the pool is inversely proportional to the superheat (15.8 mm at 30 °C and 6.2 mm at 110 °C).
• Parametric studies further established that low superheat (30 °C) increased melt viscosity, restricted convection, and promoted coarse columnar grains (equiaxed fraction: 8.9%), whereas high superheat (110 °C) enhanced fluid renewal and equiaxed nucleation (26.5%) despite lower total solidification (8.3%).
• For AISI 304 stainless steel, expanding the equiaxed zone improved ductility, while grain refinement contributed to boundary strengthening. Consequently, control of superheat enables solidification structure to be adjusted according to the target mechanical properties. In industry, monitoring the location of the kiss point can enable real-time diagnosis of solidification, rolling force, and quality risks of steel strips.

This study enables optimized process parameters for AISI 304 stainless steel twin-roll strip casting, reducing trial costs while enhancing strip quality and performance. Future integration into industrial digital twins will advance process–structure–property digitalization.