Composition Design and Property Prediction for AlCoCrCuFeNi High-Entropy Alloy Based on Machine Learning
Abstract
1. Introduction
2. Materials and Methods
2.1. Gaussian Noise
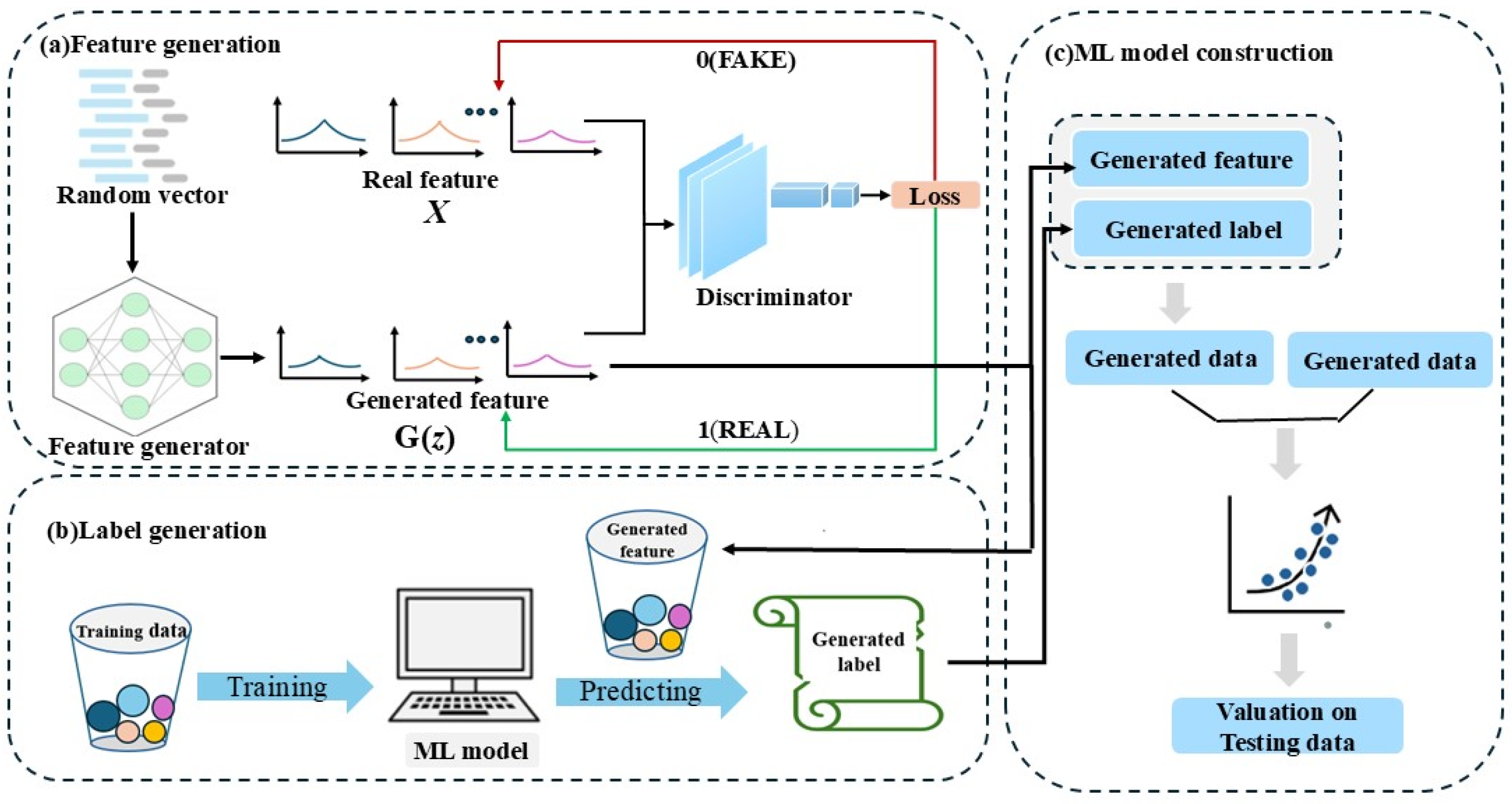
2.2. Generative Adversarial Network
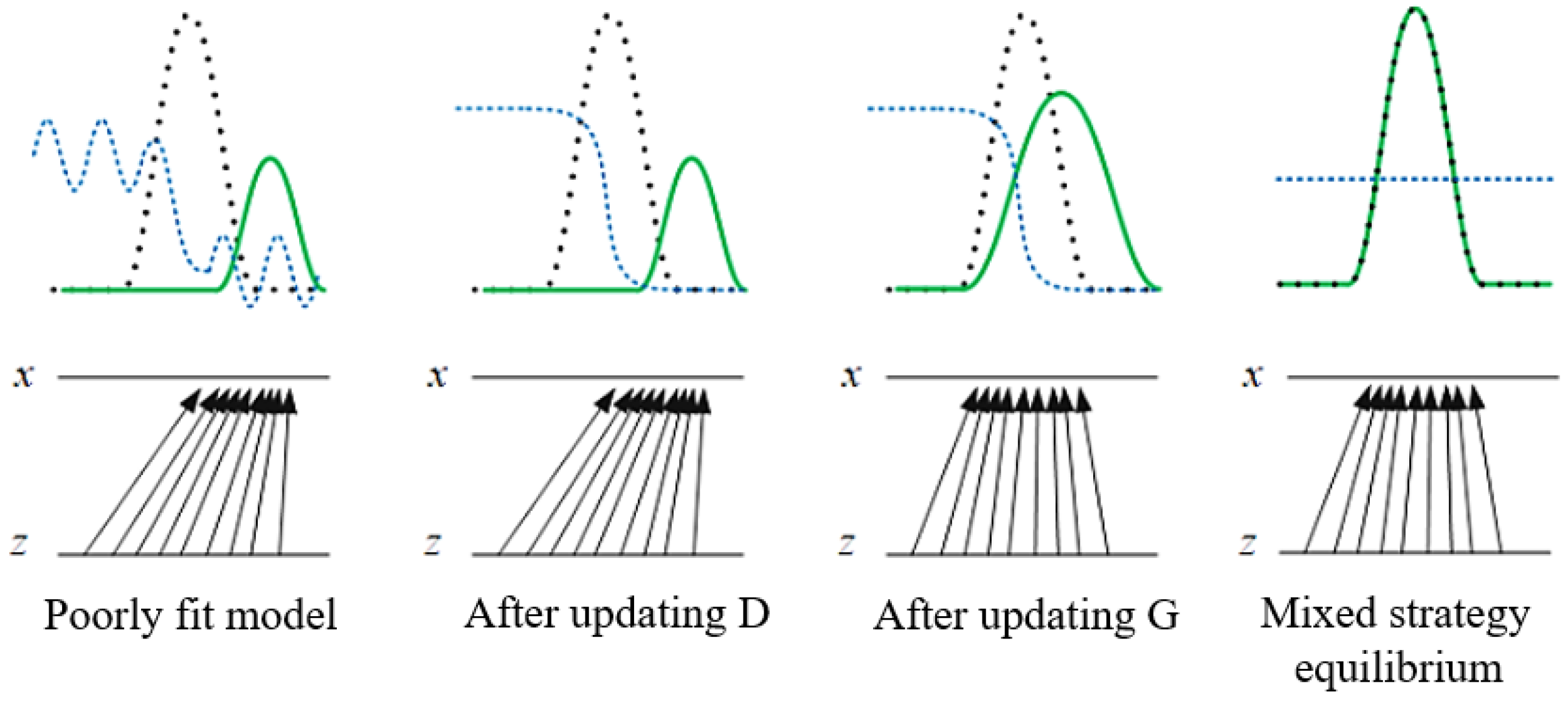
2.2.1. Principle of GAN
2.2.2. Principle of GANPro
2.3. Machine Learning Evaluation Index
3. Results
3.1. Enhancement and Expansion of the Alloy Dataset Using Gaussian Noise and Analysis of Performance Improvement
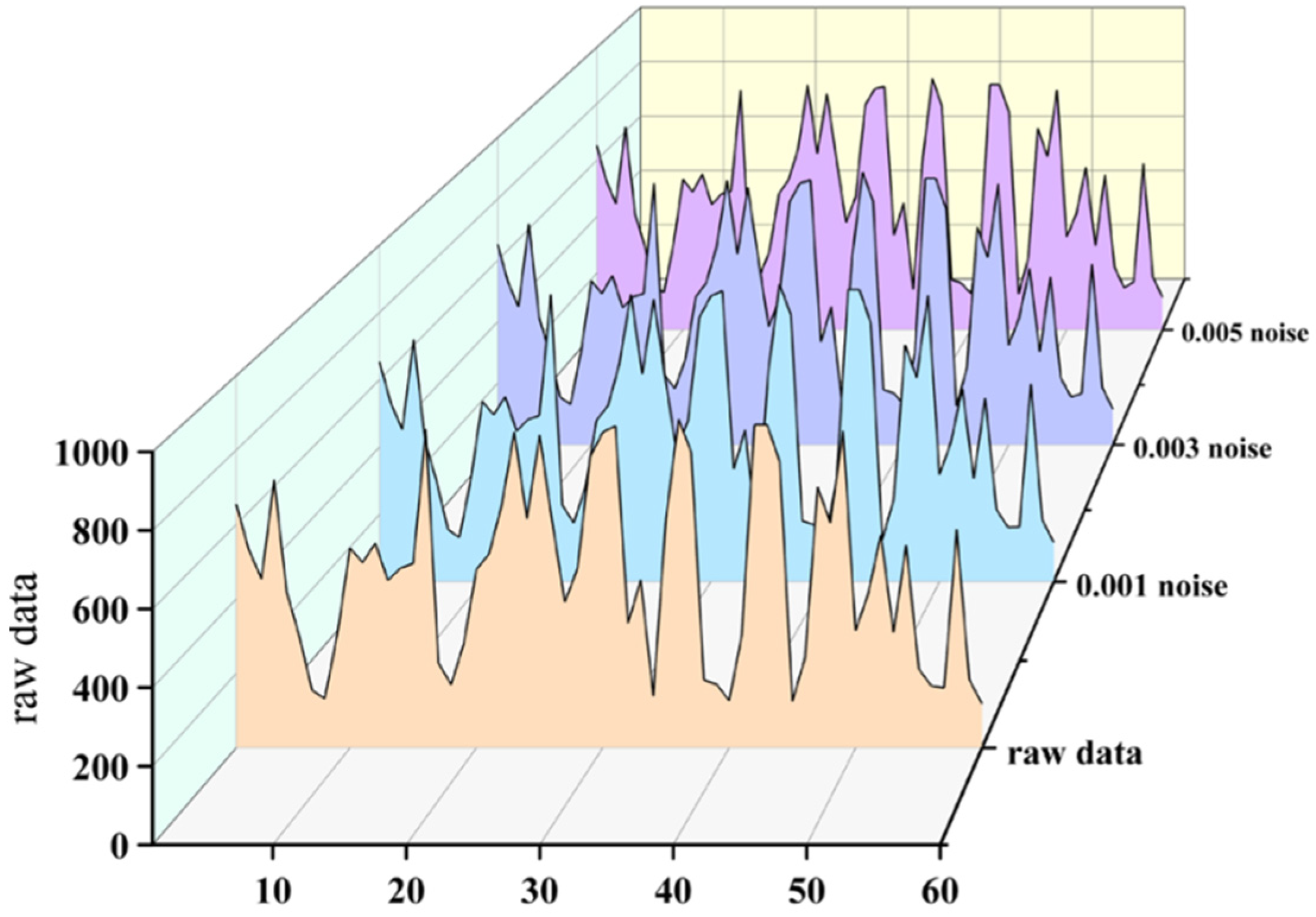
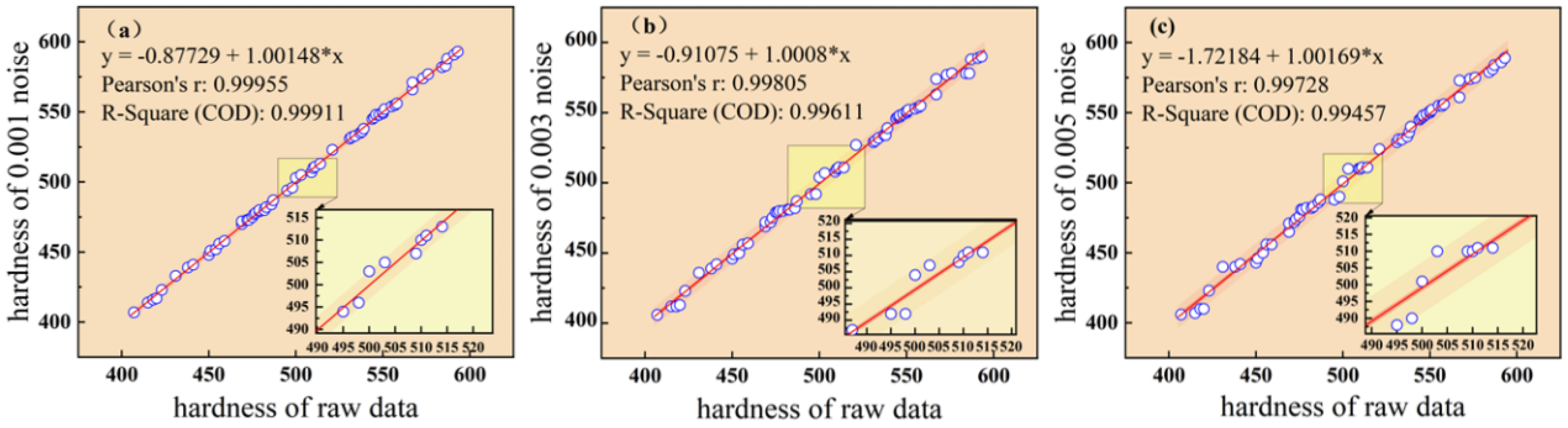
3.1.1. Analysis of Data Augmentation by Adding Different Noises
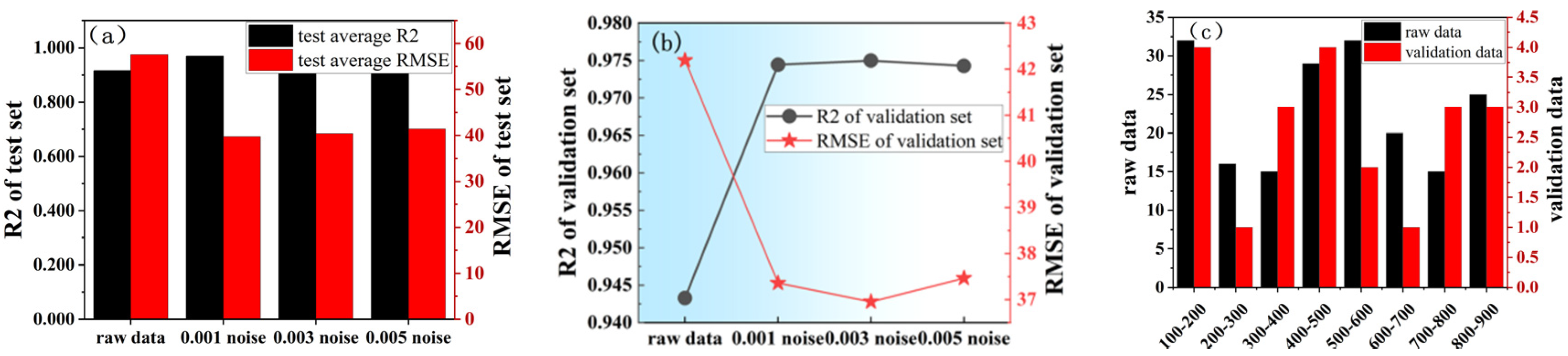
3.1.2. Effect of Different Noise on Model Performance
3.2. Enhancement and Expansion of the Alloy Dataset Using Generative Adversarial Networks (GAN) and Its Performance Improvement Analysis
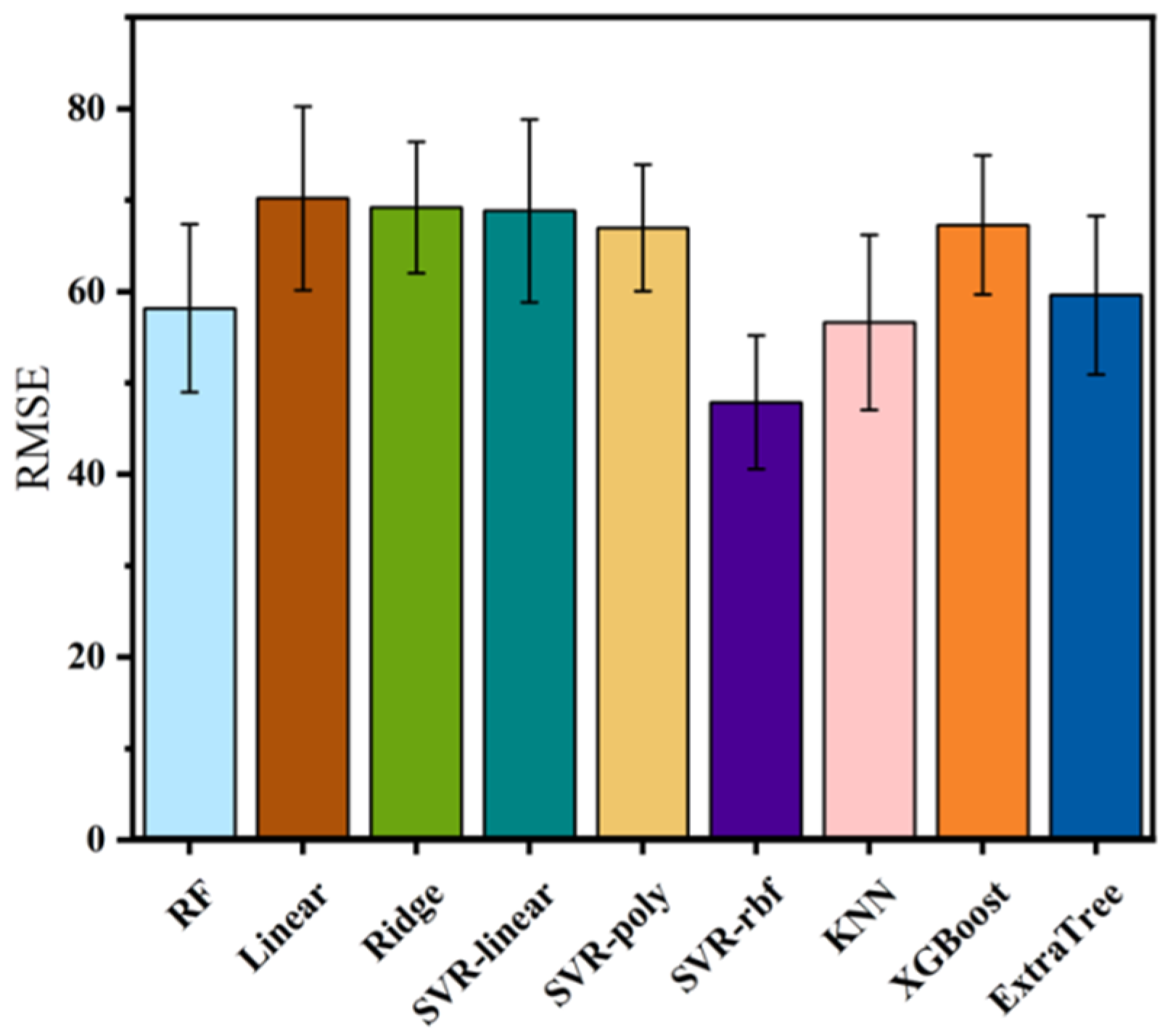
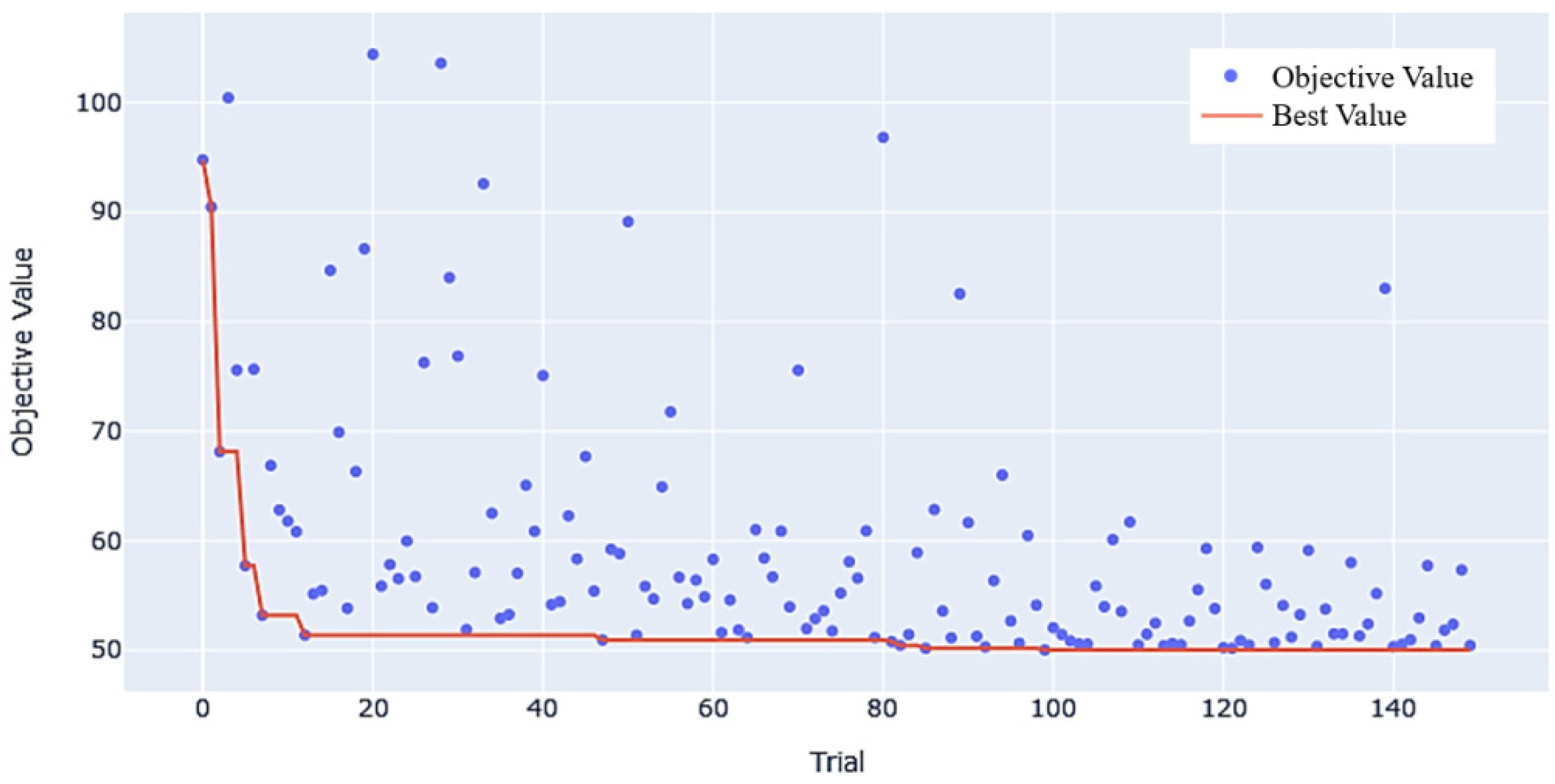
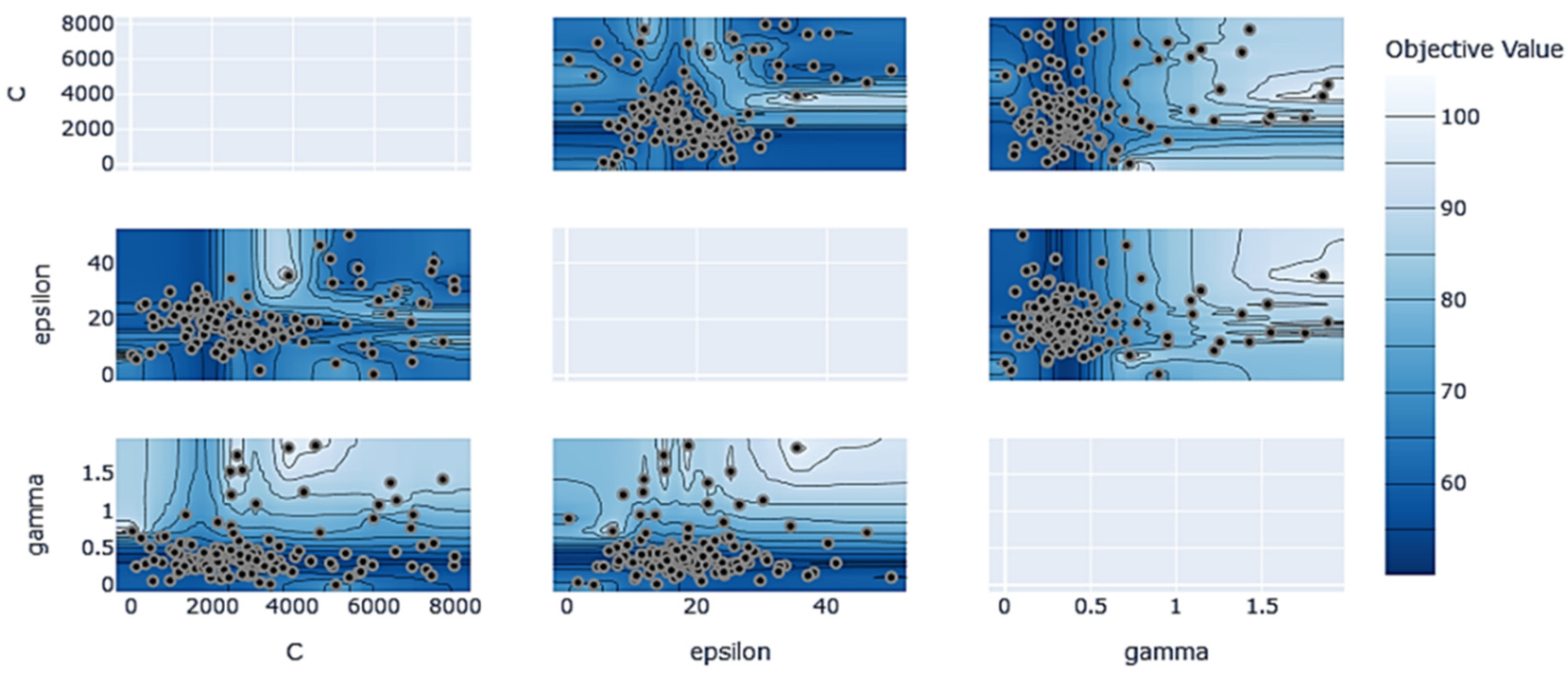
3.2.1. Evaluation of Different Algorithm Modelling
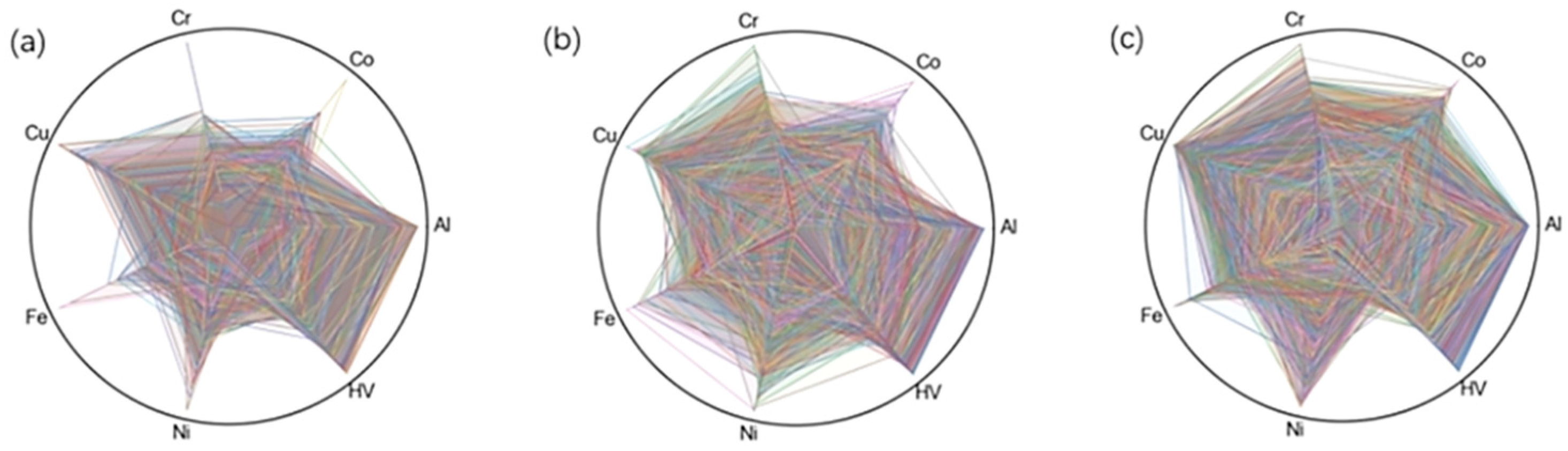
3.2.2. Distribution of Generated Data
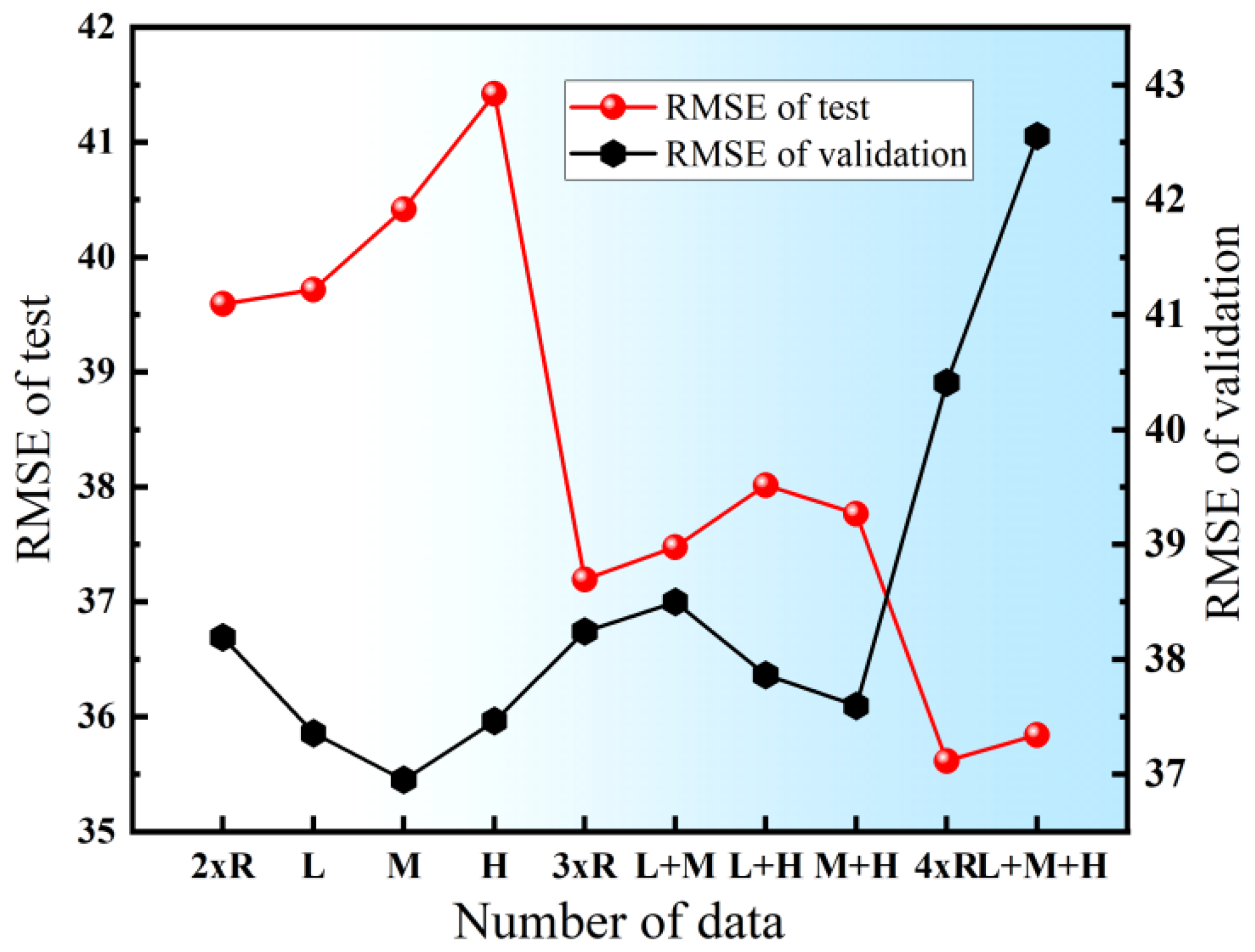
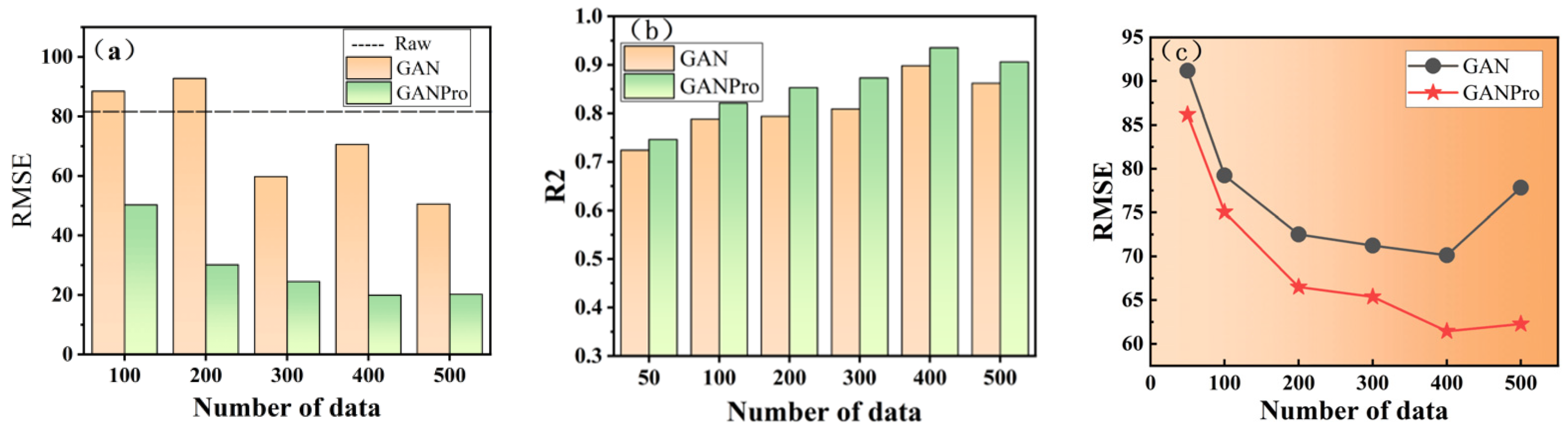
3.2.3. Impact of the Amount of Generated Data on Model Performance
3.3. Comparison Between Gaussian Noise and Generative Adversarial Network in Regression Data Augmentation
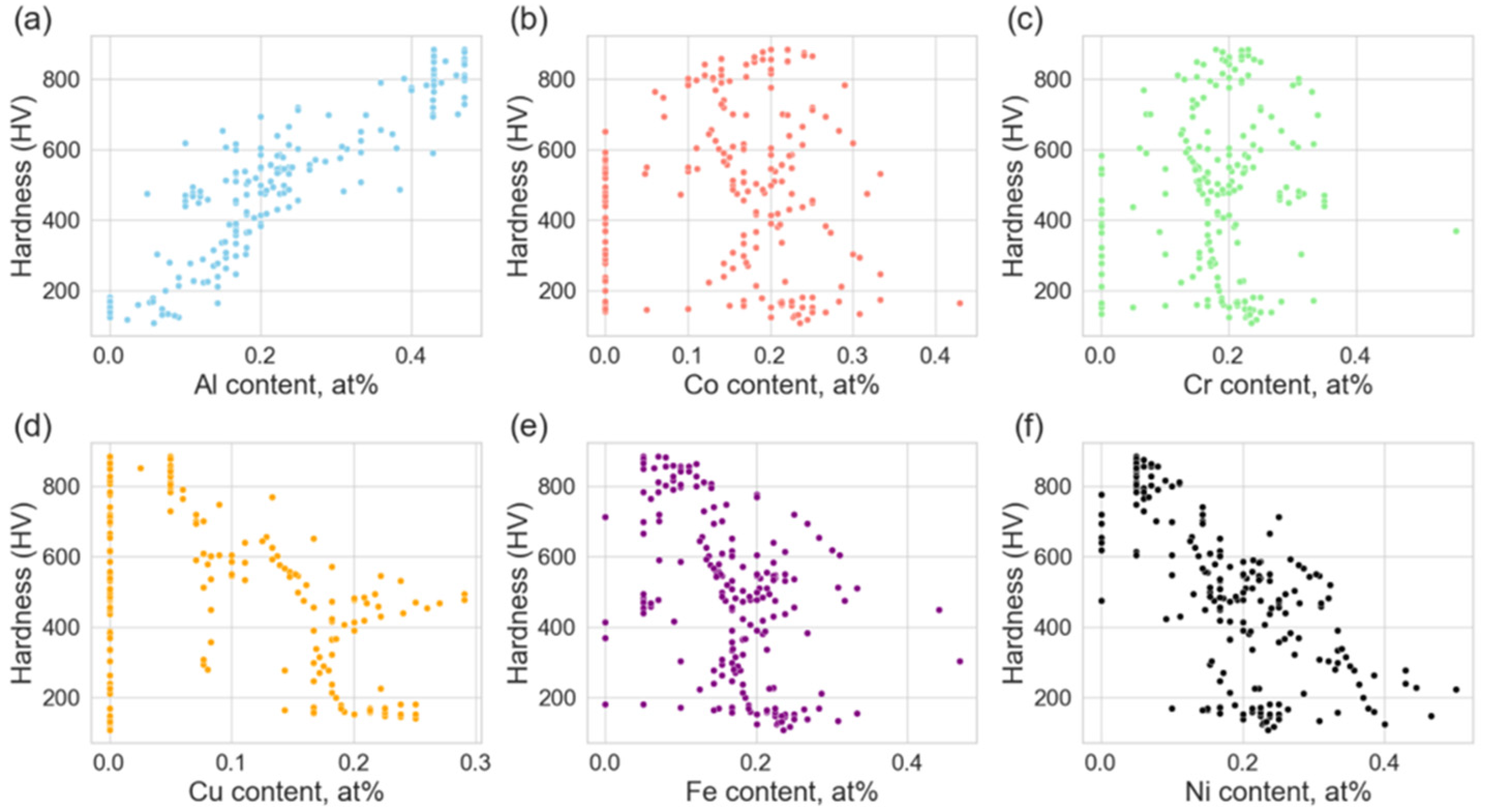
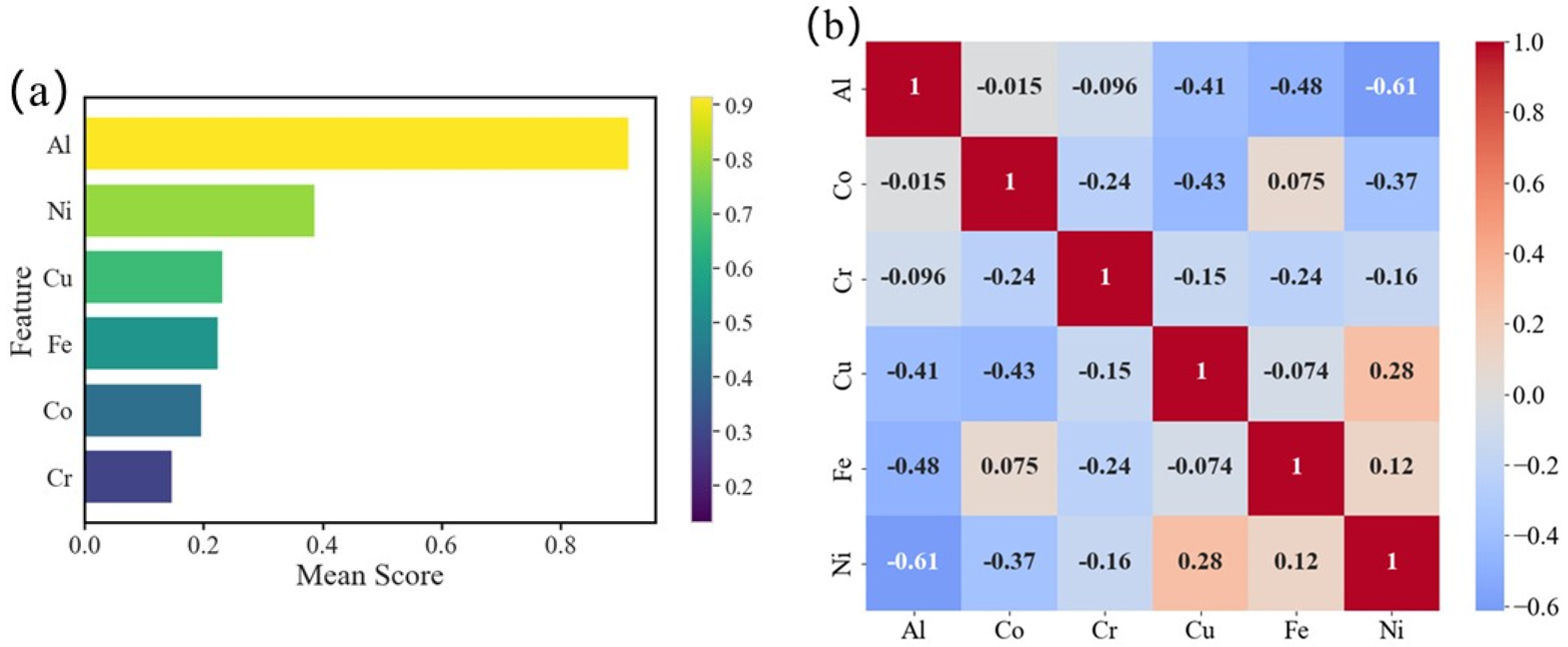
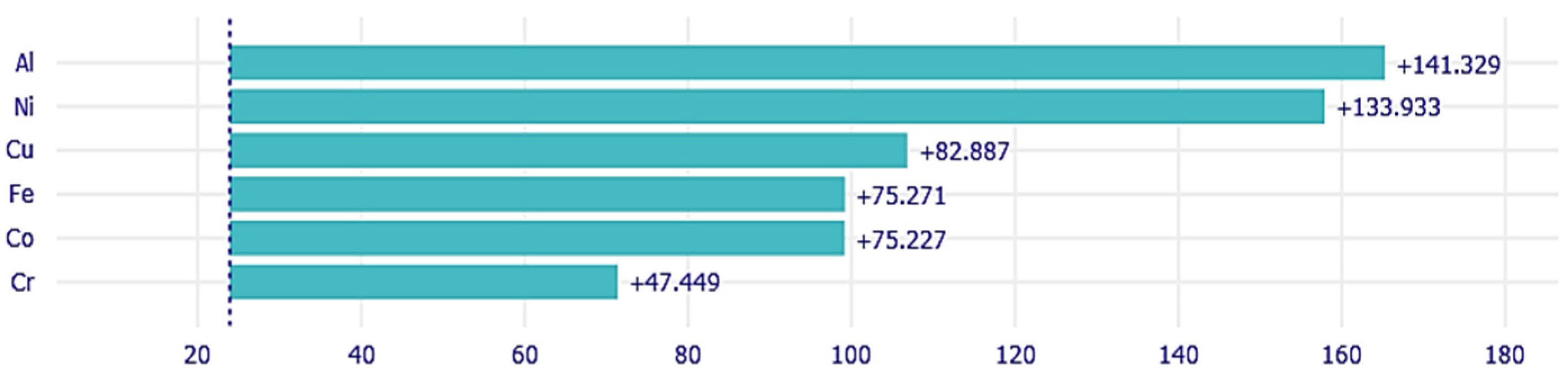
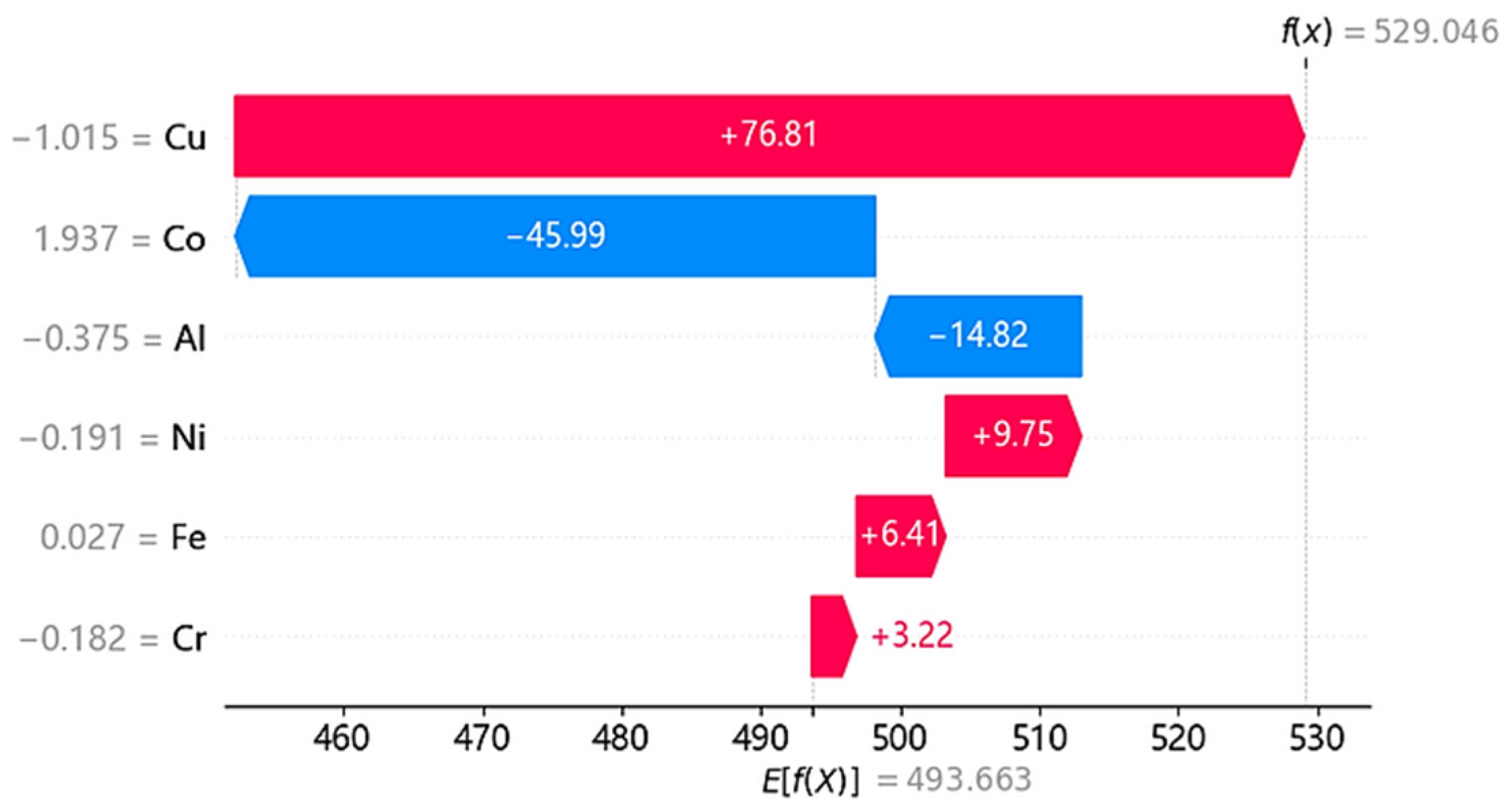
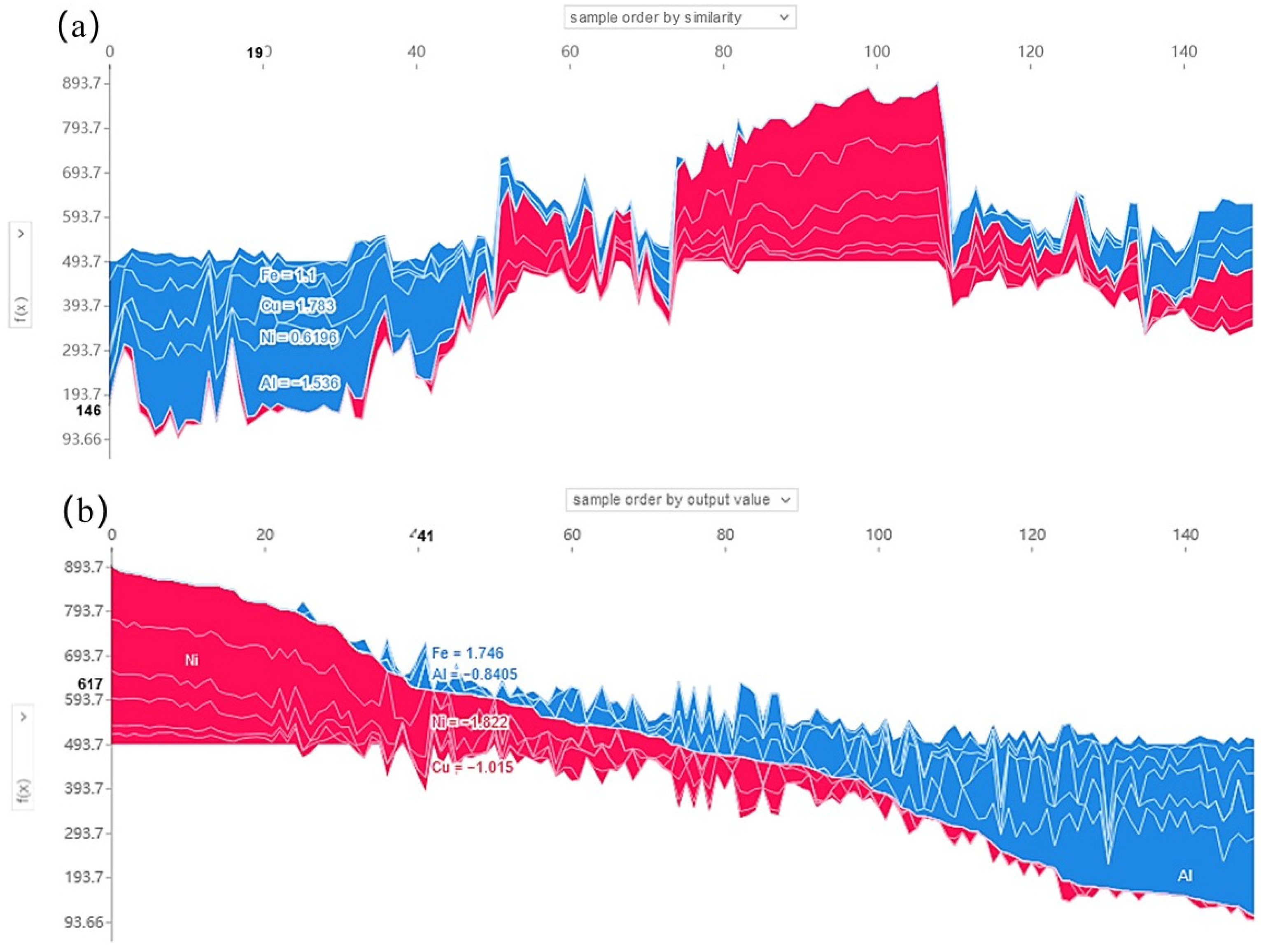
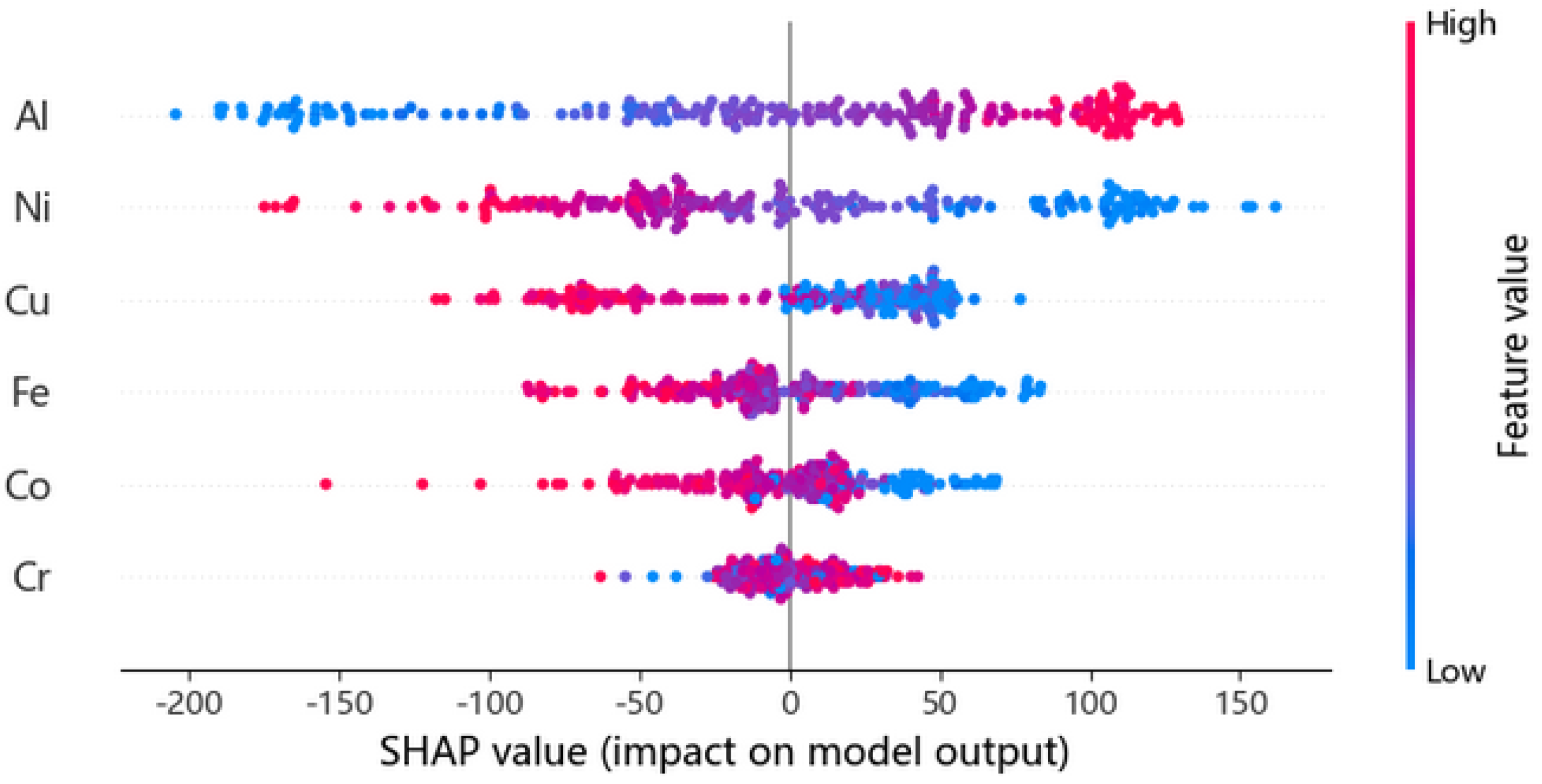
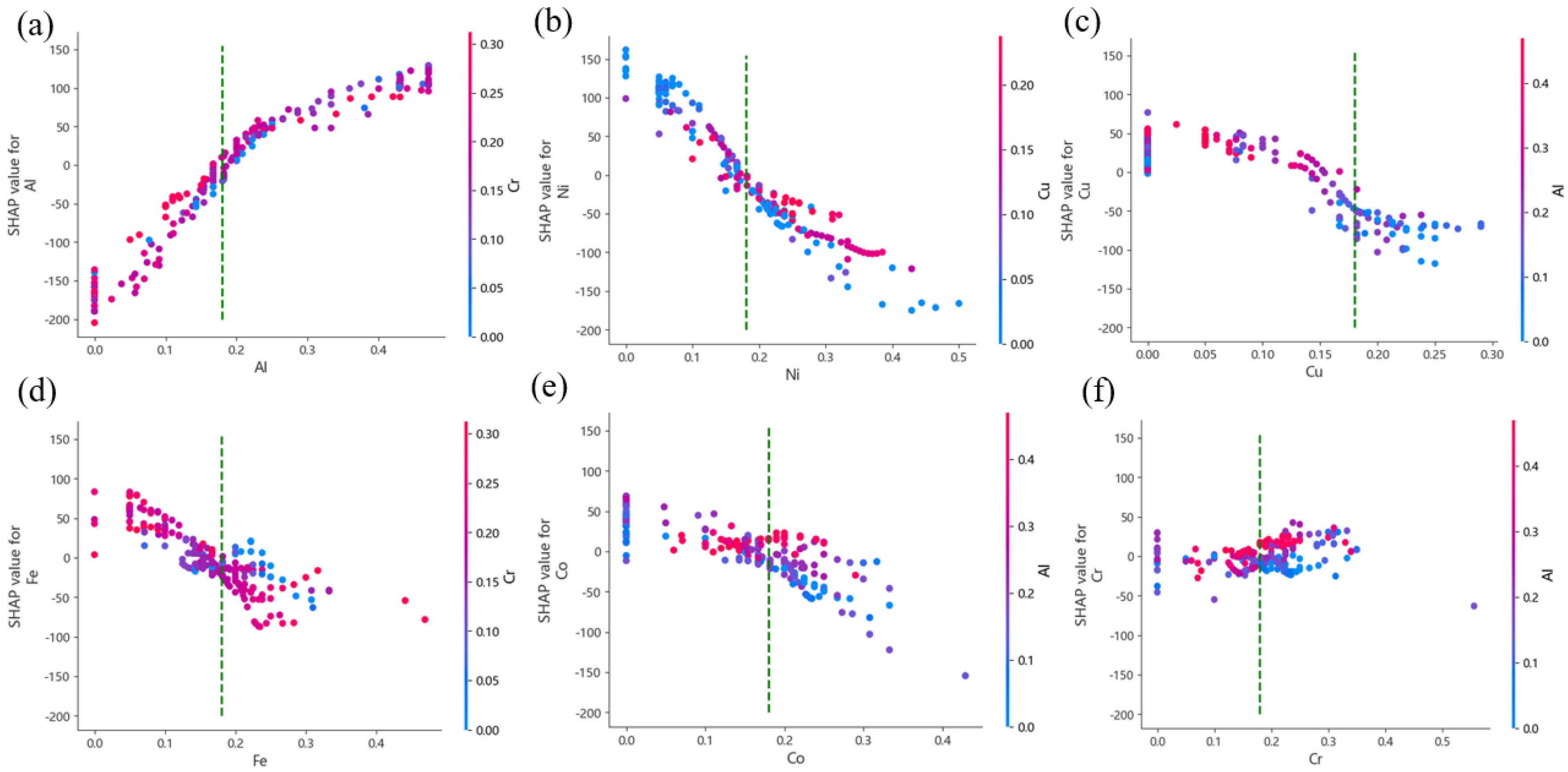
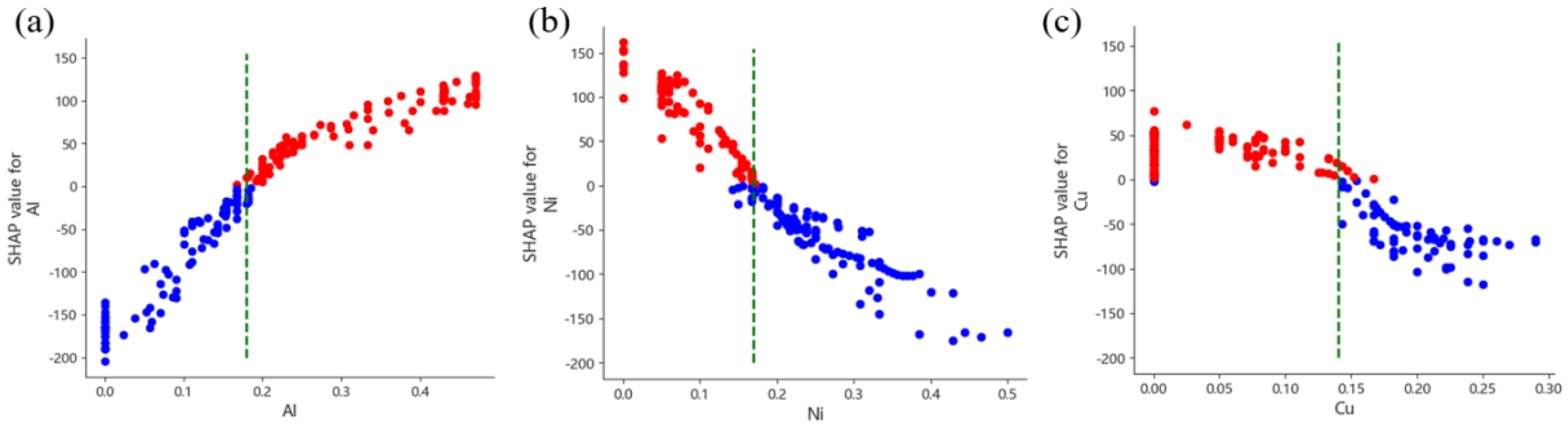
3.4. Interpretability Analysis of HEAs’ Hardness Prediction
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yeh, J.W.; Chen, S.K.; Lin, S.J.; Gan, G.P.; Chin, T.S. Nanostructured High-Entropy Alloys with Multiple Principal Elements: Novel Alloy Design Concepts and Outcomes. Adv. Eng. Mater. 2004, 6, 299–303. [Google Scholar] [CrossRef]
- Cantor, B.; Chang, I.T.H.; Knight, P.; Vincent, A.J.B. Microstructural development in equiatomic multicomponent alloys. Mater. Sci. Eng. A 2004, 375–377, 213–218. [Google Scholar] [CrossRef]
- Miracle, D.B.; Senkov, O.N. A Critical Review of High Entropy Alloys and Related Concepts. Acta Mater. 2017, 122, 448–511. [Google Scholar] [CrossRef]
- Qiao, L.; Liu, Y.; Zhu, J.; Cao, C.; Li, Z. A Focused Review on Machine Learning Aided High-Throughput Methods in High Entropy Alloy. J. Alloys Compd. 2021, 877, 160295. [Google Scholar] [CrossRef]
- Shi, Y.; Collins, L.; Feng, R.; Zhang, C.; Liaw, P.K. Homogenization of AlxCoCrFeNi high-entropy alloys with improved corrosion resistance. Corros. Sci. 2018, 133, 120–131. [Google Scholar] [CrossRef]
- Fu, Y.; Li, J.; Luo, H.; Du, C.; Li, X. Recent advances on environmental corrosion behavior and mechanism of high-entropy alloys. J. Mater. Sci. Technol. 2021, 80, 217–233. [Google Scholar] [CrossRef]
- Ding, Z.Y.; Cao, B.X.; Luan, J.H.; Jiao, Z.B.; Liu, W.H.; Yang, T.; Liu, C.T. Synergistic effects of Al and Ti on the oxidation be haviour and mechanical properties of L12-strengthened FeCoCrNi high-entropy alloys. Corros. Sci. 2021, 184, 109365. [Google Scholar] [CrossRef]
- Zhang, R.P.; Zhao, S.T.; Ding, J.; Chong, Y.; Jia, T.; Ophus, C.; Asta, M.; Ritchie, R.O.; Minor, A.M. Short-range order and its impact on the Cr Co Ni medium-entropy alloy. Nature 2020, 581, 283–287. [Google Scholar] [CrossRef]
- Agrawal, A.; Choudhary, A. Perspective: Materials Informatics and Big Data: Realization of the “Fourth Paradigm” of Science in Materials Science. APL Mater. 2016, 4, 053208. [Google Scholar] [CrossRef]
- Hemanth, K.; Vastrad, C.M.; Nagaraju, S. Data Mining Technique for Knowledge Discovery from Engineering Materials Data Sets. In Proceedings of the International Conference on Computer Science and Information Technology, Bangalore, India, 23–25 December 2011; pp. 512–522. [Google Scholar]
- Lu, W.; Xiao, R.; Yang, J.; Zhang, L.; Chen, X. Data Mining-Aided Materials Discovery and Optimization. J. Mater. 2017, 3, 191–201. [Google Scholar] [CrossRef]
- Liu, Y.; Zhao, T.; Ju, W.; Shi, S. Materials Discovery and Design Using Machine Learning. J. Mater. 2017, 3, 159–177. [Google Scholar] [CrossRef]
- Li, J.; Xie, B.; Fang, Q.; Liu, B. High-Throughput Simulation Combined Machine Learning Search for Optimum Elemental Composition in Medium Entropy Alloy. J. Mater. Sci. Technol. 2021, 68, 70–75. [Google Scholar] [CrossRef]
- Feng, S.; Fu, H.; Zhou, H.; Zhang, W. A General and Transferable Deep Learning Framework for Predicting Phase Formation in Materials. npj Comput. Mater. 2021, 7, 10. [Google Scholar] [CrossRef]
- Lookman, T.; Balachandran, P.V.; Xue, D.Z.; Hogden, J. Active learning in materials science with emphasis on adaptive sampling using uncertainties for targeted design. npj Comput. Mater. 2019, 5, 21. [Google Scholar] [CrossRef]
- Schmidt, J.; Marques, M.R.G.; Botti, S.; Marques, M.A.L. Recent advances and applications of machine learning in solid-state materials science. npj Comput. Mater. 2019, 5, 83. [Google Scholar] [CrossRef]
- Wei, X.; van der Zwaag, S.; Jia, Z.; Wang, C.; Xu, W. On the use of transfer modeling to design new steels with excellent rotating bending fatigue resistance even in the case of very small calibration datasets. Acta Mater. 2022, 235, 118103. [Google Scholar] [CrossRef]
- Zhao, Z.; You, J.; Zhang, J.; Zhou, X.; Ma, W. Data enhanced iterative few-sample learning algorithm-based inverse design of 2D programmable chiral metamaterials. Nanophotonics 2022, 11, 4465–4478. [Google Scholar] [CrossRef]
- Li, Z.; Nash, W.; O’Brien, S.; Lu, C.; Olson, G.B. Cardigan: A Generative Adversaria NetworkModel for Design and Discovery of Multi Principal Element Alloys. J. Mater. Sci. Technol. 2022, 125, 81–96. [Google Scholar] [CrossRef]
- Creswell, A.; White, T.; Dumoulin, V.; Arulkumaran, K.; Sengupta, B.; Bharath, A.A. Generative Adversarial Networks: An Overview. IEEE Signal Process. Mag. 2018, 35, 53–65. [Google Scholar] [CrossRef]
- Hart, G.L.W.; Mueller, T.; Toher, C.; Curtarolo, S. Machine learning for alloys. Nat. Rev. Mater. 2021, 6, 730. [Google Scholar] [CrossRef]
- Liu, Y.L.; Niu, C.; Wang, Z.; Du, Y. Machine learning in materials genomeinitiative: A review. J. Mater. Sci. Technol. 2020, 57, 113. [Google Scholar] [CrossRef]
- Chen, C.; Zuo, Y.; Ye, W.; Li, X.; Deng, Z.; Ong, S.P. A critical review of machine learn-ing of energy materials. Adv. Energy Mater. 2020, 10, 1903242. [Google Scholar] [CrossRef]
- Ramprasad, R.; Batra, R.; Pilania, G.; Mannodi-Kanakkithodi, A.; Kim, C. Machine learning in materials informatics: Recent applications and prospects. npj Comput. Mater. 2017, 3, 54. [Google Scholar] [CrossRef]
- Li, S.; Li, S.; Liu, D.; Zhang, Y.; Li, Q. Hardness prediction of high entropy alloys with machine learning and material descriptors selection by improved genetic algorithm. Comput. Mater. Sci. 2022, 205, 111185. [Google Scholar] [CrossRef]
- Wen, C.; Zhang, Y.; Wang, C.; Shang, S.-L.; Liu, Z.-K. Machine learning assisted design of high entropy alloys with desired property. Acta Mater. 2019, 170, 109–117. [Google Scholar] [CrossRef]
- Borg, C.K.H.; Frey, C.; Moh, J.; Laws, K.; Ramprasad, R. Expanded dataset of mechanical properties and observed phases of multi-principal element alloys. Sci. Data 2020, 7, 430. [Google Scholar] [CrossRef] [PubMed]
- Roy, A.; Hussain, A.; Sharma, P.; Singh, A.K. Rapid discovery of high hardness multi-principal-element alloys using a generative adversarial network model. Acta Mater. 2023, 257, 119177. [Google Scholar] [CrossRef]
- Prince, S.; Chayan, D.; Praveen, S.; Kumar, M.A.; Korla, R. Additively Manufactured Lightweight and Hard High-Entropy Alloys by Thermally Activated Solvent Extraction. High Entropy Alloys Mater. 2024, 2, 41–47. [Google Scholar]
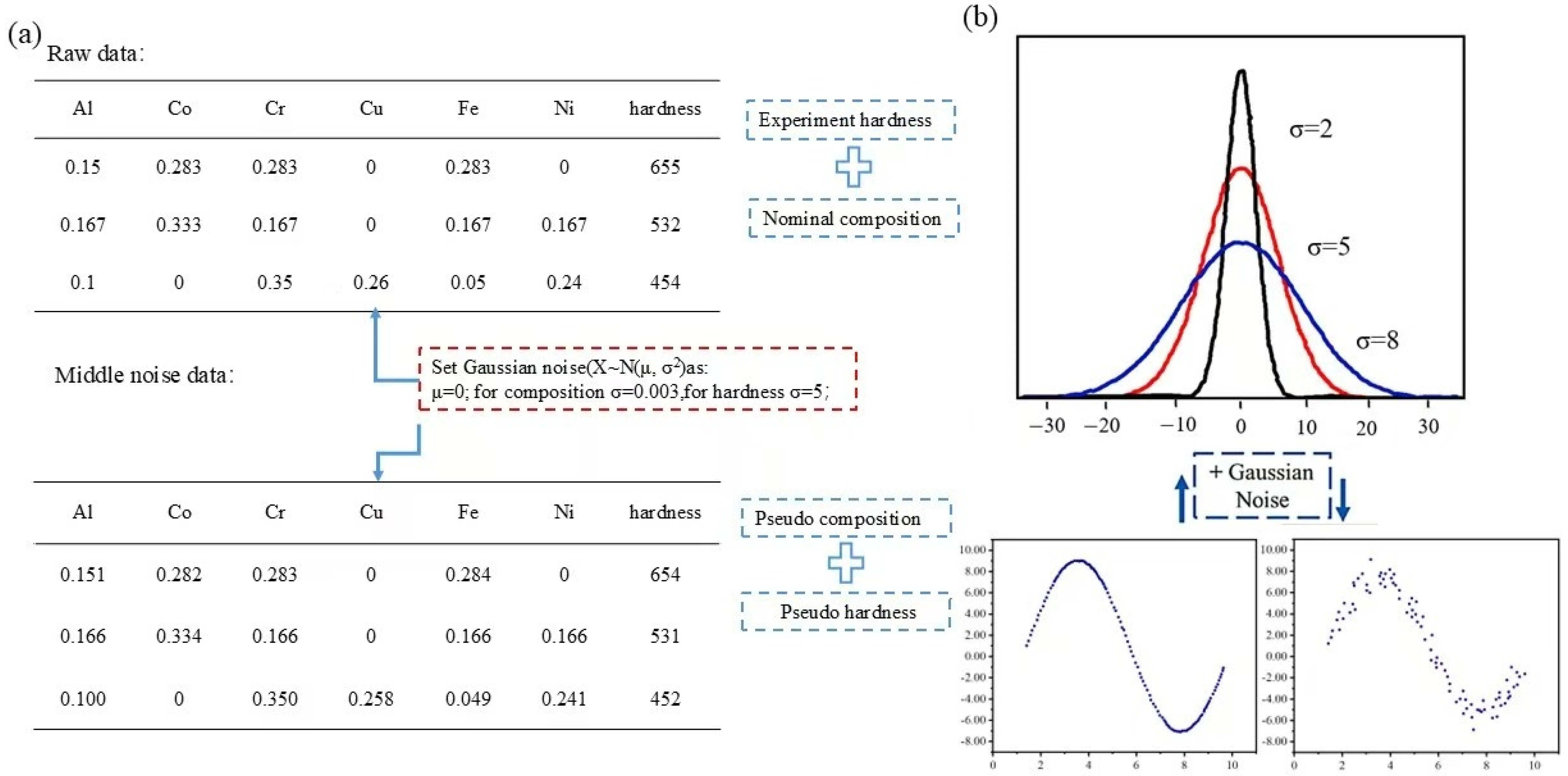
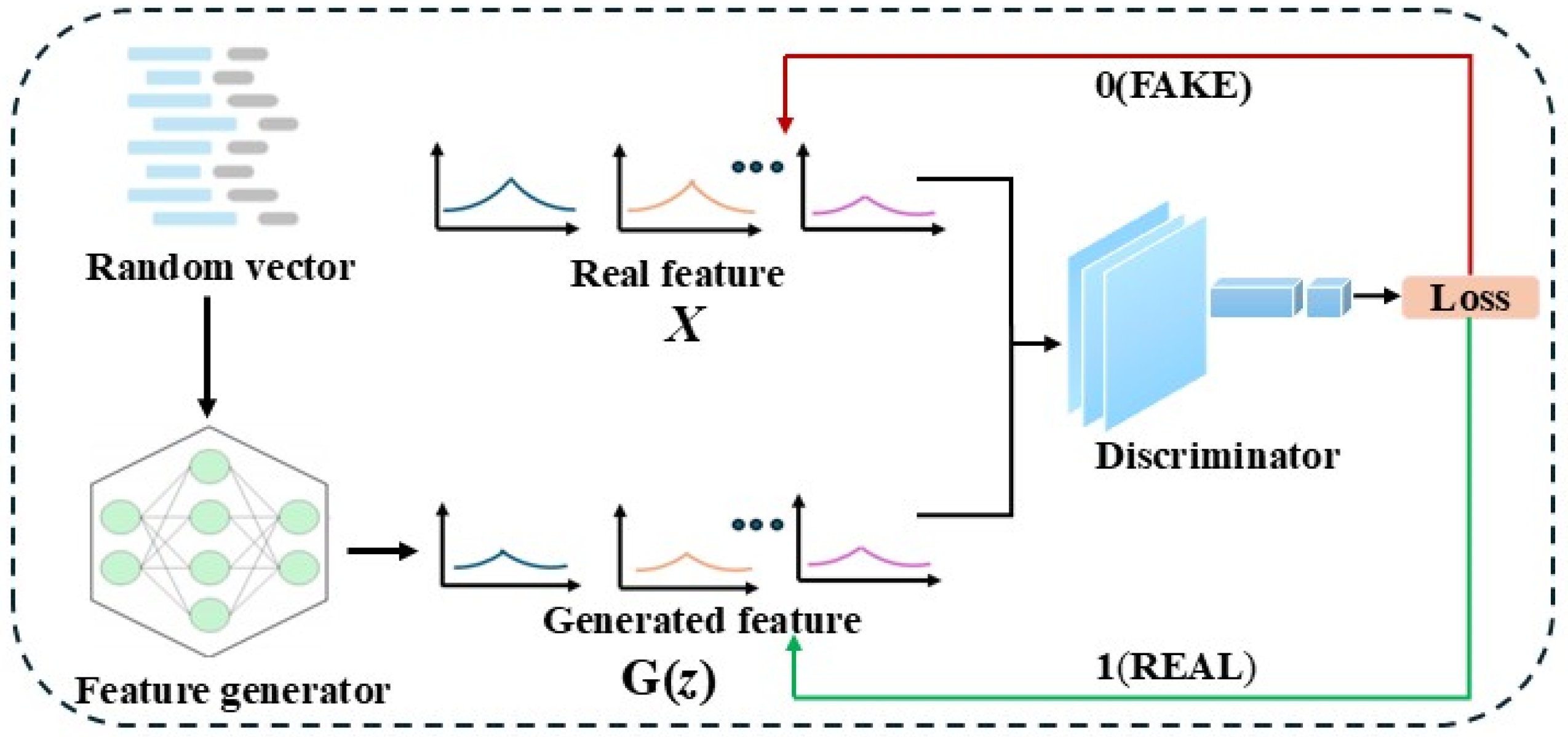
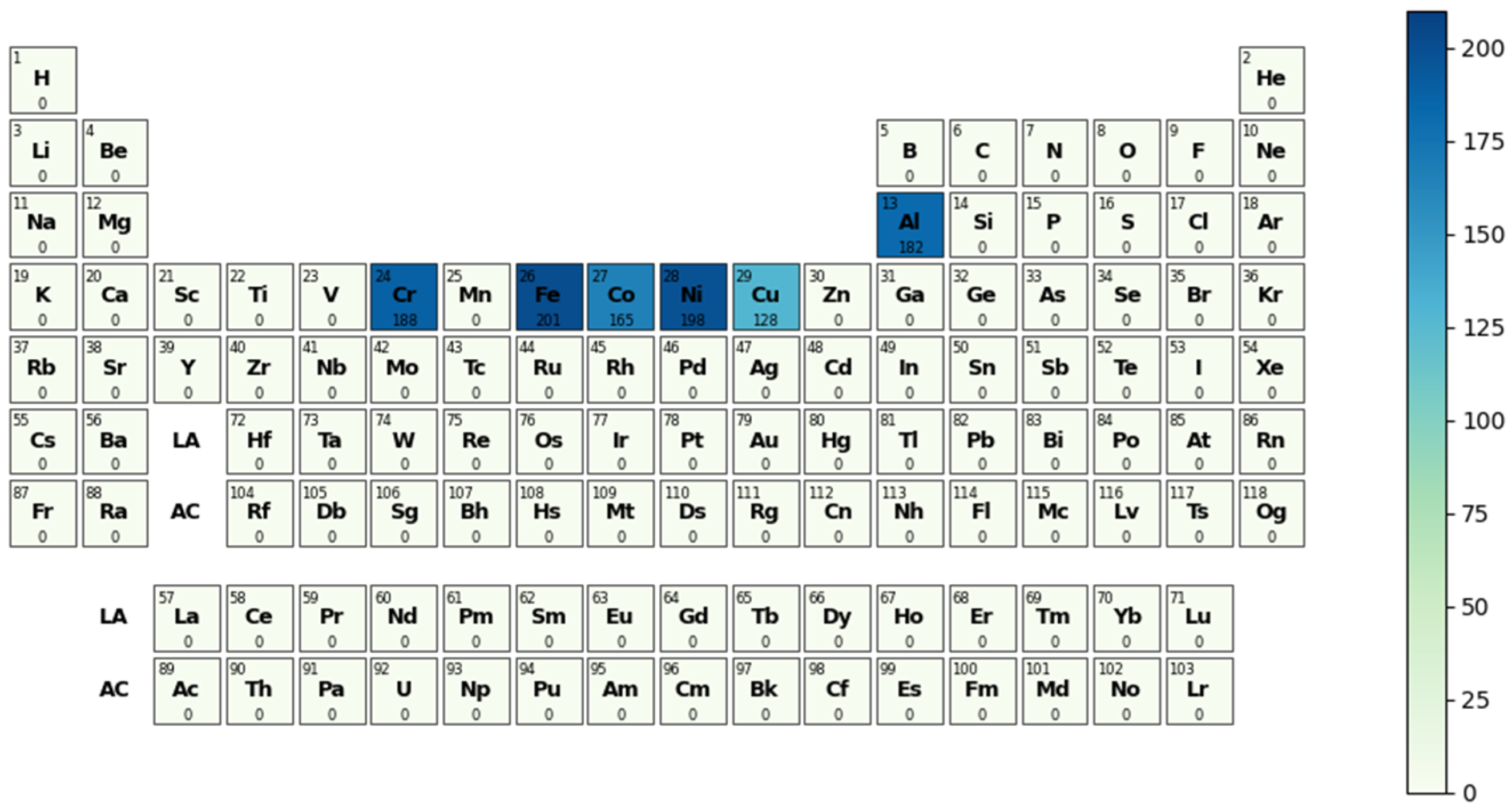

| Materials | Raw Data | 0.001 Noise | 0.003 Noise | 0.005 Noise |
|---|---|---|---|---|
| Al | 0.2310 | 0.2314 | 0.2327 | 0.2339 |
| Co | 0.1540 | 0.1541 | 0.1548 | 0.1555 |
| Cr | 0.1540 | 0.1514 | 0.1466 | 0.1418 |
| Cu | 0.1540 | 0.1536 | 0.1532 | 0.1528 |
| Fe | 0.1540 | 0.1547 | 0.1565 | 0.1583 |
| Ni | 0.1540 | 0.1545 | 0.1559 | 0.1574 |
| HV | 498 | 496 | 497 | 488 |
| Number | Mean | Std | ||||||
|---|---|---|---|---|---|---|---|---|
| Raw data | 0.001 noise | 0.003 noise | 0.005 noise | Raw data | 0.001 noise | 0.003 noise | 0.005 noise | |
| 1 | 0.2209 | 0.2207 | 0.2205 | 0.2203 | 0.1442 | 0.1442 | 0.1442 | 0.1442 |
| 2 | 0.1543 | 0.1544 | 0.1548 | 0.1547 | 0.0924 | 0.0924 | 0.0924 | 0.0925 |
| 3 | 0.1828 | 0.1828 | 0.1828 | 0.1829 | 0.0875 | 0.0874 | 0.0873 | 0.0874 |
| 4 | 0.0906 | 0.0906 | 0.0905 | 0.0904 | 0.0895 | 0.0895 | 0.0894 | 0.0894 |
| 5 | 0.1649 | 0.1648 | 0.1649 | 0.1650 | 0.0775 | 0.0776 | 0.0776 | 0.0778 |
| 6 | 0.1865 | 0.1865 | 0.1865 | 0.1866 | 0.1026 | 0.1024 | 0.1022 | 0.1020 |
| Number | Min | Max | ||||||
|---|---|---|---|---|---|---|---|---|
| Raw data | 0.001 noise | 0.003 noise | 0.005 noise | Raw data | 0.001 noise | 0.003 noise | 0.005 noise | |
| 1 | 0 | 0 | 0 | 0 | 0.470 | 0.472 | 0.476 | 0.480 |
| 2 | 0 | 0 | 0 | 0 | 0.333 | 0.428 | 0.429 | 0.430 |
| 3 | 0 | 0 | 0 | 0 | 0.317 | 0.554 | 0.551 | 0.549 |
| 4 | 0 | 0 | 0 | 0 | 0.225 | 0.290 | 0290 | 0.291 |
| 5 | 0 | 0 | 0 | 0 | 0.317 | 0.470 | 0.475 | 0.479 |
| 6 | 0 | 0 | 0 | 0 | 0.385 | 0.500 | 0.501 | 0.502 |
| Algorithm | RF | Linear | Ridge | SVR-Linear | SVR-Poly | SVR-rbf | KNN | XGBoost |
|---|---|---|---|---|---|---|---|---|
| R2(100%) | 92.1 | 87.3 | 90.6 | 90.8 | 92.6 | 96.4 | 93.6 | 90.2 |
| Generator Network | Discriminator Network | ||||
|---|---|---|---|---|---|
| Layer | Type | Dimension | Layer | Type | Dimension |
| Input | Latent | 10 | Input | Latent | 6 |
| Hidden1 | Dense layer | 128 | Hidden1 | Dense layer | 128 |
| Batch normalization | Batch normalization | ||||
| LeakyRelu | LeakyRelu | ||||
| Dense layer | 64 | Dense layer | 64 | ||
| Hidden2 | Batch normalization | Hidden2 | Batch normalization | ||
| LeakyRelu | LeakyRelu | ||||
| Dense layer | 32 | Dense layer | 32 | ||
| Hidden3 | Batch normalization | Hidden3 | Batch normalization | ||
| LeakyRelu | LeakyRelu | ||||
| output | Dense layer | 6 | output | Dense layer | 7 |
| Tanh activation | Tanh activation | ||||
| Number | Mean | Std | ||||
|---|---|---|---|---|---|---|
| Raw | GAN | GANpro | Raw | GAN | GANpro | |
| 1 | 0.221 | 0.222 | 0.223 | 0.001 | 0.062 | 0.226 |
| 2 | 0.153 | 0.152 | 0.149 | 0.148 | 0.019 | 0.019 |
| 3 | 0.185 | 0.175 | 0.183 | 0.058 | 0.029 | 0.010 |
| 4 | 0.091 | 0.089 | 0.089 | 0.129 | 0.014 | 0.188 |
| 5 | 0.164 | 0.160 | 0.165 | 0.058 | 0.012 | 0.131 |
| 6 | 0.185 | 0.185 | 0.185 | 0.097 | 0.037 | 0.085 |
| Number | Min | Max | ||||
|---|---|---|---|---|---|---|
| Raw | GAN | GANpro | Raw | GAN | GANpro | |
| 1 | 0 | 0 | 0 | 0.470 | 0.049 | 0.469 |
| 2 | 0 | 0 | 0 | 0.429 | 0.338 | 0.409 |
| 3 | 0 | 0 | 0 | 0.556 | 0.501 | 0.551 |
| 4 | 0 | 0 | 0 | 0.290 | 0.272 | 0288 |
| 5 | 0 | 0 | 0 | 0.469 | 0.407 | 0.422 |
| 6 | 0 | 0 | 0 | 0.500 | 0.471 | 0.498 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, C.; Meng, M.; Luo, X. Composition Design and Property Prediction for AlCoCrCuFeNi High-Entropy Alloy Based on Machine Learning. Metals 2025, 15, 733. https://doi.org/10.3390/met15070733
Liu C, Meng M, Luo X. Composition Design and Property Prediction for AlCoCrCuFeNi High-Entropy Alloy Based on Machine Learning. Metals. 2025; 15(7):733. https://doi.org/10.3390/met15070733
Chicago/Turabian StyleLiu, Cuixia, Meng Meng, and Xian Luo. 2025. "Composition Design and Property Prediction for AlCoCrCuFeNi High-Entropy Alloy Based on Machine Learning" Metals 15, no. 7: 733. https://doi.org/10.3390/met15070733
APA StyleLiu, C., Meng, M., & Luo, X. (2025). Composition Design and Property Prediction for AlCoCrCuFeNi High-Entropy Alloy Based on Machine Learning. Metals, 15(7), 733. https://doi.org/10.3390/met15070733







