Density Functional Theory-Based Study of UC2 and Cr-Doped UO2
Abstract
1. Introduction
2. Methodology
2.1. Elastic Constants
2.2. Lattice Assisted Thermal Conductivity
2.3. Electronic Thermal Conductivity
2.4. Total Thermal Conductivity
3. Results
3.1. Initial Ground State Structures
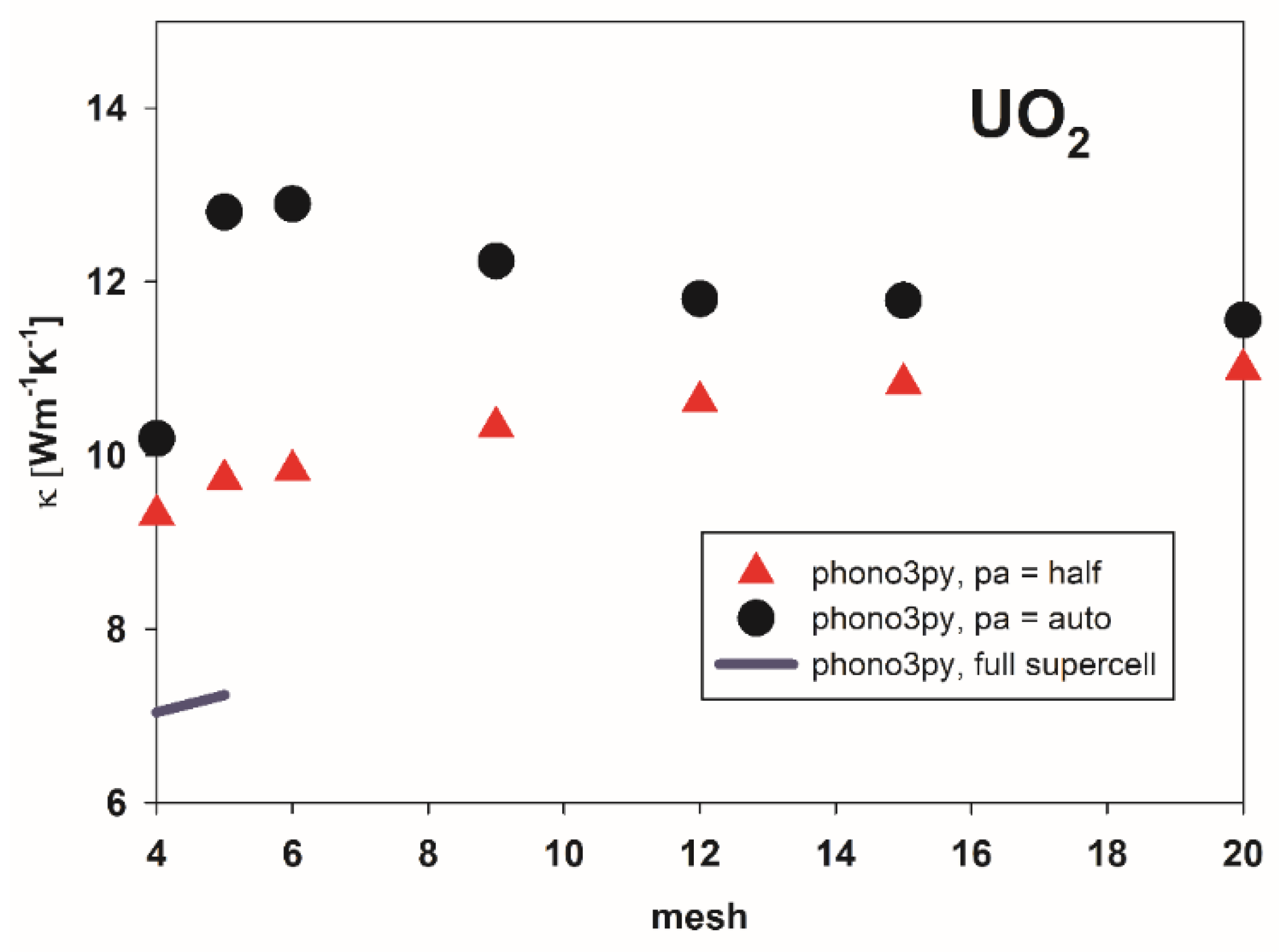
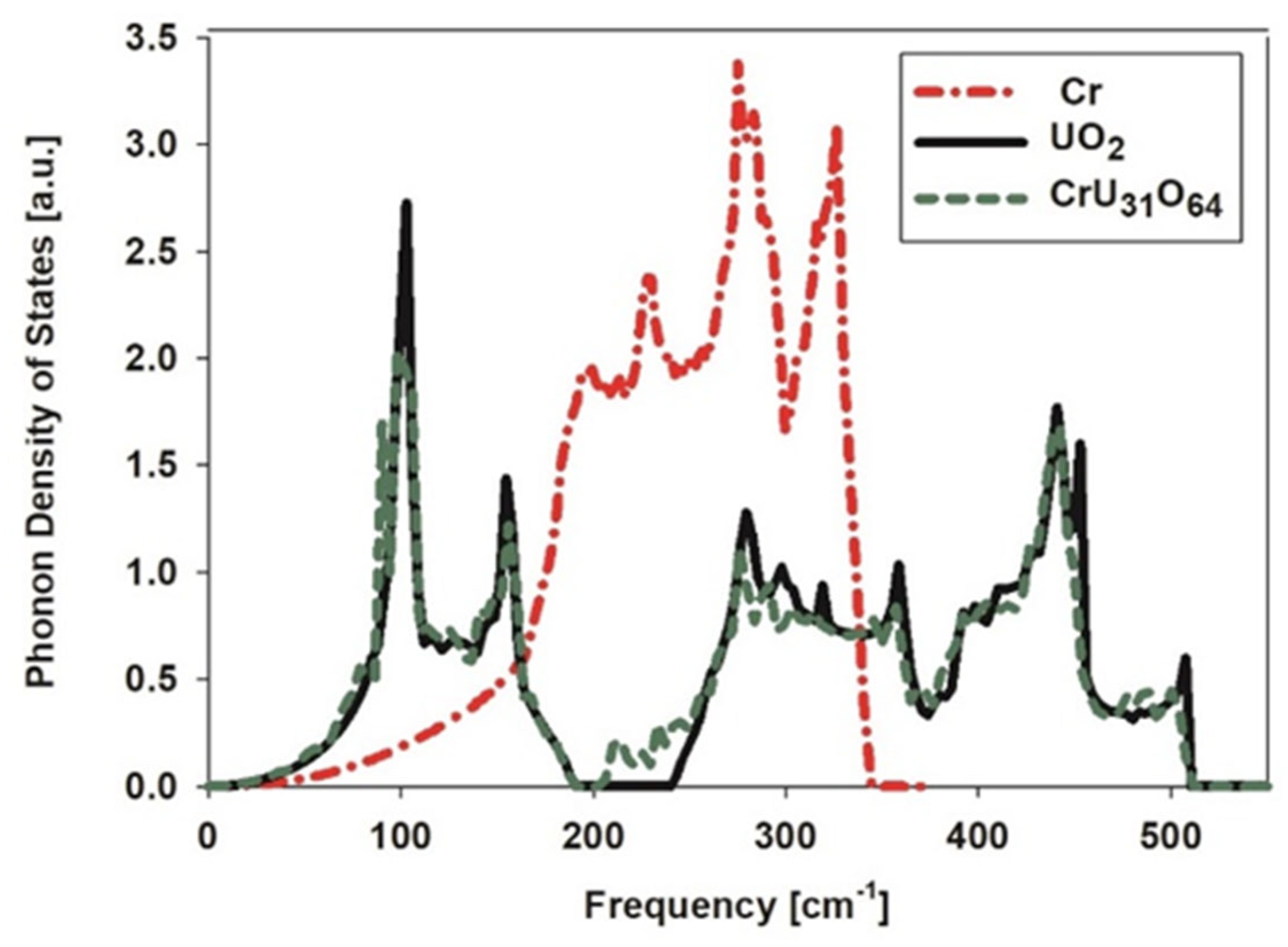
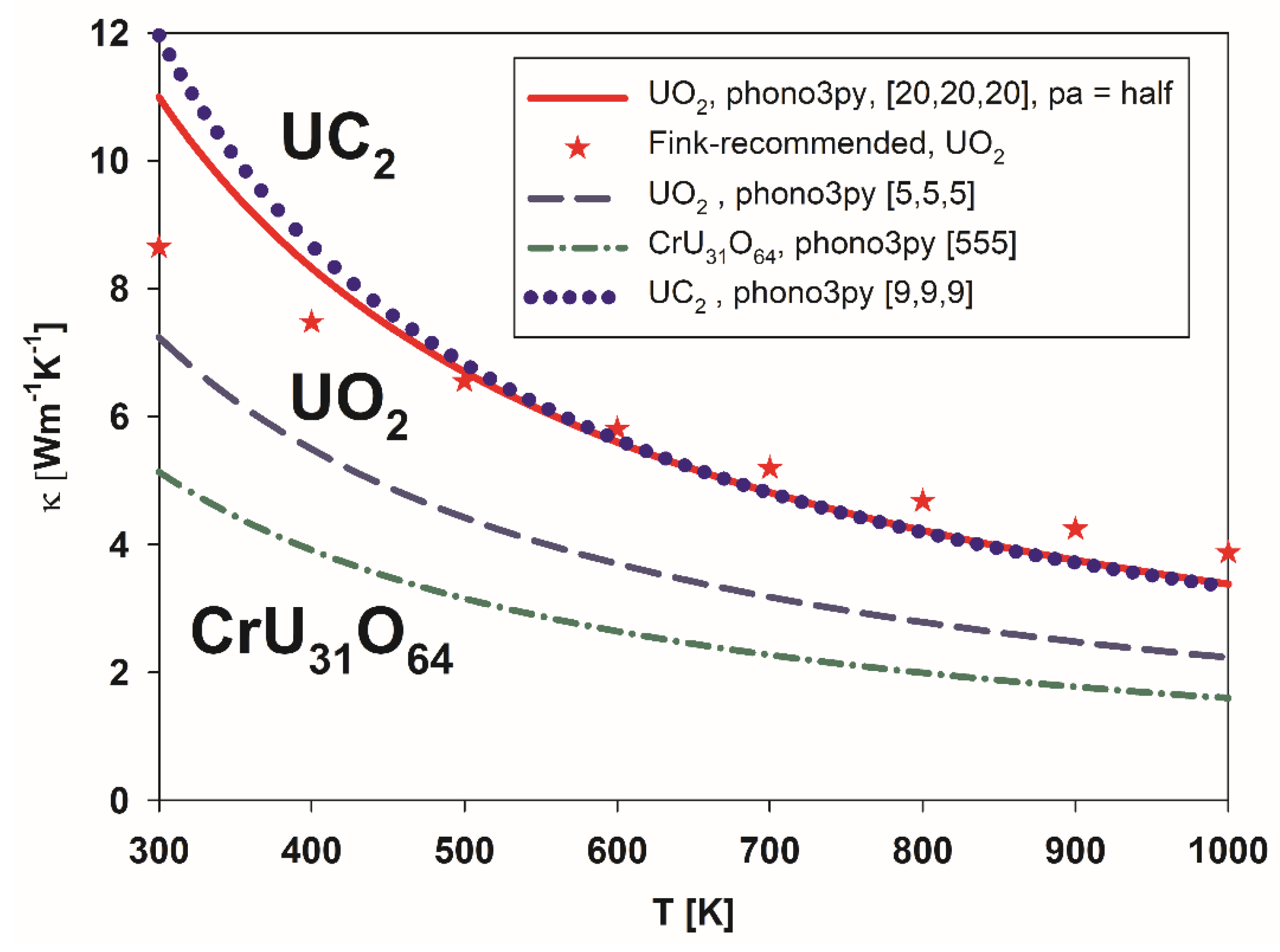
3.2. Thermal Conductivity of Pure UO2 and U1-xCrxO2
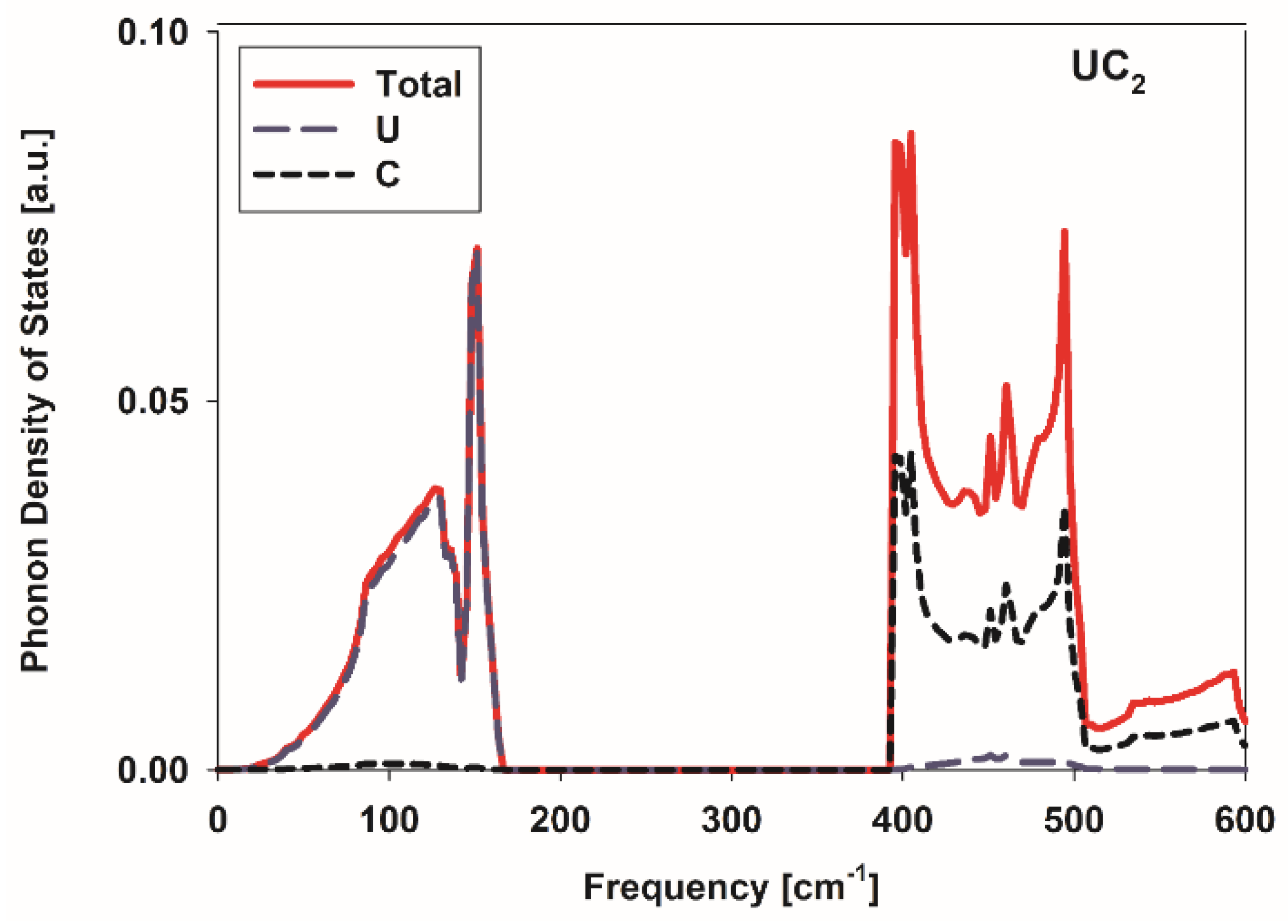
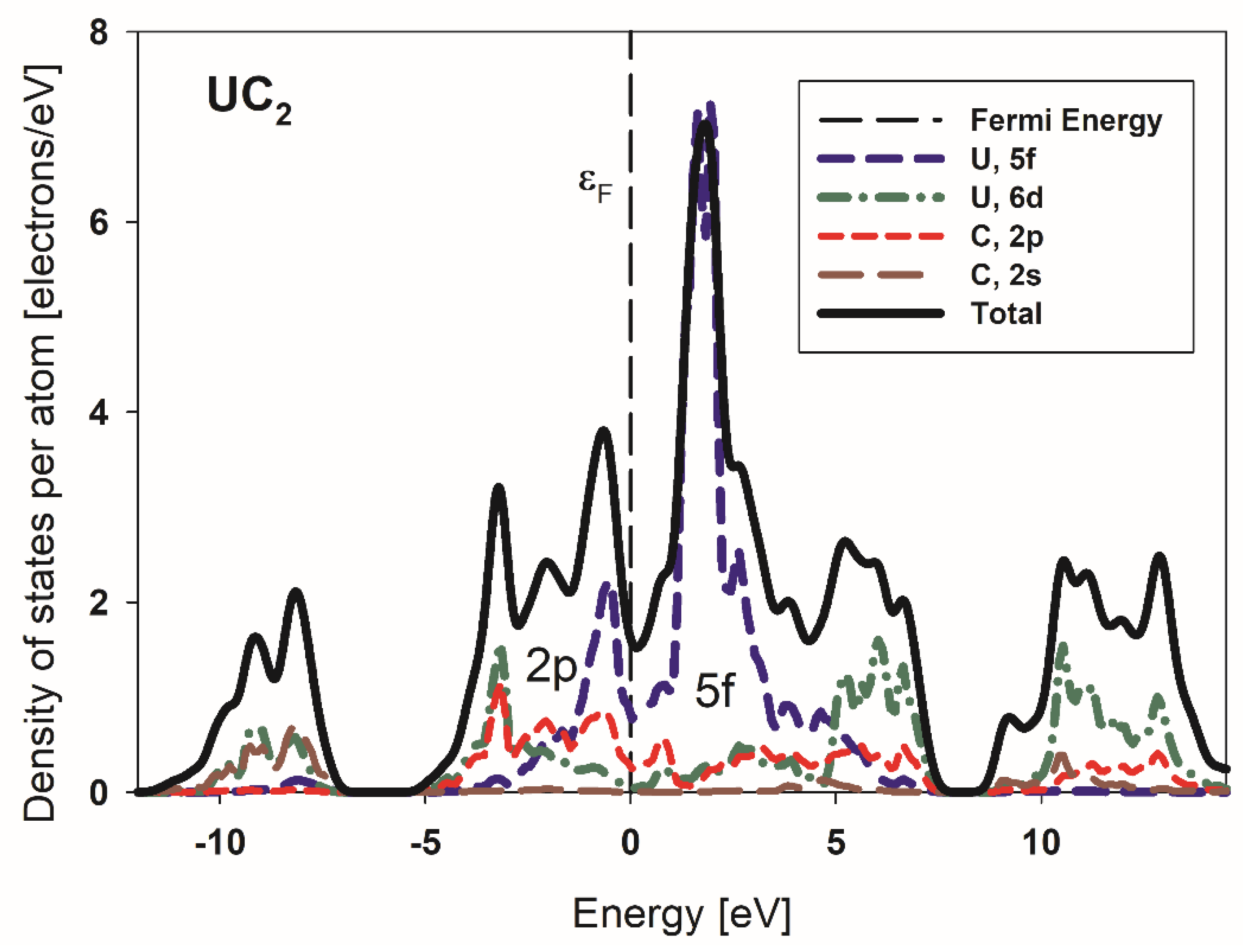
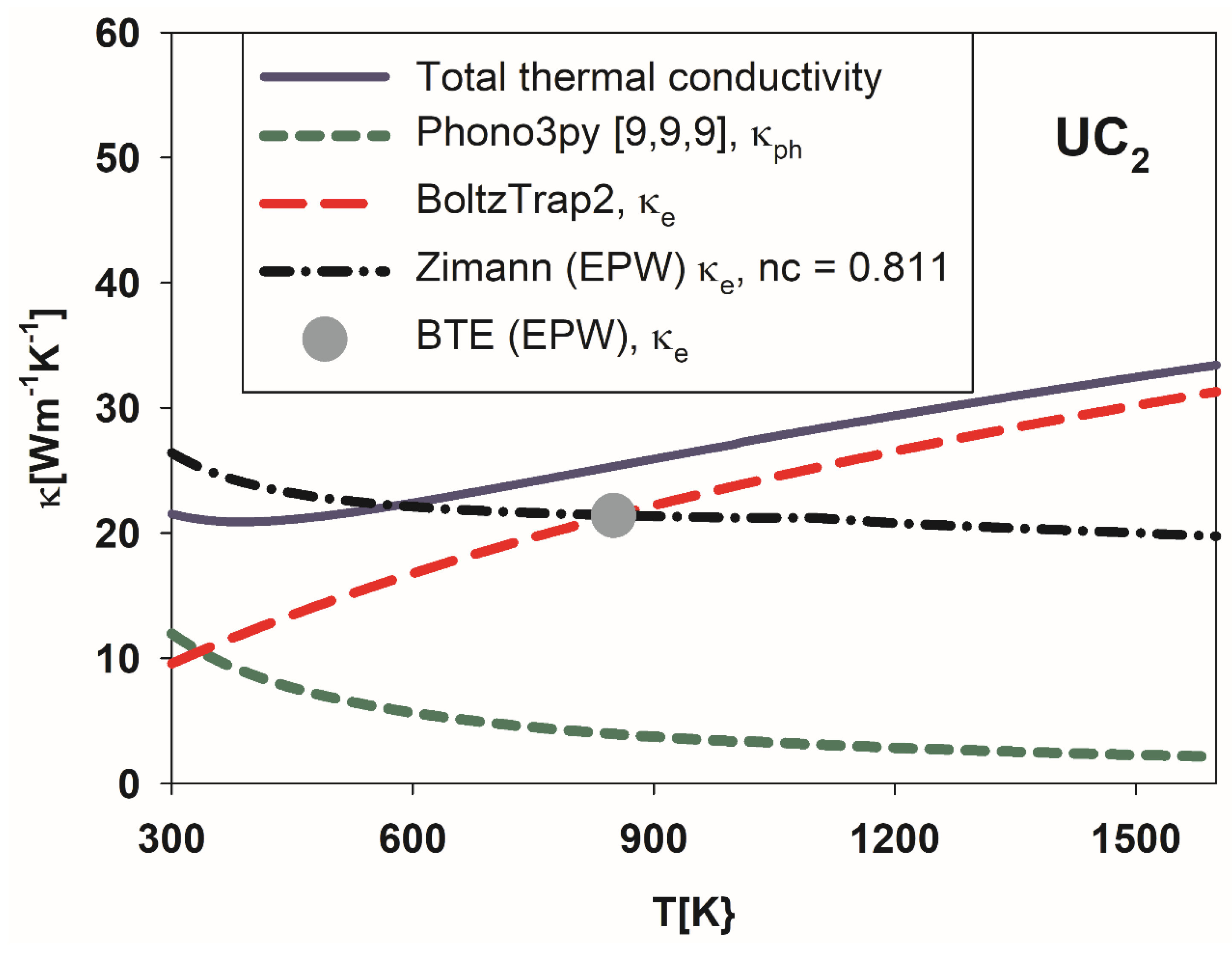
3.3. Conductivity of Metallic UC2
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ray, L.F.; Thiele, H.; Matzke, H. Transmission electron microscopy study of fission product behaviour in high burnup UO2. J. Nucl. Mater. 1992, 188, 90–95. [Google Scholar] [CrossRef]
- Tucker, M.O.; White, R.J. The release of unstable fission products from UO2 during irradiation. J. Nucl. Mater. 1979, 87, 1–10. [Google Scholar] [CrossRef]
- Sato, I.; Onishi, T.; Tanaka, K.; Iwasaki, M.J. Influence of boron vapor on transport behavior of deposited CsI during heating test simulating a BWR severe accident condition. Nucl. Mater. 2015, 461, 22–28. [Google Scholar] [CrossRef]
- Milena-Pérez, A.; Bonales, L.J.; Gómez-Mancebo, M.B.; Galán, H. Oxidation of accident tolerant fuels models based on Cr-doped UO2 for the safety of nuclear storage facilities. Nucl. Mater. 2023, 582, 13–19. [Google Scholar] [CrossRef]
- Olander, D.R. Fundamental Aspects of Nuclear Reactor Fuel Elements (TID-26711-P1); California University: Berkeley, CA, USA, 1976. [Google Scholar]
- Lyons, M.F.; Boyle, R.F.; Davies, J.H.; Hazel, V.E.; Rowland, T.C. UO2 properties affecting performance. Nucl. Eng. Des. 1972, 21, 167–199. [Google Scholar] [CrossRef]
- IAEA. Advanced Fuel Pellet Materials and Designs for Water Cooled Reactors/TECDOC-1416. In Proceedings of the Technical Committee Meeting, Brussels, Belgium, 4 June 2004. [Google Scholar]
- Singh, G.P.; Ram, S.; Eckert, J.J. Mechanical behaviour of metallic glasses related to thermal properties. Phys. Conf. Ser. 2009, 144, 012088. [Google Scholar]
- Cordara, T.; Cordara, T.; Smith, H.; Mohun, R.; Gardner, L.J.; Stennett, M.C.; Hyatt, N.C.; Corkhill, C.L. Hot Isostatic Pressing (HIP): A novel method to prepare Cr-doped UO2 nuclear fuel. MRS Adv. 2020, 5, 45–53. [Google Scholar] [CrossRef]
- Leenaers, A.; De Tollenaere, L.; Van den Berghe, S.J. On the solubility of chromium sesquioxide in uranium dioxide fuel. Nucl. Mater. 2003, 317, 62–68. [Google Scholar] [CrossRef]
- Hong, M. Role of electronic effects on the incorporation of Cr at a Σ5 grain boundary in UO2. Comput. Mater. Sci. 2013, 78, 29–33. [Google Scholar]
- Peres, V.; Favergeo, L.; Andrieu, M.; Palussière, J.C.; Balland, J.; Delafoy, C.; Pijolat, M. High emperatura chromium volatilization from Cr2O3 powder and Cr2O3-doped UO2 pellets in reducing atmospheres. J. Nucl. Mater. 2012, 423, 93–101. [Google Scholar] [CrossRef]
- Kegler, P.; Klinkenberg, M.; Bukaemskiy, A.; Murphy, G.L.; Deissmann, G.; Brandt, F.; Bosbach, D. Chromium Doped UO2-Based Ceramics: Synthesis and Characterization of Model Materials for Modern Nuclear Fuels. Materials 2021, 14, 6160. [Google Scholar] [CrossRef]
- Cardinaels, T.; Govers, K.; Vos, B.; Van den Berghe, S.; Verwerft, M.; De Tollenaere, L.; Maier, G.; Delafoy, C. Chromia doped UO2 fuel: Investigation of the lattice parameter. J Nucl Mater. 2012, 424, 252–260. [Google Scholar] [CrossRef]
- Killeen, J.C. Fission gas release and swelling in UO2 doped with Cr2O3. J. Nucl. Mater. 1980, 88, 177–184. [Google Scholar] [CrossRef]
- Middleburgh, S.C.; Dumbill, S.; Qaisar, A.; Vatter, I.; Owen, M.; Vallely, S.; Goddard, D.; Eaves, D. Enrichment of Chromium at Grain Boundaries in Chromia Doped UO2. J. Nucl. Mater. 2023, 575, 154250. [Google Scholar] [CrossRef]
- Riglet-Martial, C.J. Thermodynamics of chromium in UO2 fuel: A solubility model. Nucl. Mater. 2014, 447, 63–72. [Google Scholar] [CrossRef]
- Murphy, G.L.; Gericke, R.; Gilson, S.; Bazarkina, E.F.; Rossberg, A.; Kaden, P.; Thümmler, R.; Klinkenberg, M.; Henkes, M.; Kegler, P.; et al. Deconvoluting Cr states in Cr-doped UO2 nuclear fuels via bulk and single crystal spectroscopic studies. Nat. Commun. 2023, 14, 2455. [Google Scholar] [CrossRef]
- Pioro, I.L.; Khan, M.; Hopps, V.; Jacobs, C.S.C.W. Pressure-Channel Nuclear Reactor Some Design Features. J. Power Energy Syst. 2008, 2, 874–888. [Google Scholar] [CrossRef]
- Nuclear Science. State-of-the Art Report on Light Water Reactor Accident-Tolerant Fuels (OECD 2018); NEA No. 7317; OECD Publishing: Paris, France, 2018; p. 367. [Google Scholar]
- Vasudevamurthy, G.; Nelson, A.T. Uranium carbide properties for advanced fuel modeling-A review. J. Nucl. Mater. 2022, 558, 153145. [Google Scholar] [CrossRef]
- Shia, H.; Zhang, P.; Lib, S.-S.; Wangd, B.; Suna, B.J. First-principles study of UC2 and U2C3. Nucl. Mater. 2010, 396, 218–222. [Google Scholar] [CrossRef]
- Dancausse, J.-P.; Heathman, S.; Benedict, U.; Gerward, L.; Olsen, J.S.; Hulliger, F. Effect of N, C and B interstitial atoms on local bonding structure in mechanically activated TiH2/h-BN, TiH2/C, and TiH2/B mixtures. J. Alloys Compd. 1993, 191, 309–312. [Google Scholar] [CrossRef]
- Hafner, J. Ab-initio simulations of materials using VASP: Density-functional theory and beyond. Sol. Stat. Chem. 2008, 29, 2044–2078. [Google Scholar]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868, Erratum in Phys. Rev. Lett. 1997, 78, 1396. [Google Scholar] [CrossRef] [PubMed]
- Dudarev, S.L.; Botton, G.A.; Savrasov, S.Y.; Humphreys, C.J.; Sutton, A.P. Electron-energy-loss spectra and the structural stability of nickel oxide: An LSDA+U study. Phys. Rev. B 1998, 57, 1505–1509. [Google Scholar] [CrossRef]
- Szpunar, B.; Szpunar, J.A. Application of density functional theory in assessing properties of thoria and recycled fuels. Nucl. Mater. 2013, 439, 243–250. [Google Scholar] [CrossRef]
- Perdew, J.P.; Ruzsinszky, A.; Csonka, G.I.; Vydrov, O.A.; Scuseria, G.E.; Constantin, L.A.; Zhou, X.; Burke, K. Restoring the Density-Gradient Expansion for Exchange in Solids and Surfaces. Phys. Rev. Lett. 2008, 100, 136406, Erratum in Phys. Rev. Lett. 2009, 102, 039902. [Google Scholar] [CrossRef]
- Giannozzi, P.; Baroni, S.; Bonini, N.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Chiarotti, G.L.; Cococcioni, M.; Dabo, I.; et al. QUANTUM ESPRESSO: A modular and open-source software project for quantum simulations of materials. J. Phys. Condens. Matter 2009, 21, 395502–395521. [Google Scholar] [CrossRef] [PubMed]
- Jochym, T.; Parlinski, K. Ab Initio Lattice Dynamics and Elastic Constants of ZrC. Europ. Phys. J. B15 2000, 2, 265–268. [Google Scholar] [CrossRef]
- Arrigoni, M.; Carrete, J.; Mingo, N.; Madsen, G.K.H. First-principles quantitative prediction of the lattice thermal conductivity in random semiconductor alloys: The role of force-constant disorder. Phys. Rev. B 2018, 98, 115205. [Google Scholar] [CrossRef]
- Carruthers, P. Theory of Thermal Conductivity of Solids at Low Temperatures. Rev. Mod. Phys. 1961, 33, 93–138. [Google Scholar] [CrossRef]
- Togo, A.; Chaput, L.; Tadano, T.; Tanaka, I.; Conclusion, X.; Introduction, I. Implementation strategies in phonopy and phono3py. J. Phys. Condens. Matter 2023, 35, 353001. [Google Scholar] [CrossRef]
- Wiedemann, F.R. Ueber die Wärme-Leitungsfähigkeit der Metalle. Ann. Der Physik. 1853, 165, 497–531. (In German) [Google Scholar]
- Madsen, G.K.; Carrete, J.; Verstraete, M.J. BoltzTraP2, a program for interpolating band structures and calculating semi-classical transport coefficients. Comput. Phys. Commun. 2018, 231, 140–145. [Google Scholar] [CrossRef]
- Szpunar, B.; Ranasinghe, J.I.; Malakkal, L.; Szpunar, J.A. First principles investigation of thermal transport of uranium mononitride. Phys. Chem. Solids 2020, 146, 109636. [Google Scholar] [CrossRef]
- Poncé, S.; Margine, E.R.; Verdi, C.; Giustino, F. EPW: Electron–phonon coupling, transport and superconducting properties using maximally localized Wannier functions. Comput. Phys. Commun. 2016, 209, 116–133. [Google Scholar] [CrossRef]
- Wyckoff, R.W.G. (Ed.) Crystal Structures, 2nd ed.; John Wiley & Sons, Inc.: New York, NY, USA, 1963; Volume 2, p. 467. [Google Scholar]
- Fritz, I.J. Elastic properties of UO2 at high pressure. J. Appl. Phys. 1976, 47, 4353–4357. [Google Scholar] [CrossRef]
- Idiri, M.; Le Bihan, T.; Heathman, S.; Rebizant, J. Behavior of actinide dioxides under pressure: UO2 and ThO2. Phys. Rev. B—Condens. Matter Mater. Phys. 2004, 70, 1–8. [Google Scholar] [CrossRef]
- Chang, R. Trans 1829 C, CaF2. A diffusionless UC2 (cubic) to UC2 (tetragonal) transformation. Acta Crystallogr. 1961, 14, 1097. [Google Scholar] [CrossRef]
- Pang, J.W.L.; Chernatynskiy, A.; Larson, B.C.; Buyers, W.J.L.; Abernathy, D.L.; McClellan, K.J.; Phillpot, S.R. Phonon density of states and anharmonicity of UO2. Phys. Rev. B-Condens. Matter Mater. Phys. 2014, 89, 1–11. [Google Scholar] [CrossRef]
- Dolling, G.; Cowley, R.A.; Woods, A.D.B. The crystal dynamics of uranium dioxide. J. Phys. 1965, 43, 1397–1413. [Google Scholar] [CrossRef]
- Fink, J.K. Thermophysical properties of uranium dioxide. J. Nucl. Mater. 2000, 279, 1–18. [Google Scholar] [CrossRef]
- Camarano, D.D.M.; Mansur, F.A.; Meas, A.M.M.D.S. Experimental Investigations of Additives on the Thermal Conductivity UO2 Pellets; ABEN: Rio de Janeiro, Brazil, 2021; Volume 18, pp. 1–4. [Google Scholar]
- Terricabras, A.J.; Drewry, S.M.; Campbell, K.; Judge, E.J.; Byler, D.D.; Teti, E.S.; van Veelen, A.; Paisner, S.W.; White, J.T. Performance and properties evolution of near-term accident tolerant fuel: Cr-doped UO2. J. Nucl. Mater. 2024, 594, 10. [Google Scholar] [CrossRef]
- Zhong, Y.; Gao, R.; Li, B.; Yang, Z.; Huang, Q.; Wang, Z.; Duan, L.; Liu, X.; Chu, M.; Zhang, P.; et al. Preparation and Characterization of Large Grain UO2 for Accident Tolerant Fuel. Front. Mater. 2021, 8, 651074. [Google Scholar] [CrossRef]

| Compound | UO2 (HU 2.5 eV) | Exp. UO2 | UC2 | Exp.: UC2 |
|---|---|---|---|---|
| acalc [nm] | 0.537 (0.5457) | 0.54582 [38,39] (0.543 at 0 K) | 0.538 | 0.541 [41] |
| B [GPa] | 208.8 (192.6) | 208.9 | 198.7 | |
| C11 [GPa] | 400.9 (369.0) | 389.3 | 267.5 | |
| C12 [GPa] | 112.7 (104.5) | 118.7 | 164.3 | |
| C44 [GPa] | 82.9 (82.2) | 59.7 | 145.8 | |
| G [GPa] | 107.4 (102.2) | 108.12 | ||
| Y [GPa] | 275.0 (260.5) | 274.6 | ||
| G/B | 0.51 (0.53) | 0.54 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Szpunar, B.; Ranasinghe, J.I.; Szpunar, J.A. Density Functional Theory-Based Study of UC2 and Cr-Doped UO2. Metals 2025, 15, 727. https://doi.org/10.3390/met15070727
Szpunar B, Ranasinghe JI, Szpunar JA. Density Functional Theory-Based Study of UC2 and Cr-Doped UO2. Metals. 2025; 15(7):727. https://doi.org/10.3390/met15070727
Chicago/Turabian StyleSzpunar, Barbara, Jayangani I. Ranasinghe, and Jerzy A. Szpunar. 2025. "Density Functional Theory-Based Study of UC2 and Cr-Doped UO2" Metals 15, no. 7: 727. https://doi.org/10.3390/met15070727
APA StyleSzpunar, B., Ranasinghe, J. I., & Szpunar, J. A. (2025). Density Functional Theory-Based Study of UC2 and Cr-Doped UO2. Metals, 15(7), 727. https://doi.org/10.3390/met15070727







