Hot Deformation Behavior, Processing Maps, and Microstructure Evolution of 7E97 Alloy
Abstract
1. Introduction
2. Materials and Methods
3. Results and Discussion
3.1. Construct the Stress Constitutive Equation
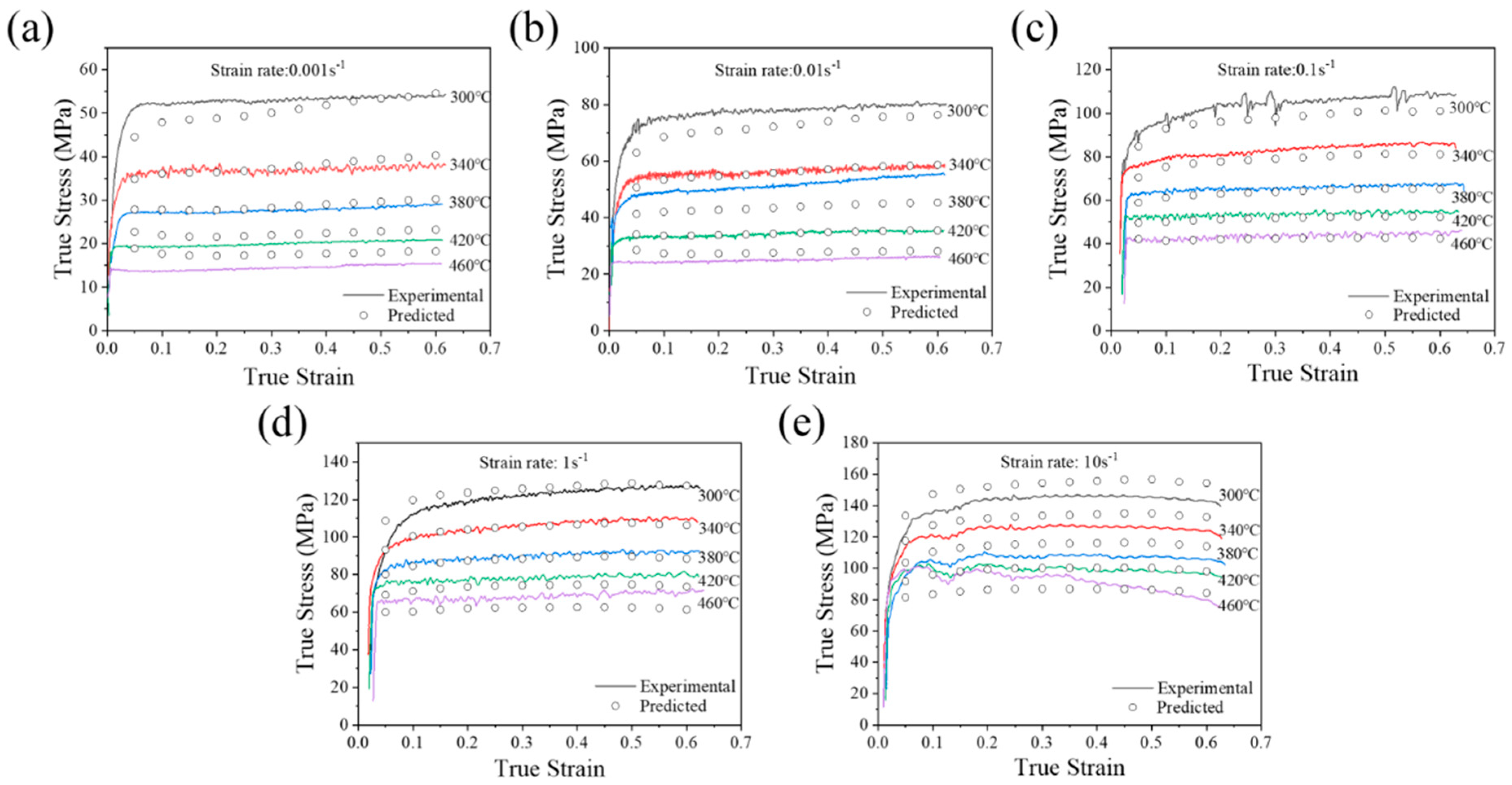
3.1.1. True Stress–True Strain Curve
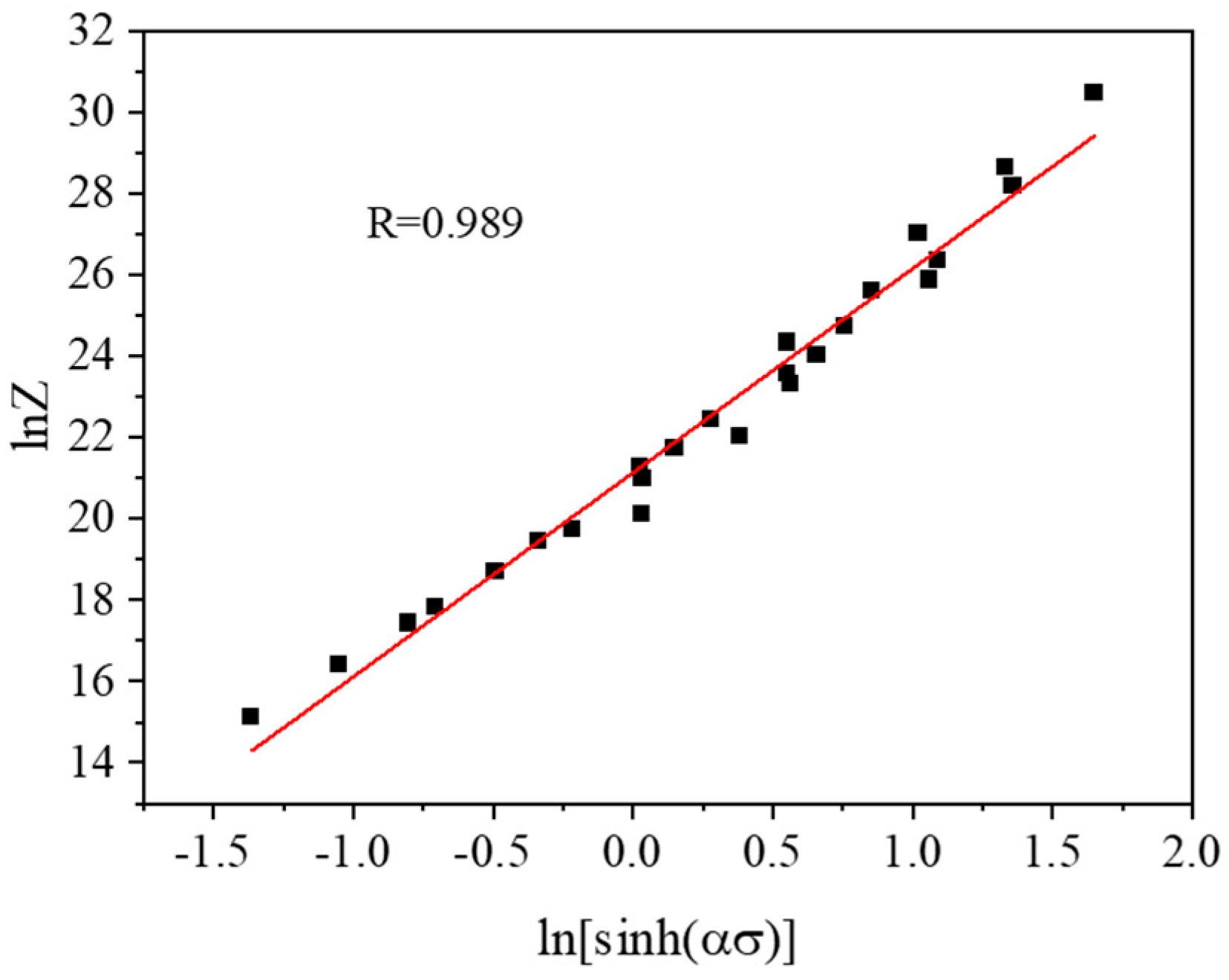
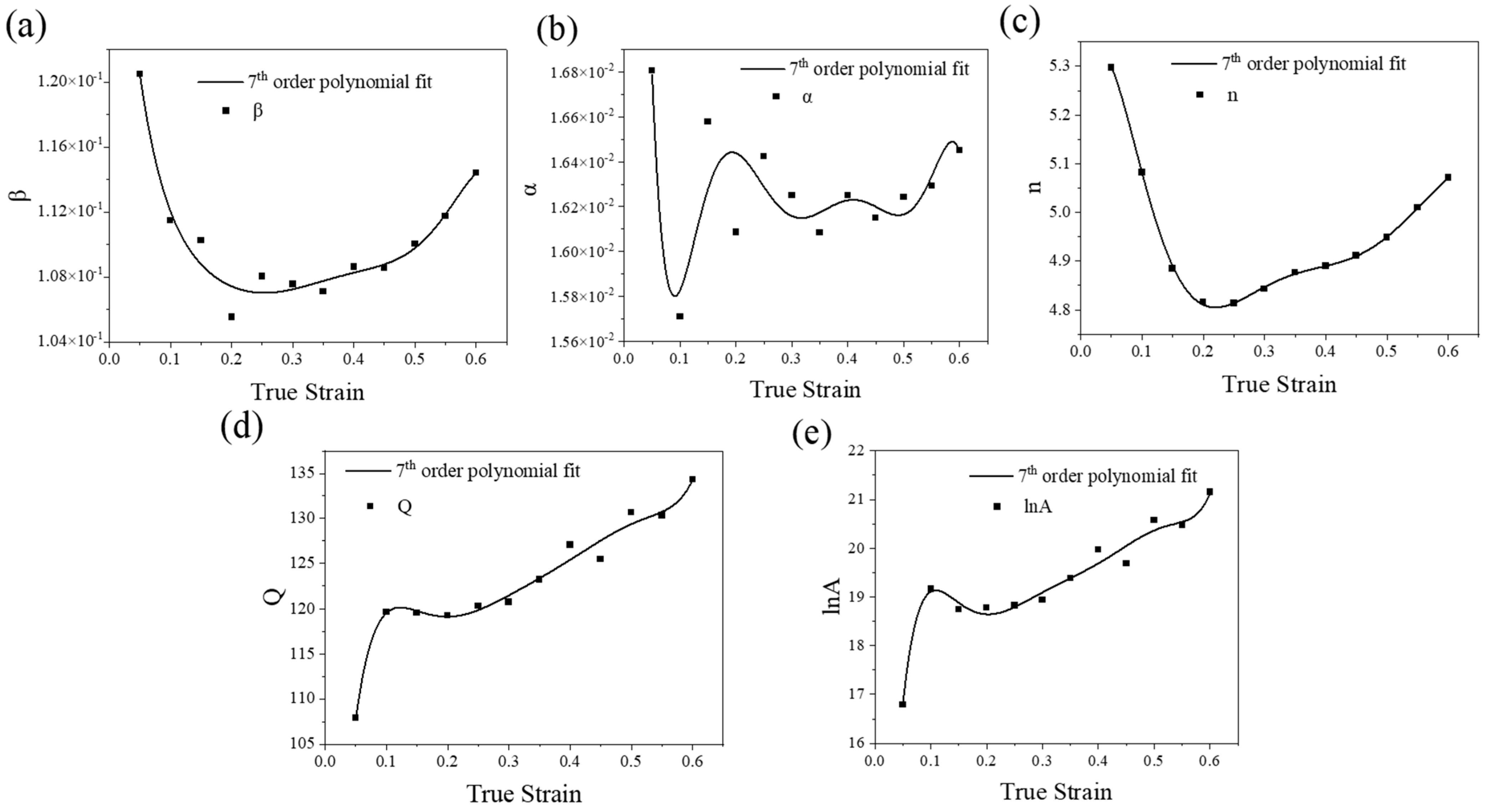
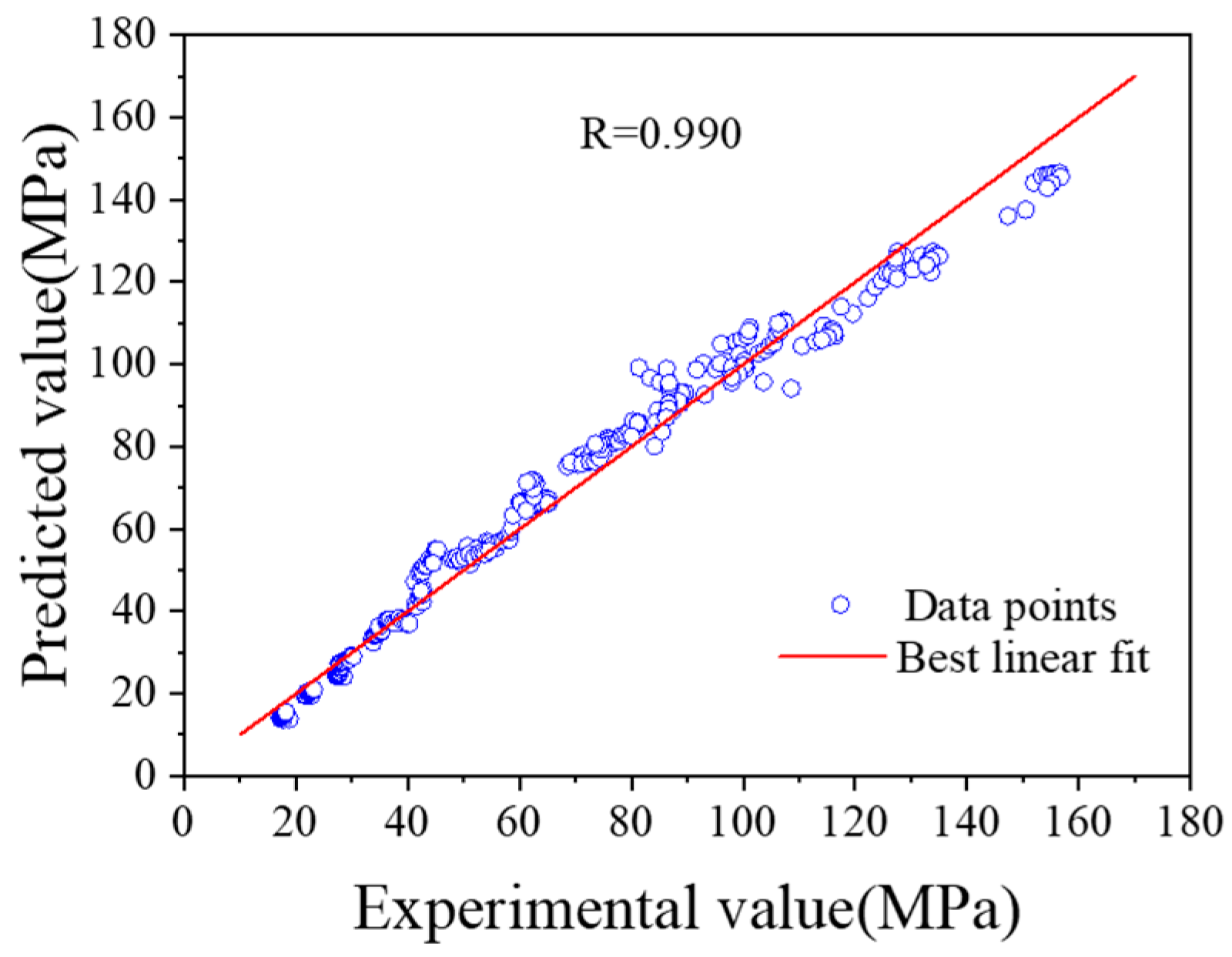
3.1.2. Constitutive Modeling
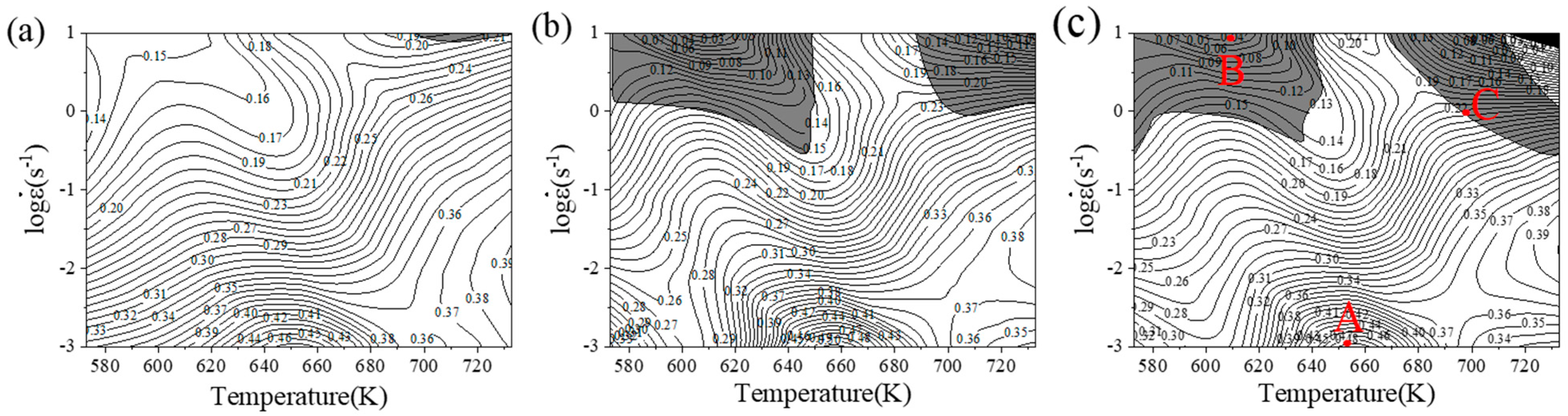
3.2. Hot Processing Maps
3.3. Microstructural Analysis
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Dong, P.; Chen, S.; Chen, K. Effects of Cu content on microstructure and properties of super-high-strength Al-9.3Zn-2.4Mg-xCu-Zr alloy. J. Alloy. Compd. 2019, 788, 329–337. [Google Scholar] [CrossRef]
- Hua, L.; Zhang, W.; Hu, L.; Zhang, Z.; Hu, Z. Mechanical responses and microstructure evolution of a 7A09 aluminum alloy extrusion profile during novel stretch bending. Mater. Charact. 2024, 212, 113938. [Google Scholar] [CrossRef]
- Wang, Z.; Geng, J.; Pu, Q.; Li, K.; Luo, T.; Li, Y.; Xia, P.; Li, X.; Chen, D.; Sha, G.; et al. Achieving high performance by optimized heat treatment in a spray formed Al–Zn–Mg–Cu alloy. Mater. Sci. Eng. A 2024, 893, 146134. [Google Scholar] [CrossRef]
- Liang, J.; Sun, J.; Li, X.; Zhang, Y.; Peng, L. Development and application of aluminum alloy drill rod in geologic drilling. Procedia Eng. 2014, 73, 84–90. [Google Scholar]
- Zhao, J.; Zhiyi, l.; Bai, S.; Huang, T.; Wang, J.; Xie, H.; Zeng, D.; Luo, L. Effect of various aging treatment on thermal stability of a novel Al-Zn-Mg-Cu alloy for oil drilling. Mater. Sci. Eng. A 2021, 803, 140490. [Google Scholar] [CrossRef]
- Wang, Y.-c.; Wu, X.-d.; Yue, L.; Guo, M.-x.; Cao, L.-f. Aging precipitation behavior and properties of Al–Zn–Mg–Cu–Zr–Er alloy at different quenching rates. Trans. Nonferrous Met. Soc. China 2022, 32, 1070–1082. [Google Scholar] [CrossRef]
- Martin, J.H.; Yahata, B.D.; Hundley, J.M.; Mayer, J.A.; Schaedler, T.A.; Pollock, T.M. 3D printing of high-strength aluminium alloys. Nature 2017, 549, 365–369. [Google Scholar] [CrossRef]
- Li, D.; Zhang, Z.; Li, S.; Yang, J.; Zhang, S.; Bian, X.; Zhang, Y.; Qi, L.; Ojo, O.A. Microstructure, mechanical properties and fatigue crack growth behavior of an Al-Zn-Mg-Cu-Si-Zr-Er alloy fabricated by laser powder bed fusion. Int. J. Fatigue 2023, 172, 107636. [Google Scholar] [CrossRef]
- Li, B.; Pan, Q.; Yin, Z. Characterization of hot deformation behavior of as-homogenized Al–Cu–Li–Sc–Zr alloy using processing maps. Mater. Sci. Eng. A 2014, 614, 199–206. [Google Scholar] [CrossRef]
- Rong, Z.; Wu, X.; He, F.; Wen, S.; Xiong, X.; Gao, K.; Wei, W.; Huang, H.; Nie, Z. Hot deformation behavior, dynamic recrystallization and precipitation behavior of a novel Er, Zr-microalloyed Al–Cu–Mg alloy. J. Mater. Res. Technol. 2025, 36, 5381–5395. [Google Scholar] [CrossRef]
- Jiang, F.; Zhang, H.; Li, L.; Chen, J. The kinetics of dynamic and static softening during multistage hot deformation of 7150 aluminum alloy. Mater. Sci. Eng. A 2012, 552, 269–275. [Google Scholar] [CrossRef]
- Tang, J.; Zhang, H.; Teng, J.; Fu, D.; Jiang, F. Effect of Zn content on the static softening behavior and kinetics of Al–Zn–Mg–Cu alloys during double-stage hot deformation. J. Alloy. Compd. 2019, 806, 1081–1096. [Google Scholar] [CrossRef]
- Hong, L.; Wu, X.; Xiong, X.; Gao, K.; Wen, S.; Wei, W.; Rong, L.; Huang, H.; Nie, Z.; Dong, Y.; et al. Study of dynamic recrystallization behavior of Al-Zn-Mg-Cu-Er-Zr alloy during isothermal compression. J. Mater. Res. Technol. 2025, 34, 1399–1409. [Google Scholar] [CrossRef]
- Cheng, Z.; Zhang, C.; Chu, G.; Liu, Z.; Wang, K.; Meng, Z.; Chen, L.; Sun, L.; Zhao, G. Dynamic precipitation and recrystallization behavior during hot deformation of Al-Zn-Mg-Cu alloy: Experiment and modeling. Int. J. Plast. 2024, 178, 103995. [Google Scholar] [CrossRef]
- Wang, H.; Qin, G.; Li, C.; Liang, G. Effect of deformation parameters and Al2Cu evolution on dynamic recrystallization of 2219-O Al alloy during hot compression. J. Mater. Res. Technol. 2023, 26, 4093–4106. [Google Scholar] [CrossRef]
- Xu, C.; Huang, J.; Jiang, F.; Jiang, Y. Dynamic recrystallization and precipitation behavior of a novel Sc, Zr alloyed Al-Zn-Mg-Cu alloy during hot deformation. Mater. Charact. 2022, 183, 111629. [Google Scholar] [CrossRef]
- Feng, D.; Zhang, X.M.; Liu, S.D.; Deng, Y.L. Constitutive equation and hot deformation behavior of homogenized Al-7.68Zn-2.12Mg-1.98Cu-0.12Zr alloy during compression at elevated temperature. Mater. Sci. Eng. A 2014, 608, 63–72. [Google Scholar] [CrossRef]
- Lu, B.; Li, Y.; Yu, W.; Wang, H.; Wang, Y.; Wang, Z.; Xu, G. Strength and ductility enhancement of twin-roll cast Al-Zn-Mg-Cu alloys with high solidification intervals through a synergistic segregation-controlling strategy. J. Mater. Sci. Technol. 2023, 142, 225–239. [Google Scholar] [CrossRef]
- Wu, M.; Xiao, D.; Yuan, S.; Li, Z.; Yin, X.; Wang, J.; Huang, L.; Liu, W. Synergy of strength-ductility in a novel Al-Zn-Mg-Cu-Zr-Sc-Hf alloy through optimizing hierarchical microstructures. J. Mater. Sci. Technol. 2025, 212, 105–122. [Google Scholar] [CrossRef]
- Zhang, J.; Yi, Y.; Huang, S.; Mao, X.; He, H.; Tang, J.; Guo, W.; Dong, F. Dynamic recrystallization mechanisms of 2195 aluminum alloy during medium/high temperature compression deformation. Mater. Sci. Eng. A 2021, 804, 140650. [Google Scholar] [CrossRef]
- Li, J.; Wu, X.; Cao, L.; Liao, B.; Wang, Y.; Liu, Q. Hot deformation and dynamic recrystallization in Al-Mg-Si alloy. Mater. Charact. 2021, 173, 110976. [Google Scholar] [CrossRef]
- Anand, L. Constitutive equations for hot-working of metals. Int. J. Plast. 1985, 1, 213–231. [Google Scholar] [CrossRef]
- Hou, H.; Zhao, G.; Yu, J.; Wei, D. A unified physically-based model describing complex unloading behavior in cold and hot deformation process of aluminum alloys. Eur. J. Mech. A-Solids 2024, 105, 105266. [Google Scholar] [CrossRef]
- Sellars, C.M.; McTegart, W.J. On the mechanism of hot deformation. Acta Metall. 1966, 14, 1136–1138. [Google Scholar] [CrossRef]
- Mann, J.B.; Chandrasekar, S.; Compton, W.D.; Trumble, K.P.; Saldana, C.; Swaminathan, S.; John, G.E.; Moscoso, W.; Murthy, T.G. 7—Severe plastic deformation and the production of nanostructured alloys by machining. In Nanostructured Metals and Alloys; Whang, S.H., Ed.; Woodhead Publishing: Cambridge, UK, 2011; pp. 178–210. [Google Scholar]
- Prasad, Y.V.R.K.; Gegel, H.L.; Doraivelu, S.M.; Malas, J.C.; Morgan, J.T.; Lark, K.A.; Barker, D.R. Modeling of dynamic material behavior in hot deformation: Forging of Ti-6242. Metall. Trans. A 1984, 15, 1883–1892. [Google Scholar] [CrossRef]
- Wei, D.; Han, L.; Lv, Z.; Wang, G.; Zhao, G. Investigation of constitutive models and microstructure evolution during hot deformation and solution treatment of Al–Zn–Mg–Cu alloy. J. Mater. Res. Technol. 2024, 32, 1028–1045. [Google Scholar] [CrossRef]
- Chen, G.; Chen, W.; Ma, L.; Guo, A.; Lü, J.; Zhang, Z.; Zheng, S. Strain-Compensated Arrhenius-Type Constitutive Model for Flow Behavior of Al-12Zn-2.4Mg-1.2Cu Alloy. Rare Metal Mat. Eng. 2015, 44, 2120–2125. [Google Scholar]
- Tang, J.; Jiang, F.; Luo, C.; Bo, G.; Chen, K.; Teng, J.; Fu, D.; Zhang, H. Integrated physically based modeling for the multiple static softening mechanisms following multi-stage hot deformation in Al-Zn-Mg-Cu alloys. Int. J. Plast. 2020, 134, 102809. [Google Scholar] [CrossRef]
- Yue, X.-h.; Liu, C.-f.; Liu, H.-h.; Xiao, S.-f.; Tang, Z.-h.; Tang, T. Effects of hot compression deformation temperature on the microstructure and properties of Al–Zr–La alloys. Int. J. Miner. Metall. Mater. 2018, 25, 236–243. [Google Scholar] [CrossRef]
- Huang, K.; Logé, R.E. A review of dynamic recrystallization phenomena in metallic materials. Mater. Des. 2016, 111, 548–574. [Google Scholar] [CrossRef]
- Ebrahimi, R.; Najafizadeh, A. A new method for evaluation of friction in bulk metal forming. J. Mater. Process. Technol. 2004, 152, 136–143. [Google Scholar] [CrossRef]
- Sellars, C.M.; Tegart, W.J. Hot workability. Int. Metall. Rev. 1972, 17, 1–24. [Google Scholar] [CrossRef]
- McQueen, H.J.; Yue, S.; Ryan, N.D.; Fry, E. Hot working characteristics of steels in austenitic state. J. Mater. Process. Technol. 1995, 53, 293–310. [Google Scholar] [CrossRef]
- Zener, C.; Hollomon, J.H. Effect of Strain Rate Upon Plastic Flow of Steel. J. Appl. Phys. 1944, 15, 22–32. [Google Scholar] [CrossRef]
- Gegel, H.L.; Malas, J.C.; Doraivelu, S.M. Process Modeling of P/M Extrusion. In Innovations in Materials Processing; Bruggeman, G., Weiss, V., Eds.; Springer: Boston, MA, USA, 1985; pp. 137–159. [Google Scholar]
- Liu, C.; Liu, Y.; Huang, Y.; Sheng, Z.; Fan, X.; Wu, Z.; Feng, W.; Liu, P. Investigation of hot deformation behavior and optimization of hot workability for a novel Zr, Sc alloyed Al-Mg-Mn alloy. J. Alloy. Compd. 2025, 1017, 178943. [Google Scholar] [CrossRef]
- Wu, H.; Wen, S.P.; Huang, H.; Gao, K.Y.; Wu, X.L.; Wang, W.; Nie, Z.R. Hot deformation behavior and processing map of a new type Al-Zn-Mg-Er-Zr alloy. J. Alloy. Compd. 2016, 685, 869–880. [Google Scholar] [CrossRef]
- Dai, Y.; Yan, L.; Sun, S.; Zhang, J.; Li, X.; Liu, J.; Liu, X. In-depth investigation of microstructural evolution induced by Sc, V, and Ni microalloying in Al-Zn-Mg-Cu alloy during hot compression. Mater. Des. 2025, 253, 113857. [Google Scholar] [CrossRef]
- Jagan Reddy, G.; Srinivasan, N.; Gokhale, A.A.; Kashyap, B.P. Processing map for hot working of spray formed and hot isostatically pressed Al–Li alloy (UL40). J. Mater. Process. Technol. 2009, 209, 5964–5972. [Google Scholar] [CrossRef]
- Tang, J.; Yi, Y.; He, H.; Huang, S.; Zhang, J.; Dong, F. Hot deformation behavior and microstructural evolution of the Al-Cu-Li alloy: A study with processing map. J. Alloy. Compd. 2023, 934, 167755. [Google Scholar] [CrossRef]
- Kulkarni, S.S.; Starke, E.A.; Kuhlmann-Wilsdorf, D. Some observations on deformation banding and correlated microstructures of two aluminum alloys compressed at different temperatures and strain rates. Acta Mater. 1998, 46, 5283–5301. [Google Scholar] [CrossRef]
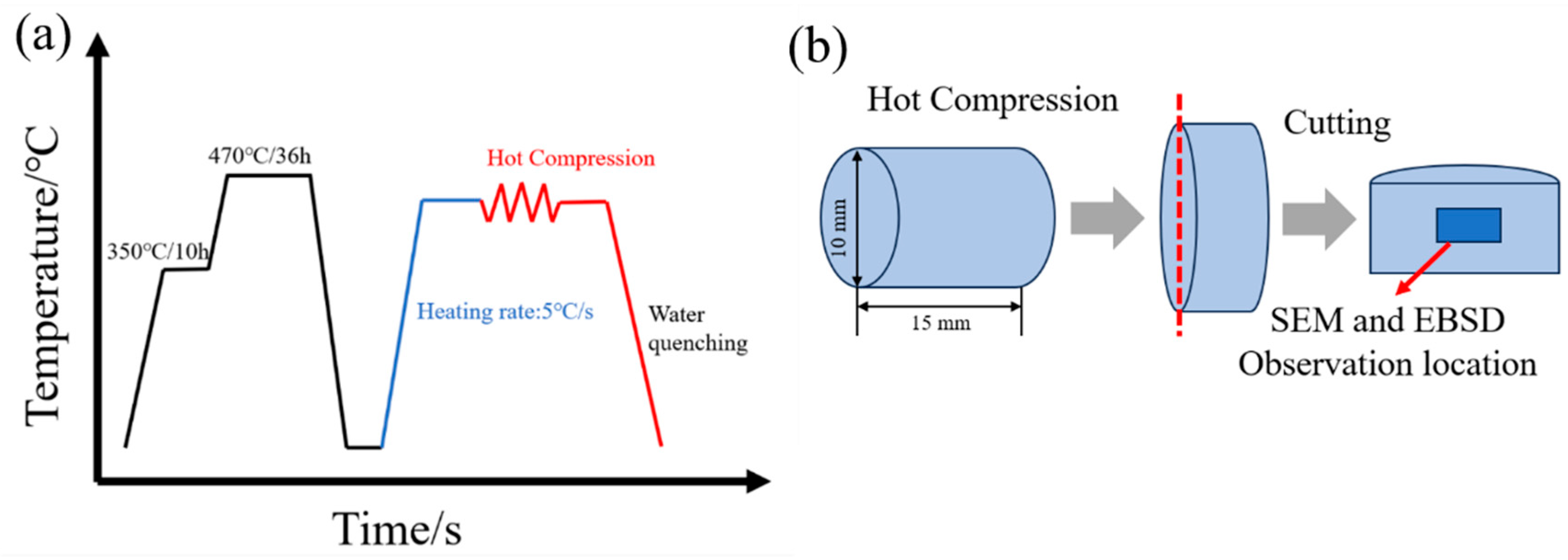
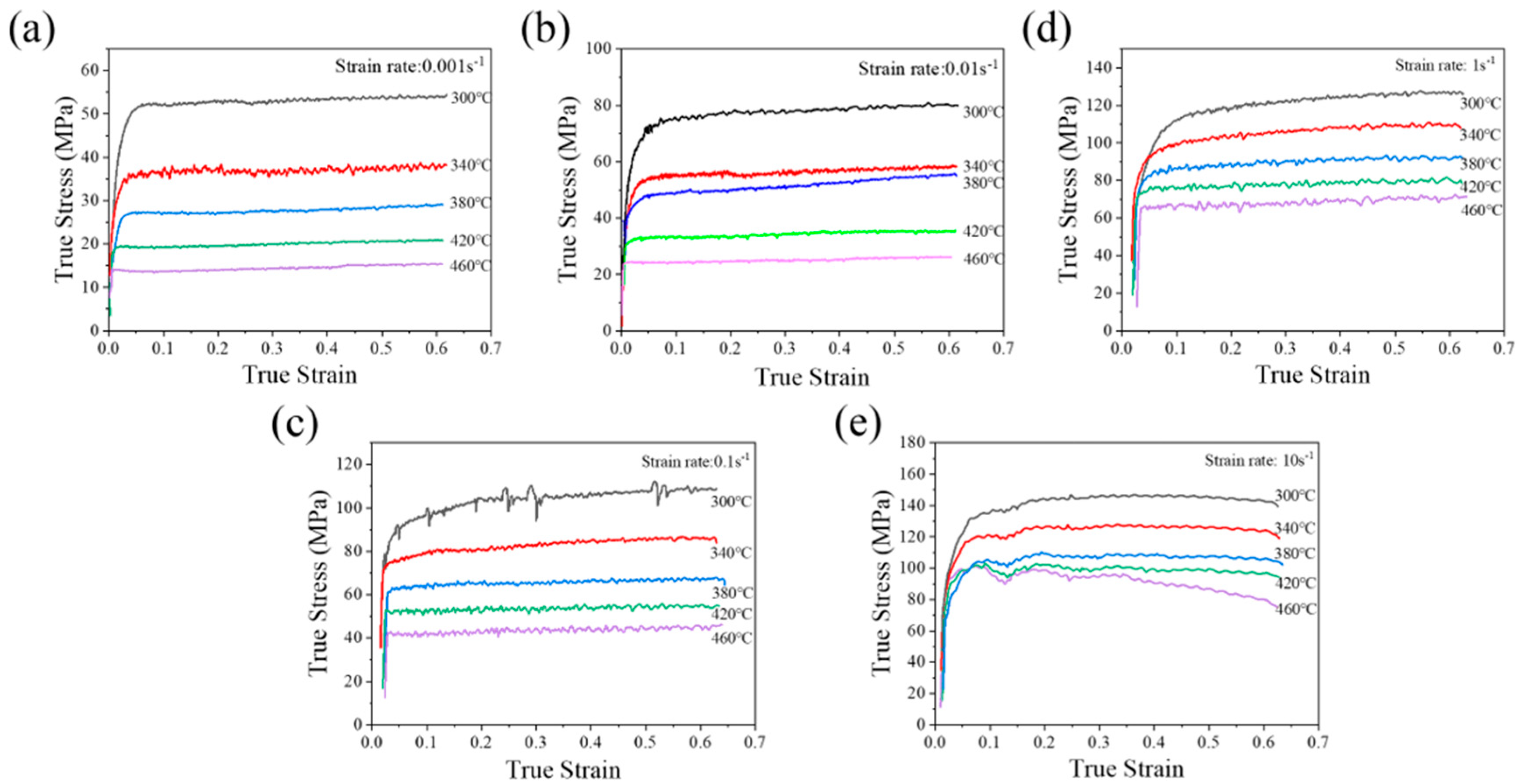



| Element | Zn | Mg | Cu | Mn | Er | Zr | Fe | Si | Al |
|---|---|---|---|---|---|---|---|---|---|
| 7.62 | 2.22 | 0.90 | 0.30 | 0.09 | 0.13 | 0.09 | 0.03 | Bal. |
| lnZ | 300 °C | 340 °C | 380 °C | 420 °C | 460 °C |
|---|---|---|---|---|---|
| 0.001 s−1 | 21.3 | 19.4 | 17.8 | 16.4 | 15.1 |
| 0.01 s−1 | 23.6 | 21.8 | 20.1 | 18.7 | 17.4 |
| 0.1 s−1 | 25.9 | 24.1 | 22.4 | 21.0 | 19.7 |
| 1 s−1 | 28.2 | 26.4 | 24.7 | 23.3 | 22.0 |
| 10 s−1 | 30.5 | 28.7 | 27.0 | 25.6 | 24.3 |
| Material Parameters | (MPa−1) | (MPa−1) | n | A (s−1) | Q (kJ/mol) |
|---|---|---|---|---|---|
| 0.114 | 0.016 | 5.0715 | 1.538 × 109 | 134.357 |
| Material Parameters | n | lnA | Q | ||
|---|---|---|---|---|---|
| B0 | 0.0249 | 0.1427 | 5.1974 | 4.6122 | 56.3937 |
| B1 | −0.3073 | −0.6830 | 9.6117 | 430.6676 | 1764.1733 |
| B2 | 3.9319 | 6.2542 | −215.2027 | −4977.5198 | −19,320.1369 |
| B3 | −24.7165 | −34.1283 | 1496.4479 | 29,133.3694 | 108,846.2525 |
| B4 | 84.9971 | 113.6882 | −5050.3063 | −95,321.0135 | −346,403.1307 |
| B5 | −163.1830 | −222.4811 | 9066.2437 | 177,382.1859 | 633,407.3081 |
| B6 | 164.1890 | 232.9456 | −8320.1573 | −175,528.1019 | −621,247.6001 |
| B7 | −67.4343 | −100.0344 | 3074.3235 | 71,696.2367 | 253,232.2171 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, F.; Wu, X.; Wen, S.; Hong, L.; Rong, Z.; Chen, H.; Gao, K.; Wei, W.; Huang, H.; Nie, Z. Hot Deformation Behavior, Processing Maps, and Microstructure Evolution of 7E97 Alloy. Metals 2025, 15, 725. https://doi.org/10.3390/met15070725
He F, Wu X, Wen S, Hong L, Rong Z, Chen H, Gao K, Wei W, Huang H, Nie Z. Hot Deformation Behavior, Processing Maps, and Microstructure Evolution of 7E97 Alloy. Metals. 2025; 15(7):725. https://doi.org/10.3390/met15070725
Chicago/Turabian StyleHe, Fangyan, Xiaolan Wu, Shengping Wen, Liang Hong, Zhizheng Rong, Hanyu Chen, Kunyuan Gao, Wu Wei, Hui Huang, and Zuoren Nie. 2025. "Hot Deformation Behavior, Processing Maps, and Microstructure Evolution of 7E97 Alloy" Metals 15, no. 7: 725. https://doi.org/10.3390/met15070725
APA StyleHe, F., Wu, X., Wen, S., Hong, L., Rong, Z., Chen, H., Gao, K., Wei, W., Huang, H., & Nie, Z. (2025). Hot Deformation Behavior, Processing Maps, and Microstructure Evolution of 7E97 Alloy. Metals, 15(7), 725. https://doi.org/10.3390/met15070725






