DFT Study of Hydrostatic Pressure Effects up to 1.0 GPa on the Electronic and Magnetic Properties of Laves Phases ErAl2 and ErNi2
Abstract
1. Introduction
2. Computational Method
3. Results and Discussion
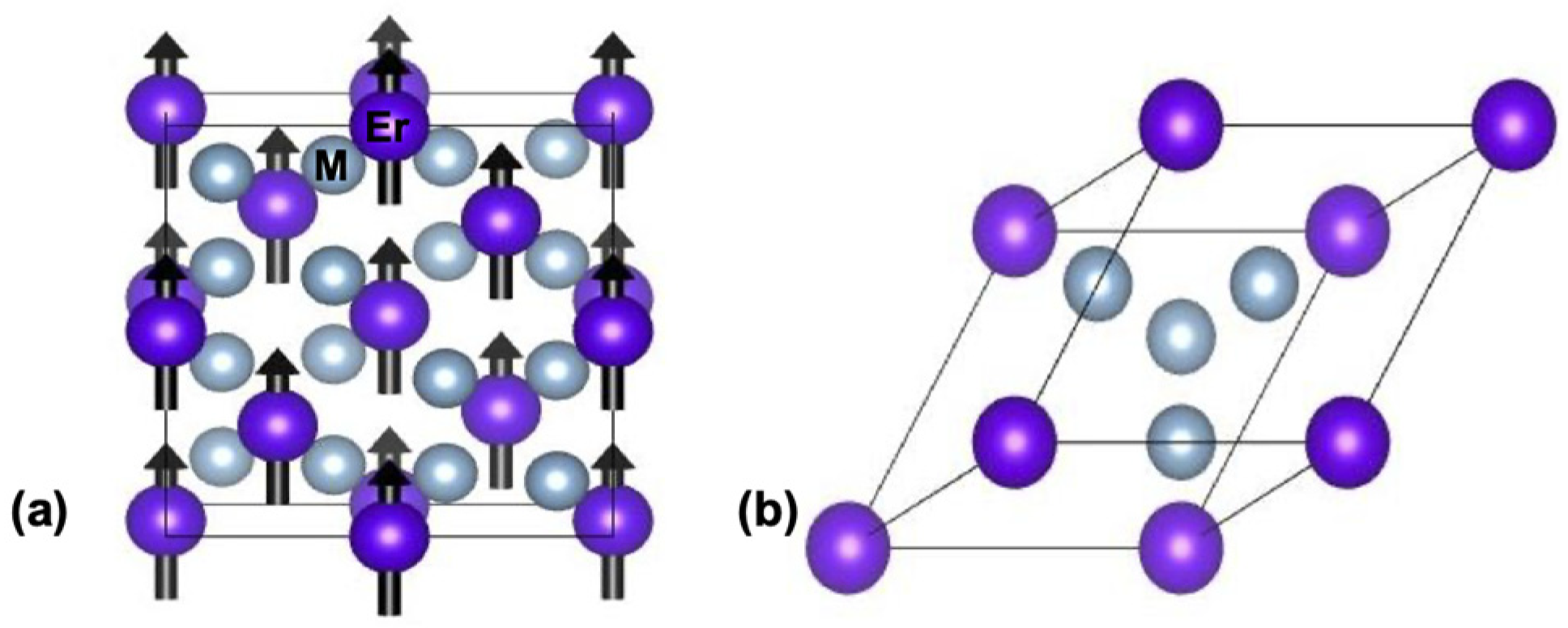
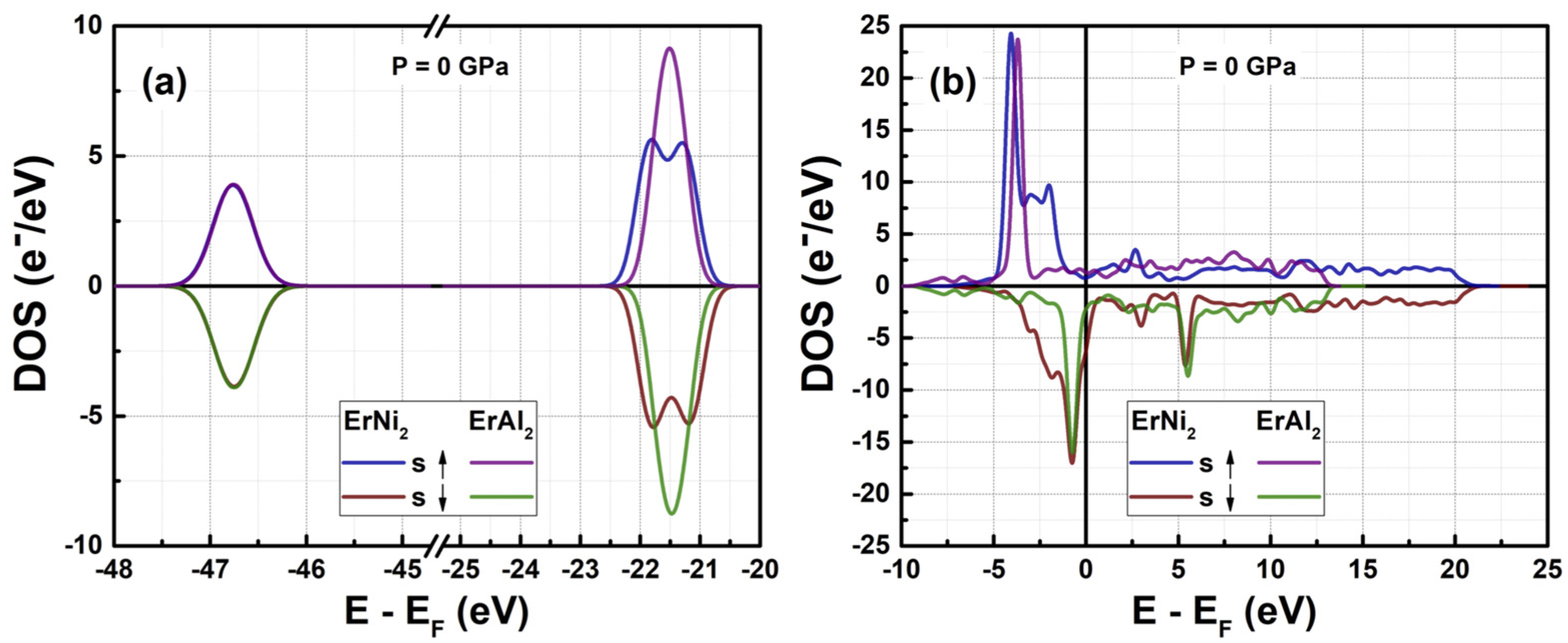
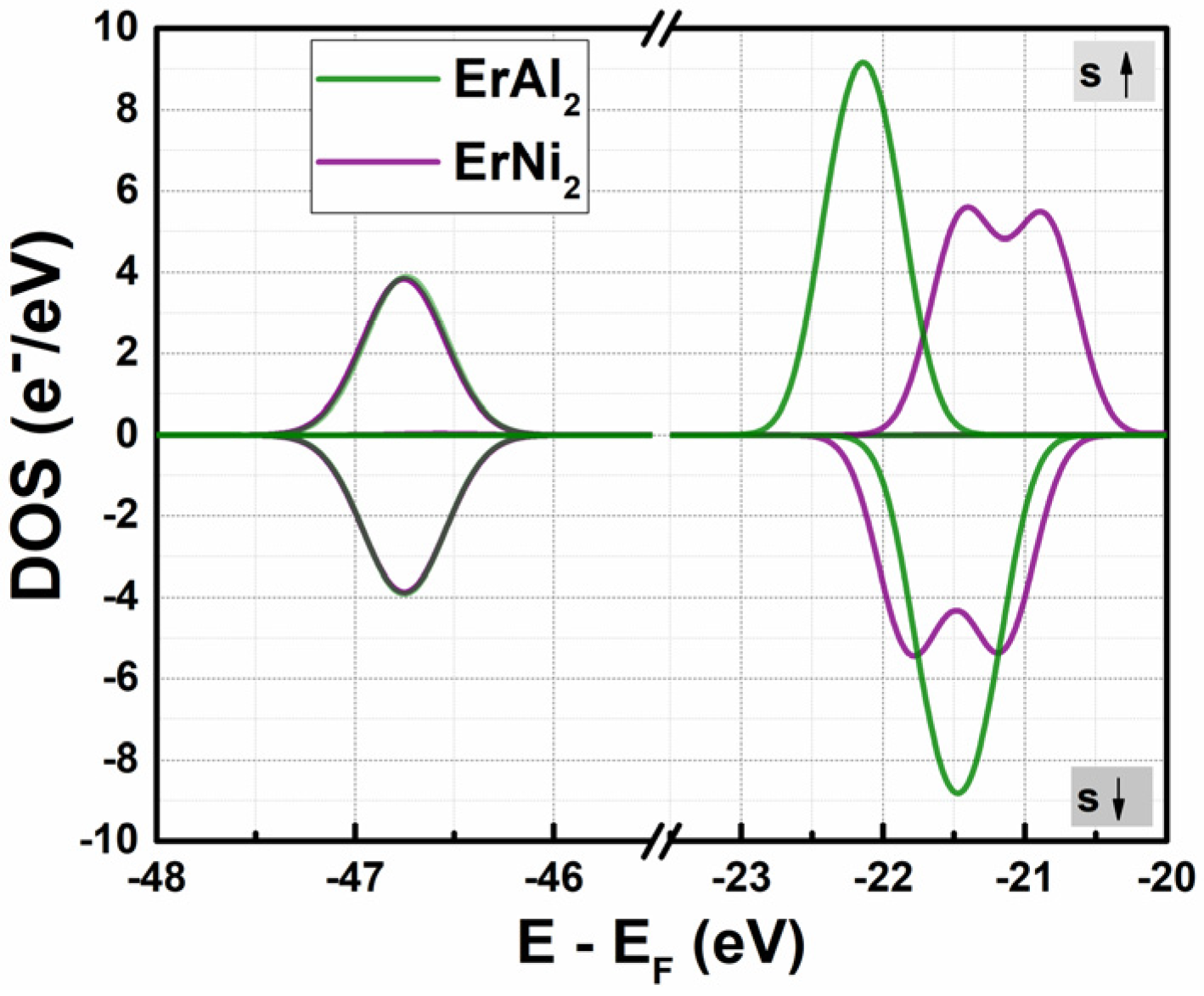
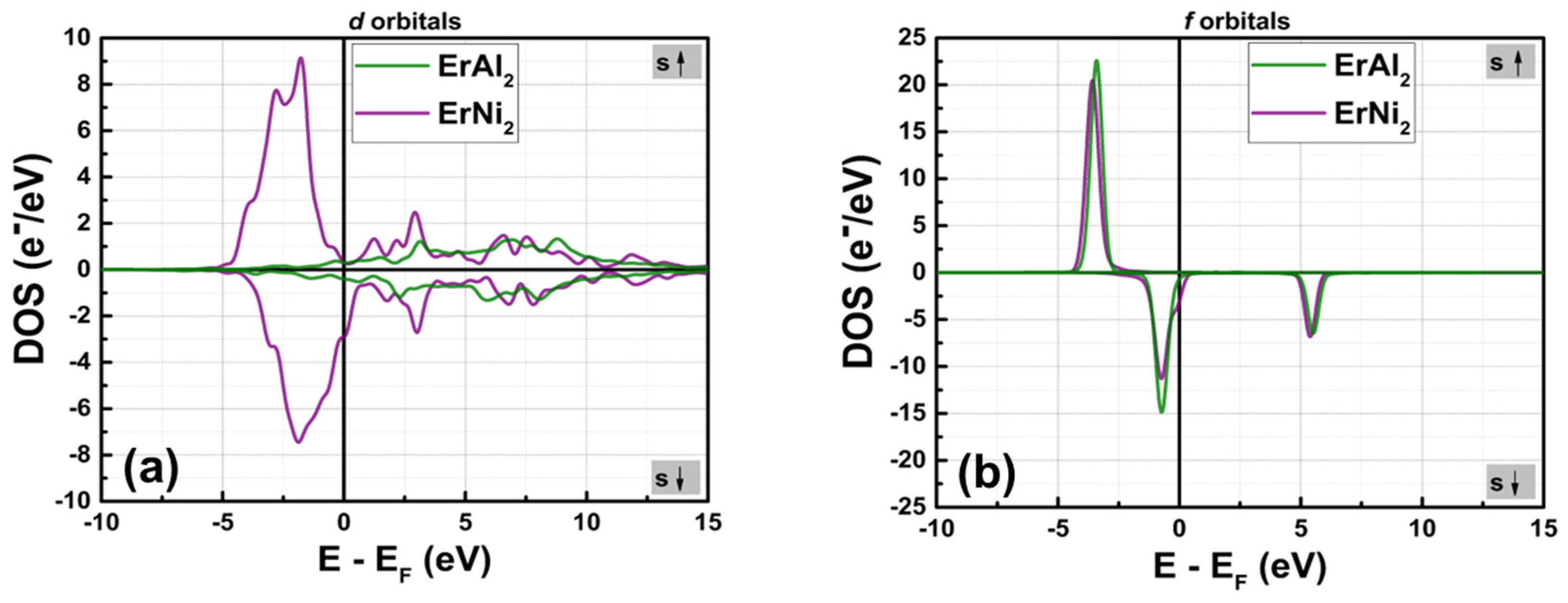
3.1. Electronic Structure at Normal Pressure
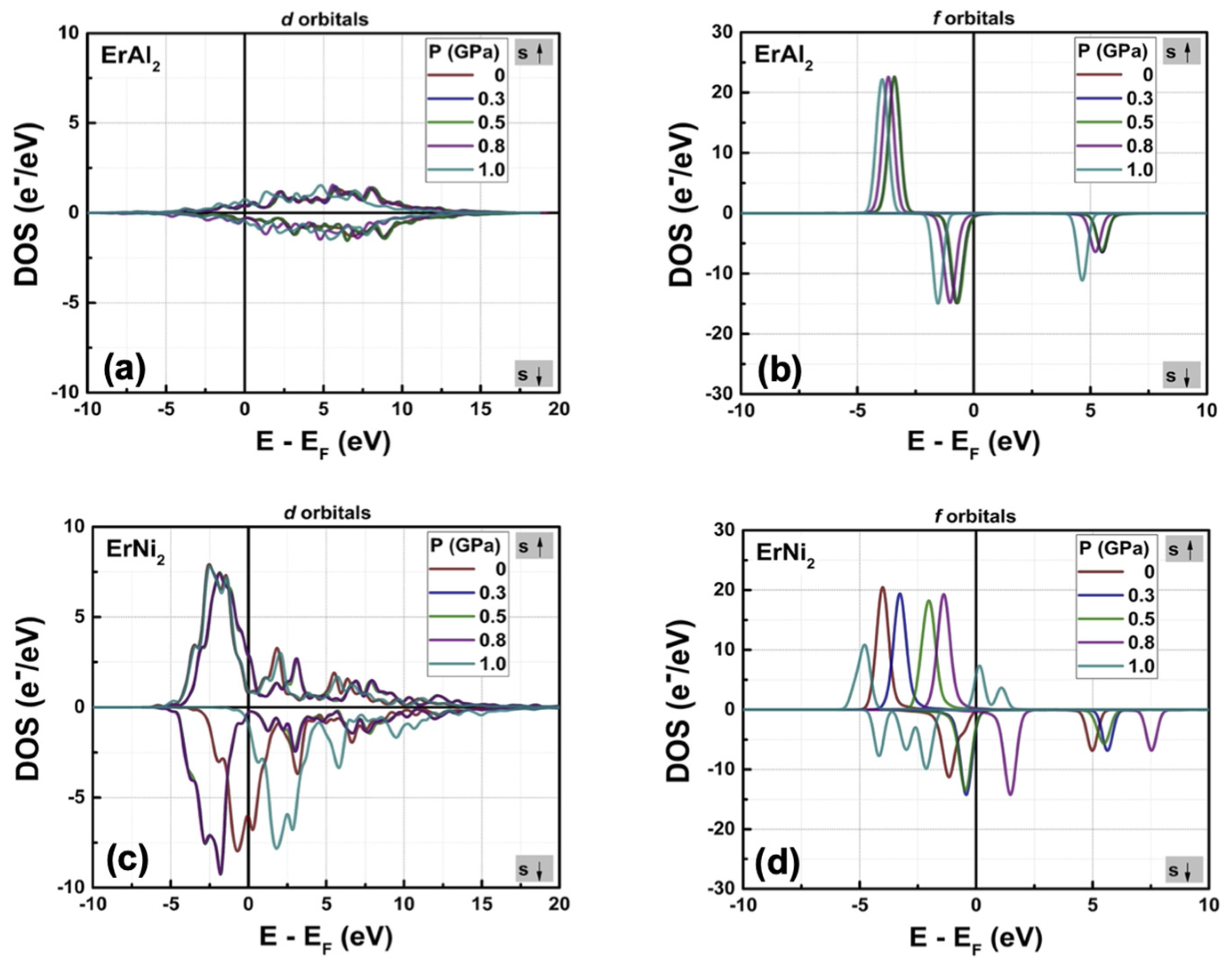
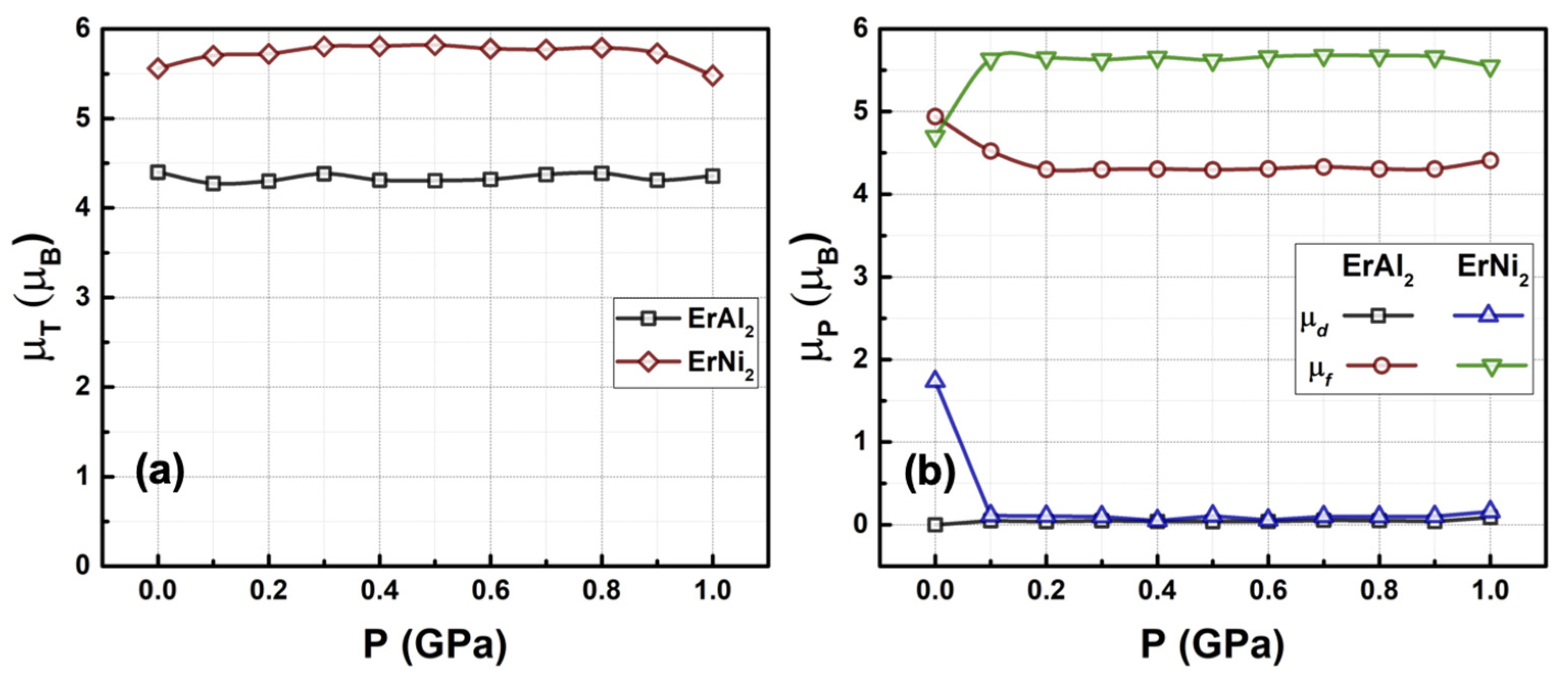
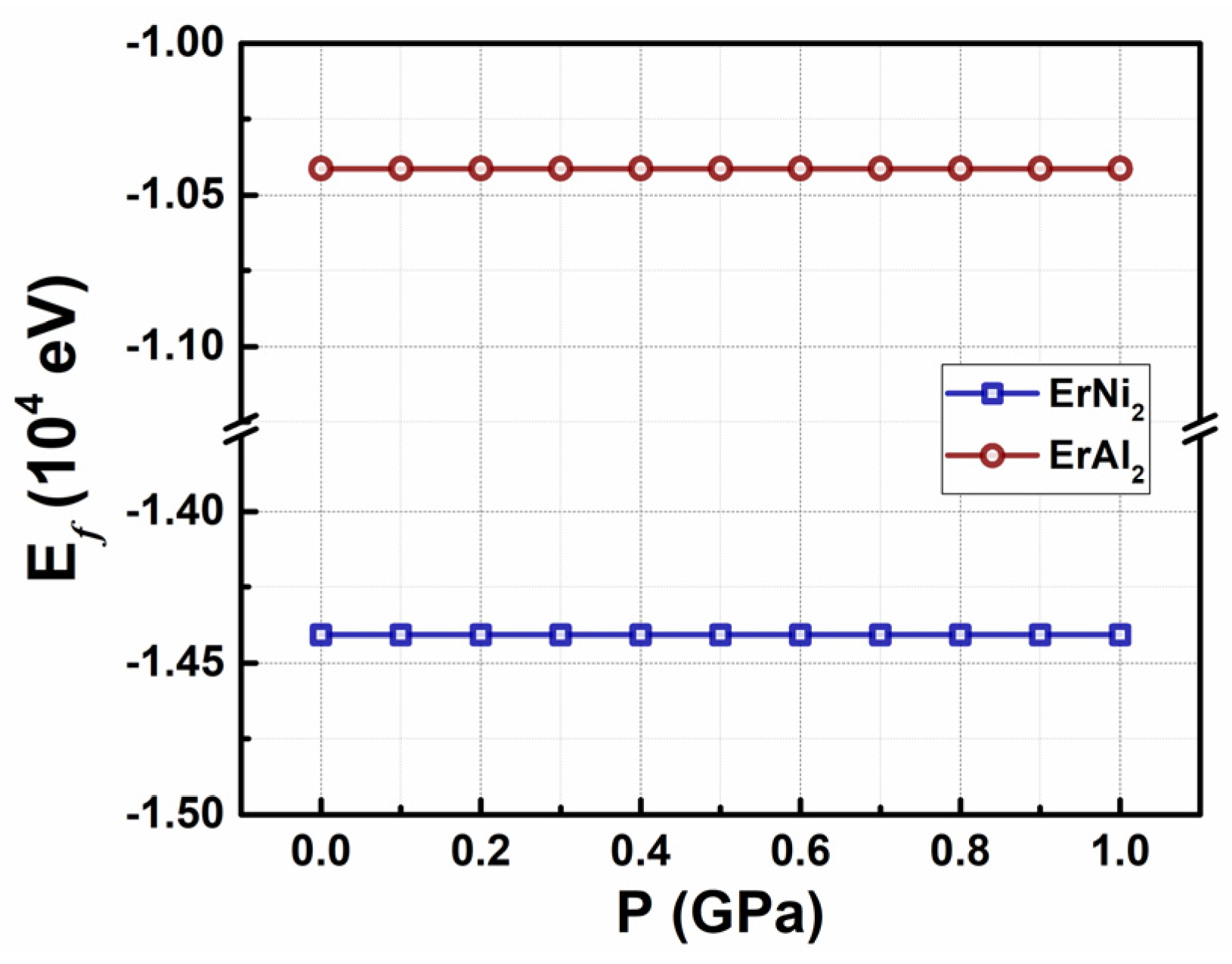
3.2. Electronic Structure at Moderate Hydrostatic Pressures
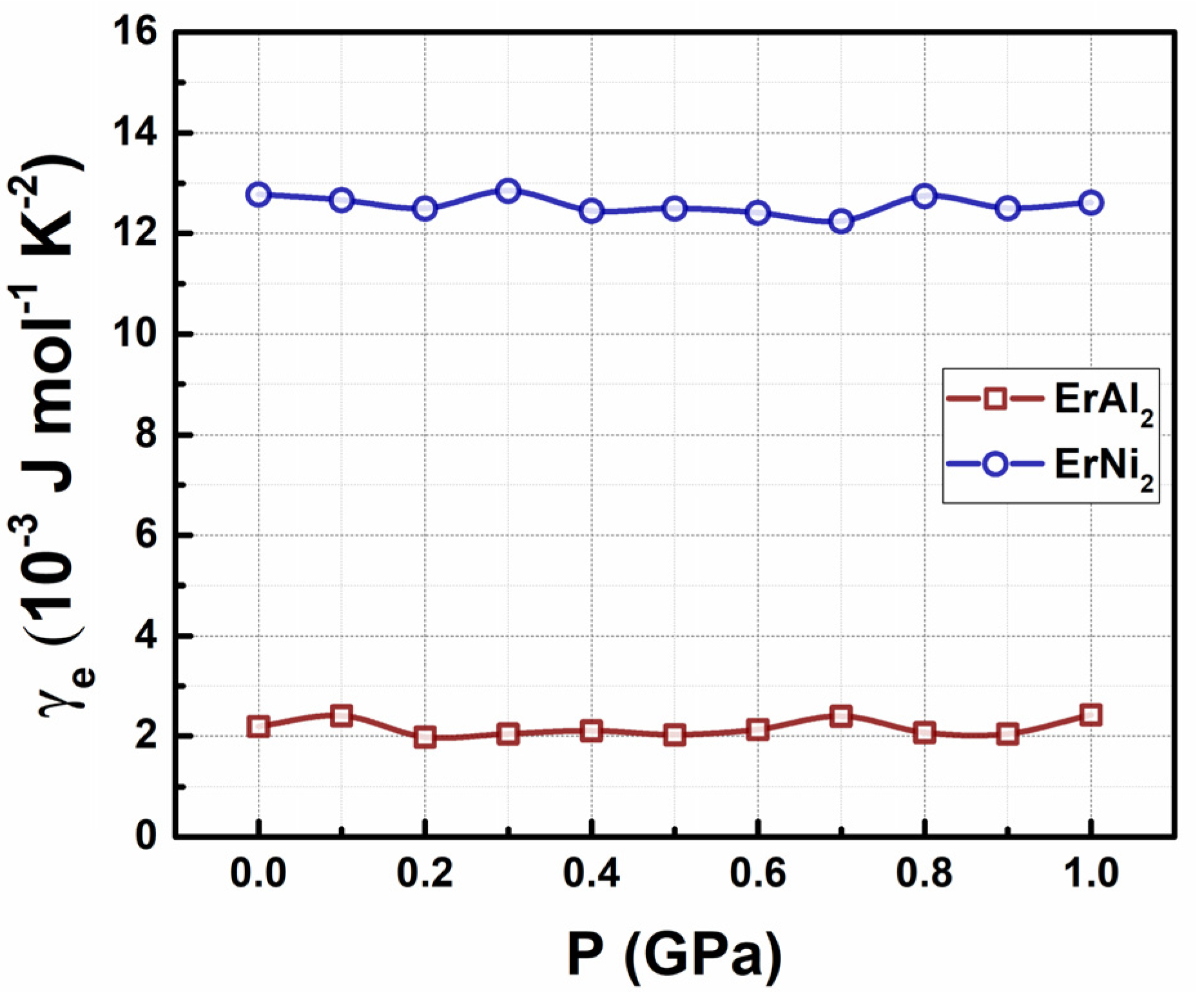
3.3. Determination of Electronic Coefficient in Specific Heat Capacity
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pecharsky, V.K.; Gschneider, K.A., Jr. Magnetocaloric effect and magnetic refrigeration. J. Magn. Magn. Mater. 1999, 200, 44–56. [Google Scholar] [CrossRef]
- Moya, X.; Mathur, N.D. Caloric materials for cooling and heating. Science 2020, 370, 797–803. [Google Scholar] [CrossRef] [PubMed]
- Moya, X.; Kar-Narayan, S.; Mathur, N.D. Caloric materials near ferroic phase transitions. Nat. Mater. 2014, 14, 439–450. [Google Scholar] [CrossRef] [PubMed]
- Franco, V.; Blázquez, J.S.; Ipus, J.J.; Law, J.Y.; Moreno-Ramírez, L.M.; Conde, A. Magnetocaloric effect: From materials research to refrigeration devices. Prog. Mater. Sci. 2018, 93, 112–232. [Google Scholar] [CrossRef]
- Tang, X.; Sepehri-Amin, H.; Terada, N.; Martin-Cid, A.; Kurniawan, I.; Kobayashi, S.; Kotani, Y.; Takeya, H.; Lai, J.; Matsushita, Y.; et al. Magnetic refrigeration material operating at a full temperature range required for hydrogen liquefaction. Nat. Commun. 2022, 13, 1817. [Google Scholar] [CrossRef]
- Smith, A.; Bahl, C.R.H.; Bjørk, R.; Engelbrecht, K.; Nielsen, K.K.; Pryds, N. Materials challenges for high performance magnetocaloric refrigeration devices. Adv. Energy Mater. 2012, 2, 1288–1318. [Google Scholar] [CrossRef]
- Pecharsky, V.K.; Gschneidner, K.A., Jr. Giant magnetocaloric effect in Gd5(Si2Ge2). Phys. Rev. Lett. 1997, 78, 4494. [Google Scholar] [CrossRef]
- Kitanovski, A. Energy applications of magnetocaloric materials. Adv. Energy Mater. 2020, 10, 1903741. [Google Scholar] [CrossRef]
- Lyubina, J. Magnetocaloric materials for energy efficient cooling. J. Phys. D Appl. Phys. 2017, 50, 053002. [Google Scholar] [CrossRef]
- Gschneidner, K.A., Jr.; Pecharsky, V.K. Binary rare earth Laves phases—An overview. Zeitschrift Kristallogr. 2006, 221, 375–381. [Google Scholar] [CrossRef]
- Stein, F.; Leineweber, A. Laves phases: A review of their functional and structural applications and an improved fundamental understanding of stability and properties. J. Mater. Sci. 2021, 56, 5321–5427. [Google Scholar] [CrossRef]
- Liu, W.; Bykov, E.; Taskaev, S.; Bogush, M.; Khovaylo, V.; Fortunato, N.; Aubert, A.; Zhang, H.; Gottschall, T.; Wosnitza, J.; et al. A study on rare-earth Laves phases for magnetocaloric liquefaction of hydrogen. Appl. Mat. Today 2022, 29, 101624. [Google Scholar] [CrossRef]
- Gschneidner, K.A., Jr.; Pecharsky, V.K.; Tsokol, A.O. Recent developments in magnetocaloric materials. Rep. Prog. Phys. 2005, 68, 1479. [Google Scholar] [CrossRef]
- Kumar, K.S.; Hazzledine, P.M. Polytypic transformations in Laves phases. Intermetallics 2004, 12, 763–770. [Google Scholar] [CrossRef]
- Sánchez Llamazares, J.L.; Zamora, J.; Sánchez-Valdés, C.F.; Álvarez-Alonso, P. Design and fabrication of a cryogenic magnetocaloric composite by spark plasma sintering based on the RAl2 Laves phases (R = Ho, Er). J. Alloys Compd. 2020, 831, 154779. [Google Scholar] [CrossRef]
- Sánchez Llamazares, J.L.; Ibarra-Gaytán, P.; Sánchez-Valdés, C.F.; Ríos-Jara, D.; Álvarez-Alonso, P. Magnetocaloric effect in ErNi2 melt-spun ribbons. J. Rare Earths. 2020, 38, 612–616. [Google Scholar] [CrossRef]
- Biswas, A.; Pathak, A.K.; Zarkevich, N.A.; Liu, X.; Mudryk, Y.; Balema, V.; Johnson, D.D.; Pecharsky, V.K. Designed materials with the giant magnetocaloric effect near room temperature. Acta Mater. 2019, 180, 341–348. [Google Scholar] [CrossRef]
- Hafner, J.; Wolverton, C.; Ceder, G. Toward computational materials design: The impact of density functional theory on materials research. MRS Bull. 2006, 31, 659–668. [Google Scholar] [CrossRef]
- Pan, F.-C.; Lin, X.-l.; Li, J.; Ma, L.; Ma, L.-C.; Cheng, H.M. The electronic structures and Ferromagnetism of Cu-Doped ZnO: The first-principle calculation Study. J. Supercond. Nov. Magn. 2018, 31, 2103–2110. [Google Scholar] [CrossRef]
- Patel, P.D.; Shinde, S.; Gupta, S.D. First principle calculation of structural, electronic and magnetic properties of Mn2RhSi Heusler alloy. AIP Conf. Proc. 2018, 2005, 040004. [Google Scholar] [CrossRef]
- Wang, S. First-principles prediction of ferromagnetism in transition-metal doped monolayer AlN. Superlattices Microstruct. 2019, 122, 171–180. [Google Scholar] [CrossRef]
- Odkhuu, D.; Tsevelmaa, T.; Sangaa, D.; Tsogbadrakh, N.; Rhim, S.H.; Hong, S.C. First-principles study of magnetization reorientation and perpendicular magnetic anisotropy in CuFe2O4/MgO heterostructures. Phys. Rev. B 2018, 98, 094408. [Google Scholar] [CrossRef]
- Kanomata, T.; Endo, H.; Mori, S.; Okajima, H.; Hihara, T.; Sumiyama, K.; Kaneko, T.; Suzuki, K. Specific heat of MnAlGe, MnGaGe and MnZnSb. J. Magn. Magn. Mater. 1995, 140–144 Pt 1, 133–134. [Google Scholar] [CrossRef]
- Aschauer, U.; Braddell, R.; Brechbuhl, S.A.; Derlet, P.M.; Spaldin, N.A. Strain-induced structural instability in FeRh. Phys. Rev. B 2016, 94, 014109. [Google Scholar] [CrossRef]
- He, L.; Zhu, J.; Zhang, L. First-principles study of Structural phase transition, electronic, elastic and thermodynamic properties of C15-type Laves phases TiCr2 under pressure. Physica B Condens. Matter. 2018, 531, 79–84. [Google Scholar] [CrossRef]
- Purwins, H.G.; Walker, E.; Barbara, B.; Rossignol, M.F.; Furrer, A. Single crystal magnetization of ErAl2 and interpretation in terms of the crystalline field. J. Phys. C Solid State Phys. 1976, 9, 1025–1030. [Google Scholar] [CrossRef]
- Gignoux, D.; Givord, F. Quadrupolar interactions in ErNi2. J. Magn. Magn. Mater. 1983, 31–34, 217–218. [Google Scholar] [CrossRef]
- Ibarra-Gaytán, P.J.; Sánchez Llamazares, J.L.; Álvarez-Alonso, P.; Sánchez-Valdés, C.F.; Gorria, P.; Blanco, J.A. Magnetic entropy table-like shape in RNi2 composites for cryogenic refrigeration. J. Appl. Phys. 2015, 117, 17C116. [Google Scholar] [CrossRef]
- Eyert, V. A comparative study on methods for convergence acceleration of iterative vector sequences. J. Comput. Phys. 1996, 124, 271–285. [Google Scholar] [CrossRef]
- Pfrommer, B.G.; Côté, M.; Louie, S.G.; Cohen, M.L. Relaxation of crystals with the quasi-Newton method. J. Comput. Phys. 1997, 131, 233–240. [Google Scholar] [CrossRef]
- Lewars, E. Computational Chemistry: Introduction to the Theory and Applications of Molecular and Quantum Mechanics, 1st ed.; Springer: Dordrecht, The Netherland, 2004; ISBN 0-306-48391-2. [Google Scholar]
- Clark, S.J.; Seagall, M.D.; Pickard, C.J.; Hasnip, P.J.; Probert, M.I.J.; Refson, K.; Payne, M.C. First principles methods using CASTEP. Z. Kristallogr. 2005, 220, 567–570. [Google Scholar] [CrossRef]
- Bader, R.F.W. The density in density functional theory. J. Mol. Struct. THEOCHEM 2010, 943, 2–18. [Google Scholar] [CrossRef]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
- Cococcioni, M.; de Gironcoli, S. Linear response approach to the calculation of the effective interaction parameters in the LDA+U method. Phys. Rev. B 2005, 71, 035105. [Google Scholar] [CrossRef]
- Anisimov, V.I.; Zaanen, J.; Andersen, O.K. Band theory and Mott insulators: Hubbard U instead of Stoner I. Phys. Rev. B 1991, 44, 943–954. [Google Scholar] [CrossRef]
- Moroni, E.G.; Kresse, G.; Hafner, J.; Furthmüller, J. Ultrasoft pseudopotentials applied to magnetic Fe, Co, and Ni: From atoms to solids. Phys. Rev. B 1997, 56, 15629. [Google Scholar] [CrossRef]
- Staroverov, V.N.; Scuseria, G.E.; Tao, J.; Perdew, J.P. Test of the ladder of density functionals for bulk solids and surfaces. Phys. Rev. B 2004, 69, 075102. [Google Scholar] [CrossRef]
- Cyrot, M.; Lavagna, M. Density of states and magnetic properties of the rare-earth compounds RFe2, RCo2 and RNi2. J. Physique 1979, 40, 763–771. [Google Scholar] [CrossRef]
- Taylor, K.N.R. Intermetallic rare-earth compounds. Adv. Phys. 1971, 20, 551–660. [Google Scholar] [CrossRef]
- Harris, I.R.; Mansey, R.C.; Raynor, G.V. Rare earth intermediate phases: III. The cubic laves phases formed with aluminium and cobalt. J. Less Common Met. 1965, 9, 270–280. [Google Scholar] [CrossRef]
- Gschneidner, K.A., Jr.; Eyring, L. Handbook on the Physics and Chemistry of Rare Earths. In Alloys and Intermetallics; North-Holland: Amsterdam, The Netherlands, 1978; Volume 2, ISBN 0444850228. [Google Scholar]
- Tipler, P.A.; Llewellyn, R. Modern Physics, 5th ed.; W.H. Freeman and Company: New York, NY, USA, 2008; ISBN 13 978-0-7167-7550-8/10 0-7167-7550-6. [Google Scholar]

| Compound | nS↑ (EF) (e−/eV) | nS↓ (EF) (e−/eV) | Δn(EF) (e−/eV) | (µB/f.u.) | (µB/f.u.) | (µB/f.u.) | (µB/f.u.) | Magnetization Axis | Reference |
|---|---|---|---|---|---|---|---|---|---|
| ErAl2 | 1.31 | −2.24 | −0.93 | 30.19 | −25.80 | 4.40 | 4.40 4.75 † | hard | [40] [26] |
| ErNi2 | 0.78 | −6.20 | −5.42 | 36.46 | −30.40 | 5.56 | 5.30 ‡ 6.23 | easy | [27] [40] |
| Laves Phase | μs (μB/f.u.) | μ p (μB/f.u.) | μd (μB/f.u.) | μf (μB/f.u.) | μP (μB/f.u.) |
|---|---|---|---|---|---|
| ErAl2 | −0.005 | −0.002 | −0.001 | 4.940 | 4.932 |
| ErNi2 | −0.058 | −0.249 | 1.737 | 4.701 | 6.131 |
| Alloy | ErAl2 | ErNi2 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| P (GPa) | a (Å) | dAl-Al (Å) | dEr-Al (Å) | VP (Å3) | Δ (%) | B (GPa) | σij (GPa) | a (Å) | dNi-Ni (Å) | dEr-Ni (Å) | VP (Å3) | Δ (%) | B (GPa) | σij (GPa) |
| 0.0 | 5.5551 | 2.777 | 3.257 | 121.218 | 0.000 | 63.76 | –0.00184 | 5.1030 | 2.551 | 2.991 | 93.949 | 0.000 | 128.13 | –0.00631 |
| 0.1 | 5.5530 | 2.776 | 3.256 | 121.090 | –0.105 | 64.53 | –0.06960 | 5.1023 | 2.550 | 2.990 | 93.853 | –0.101 | 128.56 | –0.10767 |
| 0.2 | 5.5503 | 2.775 | 3.254 | 120.908 | –0.255 | 64.87 | –0.16420 | 5.1010 | 2.549 | 2.989 | 93.737 | –0.225 | 129.90 | –0.22623 |
| 0.3 | 5.5455 | 2.772 | 3.251 | 120.590 | –0.517 | 65.76 | –0.31888 | 5.0999 | 2.548 | 2.988 | 93.653 | –0.314 | 129.89 | –0.31054 |
| 0.4 | 5.5434 | 2.771 | 3.250 | 120.456 | –0.628 | 65.96 | –0.38991 | 5.0973 | 2.547 | 2.987 | 93.560 | –0.413 | 130.11 | –0.40776 |
| 0.5 | 5.5412 | 2.770 | 3.249 | 120.310 | –0.748 | 66.14 | –0.47108 | 5.0956 | 2.546 | 2.986 | 93.464 | –0.516 | 130.82 | –0.50732 |
| 0.6 | 5.5374 | 2.768 | 3.247 | 120.062 | –0.953 | 66.98 | –0.59076 | 5.0939 | 2.546 | 2.985 | 93.366 | –0.620 | 131.39 | –0.61002 |
| 0.7 | 5.5345 | 2.767 | 3.245 | 119.873 | –1.108 | 67.08 | –0.69311 | 5.0921 | 2.545 | 2.984 | 93.270 | –0.722 | 131.91 | –0.71256 |
| 0.8 | 5.5315 | 2.765 | 3.243 | 119.677 | –1.270 | 67.56 | –0.79821 | 5.0904 | 2.544 | 2.983 | 93.182 | –0.816 | 132.08 | –0.80705 |
| 0.9 | 5.5275 | 2.763 | 3.242 | 119.324 | –1.561 | 67.96 | –0.88224 | 5.0888 | 2.543 | 2.982 | 93.102 | –0.901 | 132.88 | –0.89113 |
| 1.0 | 5.5259 | 2.762 | 3.240 | 119.318 | –1.566 | 68.04 | –0.99389 | 5.0853 | 2.542 | 2.981 | 92.994 | –1.015 | 133.12 | –1.00668 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
López-Solenzal, T.; Sánchez Llamazares, J.L.; Enríquez-Carrejo, J.L.; Sánchez-Valdés, C.F. DFT Study of Hydrostatic Pressure Effects up to 1.0 GPa on the Electronic and Magnetic Properties of Laves Phases ErAl2 and ErNi2. Metals 2025, 15, 680. https://doi.org/10.3390/met15060680
López-Solenzal T, Sánchez Llamazares JL, Enríquez-Carrejo JL, Sánchez-Valdés CF. DFT Study of Hydrostatic Pressure Effects up to 1.0 GPa on the Electronic and Magnetic Properties of Laves Phases ErAl2 and ErNi2. Metals. 2025; 15(6):680. https://doi.org/10.3390/met15060680
Chicago/Turabian StyleLópez-Solenzal, Tomás, José Luis Sánchez Llamazares, José Luis Enríquez-Carrejo, and César Fidel Sánchez-Valdés. 2025. "DFT Study of Hydrostatic Pressure Effects up to 1.0 GPa on the Electronic and Magnetic Properties of Laves Phases ErAl2 and ErNi2" Metals 15, no. 6: 680. https://doi.org/10.3390/met15060680
APA StyleLópez-Solenzal, T., Sánchez Llamazares, J. L., Enríquez-Carrejo, J. L., & Sánchez-Valdés, C. F. (2025). DFT Study of Hydrostatic Pressure Effects up to 1.0 GPa on the Electronic and Magnetic Properties of Laves Phases ErAl2 and ErNi2. Metals, 15(6), 680. https://doi.org/10.3390/met15060680







