Dislocation Avalanches in Compressive Creep and Shock Loadings
Abstract
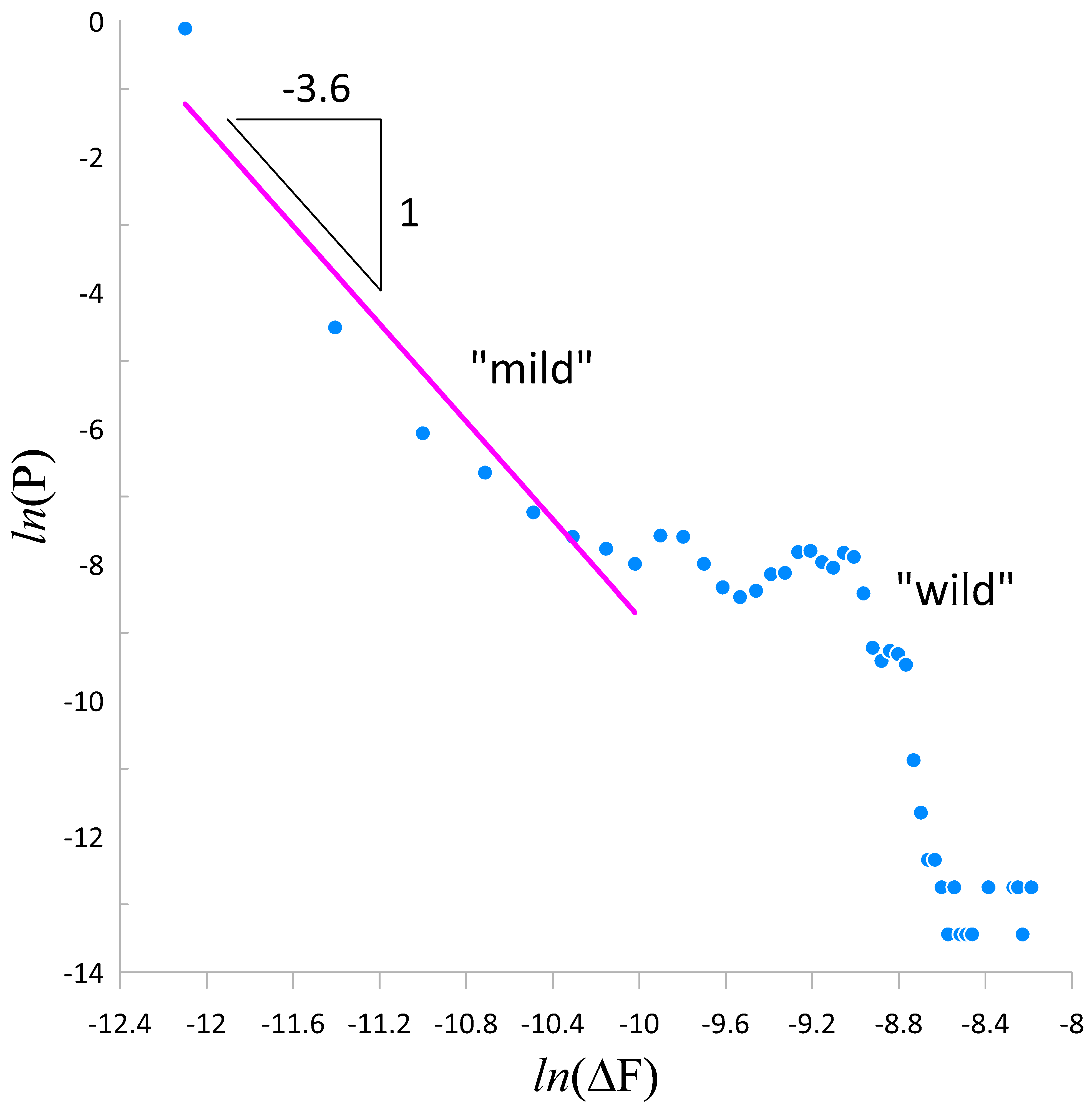
1. Background: Dislocation Avalanches
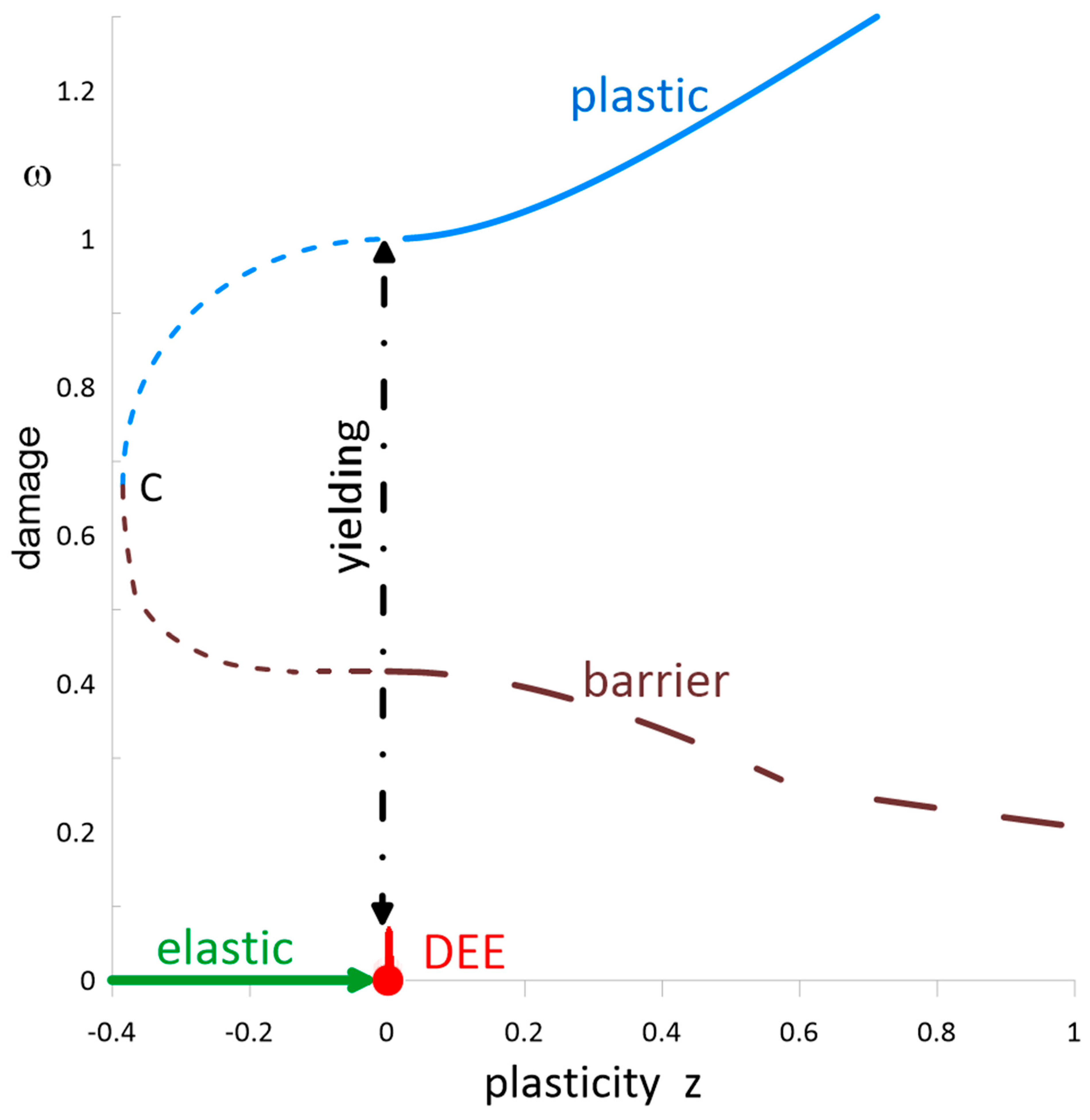
2. Dislocation-Mediated Bifurcation Theory of Plasticity
2.1. Bifurcation Theory of Plasticity
2.2. Dislocation-Mediated Plasticity
2.3. Gradient Plasticity
2.4. Dynamics of Damage
3. Time Evolution of Deformation
3.1. Evolution of Strain
3.2. Evolution of Damage
3.3. Free-Energy Balance
3.4. Dislocation Emission Event
3.5. Initial and Boundary Conditions
3.6. Scaling and Dimensionless Properties
4. Numerical Implementation
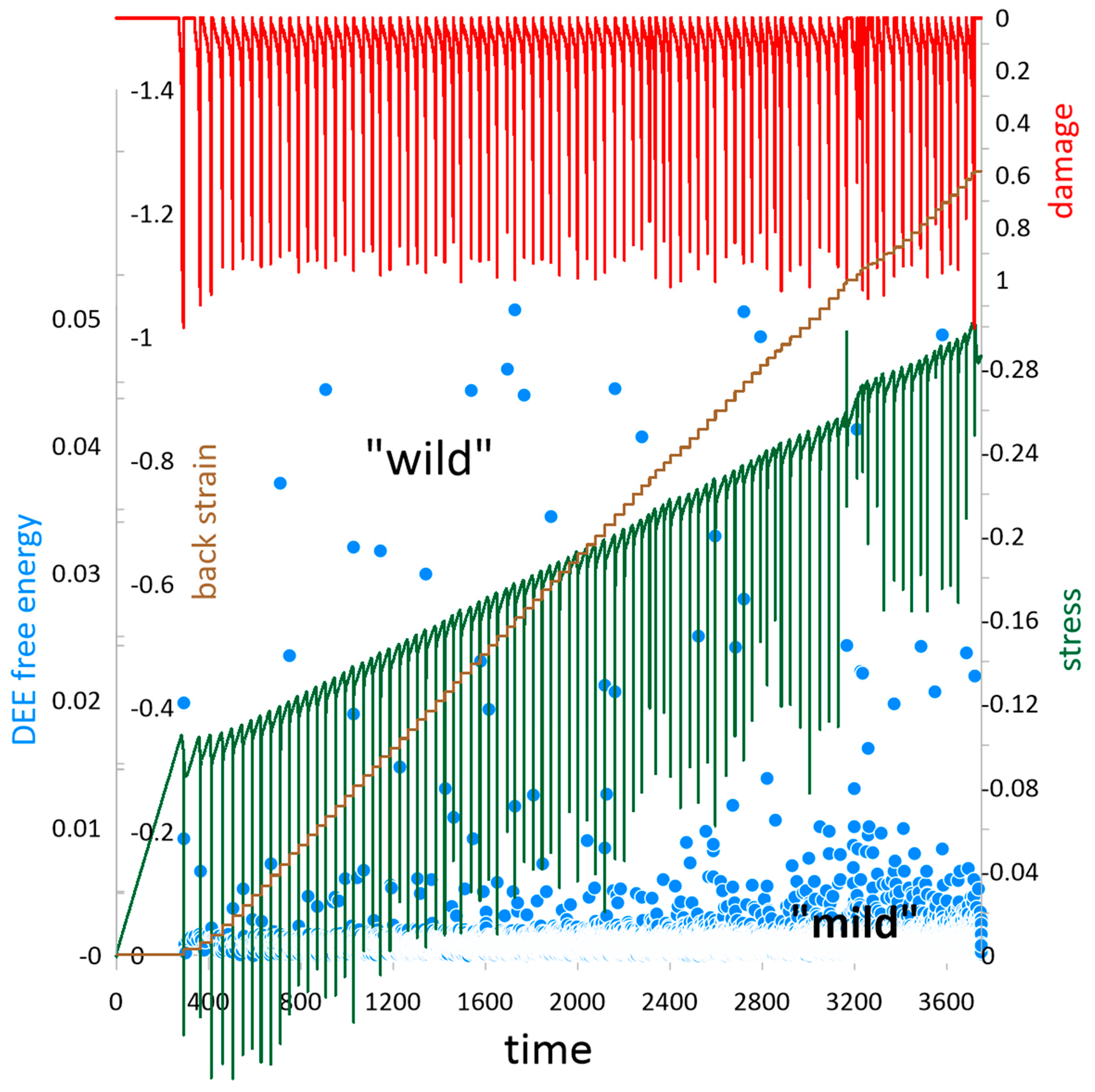
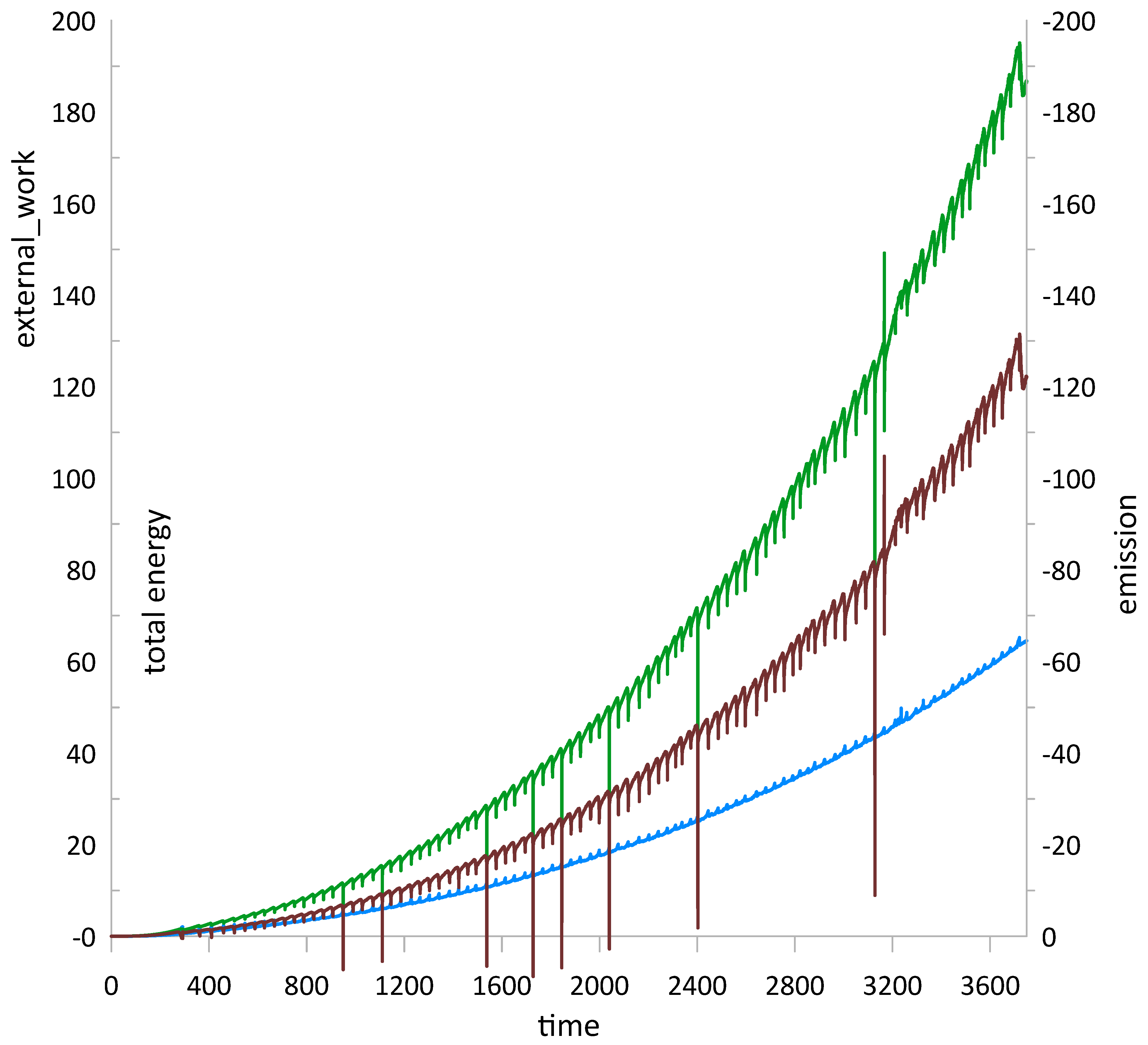
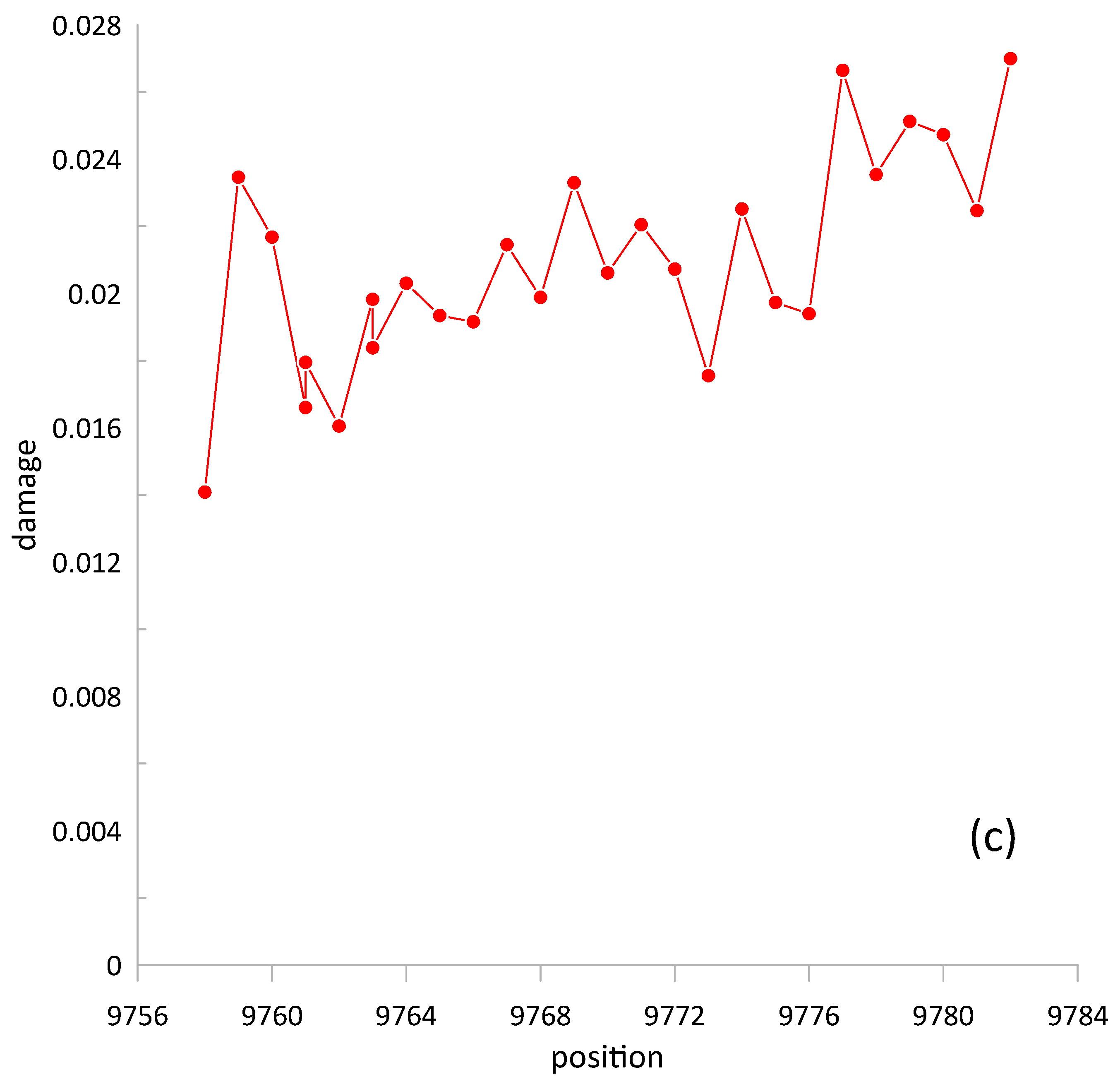
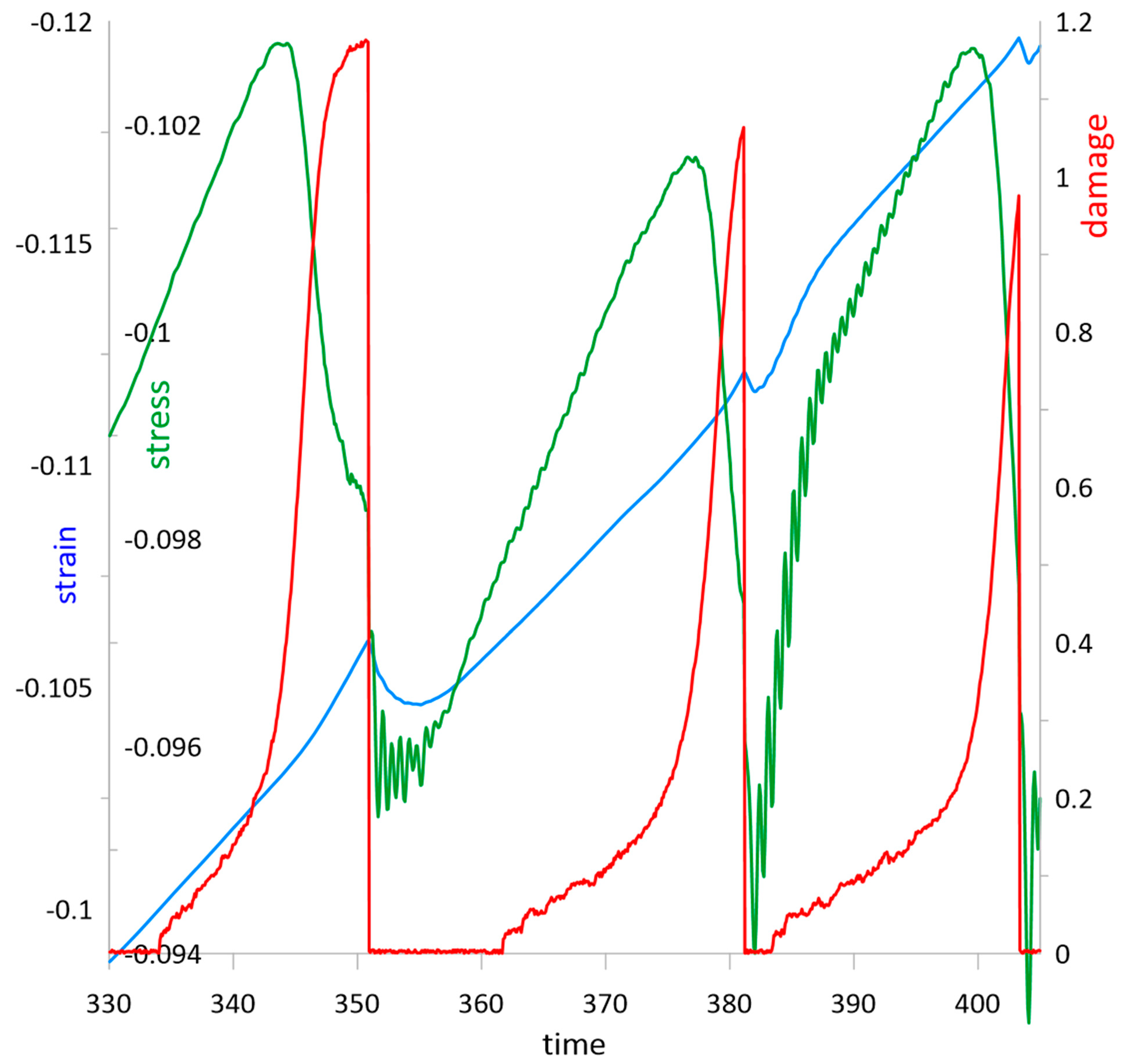
5. Compressive Creep
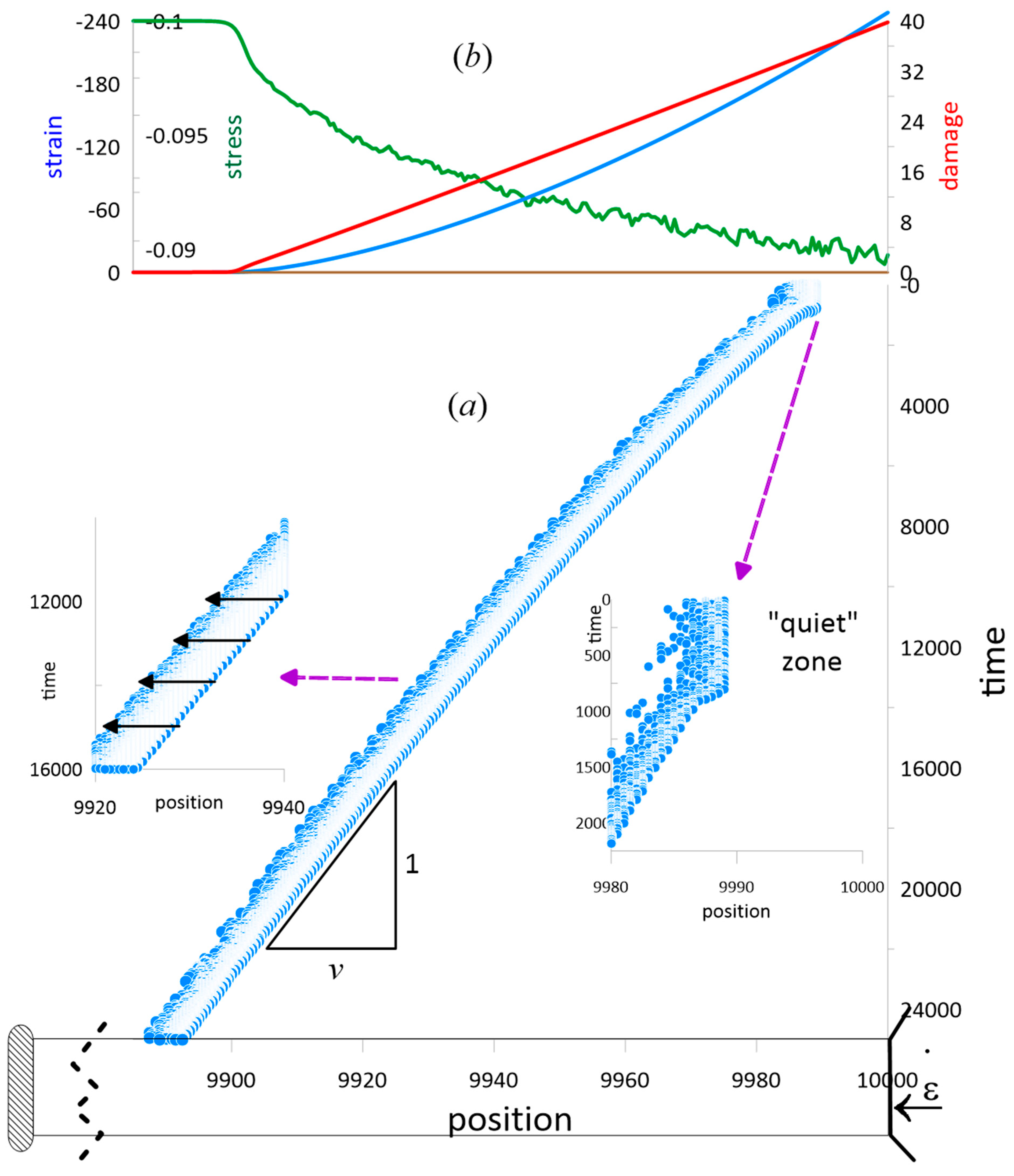
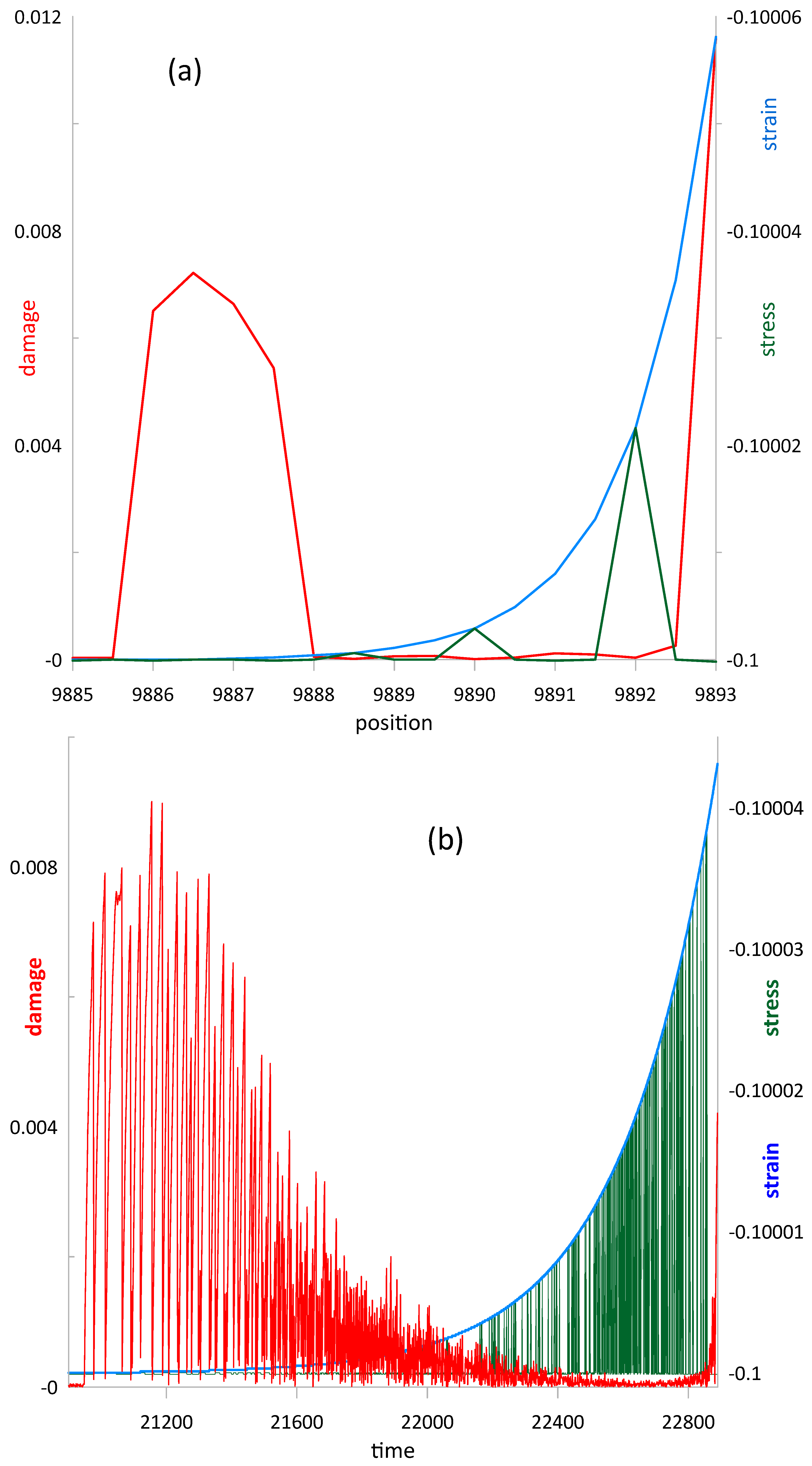
6. Shock Compression
7. Discussion
8. Conclusions
- Dislocation emission events are local unloadings of representative volumes.
- In physical space, DEEs self-organize into slip bans and avalanches.
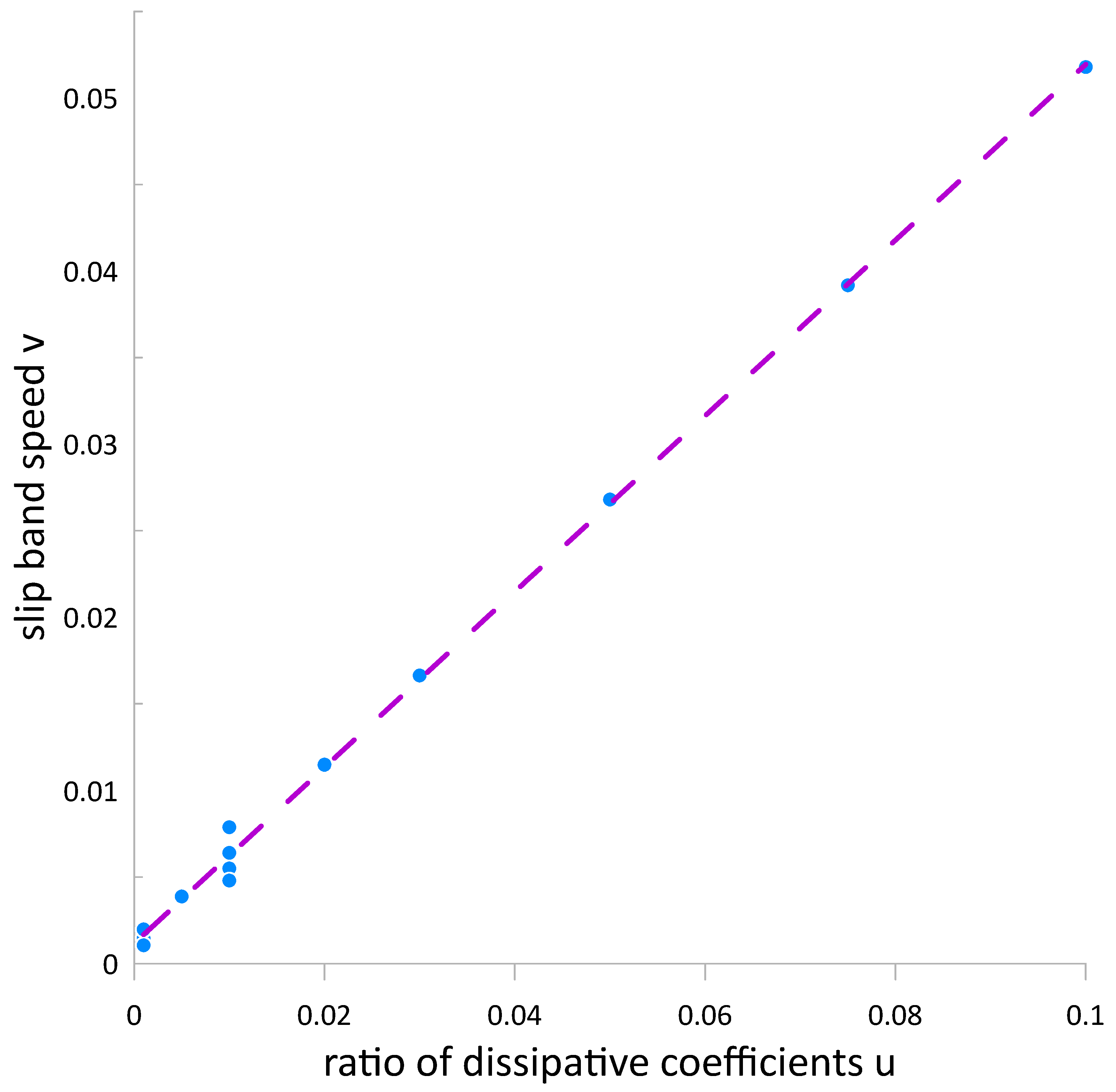
- Speed of slip band propagation is .
- Dislocation avalanches propagate at a speed higher than the speed of sound.
- In the deformation phase space, DEEs take place on the yield surface.
Funding
Data Availability Statement
Conflicts of Interest
References
- Zaiser, M. Scale invariance in plastic flow of crystalline solids. Adv. Phys. 2006, 55, 185–245. [Google Scholar] [CrossRef]
- Papanikolaou, S.; Cui, Y.; Ghoniem, N. Avalanches and plastic flow in crystal plasticity: An overview. Model. Simul. Mater. Sci. Eng. 2018, 26, 013001. [Google Scholar] [CrossRef]
- Dimiduk, D.M.; Woodward, C.; LeSar, R.; Uchic, M.D. Scale-free intermittent flow in crystal plasticity. Science 2006, 312, 1188–1190. [Google Scholar] [CrossRef] [PubMed]
- Rizzardi, Q.; McElfresh, C.; Sparks, G.; Stauffer, D.D.; Marian, J.; Maaß, R. Mild-to-wild plastic transition is governed by athermal screw dislocation slip in bcc Nb. Nat. Commun. 2022, 13, 1010. [Google Scholar] [CrossRef] [PubMed]
- Alcalá, J.; Očenášek, J.; Varillas, J.; El-Awady, J.A.; Wheeler, J.M.; Michler, J. Statistics of dislocation avalanches in FCC and BCC metals: Dislocation mechanisms and mean swept distances across microsample sizes and temperatures. Sci. Rep. 2020, 10, 19024. [Google Scholar] [CrossRef] [PubMed]
- Weiss, J.; Grasso, J.-R.; Miguel, M.-C.; Vespignani, A.; Zapperi, S. Complexity in dislocation dynamics: Experiments. Mater. Sci. Eng. 2001, A309–310, 360–364. [Google Scholar] [CrossRef]
- Weiss, J.; Marsan, D. Three-dimensional mapping of dislocation avalanches: Clustering and space/time coupling. Science 2003, 299, 89–92. [Google Scholar] [CrossRef] [PubMed]
- Weiss, J.; Richeton, T.; Louchet, F.; Chmelík, F.; Dobroň, P.; Entemeyer, D.; Lebyodkin, M.; Lebedkina, T.; Fressengeas, C.; McDonald, R.J. Evidence for universal intermittent crystal plasticity from acoustic emission and high-resolution extensometry experiments. Phys. Rev. 2007, B76, 224110. [Google Scholar] [CrossRef]
- Ispánovity, P.D.; Ugi, D.; Péterffy, G.; Knapek, M.; Kalácska, S.; Tuzes, D.; Dankházi, Z.; Máthis, K.; Chmelík, F.; Groma, I. Dislocation avalanches are like earthquakes on the micron scale. Nat. Commun. 2022, 13, 1975. [Google Scholar] [CrossRef] [PubMed]
- Bulatov, V.V.; Cai, W. Computer Simulations of Dislocations, Oxford Series on Materials Modeling; Sutton, A.P., Rudd, R.E., Eds.; Oxford University Press: Oxford, UK, 2006. [Google Scholar]
- Kubin, L. Dislocations, Mesoscale Simulations and Plastic Flow; Oxford Series on Materials Modeling; Sutton, A.P., Rudd, R.E., Eds.; Oxford University Press: Oxford, UK, 2013. [Google Scholar]
- Miguel, M.-C.; Vespignani, A.; Zapperi, S.; Weiss, J.; Grasso, J.-R. Intermittent dislocation flow in viscoplastic deformation. Nature 2001, 410, 667–671. [Google Scholar] [CrossRef] [PubMed]
- Berdichevsky, V.L. Beyond classical thermodynamics: Dislocation-mediated plasticity. J. Mech. Phys. Solids 2019, 129, 83–118. [Google Scholar] [CrossRef]
- Csikor, F.F.; Motz, C.; Weygand, D.; Zaiser, M.; Zapperi, S. Dislocation Avalanches, Strain Bursts, and the Problem of Plastic Forming at the Micrometer Scale. Science 2007, 318, 251–254. [Google Scholar] [CrossRef] [PubMed]
- Devincre, B.; Hoc, T.; Kubin, L. Dislocation Mean Free Paths and Strain Hardening of Crystals. Science 2008, 320, 1745–1748. [Google Scholar] [CrossRef] [PubMed]
- Chan, P.Y.; Tsekenis, G.; Dantzig, J.; Dahmen, K.A.; Goldenfeld, N. Plasticity and dislocation dynamics in a phase field crystal model. Phys. Rev. Lett. 2010, 105, 015502. [Google Scholar] [CrossRef] [PubMed]
- Koslowski, M.; LeSar, R. Thomson R Avalanches and scaling in plastic deformation. Phys. Rev. Lett. 2004, 93, 125502. [Google Scholar] [CrossRef] [PubMed]
- Umantsev, A. Bifurcation Theory of Plasticity, Damage and Failure. Mater. Today Comm. 2021, 26, 102121, Corrigendum in Mater. Today Comm. 2023, 37, 107377. [Google Scholar] [CrossRef]
- Umantsev, A. Thermodynamically Consistent Model of Dislocation-Mediated Plasticity. Phil. Mag. Part A Mater. Sci. 2024, 105, 2408383. [Google Scholar] [CrossRef]
- Umantsev, A. Multiscale Theory of Dislocation Plasticity. J. Mater. Sci. Mater. Theory, 2025; to be submitted. [Google Scholar]
- Mayergoyz, I.D. Mathematical Models of Hysteresis; Springer: Berlin, Germany, 1991. [Google Scholar]
- Landau, L.D.; Lifshitz, E.M. Theory of Elasticity; Pergamon Press: Oxford, UK, 1970. [Google Scholar]




| Property | Designation | Unit | Experimental Quantity |
|---|---|---|---|
| Shear modulus | μ | Pa | 5 × 1010 |
| Mass density | kg/m3 | 5 × 104 | |
| Speed of sound | c | m/s | 103 |
| 0.2%-yield strength | Pa | 108 | |
| Yielding | 2 × 10−3 | ||
| Ductility | 0.5 | ||
| Burgers vector | b | m | 10−10 |
| Dislocation density scale of plastic state | 1/m2 | 1014 | |
| Dislocation density scale of elastic state | 1/m2 | 109 | |
| Strain gradient coefficient | J/m | 10−5 | |
| Dislocation gradient coefficient | J/m | 10−5 | |
| Viscosity | η | Pa·s | 104 |
| Relaxation coefficient | γ | (Pa·s)−1 | 10−2 |
| Damage scale | 10−3 | ||
| Length scale | nm | 14 | |
| Time scale | ns | 2 | |
| Shock length scale | μm | 4 | |
| Creep time scale | μs | 0.2 | |
| Stress scale | Pa | 5 × 107 | |
| Energy density scale | J/m3 | 5 × 104 | |
| Noise scale | 1/s | 5 × 105 | |
| Ratio of speed scales | 2 × 104 | ||
| Ratio of time scales | 102 | ||
| Ratio of gradient coefficients | 1 |
| (s−1) | (μm) | (μs) | G | u | |
|---|---|---|---|---|---|
| Creep | 5 | 1.4 × 102 | 5 × 103 | 0.001 ÷ 1 | |
| Shock | 5 × 103 | 4 × 104 | 7.5 | 5 ÷ 20 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Umantsev, A.R. Dislocation Avalanches in Compressive Creep and Shock Loadings. Metals 2025, 15, 626. https://doi.org/10.3390/met15060626
Umantsev AR. Dislocation Avalanches in Compressive Creep and Shock Loadings. Metals. 2025; 15(6):626. https://doi.org/10.3390/met15060626
Chicago/Turabian StyleUmantsev, Alexander R. 2025. "Dislocation Avalanches in Compressive Creep and Shock Loadings" Metals 15, no. 6: 626. https://doi.org/10.3390/met15060626
APA StyleUmantsev, A. R. (2025). Dislocation Avalanches in Compressive Creep and Shock Loadings. Metals, 15(6), 626. https://doi.org/10.3390/met15060626






