Laser–Arc Welding Adaptive Model of Multi-Pre-Welding Condition Based on GA-BP Neural Network
Abstract
1. Introduction
2. Experimental Section
2.1. Experimental Materials
2.2. Experimental Equipment and Process
3. GA-BP Neural Network Modeling
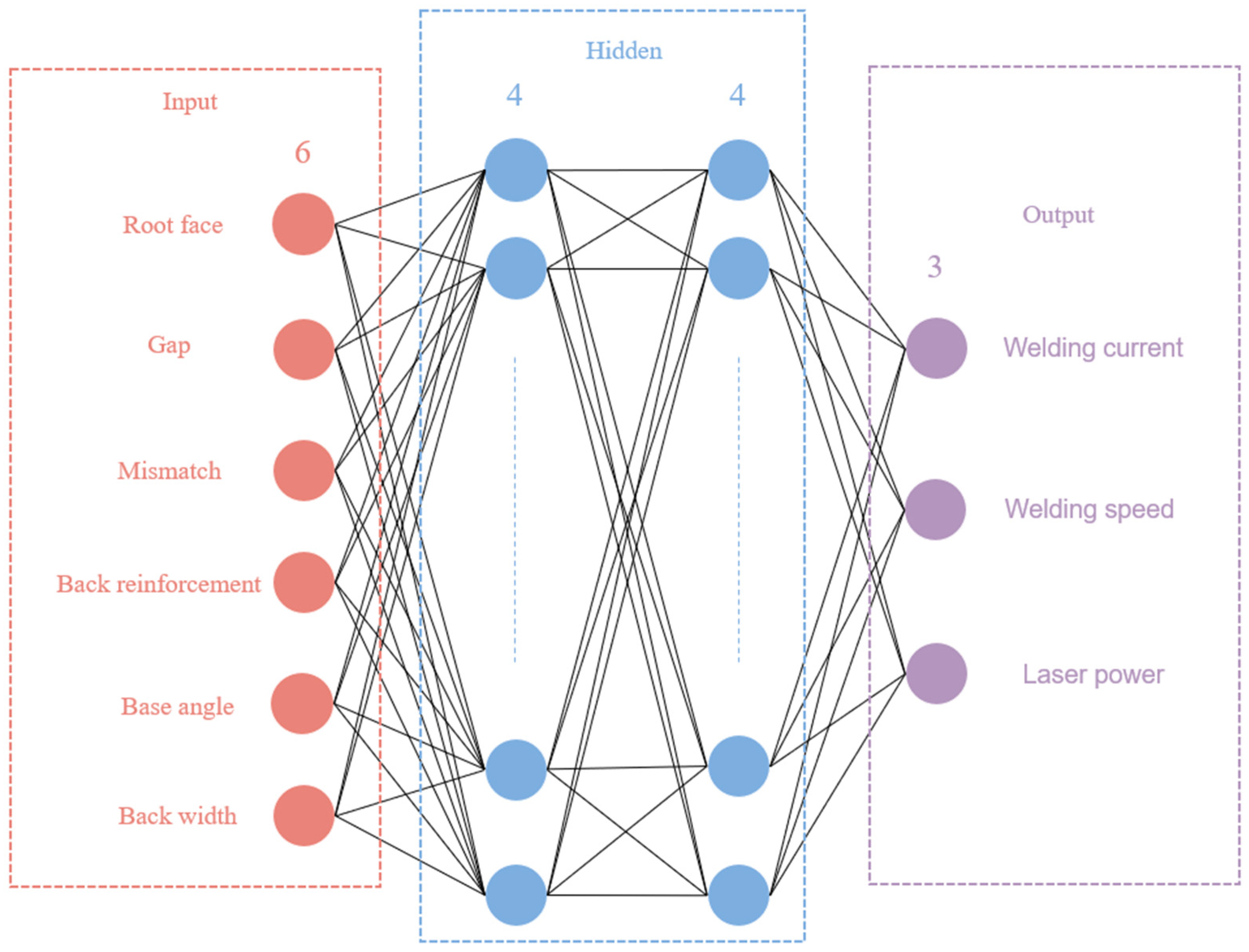
3.1. BP Neural Network Structure
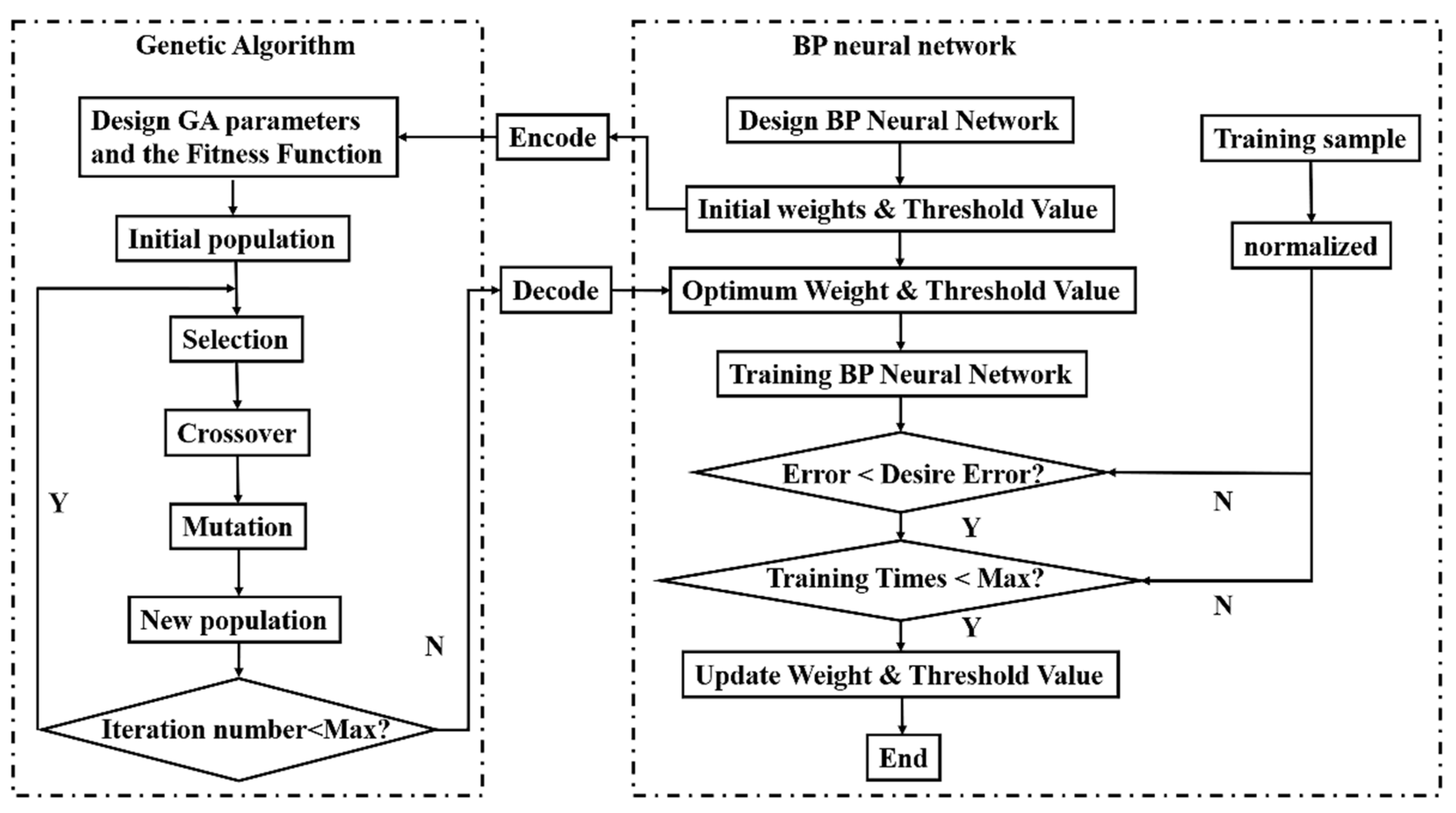
3.2. Genetic Algorithm (GA)
3.2.1. GA Design
- Population Initialization
- 2.
- Fitness Function
- 3.
- Selection
- 4.
- Crossover
- 5.
- Mutation
3.2.2. GA Parameters
4. Results and Discussion
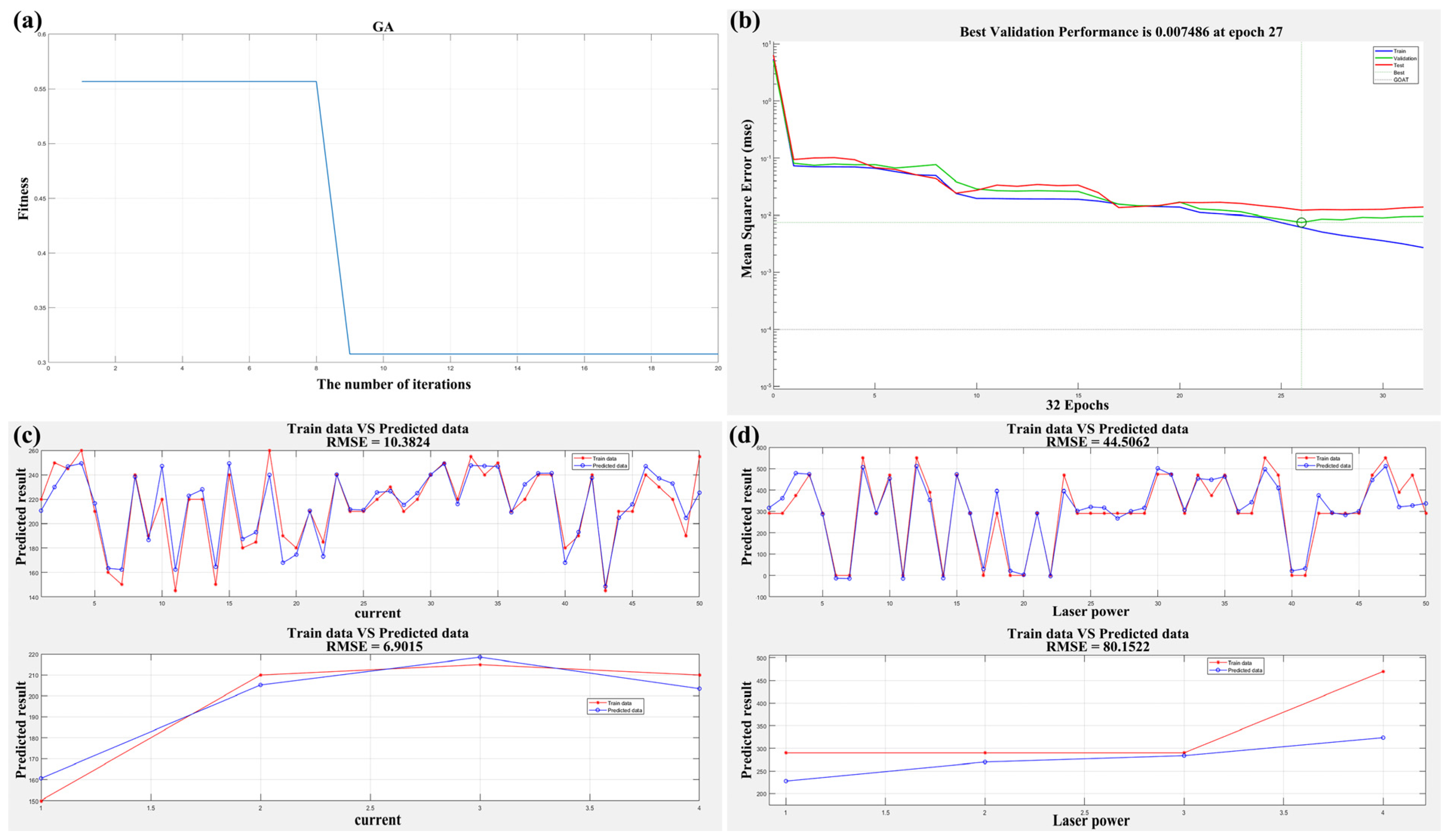
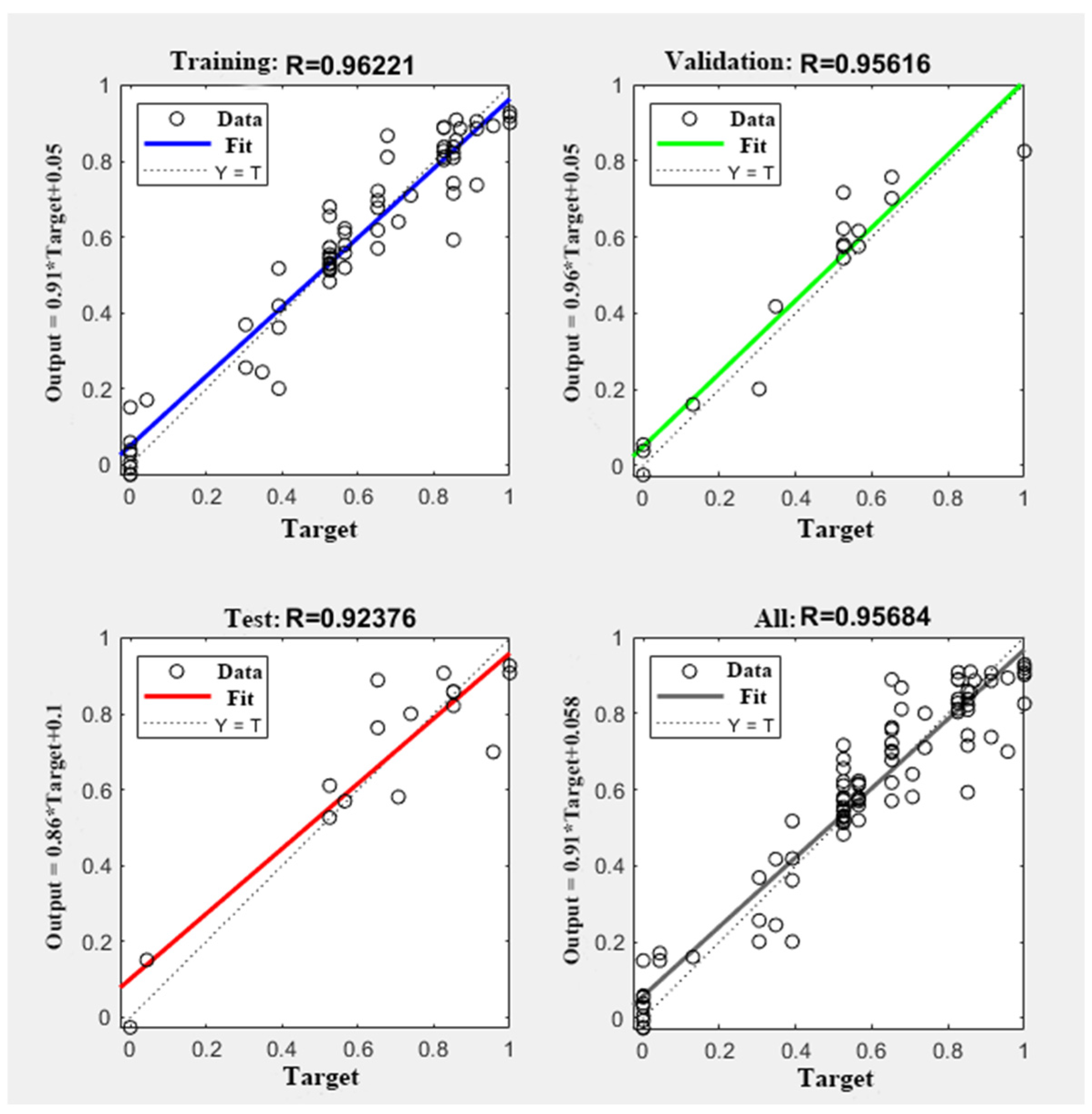
4.1. Testing the GA-BP Neural Network
4.2. Validation of GA-BPNN Through Experimentation
5. Conclusions
- (1)
- An adaptive welding model for flexible laser–arc hybrid welding was developed via a GA-BP neural network. The input layer consists of six neurons, representing the mismatch, gap, base angle, back reinforcement, and back width. The output layer includes three neurons for the welding current, welding speed, and laser power. This model can predict the welding process parameters based on different pre-welding grooves.
- (2)
- Laser-GMAW can be achieved by adjusting the balance between the laser power and arc power. This adjustment controls the melting penetration of medium–thick mild steel plates under various pre-welding groove conditions.
- (3)
- The experimental results indicated that the adaptive model based on the GA-BPNN was effective in describing the relationship between the pre-welding structure dimensions, the ideal geometric parameters of weld beads, and the optimized welding parameters to produce the ideal welds.
- (4)
- The adaptive model established by the GA-BPNN lays the foundation for the adaptive control of pre-welding grooves with variations in the groove dimensions in the welding process.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Le, G.E.; Fabbro, R.; Carin, M.; Coste, F.; Le, M.P. Analysis of hybrid Nd: YAG laser-MAG arc welding processes. Opt. Laser Technol. 2011, 43, 1155–1166. [Google Scholar] [CrossRef]
- Unt, A.; Poutiainen, I.; Grünenwald, S.; Sokolov, M.; Salminen, A. High Power Fiber Laser Welding of Single Sided T-Joint on Shipbuilding Steel with Different Processing Setups. Appl. Sci. 2017, 7, 1276. [Google Scholar] [CrossRef]
- Steen, W.M. Arc augmented laser processing of materials. J. Appl. Phys. 1980, 51, 5636–5641. [Google Scholar] [CrossRef]
- Górka, J.; Stano, S. Microstructure and Properties of Hybrid Laser Arc Welded Joints (Laser Beam-MAG) in Thermo-Mechanical Control Processed S700MC Steel. Metals 2018, 8, 132. [Google Scholar] [CrossRef]
- Agrawal, B.P.; Kumar, R. Challenges in application of pulse current gas metal arc welding process for preparation of weld joint with superior quality. Int. J. Eng. Res. Technol. 2016, 5, 319–327. [Google Scholar]
- Tarng, Y.S.; Yang, W.H. Optimisation of the weld bead geometry in gas tungsten arc welding by the Taguchi method. Int. J. Adv. Manuf. Technol. 1998, 14, 549–554. [Google Scholar] [CrossRef]
- Lee, J.; Song, C.-Y. Estimation of submerged-arc welding design parameters using Taguchi method and fuzzy logic. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2013, 227, 532–542. [Google Scholar] [CrossRef]
- Cao, X.B.; Li, Z.; Zhou, X.F.; Luo, Z.; Duan, J. Modeling and optimization of resistance spot welded aluminum to Al-Si coated boron steel using response surface methodology and genetic algorithm. Measurement 2021, 171, 108766. [Google Scholar] [CrossRef]
- Liu, G.Q.; Gao, X.D.; Peng, C.; Huang, Y.J.; Fang, H.J.; Zhang, Y.X.; You, D.Y.; Zhang, N.F. Optimization of laser welding of DP780 to Al5052 joints for weld width and lap-shear force using response surface methodology. Opt. Laser Technol. 2020, 126, 106072. [Google Scholar] [CrossRef]
- Zhou, Z.; Gao, X.; Ma, B.; Zhang, Y. Residual regression on laser welding of CFRP-metal hybrid structures. J. Adhes. Sci. Technol. 2023, 38, 2128–2146. [Google Scholar] [CrossRef]
- Yu, J. Quality estimation of resistance spot weld based on logistic regression analysis of welding power signal. Int. J. Precis. Eng. Manuf. 2015, 16, 2655–2663. [Google Scholar] [CrossRef]
- Chang, Y.S.; Yue, J.F.; Guo, R.; Liu, W.J.; Li, L.Y. Penetration quality prediction of asymmetrical fillet root welding based on optimized BP neural network. J. Manuf. Process. 2020, 50, 247–254. [Google Scholar] [CrossRef]
- Wang, H.Y.; Zhang, Z.X.; Liu, L.M. Prediction and fitting of weld morphology of Al alloy-CFRP welding-rivet hybrid bonding joint based on GA-BP neural network. J. Manuf. Process. 2021, 63, 109–120. [Google Scholar] [CrossRef]
- Manvatkar, V.D.; Arora, A.; De, A.; Roy, T. Neural network models of peak temperature, torque, traverse force, bending stress and maximum shear stress during friction stir welding. Sci. Technol. Weld. Join. 2012, 17, 460–466. [Google Scholar] [CrossRef]
- Zelalem, Y.A.; Tsegaw, A.A. Process parameter optimization of submerged arc welding on mild steel AISI 1020 using an artificial neural network trained with multi-objective Jaya algorithm. Int. J. Adv. Manuf. Technol. 2024, 134, 3877–3891. [Google Scholar] [CrossRef]
- Siamakmanesh, N.; Mostafaei, M.A. A novel approach to investigate the effect of friction stir welding parameters on hardness and grain size of pure titanium using artificial Neural Network. Mater. Today Commun. 2024, 38, 108404. [Google Scholar] [CrossRef]
- Liu, B.W.; Jin, W.T.; Lu, A.J.; Liu, K.; Wang, C.M.; Mi, G.Y. Optimal design for dual laser beam butt welding process parameter using artificial neural networks and genetic algorithm for SUS316L austenitic stainless steel. Opt. Laser Technol. 2020, 125, 106027. [Google Scholar] [CrossRef]
- Xiong, X.H.; Wang, C.; Wang, F.S.; Cui, X.; Li, G.Y. Optimization of process parameters for induction welding of composite materials based on NSGA-II and BP neural network. Mater. Today Commun. 2022, 33, 104749. [Google Scholar] [CrossRef]
- Lei, Z.L.; Shen, J.X.; Wang, Q.; Chen, Y.B. Real-time weld geometry prediction based on multi-information using neural network optimized by PCA and GA during thin-plate laser welding. J. Manuf. Process. 2019, 43, 207–217. [Google Scholar] [CrossRef]
- Meng, K.Q.; Wang, T.Q.; He, J.J.; Du, L.F. Robot welding process planning and process parameter prediction of medium-thick plate based on three-line laser. Measurement 2024, 233, 114740. [Google Scholar] [CrossRef]
- Zhao, D.W.; Wang, W.T.; Ren, D.X.; Zhao, K.M. Research on ultrasonic welding of copper wire harness and aluminum alloy: Based on experimental method and GA-ANN model. J. Mater. Res. Technol. 2023, 22, 3180–3191. [Google Scholar] [CrossRef]
- Lupo, M.; Sofia, D.; Barletta, D.; Poletto, M. Calibration of Dem Simulation of Cohesive Particles. Chem. Eng. Trans. 2019, 74, 379–384. [Google Scholar] [CrossRef]
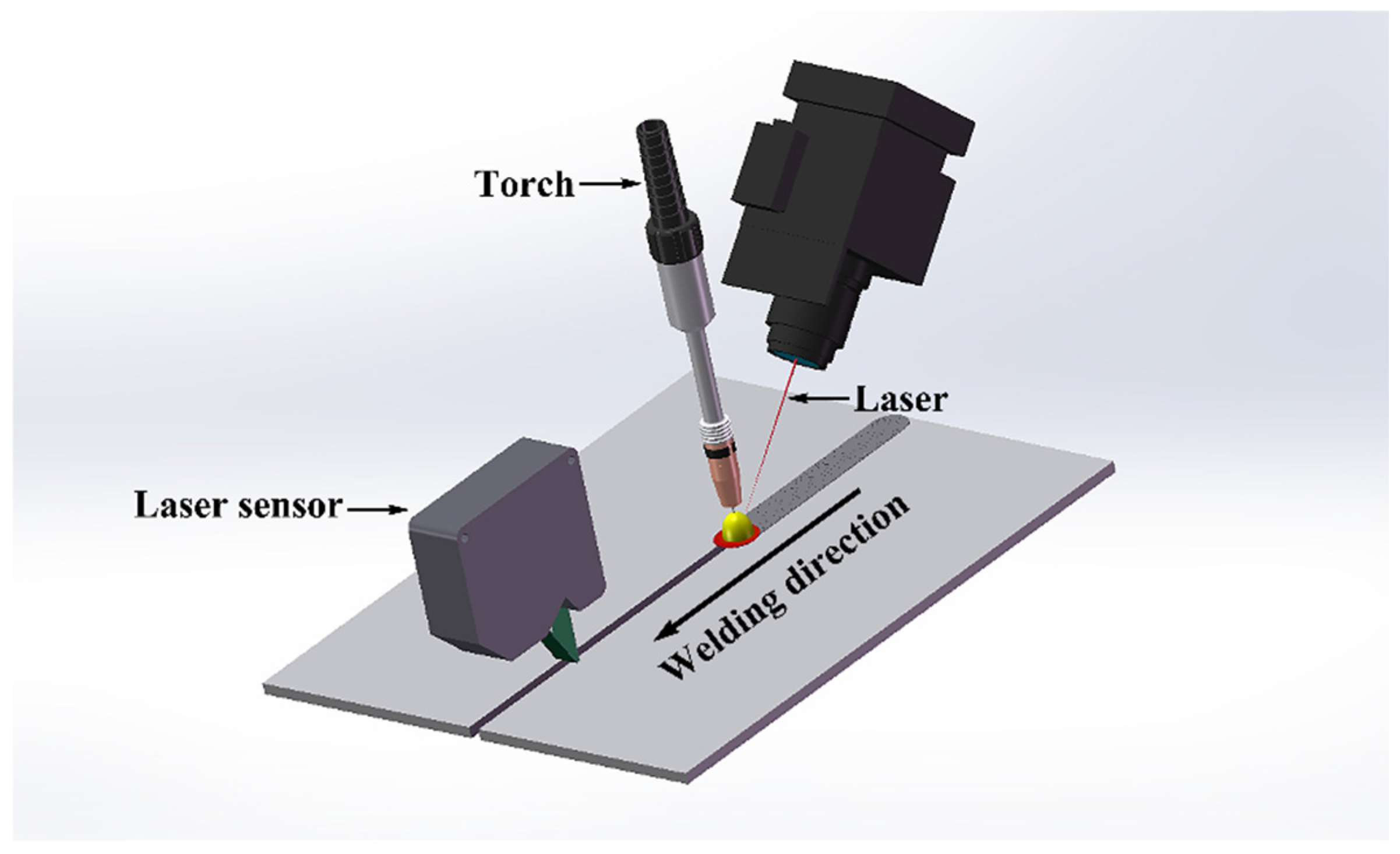
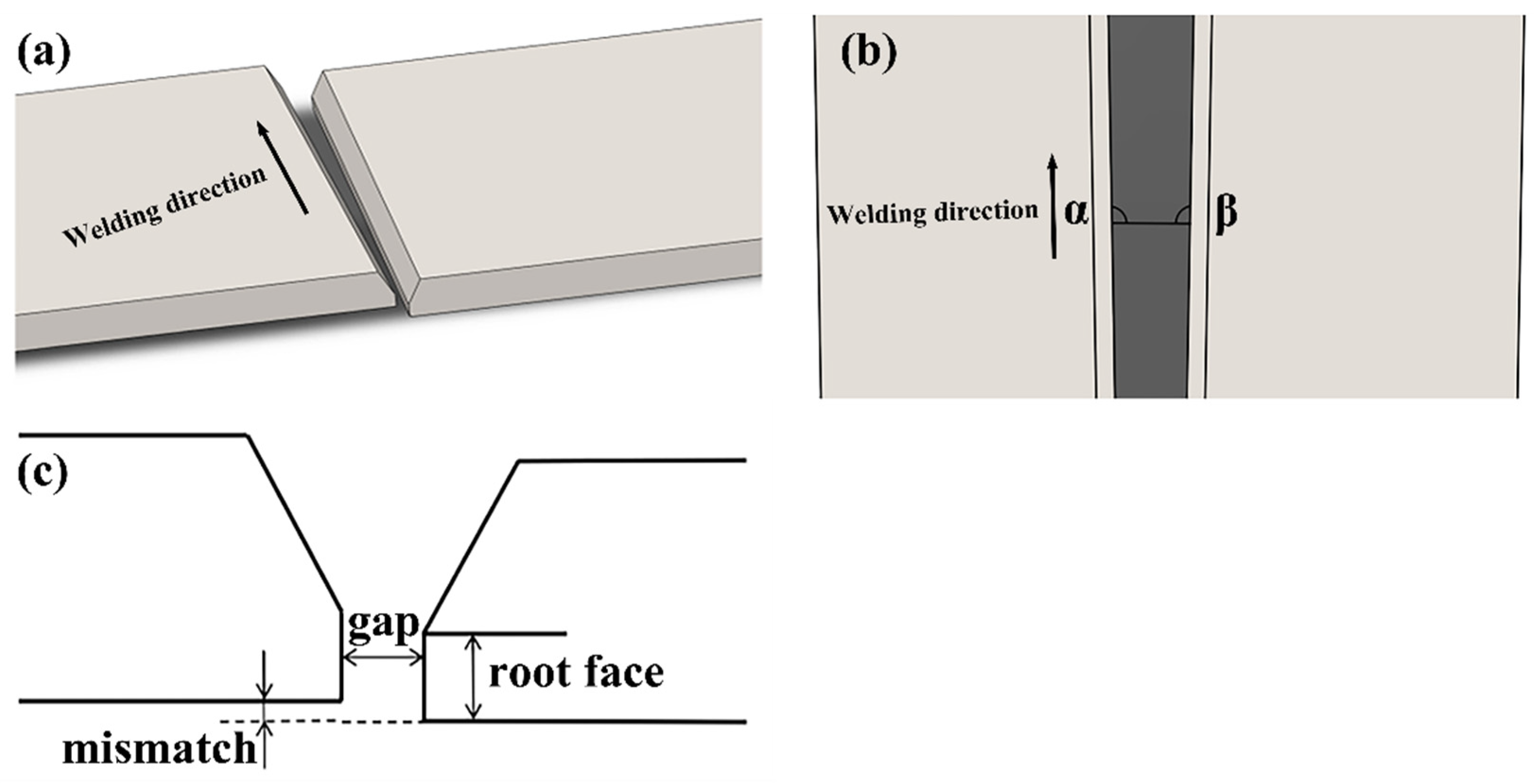


| Material | C | Si | Mn | Cu | Ni | Cr | P | S |
|---|---|---|---|---|---|---|---|---|
| Q345 | 0.20 | 0.55 | 1.70 | - | - | 0.01 | 0.045 | 0.030 |
| ER50-6 | 0.077 | 0.90 | 1.45 | 0.50 | 0.015 | 0.15 | 0.025 | 0.025 |
| No. | RF | Gap | BA | Mismatch | BR | BW | I | V | P |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 1.5 | 0 | 180 | 0 | 1.37 | 4.21 | 240 | 10 | 290 |
| 2 | 1.5 | 1 | 180 | 1 | 0.50 | 2.39 | 210 | 10 | 290 |
| 3 | 1.5 | 2 | 180 | 0.5 | 0.54 | 1.98 | 150 | 10 | 0 |
| 4 | 2 | 0 | 180 | 1 | 2.30 | 3.83 | 240 | 10 | 470 |
| 5 | 2 | 1 | 180 | 0.5 | 1.08 | 3.38 | 210 | 10 | 290 |
| 6 | 2 | 2 | 180 | 0 | 0.54 | 2.71 | 160 | 10 | 0 |
| 7 | 2.5 | 0 | 180 | 0.5 | 2.12 | 3.92 | 240 | 10 | 470 |
| 8 | 2.5 | 1 | 180 | 0 | 2.03 | 4.83 | 210 | 10 | 290 |
| 9 | 2.5 | 2 | 180 | 1 | 1.40 | 3.07 | 150 | 10 | 290 |
| 10 | 1.5 | 0 | 180.004 | 0 | 1.62 | 4.11 | 215 | 10 | 290 |
| 11 | 1.5 | 1 | 180.004 | 1 | 1.33 | 3.79 | 190 | 10 | 290 |
| 12 | 1.5 | 0 | 180.006 | 0.5 | 1.04 | 3.61 | 210 | 10 | 470 |
| 13 | 2 | 0 | 180.004 | 1 | 1.89 | 3.24 | 255 | 10 | 290 |
| 14 | 2 | 1 | 180.004 | 0.5 | 1.17 | 3.47 | 185 | 10 | 0 |
| 15 | 2 | 0 | 180.006 | 0 | 0.72 | 3.52 | 190 | 10 | 0 |
| 16 | 2.5 | 0 | 180.004 | 0.5 | −2.21 | 0 | 240 | 10 | 552 |
| 17 | 2.5 | 1 | 180.004 | 0 | 1.22 | 3.70 | 190 | 10 | 0 |
| 18 | 2.5 | 0 | 180.006 | 1 | −2.26 | 0 | 230 | 10 | 552 |
| 19 | 1.5 | 1 | 179.996 | 0 | 0.95 | 3.74 | 240 | 10 | 470 |
| 20 | 1.5 | 2 | 179.996 | 1 | 0.27 | 2.71 | 210 | 10 | 290 |
| 21 | 1.5 | 2 | 179.994 | 0.5 | 1.13 | 3.83 | 220 | 10 | 290 |
| 22 | 2 | 1 | 179.996 | 1 | 0 | 0 | 245 | 10 | 374 |
| 23 | 2 | 2 | 179.996 | 0.5 | 1.22 | 3.20 | 210 | 10 | 290 |
| 24 | 2 | 2 | 179.994 | 0 | 0.21 | 1.62 | 220 | 10 | 390 |
| 25 | 2.5 | 1 | 179.996 | 0.5 | −1.71 | 0 | 240 | 10 | 474 |
| 26 | 2.5 | 2 | 179.996 | 0 | 0.63 | 2.98 | 220 | 10 | 290 |
| 27 | 2.5 | 2 | 179.994 | 1 | 1.31 | 2.93 | 240 | 10 | 470 |
| 28 | 1.5 | 0 | 180 | 0 | 1.30 | 3.82 | 260 | 10 | 290 |
| 29 | 1.5 | 1 | 180 | 1 | 0.80 | 2.44 | 210 | 10 | 290 |
| 30 | 1.5 | 2 | 180 | 0.5 | 0.77 | 2.10 | 145 | 10 | 0 |
| 31 | 2 | 0 | 180 | 1 | 1.80 | 3.77 | 255 | 10 | 470 |
| 32 | 2 | 1 | 180 | 0.5 | 1.20 | 3.55 | 220 | 10 | 290 |
| 33 | 2 | 2 | 180 | 0 | 0.80 | 2.33 | 150 | 10 | 0 |
| 34 | 2.5 | 0 | 180 | 0.5 | 1.22 | 3.88 | 260 | 10 | 470 |
| 35 | 2.5 | 1 | 180 | 0 | 1.85 | 4.55 | 210 | 10 | 290 |
| 36 | 2.5 | 2 | 180 | 1 | 0.95 | 3.66 | 145 | 10 | 290 |
| 37 | 1.5 | 0 | 180.004 | 0 | 1.22 | 4.21 | 220 | 10 | 290 |
| 38 | 1.5 | 1 | 180.004 | 1 | 1.11 | 3.85 | 180 | 10 | 290 |
| 39 | 1.5 | 0 | 180.006 | 0.5 | 0.95 | 3.75 | 190 | 10 | 470 |
| 40 | 2 | 0 | 180.004 | 1 | 1.44 | 3.56 | 250 | 10 | 290 |
| 41 | 2 | 1 | 180.004 | 0.5 | 1.20 | 3.66 | 180 | 10 | 0 |
| 42 | 2 | 0 | 180.006 | 0 | 1.13 | 3.48 | 185 | 10 | 0 |
| 43 | 2.5 | 0 | 180.004 | 0.5 | 0.95 | 3.11 | 240 | 10 | 552 |
| 44 | 2.5 | 1 | 180.004 | 0 | 1.22 | 3.70 | 180 | 10 | 0 |
| 45 | 2.5 | 0 | 180.006 | 1 | 1.45 | 4.23 | 220 | 10 | 552 |
| 46 | 1.5 | 1 | 179.996 | 0 | 0.96 | 4.11 | 240 | 10 | 470 |
| 47 | 1.5 | 2 | 179.996 | 1 | 0.52 | 3.85 | 210 | 10 | 290 |
| 48 | 1.5 | 2 | 179.994 | 0.5 | 0.85 | 3.83 | 220 | 10 | 290 |
| 49 | 2 | 1 | 179.996 | 1 | 0.75 | 3.95 | 240 | 10 | 374 |
| 50 | 2 | 2 | 179.996 | 0.5 | 0.22 | 3.13 | 210 | 10 | 290 |
| 51 | 2 | 2 | 179.994 | 0 | 0.75 | 3.65 | 220 | 10 | 390 |
| 52 | 2.5 | 1 | 179.996 | 0.5 | 0.94 | 3.88 | 250 | 10 | 474 |
| 53 | 2.5 | 2 | 179.996 | 0 | 0.75 | 3.95 | 230 | 10 | 290 |
| 54 | 2.5 | 2 | 179.994 | 1 | 1.11 | 4.33 | 220 | 10 | 470 |
| No. | RF/mm | M/mm | BA/mm | Gap/mm | Experimental Parameters | Desired Geometry Size | Actual Geometry Size | |||
|---|---|---|---|---|---|---|---|---|---|---|
| P/W | I/A | BW/mm | BR/mm | BW/mm | BR/mm | |||||
| S1 | 2 | 0 | 180 | 0 | 450 | 240 | 3 | 0.5 | 2.82 | 0.51 |
| S2 | 1.5 | 1 | 180.004 | 2 | 0 | 145 | 3 | 0.5 | 2.91 | 0.46 |
| S3 | 2.5 | 0.5 | 179.006 | 1 | 460 | 250 | 3 | 0.5 | 3.1 | 0.43 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Z.; Zhang, Z.; Song, G. Laser–Arc Welding Adaptive Model of Multi-Pre-Welding Condition Based on GA-BP Neural Network. Metals 2025, 15, 611. https://doi.org/10.3390/met15060611
Wu Z, Zhang Z, Song G. Laser–Arc Welding Adaptive Model of Multi-Pre-Welding Condition Based on GA-BP Neural Network. Metals. 2025; 15(6):611. https://doi.org/10.3390/met15060611
Chicago/Turabian StyleWu, Zesheng, Zhaodong Zhang, and Gang Song. 2025. "Laser–Arc Welding Adaptive Model of Multi-Pre-Welding Condition Based on GA-BP Neural Network" Metals 15, no. 6: 611. https://doi.org/10.3390/met15060611
APA StyleWu, Z., Zhang, Z., & Song, G. (2025). Laser–Arc Welding Adaptive Model of Multi-Pre-Welding Condition Based on GA-BP Neural Network. Metals, 15(6), 611. https://doi.org/10.3390/met15060611






