Optimal Diamond Burnishing of Chromium–Nickel Austenitic Stainless Steels Based on the Finishing Process–Surface Integrity–Operating Behavior Correlations

Abstract

Chromium–nickel austenitic stainless steels are widely used in various industries after their initial hardness and strength are increased. Apart from low-temperature thermal–chemical diffusion, the mechanical properties can be improved by surface cold working (SCW). A cheap and reliable form of static SCW is diamond burnishing (DB), which drastically improves the surface integrity (SI) and hence the operational behavior of the processed component. To be maximally effective, the DB parameters must be optimized according to a relevant criterion, depending on the desired effect. For high fatigue strength and/or high wear resistance, complex experimental tests are necessary, which require significant time and financial resources. This study presents a cost-effective optimization approach based on the DB process–SI–operating behavior correlations. Using these correlations, in addition to the correlations between appropriately selected SI characteristics, the proposed approach relies on the control of only three easy-to-measure roughness parameters, namely the arithmetic average roughness, skewness, and kurtosis, which, in turn, depend on the governing factors of the DB process.

1. Introduction

Chromium–nickel austenitic stainless steels find widespread use in many industries owing to their corrosion resistance, facile machinability by cutting and plastic deformation, and reliable weldability. The wider application of these steels is limited by their susceptibility to intergranular corrosion in the temperature range of 500–700 °C and their initially low hardness and strength. Increasing the hardness and the strength is achieved through two main approaches: bulk cold working [1,2] and modification of the surface layers (SLs). A disadvantage of bulk cold working is the need for significant energy resources. In addition, this approach applies to a limited range of blanks and parts made of sheet material. Alternatively, the SL can be modified by low-temperature thermo-chemical diffusion processes (nitriding and/or carburizing) aimed at forming a supersaturated surface S-phase [3,4], surface cold working (SCW) processes [5,6], or a combination of both [7,8].

The SL and substrate can be viewed as a functionally linked system, and modification of the SL is required to prepare the system for the desired application. Hence, studies focus on significantly improving the desired properties of SLs, such as hardness, strength, wear resistance, crack resistance, and corrosion resistance, for specific applications in the most cost-effective manner. At the same time, the bulk material remains raw and tough; therefore, this approach is energy efficient, economical, provides added value, and is environmentally friendly in many cases.

The SLs are typically exposed to various external influences, including contact between SLs and other surfaces; high working stresses under load-bearing conditions, which are maximum in these layers; and direct exposure to the environment, which is often aggressive (seawater or other chemically active environments). As a result, the operational behavior of steel parts is directly correlated with the complex state of the SL, known as surface integrity (SI) [9]. To achieve high efficiency in the SL modification processes, an integrated approach is needed to study the finishing process–SI–operating behavior correlations [10].

An effective approach for modifying SLs is static SCW (i.e., burnishing), which is implemented using a rigid and smooth deforming element that is pressed with a constant static force and relative motion against the surface being machined. Thus, the SL deforms plastically at a temperature lower than the recrystallization temperature of the processed material. As a result, the SL is modified owing to the following effects: (1) smoothing of microscale roughness (smoothing effect); (2) a significant increase in surface microhardness (strain-hardening effect); (3) introduction of useful residual compressive stresses in the surface and nearby subsurface layers; and (4) modification of the microstructure in the direction of grain refinement and orientation. Static SCW processes mainly differ from dynamic SCW processes in terms of the surface texture parameters. Notably, the smoothing effect is generally not observed in dynamic SCW processes [11]. This result has also been confirmed for austenitic stainless steels after shot peening [12] and laser shock peening [13]. Unlike dynamic SCW, static SCW processes rely on a deforming element (tool) with a defined geometry and kinematics that precisely determine the interaction between the tool and the machined surface in time and space. This creates topographically anisotropic surfaces characterized by a drastic reduction in the roughness height parameters, such as the average roughness (Ra). In addition, the roughness shape parameters, namely skewness (Rsk) and kurtosis (Rku) [14], are particularly sensitive to the type of tangential contact (roller friction or sliding friction) and the variation of the technological parameters in the corresponding static SCW process [15,16].

The four modification effects occur simultaneously because they have a common physical basis: severe surface plastic deformation in the SL. Therefore, for a specific material, the obtained SI characteristics (as quantitative indicators of these effects) are interdependent and influenced by the combination of technological SCW parameters. The surface texture parameters are correlated with the equivalent plastic deformation in SLs, of which the surface microhardness is a quantitative indicator.

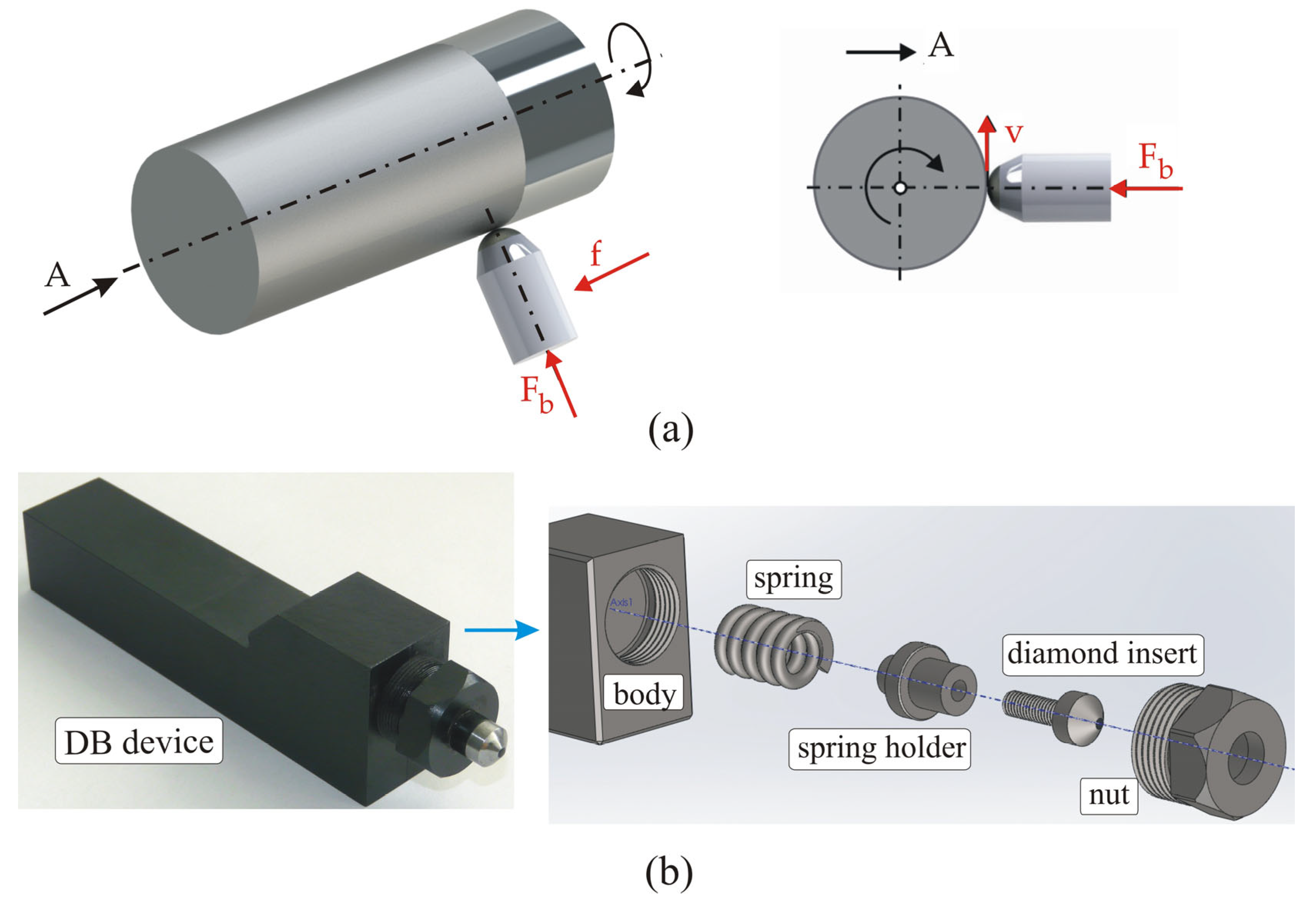
When the tangential contact between the deforming element and the SL is sliding friction, static SCW is known as slide burnishing. When slide burnishing is implemented using a diamond deforming insert, the method is called diamond burnishing (DB). DB was introduced in 1962 by General Electric to improve the SI of metal components. DB is a simple and effective finishing technique, and its main advantages over burnishing methods with rolling contact (e.g., hydrostatic ball burnishing) are the significantly simpler equipment and kinematics.

Extensive studies have been conducted on the influence of the governing factors in the DB process on the SI of samples made of chromium–nickel austenitic steels [17,18,19,20,21]. These studies mainly considered the DB process–Ra 2D roughness parameter correlation [18,19] and the DB process–3D height and shape roughness parameter correlations [17,20,21]. DB is an effective finishing process that provides a significant strain-hardening effect in austenitic stainless steels, indicated by significantly increased microhardness and residual compressive stresses [18,19,20,21]. Korzynski et al. [20] predicted that the durability of the friction couple formed by 317Ti austenitic steel stem and graphite cord is increased by up to four times after DB, employing a reciprocating motion. To improve the fatigue behavior of AISI 304 austenitic stainless steels, Maximov et al. [18,19] examined the DB process–SI–rotating bending fatigue test correlations. Different types of DB processes increased the fatigue strength of AISI 304 steel by 23–38% compared with fine turning and polishing [18]. The effects of DB and heat treatment on the rotating fatigue strength and corrosion resistance of AISI 304 austenitic stainless steel were also observed for two initial states, in correlation with the SI [19].

However, these studies [17,18,19,20,21] lack explicit correlations between the characteristics of SI obtained via DB and the operating behavior. For the first time [10], the explicit correlations between SI characteristics (including skewness and kurtosis shape roughness parameters) on the one hand and the rotating bending fatigue limit of diamond-burnished AISI 304 chromium–nickel austenitic stainless steels on the other hand were established. It was found that with the increase in both the skewness (as an algebraic number) and kurtosis shape roughness parameters, the fatigue limit increases. At the same time, the fatigue limit increases as the microhardness increases. Therefore, the maximization of surface microhardness is a very important factor in maximizing the fatigue limit of chromium–nickel austenitic steels processed by static SCW. Moreover, the increase in surface microhardness is an indicator of a more pronounced strain-hardening effect in the SL and thus is an important factor for increasing the wear resistance of contacting surfaces. The effectiveness of DB for increasing the sliding wear resistance of SLs in CuAl8Fe3 aluminum bronze [22] and CuAl9Fe4 sliding bearing bushings [23] was compared with that of fine turning under boundary lubrication and dry friction conditions.

To improve the operational behavior (e.g., tribological, fatigue, corrosion) of austenitic stainless steel, it is necessary to determine the appropriate combination of DB technological parameters (i.e., governing factors) that provide the desired combination of SI characteristics under specific operating conditions. Hence, DB can be implemented as a smoothing, hardening, or mixed process [24]. The primary aim of smoothing DB is to achieve a high-quality, smooth surface, whereas the hardening DB process aims to achieve maximum surface microhardness. There are combinations of technological parameters that provide both a low roughness and a high fatigue limit without reaching their corresponding extreme values. Such a compromise can be achieved through mixed DB. To define a specific process, DB optimization is required. One-objective optimization is often conducted using Taguchi’s method or analysis of variance because the objective function generally describes the roughness, microhardness, or wear resistance. To optimize the static SCW process for roughness and microhardness/hardness criteria, Taguchi’s orthogonal array technique [25,26,27,28,29], fuzzy logic [30], the Sugeno fuzzy neural system [31], and artificial neural networks [32] have been implemented. One-objective optimization of the roughness obtained in the ball burnishing process was carried out using an analysis of variance [33,34], as well as a response surface methodology and desirability function [35].

Regarding multi-objective optimization, Taguchi’s method and analysis of variance are not applied. Typically, multi-objective optimizations are aimed at minimizing roughness and maximizing microhardness. The following approaches are used in this case: the Grey-based Taguchi method [36,37], MiniTab software [38], a desirability function approach [39], and non-dominated sorting genetic algorithm II (NSGA II) [40,41].

In these optimizations, the 2D roughness parameter Ra is often used for evaluating the resulting roughness. The DB process–SI–operating behavior correlations can be the basis for the cost-effective multi-objective optimization of DB when easy-to-measure SI characteristics with experimentally confirmed functional significance on the operating behavior are selected as objective functions.

Among them, the most accessible and easy-to-measure SI characteristics are the 2D and 3D roughness parameters. Although the standard 2D and 3D roughness height parameters Ra and Rq (Sa, Sq) are commonly used to identify the roughness level of contact surfaces, they are not sufficient to determine the operational behavior of the corresponding components. Notably, the functional significance of the skewness and kurtosis shape roughness parameters on tribological behavior under boundary lubrication and dry friction conditions has been investigated [15,42,43,44,45]. Sedlacek et al. [42] found that the combination of high kurtosis (Sku > 3) and negative skewness (Ssk < 0) at a constant mean roughness value (Sa = const.) reduced the friction and wear of hardened AISI 52,100 ball-bearing steel under boundary lubrication conditions. With this combination of shape parameters, the valleys of the SL function as micro-reservoirs that retain the lubricating substance. It is important to emphasize that the most dominant shape parameter is the Ssk parameter: the more negative the Ssk, the less friction and wear. In general, the negative skewness of smooth surfaces can improve the contact and lubrication conditions. Chang and Jeng [43] found that $\mathrm{Ssk}=-1$ reduces the friction coefficient under boundary lubrication by two times compared with the surface characterized by a Gaussian ordinate distribution (i.e., when $\mathrm{Ssk}=0$). Furthermore, negatively skewed surfaces of smooth [44] and rough [45] 42CrMo4 steel discs improved the tribological behavior under dry sliding conditions. In their purest form, the shape roughness parameters–tribological behavior correlations have been established for conventionally processed surfaces, in which the influence of the surface plastic deformation is practically isolated [42,43,44,45].

When metal components are subjected to dynamic (cyclic) loading, the requirements for roughness parameters are different. Zabala et al. [46] assumed that the influence of SL valleys on fatigue behavior dominates: a negative skewness shape parameter with larger absolute values is an indicator of deep valleys acting as micro-stress concentrators. Accordingly, to improve fatigue behavior, the respective machining process should provide positive skewness (Ssk > 0) and kurtosis less than 3 (Sku < 3) in combination with low values of the integral height parameters Ra (Sa) or Rq (Sq). Meanwhile, the main factors improving fatigue behavior are increased surface microhardness, modified microstructure, and the introduced residual compressive stresses in the surface and nearby subsurface layers [10,18,19]. Hence, to more accurately predict the operational behavior of diamond-burnished components, it is necessary to know the correlations between the various SI characteristics, with a focus on the correlations between shape roughness parameters and surface microhardness. Such information ensures the correct selection of the governing factors in the DB process, thereby achieving the desired operating behavior of the diamond-burnished metal component.

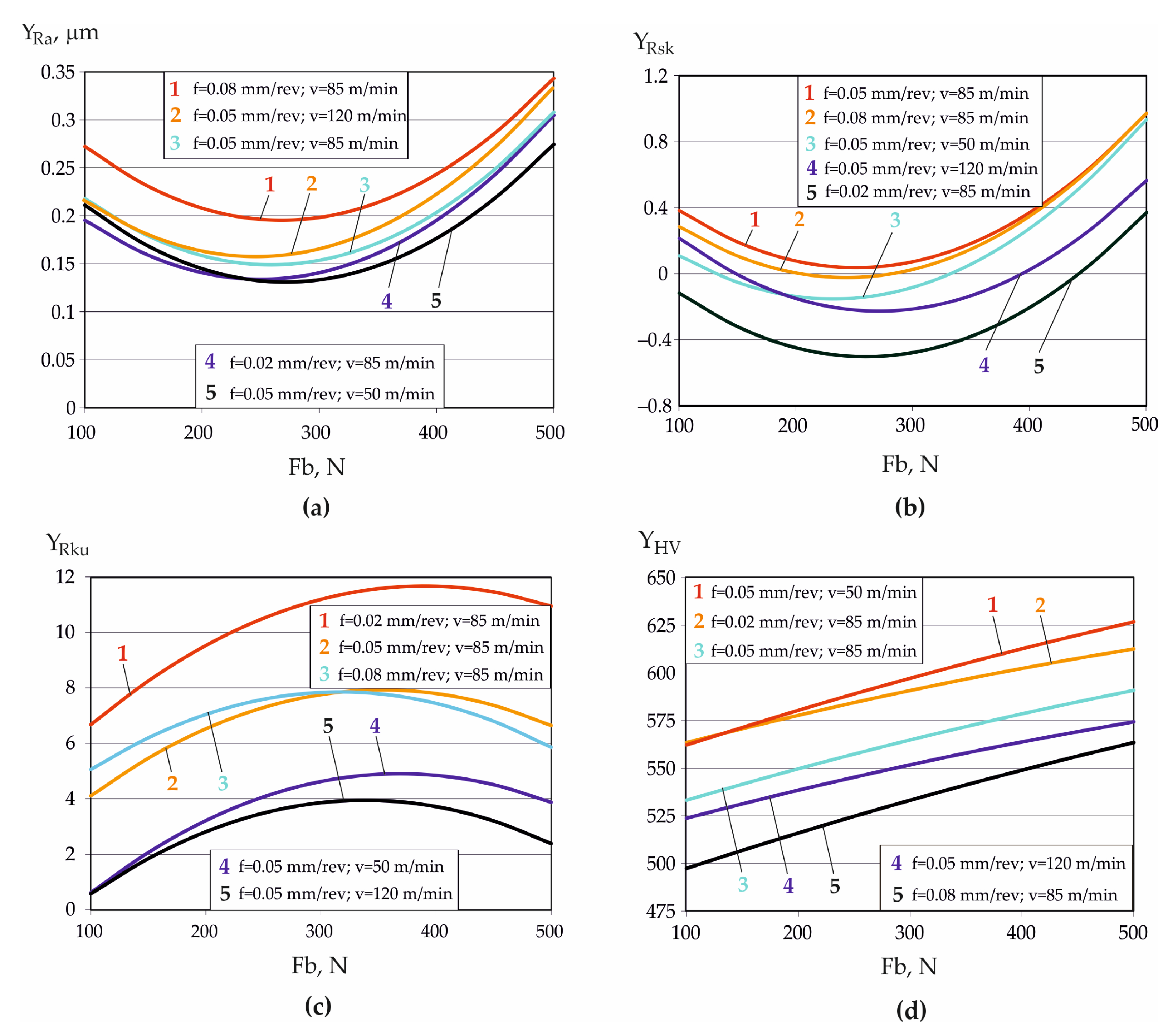
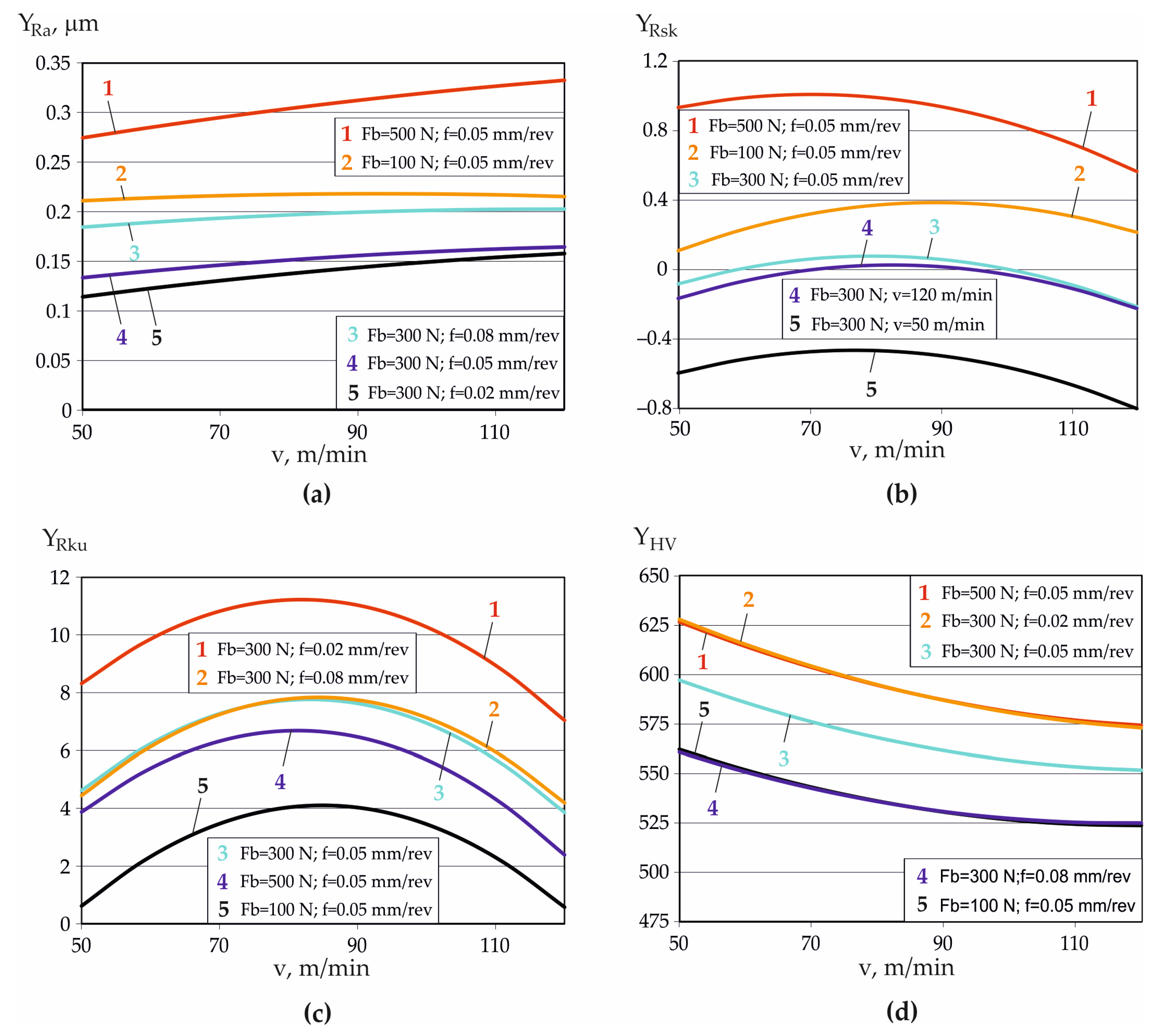
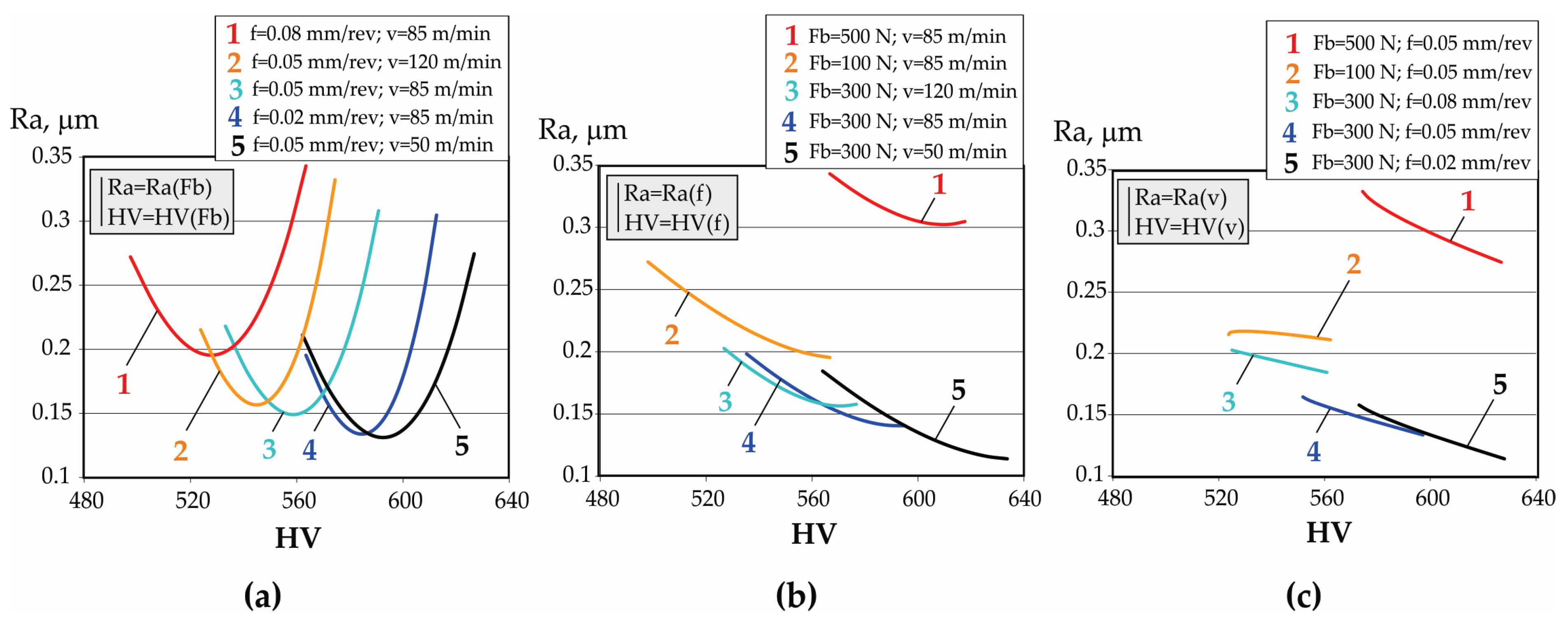
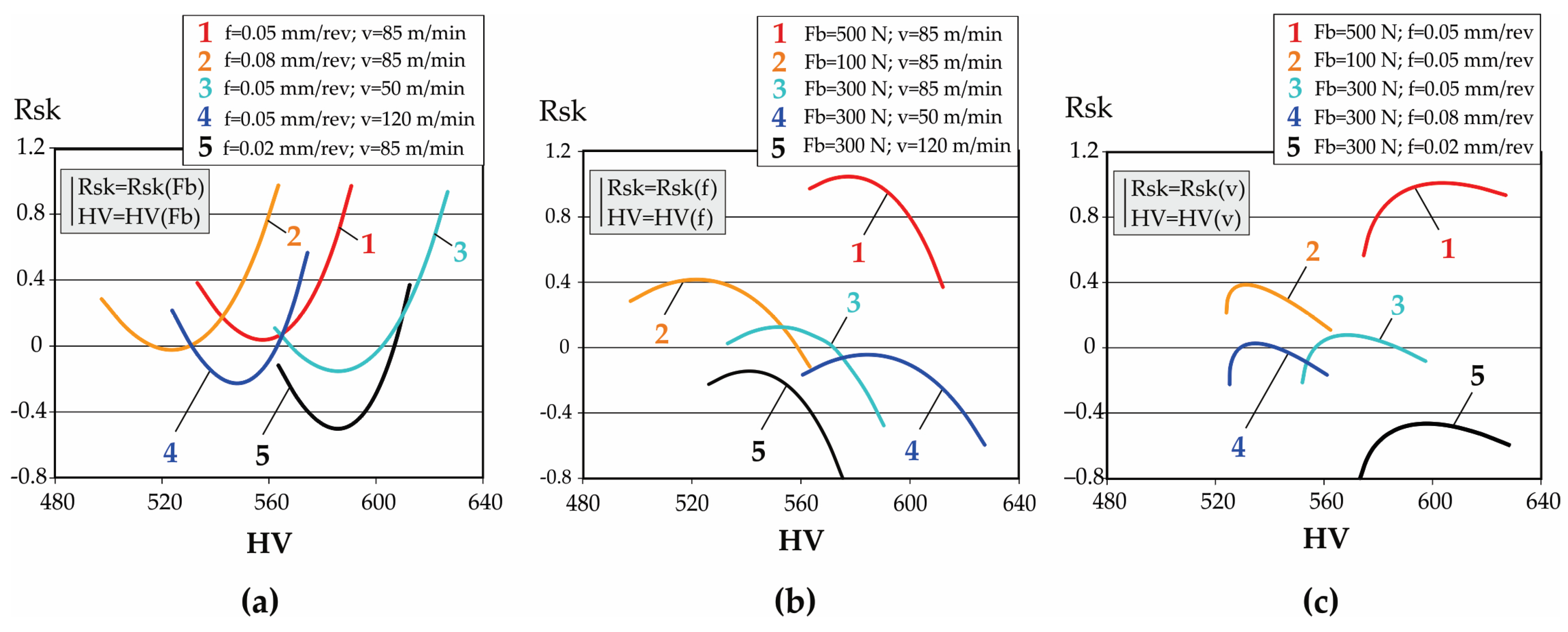
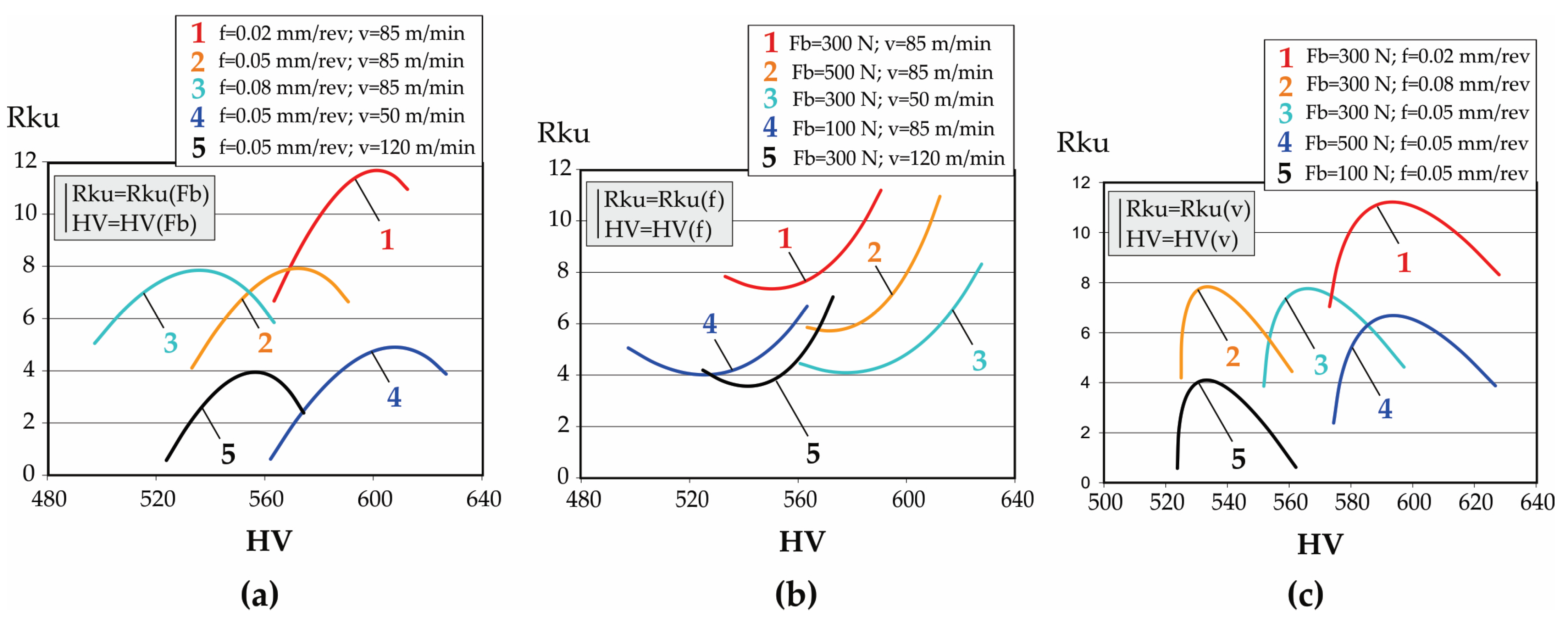
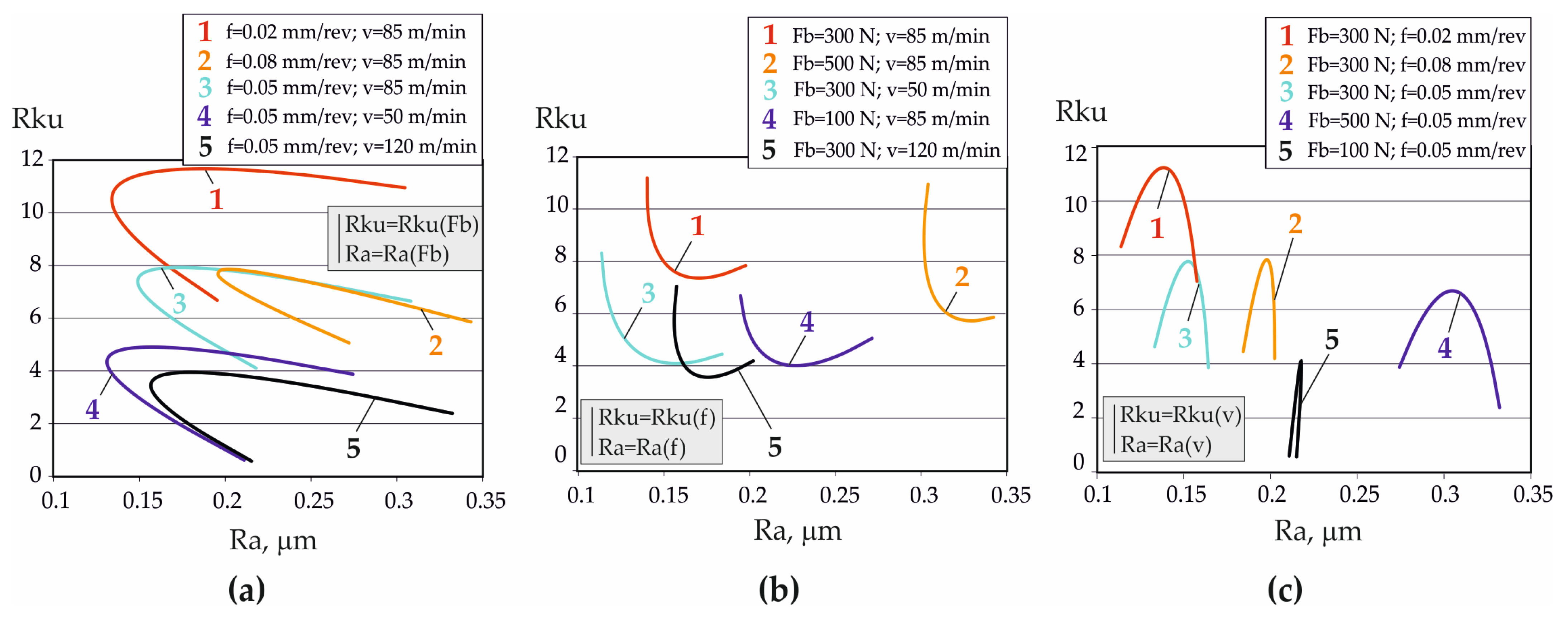
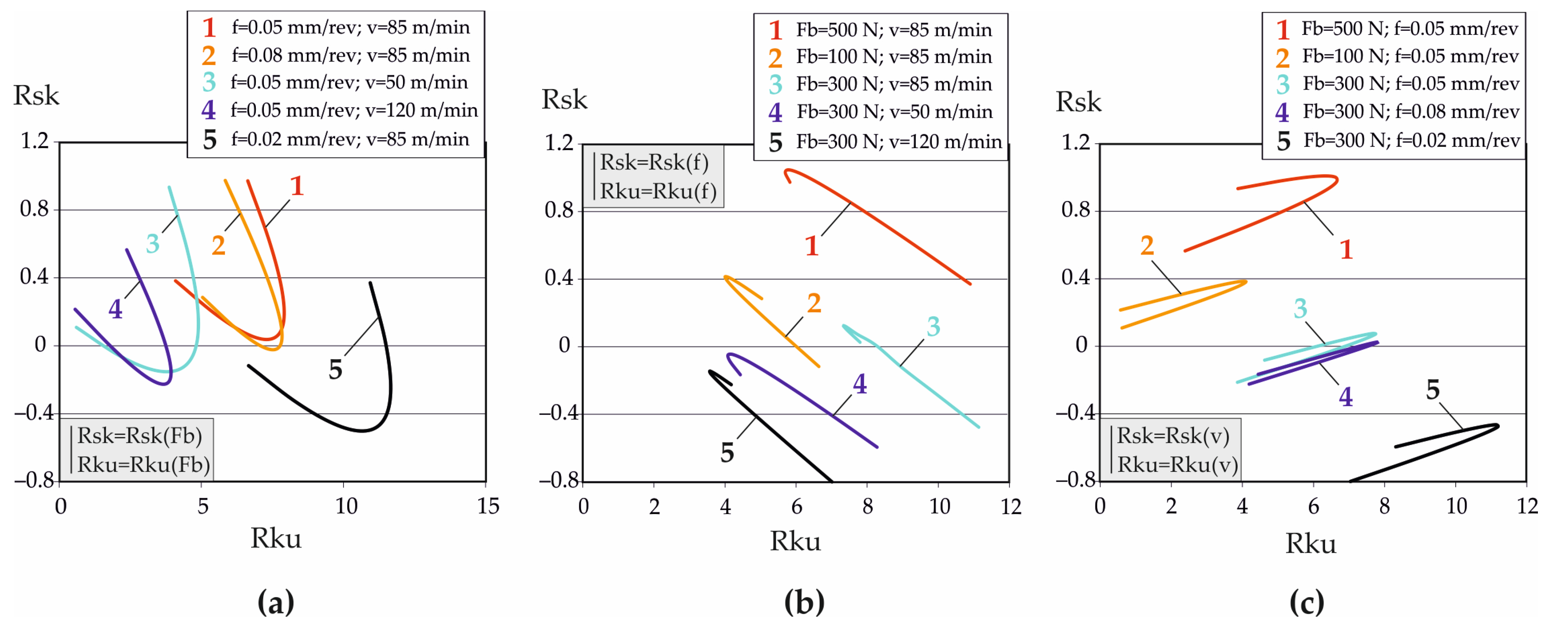
In this context, knowledge of the DB process–roughness parameters–operating behavior correlations reduces the required variables to only three easy-to-measure roughness parameters (Ra, Rsk, Rku), and depending on the intended purpose of the surface, the appropriate magnitudes of the governing factors in the DB process can be chosen.

Thus, the present study aims to determine the explicit dependencies between the main parameters of the DB process for AISI 304 stainless steel and three functionally relevant roughness parameters, as well as the explicit correlations between selected characteristics of SI, while considering results from previous studies to support the cost-effective optimization of the DB process, depending on the intended function of the diamond-burnished surface.

2. Materials and Methods

2.1. AISI 304 Steel

AISI 304 was chosen because it is the most commonly used grade of chromium–nickel austenitic stainless steel in engineering practice. The material arrived as hot-rolled bars with diameters of 16 mm and was used in an as-received state. The chemical composition was confirmed using an optical emission spectrometer (Foundry-Master Optimum, HITACHI, Tokyo, Japan). Tensile tests were carried out at room temperature using a Zwick/Roell Vibrophore 100 testing machine (Ulm, Germany). The tensile test specimens had a gauge diameter of 6 mm and a gauge length of 30 mm. The material hardness was measured using a VEB-WPM tester (Markkleeberg, Germany) equipped with a spherical-ended indenter (diameter of 2.5 mm), loading of 63 kg, and holding time of 10 s. The phase analysis was performed using a Bruker D8 Advance X-ray diffractometer (Billerica, MA, USA), and the Crystallography Open Database was used to determine the peak positions. After polishing and etching with royal water, the cross-sectional microstructure of the as-received bar was observed by optical microscopy (NEOPHOT 2, Carl Zeiss, Jena, Germany).

2.2. Turning and DB Implementation

Turning (i.e., premachining) and DB (Figure 1a) were implemented using an Index Traub CNC lathe (Esslingen am Neckar, Germany) with conventional flood lubrication (Blaser Swisslube Vasco 6000, Rüegsau, Switzerland) in a one-clamping process to minimize the concentric run-out in DB. A VCMT 160404-F3P carbide cutting insert (main back angle ${\mathrm{\alpha }}_0=7°$, tool tip radius 0.4 mm) was used for turning. An SVJCR 2525M-16 holder was used, with main and auxiliary setting angles of ${\mathrm{\chi }}_{\mathrm{c}}=93°$ and ${{\mathrm{\chi }}^{\prime }}_{\mathrm{c}}=52°$, respectively. The cutting insert and the holder were manufactured by ISCAR Bulgaria (Kazanlak, Bulgaria). The turning governing factors were as follows: cutting depth ${\mathrm{a}}_{\mathrm{c}}=0.1 \mathrm{mm}$, feed rate $\mathrm{f}=0.1 \mathrm{mm}/\mathrm{rev}$, and cutting velocity ${\mathrm{v}}_{\mathrm{c}}=110 \mathrm{m}/\min$. The average value of the Ra roughness parameter before DB was $\mathrm{R}{\mathrm{a}}^{\mathrm{init}}=0.529 \mathrm{\mu }\mathrm{m}$.

DB was performed using a spherical-ended polycrystalline diamond insert with a radius of 2 mm. The burnishing device (Figure 1b) provided elastic normal contact between the deforming element and the treated surface.

2.3. SI Characterization

The 2D roughness parameters were measured using a Mitutoyo Surftest SJ-210 surface roughness tester (Kawasaki, Japan) and a 0.8 mm base length. The average arithmetic values were calculated from the measurements of six equally spaced sample generatrixes. A ZHVµ Zwick/Roell microhardness tester (Ulm, Germany) was used to evaluate the surface microhardness. The loading force and holding time were 0.05 kgf and 10 s, respectively. The final surface microhardness value, expressed as Vickers hardness (HV), was determined based on the clustering center of ten measurements.

3. Experimental Results

3.1. Characteristics of the Study Material

Table 1. Chemical composition (in wt%) of the used AISI 304 stainless steel.

Fe	C	Si	Mn	P	S	Cr	Ni	Mo	Cu	Co	V	W	Other
69.51	0.023	0.271	1.600	0.047	0.034	19.19	7.98	0.243	0.637	0.161	0.060	0.041	Balance

shows the chemical composition of the AISI 304 stainless steel. The remaining chemical elements (0.203 wt%) are Ti, Al, Pb, Sn, Nb, B, As, Zn, Bi, Zr, and Ca. The main mechanical characteristics of the material in the as-received state are shown in

Table 2. Main mechanical characteristics of the tested AISI 304 stainless steel (as received).

Yield Limit, MPa	Tensile Strength, MPa	Elongation, %	Hardness, HB
${338}^{\begin{array}{l}+9\\ -18\end{array}}$	${733}^{\begin{array}{l}+12\\ -10\end{array}}$	${44.7}^{\begin{array}{l}+0.3\\ -0.2\end{array}}$	${250}^{\pm 8}$

. Figure 2 shows the diffraction pattern of AISI 304 steel after turning. Three peaks of γ-ferrite, namely the (111), (200), and (220) planes, were observed. No broadening or displacement of the peaks was observed. The relative intensity of the three peaks coincides with that from the databases. These results indicate that there are no texturing or significant deformations in the steel. The presence of other phases is not observed. Figure 3 shows the as-received steel microstructure in two characteristic areas: near the surface (after turning) and in the core. Overall, structural inhomogeneity is observed: zones with sliding stripes, zones with equiaxed austenite grains with an average size of 35 μm, twins, and sliding zones within the grains themselves.

3.2. DB Experiment

3.2.1. Governing Factors, Levels, and Objective Functions

The selected governing factors were burnishing force ${\mathrm{F}}_{\mathrm{b}}$, feed rate $\mathrm{f}$, and burnishing velocity v (Figure 1a). The radius of the spherical-ended polycrystalline diamond insert was 2 mm, and all tests were performed with one tool pass. The governing factor magnitudes (

Table 3. Governing factors and their levels.

Governing Factors	Levels
	$\mathbf{Natural}, {\tilde{\mathbf{x}}}_{\mathbf{i}}$				$\mathbf{Coded}, {\mathbf{x}}_{\mathbf{i}}$
Burnishing force ${\mathrm{F}}_{\mathrm{b}} [\mathrm{N}]$	${\tilde{\mathrm{x}}}_1$	100	300	500	${\mathrm{x}}_1$	–1	0	1
Feed rate $\mathrm{f} [\mathrm{m}\mathrm{m}/\mathrm{rev}]$	${\tilde{\mathrm{x}}}_2$	0.02	0.05	0.08	${\mathrm{x}}_2$	–1	0	1
Burnishing velocity v [m/min]	${\tilde{\mathrm{x}}}_3$	50	85	120	${\mathrm{x}}_3$	–1	0	1

) were selected based on previous results [18], which were obtained using the one-factor-at-a-time method. These results indicate that (1) a burnishing force greater than 500 N and less than 100 N deteriorates the Ra roughness parameter; and (2) a feed rate greater than 0.08 mm/rev also deteriorates the Ra height parameter. In addition, the maximum value of the burnishing velocity is limited to 120 m/min because higher speeds lead to the so-called softening effect, reducing surface microhardness and residual compressive stresses [47].

The transformation from physical (natural) ${\tilde{\mathrm{x}}}_{\mathrm{i}}$ to coded (dimensionless) ${\mathrm{x}}_{\mathrm{i}}$ variables is expressed as follows:

$${\mathrm{x}}_{\mathrm{i}}={\displaystyle \frac{\left({\tilde{\mathrm{x}}}_{\mathrm{i}}-{\tilde{\mathrm{x}}}_{\mathrm{i},0}\right)}{\left({\tilde{\mathrm{x}}}_{\mathrm{i},\max }-{\tilde{\mathrm{x}}}_{\mathrm{i},0}\right)}}.$$

(1)

where ${\tilde{\mathrm{x}}}_{\mathrm{i},0}$ and ${\tilde{\mathrm{x}}}_{\mathrm{i},\max }$ are the average and maximum values of the physical variable, respectively.

The objective functions were Ra, Rsk, and Rku roughness parameters, and the microhardness was ${\mathrm{Y}}_{\mathrm{R}\mathrm{a}}$, ${\mathrm{Y}}_{\mathrm{s}\mathrm{k}}$, ${\mathrm{Y}}_{\mathrm{k}\mathrm{u}}$, and ${\mathrm{Y}}_{\mathrm{H}\mathrm{V}}$, respectively. These three roughness parameters were chosen for the following reasons: (1) the Ra roughness parameter is representative of the roughness height (amplitude) parameters and is the most widely used roughness parameter in engineering practice and (2) the roughness shape parameters (skewness and kurtosis) play a significant role in the operational behavior of the diamond-burnished surface [10,23,42,46]. Ra and Rku are positive numbers, whereas skewness can be positive, negative, or equal to zero. The microhardness is associated with the strength and mechanical performance of components.

3.2.2. Experimental Design and Models of the Objective Functions

A planned experiment and a second-order optimal composition design were used (

Table 4. Experimental design and results.

№	${\mathbf{x}}_1$	${\mathbf{x}}_2$	${\mathbf{x}}_3$	Ra, μm		Rsk		Rku		HV
				Exper.	Model	Exper.	Model	Exper.	Model	Exper.	Model
1	–1	–1	–1	0.176	0.182	−0.149	−0.354	3.090	3.438	595	597.2
2	1	–1	–1	0.249	0.264	0.512	0.371	7.833	8.438	658	653.3
3	–1	1	–1	0.268	0.271	−0.073	−0.025	2.202	1.311	523	521.6
4	1	1	–1	0.328	0.315	0.723	0.900	2.747	2.832	590	594.7
5	–1	–1	1	0.187	0.199	−0.144	−0.321	2.973	2.888	554	549.3
6	1	–1	1	0.339	0.335	−0.024	−0.071	5.551	6.441	590	591.4
7	–1	1	1	0.279	0.263	0.012	0.153	2.384	1.779	488	492.7
8	1	1	1	0.367	0.361	0.399	0.604	2.203	1.854	554	551.8
9	–1	0	0	0.224	0.217	0.189	0.383	2.875	4.106	534	533.2
10	1	0	0	0.302	0.308	1.165	0.971	7.876	6.644	590	590.8
11	0	–1	0	0.171	0.141	−0.549	−0.477	12.951	11.191	585	590.8
12	0	1	0	0.168	0.198	0.598	0.026	6.075	7.834	539	533.2
13	0	0	–1	0.147	0.133	−0.204	−0.082	4.774	4.625	598	597
14	0	0	1	0.151	0.164	−0.091	−0.213	3.712	3.861	551	551.8
T				0.529		0.490		2.613		421

T—after fine turning (i.e., before DB).

).

The experimental results are shown in Table 4. Regression analyses were performed using QStatLab software, v. 6.1.1.3 [47]. Based on the chosen experimental design, the approximating polynomials are no higher than the second order:

$${\mathrm{Y}}^{(\mathrm{k})}\left(\left\{\mathrm{X}\right\}\right)={\mathrm{b}}_0^{(\mathrm{k})}+{\displaystyle \sum _{\mathrm{i}=1}^3{\mathrm{b}}_{\mathrm{i}}^{(\mathrm{k})}{\mathrm{x}}_{\mathrm{i}}+{\displaystyle \sum _{\mathrm{i}=1}^2{\displaystyle \sum _{\mathrm{j}=\mathrm{i}-1}^3{\mathrm{b}}_{\mathrm{i}\mathrm{j}}^{(\mathrm{k})}{\mathrm{x}}_{\mathrm{i}}{\mathrm{x}}_{\mathrm{j}}}}}+{\displaystyle \sum _{\mathrm{i}=1}^3{\mathrm{b}}_{\mathrm{i}\mathrm{i}}^{(\mathrm{k})}{\mathrm{x}}_{\mathrm{i}}^2}, \mathrm{k}=1, 2, 3$$

(2)

where $\left\{\mathrm{X}\right\}$ is the vector of the governing factors ${\mathrm{x}}_{\mathrm{i}}$, and $\mathrm{k}=1, 2, 3$ refers to the corresponding objective function: ${\mathrm{Y}}_{\mathrm{R}\mathrm{a}}$, ${\mathrm{Y}}_{\mathrm{s}\mathrm{k}}$, and ${\mathrm{Y}}_{\mathrm{k}\mathrm{u}}$, respectively.

The polynomial coefficients of the four models (Ra, Rsk, Rku, and HV) are shown in

Table 5. Regression coefficients.

${\mathbf{Y}}_{\mathbf{K}}$	${\mathbf{b}}_0^{(\mathbf{k})}$	${\mathbf{b}}_1^{(\mathbf{k})}$	${\mathbf{b}}_2^{(\mathbf{k})}$	${\mathbf{b}}_3^{(\mathbf{k})}$	${\mathbf{b}}_{11}^{(\mathbf{k})}$	${\mathbf{b}}_{22}^{(\mathbf{k})}$	${\mathbf{b}}_{33}^{(\mathbf{k})}$	${\mathbf{b}}_{12}^{(\mathbf{k})}$	${\mathbf{b}}_{23}^{(\mathbf{k})}$	${\mathbf{b}}_{13}^{(\mathbf{k})}$
${\mathrm{Y}}_{\mathrm{R}\mathrm{a}}$	0.15369	0.04510	0.0288	0.0155	0.10931	0.01581	−0.0047	−0.0096	−0.00637	0.013375
${\mathrm{Y}}_{\mathrm{s}\mathrm{k}}$	0.07350	0.2940	0.2513	−0.066	0.6035	−0.2990	−0.2210	0.05025	0.0365	−0.11875
${\mathrm{Y}}_{\mathrm{k}\mathrm{u}}$	7.75431	1.2686	−1.679	−0.382	−2.3788	1.75869	−3.5113	−0.8696	0.254625	−0.36138
${\mathrm{Y}}_{\mathrm{H}\mathrm{V}}$	564.75	28.8	−28.8	−22.7	−2.75	−2.75	9.75	4.25	4.75	−3.5

. The probability of a coefficient being insignificant is p = 0.05. However, all coefficients are included in the models in order to minimize the residual (Yexp − Ymodel). Table 4 shows the values predicted by the models at the experimental points. The experimental results are consistent with the model results.

Statistical analysis of the regression models was performed using QStatlab. The critical value of the Student statistic (T), Fisher statistic (F), residual standard deviation (ResStDev), determination coefficient (R-sq), and adjusted determination coefficient (Radj-sq) [48] for the four models are shown in

Table 6. Results of statistical analysis of regression models.

Model	T	F	ResStDev	R-sq	Radj-sq
${\mathrm{Y}}_{\mathrm{R}\mathrm{a}}$	2.77645	5.99878	0.028147	0.95693	0.86003
${\mathrm{Y}}_{\mathrm{S}\mathrm{k}}$	2.77645	5.99878	0.48789	0.83884	0.75122
${\mathrm{Y}}_{\mathrm{k}\mathrm{u}}$	2.77645	5.99878	1.7209	0.90289	0.7844
${\mathrm{Y}}_{\mathrm{H}\mathrm{V}}$	2.77645	5.99878	6.5536	0.99239	0.97526

. The results confirm the adequacy of the models.

3.3. Effects of DB-Governing Factors on the Selected SI Characteristics

After substituting (1) into (2), the dependencies of the objective functions on the physical variables (governing factors) are obtained. Figure 4, Figure 5 and Figure 6 show cross-sections of the hypersurfaces of the objective functions with characteristic planes. These cross-sections are used to visualize the dependence of each objective function on the corresponding governing factor.

3.3.1. Effects of Burnishing Force on Ra, Rsk, Rku, and HV

The dependence of Ra on the burnishing force for different combinations of the other two governing factors shows a pronounced minimum around ${\mathrm{F}}_{\mathrm{b}}=250 \mathrm{N}$ (Figure 4a). Lower values of the burnishing force are insufficient for the plastic deformation of the tips. However, values above 300 N deteriorate the roughness height. The skewness shows a clear minimum for the burnishing force range of 230–280 N for all combinations of feed rate and burnishing velocity (Figure 4b). The combination of minimal feed rate and ${\mathrm{F}}_{\mathrm{b}}<450 \mathrm{N}$ provides negative skewness, which is essential for increased wear resistance under boundary lubrication friction conditions [23,42]. As the burnishing force increases to approximately 340–370 N, kurtosis increases and then gradually decreases (Figure 4c). The microhardness increases with increasing burnishing force and reaches a maximum value when the burnishing force is maximal (Figure 4d). Microhardness is directly proportional to the equivalent plastic deformation in the SL, which increases as the burnishing force increases.

3.3.2. Effects of Feed Rate on Ra, Rsk, Rku, and HV

Ra increases with increasing feed rate for all combinations of burnishing force and burnishing velocity (Figure 5a). The minimum Ra is obtained when the feed rate is also minimized. When the feed rate increases, Ra increases in a non-linear law, consistent with previous work [49]. By increasing the feed rate to approximately 0.065 mm/rev, the skewness increases (as an algebraic number) and then slightly decreases (Figure 5b), whereas the kurtosis decreases and then gradually increases (Figure 5c). The minimum feed rate provides maximum kurtosis. Microhardness decreases monotonically with increasing feed rate (Figure 5d). The smaller the feed rate, the greater the cyclic loading coefficient [50], which is a measure of strain hardening.

3.3.3. Effects of Burnishing Velocity on Ra, Rsk, Rku, and HV

The influence of burnishing velocity on Ra is similar to that of the feed rate but less pronounced (Figure 6a). For the entire range of feed rate variation, Ra slightly increases with increasing burnishing force. However, the increase in Ra is not uniform for different values of burnishing force: with increasing burnishing force, the influence of burnishing velocity on Ra increases. The influence of burnishing velocity on skewness is also similar to that of the feed rate but less pronounced (Figure 6b). Skewness is minimal when the burnishing velocity is maximum. When the feed rate is minimal and the burnishing force is mid-range

(${\mathrm{F}}_{\mathrm{b}}=300 \mathrm{N}$), the skewness is negative for the entire range of burnishing velocity. By increasing the burnishing velocity to the middle of the range

($\mathrm{v}=85 \mathrm{m}/\mathrm{m}\mathrm{i}\mathrm{n}$), kurtosis increases and then decreases (Figure 6c). With increasing burnishing velocity, the microhardness decreases, but at a decreasing rate (Figure 6d). This is attributed to the softening effect [50] induced by the heat generated from friction and surface plastic deformation.

Note that these conclusions are valid for the given radius of the diamond insert ($\mathrm{r}=2 \mathrm{m}\mathrm{m}$) and the range of variation among the variables shown in Table 2.

3.4. Correlations Between Selected SI Characteristics

The objective function models ${\mathrm{Y}}_{\mathrm{i}}$ are hypersurfaces that depend on the three variables (governing factors), ${\mathrm{x}}_{\mathrm{i}}$(i = 1, 2, 3). Each pair of objective functions ${\mathrm{Y}}_{\mathrm{i}}\left(\left\{\mathrm{X}\right\}\right)$ and ${\mathrm{Y}}_{\mathrm{j}}\left(\left\{\mathrm{X}\right\}\right)$ defines the intersection of the two hypersurfaces in parametric form with the parameter vector $\left\{\mathrm{X}\right\}={\left[{\mathrm{x}}_1 {\mathrm{x}}_2 {\mathrm{x}}_3\right]}^{\mathrm{T}}$, where ${\mathrm{x}}_{\mathrm{i}}$ represents the governing factors. If any pair of the governing factors takes on constant values, then the pair of objective functions ${\mathrm{Y}}_{\mathrm{i}}$ and ${\mathrm{Y}}_{\mathrm{j}}$ will depend on only one parameter (governing factor), ${\mathrm{x}}_{\mathrm{k}}$. Consequently, ${\mathrm{Y}}_{\mathrm{i}}\left({\mathrm{x}}_{\mathrm{k}}\right)$ and ${\mathrm{Y}}_{\mathrm{j}}\left({\mathrm{x}}_{\mathrm{k}}\right)$ define the plane curve ${\mathrm{Y}}_{\mathrm{i}}={\mathrm{Y}}_{\mathrm{i}}\left({\mathrm{Y}}_{\mathrm{j}}\right)$, which elucidates the relationship between the two objective functions when two of the three governing factors are constant quantities. Thus, by assuming constant values at both ends and in the middle of each variable’s range from the selected pair of constant governing factors, dependencies between the two objective functions ${\mathrm{Y}}_{\mathrm{i}}$ and ${\mathrm{Y}}_{\mathrm{j}}$ can be represented and visualized on a single plane.

3.4.1. Correlation Between Ra and HV

The correlation between Ra and HV shows that there are areas of their cross-section in which Ra takes minimum values and HV takes values close to the maximum (Figure 7). The combinations of governing factors that define these areas are expected to improve the performance of the diamond-burnished component.

3.4.2. Correlation Between Rsk and HV

The correlation between skewness and HV is depicted in Figure 8. There are areas where both more negative skewness and significant positive skewness are combined with large HV values. The area in the first case is suitable for improving the tribological behavior under boundary lubrication conditions [42], and the second case (significant positive skewness and large microhardness values) is favorable for improving fatigue strength [10].

3.4.3. Correlation Between Rku and HV

A kurtosis greater than three combined with more negative skewness is suitable for a surface that requires increased wear resistance under boundary lubrication friction conditions [42]. Figure 9 shows that there are areas where high kurtosis is combined with HV greater than 600.

3.4.4. Correlation Between Rsk and Ra

Figure 10 shows the presence of areas where minimal (as an algebraic number) skewness and Ra values below 0.17 μm are combined, which favors beneficial tribological behavior under boundary lubrication friction conditions [22,23,42].

3.4.5. Correlation Between Rku and Ra

Figure 11 shows that there are areas where significant kurtosis is combined with Ra values below 0.17 μm. These areas improve the fatigue behavior [10].

3.4.6. Correlation Between Rsk and Rku

Figure 12 shows the presence of areas in which significant negative and positive skewness are combined with large kurtosis values (above 5). The former area favors tribological behavior under boundary friction conditions [42], and the latter area improves the fatigue strength [10].

4. Optimization Procedures

4.1. Justification of the Optimization Based on the Type of DB Process

DB can be implemented as smoothing, hardening, or mixed processes [24]. The main purpose of the smoothing DB process is to achieve a high-quality, smooth surface with a mirror-like finish. The other beneficial effects (increased microhardness and compressive residual stresses) are also present but are less pronounced than those observed in the hardening and mixed processes. Thus, the smoothing DB process requires one-objective optimization, based on minimizing the ${\mathrm{Y}}_{\mathrm{R}\mathrm{a}}$ function.

The hardening DB process maximizes the strain hardening effects, which are characterized by a high microhardness of the surface and subsurface layers, large residual compressive stresses in a depth of up to 0.8 mm, and a grain-refined microstructure within these layers. As a result, the rotating bending fatigue strength of the corresponding component increases significantly, but the roughness height parameters are larger than those obtained by smoothing DB. A correlation between the rotating bending fatigue limit and the microhardness of diamond-burnished AISI 304 steel was previously established [10]; as the microhardness increases, the fatigue limit increases at an increasing rate. This occurs because microhardness and residual macro-stresses have a common physical basis, namely the equivalent plastic deformation of the SL. Thus, with the increasing microhardness, the depth of the zone with residual compressive stresses increases (macroeffect) and the microstructure of the SLs is modified (microeffect), resulting in finer grains, favorable grain orientations, and increased fatigue strength. Therefore, the hardening DB process requires one-objective optimization, based on maximizing the ${\mathrm{Y}}_{\mathrm{H}\mathrm{V}}$ function.

The mixed DB process achieves a compromise between roughness on the one hand and microhardness and fatigue strength on the other hand. Hence, the mixed DB process requires multi-objective optimization. In the present study, a new cost-effective optimization approach is developed based on the DB process–SI–operating behavior correlations. Using these correlations, in addition to the correlations between appropriately selected SI characteristics, the proposed optimization approach requires the control of only three roughness parameters, namely the arithmetic average roughness Ra, skewness Rsk, and kurtosis Rku, which, in turn, depend on the DB process governing factors.

4.2. One-Objective Optimizations

4.2.1. Smoothing DB Process

To find the minimum Ra value and the values of the governing factors that provide it, the minimum of the ${\mathrm{Y}}_{\mathrm{R}\mathrm{a}}$ objective function was determined using QstatLab and non-dominated sorting genetic algorithm II (NSGA II) [40,48]. The ${\mathrm{x}}_{\mathrm{i}}\to {\tilde{\mathrm{x}}}_{\mathrm{i}}$ transformation was performed according to formula (2).

Table 7. Values of the governing factors ensuring minimum roughness Ra.

Optimal Values of the Governing Factors						Min Ra, μm
Codded (Dimensionless)			Natural (Physical)
${\mathrm{x}}_1^{*}$	${\mathrm{x}}_2^{*}$	${\mathrm{x}}_3^{*}$	${\mathrm{F}}_{\mathrm{b}}^{*}, \mathrm{N}$	${\mathrm{f}}^{*}, \mathrm{m}\mathrm{m}/\mathrm{r}\mathrm{e}\mathrm{v}$	${\mathrm{v}}^{*}, \mathrm{m}/\min$
−0.1892	−1	−1	262	0.02	50	0.1102

shows the results.

4.2.2. Hardening DB Process

To find the maximum microhardness value and the values of governing factors that provide it, the maximum of the ${\mathrm{Y}}_{\mathrm{H}\mathrm{V}}$ objective function was determined using QstatLab and NSGA II. The results were obtained using the ${\mathrm{x}}_{\mathrm{i}}\to {\tilde{\mathrm{x}}}_{\mathrm{i}}$ transformation (formula (2)), as shown in

Table 8. Values of the governing factors ensuring maximum surface microhardness.

Optimal Values of the Governing Factors						Max HV
Codded (Dimensionless)			Natural (Physical)
${\mathrm{x}}_1^{*}$	${\mathrm{x}}_2^{*}$	${\mathrm{x}}_3^{*}$	${\mathrm{F}}_{\mathrm{b}}^{*}, \mathrm{N}$	${\mathrm{f}}^{*}, \mathrm{m}\mathrm{m}/\mathrm{r}\mathrm{e}\mathrm{v}$	${\mathrm{v}}^{*}, \mathrm{m}/\min$
1	−1	−1	500	0.02	50	653

. The maximum value of the surface microhardness corresponds to experimental point No. 2 of the experimental plan (see Table 4).

4.3. Multi-Objective Optimizations

4.3.1. Maximizing Wear Resistance Under the Boundary Lubrication Friction Condition

Sedlacek et al. [42] investigated the correlation between the roughness shape parameters (i.e., skewness and kurtosis) and the tribological behavior of contact surfaces, showing that the wear resistance was maximized for more negative skewness and kurtosis greater than three, under boundary lubrication friction conditions. For diamond-burnished surfaces, this observation was confirmed by Duncheva et al. [22,23]. In addition, an increased surface microhardness promotes high wear resistance [47]. From the correlations between the SI characteristics (Figure 7, Figure 8 and Figure 9), there are regions of the factor space in which the microhardness is close to the maximum, and in the same regions, the Ra is minimal, the skewness is negative, and the kurtosis is significantly greater than three. Meanwhile, Figure 4d, Figure 5d, and Figure 6d show that microhardness takes high values under a high burnishing force with a minimum feed rate and burnishing velocity.

To find the values of the governing factors that maximize the wear resistance under the boundary lubrication friction condition of the diamond-burnished AISI 304 steel, the following multi-objective optimization task is defined: The vector of the objective functions is $\left\{\mathrm{Y}\left(\left\{\mathrm{X}\right\}\right)\right\}={\left[{\mathrm{Y}}_{\mathrm{R}\mathrm{a}} {\mathrm{Y}}_{\mathrm{R}\mathrm{s}\mathrm{k}} {\mathrm{Y}}_{\mathrm{R}\mathrm{k}\mathrm{u}}\right]}^{\mathrm{T}}$, where $\left\{\mathrm{X}\right\}={\left[{\mathrm{x}}_1 {\mathrm{x}}_2 {\mathrm{x}}_3\right]}^{\mathrm{T}}$ is the vector of the governing factors. The numerical vector ${\left\{\mathrm{X}\right\}}^{*}$ must be determined, for which ${\mathrm{Y}}_{\mathrm{R}\mathrm{a}}\left({\left\{\mathrm{X}\right\}}^{*}\right)\to \min$, ${\mathrm{Y}}_{\mathrm{R}\mathrm{s}\mathrm{k}}\left({\left\{\mathrm{X}\right\}}^{*}\right)\to \min$, and ${\mathrm{Y}}_{\mathrm{R}\mathrm{k}\mathrm{u}}\left({\left\{\mathrm{X}\right\}}^{*}\right)\to \max$, where ${\left\{\mathrm{X}\right\}}^{*}={\left[{\mathrm{x}}_1^{*} {\mathrm{x}}_2^{*} {\mathrm{x}}_3^{*}\right]}^{\mathrm{T}}$ and ${\mathrm{x}}_{\mathrm{i}}^{*}, \mathrm{i}=1, 2, 3$ represent the optimal compromise values of the governing factors. The following functional constraints are imposed: ${\mathrm{Y}}_{\mathrm{R}\mathrm{s}\mathrm{k}}<0$, ${\mathrm{Y}}_{\mathrm{R}\mathrm{k}\mathrm{u}}>3$, ${\mathrm{Y}}_{\mathrm{R}\mathrm{a}}<0.3 \mathrm{\mu }\mathrm{m}$. The task is solved by searching for the Pareto optimal solution [24] using QstatLab and NSGA II. From the resulting Pareto front (Figure 13a), the best five compromise solutions are selected using the results obtained in Section 3.3 (

Table 9. Selected optimal solutions from the found Pareto front and objective function values.

№	${\mathbf{x}}_1^{*}$	${\mathbf{x}}_2^{*}$	${\mathbf{x}}_3^{*}$	${\mathbf{Y}}_{\mathbf{R}\mathbf{a}}^{*}, \mathbf{\mu }\mathbf{m}$	${\mathbf{Y}}_{\mathbf{R}\mathbf{s}\mathbf{k}}^{*}$	${\mathbf{Y}}_{\mathbf{R}\mathbf{k}\mathbf{u}}^{*}$	${\mathbf{Y}}_{\mathbf{H}\mathbf{V}}^{*}$
	Proposed Approach
1	–0.1911	–1.0000	–1.0000	0.1102	–0.6428	7.7529	622.54
2	–0.1179	–0.9982	–0.9740	0.1116	–0.6195	8.1446	623.40
3	–0.1517	–1.0000	–1.0000	0.1104	–0.6367	7.8834	623.68
4	–0.1647	–1.0000	–1.0000	0.1103	–0.6389	7.8411	623.30
5	–0.1188	–1.0000	–1.0000	0.1108	−0.6301	7.9868	624.63
	Conventional Approach
1	–0.0045	–1.0000	–1.0000	0.1140	−0.5972	8.3061	627.87
2	–0.1756	–1.0000	–0.9999	0.1103	–0.6406	7.8058	622.98
3	–0.1031	–0.9999	–1.0000	0.1110	–0.6265	8.0337	625.07
4	–0.0737	–0.9942	–0.9993	0.1117	–0.6141	8.0935	625.72
5	–0.1126	–1.0000	–0.9998	0.1109	–0.6287	8.0070	624.80

).

To demonstrate the effectiveness of the proposed optimization approach, a re-optimization is performed using a conventional approach where the microhardness function is included in the vector of objective functions $\left\{\mathrm{Y}\left(\left\{\mathrm{X}\right\}\right)\right\}={\left[{\mathrm{Y}}_{\mathrm{R}\mathrm{a}} {\mathrm{Y}}_{\mathrm{R}\mathrm{s}\mathrm{k}} {\mathrm{Y}}_{\mathrm{R}\mathrm{k}\mathrm{u}} {\mathrm{Y}}_{\mathrm{H}\mathrm{V}}\right]}^{\mathrm{T}}$, and the desired numerical vector ${\left\{\mathrm{X}\right\}}^{*}$ must additionally satisfy the condition ${\mathrm{Y}}_{\mathrm{H}\mathrm{V}}\left({\left\{\mathrm{X}\right\}}^{*}\right)\to \max$ while the functional constraints remain the same (${\mathrm{Y}}_{\mathrm{R}\mathrm{s}\mathrm{k}}<0$, ${\mathrm{Y}}_{\mathrm{R}\mathrm{k}\mathrm{u}}>3$, ${\mathrm{Y}}_{\mathrm{R}\mathrm{a}}<0.3 \mathrm{\mu }\mathrm{m}$). The resulting Pareto front is shown in Figure 13b and is similar to the one obtained using the proposed approach (Figure 13a). The five best compromise solutions selected from the resulting Pareto front (Figure 13b) are shown in Table 8. A visual inspection of Table 8 shows that the two groups of selected solutions are practically equivalent, which confirms the effectiveness of the proposed optimization approach. Using the inverse transformation ${\mathrm{x}}_{\mathrm{i}}\to {\tilde{\mathrm{x}}}_{\mathrm{i}}$ shown in formula (2) and choosing the third solution from Table 8, which was obtained through the proposed optimization approach, the maximum wear resistance is achieved under boundary lubrication friction conditions for the following values of the governing factors: ${\mathrm{F}}_{\mathrm{b}}^{*}=270 \mathrm{N}$, ${\mathrm{f}}^{*}=0.02 \mathrm{m}\mathrm{m}/\mathrm{r}\mathrm{e}\mathrm{v}$, and ${\mathrm{v}}^{*}=50 \mathrm{m}/\min$.

4.3.2. Maximizing the Effects of the Mixed DB Process

It is known that minimal Ra values are favorable for high fatigue strength because they reduce the surface stress concentrators [15]. Conversely, a more negative skewness inversely affects fatigue strength owing to the deep valleys, which are natural stress concentrators. A larger positive skewness leads to a higher rotating bending fatigue limit of diamond-burnished 304 steel specimens [10]. According to Zabala et al. [46], kurtosis greater than three worsens the fatigue behavior. This statement has a solid physical basis given the sharp peaks and deep valleys of the roughness profile. However, the surface texture is not an independent factor when formed by DB because the severe surface plastic deformation (characteristic of DB) introduces beneficial effects such as high surface microhardness, residual compressive stresses, and grain refinement. For example, it was experimentally shown that increasing kurtosis increases the rotating bending fatigue limit of diamond-burnished 304 steel specimens [10]. With increasing burnishing force and number of passes, kurtosis increases, but at the same time, the microhardness and depth of the zone with residual compressive stresses increase. The latter two positive effects neutralize the isolated negative effect of kurtosis and increase the fatigue strength. Thus, a high kurtosis value for a diamond-burnished surface is an indicator of significant residual compressive stresses and high surface microhardness.

To find the values of the control factors that maximize the effect of the mixed DB process for AISI 304 steel components, the following multi-objective optimization task is defined: The vector of the objective functions is $\left\{\mathrm{Y}\left(\left\{\mathrm{X}\right\}\right)\right\}={\left[{\mathrm{Y}}_{\mathrm{R}\mathrm{a}} {\mathrm{Y}}_{\mathrm{R}\mathrm{s}\mathrm{k}} {\mathrm{Y}}_{\mathrm{R}\mathrm{k}\mathrm{u}}\right]}^{\mathrm{T}}$. The compromise values ${\mathrm{x}}_{\mathrm{i}}^{*}, \mathrm{i}=1, 2, 3$ of the controlling factors must be determined, for which ${\mathrm{Y}}_{\mathrm{R}\mathrm{a}}\left({\left\{\mathrm{X}\right\}}^{*}\right)\to \min$, ${\mathrm{Y}}_{\mathrm{R}\mathrm{s}\mathrm{k}}\left({\left\{\mathrm{X}\right\}}^{*}\right)\to \max$, and ${\mathrm{Y}}_{\mathrm{R}\mathrm{k}\mathrm{u}}\left({\left\{\mathrm{X}\right\}}^{*}\right)\to \max$. The following functional constraints are imposed: ${\mathrm{Y}}_{\mathrm{R}\mathrm{s}\mathrm{k}}>0$, ${\mathrm{Y}}_{\mathrm{R}\mathrm{k}\mathrm{u}}>3$, and ${\mathrm{Y}}_{\mathrm{R}\mathrm{a}}<0.3 \mathrm{\mu }\mathrm{m}$, and the Pareto optimal solution approach, QstatLab, and NSGA II were used. The best five compromise solutions (

Table 10. Selected optimal solutions from the found Pareto front and objective function values.

№	${\mathbf{x}}_1^{*}$	${\mathbf{x}}_2^{*}$	${\mathbf{x}}_3^{*}$	${\mathbf{Y}}_{\mathbf{R}\mathbf{a}}^{*}, \mathbf{\mu }\mathbf{m}$	${\mathbf{Y}}_{\mathbf{R}\mathbf{s}\mathbf{k}}^{*}$	${\mathbf{Y}}_{\mathbf{R}\mathbf{k}\mathbf{u}}^{*}$	${\mathbf{Y}}_{\mathbf{H}\mathbf{V}}^{*}$
	Proposed Approach
1	0.8249	–0.2796	–0.3143	0.2513	0.6543	7.8788	602.91
2	0.5687	0.1006	–0.7315	0.1982	0.4375	6.0379	600.48
3	0.6078	–0.0111	–0.6218	0.2047	0.4725	6.6896	600.77
4	0.7747	–0.2076	–0.6639	0.2304	0.6026	6.8007	612.41
5	0.5699	–0.0317	–0.7807	0.1949	0.4142	5.9506	604.53
	Conventional Approach
1	0.7226	–0.1420	–0.7427	0.2186	0.5486	6.3599	612.34
2	0.8898	–0.1475	–0.5766	0.2598	0.7912	6.6595	610.36
3	0.7619	–0.6052	–0.5391	0.2270	0.3950	8.8183	607.61
4	0.7939	–0.4685	–0.5904	0.2301	0.5127	7.9997	606.94
5	0.6493	–0.4936	–0.5577	0.2051	0.3268	8.4330	612.74

) are selected from the Pareto front (Figure 14a).

To demonstrate the effectiveness of the proposed optimization approach, a re-optimization is performed using a conventional approach where the microhardness function is included in the vector of objective functions $\left\{\mathrm{Y}\left(\left\{\mathrm{X}\right\}\right)\right\}={\left[{\mathrm{Y}}_{\mathrm{R}\mathrm{a}} {\mathrm{Y}}_{\mathrm{R}\mathrm{s}\mathrm{k}} {\mathrm{Y}}_{\mathrm{R}\mathrm{k}\mathrm{u}} {\mathrm{Y}}_{\mathrm{H}\mathrm{V}}\right]}^{\mathrm{T}}$, and the numerical vector ${\left\{\mathrm{X}\right\}}^{*}$ must additionally satisfy the condition ${\mathrm{Y}}_{\mathrm{H}\mathrm{V}}\left({\left\{\mathrm{X}\right\}}^{*}\right)\to \max$. The functional constraints remain the same (${\mathrm{Y}}_{\mathrm{R}\mathrm{s}\mathrm{k}}>0$, ${\mathrm{Y}}_{\mathrm{R}\mathrm{k}\mathrm{u}}>3$, ${\mathrm{Y}}_{\mathrm{R}\mathrm{a}}<0.3 \mathrm{\mu }\mathrm{m}$). The Pareto front is shown in Figure 14b and is similar to the one obtained using the proposed approach (Figure 14a). The five best compromise solutions selected from the resulting Pareto front (Figure 14b) are shown in Table 9. A visual inspection of Table 9 shows that the two groups of selected solutions are practically equivalent, indicating the effectiveness of the proposed optimization approach. Using the inverse transformation ${\mathrm{x}}_{\mathrm{i}}\to {\tilde{\mathrm{x}}}_{\mathrm{i}}$ defined in formula (2) and choosing the fourth solution from Table 9, obtained through the proposed optimization approach, the maximum effect of the mixed DB process for 304 steel is achieved for the following values of the governing factors: ${\mathrm{F}}_{\mathrm{b}}^{*}=455 \mathrm{N}$, ${\mathrm{f}}^{*}=0.044 \mathrm{m}\mathrm{m}/\mathrm{r}\mathrm{e}\mathrm{v}$, and ${\mathrm{v}}^{*}=62 \mathrm{m}/\min$.

5. Conclusions

This study was designed to find explicit dependencies between the main parameters of the DB process for AISI 304 stainless steel and three functionally relevant roughness parameters, as well as explicit correlations between selected SI characteristics, while considering results from previous studies to develop cost-effective optimization procedures for the DB process, depending on the intended application of the diamond-burnished surface. The major findings are summarized as follows:

• A new multi-objective cost-effective optimization approach based on the DB process–SI–operating behavior correlations was justified and developed. Using these correlations, in addition to the correlations between appropriately selected SI characteristics, the proposed optimization procedures require the control of only three easy-to-measure roughness parameters, specifically the arithmetic average roughness Ra, skewness Rsk, and kurtosis Rku, which depend on the governing factors of the DB process. Thus, the need to conduct time-consuming and expensive fatigue and tribological tests, which typically precede the multi-objective optimization of DB, is eliminated.
• Explicit correlations were established between the basic governing factors of DB for AISI 304 steel and (1) the roughness parameters, as well as (2) the selected easy-to-measure SI characteristics.
• When increased wear resistance is required for diamond-burnished surfaces under boundary lubrication friction conditions, the compromise values of the single-pass DB governing factors are ${\mathrm{F}}_{\mathrm{b}}^{*}=270 \mathrm{N}$, ${\mathrm{f}}^{*}=0.02 \mathrm{m}\mathrm{m}/\mathrm{r}\mathrm{e}\mathrm{v}$, and ${\mathrm{v}}^{*}=50 \mathrm{m}/\min$, using a spherical-ended polycrystalline diamond insert with a radius of 2 mm.
• To maximize the effect of the mixed single-pass DB process, the compromise values of the governing factors are ${\mathrm{F}}_{\mathrm{b}}^{*}=455 \mathrm{N}$, ${\mathrm{f}}^{*}=0.044 \mathrm{m}\mathrm{m}/\mathrm{r}\mathrm{e}\mathrm{v}$, and ${\mathrm{v}}^{*}=62 \mathrm{m}/\min$, using a diamond insert with a radius of 2 mm.