An Investigation of Heat Treatment Residual Stress of Type I, II, III for 8Cr4Mo4V Steel Bearing Ring Using FEA-CPFEM-GPA Method
Abstract
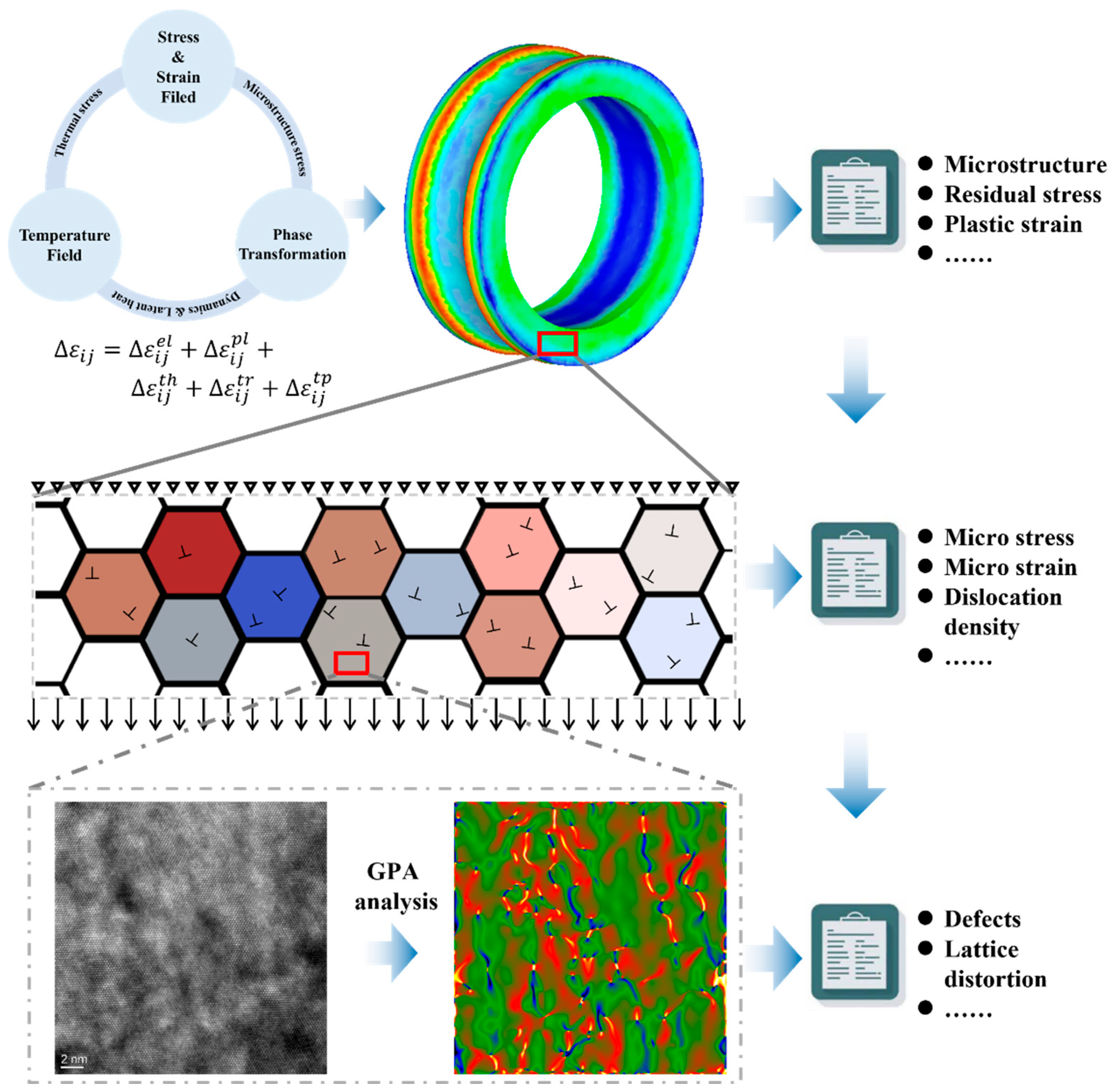
1. Introduction
2. Materials and Methods
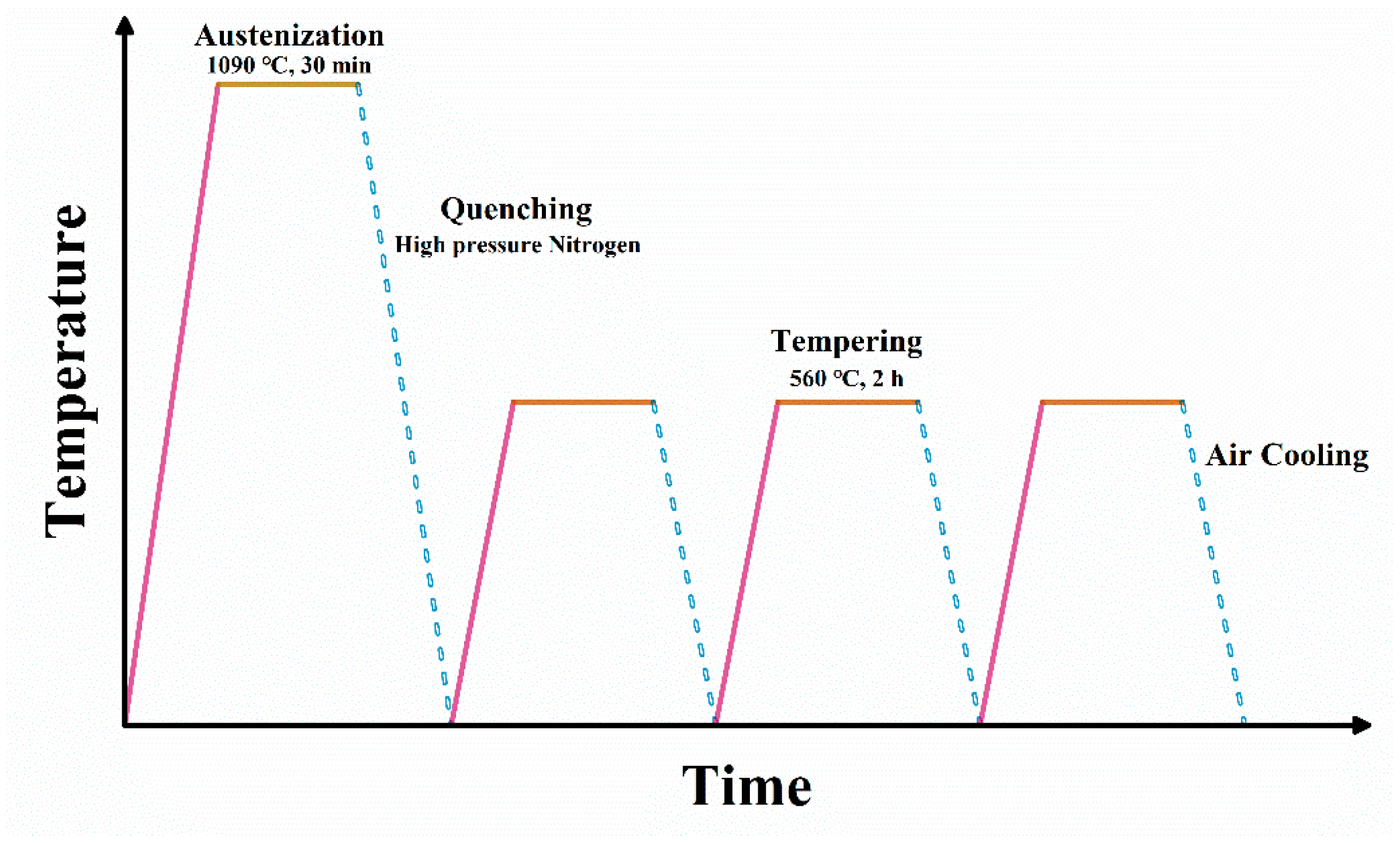
2.1. Materials and Heat Treatment
2.2. Numerical Simulation Method
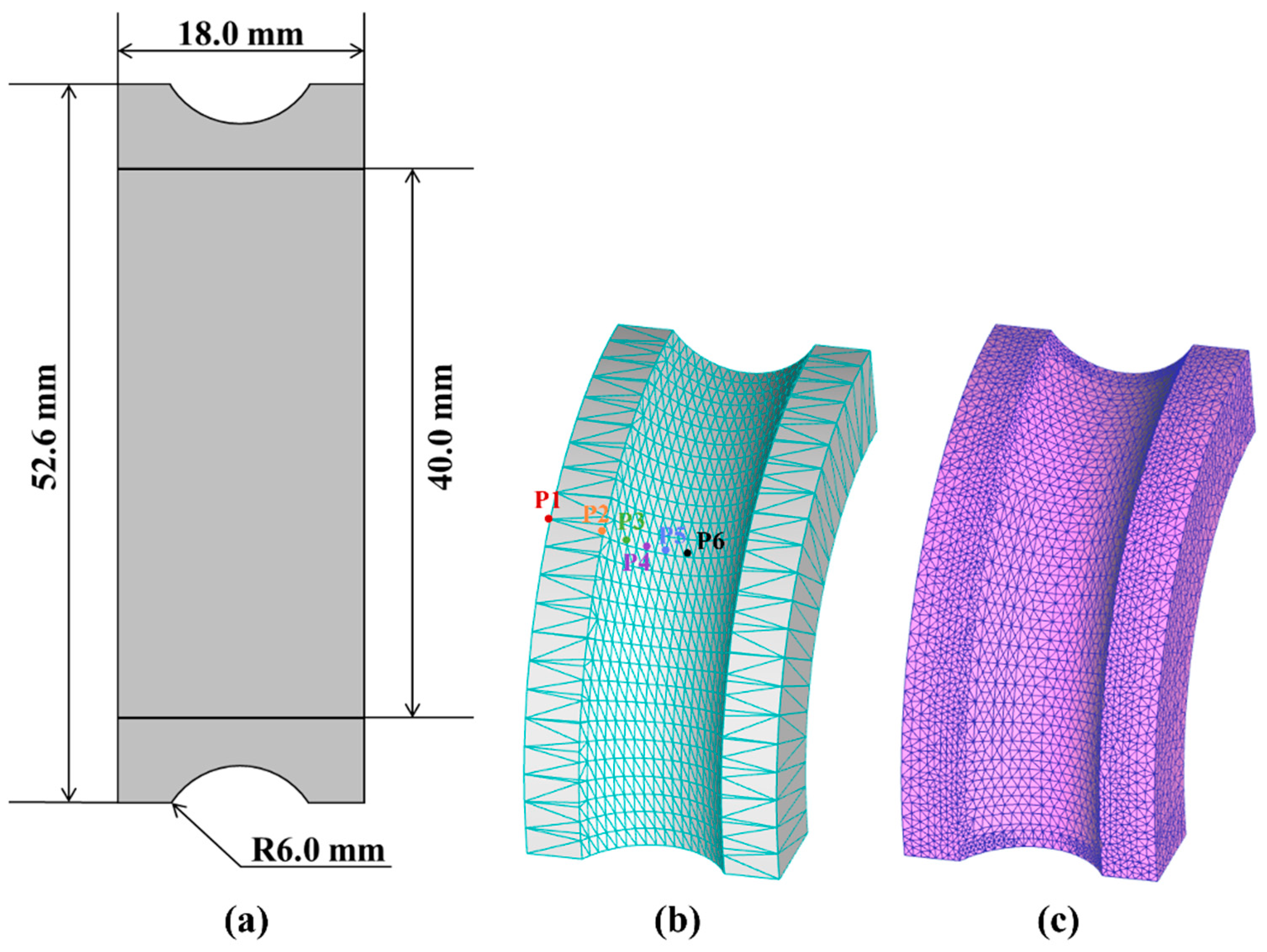
2.2.1. Finite Element Analysis
2.2.2. Crystal Plasticity Finite Element Analysis
2.3. Microstructure Characterization
2.4. Geometric Phase Analysis
3. Results and Discussion
3.1. Numerical Simulation Results Analysis
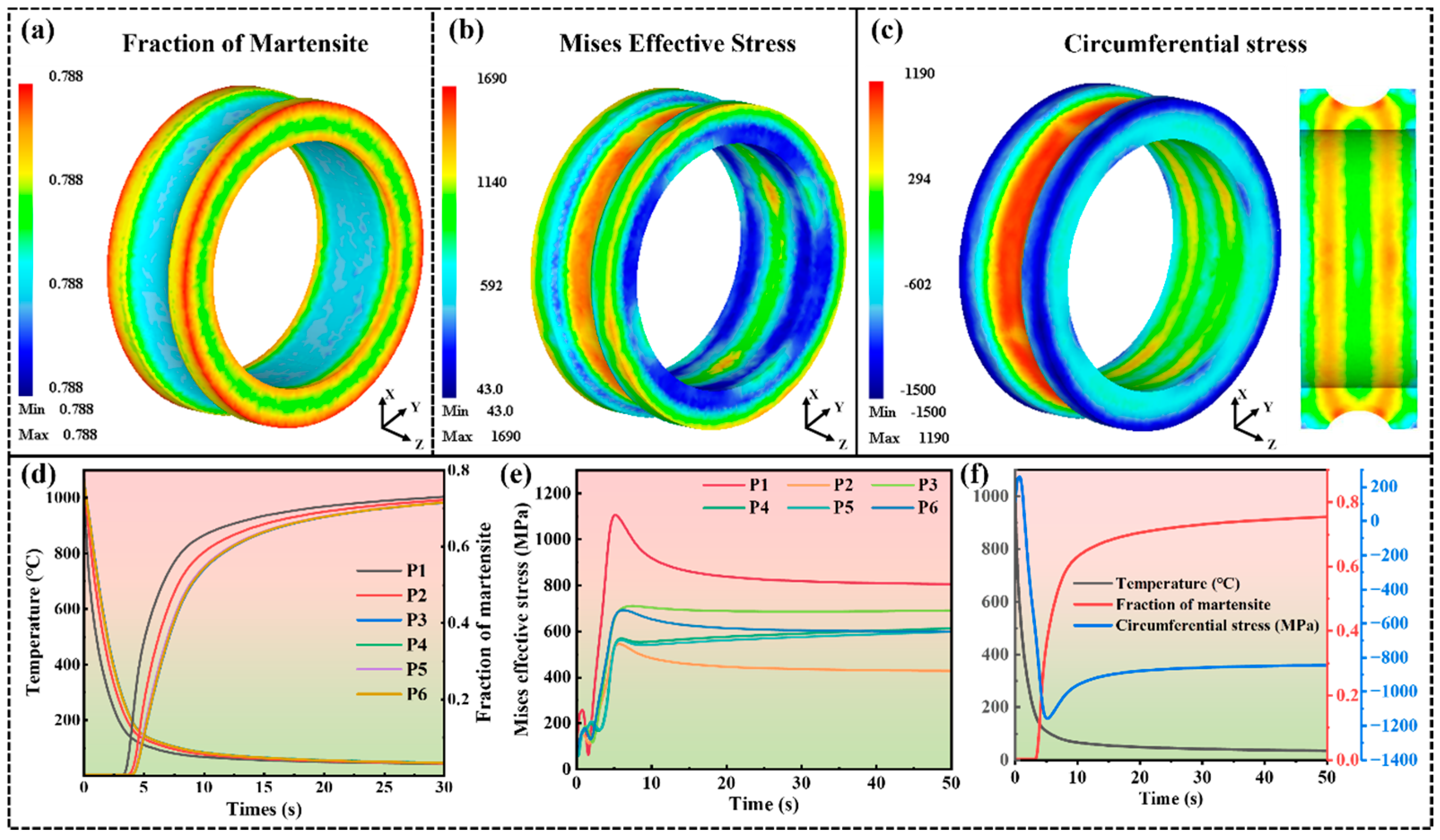
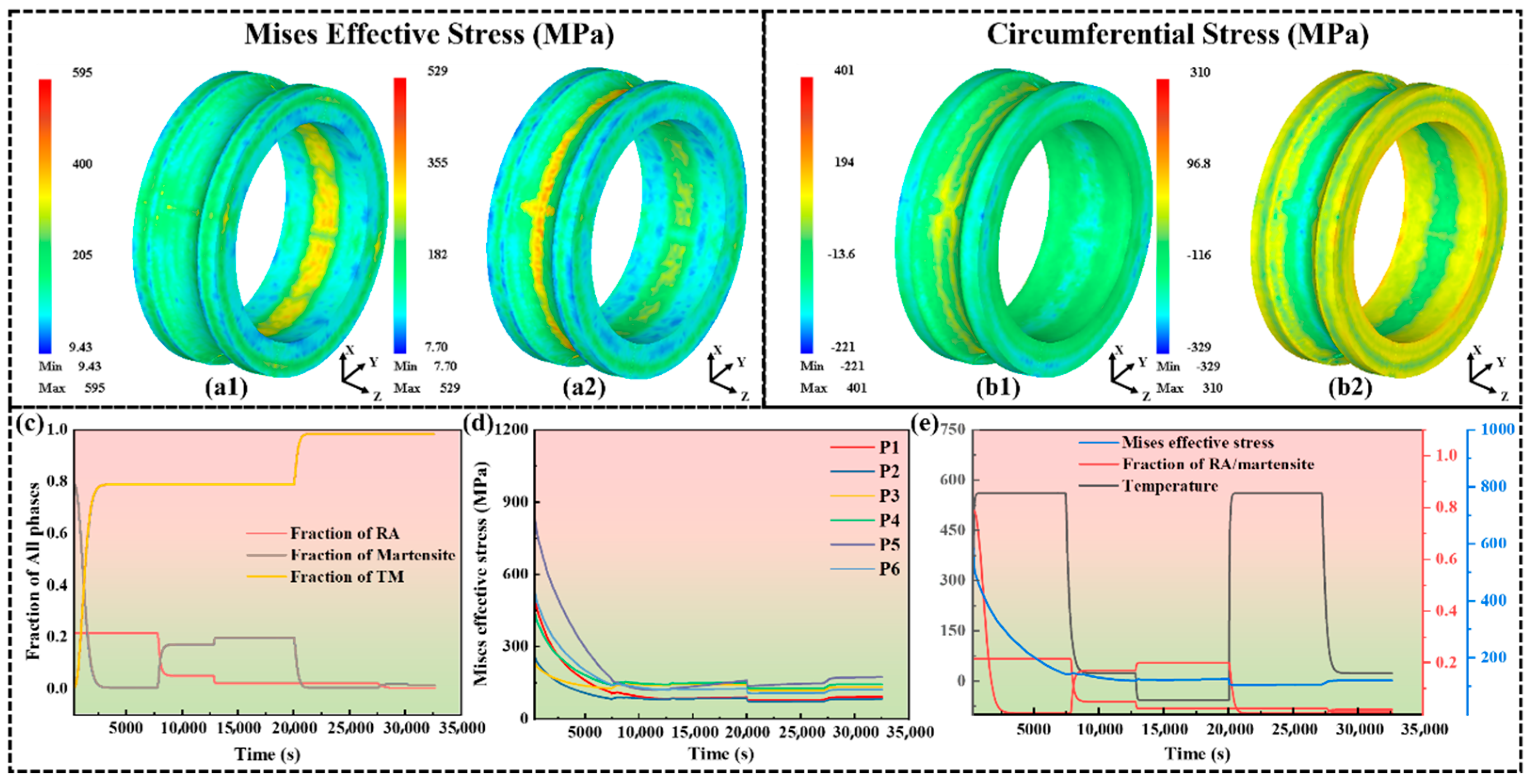
3.1.1. Macroscopic Stress Evolution During Quenching
3.1.2. Macroscopic Stress Evolution During Tempering
3.2. CPFEM Analysis Type II Residual Stress
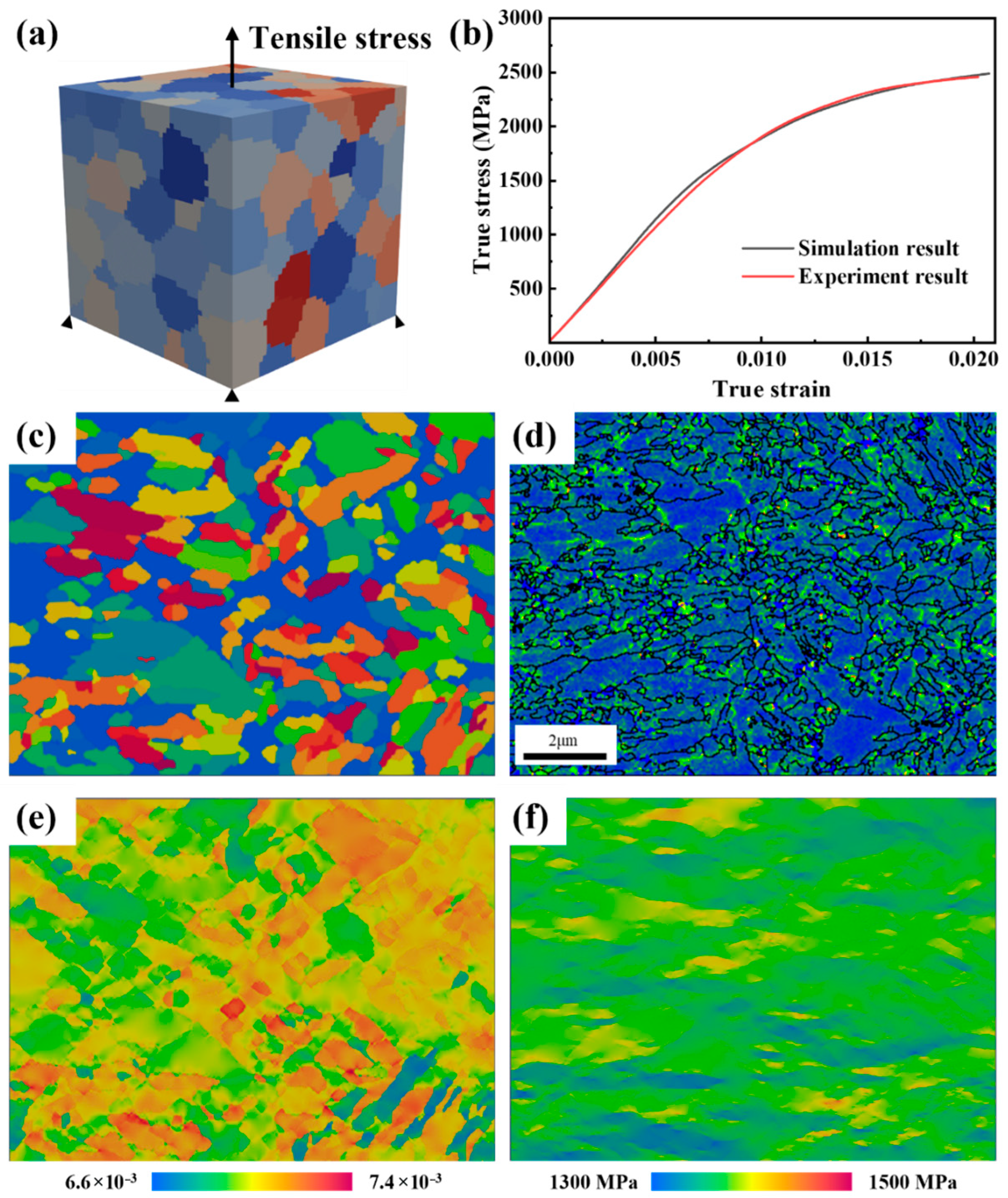
3.2.1. Crystal Plastic Constitutive Parameters
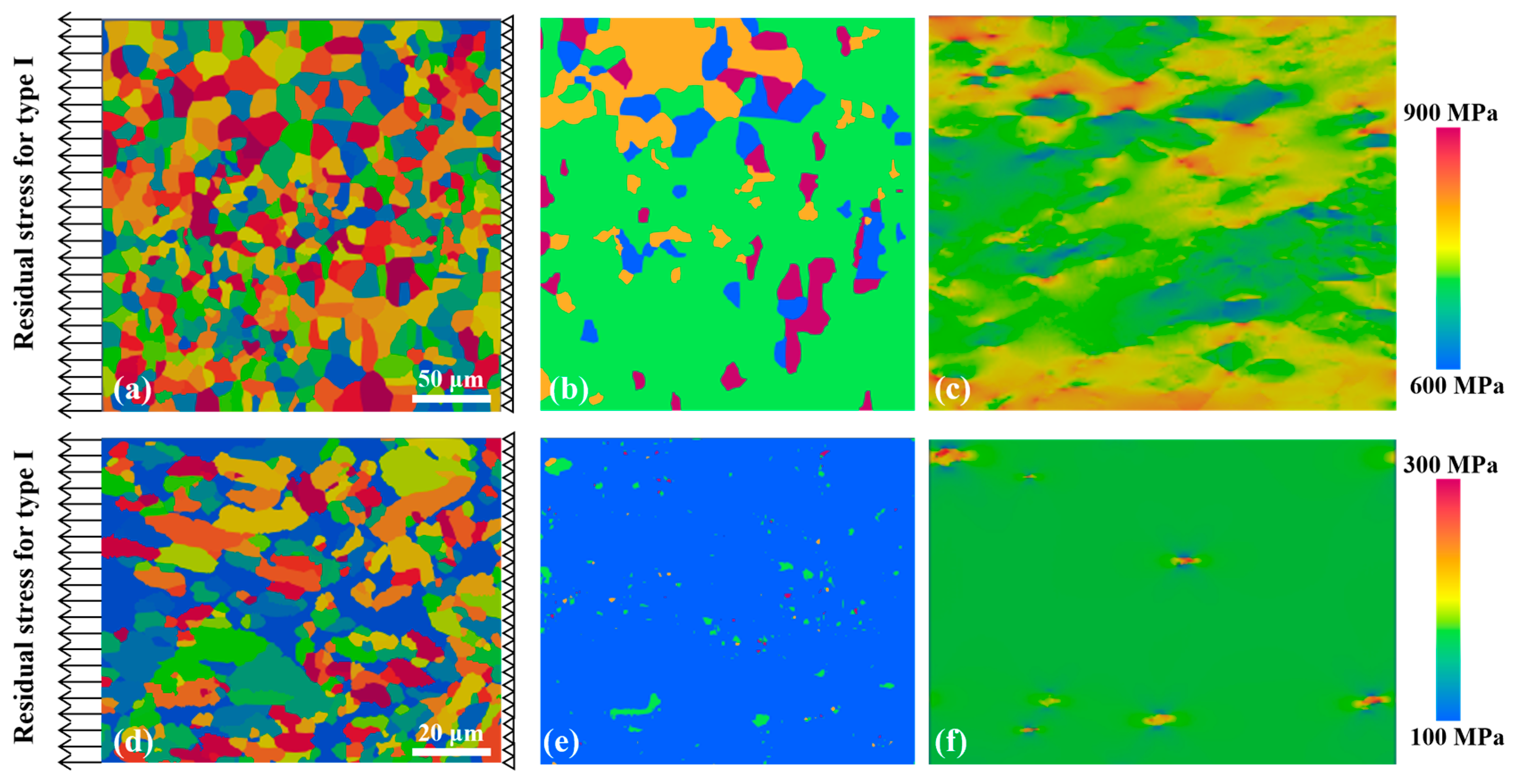
3.2.2. Analysis Residual Stress of Type II After Heat Treatment
3.3. Geometry Phase Analysis Type III Residual Stress
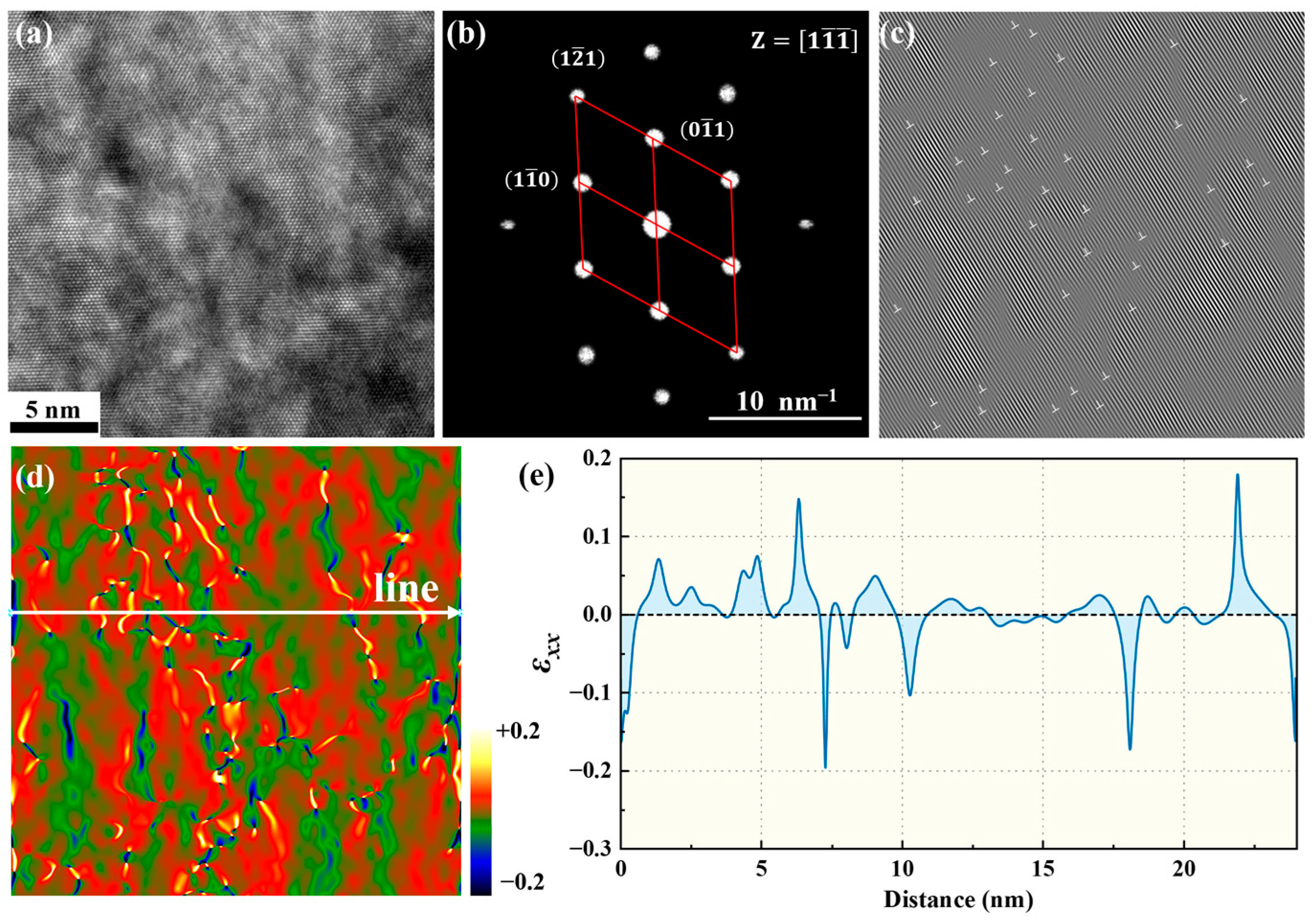
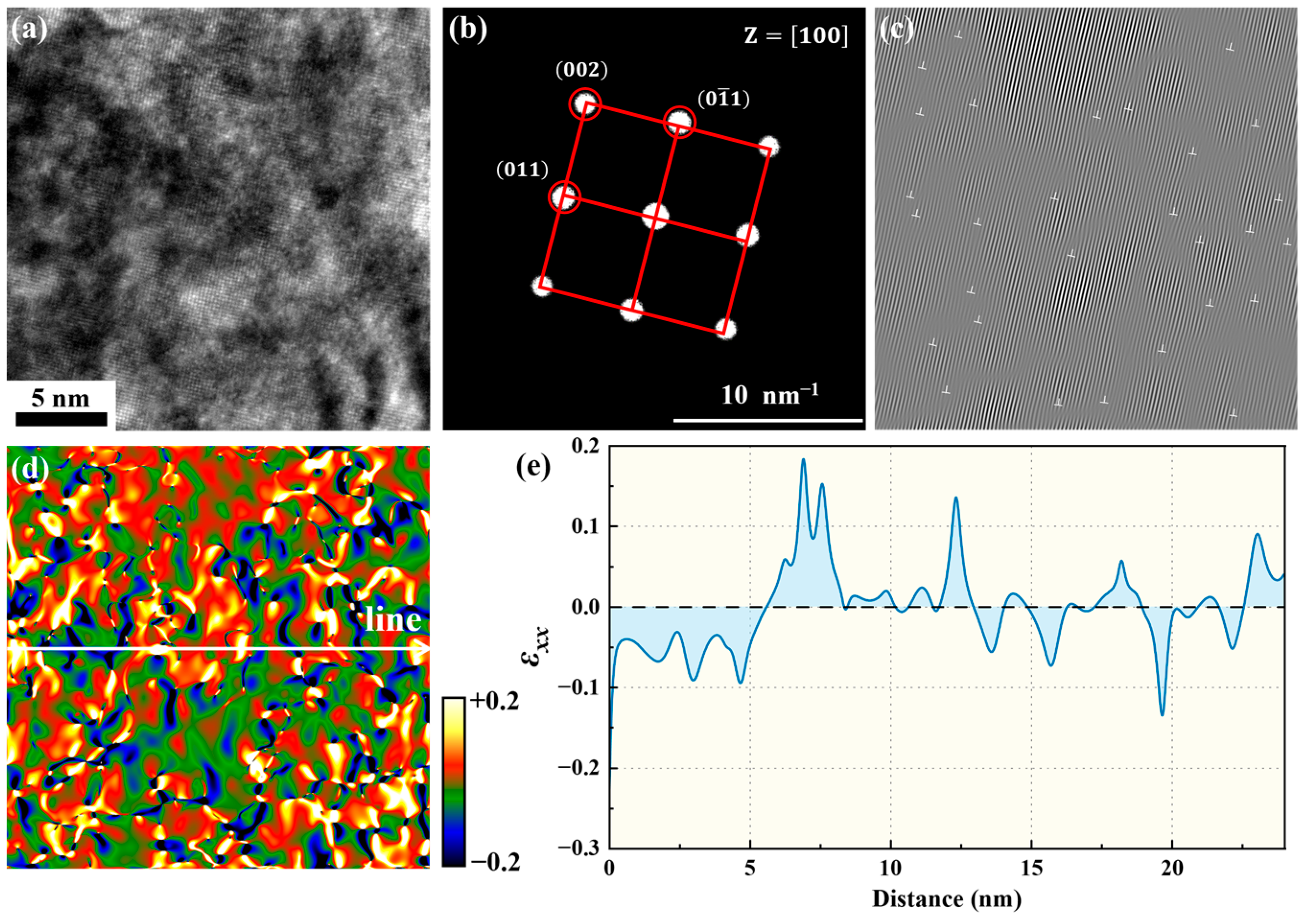
3.3.1. Geometry Phase Analysis of Quenched Martensite
3.3.2. Geometry Phase Analysis of Tempered Martensite
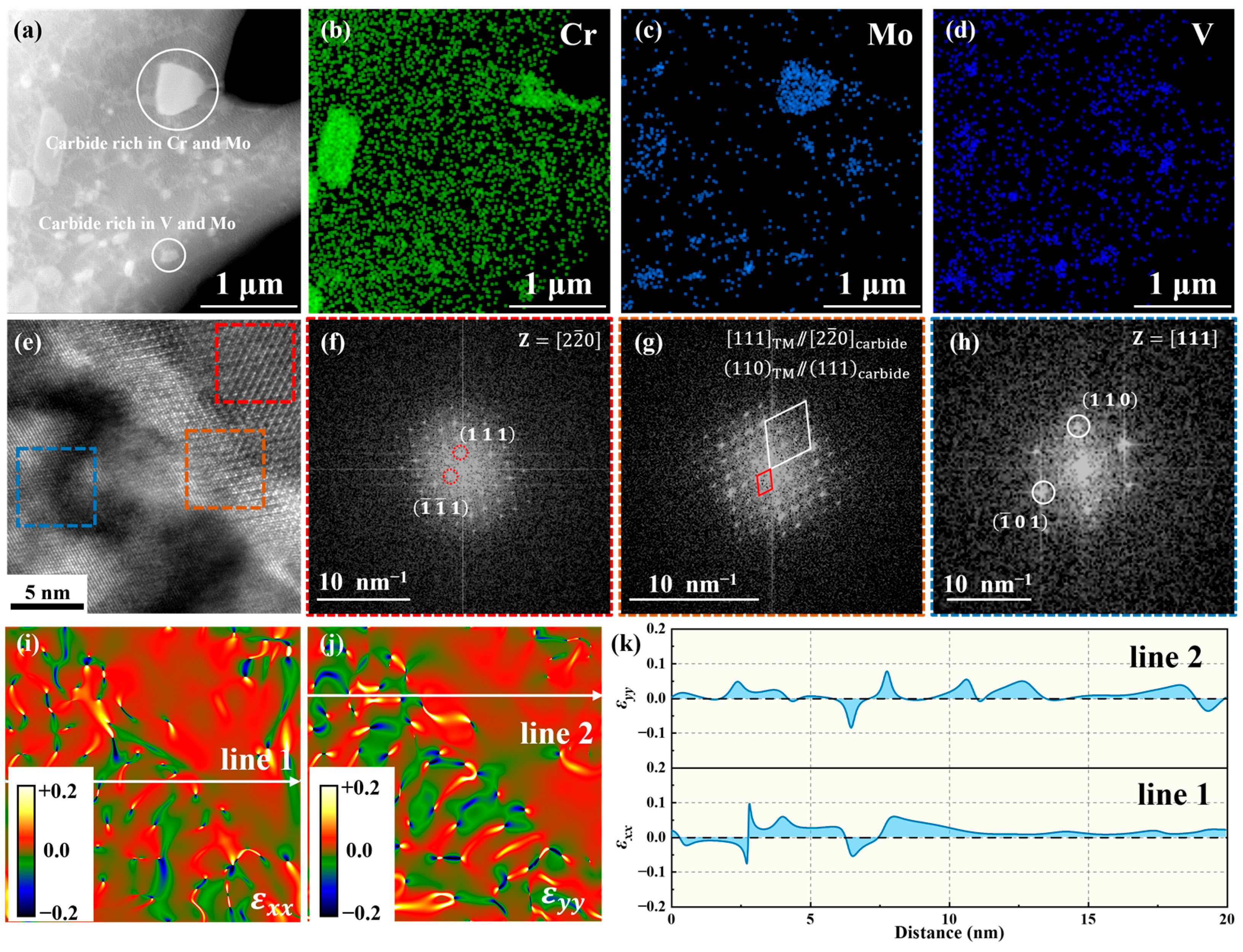
3.3.3. Geometry Phase Analysis of Phase Interface
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gloeckner, P.; Rodway, C. The Evolution of Reliability and Efficiency of Aerospace Bearing Systems. Engineering 2017, 9, 962–991. [Google Scholar] [CrossRef]
- Rejith, R.; Kesavan, D.; Chakravarthy, P.; Narayana Murty, S.V.S. Bearings for Aerospace Applications. Tribol. Int. 2023, 181, 108312. [Google Scholar] [CrossRef]
- Zhang, B.; Liu, H.; Zhang, M.; Dai, C.; Xie, Z.; Ma, X.; Sun, Y. New Layering Strategy and the Gradient Microstructure Distribution of Surface Metamorphic Layer for 8Cr4Mo4V Steel by Grinding. Arch. Civ. Mech. Eng. 2024, 24, 42. [Google Scholar] [CrossRef]
- Li, Z.; Li, K.; Qian, C.; Wang, D.; Ji, W.; Wu, Y.; Cai, Z.; Liu, Q. Effect of Pulsed Magnetic Field on Retained Austenite of Quenched 8Cr4Mo4V Steel under Cryogenic Condition. J. Mater. Res. Technol. 2023, 23, 5004–5015. [Google Scholar] [CrossRef]
- Wang, F.; Qian, D.; Hua, L.; Mao, H.; Xie, L.; Song, X.; Dong, Z. Effect of High Magnetic Field on the Microstructure Evolution and Mechanical Properties of M50 Bearing Steel during Tempering. Mater. Sci. Eng. A 2020, 771, 138623. [Google Scholar] [CrossRef]
- Jiang, H.; Song, Y.; Wu, Y.; Shan, D.; Zong, Y. Macrostructure, Microstructure and Mechanical Properties Evolution during 8Cr4Mo4V Steel Roller Bearing Inner Ring Forging Process. Mater. Sci. Eng. A 2020, 798, 140196. [Google Scholar] [CrossRef]
- Zhu, F.; Jiang, D.; Sun, S.; Wu, H.; Zhang, Z.; Wang, J.; Ren, Z. Effect of Alternating Magnetic Field on Microstructure Evolution and Mechanical Properties of M50 Bearing Steel during Tempering Process. J. Mater. Res. Technol. 2023, 26, 4516–4525. [Google Scholar] [CrossRef]
- Zhou, L.; Tang, G.; Ma, X.; Wang, L.; Zhang, X. Relationship between Microstructure and Mechanical Properties of M50 Ultra-High Strength Steel via Quenching-Partitioning-Tempering Process. Mater. Charact. 2018, 146, 258–266. [Google Scholar] [CrossRef]
- Niu, J.B.; Zhang, X.H.; Ma, X.X.; Liu, Y.; Wang, L.Q.; Wu, T.B. Characterization of Vein-like Structures Formed in Nitrided Layers during Plasma Nitriding of 8Cr4Mo4V Steel. Materialia 2022, 22, 101378. [Google Scholar] [CrossRef]
- Esfahani, A.K.; Babaei, M.; Sarrami-Foroushani, S. A Numerical Model Coupling Phase Transformation to Predict Microstructure Evolution and Residual Stress during Quenching of 1045 Steel. Math. Comput. Simul. 2021, 179, 1–22. [Google Scholar] [CrossRef]
- Niu, J.B.; Waqas Qureshi, M.; Ding, Z.F.; Ma, X.X.; He, Y. Effect of Nitriding on the Transformation of Alloy Carbides (VC and Mo2C) in 8Cr4Mo4V Steel. Appl. Surf. Sci. 2023, 610, 155561. [Google Scholar] [CrossRef]
- Hou, X.-Q. Formation Mechanism and Influence of White Etching Area on Contact Fatigue Spalling of M50 Bearing Steel. Eng. Fail. Anal. 2022, 139, 106273. [Google Scholar] [CrossRef]
- Schönbauer, B.M.; More, S.S.; Morales-Espejel, G.E.; Mayer, H. Influence of Elevated Temperature on the Very High Cycle Fatigue Properties of Bearing Steels. Int. J. Fatigue 2023, 176, 107847. [Google Scholar] [CrossRef]
- Oezel, M. Formation of White Etching Areas in SAE 52100 Bearing Steel under Rolling Contact Fatigue—Influence of Diffusible Hydrogen. Wear 2018, 414–415, 352–365. [Google Scholar] [CrossRef]
- Guan, J.; Wang, L.; Zhang, C.; Ma, X. Effects of Non-Metallic Inclusions on the Crack Propagation in Bearing Steel. Tribol. Int. 2017, 106, 123–131. [Google Scholar] [CrossRef]
- Curd, M.E.; Burnett, T.L.; Fellowes, J.; Yan, P.; Withers, P.J. Redistribution of Carbon Caused by Butterfly Defects in Bearing Steels. Acta Mater. 2020, 183, 390–397. [Google Scholar] [CrossRef]
- Steinweg, F.; Mikitisin, A.; Zhang, J.-L.; Weirich, T.E.; Wang, J.; Chauhan, D.; Schwedt, A.; Richter, S.; Zander, D.; Mayer, J.; et al. Discovery of White Etching Areas in High Nitrogen Bearing Steel X30CrMoN15-1: A Novel Finding in Rolling Contact Fatigue Analysis. Wear 2024, 558–559, 205556. [Google Scholar] [CrossRef]
- Kürten, D.; Khader, I.; Raga, R.; Casajús, P.; Winzer, N.; Kailer, A.; Spallek, R.; Scherge, M. Hydrogen Assisted Rolling Contact Fatigue Due to Lubricant Degradation and Formation of White Etching Areas. Eng. Fail. Anal. 2019, 99, 330–342. [Google Scholar] [CrossRef]
- Peela, A.; Spille, J.; Steinweg, F.; Janitzky, T.; Schwedt, A.; Mayer, J.; Broeckmann, C. Multiscale Modelling and Simulation of Subsurface Carbide Deformation during the Formation of White Etching Areas. Wear 2023, 512–513, 204542. [Google Scholar] [CrossRef]
- Li, S.-X.; Su, Y.-S.; Shu, X.-D.; Chen, J.-J. Microstructural Evolution in Bearing Steel under Rolling Contact Fatigue. Wear 2017, 380–381, 146–153. [Google Scholar] [CrossRef]
- Wei, Y.H.; Yu, X.F.; Su, Y.; Shen, X.Y.; Xia, Y.Z.; Yang, W.W. Effect of Residual Stress and Microstructure Evolution on Size Stability of M50 Bearing Steel. J. Mater. Res. Technol. 2021, 10, 651–661. [Google Scholar] [CrossRef]
- Samuel, A.; Prabhu, K.N. Residual Stress and Distortion during Quench Hardening of Steels: A Review. J. Mater. Eng. Perform. 2022, 31, 5161–5188. [Google Scholar] [CrossRef]
- Li, H.; Zhao, G.; Huang, C.; Niu, S. Technological Parameters Evaluation of Gas Quenching Based on the Finite Element Method. Comput. Mater. Sci. 2007, 40, 282–291. [Google Scholar] [CrossRef]
- Li, W.; Meng, X.; Shu, K.; Zheng, D.; Wang, T.; Gu, L.; Wang, L.; Zhang, C. Effect of Dented Residual Stress on the Surface-Defect-Induced Pitting under Rolling Contact Loading of M50 Bearing Steel. Tribol. Int. 2024, 194, 109492. [Google Scholar] [CrossRef]
- Guan, J. A Continuum Damage Mechanics Based Approach to Damage Evolution of M50 Bearing Steel Considering Residual Stress Induced by Shot Peening. Tribol. Int. 2018, 126, 218–228. [Google Scholar] [CrossRef]
- Salvati, E.; Korsunsky, A.M. An Analysis of Macro- and Micro-Scale Residual Stresses of Type I, II and III Using FIB-DIC Micro-Ring-Core Milling and Crystal Plasticity FE Modelling. Int. J. Plast. 2017, 98, 123–138. [Google Scholar] [CrossRef]
- Wang, R.; Jiang, H.; Shao, W.; Yang, S.; Sun, X.; Cao, J.; Zhen, L. Quenching Induced Residue Stress in M50 Steel Ring: A FEM Simulation. J. Mater. Res. Technol. 2023, 24, 5298–5308. [Google Scholar] [CrossRef]
- Akbarzadeh, I.; Attarha, M.J.; Salehi, M.; Sattari-Far, I. Numerical and Experimental Study on the Effect of Post-Weld Heat Treatment Parameters on the Relaxation of Welding Residual Stresses. J. Strain Anal. Eng. Des. 2011, 46, 79–86. [Google Scholar] [CrossRef]
- Carro-Sevillano, G.; Fernández, R.; Bokuchava, G.; Millán, L.; González-Doncel, G. Residual Stress Distribution after Quenching Treatment Obtained from Diffraction Experiments and Simulation by Finite Element Method. J. Synch. Investig. 2021, 15, 537–541. [Google Scholar] [CrossRef]
- Guo, Y.; Abdolvand, H.; Britton, T.B.; Wilkinson, A.J. Growth of {} Twins in Titanium: A Combined Experimental and Modelling Investigation of the Local State of Deformation. Acta Mater. 2017, 126, 221–235. [Google Scholar] [CrossRef]
- Zhang, W.X.; Cong, Y.B.; Wang, J.; Li, C.; Wan, J.; Chen, Y.Z. Revealing the Effects of Martensitic Transformation and Dislocation Slip in Austenite on the Micromechanical Behaviors of a 9Ni Steel Using Crystal Plasticity Finite Element Method. Int. J. Plast. 2024, 174, 103869. [Google Scholar] [CrossRef]
- Lunt, A.J.G.; Korsunsky, A.M. A Review of Micro-Scale Focused Ion Beam Milling and Digital Image Correlation Analysis for Residual Stress Evaluation and Error Estimation. Surf. Coat. Technol. 2015, 283, 373–388. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, X.P.; Qin, G.W. Investigation of Misfit Dislocations in α-Fe2O3/α-Al2O3 Interface by Geometric Phase Analysis and Dislocation Density Tensor Analysis. Mater. Charact. 2015, 106, 308–316. [Google Scholar] [CrossRef]
- Wang, S.Y.; Lang, F.C.; Xing, Y.M. Geometric Phase Analysis for Characterization of 3D Morphology of Carbon Fiber Reinforced Composites. Compos. Sci. Technol. 2023, 242, 110215. [Google Scholar] [CrossRef]
- Xia, T.; Chen, Y.; Song, T.; Cui, P.; Liu, Y.; Zhu, J. Optimization of Heat Treatment Process Parameters for 8Cr4Mo4V Bearing Ring Using FEA-NN-PSO Method. Met. Mater. Int. 2025. [Google Scholar] [CrossRef]
- Liu, Y.; Qin, S.; Hao, Q.; Chen, N.; Zuo, X.; Rong, Y. Finite Element Simulation and Experimental Verification of Internal Stress of Quenched AISI 4140 Cylinders. Met. Mater. Trans. A 2017, 48, 1402–1413. [Google Scholar] [CrossRef]
- Koistinen, D.; Marburger, R. A General Equation Prescribing the Extent of the Austenite-Martensite Transformation in Pure Iron-Carbon Alloys and Plain Carbon Steels. Acta Metall. 1959, 7, 59–60. [Google Scholar] [CrossRef]
- Zhou, Y.; Lin, W.; Yang, F.; Fang, W.; Huang, J.; Li, Q. Insights into Formation Kinetics of Gold Nanoparticles Using the Classical JMAK Model. Chem. Phys. 2014, 441, 23–29. [Google Scholar] [CrossRef]
- Roters, F.; Eisenlohr, P.; Kords, C.; Tjahjanto, D.D.; Diehl, M.; Raabe, D. DAMASK: The Düsseldorf Advanced MAterial Simulation Kit for Studying Crystal Plasticity Using an FE Based or a Spectral Numerical Solver. Procedia Iutam 2012, 3, 3–10. [Google Scholar] [CrossRef]
- Lee, E.H.; Liu, D.T. Finite-Strain Elastic—Plastic Theory with Application to Plane-Wave Analysis. J. Appl. Phys. 1967, 38, 19–27. [Google Scholar] [CrossRef]
- Liu, X.; Xia, T.; Li, H.; Song, T.; Qu, N.; Liu, Y.; Zhu, J. Microstructure Evolution and Mechanical Properties of Grinding Metamorphic for 8Cr4Mo4V Steel. Materials 2025, 18, 1092. [Google Scholar] [CrossRef]
- Roters, F.; Eisenlohr, P.; Hantcherli, L.; Tjahjanto, D.D.; Bieler, T.R.; Raabe, D. Overview of Constitutive Laws, Kinematics, Homogenization and Multiscale Methods in Crystal Plasticity Finite-Element Modeling: Theory, Experiments, Applications. Acta Mater. 2010, 58, 1152–1211. [Google Scholar] [CrossRef]
- Groeber, M.A.; Jackson, M.A. DREAM.3D: A Digital Representation Environment for the Analysis of Microstructure in 3D. Integr. Mater. Manuf. Innov. 2014, 3, 56–72. [Google Scholar] [CrossRef]
- Hÿtch, M.J.; Snoeck, E.; Kilaas, R. Quantitative Measurement of Displacement and Strain Fields from HREM Micrographs. Ultramicroscopy 1998, 74, 131–146. [Google Scholar] [CrossRef]
- Takeda, M.; Suzuki, J. Crystallographic Heterodyne Phase Detection for Highly Sensitive Lattice-Distortion Measurements. J. Opt. Soc. Am. A 1996, 13, 1495. [Google Scholar] [CrossRef]
- Tasan, C.C.; Hoefnagels, J.P.M.; Diehl, M.; Yan, D.; Roters, F.; Raabe, D. Strain Localization and Damage in Dual Phase Steels Investigated by Coupled In-Situ Deformation Experiments and Crystal Plasticity Simulations. Int. J. Plast. 2014, 63, 198–210. [Google Scholar] [CrossRef]
- Tjahjanto, D.D.; Turteltaub, S.; Suiker, A.S.J. Crystallographically Based Model for Transformation-Induced Plasticity in Multiphase Carbon Steels. Contin. Mech. Thermodyn. 2008, 19, 399–422. [Google Scholar] [CrossRef]
- Du, H. GPA—Geometrical Phase Analysis Software (2018). Available online: https://er-c.org/index.php/software/stem-data-analysis/gpa/ (accessed on 1 January 2018).
| C | Cr | Mo | V | Mn | Fe |
|---|---|---|---|---|---|
| 0.8 | 4.0 | 4.0 | 1.0 | 0.2 | Bal. |
| Parameter | Martensite [46] | Tempered Martensite |
|---|---|---|
| C11 (GPa) | 417.4 | 309.1 |
| C12 (GPa) | 242.4 | 132.5 |
| C44 (GPa) | 211.1 | 88.3 |
| g0{111} (MPa) | 406 | 605 |
| gꝏ{111} (MPa) | 873 | 972 |
| g0{112} (MPa) | 457 | 656 |
| gꝏ{112} (MPa) | 971 | 1071 |
| 0.001 | 0.001 | |
| n | 20 | 12 |
| a | 2.25 | 1.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xia, T.; Cui, P.; Song, T.; Liu, X.; Liu, Y.; Zhu, J. An Investigation of Heat Treatment Residual Stress of Type I, II, III for 8Cr4Mo4V Steel Bearing Ring Using FEA-CPFEM-GPA Method. Metals 2025, 15, 548. https://doi.org/10.3390/met15050548
Xia T, Cui P, Song T, Liu X, Liu Y, Zhu J. An Investigation of Heat Treatment Residual Stress of Type I, II, III for 8Cr4Mo4V Steel Bearing Ring Using FEA-CPFEM-GPA Method. Metals. 2025; 15(5):548. https://doi.org/10.3390/met15050548
Chicago/Turabian StyleXia, Tao, Puchang Cui, Tianpeng Song, Xue Liu, Yong Liu, and Jingchuan Zhu. 2025. "An Investigation of Heat Treatment Residual Stress of Type I, II, III for 8Cr4Mo4V Steel Bearing Ring Using FEA-CPFEM-GPA Method" Metals 15, no. 5: 548. https://doi.org/10.3390/met15050548
APA StyleXia, T., Cui, P., Song, T., Liu, X., Liu, Y., & Zhu, J. (2025). An Investigation of Heat Treatment Residual Stress of Type I, II, III for 8Cr4Mo4V Steel Bearing Ring Using FEA-CPFEM-GPA Method. Metals, 15(5), 548. https://doi.org/10.3390/met15050548







