Study of Tensile Fracture and Interfacial Strength of 316L/Q345R Stainless Steel Composite Plate Based on Molecular Dynamics
Abstract
1. Introduction
2. MD Simulation and Methods
2.1. Model Establishment
2.2. Simulation Method
3. Results and Discussion
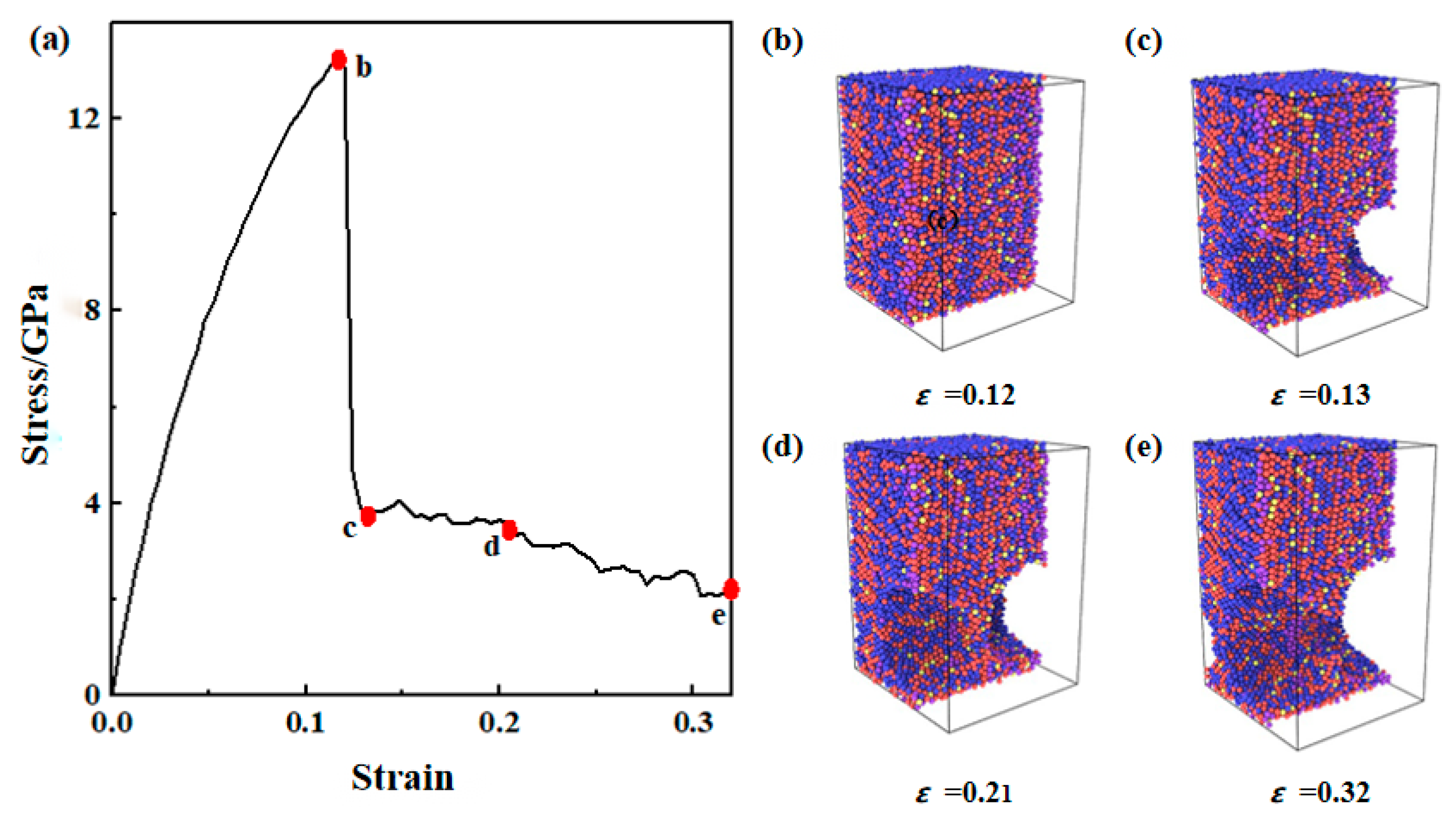
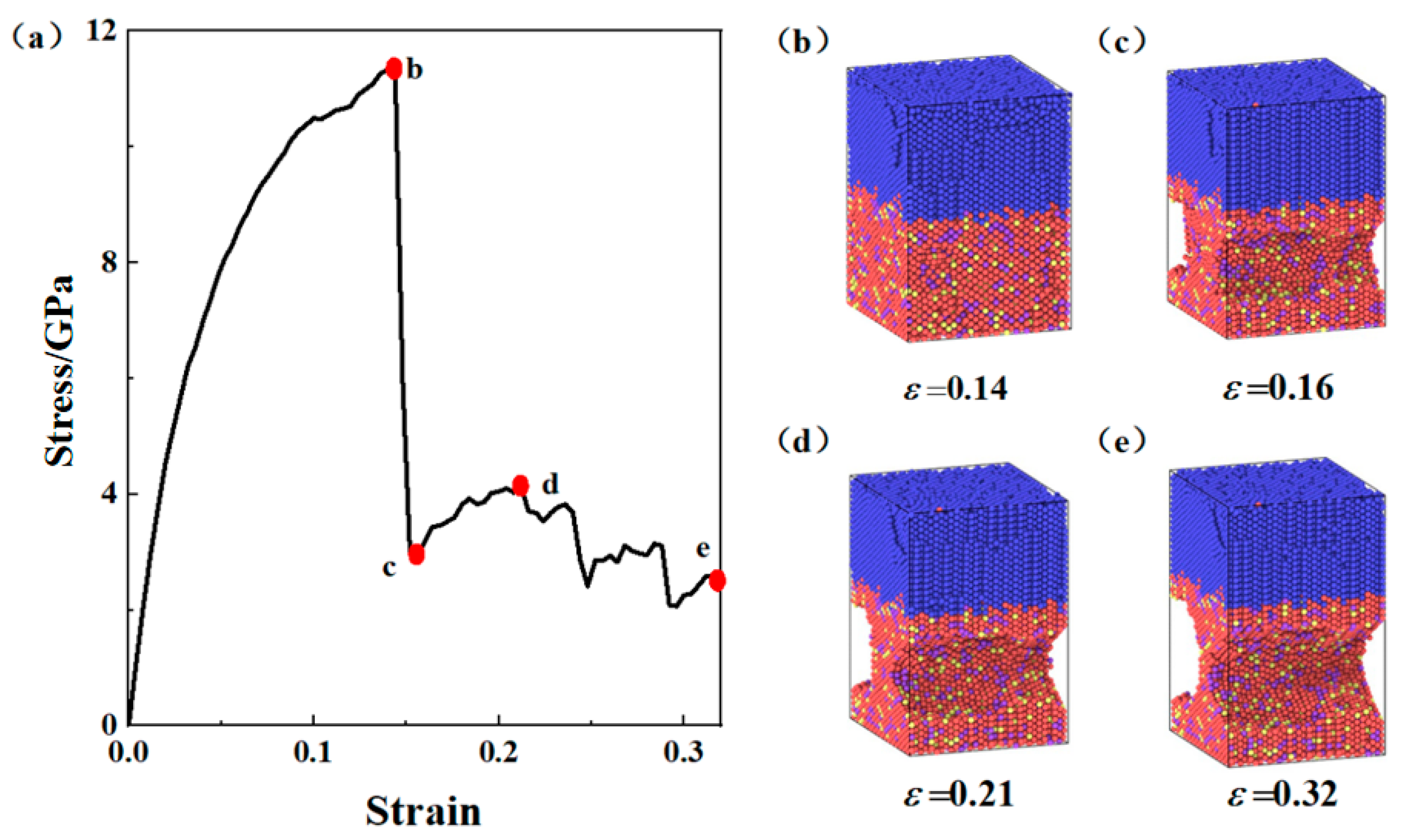
3.1. Tensile Deformation Process of the Composite Plate Interface
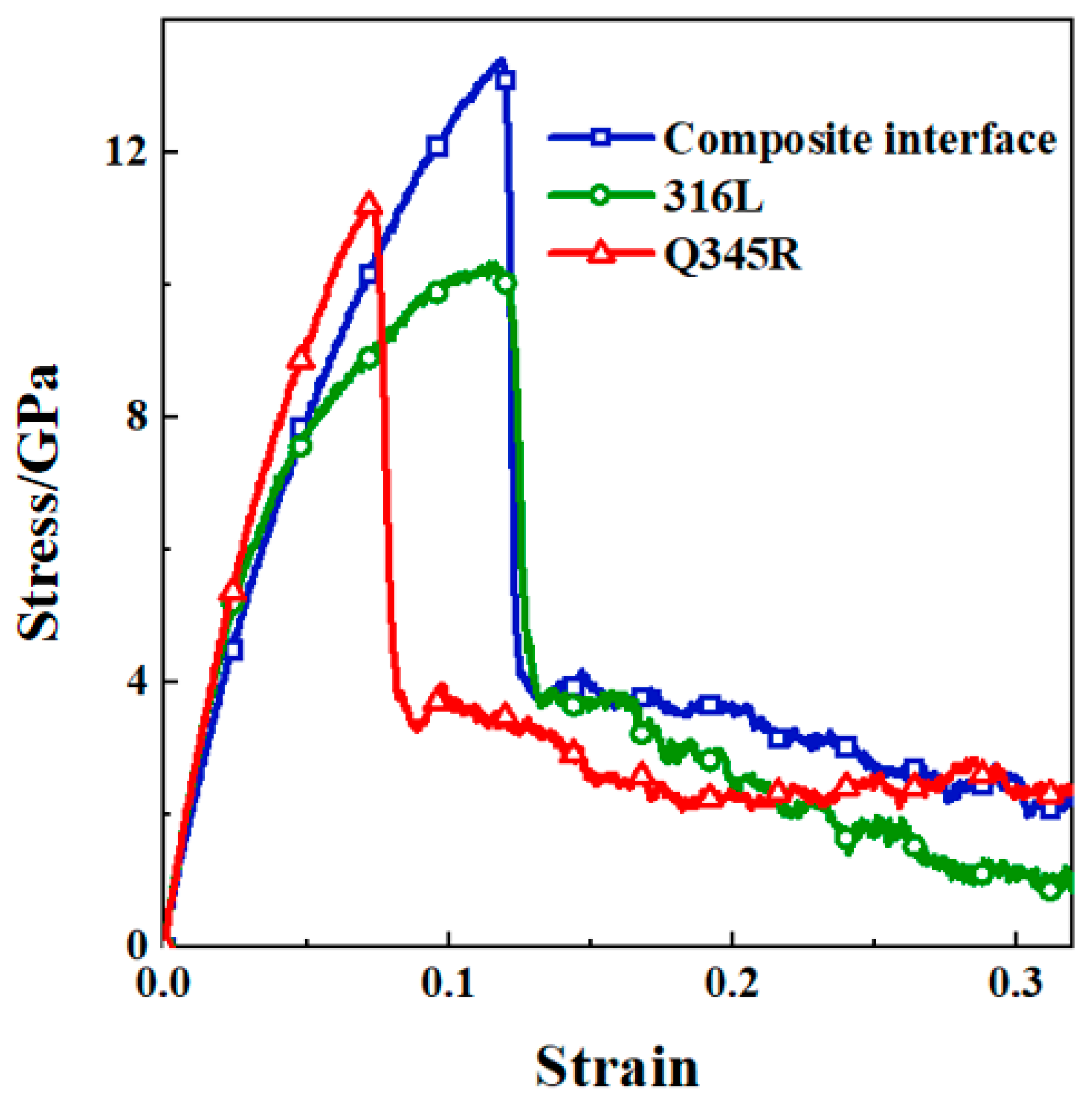
3.2. Strength Comparison Between Composite Board Interface and Substrate Materials
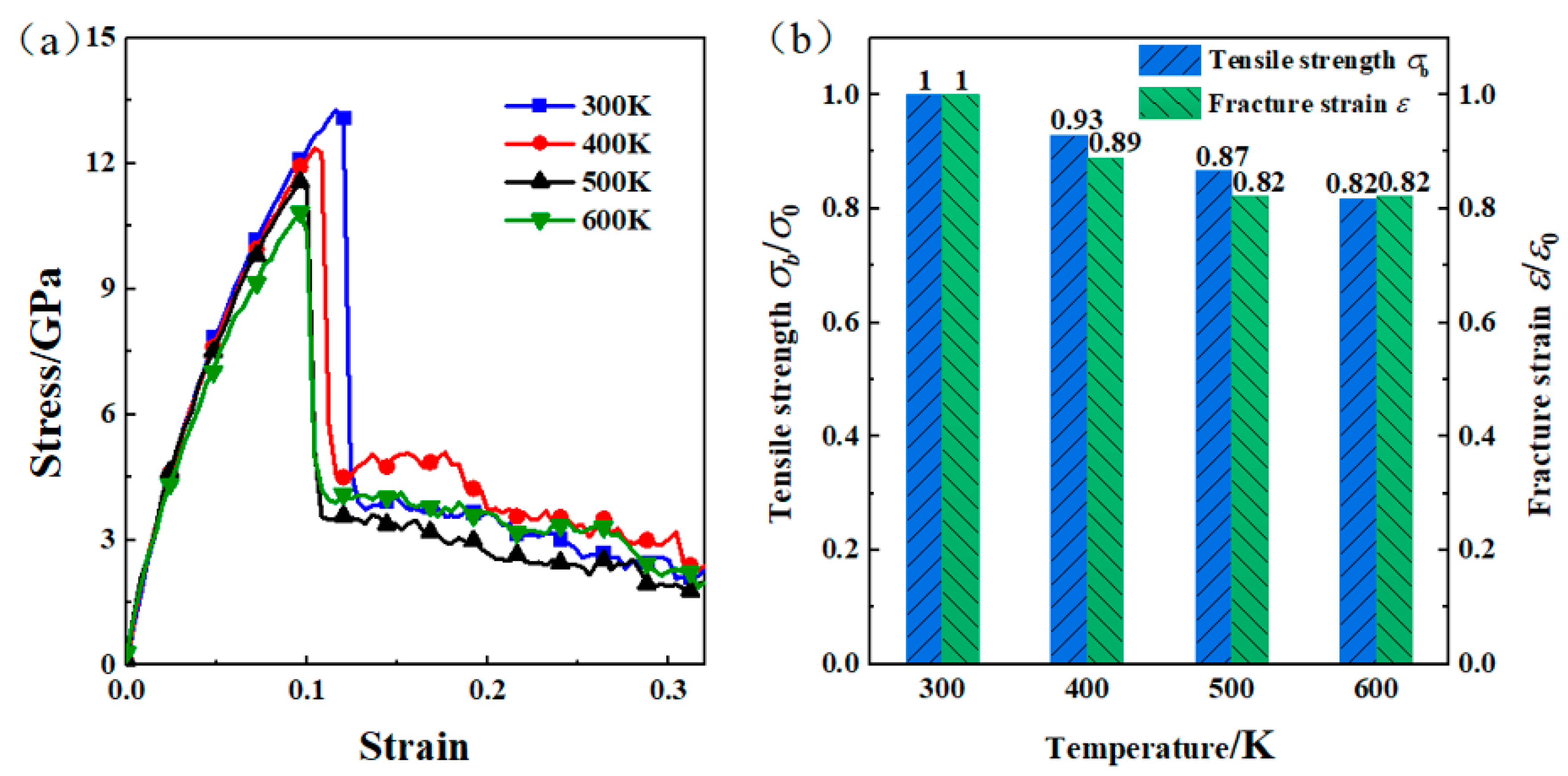
3.3. The Effect of Temperature on the Interfacial Bonding Strength of Composite Panels
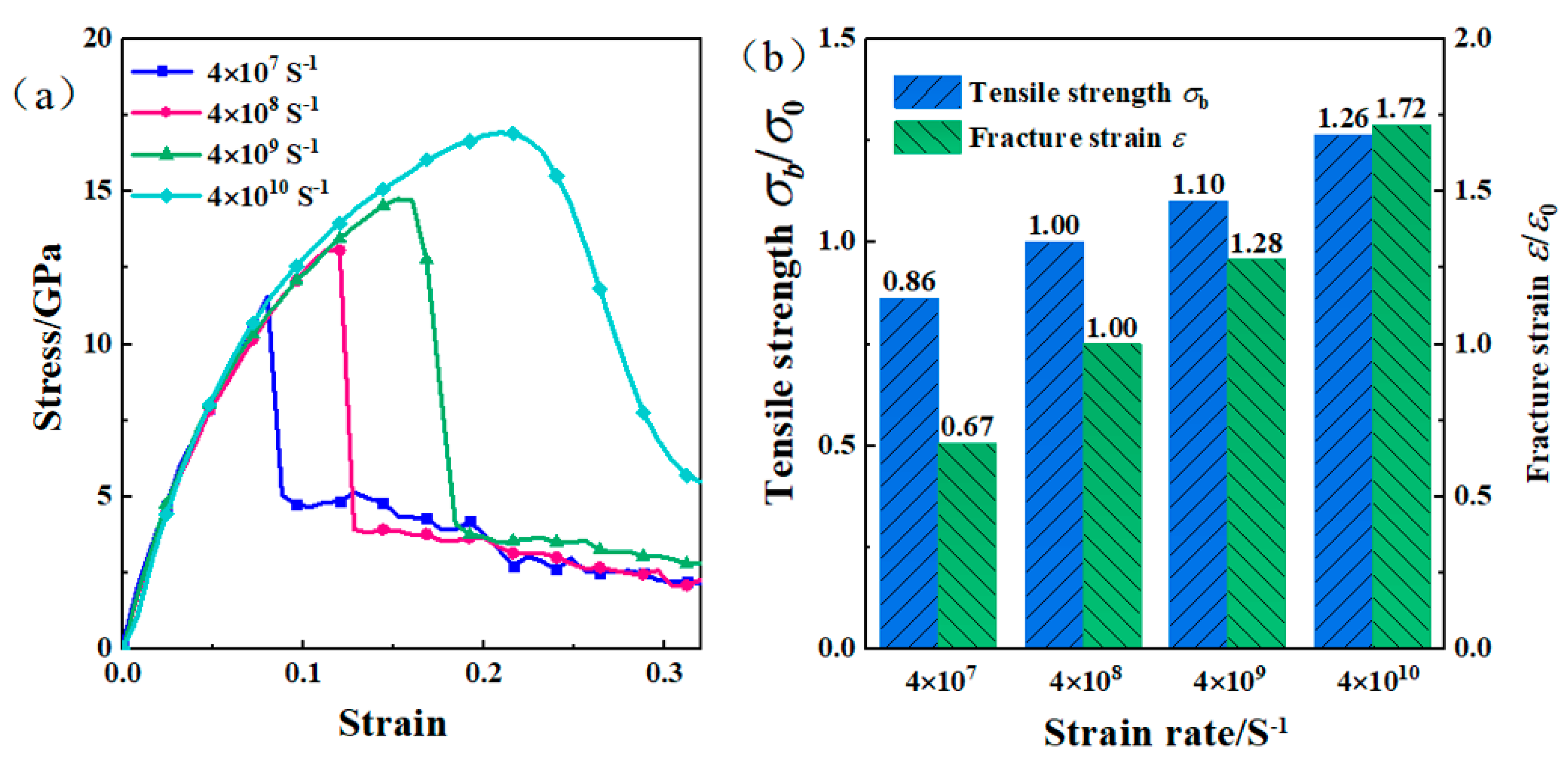
3.4. Effect of Strain Rate on the Interface Bonding Strength of Composite Plates
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| MD | Molecular Dynamics |
| FCC | Face-Centered Cubic |
| BCC | Body-Centered Cubic |
| 316L | AISI 316L Stainless Steel |
| Q345R | Chinese Standard Low-Carbon Steel |
| EAM | Embedded-Atom Method |
| OVITO | Open Visualization Tool |
| NPT | Isothermal–Isobaric Ensemble |
| NVT | Canonical Ensemble (Constant N, V, and T) |
| ps | Picosecond |
| σ | Stress |
| ε | Strain |
| σ0, ε0 | Ultimate Stress and Strain at Baseline Condition (300 K, 4 × 10⁸ s−1) |
References
- Make, A.; Schultz, B.F.; Rohatgi, P. Metal matrix composites. Adv. Mater. Process. 2012, 170, 19–23. [Google Scholar]
- Kaczmar, J.W.; Pietrzak, K.; Włosiński, W. The Production and Application of Metal Matrix Composite Materials. J. Mater. Process. Technol. 2000, 106, 58–67. [Google Scholar] [CrossRef]
- Abbasi, M.; Salehi, M.T.; Karimi Taheri, A. An Investigation on Cold Roll Welding of Copper to Aluminum Using Electrical Resistivity. Int. J. Mater. Res. 2001, 92, 423–430. [Google Scholar]
- Wang, T.; Sidhar, H.; Mishra, R.S.; Hovanski, Y.; Upadhyay, P.; Carlson, B. Friction Stir Welding of Dissimilar Alloys: Influence of Tool Offset on Microstructure and Mechanical Properties. Mater. Des. 2019, 174, 107795. [Google Scholar] [CrossRef]
- Manesh, H.D.; Taheri, A.K. Investigation of Mechanical Properties of Cold Roll Bonded Aluminum Strips. Mech. Mater. 2005, 37, 531–543. [Google Scholar] [CrossRef]
- Kim, Y.K.; Hong, S.I. Effect of interfacial intermetallic compounds evolution on the mechanical response and fracture of layered Ti/Cu/Ti clad materials. Mater. Sci. Eng. A 2019, 767, 138802. [Google Scholar] [CrossRef]
- Pozuelo, M.; Carreño, F.; Ruano, O.A. Processing and impact properties of steel-based laminated composites. Compos. Sci. Technol. 2006, 66, 2671–2680. [Google Scholar] [CrossRef]
- Borchers, C.; Lenz, M.; Deutges, M.; Klein, H.; Gärtner, F.; Hammerschmidt, M.; Kreye, H. Microstructure and mechanical properties of medium-carbon steel bonded on low-carbon steel by explosive welding. Mater. Des. 2016, 89, 369–376. [Google Scholar] [CrossRef]
- Kaya, Y.; Kahraman, N.; Durgutlu, A.; Gülenç, B. AISI 316 Austenitic Stainless Steel and AISI 430 Ferritic Stainless Steel Plates Explosive Welding: Effect of Explosive Ratio on Interface Formation. Metall. Mater. Trans. A 2017, 48, 3721–3730. [Google Scholar] [CrossRef]
- Kwiecień, M.; Majta, J.; Dziedzic, D. Shear deformation and failure of explosive welded Inconel-microalloyed steels bimetals. Arch. Civ. Mech. Eng. 2014, 14, 32–39. [Google Scholar] [CrossRef]
- Li, S.; Chen, Y.; Zhou, X.; Kang, J.; Huang, Y.; Deng, H. Effect of heat treatment on the microstructure and mechanical properties of a Cu–Ni–Sn–P alloy. Mater. Lett. 2019, 234, 155–158. [Google Scholar] [CrossRef]
- Camanho, P.; Erçin, G.; Catalanotti, G.; Mahdi, S.; Linde, P. A finite fracture mechanics model for the prediction of the open-hole strength of composite laminates. Compos. Part A Appl. Sci. Manuf. 2012, 43, 1219–1225. [Google Scholar] [CrossRef]
- Adams, R.D.; Coppendale, J. The measurement of the elastic moduli of structural adhesives by a resonant bar technique. J. Adhesion 1979, 10, 49–55. [Google Scholar] [CrossRef]
- Wu, Z. Influence of surface treatment on the strength of adhesive joints. Int. J. Adhes. Adhes. 2017, 77, 29–35. [Google Scholar] [CrossRef]
- Felger, J.; Stein, N.; Frey, C.; Becker, W. Experimental investigation of the mechanical behavior of adhesive joints under mixed-mode loading. Compos. Struct. 2018, 208, 546–556. [Google Scholar] [CrossRef]
- Ma, B.; Rao, Q.; He, Y. Phase-field modeling of microstructure evolution in solidification of binary alloys. Comput. Mater. Sci. 2016, 117, 40–47. [Google Scholar] [CrossRef]
- Chang, L.; Zhou, C.-Y.; Wen, L.-L.; Li, J.; He, X.-H. Molecular dynamics study of the deformation behavior and strengthening mechanisms of Cu/graphene composites under nanoindentation. Comput. Mater. Sci. 2017, 128, 348–355. [Google Scholar] [CrossRef]
- Choi, B.K.; Yoon, G.H.; Lee, S. Molecular dynamics studies of CNT-reinforced aluminum composites under uniaxial tensile loading. Compos. Part B Eng. 2016, 91, 119–125. [Google Scholar] [CrossRef]
- Tomar, V.; Zhou, M. Analyses of tensile deformation of nanocrystalline α-Fe2O3+fcc-Al composites using molecular dynamics simulations. J. Mech. Phys. Solids 2007, 55, 1053–1085. [Google Scholar] [CrossRef]
- Zhu, H.; Sun, W.; Kong, F.; Wang, X.; Song, Z.; Chen, Y. Cyclic behaviours of superelastic shape-memory alloy plates joined by tungsten inert gas welding. Mater. Sci. Eng. A 2019, 742, 704–710. [Google Scholar] [CrossRef]
- Kardani, A.; Montazeri, A. Temperature-based plastic deformation mechanism of Cu/Ag nanocomposites: A molecular dynamics study. Comput. Mater. Sci. 2018, 144, 223–231. [Google Scholar] [CrossRef]
- Zhou, Y.; Hu, M. Molecular dynamics simulations of the mechanical properties of graphene oxide nanosheets. Comput. Mater. Sci. 2017, 129, 129–135. [Google Scholar] [CrossRef]
- Chen, S.; Wu, Z.; Liu, K.; Li, X.; Luo, N.; Lu, G. Atomic diffusion behavior in Cu–Al explosive welding process. J. Appl. Phys. 2013, 113, 205–209. [Google Scholar] [CrossRef]
- Qin, Q.; He, W.; Xie, L.; Deng, J.; Zhu, X.; Peng, Q. Nonlinear diffusion, bonding, and mechanics of the interface between austenitic steel and iron. Phys. Chem. Chem. Phys. 2019, 21, 1464–1473. [Google Scholar] [CrossRef]
- Chen, Y.; Shao, S.; Liu, X.-Y.; Yadav, S.K.; Li, N.; Mara, N.; Wang, J. Misfit dislocation patterns of Mg-Nb interfaces. Acta Mater. 2017, 126, 552–563. [Google Scholar] [CrossRef]
- Zhang, R.F.; Beyerlein, I.J.; Zheng, S.J.; Zhang, S.H.; Stukowski, A.; Germann, T.C. Dislocation and twin interactions in a magnesium alloy: A molecular dynamics study. Acta Mater. 2016, 113, 194–205. [Google Scholar] [CrossRef]
- Stukowski, A. Visualization and analysis of atomistic simulation data with OVITO—The Open Visualization Tool. Modell. Simul. Mater. Sci. Eng. 2009, 18, 015012. [Google Scholar] [CrossRef]
- Plimpton, S. Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Bonny, G.; Castin, N.; Terentyev, D. Interatomic potential for studying ageing under irradiation in stainless steels: The FeNiCr model alloy. Modell. Simul. Mater. Sci. Eng. 2013, 21, 085004. [Google Scholar] [CrossRef]
| Name | Fe | C | Si | Mn | P | S | Cr | Ni | Mo | Al | Ti |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Q345R | 98.0 | 0.17 | 0.2 | 1.4 | 0.01 | 0.00 | 0.02 | 0.02 | <0.01 | <0.01 | <0.01 |
| SUS316L | 70.26 | 0.017 | 0.42 | 1.26 | 0.031 | 0.003 | 16.03 | 10.03 | 1.95 | - | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, L.; Kang, J.; Fu, X.; Wang, W. Study of Tensile Fracture and Interfacial Strength of 316L/Q345R Stainless Steel Composite Plate Based on Molecular Dynamics. Metals 2025, 15, 502. https://doi.org/10.3390/met15050502
Xie L, Kang J, Fu X, Wang W. Study of Tensile Fracture and Interfacial Strength of 316L/Q345R Stainless Steel Composite Plate Based on Molecular Dynamics. Metals. 2025; 15(5):502. https://doi.org/10.3390/met15050502
Chicago/Turabian StyleXie, Lu, Junhao Kang, Xuefei Fu, and Wenrui Wang. 2025. "Study of Tensile Fracture and Interfacial Strength of 316L/Q345R Stainless Steel Composite Plate Based on Molecular Dynamics" Metals 15, no. 5: 502. https://doi.org/10.3390/met15050502
APA StyleXie, L., Kang, J., Fu, X., & Wang, W. (2025). Study of Tensile Fracture and Interfacial Strength of 316L/Q345R Stainless Steel Composite Plate Based on Molecular Dynamics. Metals, 15(5), 502. https://doi.org/10.3390/met15050502






