Application of Artificial Intelligence to Support Design and Analysis of Steel Structures

Abstract

In steel structural engineering, artificial intelligence (AI) and machine learning (ML) are improving accuracy, efficiency, and automation. This review explores AI-driven approaches, emphasizing how AI models improve predictive capabilities, optimize performance, and reduce computational costs compared to traditional methods. Inverse Machine Learning (IML) is a major focus since it helps engineers to minimize reliance on iterative trial-and-error by allowing them to identify ideal material properties and geometric configurations depending on predefined performance targets. Unlike conventional ML models that focus mostly on forward predictions, IML helps data-driven design generation, enabling more adaptive engineering solutions. Furthermore, underlined is Explainable Artificial Intelligence (XAI), which enhances model transparency, interpretability, and trust of AI. The paper categorizes AI applications in steel construction based on their impact on design automation, structural health monitoring, failure prediction and performance evaluation throughout research from 1990 to 2025. The review explores challenges such as data limitations, model generalization, engineering reliability, and the need for physics-informed learning while examining AI’s role in bridging research and real-world structural applications. By integrating AI into structural engineering, this work supports the adoption of ML, IML, and XAI in structural analysis and design, paving the way for more reliable and interpretable engineering practices.

1. Introduction

Structural engineering depends on both exact design specification and extensive analysis to ensure that infrastructure and buildings satisfy safety and performance criteria. Although conventional structural engineering depends on analytical calculations, experimental testing, and numerical simulations, modern developments demand a change toward data-driven methods and automation. Like they once moved from hand calculations to computational tools like finite element (FE) analysis, engineers have to adopt fresh approaches to solve problems as technology develops. The increasing application of artificial intelligence (AI) and machine learning (ML) in structural engineering [1,2,3] presents a similar challenge and demands experts to become familiar with AI-driven tools. These new technologies reinforce decision-making with adaptive, data-supported solutions rather than replacing conventional knowledge; they are instead extensions of engineering intuition [4]. Structural engineering guarantees design and analysis accuracy by means of methodical processes and uniform guidelines. These approaches have been included into software tools over time to automatically complete compliance checks and regular computations. Large-scale steel buildings, however, often call for high-performance workstations and licensed tools since they demand significant computational resources, specialized simulation software, and expert oversight.

Among the deterministic, physics-based models supporting most conventional structural engineering approaches are reliability-based optimization frameworks, Computational Fluid Dynamics (CFD), and the Finite Element Method (FEM). These reliable methods provide engineers with complete awareness of mechanical behavior, stress distribution, failure modes, and safety margins. However, the application of structural systems becomes more challenging and computationally expensive as they get larger and include nonlinearities, material heterogeneity, or advanced loading scenarios. Even with strong simulation tools, each analysis iteration requires manual intervention, time, and expert interpretation—factors that can slow down the design and optimization process. Another paradigm comes from AI—in particular from ML. ML models learn from patterns in past datasets, derived from experiments, simulations, or hybrid sources, instead of solving governing equations repeatedly. Once trained, these models can save computational time, let engineers rapidly investigate large design areas, and offer almost instantaneous predictions for new designs. This capacity underlies early-stage design, parametric sensitivity studies, and multi-objective optimization where speed and adaptability are particularly critical. From a structural perspective, ML techniques have been used to precisely predict material strength, buckling resistance, joint behavior, and global system performance. From the AI side, the use of surrogate modeling, ensemble learning, and neural networks has made it possible to capture highly nonlinear relationships that are difficult to express analytically. Acting as a fast, approximative evaluator, trained ML models enable real-time structural assessment, uncertainty-based optimization, or integration with digital twin systems. This synergy between physics-based rigor and data-driven intelligence marks a potential revolution in how future structures are conceived, assessed, and optimized.

Analyzing a structure and designing it, have different uses and needs for different skill sets in structural engineering. Analysis is mostly concerned with how a structure responds to external forces; design is the process of developing answers that fit performance criteria and practical limitations. These two disciplines sometimes have different logical frameworks. Analysis depends on scientific ideas and deterministic models while design is adaptive, iterative, and affected by outside events including material availability, cost, and safety rules. One challenge of engineering education is that students are mostly taught mathematical and computational methods, which stress strict formulations and simulations. However, when they enter the industry, they must deal with real-world design problems that require creative problem-solving, adaptability, and decision-making under uncertainty. This gap emphasizes the need of bridging analytical precision with design intuition so that engineers may properly move from knowledge of structural behavior to developing practical, efficient, creative designs that satisfy real-world needs [5].

Particularly in inverse design, ML is becoming more popular since it lets engineers directly decide ideal material properties, geometric layouts, and performance criteria depending on predefined structural goals [4,6]. Inverse Machine Learning (IML) allows a data-driven approach to quickly find the best design solutions in steel constructions, not only iteratively improving designs through simulations.

Apart from predictive powers, the growing complexity of ML models has generated questions about interpretability and transparency in structural engineering uses [7]. Explainable machine learning (XML) has become increasingly important in order to meet these difficulties since it guarantees that ML-driven models produce justifiable, clear, and understandable results [8]. By means of explainability techniques including feature importance analysis and SHapley Additive exPlanations (SHAP) [9], engineers can better grasp the contribution of various design parameters in decision-making, rendering ML-based structural analysis more reliable and useful. The identification of possible biases, validation of model reliability, and enhancement of decision-making confidence in safety-critical applications including load-bearing assessments, failure predictions, and material selection also quite heavily depend on XML techniques [10].

Typically addressing different engineering challenges, three main categories define ML techniques: supervised learning, unsupervised learning, and reinforcement learning. Supervised learning, which relies on labeled datasets, is particularly effective for regression tasks such as estimating material properties and classification problems like detecting structural damage [11]. Conversely, unsupervised learning is useful for predictive maintenance and structural design optimization since it finds hidden trends in engineering data without depending on predefined labels [12]. Though less often used, reinforcement learning is very important for decision-making under uncertainty—especially in dynamic structural analysis [13].

Table 1. Overview of main ML categories.

ML Category	Core Principle	Common Algorithms	Applications in Structural Engineering	Limitations
Supervised Learning	Learns from labeled datasets to predict outcomes	Linear Regression, Random Forest, ANN	Material property estimation, damage classification, load prediction	Requires large, labeled datasets; limited in extrapolation
Unsupervised Learning	Finds hidden patterns or groupings in unlabeled data	K-means, PCA, Autoencoders	Structural health monitoring, design clustering, pattern discovery in sensor data	Results may lack clear interpretation; requires expert analysis
Reinforcement Learning	Learns via trial-and-error interactions to maximize rewards over time	Q-learning, Deep Q-Networks	Real-time structural control, decision-making under uncertainty, adaptive load redistribution	High computational cost; limited adoption due to training complexity

provides a comparative overview of these three categories—highlighting their underlying logic, typical algorithms, structural applications, and key limitations.

In structural engineering, ML first emerged in the late 1980s when researchers started working on design tasks using artificial neural networks (ANN) [14]. Recent advances in data-driven design methods, ML-driven predictive modeling, and optimization techniques have expanded its opportunities. Although more and more studies on AI in civil and structural engineering are available, there is still a dearth of targeted studies methodically analyzing ML uses in steel constructions. Emphasizing improved accuracy, efficiency, and automation, this review shows how AI is transforming steel structure engineering and synthesizing recent developments from 1994 to 2025. Previous studies have mostly focused on particular AI techniques in structural engineering, including pattern recognition for structural health monitoring, genetic algorithms in optimization problems, ML applications in concrete structures, and steel–concrete composite structures. Although these works offer insightful analysis, their scope is usually more general and they do not particularly address the function of ML in steel structure engineering.

This review paper provides a concentrated study of AI applications in design and analysis of steel structures. It also underlines the increasing relevance of IML, which allows engineers to directly choose optimal material properties and design criteria independent of iterative trial-and-error processes. By learning complicated interactions between input parameters and structural behavior, ML models can accelerate the design process, increase prediction accuracy, and maximize structural performance unlike conventional simulation-based techniques. This review provides a basic resource for researchers and engineers by aggregating and critically evaluating the most recent ML-driven innovations in steel structure engineering, thus bridging the gap between conventional computing methods and modern AI-enhanced approaches. The aim of this work is to enable the acceptance of ML, IML, and XML in steel structure design and analysis so guaranteeing more effective, transparent, and data-driven engineering solutions.

Objectives of This Review

• Providing a Focused Overview of ML in Steel Structure Engineering:

This paper attempts to give a thorough study of the part ML plays in the design and analysis of steel buildings. This work will show how ML-driven approaches are improving structural performance prediction, material selection, load-bearing capacity estimate, and failure assessment by aggregating significant developments. The paper will also discuss how ML is changing conventional design methods, thus enabling structural engineering to be more efficient, data-driven, and optimized.

• Exploring the Role of IML in Steel Structure Design:

This work tries to show a thorough investigation of the part ML does in the design and analysis of steel buildings. IML allows engineers, free from trial-and-error methods, to directly choose ideal design parameters including geometric configurations, material properties, and performance criteria unlike conventional iterative approaches. This review will examine how application of IML is improving steel structure optimization.

• Investigating XML for Transparent Structural Engineering

The growing complexity of ML models raises questions about interpretability and confidence in structural engineering uses. This paper will review XML techniques to show how engineers might better understand and validate AI-driven predictions. By means of better model transparency, XML can help to identify significant influencing factors, guarantee safety compliance, and improve reliability in steel analysis and design.

• Addressing Challenges, Limitations, and Future Directions

Even if ML has great promise for structural engineering, several issues have to be resolved before general acceptance. Important questions including data shortage, model interpretability, generalization, and integration of physics-informed learning to improve engineering accuracy are investigated in this review. Moreover, covered are problems with feature engineering, uncertainty quantification, and regulatory approval of ML-driven models in structural safety assessments. Future research directions are also under discussion, underlining the need of hybrid AI-physics models, industry-driven validation, and responsible AI application in design and analysis processes.

2. Research Data Extraction Process

This research evaluates steel building design and analysis through bibliometric methods and content analysis to investigate the implementation of AI techniques.

Scopus’s extensive scholarly coverage enabled this study to compile a comprehensive dataset for examining the impact of AI on the design and analysis of steel structures. The selected papers included applications of ML, IML, deep learning, fuzzy logic, genetic algorithms, optimization, surrogate modeling, and XML across various domains of structural engineering. Special attention was given to steel building components such as cold-formed steel, stainless steel, high-strength steel, beams, columns, plates, trusses, connections, and full steel frames. The dataset also included research on design strategies—such as structural optimization, topology optimization, reliability analysis, uncertainty quantification, and performance-based design—and structural analysis techniques including FEM, numerical simulations, structural health monitoring, load capacity evaluation, fatigue assessment, buckling behavior, seismic performance, wind load effects, and fire resistance.

The following inclusion criteria ensured both scientific quality and thematic relevance: only peer-reviewed journal articles were selected; the search was limited to publications between 1994 and 2025; all chosen papers explicitly focused on the application of artificial intelligence in steel structural engineering, excluding studies centered solely on concrete, timber, or hybrid systems; and the selected studies were required to demonstrate either methodological innovation or practical relevance in structural modeling, performance prediction, or design optimization. A keyword-based search was conducted in Scopus using combinations of terms such as “steel structures”, “machine learning”, “artificial intelligence”, “predictive modeling”, and “structural optimization”. Duplicate records, non-English publications, editorials, and studies without accessible full texts were excluded.

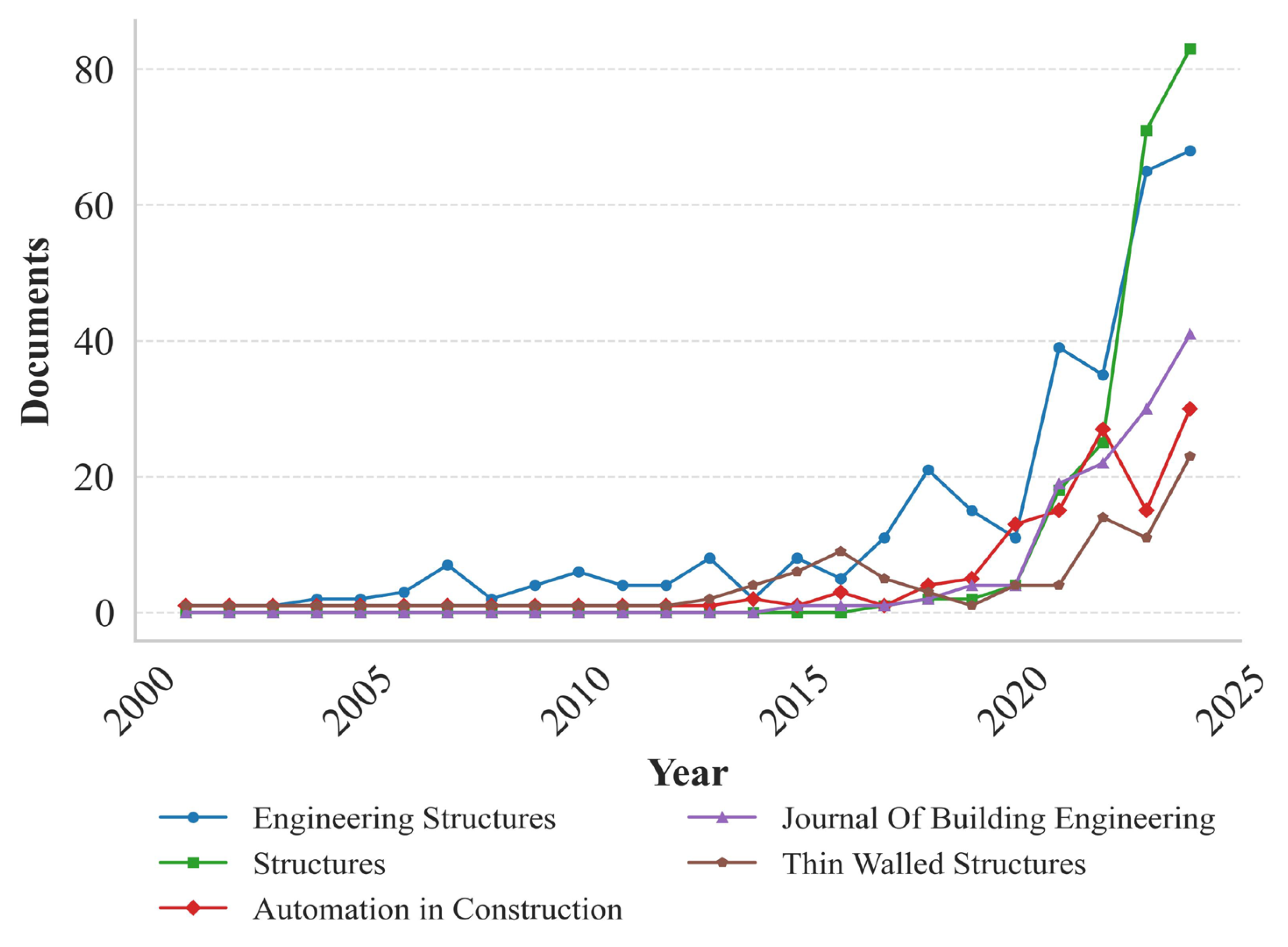
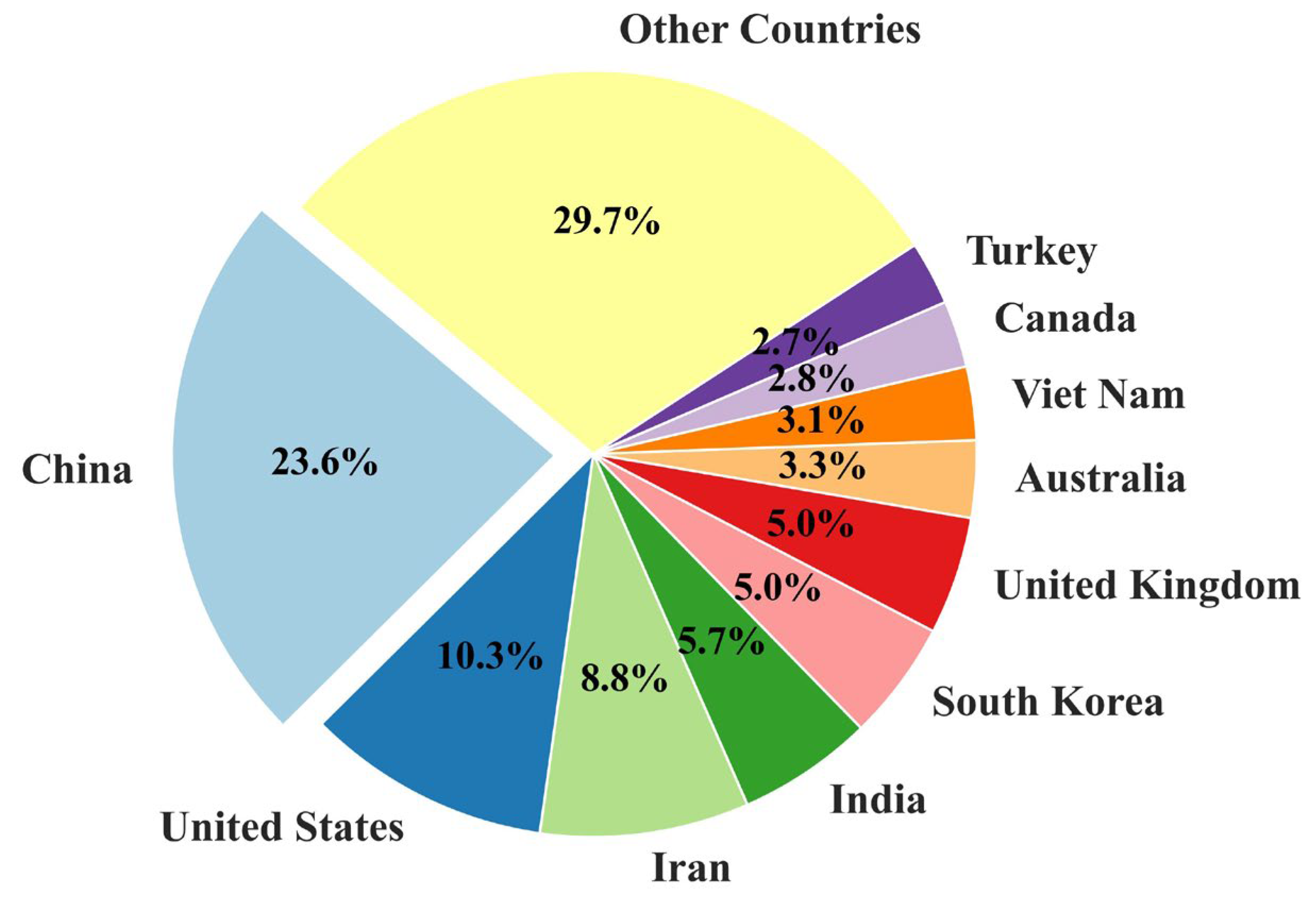
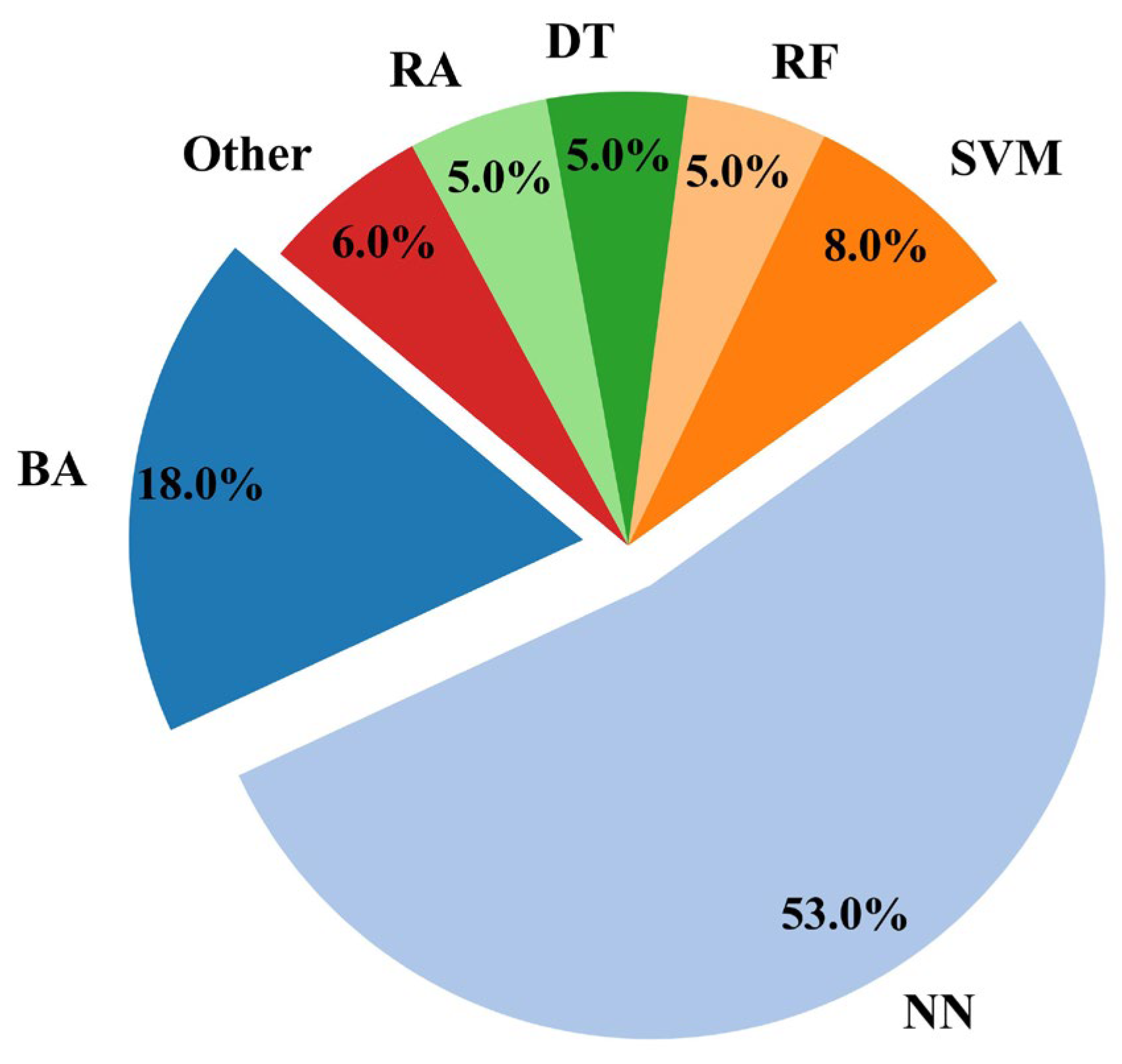
Overview of Research Contributions in AI-Driven Steel Structure Studies

A two-stage screening process was applied. In the first stage, papers were screened depending on title, abstract, and keywords to ensure relevance. The second stage involved a thorough review to select studies focusing on ML-driven structural analysis and design strategies. The bibliometric analysis identified 2291 English-language publications, as shown in

Table 2. Core Data Insights.

Detailed Overview	Outcomes
Citations	50,893
Authors	1277
Organization	1367
Countries	85
Journal	159
Documents	2291
Average citations per year	2035.72
Average citations per document	22.21
Time span	1994–2025

, highlighting the growing scholarly attention on AI’s role in structural engineering. This collection shows a wide international collaboration, with contributions from 1277 researchers affiliated with 1367 institutions across 85 countries. Covering from 1994 to 2025, the dataset captures three decades of increasing interest in AI-driven structural performance evaluation and optimization. Of the collected works published across 159 scientific journals, 2227 are research articles and 64 are review papers. The citation impact is also noteworthy, with a total of 50,893 citations and an average of 22.21 citations per paper. An annual citation rate of 2035.72 further emphasizes the rapid acceptance and industrial relevance of AI-based technologies in steel construction engineering.

The Citation Overview graph (Figure 1) displays the annual publication and citation distribution in the field of AI-driven steel structure research. From 2000 to about 2015, the results show a slow but steady increase in research activity despite rather low numbers of publications and citations. Starting in 2015, however, both measures clearly speed forward, a reflection of structural engineering’s increasing integration of AI and data-driven approaches. This trend fits world developments in computational modeling, deep learning, and ML, which have made AI-based solutions more pragmatic and successful for engineering use.

Publications pointing a shift toward AI acceptance in the field began to appear around 2018. This development confirms that the research community is placing increasing emphasis on AI applications in structural analysis, optimization, and design. Interest continues to rise, reaching its highest levels between 2022 and 2024. Citation counts follow a similar trend, showing a marked increase from 2015 onward and peaking in 2024. This trend underlines both the growing academic weight of AI-related research and its relevance in addressing challenging engineering problems.

Figure 2 shows the publication trends of AI-driven structural engineering research across several journals from 2000 to 2024. Among the most prominent sources, only the top five journals with the highest number of publications are considered: Engineering Structures, Structures, Automation in Construction, Journal of Building Engineering, and Thin-Walled Structures. These journals are important venues for disseminating innovative research, since their major contributions to the development of AI applications in structural engineering have played a major contribution in advancing the field. The statistics show a slow rise in research activity in the early years followed by a sudden surge in publications after 2015, suggesting an increasing interest in AI applications within this field. Engineering Structures and Structures show the most notable rise among the sources, especially starting from 2020 forward. This trend implies that in steel structure engineering, these publications now serve as main venues for publishing research on AI. Particularly noteworthy is the fast rise in publications within Structures after 2020, which reflects a recent surge in research contributions most likely driven by the growing acceptance of ML, optimization strategies, and computational modeling in structural design.

Though at a rather slower pace, other journals including Automation in Construction, Journal of Building Engineering, and Thin-Walled Structures—also exhibit a consistent upward trend in AI-related publications. Particularly from 2018 onward, these journals have gained popularity as AI-based approaches are increasingly applied across multiple domains, including structural design, optimization, and performance assessment. This steady rise in publication frequency suggests that AI methods are expanding beyond traditional design principles into broader applications, such as structural resilience evaluation, real-time monitoring, and automated construction.

Figure 3 shows the worldwide distribution of structural engineering research motivated by AI and identifies important contributing nations. Reflecting its strong investment in data-driven approaches and computational technologies, China (23.6%) leads the field, followed by the United States (10.3%), which continues to be a major center for structural analysis and design. Iran (8.8%) and India (5.7%)—both actively advancing structural performance evaluation and optimization—are other major contributors. Similarly, the United Kingdom (5.0%) and South Korea (5.0%) have made significant contributions, with a focus on enhancing the accuracy and efficiency of the engineering process. Apart from these leading countries, Australia (3.3%), Vietnam (3.1%), Canada (2.8%), and Turkey (2.7%) have also played instrumental roles in shaping AI-driven structural engineering research. The “Other Countries” category, accounting for 29.7%, emphasizes the global reach and growing relevance of artificial intelligence applications in structural engineering across many regions.

Visualizing the most often used terms in AI-driven structural engineering research, the keyword co-occurrence network (Figure 4) shows their interconnections and thematic clusters. Comprising several color-coded clusters, each with a different research focus, the network is each keyword’s size reflects its importance in the dataset; conversely, the proximity and connecting lines show the strength of terms’ relationships. Key words including “machine learning”, “prediction”, “model”, “structure”, “analysis”, “method”, and “genetic algorithm” appear most at the center of the network. This implies that research in this domain heavily emphasizes predictive modeling, structural analysis, and algorithmic optimization. Emphasizing its use in structural performance enhancement, the term “genetic algorithm” is tightly related to “optimization”, “frame”, and “optimal design”. The red cluster is centered around “machine learning”, “prediction”, and “strength”, indicating a focus on AI-driven approaches for capacity estimation, structural behavior modeling, and material property analysis. This cluster includes terms such as “fire resistance”, “column”, “shear strength”, and “capacity prediction”, showing the role of AI in evaluating load-bearing capacities and failure mechanisms in steel structures. The blue cluster emphasizes “structural health monitoring”, “detection”, and “classification”, indicating a strong research focus on damage detection, real-time assessment, and digital twin technology. This fits the growing acceptance of computer vision techniques and deep learning for automated structural inspection and reliability assessment. The green cluster—which centers on “genetic algorithm”, “frame”, and “optimization design”—represents another important area. This points to the focus of research on seismic reliability analysis, structural optimization methods driven by AI, and improvement of steel frame performance. Terms like “finite element simulation”, “deep learning method”, and “graph neural network” point to the way AI is being combined with cutting-edge computational approaches. In engineering applications, structural reliability, performance evaluation, and uncertainty quantification all depend on this integration. The keyword network (Figure 4) shows generally the increasing importance of AI, deep learning, and optimization methods in structural engineering research. The grouping of related keywords emphasizes how AI is being used in predictive modeling, performance analysis, structural monitoring, and optimization, determining the course of data-driven engineering solutions.

The integration of AI in structural engineering has obviously evolved over the last two decades. Early years mostly focused on rule-based systems, genetic algorithms, and shallow neural networks—mostly used for design optimization or basic capacity prediction. As the field matured, researchers gradually shifted toward more sophisticated methods, including support vector machines, ensemble learning models, and metaheuristic optimization frameworks. After 2015, with increasing computational resources and access to larger datasets, deep learning techniques—particularly convolutional and recurrent neural networks—began to dominate studies focused on structural health monitoring, damage detection, and time-series forecasting. Reflecting the need for transparency in safety-critical domains, most recently the interest has grown into Explainable AI (XAI) and hybrid approaches.

Three main applications—ML, IML, and XML—are investigated in our scientometric analysis. Section 3, Section 4 and Section 5 include representative studies that demonstrate how these approaches tackle complex engineering problems to show an extensive view of AI applications in the field.

3. An Overview of ML Application in Steel Structures

To maintain focus and ensure scientific clarity, this review concentrates on supervised learning algorithms, which represent the most widely applied category in structural engineering tasks. Although other machine learning paradigms such unsupervised and reinforcement learning have great value, a thorough review of all current ML models would exceed the scope and intended length of this paper. Therefore, a curated set of algorithms with a demonstrated applicability to structural prediction, optimization, and evaluation is examined in the sections that follow. To help better navigate the hierarchy and relationships among these supervised learning techniques, Figure 5 offers a graphical summary of their classification.

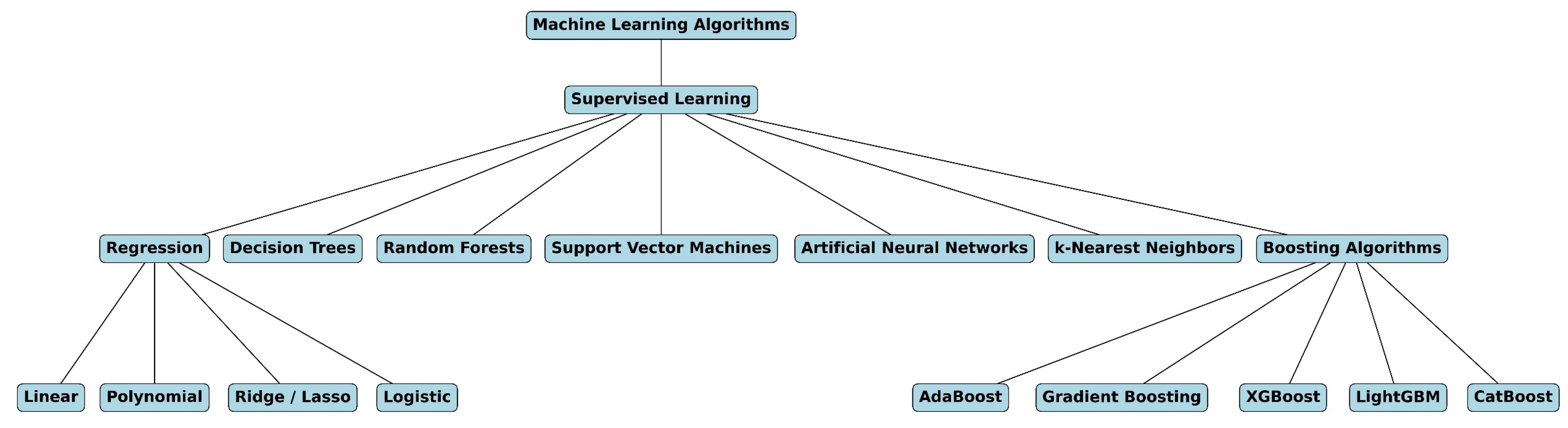
3.1. Supervised ML Algorithms

3.1.1. Regression Algorithms

One of the simplest regression models, linear regression, uses a straight-line equation to build a direct link between input and output variables. This approach is categorized as simple linear regression (for a single predictor) or multiple linear regression (for many predictors) depending on the count of input variables. Expanding on regression techniques, multivariate regression extends multiple linear regression by concurrently predicting several output variables, thus helping to understand interdependencies between inputs and outputs in complex systems. By including higher-degree polynomial terms in the equation, polynomial regression unlike linear models captures nonlinear relationships. Lasso regression adds an L1 regularization term to handle problems with correlated input features, helping to shrink less relevant coefficients toward zero and so accomplish feature selection. Another type of regularized linear regression, ridge regression, maintains all variables in the model by using L2 regularization to lower the impact of less important features. Although these methods are meant for continuous variable prediction, logistic regression is extensively applied for classification problems by estimating the probability of an outcome and mapping inputs to discrete categories. In structural engineering, each of these regression techniques has unique uses; linear regression is appropriate for simple predictions like load-bearing estimates, polynomial regression is helpful for modeling nonlinear material behavior, and logistic regression helps in binary classification tasks including evaluating structural safety compliance [15,16].

3.1.2. Decision Tree

Considered a generally used ML method with simplicity and interpretability [17], decision tree (DT) analysis is particularly useful for classification and regression activities. This approach methodically divides difficult datasets into smaller pieces. A DT is a nonparametric model that divides the input space into discrete areas, each matching a particular decision result. The structure comprises a root node, which acts as the starting point for decision-making, branches reflecting various conditions, decision nodes performing feature-based tests, and leaf nodes, indicating final predictions. The learning process alternately divides the dataset depending on chosen criteria, such minimizing Mean Squared Error (MSE) in regression problems. With each leaf node serving as a last classification or prediction, the path from root to leaf defines the decision rules within the tree. The aim is to build a compact tree with few decision nodes such that predictive accuracy is maintained. Avoiding overfitting depends on appropriate stopping criteria that limit tree depth or stop too frequent divisions. DTs demand minimal data preparation, are quite flexible, able of managing both numerical and categorical data. Their sensitivity to small data variations and overfitting sensitivity, however, can cause instability and accuracy loss relative to more sophisticated tree-based models like Random Forests and Boosting Algorithms. Regularizing methods—such as pruning or limiting tree complexity—are widely used to improve performance, guaranteeing better generalization to unseen data.

3.1.3. Random Forest

Widely used in both classification and regression tasks, Random Forest (RF) [18] is a potent ensemble learning method. RF improves predictive accuracy by building several DTs and aggregating their outputs, thus lowering the overfitting risk. The basis of RF, the idea of ensemble learning, depends on the combined ability of several models to generate more consistent results. Bootstrapped aggregation (bagging), in which the dataset is randomly split into several subsets and separate classifiers are trained on each subset, is one of the most successful ensemble techniques available within RF. This method reduces variance and enhances model stability by means of some data points appearing in several subsets. Majority voting (for classification) or averaging (for regression) determines the last prediction, thus guaranteeing better generalization on fresh data. RF is unique in that it randomly chooses features during tree building, thus lowering correlation between individual trees and improving model performance. For handling high-dimensional datasets with many input variables—a difficulty that conventional Decision Trees often face—this randomness makes RF especially efficient. While training many trees is computationally efficient, producing predictions from a trained RF model can be time-intensive because the demand to process several trees concurrently. Among RF’s main benefits are its lower sensitivity to overfitting and greater resilience than of a single Decision Tree. RF is easily available for users without strong knowledge in ML since it often performs well with default settings even without great fine-tuning.

3.1.4. Support Vector Machines

Support Vector Machines (SVM) are a widely used ML technique known for their effectiveness in classification tasks [19]. Originally presented for handling linearly separable data, SVM has since evolved to accommodate more complex problems including nonlinearly separable datasets, regression (Support Vector Regression, SVR), and clustering (Support Vector Clustering, SVC). Although its main use is still in classification, SVM’s flexibility lets it be applied in many fields needing strong accuracy and solid decision limits. Fundamentally, SVM seeks to identify the best separating hyperplane maximizing the margin separating several data classes.

Its orientation and position are much influenced by the support vectors, the important data points closest to the hyperplane. SVR uses a similar idea but concentrates on fitting a function that retains most data points inside a specified margin, thus allowing some flexibility in error tolerance in regression problems. SVM uses kernel functions and penalty parameters to improve its capability in situations when data are not linearly separable. While preserving a wide margin, the penalty parameter adds slack variables that enable controlled misclassifications, thus balancing accuracy with generalization. Conversely, kernel functions create a higher-dimensional space from the original input space where a linear separation is feasible. Commonly used kernels include sigmoid, linear, poisson, radial basis function (RBF), and sigmoid functions, each with different benefits contingent on the dataset.

3.1.5. Artificial Neural Networks

Inspired by the organization and capability of the human brain, artificial neural networks (ANNs) are a fundamental ML method. Originally designed for pattern recognition tasks, Rosenblatt’s perceptron model in 1958 helped to form the idea. Computational power improvements over time have allowed ANNs to develop into more advanced designs able to address challenging ML tasks. ANNs have developed into several specialized designs each intended to solve particular ML problems. The most fundamental form is the feed-forward neural network (FFNN), in which data moves just from input to output layers. Incorporating several hidden layers, an advanced form of the Multilayer Perceptron (MLP) improves processing capability. Conversely, the Radial Basis Function Neural Network (RBFNN) is especially fit for specialized uses since it uses radial basis functions as activation mechanisms. Applied in fields including structural engineering, convolutional neural networks (CNNs) are optimized for image processing and pattern recognition, playing a major part in crack detection. Designed to manage sequential data, recurrent neural networks (RNNs) and their sophisticated variant, Long Short-Term Memory (LSTM) networks, shine in capturing long-term dependencies. The Adaptive Neuro-Fuzzy Inference System (ANFIS) is another hybrid method whereby neural networks are combined with fuzzy logic to improve decision-making capacity in uncertain surroundings [20].

Inspired by the human brain, which has linked layers of neurons processing and interpreting data, ANN architecture follows Input, hidden, and output layers. The hidden layers use sophisticated computations to derive significant patterns from unprocessed data. An ANN’s efficiency mostly relies on elements like activation functions, which control signal flow across the network. The sigmoid or Rectified Linear Unit (ReLU) controls neuron activations, influencing the learning process. ANNs need hyperparameter fine-tuning of the number of layers, learning rate, and training epochs if they are to reach optimal performance. Correct optimization guarantees against overfitting or underfitting and guarantees the network can generalize to unseen data effectively.

The capacity of ANNs to replicate the learning mechanisms of the human brain defines one of their main advantages. Like neurons and synapses, these networks handle data in a way where experience shapes connections either strengthening or weakening. By means of deep feature extraction made possible by hidden layers, the network can identify complex interactions inside data. In difficult problem-solving activities, high predictive accuracy depends on this layered approach. Modern ML applications depend on ANNs since they offer a strong framework for adaptive learning by modeling biological neural paths [21].

3.1.6. k-Nearest Neighbor

Mostly used for classification and regression problems, the k-Nearest Neighbor (KNN) algorithm [22] is among the simplest yet most often used ML methods. KNN preserves the whole dataset and generates predictions depending on proximity-based decision-making unlike many other models that build an explicit function or discard training data after learning. The method assigns a class label depending on the majority vote among the k-closest data points, sometimes known as “nearest neighbors”, when classifying a new instance. KNN averages the target values of the closest neighbors to forecast a continuous value in regression problems. Being a non-parametric method, KNN does not presume any predefined data distribution. Its efficiency relies on choosing a suitable value for k and measuring data point similarity using an appropriate distance metric. When no previous domain knowledge is available, the most often used metric is the Euclidean distance; nevertheless, depending on the dataset properties other metrics, such Manhattan or Minkowski distance, could also be used. KNN is a common choice, especially for applications where model transparency is crucial, because of its simplicity and interpretability.

3.1.7. Boosting Algorithms

Combining several weak learners into a more accurate and robust model helps boosting, a ML method, increase predictive performance. Freund and Schapire [23] first proposed the idea of boosting in the middle of the 1990s, which helped to create AdaBoost, among the first adaptive boosting systems. Many sophisticated boosting techniques have been developed since then to improve computational efficiency as well as accuracy. Among the notable examples are Friedman’s Gradient Boosting Machine (GBM), which iteratively improves predictions by minimizing errors via gradient optimization. More recent developments including Extreme Gradient Boosting (XGBoost), Light Gradient Boosting Machine (LightGBM), and Categorical Gradient Boosting (CatBoost) have further optimized boosting techniques by improving speed, lowering memory use, and more effectively handling categorical data.

First presented in 1996 by Freund and Schapire [23], Adaptive Boosting (AdaBoost) was among the first boosting methods to show notable success. AdaBoost’s central concept is to prioritize challenging-to-classify samples, sequentially improving weak learners. The method starts with training a base model on the whole dataset and evaluates mistakes afterwards, strengthening the impact of misclassified events. This guarantees that next models give more of their attention on fixing past errors. Many weak learners are trained as the process runs, each tackling particular shortcomings of the previous models. The resultant ensemble model uses a weighted voting system to decide predictions, giving more weight to more accurate models. Although AdaBoost is quite successful in raising prediction accuracy, its dependence on reweighting misclassified data makes it vulnerable to outliers and noisy data, thus compromising general performance. AdaBoost’s efficiency and ability to improve simpler models help it to still be extensively used in many applications despite this restriction.

Designed to increase predictive accuracy by building models in a stepwise manner—where each new model seeks to correct the errors of the previous one—gradient boosting (GB) [24] is a ML method. GB, unlike AdaBoost, which changes instance weights, trains each next model on the mistakes left by its predecessor, minimizing the residual errors. The name “gradient” derives from the technique applied to maximize the loss function—each iteration moves in the direction most effectively lowering errors. Flexibility is one of its main advantages since it can be used with different loss functions depending on the kind of the problem. But because of its incremental character, computational cost may be high—especially in relation to big datasets.

Designed especially for speed and scalability when handling vast amounts of data, XGBoost [25] is an advanced application of the gradient boosting framework. It increases prediction accuracy by consecutively training decision trees, in which each new tree fixes the mistakes made by the one before it, same as in conventional GB. Still, XGBoost brings some improvements that boost efficiency. Its regularizing systems are an important aspect, since they stop overfitting and enhance computational efficiency.

Particularly useful for large-scale ML applications, Light Gradient Boosting Machine (LightGBM) [26] is a high-performance gradient boosting method intended for speed and efficiency. Furthermore, unique to LightGBM is its leaf-wise tree growth method, which deviates from standard level-wise methods. This enables the method to create increasingly sophisticated, deeper trees, thus improving predictive accuracy. But especially if the number of leaves is not under control, this rapid tree growth raises the possibility of overfitting. Despite this difficulty, LightGBM is still among the most effective boosting methods, since it can manage vast amounts of high computational-efficient data.

CatBoost [27] is a gradient boosting method that handles categorical features using target-based statistics, instead of one-hot encoding like many other boosting algorithms. This approach helps reduce the risk of data leakage and overfitting. CatBoost uses an ordered boosting method, where each model iteration is trained only on the data that comes before it. This helps produce stable predictions and avoids bias caused by using future data. CatBoost also uses a symmetric tree structure to maximize the search space and speed training while preserving great accuracy. It is a user-friendly option for many ML projects since it requires less hyperparameter tuning when compared to XGBoost and LightGBM. CatBoost is especially suited for uses involving structured data with multiple categorical features since it can effectively manage categorical variables and provide fast, accurate results.

Figure 6 shows the distribution of ML algorithms used in structural engineering research, based on the reviewed papers published between 1990 and 2025. Neural Networks (NN), with the largest share at 53%, remain the dominant choice across a wide range of structural applications. Boosting Algorithms (BA) follow with 18%, clearly indicating their growing presence in recent years. Support Vector Machines (SVM) account for 8% of the total, while Random Forest (RF) and Decision Trees (DT) each contribute 5%. Regression-based Approaches (RA) also represent 5%, and the remaining 6% are grouped under Other methods, which reflects a combination of various ML techniques. This distribution underscores the strong reliance on NN-based models, while also highlighting the increasing role of ensemble methods such as BA, RF, and DT in structural engineering research.

3.2. ML for Steel Joints, Connections, and Rotational Stiffness Prediction

Including ML into steel connections and joints helps to predict structural behavior with much more accuracy and efficiency, thus reducing dependence on expensive experimental testing and conventional empirical formulations [28,29,30,31,32,33]. Several research have used ML techniques to enhance the prediction of moment-rotation behavior, joint stiffness, and strength of bolted and welded connections.

Paral et al. [34] presented a deep learning-based method for evaluation of semi-rigid joint condition in steel frames. The model efficiently analyzed global vibration response signals from impulse excitation by combining Convolutional Neural Networks (CNN) with Continuous Wavelet Transform (CWT). Emphasizing moment-rotation (M-φ) correlations, Kueh [35] suggested explicit mathematical formulations for steel flush endplate beam–column connection rotational stiffness prediction. Practical formulations were derived depending on geometric and material characteristics using ANNs and MLR. In another study on moment-rotation behavior, Tran [36] examined flush end-plate connections at elevated temperatures using FE simulations and ANNs to forecast the ultimate moment (Mu) and shape parameters of an optimal M-φ model. Expanding the use of ML in bolted connections, Sarothi et al. [37] created a predictive ML framework for structural steel bearing strength estimation of double shear bolted joints. RF showed the best accuracy (R² = 0.88) above current design formulations. In a similar vein, Jiang et al. [38] investigated ML-based failure load and failure mode predictions for bolted connections of high strength steel. Training eight ML algorithms—including SVM, RF, and XGBoost—the study obtained a failure mode prediction accuracy of 97.2%, higher than the 67.9–85.3% accuracy of traditional design codes.

Beyond ANN models, Multi-Gene Genetic Programming (MGGP) has been investigated for moment-rotation prediction. In modeling semi-rigid connection behavior, Rabbani et al. [39] compared MGGP with ANN-based models and showed that MGGP displayed better accuracy and generalization capacity.

3.3. ML for Buckling and Stability Analysis

Recent developments in ML and AI have produced more exact, data-driven approaches for predicting lateral-torsional buckling (LTB), elastic and inelastic buckling, and stability failure modes in steel buildings. Several studies have also shown how well ANNs might predict LTB resistance. For LTB resistance in slender steel cellular beams, Ferreira et al. [40] created an ANN-based predictive model. The findings revealed notable progress over current analytical models, thus highlighting ML’s structural optimization potential.

The existence of web openings in steel beams presents yet another difficulty for buckling resistance estimate since it can greatly affect post-buckling strength. Developing an ANN model for web-post buckling resistance and failure modes in steel beams with elliptically based web openings, Shamass et al. [41] addressed this problem. While web opening height, width, and radius had negative effects, the study found important geometric parameters influencing buckling behavior including beam height and web thickness (which favorably affected resistance). Their results underlined how successfully ANN-based models capture intricate geometric effects on stability performance. Furthermore, difficult in LTB prediction are steel beams with perforated web geometries. De Carvalho et al. [42] investigated the lateral-torsional buckling behavior of I-beams including sinusoidal web openings. The results imply that engineers using perforated I-sections might find useful design tools in ANN-enhanced predictive models. Xing et al. [43] presented an ANN-based model for local buckling prediction in the fire-resistant design of stainless steel beams. The study trained ANN models optimized using Kruppa’s criteria and k-Fold cross-valuation by including experimental and FE results into a comprehensive dataset, thus ensuring robust and reliable buckling predictions for stainless steel I-sections under fire exposure. Rossi et al. [44] showed how well ANN-based models predicted LTB strength for steel I-beams. Their FEA parametric study investigated LTB resistance under geometric parameters and loading conditions. The ANN model gave better predictive accuracy than current design equations. Developing an ML framework for high-strength steel I-section columns, Cheng et al. [45] addressed the scattered accuracy of conventional design rules. Seven ML models were trained; Categorical Boosting turned out to be the most accurate method.

3.4. ML for Strength Prediction and Optimization of Cold-Formed Steel Structures

Cold-formed steel (CFS) buildings are rather common because of their great strength-to-weight ratio, economy, and sustainability. Predicting their strength, stability, and failure mechanisms still challenges since traditional design approaches sometimes oversimplify nonlinear interactions, residual stresses, and defects. ML is quickly becoming a great tool for load-bearing predictions, cross-section optimization, and structural reliability increase.

By addressing constraints in conventional design approaches that mostly concentrate on global buckling, Xu et al. [46] helped to predict ML-based bearing capacity for cold-formed stainless steel circular hollow section (CHS) columns. Trained on a database of 280 CHS columns, their ML-based approach showed significant accuracy improvements over current design codes, enabling improved predictive models in cold-formed steel engineering. Nguyen et al. [47] estimated the axial compression capacity of cold-formed steel oval hollow section columns using ANN and Adaptive Neural Fuzzy Inference System (ANFIS) models. Comparisons with three current design codes confirmed even more that ML-based approaches are better in estimating CFS section capacity. Fang et al. [48] developed a deep learning framework to evaluate the web crippling strength of cold-formed stainless steel channels addressing web crippling in perforated steel sections. Their DBN-based predictions exceeded conventional web crippling equations; new design equations were proposed based on the ML results. Lu et al. [49] developed a regression-classification ensemble ML model for predicting loading capacity and buckling modes of cold-formed steel built-up I-section columns. With high accuracy in both capacity estimation and buckling mode classification, XGBoost stood out among the tested models. To solve constraints in traditional fire design methods, Shaheen et al. [50] developed an ML-based predictive model for estimating the mechanical properties of high-strength steel at elevated temperatures. The work trained Deep Neural Networks (DNNs) on a large experimental dataset using temperature and chemical composition as input features to predict ultimate tensile strength, yield strength, 0.2% proof strength, and elastic modulus. Shahin et al. [51] developed hybrid ML methods for cold-formed steel-lipped channels to forecast web crippling capacity. Their work honed forecasts by combining ANN with GA and PSO. The PSO-ANN hybrid model exceeded other methods and offered more consistent strength estimates than accepted design guidelines. Yılmaz et al. [52] developed an ML-based predictive model for the load-bearing capacity of lipped channel sections. By training their model on a dataset of 2240 FE simulations, they found that flange length and section thickness were the most important parameters, underlining the importance of ML in geometry-based strength evaluations.

3.5. ML Applications in Steel Frame Design, Optimization, and Damage Detection

For automated visual inspection of steel frame structures, Kim et al. [53] presented a deep convolutional neural network-based damage locating (DCNN-DL) method. The DCNN-DL approach found and overlaid damage sites on input images, thus enabling exact, real-time steel frame inspections. Using ML models, Truong et al. [54] investigated their applicability for load-carrying capacity prediction of semi-rigid steel structures. Twelve ML techniques were tested. With regard to error metrics and determination coefficients, XGBoost showed the best accuracy among the tested models. Aiming to replicate the decision-making process of an experienced designer, Jahjouh [55] investigated the possibilities of ANNs in the design optimization of steel frames. Optimal structural designs for 2D steel frames were produced using an adaptive harmony search technique, subsequently regarded as training data for ANNs. The trained ANN models showed a 99% accuracy in forecasting appropriate designs during verification. By including real-time model training and parameter tuning, Shan et al. [56] developed an ML-assisted optimization framework for steel frame design, thus improving the efficiency of metaheuristic algorithms. The technique dynamically creates surrogate models to improve convergent accuracy and convergence.

3.6. ML-Based Structural Health Monitoring in Steel Structures

Pal et al. [57] presented a deep-learning method for structural health monitoring of a steel frame construction with bolted connections based on vibrations. Developed to extract discriminative features from time-frequency scalogram images of vibration data, a convolutional neural network (CNN) classified Bolt loosening conditions into fully loose, hand-tight, and completely tight (undamaged) categories. Focusing on connection damage identification using statistical vibration features, Naresh et al. [58] developed an ML-based health monitoring system for steel frame buildings. High accuracy in structural damage detection allowed an SVM model to classify both undamaged and damaged conditions to show Analyzing natural frequency fluctuations, Vu et al. [59] investigated ML-based damage identification in steel beams, offering a substitute for conventional structural health monitoring techniques. FEM generated a dataset of natural frequencies under several damage scenarios; ML models including ANN, XGB, and RF were trained to predict damage location, width, and depth.

Although conventional sensor-based monitoring systems—such as strain gauges, fiber Bragg grating sensors, and accelerometers—have been extensively used for damage detection in steel constructions due to their high precision and long-term stability, they are often limited to localized measurements and demand direct physical installation and continuous maintenance. Conversely, for non-contact, wide-area structural inspection, recent developments in computer vision and deep learning present interesting substitutes. These AI-powered visual techniques, particularly those using convolutional neural networks (CNNs), have shown strong performance in tasks such as surface crack segmentation, corrosion detection, and bolt loosening identification. The primary advantage of vision-based approaches lies in their scalability, cost-effectiveness, and ability to process large amounts of visual data rapidly. However, they also face practical challenges such as sensitivity to lighting, occlusion, camera angle, and the need for high-quality annotated datasets. Several recent studies suggest hybrid approaches that use the strengths of both systems to combine sensor signals with vision-based outputs, thus enabling stronger condition assessment. Integrating these two techniques could provide a more robust and interpretable structure for real-time steel structure monitoring in complex environments as the field develops.

Beyond real-time detection, one of the most exciting frontiers of AI in structural engineering is the prediction of long-term degradation in steel structures including industrial frameworks, bridges, and high-rise buildings. Recurrent neural networks (RNNs), long short-term memory (LSTM), and Bayesian networks have been investigated recently in order to forecast damage accumulation depending on operational load, climate exposure, and historical sensor data. Models have been trained, for example, to learn patterns from multi-year monitoring datasets to forecast fatigue crack propagation, coating degradation, and corrosion depth over time. Though early results are encouraging, such applications still provide practical difficulties. These comprise limited access to high-quality long-term field data, environmental condition variability, and the challenge of documenting rare but critical degradation modes. Recent efforts aiming at overcoming these constraints have concentrated on hybrid models combining AI with physics-based deterioration models, providing better interpretability and generalizability. Transfer learning methods let models developed on one structure be adjusted for others with similar typologies concurrently. These methods, which are still under development, imply that AI has great possibilities for lifecycle assessment of steel infrastructure under actual conditions and predictive maintenance planning.

Especially in the automated damage and failure mode detection in steel constructions, ML techniques have brought significant SHM advances. Deep learning and feature extraction-based models have remarkably faithfully classified bolt loosening, connection damage, and other structural failures. Moreover, ML-driven frequency analysis provides a fast approach to identify damage in steel beams and frames, thus reducing dependency on traditional sensor-based methods and hand inspections.

3.7. ML-Based Prediction of Structural Performance in Steel Components

ML uses in shear strength, bending capacity, moment resistance, and structural stability prediction in steel components is investigated in this part.

Li et al. [60] addressed errors in conventional design approaches by developing a data-driven ML model for shear strength of high-strength friction-grip bolts. Backpropagation Neural Networks (BPNN) obtained the lowest coefficient of variation and the best accuracy (93% goodness of fit) among the several ML techniques the study examined. Using 108 stainless steel lipped channels and 238 carbon steel Lite Steel sections as test data, Dissanayake et al. [61] further used ML models to forecast the shear capacity of steel channel sections. The work evaluated several ML methods and found that SVR gave the most consistent shear capacity predictions. Aiming to overcome conventional design codes, Dai et al. [62] concentrated on moment capacity prediction of cold-formed steel channel beams with edge-stiffened and un-stiffened web holes. A FEM was validated against 12 experimental datasets, and an XGBoost model was trained using a database of 1620 samples, obtaining a R² score of ~99%, much above traditional design approaches. Reliability analysis helped to validate the suggested ML-driven equations, guaranteeing adherence to AISI safety standards. Liu et al. [63] expanded this study by developing ML-based models for predicting the ultimate bending moment resistance of high-strength steel (HSS) welded I-section beams. The results confirmed that ML models greatly outperformed both European and American design codes.

To estimate the failure loads of normal and high-strength steel welded I-section beam–columns, Su et al. [64] proposed an ML-based unified design method. Traditional methods were found to understate or scatter failure load predictions when compared to Eurocode and American design rules; the ML approach produced more consistent and dependable results. Utilizing structural mechanics and ANNs to forecast point forces and distributed loads, Tusnin et al. [65] applied ML for load identification in steel structural systems. The suggested approach allows final load estimations, structural decomposition, ML-based projections, and structural integrity monitoring better accuracy in engineering inspections and structural health monitoring.

3.8. ML-Based Seismic Performance Assessment and Optimization

Aiming at seismic collapse behavior using ML, Sediek et al. [66] developed a database of over 900 experimental and numerical results for deep wide flange (W-shaped) columns. The work estimated cumulative inelastic rotation until failure under axial and lateral loading and categorized failure modes (local, global, and coupled). By raising classification accuracy by 30%, the ML models exceeded highly ductile limits and demonstrated the possibilities of data-driven methods in creating future seismic design rules. Using ML models, Imam et al. [67] investigated how best to forecast the seismic performance of steel moment-resisting frames (SMRFs). The study assembled a sizable 29,200 data point collection from 292 structural models, training RF, XGBoost, and ANN. Compared to conventional nonlinear dynamic analysis techniques, the ML-based models showed great predictive accuracy.

Addressing constraints in traditional multivariable regression models, Shin and Kim [68] developed an ML-based framework for estimating the hysteretic behavior of two-sided clamped steel shear walls (TCSSWs). Under cyclic load, the ML-based model shown efficiency in automating and enhancing the hysteretic behavior modeling of steel shear walls. Cho and Han [69] developed a numerical material model to simulate the cyclic behavior of high-strength steel (HSS), thus extending ML applications in seismic engineering. Eliminating the need for expensive LCF tests, empirical equations were proposed to estimate model parameters using just monotonic tensile test data, improving practical applicability.

Hu et al. [70] presented an ML-aided peak and residual displacement-based design (PRDBD) method to use self-centering braces to increase the seismic resilience of SMRFs. Conventional SMRFs dissipate energy through steel yielding, producing significant residual displacements that sometimes call for expensive post-earthquake demolition. Samadian et al. [71] developed surrogate models for seismic and pushover responses of SMRFs, furthering ML applications in seismic engineering. Providing a computationally efficient substitute for traditional nonlinear time history and pushover analyses, CatBoost models emerged as the most effective in the study. Salama [72] investigated ML techniques to maximize the seismic resilience of vertically irregular steel building. Using XGBoost with Owl Search Algorithm (OSA) for hyperparameter tuning produced accurate seismic behavior predictions. The results underlined the great reliance of base shear capacity and general seismic performance on structural irregularities.

3.9. AI Applications in Real-World Steel Structures

In bridge engineering, AI-based inspection and SHM systems are advancing safety, automation, and predictive maintenance. Huang et al. [73] developed a CNN-based deep learning method for structural damage identification (SDI) on steel truss bridges, achieving high detection accuracy using field data. Iacussi et al. [74] explored a drive-by monitoring approach, where smart sensor nodes on moving vehicles predicted bridge deflection shapes with strong agreement to installed sensors. Wang et al. [75] introduced SBDNet, a segmentation network trained on real crack images, enabling pixel-level fatigue crack detection on steel bridge surfaces. Svendsen et al. [76] proposed a hybrid SHM framework combining numerical simulations with experimental data to detect loose bolts and member failure on full-scale steel bridges under environmental fluctuations. In high-rise buildings, Zhou et al. [77] monitored a 300 m twin-tower steel frame where smartphone videos were processed with computer vision to extract vibration patterns. Ghaffari et al. [78] developed an RNN model trained on multi-hazard FE data to predict the dynamic response of tall steel structures, achieving less than 1% error compared to actual displacements.

For offshore and tower structures, AI tools have demonstrated strong practical potential. Wang et al. [79] introduced an ensemble deep learning model (CNN + BiLSTM + SENet) to detect damage in jacket platforms with 95% accuracy, validated by experimental results. Martzikos et al. [80] used field data from scaled floating steel platforms to train ANN models predicting mooring line forces under wave loading. Kouchaki et al. [81] used ML classifiers to detect damage in transmission towers based on vibration data, achieving up to 96% accuracy even under noise-contaminated conditions. Kiyoki et al. [82] predicted bending moments in wind turbine towers using only nacelle sensor data, offering a low-cost alternative to strain-based measurements.

Beyond monitoring, AI is being embedded into design optimization and material reuse. Vlasenko et al. [83] developed an ensemble ML model to non-destructively estimate yield strength of reclaimed steel using magnetic sensor readings, enabling sustainable material reuse with real-time decisions.

Connection and joint evaluation has also benefited from AI integration. Shang et al. [84] created a machine vision system that automatically quantifies bolt loosening by detecting nut rotation angles through image processing.

In the area of maintenance and corrosion monitoring, Huang et al. [85] used an Inception-v3 deep CNN trained on laboratory corrosion images to classify rust severity levels on steel surfaces. The model achieved performance comparable to expert inspectors and enables consistent, rapid corrosion assessment across large steel structures such as bridges, towers, and tanks.

These studies collectively show that AI technologies are now being deployed in real-world settings for steel structure monitoring, inspection, design, reuse, and maintenance. As AI continues to mature, its integration into practical structural workflows will likely expand, making structural engineering more data-informed, efficient, and adaptive. This expanding body of validated applications confirms that AI is no longer limited to simulation environments but is becoming an essential companion to structural engineers in the field.

4. Inverse Machine Learning (IML) for Design Optimization and Performance Enhancement in Steel Structures

IML has become a powerful tool in structural engineering for rapidly investigating complex geometrical designs [86]. Particularly for complicated structural systems, conventional design techniques sometimes involve several iterative changes that can be computationally expensive and time-consuming. Direct mapping design objectives to optimal parameters helps IML simplify this process and enable a greater spectrum of design possibilities by lowering the need for major trial-and-error adjustments [87]. This capacity is especially important for handling complex structural designs where conventional methods might not be able to provide sufficient effective answers. In inverse modeling, one of the main challenges is the ill-posed character of inverse problems, whereby solutions could lack uniqueness or stability [88]. To solve these challenges, several computational techniques have been developed to ensure strong and consistent predictions, thus improving the applicability of IML in useful engineering environments.

In structural engineering, inverse problems mostly concern determining design parameters—such as geometry and material properties—needed to meet specific performance criteria [89]. Conversely, in forward problems structural performance is expected to be dependent on predefined input criteria. Unlike forward analyses, inverse problems are often ill-posed, meaning they can show instability or have several possible answers. Particularly for complex structural designs [90], conventional techniques—such as trial-and-error changes—rely on iterative adjustments and hence are both time-consuming and computationally demanding. IML provides a quick replacement that eliminates the need for constant hand-offering by directly predicting ideal design parameters straight from historical data and ML models. This greatly simplifies the design and optimization process, hence faster and more efficient solutions follow [91]. IML is particularly important for metamaterials and advanced structural systems where the interactions between geometry, material composition, and mechanical performance are highly nonlinear and complicated. Its application to designing buildings ideal for impact absorption, improved buckling resistance, and shape recovery [92] shows its flexibility over many engineering problems. By converting structural design into a data-driven process, IML speeds innovation in demanding structural systems, reduces computing costs, and increases accuracy.

IML Application in Steel Structures

Several studies demonstrating the possibilities of IML in steel construction analysis, fabrication, and performance prediction offer more efficient and statistically driven solutions. IML has been used to maximize steel buildings by improving geometry, mechanical aspects, and material composition.

Teimouri et al. [92] devised an IML framework for designing plate-lattice structures (PLSs) idealized for compression strength and specific recovery force (SFR) in large-scale steel constructions. Their method consisted of three validation sub-frameworks before PLS optimization, 3D-printed using a new shape memory polymer (SMP).

By considering manufacture defect and imperfections, IML has also been used to increase the mechanical robustness of steel-based systems. Glaesener et al. [93] investigated how mechanical response of periodic trusses changed with geometric flaws. Using IML-based defect prediction models, their study examined common defect types over several steel truss topologies to evaluate their impact on effective stiffness. This method actively found and reduced geometric inconsistencies, thus improving the dependability of steel trusses.

Particularly in high-strength and ultra-high-strength steel alloys, IML methods have also been heavily applied to maximize steel materials. Using deep neural networks to improve hohlraum designs for radiation temperature control, McClarren et al. [94] showed an IML-driven optimization framework in a high-performance design environment. Similar uses in steel alloy optimization have been inspired by the approach they used whereby a forward ML model forecasts results and an inverse model finds optimal parameters. Building on this, Lee et al. [95] suggested an inverse design framework for high-strength steels, thus attaining an ultimate tensile strength (UTS) above 2 GPa with improved ductility. Experimentally validated designs with improved mechanical performance resulted from a GA optimized using the Shannon diversity index investigating a high-dimensional search space of chemical compositions and austenitizing conditions. Analogous development of two ML-based materials genome integration systems for inverse microstructure analysis of steels was accomplished by Wang and Adachi [96]. These models allowed inverse design of steel microstructures and direct prediction of material properties to reach desired stress–strain behavior, tensile strength, and elongation. This method helped to create ideal steel compositions with better mechanical properties. Using microstructure image recognition to maximize the composition of martensitic and ferritic steels, Pei et al. [97] introduced an IML-based framework for inverse alloy design, thus improving steel alloy performance. Their method greatly reduced trial-and-error efforts in steel development by using neural networks to identify intricate microstructural patterns and predict alloy properties. Dealing with microstructure-property optimization, Lertkiatpeeti et al. [98] investigated the impact of martensite phase alignment in dual-phase steels by means of a Markov Chain Monte Carlo-based inverse analysis coupled with ML models. Using representative volume element (RVE) simulations incorporated new microstructure descriptors—such as Moran’s index, martensite band index, and martensite orientation—and SVR and ANN models trained on them quantify spatial effects in martensitic phase distributions. Their method effectively tuned steel microstructures for intended mechanical characteristics. Adachi et al. [99] examined IML applications in steel material design more broadly and discussed ML techniques integrating process-property-microstructure relations. The study underlined the growing relevance of IML in improving steel material development by means of automation. Important design factors are the lifetime and fatigue resistance of steel buildings; IML has been applied to maximize these features. By means of both direct and inverse analyses, He et al. [100] devised an ML-based framework to estimate fatigue life and fatigue limits of steels. A Bayesian optimization-based inverse analysis was also conducted to ascertain fatigue limits. Optimizing double-layer protective coatings used in spacecraft friction units, Kolesnikov et al. [101] developed an IML-assisted framework. While the Extra Trees method was used for feature importance analysis, their work combined FEM with adaptive sampling techniques to build a training set. By allowing coatings based on target hardness values to be designed, the inverse ML model helped to achieve predictive accuracies above R² = 0.96, offering an effective method of designing high-performance protective layers.

Relevant for hybrid steel-composite structures, IML has helped to maximize the Automated Fiber Placement (AFP) process in thermoplastic composite manufacture in manufacturing processes. To increase process control, Islam et al. [102] presented a hybrid ML framework combining ANNs, virtual sample generation, physics-based numerical simulations, and experimental data. Using an inverse property estimation framework, Masurkar et al. [88] estimated elastic constants of orthotropic laminates used in steel-composite hybrid structures. Their work structured the problem as an inverse task, whereby a deep neural network model was developed on time-series simulation data to effectively infer material properties.

In recent years, IML has been applied to achieve tangible performance gains in real-world structural components. For example, Challapalli et al. [89] developed an IML-GAN framework that optimized the internal geometry of lightweight metamaterials, leading to a 40–120% improvement in load-bearing capacity compared to traditional lattice designs. Similarly, Shen et al. [103] proposed an inverse design architecture for high-performance gradient honeycomb steel structures, where IML integration resulted in designs that offered improved stress distribution and reduced material usage under high-impact loads. Another study by Challapalli et al. [104] demonstrated how IML can be used to design thin-walled cellular structures made from shape memory polymers, achieving record-high specific recovery stress and a 200% improvement in normalized mechanical performance compared to conventional unit cells. While focused on SMPs, the underlying framework is directly applicable to lightweight steel-composite systems where strength and flexibility must be balanced. IML has also been used in dual-phase and ultra-high-strength steels to refine microstructure design, leading to higher tensile strength and optimized material utilization [105]. These examples show that IML is no longer limited to conceptual or experimental research; it is actively shaping how structural efficiency, geometry optimization, and weight minimization are achieved in modern steel engineering. Using IML on specific structural engineering problems helps to clearly notice its usefulness. In load-bearing capacity estimate, IML enables engineers to define the target resistance and quickly access the design parameters—such as cross-section dimensions or material strength—that satisfy that need. In material selection, IML considers cost, weight, or environmental impact in addition to guiding the identification of perfect material types or grades meeting performance criteria. Without involving many forward simulations, IML guides suitable forms, profiles, or arrangement patterns, thus enabling geometric optimization. These projects demonstrate how much IML can reduce demand for repeated analyses and hand-made iterations by offering a more intelligent and simplified design workflow.

These applications collectively offer not only theoretical frameworks but also clear numerical evidence for IML’s effectiveness in structural engineering. For example, IML-driven metamaterial design achieved up to 120% increases in load capacity [89], inverse alloy optimization exceeded 2 GPa tensile strength with validated experiments [95], and fatigue life estimation frameworks reached predictive accuracy above R² = 0.96 [101]. These results confirm that IML is not merely an abstract modeling concept but a practically validated tool for performance-driven structural optimization.

5. Enhancing Explainability in ML: Concepts, Methods, and Applications in Structural Engineering

Explainability in ML is the ability of models to provide open insights into their decision-making process so ensuring human comprehension of their predictions. Unlike conventional black-box models in which the internal computations are difficult to understand [106], explainable ML techniques aim to reveal the link between input features and output preferences. Transparency of model behavior supports explainability to foster responsibility, trust, and usability in AI applications [11]. One major advantage of explainable models is that they help to ensure that relevant and major events drive forecasts, reducing the risk of erroneous or biased influences [8].

Moreover, explainability facilitates the identification of prejudices in training data, thus advancing fairness and enhancing the quality of decisions made. Open models also contribute to build resilience and reliability by identifying discrepancies or anomalies that might compromise predictive accuracy [107,108]. Beyond only technical improvements, explainability supports ethical considerations since it helps users to critically evaluate model decisions and change them to fit policy, fairness, and operational goals [109,110,111]. While interpretability stresses how easily a human can grasp the reasoning behind a given prediction, explainability stresses on understanding the internal mechanisms and interactions inside a model. Although the terms explainability and interpretability are sometimes used synonymously. Both components are quite crucial in bridging the gap between advanced ML algorithms and human knowledge so that AI-driven solutions remain transparent, trustworthy, and practically relevant in many different fields [112,113,114,115]. XML aims to generate transparent, interpretable, trustworthy ML models guaranteeing their ethical and useful application [116]. Especially in high-stakes decision-making processes, one of its main objectives is to build user confidence by demonstrating that models behave consistently and regularly. While explainability is only one aspect influencing trust in AI, giving users tools to assess the reliability of a model will help to raise confidence in its predictions [117,118]. Apart from this, XAI aims to provide explanations that allow the identification of possible causal relationships inside data, thus transcending observations based on correlation [119]. While conventional ML models focus on pattern recognition, explainable methods help to identify underlying cause-and-effect dynamics, which can then be validated using specialized inference techniques. Simplifying challenging models into understandable insights is also fundamental for XAI so that users may grasp how different features interact and support predictions. By allowing AI-generated decisions to be more readily available, these justifications help to enable informed human supervision and improved integration into useful applications [120]. XAI also emphasizes the transferability of knowledge, that is, the capacity of knowledge to be applied to other problems once the decision-making process of a model is well known. On the other hand, transferring models across tasks depends on a clear awareness of their limitations and presumptions so that predictions remain relevant in new contexts [121,122]. Yet another crucial emphasis of explainability is keeping confidence and consistency in predictions. Users have to be able to assess their certainty, especially in situations when model predictions directly influence outputs produced by AI [123,124]. XAI transparency open communication of constraints and uncertainty, thus improving the dependability of automated decision-making systems. The main goal of XAI is to close the gap between technical complexity and human-centered usability so ensuring that AI solutions remain responsible, interpretable, and compliant with ethical and operational guidelines.

5.1. SHapley Additive exPlanations (SHAP)

Different approaches have developed from enhancing the interpretability of ML models; these can be usually categorized as either model-specific or model-agnostic [125]. Designed to investigate internal dynamics of particular algorithms, model-specific methods offer insights dependent on the structure of the model. By contrast, model-agnostic approaches provide a more flexible approach appropriate for any ML model independent of its underlying design.

One of the most often used model-agnostic interpretability methods [9] is SHAP, which measures the contribution of particular features to model predictions using ideas from game theory. This method views the predictive model as a cooperative game based on Shapley values, in which case features play as players and their influence on the final prediction is assessed methodically either including or excluding them from the model. The Shapley value is the average contribution of a feature across all possible combinations of input variables, guaranteeing a mathematically sound evaluation of feature importance [9].

SHAP is globally, as well as locally, interpretable. Globally, it identifies which traits have the most influence over a whole dataset, providing a general picture of the model’s decision-making pattern [9,126]. SHAP shows how specific input values produced a given result, clarifying local level individual predictions. Using binary representations, SHAP produces linear approximations clarifying their influence on predictions by indicating the presence or absence of features.

Beyond only increasing model transparency, SHAP is quite crucial for the ethical development of AI since it supports responsibility and fairness. By precisely defining the function of every feature in decision-making, SHAP helps to detect possible biases and guarantees that models remain interpretable for end users. Even as ML advances, SHAP remains a simple tool for enhancing trust and openness in complex predictive systems [127].

SHAP’s surrogate model links complex ML models with human interpretability [11] using both local and global explanations. SHAP quantifies its individual influence on a given prediction since it generates Shapley values for each local input feature. This clarifies for consumers which truly influence an outcome and which have either little or no impact on it. Globally, SHAP aggregates these local explanations to provide a more complete view of feature significance over the entire dataset [9,107]. By means of methodically evaluating the contribution of every feature, SHAP guarantees more transparency in model behavior, separating between variables influencing decision-making from those less important.

5.2. XML Application in Steel Structures

To address the complexity of several instabilities in channel sections under axial compression or bending, Mojtabaei et al. [128] created an XML-based model to forecast the buckling behavior of thin-walled structural elements. High accuracy was obtained by the trained ANN models; SHAP analysis revealed feature contributions. With regard to material properties and geometry, Hu et al. [129] then developed XML models for the probabilistic prediction of buckling stress in steel shear panel dampers. While core plate thickness (t) had little effect, SHAP and feature importance analysis found yield strength (fy), height-to-width ratio (α), width-to-thickness ratio (β), and initial imperfection (δ) as critical factors affecting buckling stress. Building on these developments, Hou et al. [130] developed an interpretable ML model to predict the probabilistic axial buckling strength of steel circular hollow section members, addressing the impact of geometric, material, and initial imperfections not explicitly accounted for in current design codes. Parameter impact was assessed using global sensitivity analysis and SHAP. While greatly lowering computational time, the ML-based probabilistic model showed that it closely matches numerical and design code predictions and provides a more detailed and effective method for axial buckling strength evaluation. Extending XML applications to more general structural systems, Samadian et al. [131] developed meta databases and a surrogate modeling framework for steel moment-resisting frames, providing a computationally efficient alternative to nonlinear time history analysis for disaster risk management. Feature importance was evaluated using random forest and SHAP analysis pointing up important elements in SMRF design. XML studies have also concentrated much on fire resistance. Liu et al. [132] created an XML-based framework to maximize cold-formed steel wall design for the economy and forecast their fire resistance time. Although SHAP analysis found important input parameters, the XGBoost model—optimized with Bayesian tuning—showcased great predictive accuracy. Further advancing ML applications in fire-resistant design, Tang et al. [133] developed an XML framework to predict the axial capacity of cold-formed steel channel sections at elevated temperatures, offering an effective alternative to conventional techniques. Features were interpreted using SHAP analysis. The results show ML’s potential to provide faster and more consistent axial capacity predictions as well as to enhance fire-resistant structural design. Apart from fire resistance, XML has helped to enhance the design and reliability of perforated and cellular steel sections. Addressing constraints in traditional design provisions, Degtyarev et al. [134] presented a probabilistic XML model based on Natural Gradient Boosting for predicting the resistance of laterally restrained cellular steel beams. Reliability studies identified the resistance reduction factors needed for compliance with European and US design frameworks; SHAP analysis was then used to improve interpretability. Beyond static loading situations, Widanage et al. [135] investigated the use of XML models for predicting blast loads on rigid structures, thus offering a time-efficient alternative to experimental and numerical methods. Model transparency was guaranteed using XML methods, thus confirming that predictions follow fundamental blast physics rules. Anand et al. [136] similarly used XML models to forecast engineering demand parameters in buckling-restrained braced frames under seismic load, thus reducing reliance on computationally costly simulations. XML methods emphasized important seismic parameters affecting BRBF behavior, thus enhancing model transparency. Fan et al. [137] suggested another creative use for an XML-based framework to forecast the axial compressive capacity of Σ-shaped cold-formed steel with web opening, thus addressing the inefficiencies of conventional finite element and experimental techniques. SHAP analysis revealed important design parameters affecting axial capacity and their interactions, thus offering interpretability. Extending on connections and fastener-related issues, Sarfarazi et al. [138] used XML techniques to forecast the shear strength of stainless-steel column web panels, addressing constraints in current design standards that do not entirely reflect the strain hardening behavior of stainless steel. Twelve machine learning models were tested; Extra Trees Regression had the best predictive accuracy. SHAP analysis identified bolt diameter and the column’s second moment of inertia as the most influential factors in shear strength. Predicting axial capacity and failure modes, Aloko et al. [139] investigated further the use of XML models in cold-formed steel built-up columns. Their work showed that, surpassing conventional strength prediction approaches, ML techniques could efficiently record buckling interactions and load-bearing behavior. The interpretability of the models supports even more the relevance of ML in design validation and optimization. Still, it is difficult to guarantee generalizability over different section geometries and loading conditions. Furthermore, helping seismic performance optimization are XML techniques. Gharagoz et al. [140] presented an XML framework including XGBoost for structural engineering optimizing seismic retrofitting techniques. Considered for seismic energy dissipation and self-centering mechanisms, the framework incorporates the Spring-rotational Friction Damper system. Transparency of models was improved using interpretable models, guaranteeing interpretability for use in decision-making. For the quick evaluation of seismic resistance in steel frames, Su et al. [141] presented an XML-based method including active learning techniques. The dataset comprised 1056 seismic response records from 250 steel frames with varying geometric characteristics and steel grades. Evaluated were seven ML models (DT, RF, SVM, KNN, ADA, XG, CB); Extreme Gradient Boosting (XG) obtained the best accuracy (97.79%). SHAP analysis provided interpretability for seismic response predictions. Applying XML models, Gatheeshgar et al. [142] projected web-crippling strength in cold-formed steel beams with staggered sloped perforations. Four ML models—KNN, RF, SVR, ANN—were assessed. Slope length and bearing plate length were found by SHAP analysis to be main determinants of web-crippling strength. Sarfarazi et al. [143] presented a hybrid XML framework for examining the mechanical response of stainless-steel beam-to-column connections.

Beyond their academic importance, these interpretability techniques now serve practical roles in engineering decision-making. For example, when SHAP values identify specific parameters (such as flange width, thickness ratio, or bolt diameter) as dominant influencers in capacity prediction, engineers can confidently prioritize these variables during section design or material selection. Similarly, in XML-based fire resistance studies, the clear identification of wall thickness or insulation parameters helps design safer cold-formed steel walls without extensive physical testing. In seismic applications, SHAP analysis pinpoints key damping and stiffness properties, allowing for informed retrofitting or configuration changes. These tools enable engineers to move from ‘black-box’ models to traceable and code-aligned decisions, strengthening both model trust and practical design outcomes.

6. Addressing Challenges, Limitations, and Future Directions

Although ML models show very good accuracy in estimating structural responses, several elements limit their usability in professional engineering practice including data availability, model reliability, interpretability, integration with conventional design methods, and regulatory acceptance. This section methodically addresses the shortcomings of current approaches, investigates the main barriers preventing the full-scale implementation of ML in structural engineering, and proposes future directions of research to close the distance between ML-driven discoveries and useful applications.

6.1. Rethinking Model Training: Advancing from Accuracy to Engineering Reliability

6.1.1. Generalization and Overfitting in Structural ML Models

The main issue with current ML applications in steel construction is the excessive emphasis of model accuracy without considering engineering reliability. Although many studies reveal low error rates and strong R² values, these measures do not always translate into safe and reliable structural designs. Overfitting is a main problem whereby a model performs remarkably on training data but fails in real-world or unseen conditions. Unlike conventional engineering models including physical laws (such as equilibrium equations and constitutive models), many ML techniques depend just on statistical learning. This can generate physically contradicting predictions whereby results seem statistically valid but violate fundamental engineering criteria.

6.1.2. Addressing the Gap in Physics-Based Learning

Unlike in computational mechanics and fluid dynamics, where Physics-Informed Neural Networks (PINNs) and hybrid solvers have gained considerable ground—most ML applications in structural engineering remain entirely data-driven [144]. Although on well-curated datasets these black-box models can show remarkable accuracy, they usually lack embedded physical constraints including equilibrium, compatibility, or constitutive relations. As a result, such models risk producing outputs that, although numerically plausible, may contradict fundamental engineering principles, especially under extrapolated or safety-critical conditions [145].

The structural engineering community is starting to investigate Physics-Informed Machine Learning (PIML) as a more reliable substitute to mitigate this shortcoming. These models directly include domain-specific physical laws including elasticity, buckling equations, or dynamic balance into the ML training process. For example, Raissi et al. [145] introduced the foundational framework of PINNs, in which governing partial differential equations (PDEs) are embedded in the neural network’s loss function. Haghighat et al. [146] later extended this method to solid mechanics problems, enabling the network to produce stress or displacement fields that respect the governing equations of structural behavior.

In parallel, hybrid ML–FEM approaches have emerged that blend neural network-based surrogates with traditional finite element formulations. These models seek to preserve mechanical integrity of the results while lowering computational effort—especially in repeated simulations. Recent models, for instance, let ML models act as fast approximators for particular FEM sub-processes including stress field estimate or crack growth under variable boundary conditions [145,147].

A comprehensive review by Habib et al. [144] cataloged over 90 PIML applications tailored to structural PDEs, spanning use cases like stiffness identification, crack propagation, and damage localization. When training data are limited or difficult to obtain—such as post-buckling behavior, fatigue evolution, or high-strain-rate responses—these techniques are especially helpful. Physics-guided constraints in such environments not only stabilize learning but also strengthen engineering confidence in model outputs.

Physics-based learning must clearly be central in bridging the gap between academic experimentation and practical adoption as structural ML develops. Including mechanical rules into data-driven models increases generalizability, transparency, and offers a necessary basis for future possible regulatory approval.

6.1.3. Future Directions for Reliability-Oriented Model Training

• Creating PIML Models
• Hybrid Engineering-ML Models
• Uncertainty Quantification (UQ)

6.2. The Overlooked Role of Feature Engineering and Domain Expertise

6.2.1. The Difficulties Using Raw Data Without Engineering Context

In structural engineering, feature engineering—the choice and modification of input variables—is among the most crucial but underappreciated elements of ML modeling. Many studies direct raw numerical data—such as cross-sectional dimensions, material strength, and loading conditions—into ML models without regard for the deeper physical interactions guiding structural behavior. For buckling failure, for instance, just entering the height, width, and thickness of a steel column might not be sufficient. Rather, engineering equation-derived features—such as slenderness ratio, moment of inertia, and effective length factor—may offer more important predictors.

6.2.2. Why Structural Analysis Driven by ML Requires Domain Knowledge

While fields like image recognition [148] or natural language processing [149] where raw data directly reflects the problem space, structural engineering calls for a complete awareness of mechanics and materials. Ignorance of domain knowledge might lead to models that memorize patterns instead of learning fundamental structural behavior. However, an often overlooked yet critical issue in ML-based structural analysis is the limited transferability of models across different steel structural typologies. A model trained on I-section beams under flexure may not perform well when applied to box-section columns or perforated trusses under axial or torsional loading. This lack of generalizability stems from fundamental differences in governing mechanics, geometric characteristics, failure modes, and load interactions. To address this, several approaches have been proposed. One promising direction is transfer learning, where a pre-trained model is fine-tuned using smaller datasets from a new typology, preserving learned features while adapting to new contexts [150]. Another emerging method is meta-learning, which aims to train models capable of quickly adapting to new structural scenarios with limited data [151]. Domain adaptation techniques are also under exploration to help models account for the shift in data distributions when moving from one structural typology to another [152]. While these techniques offer potential, their use in structural engineering remains limited and largely exploratory. Therefore, future research must systematically investigate cross-typology learning to develop truly generalizable and robust AI models for structural applications.

6.2.3. Future Directions for Feature Engineering and Domain-Driven Learning

• Creating feature selection techniques grounded in engineering
• Incorporating Expert Knowledge into Feature Engineering
• Automated Feature Extraction Techniques

6.3. From Deterministic to Probabilistic Modeling

6.3.1. The Importance of Uncertainty Quantification in Structural Predictions

ML models treat structural properties as fixed parameters rather than stochastic variables, thus providing single-value predictions. Structural materials do, however, exhibit natural variation, and operational and environmental uncertainty results in loads never exactly known. Traditional engineering methods allow for these uncertainties using safety factors; but, ML models typically ignore uncertainty. For example, a neural network forecasting the shear strength of a steel joint could produce a value of 500 kN but does not show a confidence range (e.g., 480–520 kN). The lack of probabilistic insight reduces the reliability of ML-based predictions in applications related to safety.

6.3.2. The Role of Bayesian ML and Monte Carlo Simulations

Two fundamental components of safety-critical structural design, uncertainty quantification and probabilistic risk assessment, can be supported by ML beyond point predictions. Conventional engineering frameworks like Load and Resistance Factor Design (LRFD) embed probabilistic safety margins, yet most ML models remain deterministic. This disconnect limits their practical reliability in engineering settings.

To bridge this gap, Probabilistic ML techniques such Bayesian Neural Networks (BNNs) [153] and Monte Carlo [154] dropout have been adopted to estimate predictive distributions rather than single values. These techniques help quantify epistemic uncertainty—arising from limited training data—and allow engineers to evaluate how much trust can be placed in a model’s prediction [155]. For example, a BNN can estimate that a predicted shear capacity of 480 kN has a 95% confidence range of 450–510 kN, helping decision-makers incorporate statistical safety considerations directly into their workflow.

In parallel, Gaussian Process Regression (GPR) is increasingly used to develop probabilistic surrogate models that approximate finite element responses under uncertain loads or material properties [156]. These surrogates dramatically reduce computational cost when thousands of simulations are needed, for instance, in fragility curve generation or reliability-based design optimization (RBDO). When integrated with Monte Carlo simulations or Latin Hypercube Sampling, such models enable full probabilistic risk evaluations without sacrificing computational efficiency [157].

Embedding explainable AI (XAI) tools—such as SHAP or feature sensitivity analysis—within these frameworks further enhances their credibility. Engineers can not only assess the probability of structural failure but also understand which input uncertainties most influence those risks, improving transparency and accountability [9].

These approaches are now beginning to reshape performance-based structural design, particularly under seismic and fatigue loading scenarios. While regulatory approval is still pending, this convergence of AI and probabilistic engineering offers a promising path toward data-informed, risk-conscious structural decision-making.

6.3.3. Future Directions for Probabilistic and Uncertainty-Aware Modeling

• Adopting Bayesian ML techniques
• Integrating ML with probabilistic design codes
• Developing uncertainty-aware ML models

6.4. Bridging the Gap Between Research and Practice

6.4.1. Why ML Still Is Not Often Applied in Industry?

Although many studies indicate that ML is better than conventional methods, very few ML models have been included into commercial engineering tools. Some primary factors include:

• ML models lack a universal benchmarking system unlike FEA, which follows accepted verification processes.
• Some deep learning architectures demand significant computational resources, thus they are useless for real-time analysis.
• Regulatory and Code Compliance Problems; a highly regulated discipline, structural engineering lacks formal approval of engineering codes using ML-based design methods.

Another key factor limiting the industrial uptake of AI-driven structural optimization is the associated computational cost. The training phase—particularly for deep learning models, evolutionary algorithms, or high-dimensional inverse design frameworks—often requires access to high-performance computing (HPC) environments, including GPUs or multi-core CPU clusters [158]. This is especially true when models are coupled with finite element simulations or need to explore large design spaces through surrogate modeling or generative methods.

However, it is important to note that the computational burden is mostly concentrated during the training or model development phase. Once trained, most ML and IML models are highly efficient at inference and can generate design predictions or optimize solutions in real time on standard computing hardware [159]. Additionally, the emergence of cloud-based AI platforms and lightweight optimization strategies (e.g., pruning, quantization, and knowledge distillation) now offers engineers access to powerful tools without owning dedicated HPC resources [160]. Nonetheless, to train advanced models or explore multi-objective optimizations at scale, HPC remains an enabler rather than a barrier, especially in research or enterprise settings.

6.4.2. Future Directions for Bridging the Gap Between Research and Practice

• Creating Industry-Standard Validation Benchmarks
• Developing ML-Integrated Engineering Software
• Regulatory Frameworks for AI in Structural Engineering

6.5. Expanding the Role of IML in Structural Design

6.5.1. IML and Generative AI as the Next Frontier in Structural Design Automation

While most structural ML applications remain focused on forward prediction, IML and generative AI are reshaping the early stages of structural design by allowing engineers to define performance targets and automatically generate optimized design configurations. This shift holds major implications for steel construction, where structural complexity, load-bearing demands, and geometric constraints often lead to highly iterative and labor-intensive design cycles.

In generative design, AI models such as Generative Adversarial Networks (GANs) and Variational Autoencoders (VAEs) are trained to synthesize novel structural topologies based on desired performance criteria. These models do not merely search for optimum values in a fixed design space; instead, they learn the underlying structural logic and generate entirely new configurations that satisfy both architectural intent and engineering performance. For example, Challapalli et al. [104] demonstrated an inverse design framework using GANs to generate cellular structures with record-breaking recovery stress, revealing how generative models can produce designs that outperform conventional configurations.

In the context of steel frameworks, ML-guided topology optimization—which couples finite element analysis with reinforcement learning or surrogate modeling—has emerged as a powerful technique for generating lightweight, efficient structural forms. AI algorithms explore design variants that would be computationally prohibitive to evaluate through brute-force methods. This has enabled engineers to optimize member layout, cross-sectional geometry, and bracing patterns in ways that reduce weight and material usage without sacrificing stiffness or stability.

Despite these advances, practical challenges remain. Generative models often produce non-code-compliant geometries, requiring post-processing to ensure structural safety and constructability. Additionally, real-world datasets for training such models are scarce, and integration with BIM and FEM workflows is still underdeveloped. Nonetheless, the growing synergy between IML, generative design, and performance-based engineering is paving the way for a new paradigm in steel structure design, where AI supports both creativity and compliance.

6.5.2. Future Directions for Inverse and Generative AI in Structural Design

• Integration of GANs and VAEs into Structural Topology Optimization
• Coupling Generative Design with FEM and BIM Systems
• Data-Driven Evolutionary Design Platforms for Custom Steel Systems

6.6. Regulatory Acceptance and Validation of AI Models in Structural Engineering

6.6.1. Current Regulatory Limitations and Engineering Concerns

Although AI and ML are rapidly advancing structural engineering, they are not formally approved in safety-critical design by any major code authority including the Eurocodes, AISC, or ASCE yet. Current building codes still rely on traditional analytical or empirical formulas that have been tested and validated over decades. These codes have not yet adapted to the use of complex, data-driven models like AI, especially in their “black-box” form, where internal logic may not be transparent or physically interpretable [161]. For now, any AI-based model applied in engineering has to be thoroughly tested and demonstrated to satisfy the same safety criteria established in the codes. This typically means comparing AI predictions with experimental data or ensuring that they align with the safety factors prescribed by standards. Particularly in predicting structural resistance when trained on large, high-quality datasets, several studies have shown that AI can achieve either similar or even better accuracy than conventional codes [162]. Notwithstanding this technical promise, there is still no official path for AI models to be certified or approved as direct substitutes for code-based design equations. To address this issue, researchers have proposed the idea of “engineering equivalence”. This method develops an ML model to replicate the output of a known code equation, thus guaranteeing consistent and logical behavior with accepted engineering principles [163]. If this equivalence is achieved, the AI model might be accepted as a substitute for the original equation. Although this idea is still at an early stage, it shows promise for future updates to codes. At the same time, international standards organizations such as ISO/IEC JTC1 SC42 are working on high-level AI quality and trust guidelines that could later be adapted to civil and structural engineering needs [164,165]. Even so, there are currently no specific clauses in design codes that allow general approval of AI models. In practice, if AI is used, it must typically be justified under “alternative design methods” and backed by strong validation. Explainability is one of the key causes of this uncertainty. Engineering authorities are naturally wary of adopting models that perform well but lack any evident justification for their projections. Given the generalizability of AI models [166], this becomes even more critical.

The lack of comprehensive training data is another issue. Especially catastrophic structural failures are rare and costly to test. Training datasets thus are often small, biased, or lacking important failure scenarios [167]. There are also concerns about accountability: if an AI-guided decision results in a structural failure, it is unclear who bears the legal or ethical responsibility—the software developer, the design engineer, or the authority that accepted the design [161].

These unresolved problems keep most AI applications in structural engineering in a supporting role. Although they help with design exploration, optimization, and monitoring, they are not yet accepted as replacements for code-approved methods in final decision-making. To move forward, researchers are concentrating on creating explainable and hybrid models, combining AI with physics-based rules, and suggesting more precise validation and certification guidelines [159,164]. AI will remain a complimentary but not central player in the structural engineering code environment until those efforts develop.

6.6.2. Role of Explainable AI (XAI) in Meeting Regulatory Demands

Explainable AI (XAI) models—those that integrate techniques like SHAP, and global sensitivity analysis—are especially promising for regulatory consideration. Their transparency and interpretability let engineers to trace model predictions to specific design inputs, satisfying key principles of engineering traceability. This transparency can support formal validation by offering clear reasoning, which is essential for approval in safety-critical applications. While no design code formally certifies XAI models for structural design, their fit with rising trustworthiness criteria makes them attractive candidates for future code inclusion. XAI tools remain useful as interpretive aids until codified paths develop, bridging the gap between high-performance AI models and the regulatory demand for transparent, verifiable decision-making.

Moving forward, the structural engineering community must work toward developing formal AI regulatory frameworks tailored for design approval, certification, and standardization. These frameworks should define quality control protocols, minimum interpretability thresholds, validation benchmarks against code-based methods, and pathways for certifying hybrid models that combine AI with physical principles. Establishing such standards will require coordinated input from engineers, AI researchers, code authorities (e.g., Eurocodes, AISC), and software developers. Without these regulatory foundations, the full industrial adoption of AI in structural design will remain restricted to non-critical applications or limited to use under alternative design justifications.

6.6.3. Future Directions for Regulatory Approval and Model Certification

• Establishing formal AI regulatory frameworks tailored for civil/structural engineering
• Defining interpretability thresholds and validation protocols
• Creating certification pathways for hybrid models combining AI and physical principles

6.7. Practical Barriers to Industry Adoption of AI in Structural Engineering

6.7.1. Data Scarcity, Trust, and the Need for Validation

Although many scholarly studies show the strength of AI models in structural engineering, their actual application in practice is still rather restricted. Data availability presents one of the key difficulties. Many engineering companies find that high-quality structural datasets are either difficult to gather or nonexistent. Many datasets are kept privately by businesses or organizations, and experimental results are often few. Most AI models stay limited to particular cases or academic use [162,164] without access to large and well-structured data. Lack of interpretability is another main problem. Most engineers are taught to operate using transparent models based on exact physical principles. Engineers often find AI models unreliable when they make predictions without displaying how or why, particularly in safety-critical contexts. This lack of trust becomes a serious concern when the model output could affect structural performance, risk evaluation, or code compliance [168]. The need for engineering-level validation forms a third practical obstacle. In academic research, an AI model may be sufficient to exhibit great test data accuracy. In industry, however, models are expected to satisfy code-based safety margins, pass experimental comparisons, and offer repeatable results under several design environments.

These expectations are not only technical but also linked to professional liability and public safety. As long as validation procedures for AI remain unclear or unsupported by formal standards, adoption will remain slow [161,165,167].

6.7.2. Future Directions for Industry Adoption of AI in Structural Engineering

• Enhancing access to shared structural datasets
• Promoting model transparency in safety-critical use cases
• Aligning industrial validation with regulatory expectations

6.8. Advancing Seismic Modeling Through Multi-Physics AI

6.8.1. Limitations of Current Seismic AI Models

Most structural AI applications today treat seismic performance as a simplified dynamic problem—often ignoring the coupling of multi-physical factors such as temperature variation, soil-structure interaction, and real-time degradation during earthquakes. This reductionist approach limits prediction accuracy in real-world scenarios. As structural systems become more complex, and the demand for resilient infrastructure increases, integrating AI with multi-physics modeling becomes important for seismic design and real-time monitoring.

6.8.2. Emerging Research on Multi-Physics AI Integration

Recent studies have explored the fusion of AI with multi-physics finite element methods, including soil-fluid–structure interaction, thermal-mechanical behavior under seismic excitation, and even coupled damage evolution. These models allow AI to learn from both physical laws and real-time data, creating better generalization under rare or extreme events [168,169].

Recent advancements in seismic performance prediction for steel structures highlight the effectiveness of physics-informed machine learning (PiML). By embedding fundamental physical laws into neural networks, particularly using techniques like LSTM, these models reliably predict nonlinear seismic behaviors such as interstory drift, plastic hinge formation, and collapse mechanisms. This integration enhances prediction accuracy and interpretability compared to traditional methods. However, computational demand and data calibration challenges still limit their widespread adoption in design offices.

Despite promising progress, multi-physics AI models require improved data infrastructure, standardized validation protocols, and transparent uncertainty handling to gain broader trust and usability in seismic safety-critical decisions.

6.8.3. Feature Direction for Advancing Seismic Modeling Through Multi-Physics AI

• Coupling PINNs with seismic time-history simulations
• Creating benchmark datasets for earthquake-driven ML training
• Developing real-time digital twins for seismic assessment
• Standardizing validation protocols in Eurocode 8, ASCE 41, etc.

Together, ML, IML, and XAI provide a complementary framework for reshaping structural engineering processes. Their integration has the potential to modernize design strategies while upholding safety, transparency, and regulatory integrity. To summarize their respective strengths and challenges,

Table 3. Summary of ML, IML, and XAI.

Technique	Strengths	Limitations	Key Structural Applications
Machine Learning (ML)	- Rapid prediction of structural responses once trained. - Capable of handling large, nonlinear, high-dimensional datasets. - Useful for surrogate modeling, failure classification, and load capacity estimation.	- Often acts as a “black box” with low interpretability. - Requires large and high-quality labeled datasets. - Limited generalization outside trained domains.	- Performance prediction under complex loads. - Data-driven structural health monitoring. - Load-carrying capacity and failure mode prediction.
Inverse Machine Learning (IML)	- Directly maps performance goals to optimal design parameters. - Reduces manual iteration in parametric design. - Efficient for optimization in multi-variable, constrained problems.	- Inverse problems can be ill-posed and unstable. - Often requires regularization or surrogate models to ensure convergence. - Experimental validation still limited in structural contexts.	- Automated design of cross-sections and steel profiles. - Topology optimization. - Material and microstructure tuning in steel alloy design.
Explainable AI (XAI)	- Automated design of cross-sections and steel profiles. - Topology optimization. - Material and microstructure tuning in steel alloy design.	- Still emerging in regulatory practice. - Trade-off between complexity and explainability. - Interpretations can be misused if not domain-verified.	- Code validation and transparency for AI-driven designs. - SHAP/LIME interpretation of failure risk. - Engineering decision support in safety-critical systems.

provides a comparative overview of these three approaches in terms of their structural applications, benefits, and limitations. The future trajectory of AI in structural engineering depends on bridging the gap between academic advances and industry practices through explainable methods, hybrid physics-guided models, and reliable validation procedures. Furthermore, AI will increasingly contribute to sustainable, climate-adaptive design and life-cycle optimization. Inverse ML will redefine how engineers generate solutions from desired outcomes, opening new frontiers in structural optimization. Achieving this vision requires cross-disciplinary collaboration, industrial validation, and stronger AI literacy in engineering education.

7. Conclusions

Including AI into structural engineering transforms a paradigm change in the design, analysis, and optimization of steel constructions. Over the past three decades, fast development of ML techniques has given engineers great tools to increase predictive accuracy, automate challenging tasks, and derive data-driven insights. But rather than only replacing traditional engineering knowledge, the evolution of AI in this field is about raising its capacity to negotiate the complexity of contemporary building challenges. Using AI, engineers can adopt adaptive, real-time solutions that account for uncertainty, variability, and evolving design constraints, moving beyond traditional simulation-based approaches.

Particularly in fields where more conventional methods have limits, one of the most transforming consequences of AI is its ability to enable more exact decision-making. From load-bearing studies and failure predictions to material selection and seismic performance evaluations, AI models have shown their capacity to provide engineers more complete knowledge of structural behavior. Particularly with IML, engineers can let AI select the best design solutions and directly specify target performance criteria, thus adding a new dimension in optimization. This shift represents a fundamental move away from trial-and-error methods, streamlining the design process and reducing dependence on repetitive simulations

Notwithstanding these advances, the path toward widespread acceptance of AI in structural engineering remains a long one. Practical implementation of AI-driven models still requires greater transparency, standardized practices, and alignment with regulatory codes to ensure their reliability and safety in real-world applications. Moreover, the demand for high-quality, diverse datasets is still a main challenge, since AI models are only as successful as the data they are trained on. Overlooking issues such as data limitations, overfitting, and model interpretability will confine the role of AI in structural engineering to academic research, rather than enabling its practical application

Looking ahead, AI will influence developing fields including digital twin technology, sustainability, and automated building methods beyond its traditional applications, impacting steel structure engineering. Real-time monitoring systems allow AI-powered design frameworks to interact and apply proactive structural assessments and predictive maintenance programs. Moreover, as engineering education evolves, AI literacy will become an essential skill for future professionals, ensuring that engineers not only know how to use AI tools but also critically assess their outputs within the context of engineering principles.

In structural engineering, AI is fundamentally reshaping the approach to design and analysis, going beyond mere technological advancement. Though challenges still exist, the continuous development of AI-driven technologies offers interesting paths for acquiring more intelligent, resilient, and efficient steel buildings. By supporting cooperation between academia, industry, and regulatory authorities, the engineering community can maximize AI’s possibilities and so guarantee that its application stays rooted in safety, reliability, and engineering intuition.