Finite Element Modeling of Acoustic Nonlinearity Derived from Plastic Deformation of 35CrMoA Steel
Abstract
1. Introduction
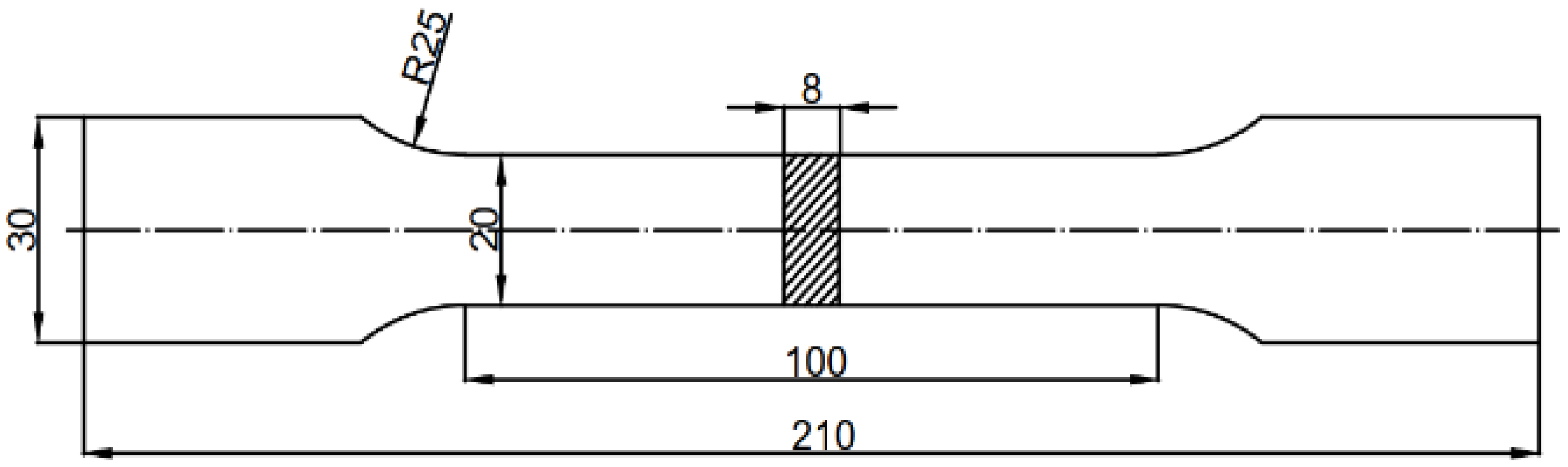
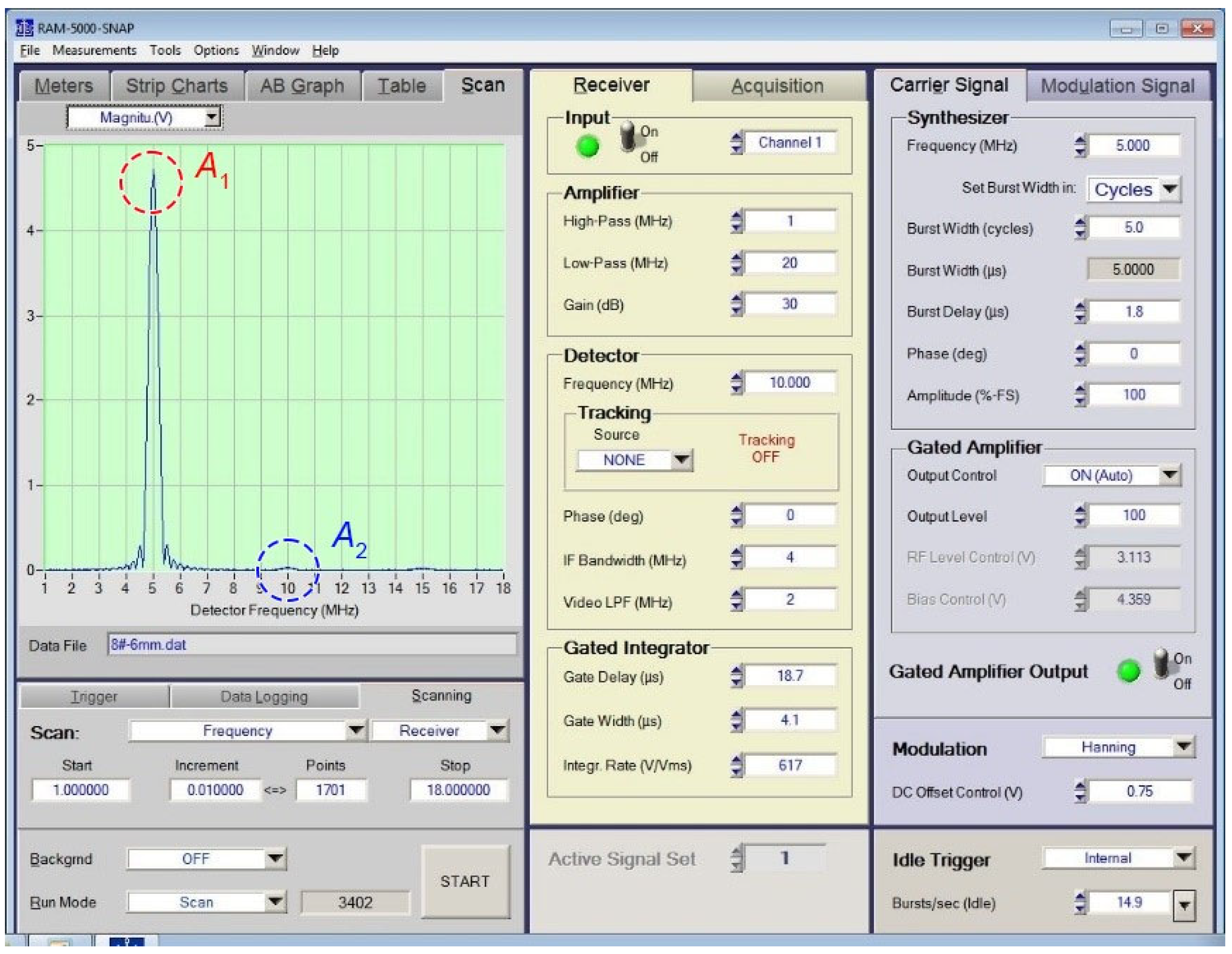
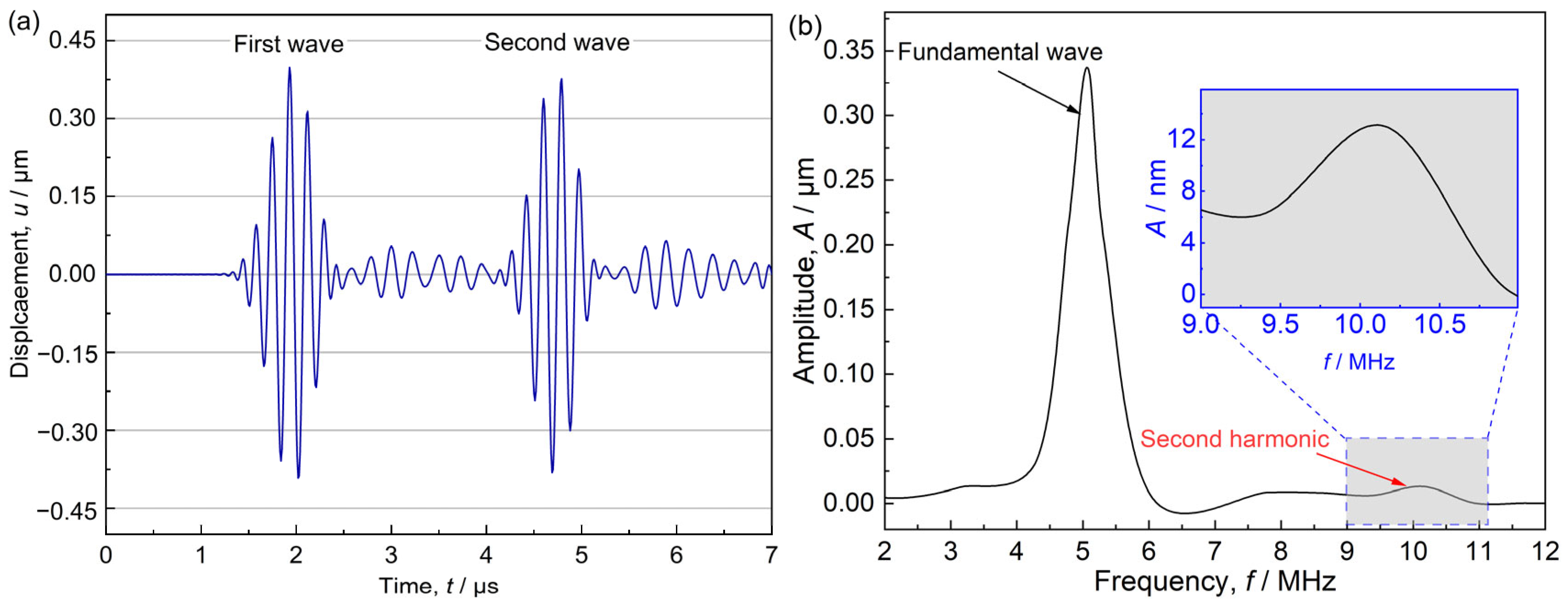
2. Experimental Procedure
3. Mathematical and Finite Element Models
3.1. Theory of Dislocation-Induced Acoustics Nonlinearity
3.2. Dislocation Density Evolution Model
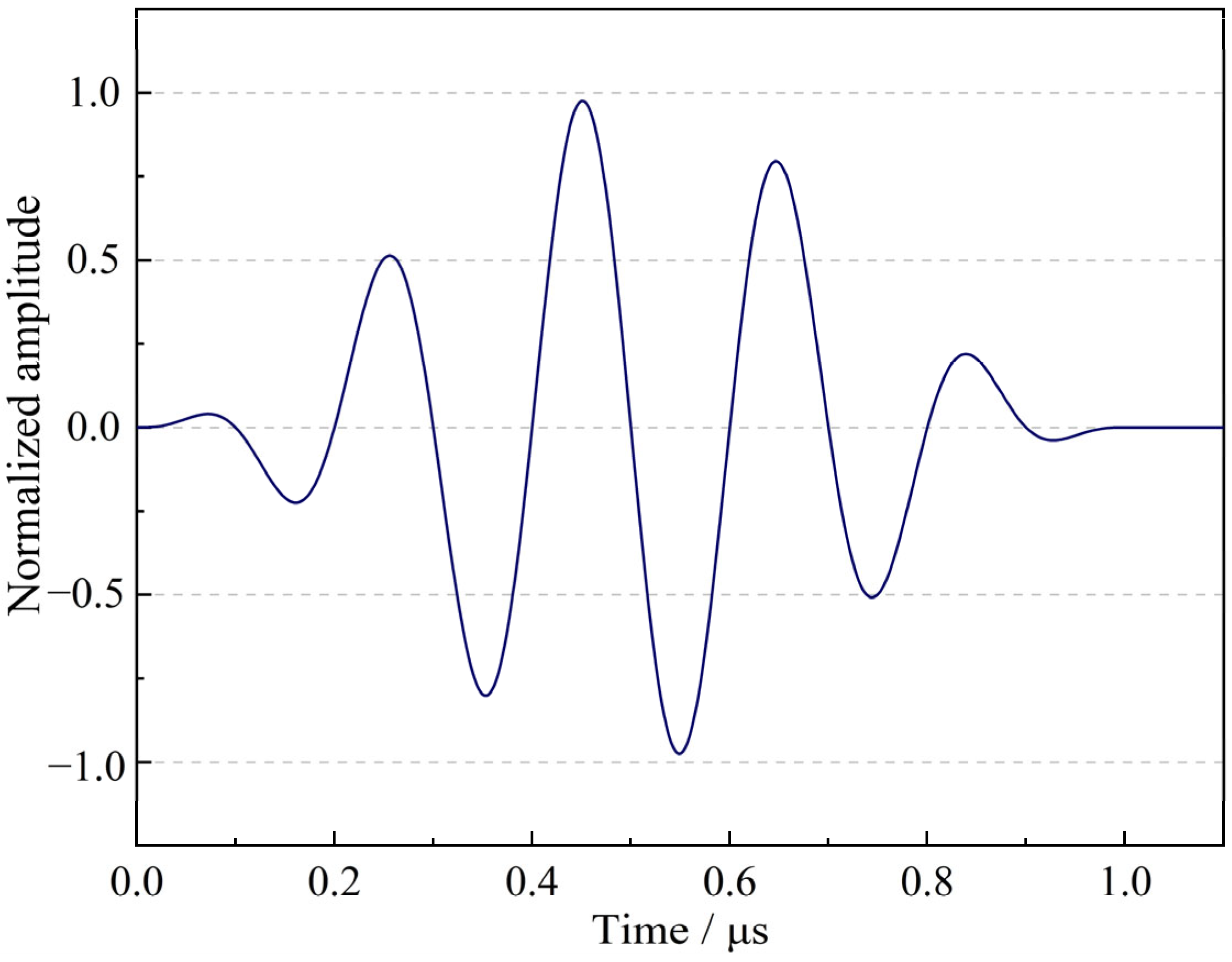
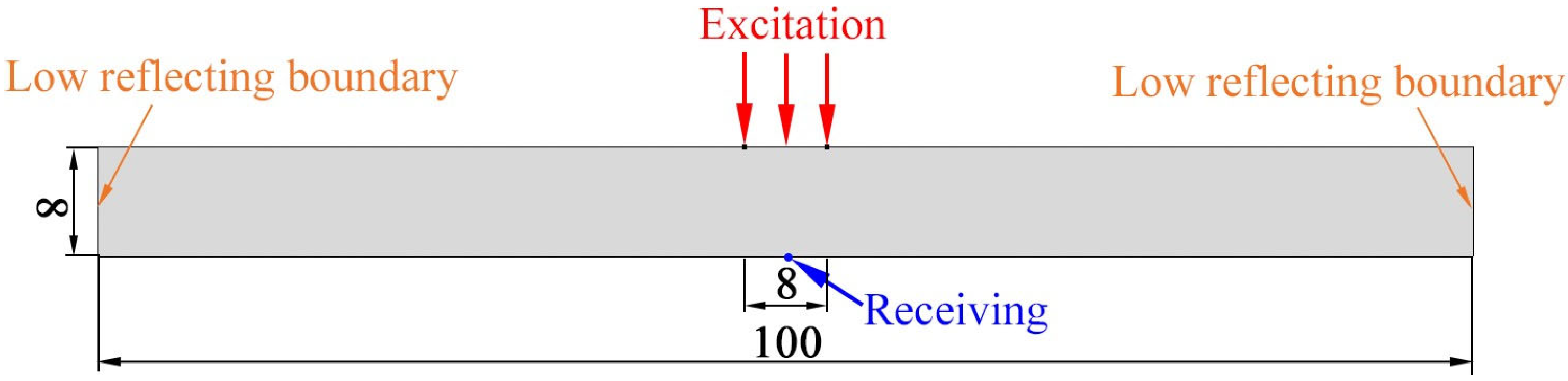
3.3. Finite Element Simulation
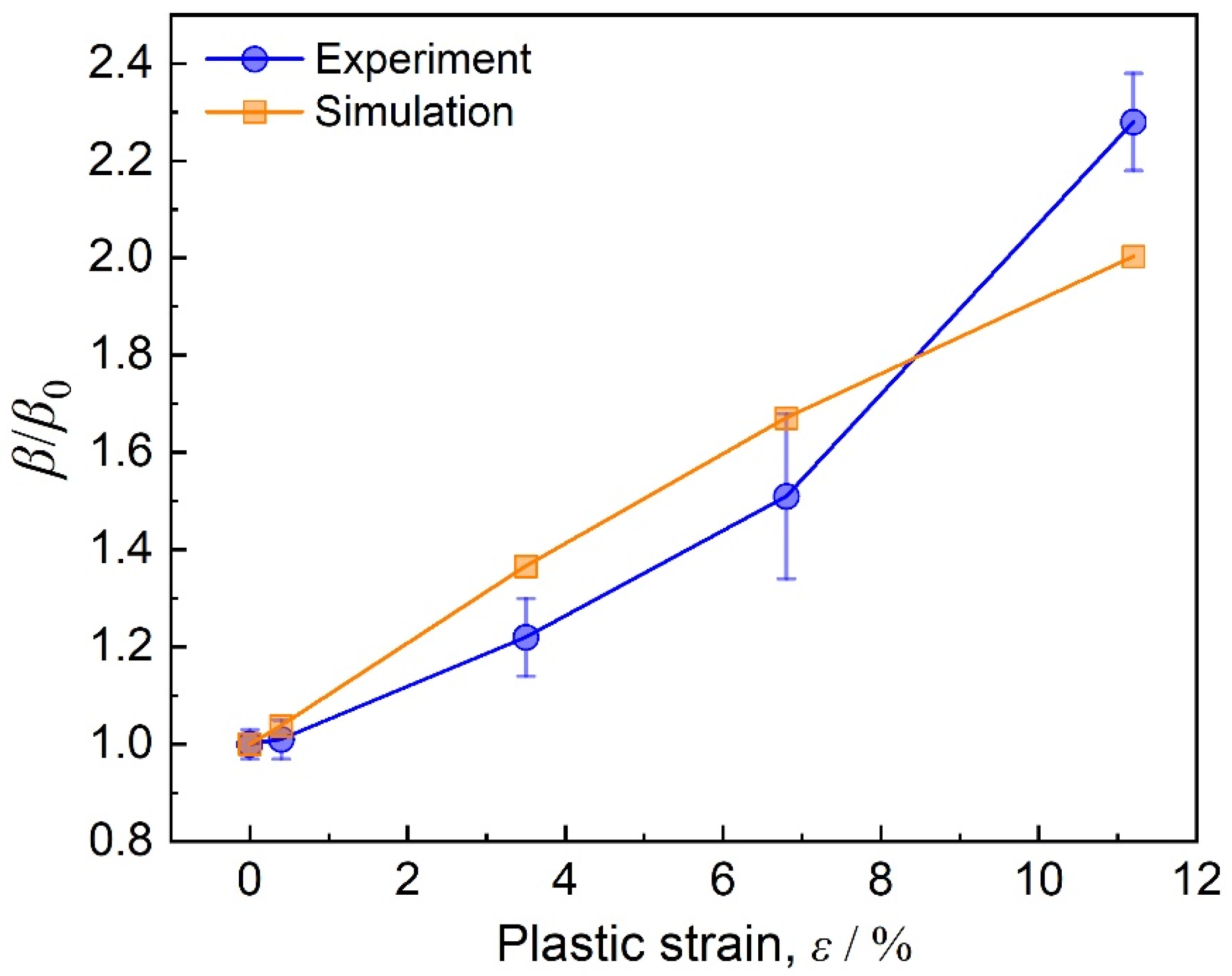
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zeng, J.; Liu, J.; Jia, Y.; Zhao, G. Study on the Deformation and Fracture Mechanisms of Plastic Metals Considering Void Damage. Metals 2023, 13, 1556. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, J.; He, Y. Formation Mechanism and Evolution of Plastic Damage in Billet during Reduction Pretreatment. Metals 2023, 13, 747. [Google Scholar] [CrossRef]
- Wang, X.; Chen, J.; Su, G.; Li, H.; Wang, C. Plastic damage evolution in structural steel and its non-destructive evaluation. J. Mater. Res. Technol. 2020, 9, 1189–1199. [Google Scholar] [CrossRef]
- Sampath, S.; Sohn, H. Detection and localization of fatigue crack using nonlinear ultrasonic three-wave mixing technique. Int. J. Fatigue 2022, 155, 106582. [Google Scholar] [CrossRef]
- Williams, C.L.; Lear, M.H.; Shokouhi, P. On the utility of linear and nonlinear ultrasound for evaluating microstructure-property relationships in laser powder bed fusion 316 L stainless steel. Addit. Manuf. 2023, 73, 103653. [Google Scholar] [CrossRef]
- Yun, H.; Rayhana, R.; Pant, S.; Genest, M.; Liu, Z. Nonlinear ultrasonic testing and data analytics for damage characterization: A review. Meas. J. Int. Meas. Confed. 2021, 186, 110155. [Google Scholar] [CrossRef]
- Bang, S.; Song, D.; Jhang, K. Comparisons of second- and third-order ultrasonic nonlinearity parameters measured using through-transmission and pulse-echo methods. NdtE Int. 2023, 133, 102757. [Google Scholar] [CrossRef]
- Ryu, S.; Park, S.; Jhang, K. Plastic properties estimation of aluminum alloys using machine learning of ultrasonic and eddy current data. NdtE Int. 2023, 137, 102857. [Google Scholar] [CrossRef]
- Nilsson, M.; Ulriksen, P.; Rydén, N. Nonlinear ultrasonic characteristics of a corroded steel plate. Nondestruct. Test. Eval. 2023, 38, 456–479. [Google Scholar] [CrossRef]
- Rauter, N.; Lammering, R. A constitutive model for the analysis of second harmonic Lamb waves in unidirectional composites. Int. J. Solids Struct. 2018, 135, 184–196. [Google Scholar] [CrossRef]
- Deng, M. Second-harmonic generation of ultrasonic guided wave propagation in an anisotropic solid plate. Appl. Phys. Lett. 2008, 92, 111910. [Google Scholar] [CrossRef]
- Masurkar, F.; Tse, P.; Yelve, N.P. Evaluation of inherent and dislocation induced material nonlinearity in metallic plates using Lamb waves. Appl. Acoust. 2018, 136, 76–85. [Google Scholar] [CrossRef]
- Xiang, Y.; Deng, M.; Liu, C.; Xuan, F. Contribution of mixed dislocations to the acoustic nonlinearity in plastically deformed materials. J. Appl. Phys. 2015, 117, 214903. [Google Scholar]
- Hikata, A.; Chick, B.B.; Elbaum, C. Dislocation Contribution to the Second Harmonic Generation of Ultrasonic Waves. J. Appl. Phys. 1965, 36, 229–236. [Google Scholar]
- Granato, A.; Lücke, K. Theory of mechanical damping due to dislocations. J. Appl. Phys. 1956, 27, 583–593. [Google Scholar]
- Cash, W.D.; Cai, W. Dislocation contribution to acoustic nonlinearity: The effect of orientation-dependent line energy. J. Appl. Phys. 2011, 109, 014915. [Google Scholar]
- Zhang, J.; Xuan, F.Z.; Xiang, Y. Dislocation characterization in cold rolled stainless steel using nonlinear ultrasonic techniques: A comprehensive model. Europhys. Lett. 2013, 103, 68003. [Google Scholar]
- Hong, M.; Su, Z.; Wang, Q.; Cheng, L.; Qing, X. Modeling nonlinearities of ultrasonic waves for fatigue damage characterization: Theory, simulation, and experimental validation. Ultrasonics 2014, 54, 770–778. [Google Scholar] [CrossRef]
- Matsuda, N.; Biwa, S. A Finite-Difference Time-Domain Technique for Nonlinear Elastic Media and Its Application to Nonlinear Lamb Wave Propagation. Jpn. J. Appl. Phys. 2012, 51, 07GB14. [Google Scholar]
- Lee, B.C.; Staszewski, W.J. Lamb wave propagation modelling for damage detection: I. Two-dimensional analysis. Smart Mater. Struct. 2007, 16, 249–259. [Google Scholar] [CrossRef]
- Zhu, W.; Deng, M.; Xiang, Y.; Xuan, F.; Liu, C.; Wang, Y. Modeling of ultrasonic nonlinearities for dislocation evolution in plastically deformed materials: Simulation and experimental validation. Ultrasonics 2016, 68, 134–141. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; He, C.; He, H.; Xie, W. Simulation and experimental research on nonlinear ultrasonic testing of composite material porosity. Appl. Acoust. 2022, 188, 108528. [Google Scholar] [CrossRef]
- Kim, J.; Park, J.; Zhu, B.; Cho, Y. Nonlinear Ultrasonic Guided Wave Method Using Semi-Analytical Finite Element (SAFE) Technique on a Damaged SWO-V Spring Coil. Metals 2021, 11, 752. [Google Scholar] [CrossRef]
- Li, F.; Zou, F. A hybrid spectral/finite element method for accurate and efficient modelling of crack-induced contact acoustic nonlinearity. J. Sound Vib. 2021, 508, 116198. [Google Scholar] [CrossRef]
- Cao, W.; Xu, L.; Su, Z.; Pang, B.; Chi, R.; Wang, L.; Wang, X. Modeling of pitting damage-induced ultrasonic nonlinearity in AL-Whipple shields of spacecraft: Theory, simulation, and experimental validation. Int. J. Mech. Sci. 2021, 207, 106659. [Google Scholar] [CrossRef]
- Chen, H.; Li, S. Collinear Nonlinear Mixed-Frequency Ultrasound with FEM and Experimental Method for Structural Health Prognosis. Processes 2022, 10, 656. [Google Scholar] [CrossRef]
- Kim, J.; Song, D.; Jhang, K. A method to estimate the absolute ultrasonic nonlinearity parameter from relative measurements. Ultrasonics 2017, 77, 197–202. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Rokhlin, S.I. Propagation and scattering of ultrasonic waves in polycrystals with arbitrary crystallite and macroscopic texture symmetries. Wave Motion 2015, 58, 145–164. [Google Scholar] [CrossRef]
- Matlack, K.H.; Kim, J.Y.; Jacobs, L.J.; Qu, J. Review of Second Harmonic Generation Measurement Techniques for Material State Determination in Metals. J. Nondestruct. Eval. 2015, 34, 273. [Google Scholar] [CrossRef]
- Zhou, W.J.; Ichchou, M.N. Wave propagation in mechanical waveguide with curved members using wave finite element solution. Comput. Method Appl. Mech. Eng. 2010, 199, 2099–2109. [Google Scholar] [CrossRef]
- Meckings, H.; Kocks, U.F. Kinetics of flow and strain-hardening. Acta Metall. 1981, 29, 1865–1875. [Google Scholar] [CrossRef]
- Xu, B.; Shen, Z.; Ni, X.; Lu, J. Numerical simulation of laser-generated ultrasound by the finite element method. J. Appl. Phys. 2004, 95, 2116–2122. [Google Scholar] [CrossRef]
- Sewell, G. The Numerical Solution of Ordinary and Partial Differential Equations, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 1989. [Google Scholar]
- Zhang, J.; Xuan, F.Z. Fatigue damage evaluation of austenitic stainless steel using nonlinear ultrasonic waves in low cycle regime. J. Appl. Phys. 2014, 115, 113. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, S.; Hu, L.; Yang, X.; Ji, X. Finite Element Modeling of Acoustic Nonlinearity Derived from Plastic Deformation of 35CrMoA Steel. Metals 2025, 15, 343. https://doi.org/10.3390/met15040343
Yu S, Hu L, Yang X, Ji X. Finite Element Modeling of Acoustic Nonlinearity Derived from Plastic Deformation of 35CrMoA Steel. Metals. 2025; 15(4):343. https://doi.org/10.3390/met15040343
Chicago/Turabian StyleYu, Shumin, Lei Hu, Xingbin Yang, and Xiangyu Ji. 2025. "Finite Element Modeling of Acoustic Nonlinearity Derived from Plastic Deformation of 35CrMoA Steel" Metals 15, no. 4: 343. https://doi.org/10.3390/met15040343
APA StyleYu, S., Hu, L., Yang, X., & Ji, X. (2025). Finite Element Modeling of Acoustic Nonlinearity Derived from Plastic Deformation of 35CrMoA Steel. Metals, 15(4), 343. https://doi.org/10.3390/met15040343




