Numerical Analysis of the Laser Forming Process of Cylindrical Surfaces
Abstract
1. Introduction
2. Material and Methods
2.1. Experimental Cases Analyzed
2.2. Numerical Simulation
| Governing equations (written in a Lagrangian description) | |
| Continuity equation | |
| Equation of motion | |
| Energy balance equation | |
| All equations are valid in the domain Ω × γ, where Ω is the spatial configuration of a body and γ is the time interval of interest, where: | |
| Determinant of the deformation gradient tensor (where , being the unity tensor and being the displacement field) | |
| : Density | |
| : Spatial gradient operator | |
| : Cauchy stress tensor (symmetric for the nonpolar case adopted in this work) | |
| : Specific heat capacity | |
| : Temperature of the body | |
| : Heat flux vector | |
| Subscript 0 | : Denotes values in the initial configuration |
| The effects of body forces, acceleration, external heat source, and heat due to mechanical work are assumed to be negligible. | |
| Thermal boundary conditions | |
| The normal heat flux boundary condition of the energy balance (considered valid in, where is the thermal boundary of the spatial configuration) is written as follows: | |
| where is the convection–radiation normal heat flux, is the normal heat flux provided by the laser beam, and is the outward unit normal vector to. The following laws are adopted: | |
| where: | |
| : Convection–radiation heat transfer coefficient. | |
| : Environmental temperature. | |
| : Absorption coefficient. It represents the fraction of incident energy that a material can absorb when irradiated by an external source. | |
| : Laser heat flux distribution function, with and being the power and diameter of the laser beam, respectively. In this work, a Gaussian distribution is adopted: , where r is the radial distance to the center of the laser beam. | |
| A parallel convection–radiation mechanism is typically assumed, i.e., , with and being the convection and radiation coefficients, respectively. In this work, a constant value is adopted for , while the radiation is described in this context as, where is the emissivity coefficient and is the Boltzmann constant. | |
| Constitutive relations | |
| Isotropic Fourier’s law | |
| Stress–strain relation | |
| Thermal Almansi strain tensor | |
| where: | |
| : Conductivity coefficient, taken from Figure 2 | |
| : Isotropic elastic constitutive tensor, Young’s modulus, and Poisson’s ratio taken from Figure 2 | |
| : Almansi strain tensor (e = 1/2 () : Plastic Almansi strain tensor | |
| : Thermal dilatation function (, with being the thermal dilatation coefficient | |
| Von Mises yield function | |
| where is the second invariant of the deviatoric part of ( is the so-called equivalent or von Mises stress), is the plastic isotropic hardening function, and is the yield strength defining the initial material elastic bound. | |
| Hardening function | |
| where: | |
| :
: : |
Hardening coefficient Hardening exponent Equivalent plastic deformation |
| Plastic model | |
| Flow rule | |
| where: | |
| : : | Lie (frame-indifferent) derivative Plastic consistency parameter (derived from the condition ) |
3. Results and Discussion
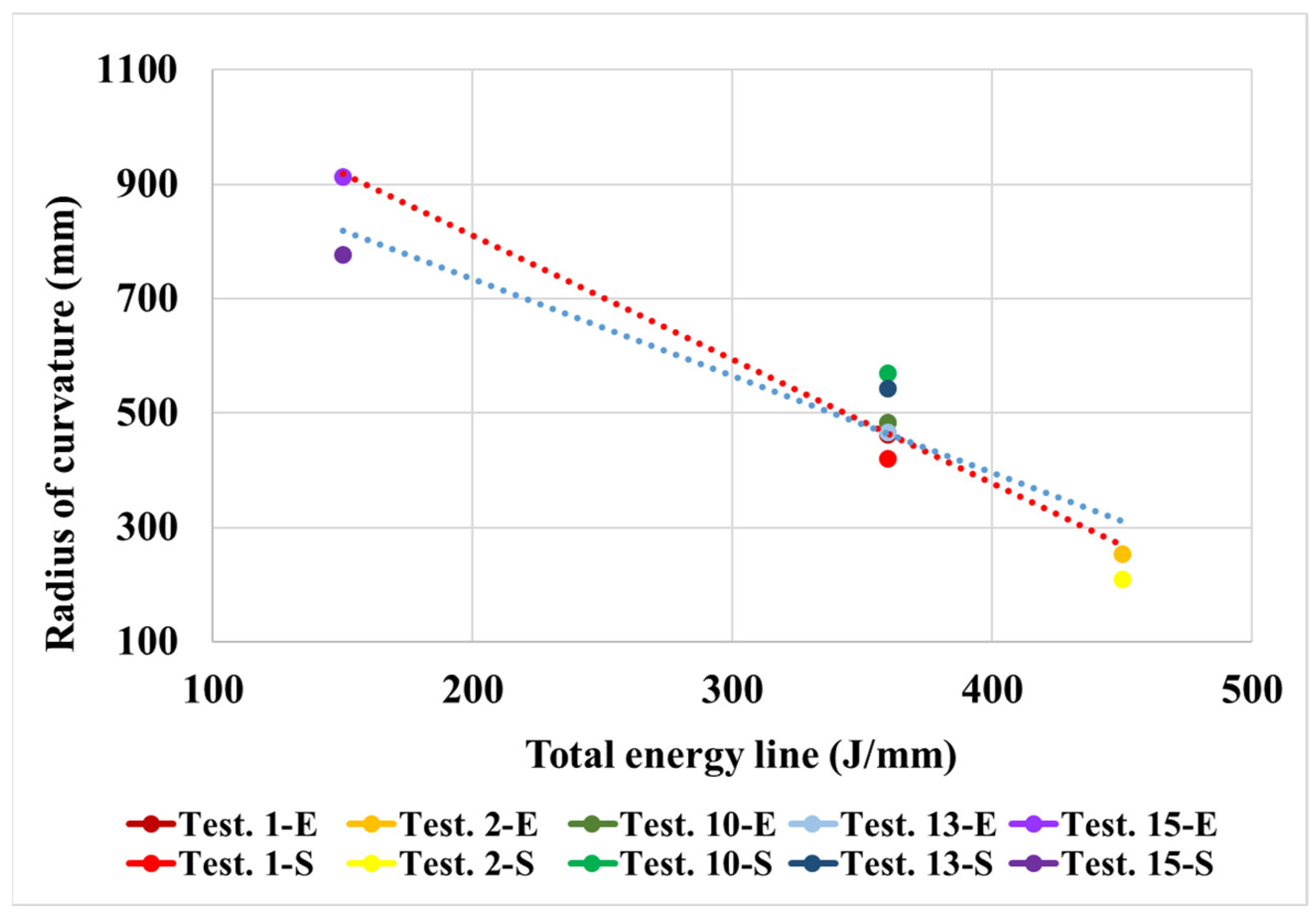
3.1. Experimental Validation of the Radius of Curvature
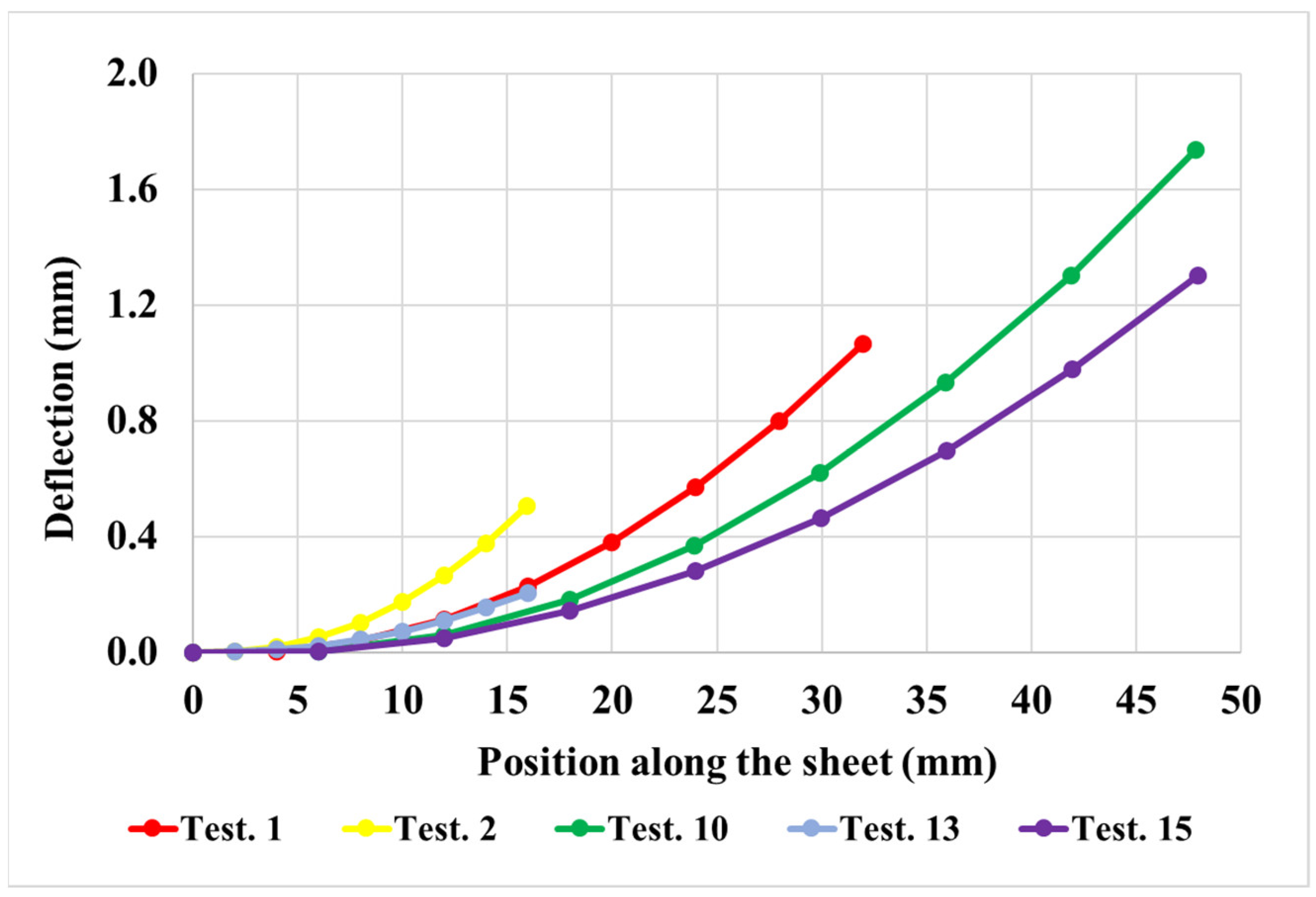
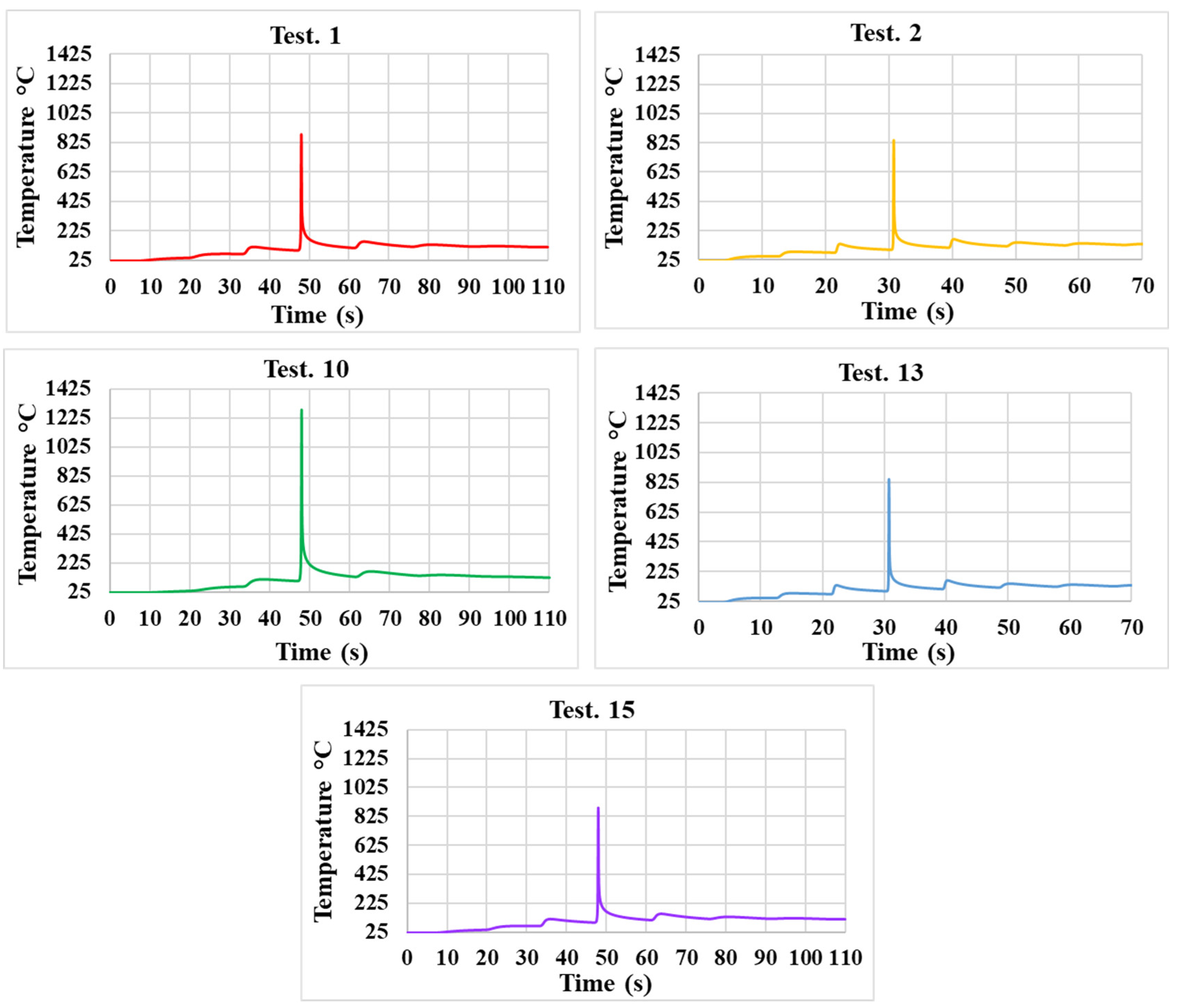
3.2. Influence of Processing Parameters on the Thermomechanical Material Response
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Dixit, U.S.; Joshi, S.N.; Kant, R. Laser forming systems: A review. Int. J. Mechatron. Manuf. Syst. 2015, 8, 160–205. [Google Scholar] [CrossRef]
- Castillo, J.I.; Celentano, D.J.; Cruchaga, M.A.; García-Herrera, C.M. Characterization of strain rate effects in sheet laser forming. Comptes Rendus Mécanique 2018, 346, 794–805. [Google Scholar] [CrossRef]
- Dong, W.; Zhang, Y.; Bao, L.; Shin, K. Effects of laser scanning strategy on bending behavior and microstructure of DP980 steel. Materials 2024, 17, 2415. [Google Scholar] [CrossRef]
- Ablat, M.A.; Qattawi, A. Numerical simulation of sheet metal forming: A review. Int. J. Adv. Manuf. Technol. 2017, 89, 1235–1250. [Google Scholar] [CrossRef]
- Bachmann, A.L.; Dickey, M.D.; Lazarus, N. Making light work of metal bending: Laser forming in rapid prototyping. Quantum. Beam Sci. 2020, 4, 44. [Google Scholar] [CrossRef]
- Zhang, Z.; Shen, H. Numerical study on deformation behaviors in intersecting rectilinear laser bending. J. Manuf. Process. 2024, 127, 98–106. [Google Scholar] [CrossRef]
- Khandai, B.K.; Gopinath, M. Modelling and monitoring of scaling effects in multi-scan laser forming. Opt. Laser Technol. 2025, 186, 112712. [Google Scholar] [CrossRef]
- Cook, F.; Celentano, D.; Ramos-Grez, J. Experimental-numerical methodology for the manufacturing of cranial prosthesis via laser forming. Int. J. Adv. Manuf. Technol. 2016, 86, 2187–2196. [Google Scholar]
- Pennuto, J.; Choi, J. Characteristics of parallel irradiations in laser forming of stainless steel. J. Laser Appl. 2005, 17, 235–242. [Google Scholar] [CrossRef]
- Shen, H.; Zhou, W.; Wang, H. Laser forming of doubly curved plates using minimum energy principle and comprehensive strain control. Int. J. Mech. Sci. 2018, 145, 42–52. [Google Scholar] [CrossRef]
- Vásquez Ojeda, C.; Ramos Grez, J. Bending of stainless steel thin sheets by a raster scanned low power CO2 laser. J. Mater. Process. Technol. 2009, 209, 2641–2647. [Google Scholar] [CrossRef]
- Maji, K.; Pratihar, D.K.; Nath, A.K. Experimental investigations, modeling, and optimization of multi-scan laser forming of AISI 304 stainless steel sheet. Int. J. Adv. Manuf. Technol. 2016, 83, 1441–1455. [Google Scholar] [CrossRef]
- Thomsen, A.N.; Kristiansen, E.; Kristiansen, M.; Endelt, B. Investigation of the profile of laser bends with variable scan distance. Procedia Manuf. 2019, 36, 192–199. [Google Scholar] [CrossRef]
- Shahabad, S.I.; Naeini, H.M.; Roohi, A.H.; Tavakoli, A.; Nasrollahzade, M. Experimental investigation of laser forming process to produce dome-shaped products. Int. J. Adv. Manuf. Technol. 2017, 90, 1051–1057. [Google Scholar] [CrossRef]
- Gollo, M.H.; Nadi, G.; Mehdi, M.; Abbaszadeh, M. Experimental and numerical study of spiral scan paths on cap laser forming. J. Laser Appl. 2015, 27, 012002. [Google Scholar] [CrossRef]
- Safari, M.; Farzin, M. Experimental investigation of laser forming of a saddle shape with spiral irradiating scheme. Opt. Laser Technol. 2015, 66, 146–150. [Google Scholar] [CrossRef]
- Safari, M.; Farzin, M.; Mostaan, H. A novel method for laser forming of two-step bending of a dome-shaped part. Iran. J. Mater. Form. 2017, 4, 1–14. [Google Scholar] [CrossRef]
- Nunobiki, M.; Okuda, K.; Hourai, K.; Shizuka, H. Bending of pure titanium sheet to curved surface shape by laser forming technique. Adv. Mater. Res. 2010, 126, 388–393. [Google Scholar] [CrossRef]
- Abolhasani, D.; Seyedkashi, S.M.H.; Kim, Y.T.; Gollo, M.H.; Moon, Y.H. A double raster laser scanning strategy for rapid die-less bending of 3D shape. J. Mater. Res. Technol. 2019, 8, 4741–4756. [Google Scholar] [CrossRef]
- Abolhasani, D.; Seyedkashi, S.M.H.; Hoseinpour Gollo, M.; Moon, Y.H. Effects of laser beam parameters on bendability and microstructure of stainless steel in three-dimensional laser forming. Appl. Sci. 2019, 9, 4463. [Google Scholar] [CrossRef]
- Wang, X.; Shi, Y.; Guo, Y.; Wang, Q. Design of 3D surface laser forming process. J. Manuf. Process. 2022, 73, 306–315. [Google Scholar] [CrossRef]
- Safari, M.; Miralaa, S.M.; Alves de Sousa, R. Experimental investigation of the effects of process parameters on the radius of curvature in laser forming process of cylindrical surfaces. Metals 2022, 13, 56. [Google Scholar] [CrossRef]
- Naqvi, S.M.R.; Haidry, A.A.; Xie, D.; Ahmad, S.; Liu, Y.; Chen, Y.; Jiao, C.; Jamil, M.; Yan, C.; Shen, L. Influence of laser beam process parameters on the bending ability of Ti-6Al-4V titanium alloy sheets. Int. J. Adv. Manuf. Technol. 2024, 133, 3445–3460. [Google Scholar] [CrossRef]
- Cook, F.; Jacobsen, V.; Celentano, D.; Ramos-Grez, J. Characterization of the absorptance of laser irradiated steel sheets. J. Laser Appl. 2015, 27, 032006. [Google Scholar] [CrossRef]
- Cook, F.; Miró, L.; Celentano, D.; Ramos-Grez, J. Effect of inclination angle on the absorptance of a graphite-coated cold-rolled steel sheet irradiated by laser. J. Laser Appl. 2016, 28, 022001. [Google Scholar] [CrossRef]
- Yamada, K.; Kushida, N.; Wada, S.; Sentoku, E.; Tanaka, R.; Sekiya, K. A machine learning approach for simulation of multi-stage laser forming process. J. Adv. Mech. Des. Syst. Manuf. 2023, 17, JAMDSM0006. [Google Scholar] [CrossRef]
- Lambiase, F.; Di Ilio, A.; Paoletti, A. Productivity in multi-pass laser forming of thin AISI 304 stainless steel sheets. Int. J. Adv. Manuf. Technol. 2016, 86, 259–268. [Google Scholar] [CrossRef]
- Nath, U.; Yadav, V.; Purohit, R. Finite element analysis of AM30 magnesium alloy sheet in the laser bending process. Adv. Mater. Process. Technol. 2022, 8, 1803–1815. [Google Scholar] [CrossRef]
- Nath, U.; Yadav, V.; Bhadauria, S.S. Effects of workpiece size on bending angle in laser forming of Al 6061-T6 sheet. Mater. Today: Proc. 2024, 113, 307–313. [Google Scholar] [CrossRef]
- Fetene, B.N.; Kumar, V.; Dixit, U.S.; Echempati, R. Numerical and experimental study on multi-pass laser bending of AH36 steel strips. Opt. Laser Technol. 2018, 99, 291–300. [Google Scholar] [CrossRef]
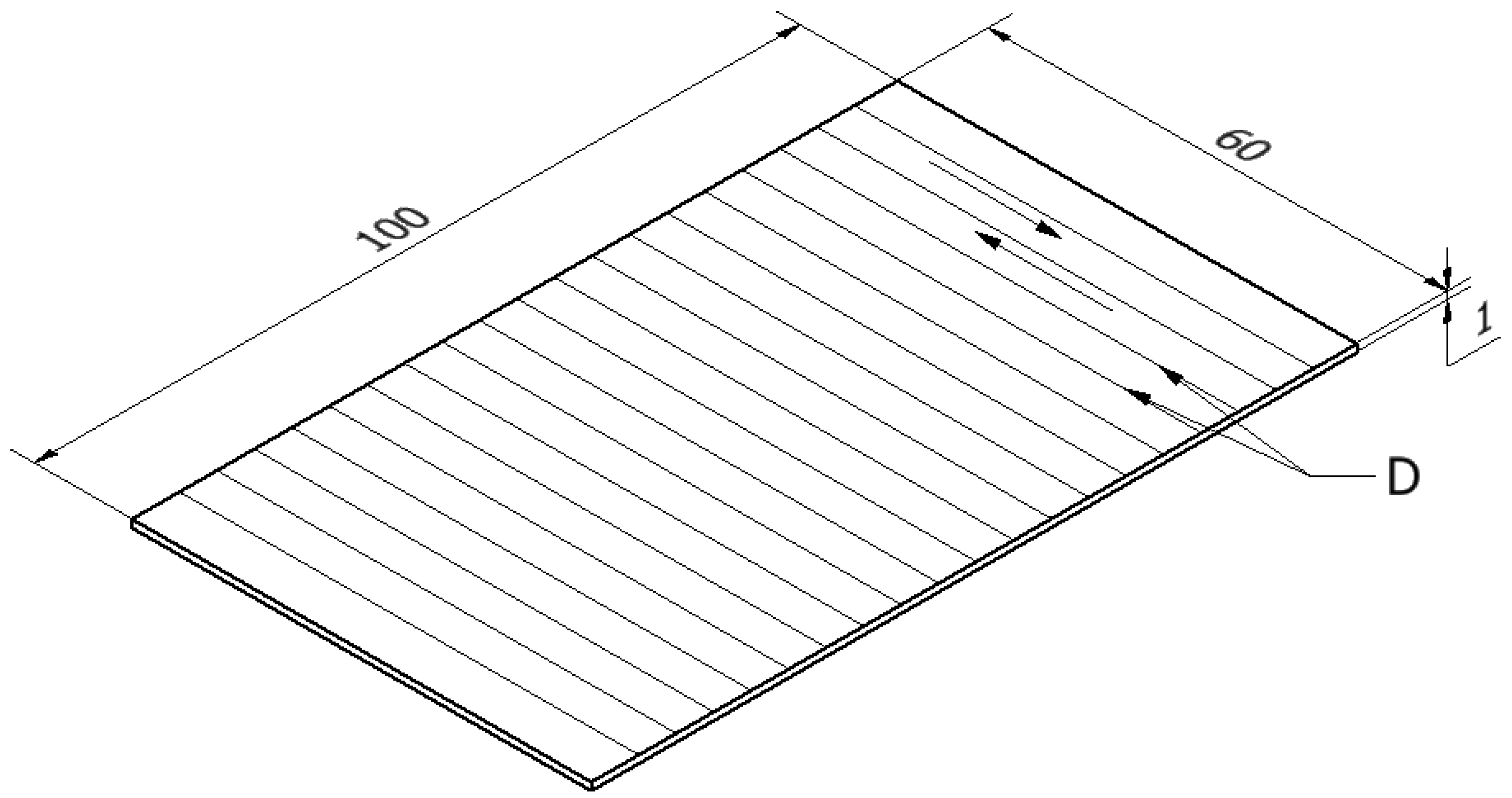
| Test Number | Laser Beam Power, P (W) | Scanning Velocity, V (mm/s) | Distance Between Irradiation Lines, D (mm) |
|---|---|---|---|
| 1 | 72 | 5 | 4 |
| 2 | 72 | 8 | 2 |
| 10 | 108 | 5 | 6 |
| 13 | 36 | 5 | 2 |
| 15 | 72 | 8 | 6 |
| Test Number | R (E) (mm) | R (S) (mm) | (%) |
|---|---|---|---|
| 1 | 463 | 420 | 9.2 |
| 2 | 254 | 210 | 17.2 |
| 10 | 484 | 571 | −17.8 |
| 13 | 467 | 544 | −16.5 |
| 15 | 913 | 776 | 15.0 |
| Test Number | Energy Line, (J/mm) | Number of Passes, | Total Energy Line, (J/mm) |
|---|---|---|---|
| 1 | 14.4 | 25 | 360 |
| 2 | 9.0 | 50 | 450 |
| 10 | 21.6 | 17 | 360 |
| 13 | 7.2 | 50 | 360 |
| 15 | 9.0 | 16 | 144 |
| Test Number | (J/mm) | Temperature (°C) | ||
|---|---|---|---|---|
| Top Face | Half Thickness | Bottom Face | ||
| 1 | 14.4 | 880 | 346 | 290 |
| 2 | 9.0 | 842 | 319 | 266 |
| 10 | 21.6 | 1279 | 489 | 403 |
| 13 | 7.2 | 501 | 216 | 187 |
| 15 | 9.0 | 748 | 241 | 191 |
| Test Number | (J/mm) | Initial Edge | Half Width | Final Edge | |||
|---|---|---|---|---|---|---|---|
| T (°C) | T (°C) | T (°C) | |||||
| 1 | 14.4 | 810 | 0.013 | 880 | 0.019 | 1019 | 0.019 |
| 2 | 9.0 | 779 | 0.011 | 842 | 0.018 | 931 | 0.016 |
| 10 | 21.6 | 782 | 0.017 | 1279 | 0.033 | 1484 | 0.044 |
| 13 | 7.2 | 465 | 0.003 | 501 | 0.007 | 579 | 0.007 |
| 15 | 9.0 | 374 | 0.005 | 748 | 0.015 | 888 | 0.016 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cabezas, D.; Celentano, D.J.; Cruchaga, M.A.; García-Herrera, C.; Monsalve, A. Numerical Analysis of the Laser Forming Process of Cylindrical Surfaces. Metals 2025, 15, 402. https://doi.org/10.3390/met15040402
Cabezas D, Celentano DJ, Cruchaga MA, García-Herrera C, Monsalve A. Numerical Analysis of the Laser Forming Process of Cylindrical Surfaces. Metals. 2025; 15(4):402. https://doi.org/10.3390/met15040402
Chicago/Turabian StyleCabezas, Daniel, Diego J. Celentano, Marcela A. Cruchaga, Claudio García-Herrera, and Alberto Monsalve. 2025. "Numerical Analysis of the Laser Forming Process of Cylindrical Surfaces" Metals 15, no. 4: 402. https://doi.org/10.3390/met15040402
APA StyleCabezas, D., Celentano, D. J., Cruchaga, M. A., García-Herrera, C., & Monsalve, A. (2025). Numerical Analysis of the Laser Forming Process of Cylindrical Surfaces. Metals, 15(4), 402. https://doi.org/10.3390/met15040402










